Talk:Field line
| This is the talk page for discussing improvements to the Field line article. This is not a forum for general discussion of the article's subject. |
Article policies
|
| Find sources: Google (books · news · scholar · free images · WP refs) · FENS · JSTOR · TWL |
| This It is of interest to the following WikiProjects: | |||||||||||||||||||||
| |||||||||||||||||||||
Regarding the proposed merger of Line of force and Field line, the two articles are about two closely related yet quite distinct concepts. The concept of Line of force and the set phrase of a Line of force have historical and physical meanings that the more mathemaitcal concept of Field line does not. It's over a month since the proposal and a lot over work has been done to Line of force that make it's distinctiveness more clear. I plan to remove the tags soon. --Firefly322 (talk) 01:36, 15 June 2008 (UTC)
- I plan to remove the tags today if there are no objections. --Firefly322 (talk) 10:30, 22 June 2008 (UTC)
There's no such thing as a "field line"
[edit]There's no such thing as a "field line". It is analogous to a topographic line in that it's drawn on a map in a region of similar height magnitude, but mountains do not actually have any lines. The same is true for magnetic fields. The whole notion of a "field line" comes from the pattern iron filings make around a magnet. The only reason it looks like continuous lines is because the magnetic field concentrates in the filings like an iron core inductor, causing more filings to be attracted to it, and further concentrating the magnetic field, all along a "topographic" region of similar magnetic magnitude. This is the most common misunderstanding in science. Even very brilliant and accomplished professionals who deal with magnetism daily do not understand that there are no discrete lines, it's a continuous field with no features that resemble lines until you put a concentrating agent like iron powder on it. —Preceding unsigned comment added by 71.219.115.168 (talk) 02:48, 20 June 2009 (UTC)
For the record, *EVERY* "brilliant and accomplished professional who deal[s] with magnetism" *absolutely* understands that *magnetic field lines do not exist*. Nobody actually thinks they do. The magnetic lines of force are a graphic and useful concept invented by Michael Faraday in the nineteenth century for representing the configuration of the continuous magnetic field, and that the are not discrete lines. Do not misrepresent your own misunderstanding of professional scientists, as a matter of fact issue. The math we use to analyze all situations is perfectly self-consistent with all known laws of physics, regardless of our layman descriptions used on (for example) Wikipedia (which is not a credible scientific source).
- I've never heard anyone make this mistake. It's a pretty bizarre mistake to make. Have you ever heard anyone say, "This is a bar magnet which has exactly sixteen field lines passing through it"? I know I haven't. Maybe I'm just lucky. But sure...if the misconception exists, and by all means the article should dispell it. :-)
- By the way, in three dimensions, field lines are still lines. They're not surfaces. You can double-check this fact in any textbook. --Steve (talk) 05:37, 20 June 2009 (UTC)
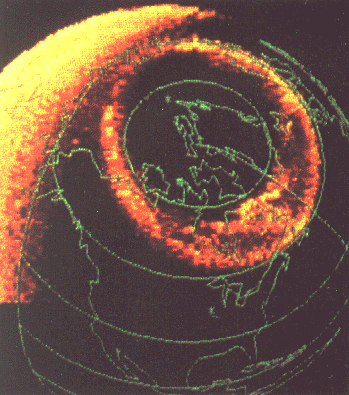
- I haven't got any textbooks handy, but the main reason for my insistence that it be pointed out that they don't actually exist is precisely because the textbooks I have seen in the past have failed to. Since the lines are artificial constructs to begin with, certainly one can draw lines in 1 or 2 dimensions, even when the physical feature the line is mapping is continuous along an entire 3 dimensional surface. For example, in a 2d topographical map, the topographic lines should be closed loops, but if you want to, you can show only a portion of the area that each line encompasses, thereby making your 2d loop into a 1d line. I have actually seen a few textbooks that get it right with with the earth's magnetic field. They show the field as an elongated onion subject to the pressure of the solar wind. So, I guess now that I think about it, a few of the textbooks I've seen have actually shown the 3 dimensional nature of magnetic fields in the context of the earth's magnetosphere. Also, the aurora at the earth's poles appear as sheets of charged particles that follow the earth's 3 dimensional magnetic field surfaces. Take a look at photos of the sheet nature of the aurora, and you'll be convinced that the magnetic field could not be mapped in 3 dimensions with just lines, it has to be shell-like surfaces, like the layered skin of an onion. —Preceding unsigned comment added by 71.219.115.168 (talk) 22:12, 20 June 2009 (UTC)
- I found some great photos of the 3d nature of field lines. Pictures are from the articles magnetosphere, solar wind, and aurora (astronomy). Which ones ought to go into the article? There's enough here to give a really good conceptual idea of what a field line is. I think we could call it a hypothetical path of similar momentum, or something of that nature, depending on the type of field. Anybody know more about what a field line is TECHNICALLY? A particle, like solar wind, will follow a repeatable path if it enters the field in the same spot at the same speed, much like the arc of an artillery shell in a gravitational field. Actually, I think it's no different from the arc of an artillery shell. That arc is literally a physical representation of a gravitational field line.
- I haven't got any textbooks handy, but the main reason for my insistence that it be pointed out that they don't actually exist is precisely because the textbooks I have seen in the past have failed to. Since the lines are artificial constructs to begin with, certainly one can draw lines in 1 or 2 dimensions, even when the physical feature the line is mapping is continuous along an entire 3 dimensional surface. For example, in a 2d topographical map, the topographic lines should be closed loops, but if you want to, you can show only a portion of the area that each line encompasses, thereby making your 2d loop into a 1d line. I have actually seen a few textbooks that get it right with with the earth's magnetic field. They show the field as an elongated onion subject to the pressure of the solar wind. So, I guess now that I think about it, a few of the textbooks I've seen have actually shown the 3 dimensional nature of magnetic fields in the context of the earth's magnetosphere. Also, the aurora at the earth's poles appear as sheets of charged particles that follow the earth's 3 dimensional magnetic field surfaces. Take a look at photos of the sheet nature of the aurora, and you'll be convinced that the magnetic field could not be mapped in 3 dimensions with just lines, it has to be shell-like surfaces, like the layered skin of an onion. —Preceding unsigned comment added by 71.219.115.168 (talk) 22:12, 20 June 2009 (UTC)



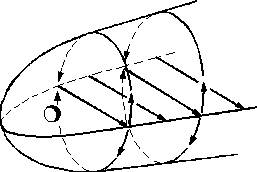



- This image is of gravitational field lines from the article parabola. Notice that the field line is different, depending on the position and velocity of the ball. I think we'd see the exact same behavior with any field line.

.
- I think variation in velocity and location of particles of solar wind account for the "moving field lines" of the aurora. Since field lines don't exist, they're literally created by physical interaction with a field by some object, and can thus vary just as the velocity of the objects making up the field can vary.

- I think the following image from the trajectory article illustrates VERY WELL how a field line is merely the path an object is confined to within the field, and how the path can vary depending NOT ON THE FIELD, but on the velocity of the object. The image demonstrates two different gravitational field lines that only vary because of differences in the objects moving in the field. The gravitational field remains the same.

- OK, this is formatted very badly. Can somebody that knows wiki markup fix it? —Preceding unsigned comment added by 71.219.115.168 (talk) 22:55, 20 June 2009 (UTC)
- Here's a great example of an extremely convoluted gravitational field line through the solar system from the Interplanetary Transport Network article. It follows paths that in theory require zero delta v to tour the entire solar system. It's a really great way to illustrate that field lines are trajectories rather than actual features of a force field, be it gravitational, magnetic, or whatever, and that they don't always look much like lines.

- Just decided to login here. It's been a while since I've done much on wikipedia. Here's a graphic of the orbits of the planets in the solar system. The planet orbits follow gravitational field lines.

- Here's another one that shows gravitational field lines from two interacting sources of the gravity field, from the orbit article.

- Here's a very complex orbit from the rosetta orbit article, where the orbit is just one small object orbiting a black hole, but still producing a very complex "field line".

- Even more complex, but showing a great 3 dimensional "field line" are these images from the heliospheric current sheet article. These are magnetic, with the particles of the solar wind following the sun's "magnetic field lines".


- After looking at all this, it's hard to figure out how the notion of a "field line" makes sense anymore. Clearly the idea of a "field line" is a gross oversimplification for much more complex phenomena. I suppose it could have some uses in mathematical simulations that can benefit from oversimplifications, such as in ballistic targeting calculations, or orbit calculations. In any case, I think all the articles I've mentioned here are actually discussing field lines of various types, and they probably out to have a link to this article in their see also sections.
- Qwasty (talk) 23:37, 20 June 2009 (UTC)
- A field line is not the same as a trajectory line. Given a vector field, you draw a field line by starting at a point, and following whatever direction the vector field is pointing where you are. For example, the gravitational field always points down for someone on the surface of earth, so the field lines are all vertical lines. The trajectories, on the other hand, are not just vertical lines, they're parabolas too. Field lines and trajectories are entirely different concepts. (Although, they can happen to be the same in certain cases, e.g. a particle with a low Reynold's number flowing in a fluid.) Here (first paragraph or two) is a nice explanation of field lines, if you don't like the one I put in the article. --Steve (talk) 05:49, 21 June 2009 (UTC)
- Then I suppose you could say that a vertical gravitational field line pointing directly down, is the trajectory that a particle beginning at rest will travel on as time progresses. At least, that's what it looks like to me. Does that sound right to you? Is that what the vector field is abstracting for us? The vector field appears to be the influences an a trajectory passing through it. Qwasty (talk) 23:44, 22 June 2009 (UTC)
- In general, if we're talking about a force field, it's the trajectory that a particle beginning at rest will start to travel on (but after that it will no longer be at rest, and inertia will come into play).
- Any vector field has field lines, but only divergence-free fields, e.g. corresponding to inverse-square force laws, have lines whose density automatically reflects the field strength if you just start with some number of lines and then simply extend them wherever they go. Much of their utility in gravity and electromagnetism arises from this special property, which is why you can (almost) think of them as "real" without getting into (too much) trouble. For general vector fields, you can draw the lines, but if you don't use other information to start and stop them (give them "ends") then they will only tell you the field direction, not strength. For example, the field f(x,y,z) = (Aex,0,0) has straight, parallel field lines that are identical to those of the divergence-free field g(x,y,z) = (A,0,0). 82.10.111.112 (talk) 23:01, 28 August 2009 (UTC)
The statement that "As a result of the divergence theorem, field lines start at sources and end at sinks of the vector field" is technically incorrect
[edit]The (correct!) view expressed in the article that the field lines of a vector field are simply what mathematicians would call the (potentially reparametrized) integral curves of the vector field in question is at odds with the statement (which as I am aware is common "wisdom") that "field lines start at sources and end at sinks of the vector field" (or otherwise have to go to infinity). One obvious counterexample is the case of an electrostatic dipole made up of two equal positive charges on the x-axis, at positions (±a,0,0). As is easy to check, any field line (in the sense of the article) starting at (x0,0,0), with 0<x0<a, will simply approach the origin from the right, never quite getting there. Similarly any field line starting at (x0,0,0), with -a<x0<0, will approach the origin from the left, never quite getting there. It can't get there because of the standard existence and uniqueness result on ODEs, i.e. if it did they it would actually be the (degenerate) field line which begins at the origin and stays there forever. These field lines are obviously "physically" distinct (with one emanating from the right charge and the other from the left charge) and thus this situation is a counterexample to what said in the article and in many textbooks. Umberto Lupo (talk) 14:51, 5 April 2016 (UTC)
- Here is the offending statement from the article, including wikilinks:
- As a result of the divergence theorem, field lines start at sources and end at sinks of the vector field.
- I came here because I thought this was wrong. Taken at face value, it denies the possibility of loops. Presumably, what was meant is that field lines that have a definite beginning start at a source, and likewise for endings and sinks. But that is not what the sentence states.
- But the counterexample offered above by Umberto Lupo also falsifies the modified statement. An observation: in that counterexample, the vector of the field vanishes at the origin, that is, it has zero magnitude. I don't know if such an anomaly is essential for constructing counterexamples, and I don't feel sufficiently knowledgeable on the subject matter to apply a correction – but a correction is needed here. --Lambiam 17:15, 27 August 2017 (UTC)
This is a comment that may clarify the matter. It is true that for a vector field the integral curves do not have end points. On the other hand, a field line (what I would call a flux curve) is not a vector field. It is a differential 2-form. When a differential 2-form is represented in pictures, the natural picture is that of flux curves that may (or may not) have starting points and ending points. They do, however, have orientations in the transverse direction. Then (in a discrete approximation) the integral of a differential 2-form over an oriented surface just counts the flux curves that cross the surface (with signs depending on relative orientation). This story makes evident that this differential 2-form picture must be independent of the coordinate system.
It also makes clear what the nature of the sources and sinks are: they are given by the 3-form that is the exterior derivative of the 2-form.
There is of course a relation between these two pictures. Given a volume 3-form, a differential 2-form may be associated with a vector field. The divergence of this vector field times the volume form is the 3-form that is the exterior derivative of the 2-form. So the divergence indeed describes the sources and sinks.
Fariswg (talk) 20:18, 23 May 2018 (UTC)
- Obviously the field line does not include the source or sink endpoints, because the electric field is not defined there. It is an open line segment. But the source and sink points are limit points of the set, so it seems to me the statement in question, "...field lines start at sources and end at sinks of the vector field." is accurate. This implies for vector fields which do not have sources or sinks the field lines must either be closed loops or must end at infinity. --ChetvornoTALK 21:53, 23 April 2019 (UTC)
Mathematical Basis of Descriptions of Vector Fields Using Curvilinear Squares ?
[edit]The general problem of describing 2-D vector fields using "curvo-linear squares" and by implication 3-D vector fields using "curvo-linear cubes" https://cldup.com/IWJrzHiWDh.pdf Rhnmcl (talk) 01:26, 13 November 2022 (UTC)
"electric field lines start at positive charges and end at negative charges"
[edit]"Gauss's law states that an electric field has sources at positive charges, sinks at negative charges, and neither elsewhere, so electric field lines start at positive charges and end at negative charges." Can't electric field lines also come from infinity and continue for infinity? For example in the case of a lone negative charge, the field lines come from infinity and end at the negative charge. In the case of a positive one they start from it and continue for infinity. [Edit: I thought about it and I feel like the text in the article mean to to say that if the field lines have a source, then it must be a positive charge, and if they have an end, then it must be a negative charge. However they can also not have a source or an end, which is when the field lines come from infinity or end at infinity. Here the wording is tricky because come from infinity and end at infinity makes it seem like they start/end somewhere when it is not the case. Anyways I would specify that the lines can come from or end at infinity (but not both at the same time).] TheGoatOfSparta (talk) 11:32, 4 July 2023 (UTC)
Is this sentence confusing or is it only me?
[edit]From the first paragraph of "Definition and description": "For two-dimensional fields the field lines are plane curves; since a plane drawing of a 3-dimensional set of field lines can be visually confusing most field line diagrams are of this type."
English is not my first language, so I may be wrong. It appears to me that the sentence actually suggests that most field line diagrams are of the confusing type. It is not entirely clear what "this" is.
By just changing word order, it appears clear to me and meaning and intent match:
"For two-dimensional fields the field lines are plane curves; most field line diagrams are of this type since a plane drawing of a 3-dimensional set of field lines can be visually confusing."
If this is nonsense: sorry! If it is useful, someone else should change it, since I do not feel that I should edit a mature text in a foreign language. Thanks! 2003:DE:4F2A:9500:D8AC:651A:4714:B83E (talk) 23:27, 20 October 2023 (UTC)


