Elongated dodecahedron: Difference between revisions
No edit summary |
No edit summary |
||
| (22 intermediate revisions by 6 users not shown) | |||
| Line 1: | Line 1: | ||
{{Short description|Polyhedron with 8 rhombic and 4 hexagonal faces}} |
|||
{{Infobox polyhedron |
{{Infobox polyhedron |
||
|image=Rhombo-hexagonal dodecahedron.png |
|image=Rhombo-hexagonal dodecahedron.png |
||
|type=[[Parallelohedron]] |
|||
|type=[[Dodecahedron#Other dodecahedra|Dodecahedron]] |
|||
|faces=8 [[rhombus|rhombi]]<br>4 [[hexagon]]s |
|faces=8 [[rhombus|rhombi]]<br>4 [[hexagon]]s |
||
|edges=28 |
|edges=28 |
||
|vertices=18 |
|vertices=18 |
||
|vertex_config=(8) 4.6.6<br>(8) 4.4.6<br>(2) 4.4.4.4 |
|vertex_config={{math|(8) 4.6.6<br>(8) 4.4.6<br>(2) 4.4.4.4}} |
||
|symmetry=[[Dihedral symmetry in three dimensions|D |
|symmetry=[[Dihedral symmetry in three dimensions|Dihedral]] {{math|(D{{sub|4h}}), [4,2], (*422),}} order 16 |
||
|net=Elongated_dodecahedron_net.png |
|net=Elongated_dodecahedron_net.png |
||
|rotation_group=D |
|rotation_group={{math|D{{sub|4}}, [4,2]{{sup|+}}, (422),}} order 8 |
||
|dual= |
|dual= |
||
|properties=[[ |
|properties= [[Convex polytope|Convex]] |
||
}} |
}} |
||
[[File:Elongated Dodecahedron.stl|thumb|alt=3D model of a elongated dodecahedron|3D model of a elongated dodecahedron]] |
|||
| ⚫ | In [[geometry]], the '''elongated dodecahedron''',<ref>Coxeter (1973) p.257</ref> '''extended rhombic dodecahedron''', '''rhombo-hexagonal dodecahedron'''<ref>Williamson (1979) p169</ref> or '''hexarhombic dodecahedron'''<ref>http://www.matha.mathematik.uni-dortmund.de/~thilo/contents/fedorov.htm</ref> is a convex [[ |
||
| ⚫ | In [[geometry]], the '''elongated dodecahedron''',<ref>Coxeter (1973) p.257</ref> '''extended rhombic dodecahedron''', '''rhombo-hexagonal dodecahedron'''<ref>Williamson (1979) p169</ref> or '''hexarhombic dodecahedron'''<ref>[https://web.archive.org/web/20080413143937/http://www.matha.mathematik.uni-dortmund.de/~thilo/contents/fedorov.htm Fedorov's five parallelohedra in R³]</ref> is a convex [[dodecahedron]] with 8 [[Rhombus|rhombic]] and 4 [[hexagon]]al faces. The hexagons can be made equilateral, or regular depending on the shape of the rhombi. It can be seen as constructed from a [[rhombic dodecahedron]] [[elongation (geometry)|elongated]] by a [[square prism]]. |
||
== Parallelohedron== |
|||
Along with the rhombic dodecahedron, it is a [[space-filling polyhedron]], one of the five types of [[parallelohedron]] identified by [[Evgraf Fedorov]] that [[Honeycomb (geometry)|tile space]] face-to-face by translations. It has 5 sets of parallel edges, called zones or belts. |
|||
: [[File:Parallelohedron edges elongated rhombic dodecahedron.png|160px]] |
|||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
== Tessellation == |
== Tessellation == |
||
* It can [[tesselate]] all space by translations. |
* It can [[tesselate]] all space by translations. |
||
* It is the [[ |
* It is the [[Wigner–Seitz cell]] for certain [[Bravais lattice|body-centered tetragonal lattices]]. |
||
{| class=wikitable |
{| class=wikitable |
||
|[[File:Rhombo-hexagonal dodecahedron tessellation.png|240px]] |
|[[File:Rhombo-hexagonal dodecahedron tessellation.png|240px]] |
||
| ⚫ | |||
|} |
|} |
||
This is related to the [[rhombic dodecahedral honeycomb]] with an elongation of zero. Projected normal to the elongation direction, the honeycomb looks like a [[square tiling]] with the [[rhombi]] projected into [[square]]s. |
This is related to the [[rhombic dodecahedral honeycomb]] with an elongation of zero. Projected normal to the elongation direction, the honeycomb looks like a [[square tiling]] with the [[rhombi]] projected into [[square]]s. |
||
| ⚫ | |||
The expanded dodecahedra can be distorted into cubic volumes, with the honeycomb as a half-offset stacking of cubes. It can also be made concave by adjusting the 8 corners downward by the same amount as the centers are moved up. |
|||
{| class=wikitable |
|||
|- align=center |
|||
|[[File:Elongated_dodecahedron_flat.png|140px]]<BR>Coplanar polyhedron |
|||
|[[File:elongated_dodecahedron_flat_net.png|200px]]<BR>Net |
|||
|[[File:Elongated_dodecahedron_flat_honeycomb.png|160px]]<BR>Honeycomb |
|||
|- align=center |
|||
|[[File:Elongated_dodecahedron_concave.png|140px]]<BR>Concave |
|||
|[[File:elongated_dodecahedron_concave_net.png|200px]]<BR>Net |
|||
|[[File:Elongated_dodecahedron_concave_honeycomb.png|160px]]<BR>Honeycomb |
|||
|} |
|||
| ⚫ | The elongated dodecahedron can be constructed as a contraction of a uniform [[truncated octahedron]], where square faces are reduced to single edges and regular hexagonal faces are reduced to 60 degree rhombic faces (or pairs of equilateral triangles). This construction alternates square and rhombi on the 4-valence vertices, and has half the symmetry, D<sub>2h</sub> symmetry, order 8. |
||
{| class=wikitable width=480 |
|||
|- align=center |
|||
| ⚫ | |||
|[[File:Contracted_truncated_octahedron_net.png|160px]]<BR>Net |
|||
| ⚫ | |||
|} |
|||
== See also== |
== See also== |
||
* [[Trapezo-rhombic dodecahedron]] |
* [[Trapezo-rhombic dodecahedron]] |
||
* [[Elongated octahedron]] |
|||
* [[Elongated gyrobifastigium]] |
|||
==References== |
==References== |
||
{{reflist}} |
{{reflist}} |
||
*{{The Geometrical Foundation of Natural Structure (book)}} ''rhombo-hexagonal dodecahedron'', p169 |
*{{The Geometrical Foundation of Natural Structure (book)}} ''rhombo-hexagonal dodecahedron'', p169 |
||
*[[H.S.M. Coxeter]], [[Regular Polytopes (book)|''Regular Polytopes'']], Third edition, (1973), Dover edition, ISBN |
*[[H.S.M. Coxeter]], [[Regular Polytopes (book)|''Regular Polytopes'']], Third edition, (1973), Dover edition, {{ISBN|0-486-61480-8}} p. 257 |
||
== External links == |
== External links == |
||
Latest revision as of 13:38, 25 December 2022
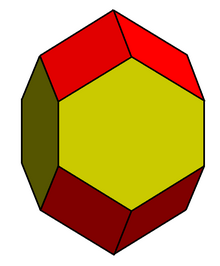
| Elongated dodecahedron | |
|---|---|
 | |
| Type | Parallelohedron |
| Faces | 8 rhombi 4 hexagons |
| Edges | 28 |
| Vertices | 18 |
| Vertex configuration | (8) 4.6.6 (8) 4.4.6 (2) 4.4.4.4 |
| Symmetry group | Dihedral (D4h), [4,2], (*422), order 16 |
| Rotation group | D4, [4,2]+, (422), order 8 |
| Properties | Convex |
| Net | |
 | |

In geometry, the elongated dodecahedron,[1] extended rhombic dodecahedron, rhombo-hexagonal dodecahedron[2] or hexarhombic dodecahedron[3] is a convex dodecahedron with 8 rhombic and 4 hexagonal faces. The hexagons can be made equilateral, or regular depending on the shape of the rhombi. It can be seen as constructed from a rhombic dodecahedron elongated by a square prism.
Parallelohedron
[edit]Along with the rhombic dodecahedron, it is a space-filling polyhedron, one of the five types of parallelohedron identified by Evgraf Fedorov that tile space face-to-face by translations. It has 5 sets of parallel edges, called zones or belts.
Tessellation
[edit]- It can tesselate all space by translations.
- It is the Wigner–Seitz cell for certain body-centered tetragonal lattices.

|
This is related to the rhombic dodecahedral honeycomb with an elongation of zero. Projected normal to the elongation direction, the honeycomb looks like a square tiling with the rhombi projected into squares.
Variations
[edit]The expanded dodecahedra can be distorted into cubic volumes, with the honeycomb as a half-offset stacking of cubes. It can also be made concave by adjusting the 8 corners downward by the same amount as the centers are moved up.
 Coplanar polyhedron |
 Net |
 Honeycomb |
 Concave |
 Net |
 Honeycomb |
The elongated dodecahedron can be constructed as a contraction of a uniform truncated octahedron, where square faces are reduced to single edges and regular hexagonal faces are reduced to 60 degree rhombic faces (or pairs of equilateral triangles). This construction alternates square and rhombi on the 4-valence vertices, and has half the symmetry, D2h symmetry, order 8.
 Contracted truncated octahedron |
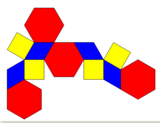 Net |
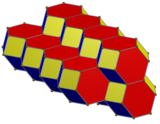 Honeycomb |
See also
[edit]References
[edit]- ^ Coxeter (1973) p.257
- ^ Williamson (1979) p169
- ^ Fedorov's five parallelohedra in R³
- Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. rhombo-hexagonal dodecahedron, p169
- H.S.M. Coxeter, Regular Polytopes, Third edition, (1973), Dover edition, ISBN 0-486-61480-8 p. 257

