Solar zenith angle: Difference between revisions
Fgnievinski (talk | contribs) No edit summary |
m Reverted edits by 2409:4081:D97:774F:0:0:4209:7C11 (talk): please use the talk page (WP:TPHELP) or be bold and fix the problem (HG) (3.4.12) |
||
| (7 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
{{Short description|Angle between the zenith and the centre of the Sun's disc}} |
{{Short description|Angle between the zenith and the centre of the Sun's disc}} |
||
The '''solar zenith angle''' is the [[zenith angle]] of the [[sun]], i.e., the angle between the sun’s rays and the [[vertical direction]]. It is |
The '''solar zenith angle''' is the [[zenith angle]] of the [[sun]], i.e., the angle between the sun’s rays and the [[vertical direction]]. It is the [[complement angle|complement]] to the '''solar altitude''' or '''solar elevation''', which is the [[altitude angle]] or [[elevation angle]] between the sun’s rays and a [[horizontal plane]].<ref>{{cite book | page = [https://archive.org/details/fundamentalsatmo00jaco/page/n332 317] | title = Fundamentals of Atmospheric Modeling | url = https://archive.org/details/fundamentalsatmo00jaco | url-access = limited | first = Mark Z. | last = Jacobson | publisher = [[Cambridge University Press]] | date = 2005 | isbn = 0521548659 | edition = 2nd}}</ref><ref name="hartmann">{{cite book | title = Global Physical Climatology | url = https://archive.org/details/globalphysicalcl00hart | url-access = limited | first = Dennis L. | last = Hartmann | publisher = [[Academic Press]] | page = [https://archive.org/details/globalphysicalcl00hart/page/n41 30] | date = 1994 | isbn = 0080571638}}</ref> At [[solar noon]], the zenith angle is at a minimum and is equal to latitude minus [[solar declination]] angle. This is the basis by which ancient mariners navigated the oceans.<ref>{{cite book |last1=Bonan |first1=Gordon |title=Ecological climatology: concepts and applications |date=2005 |publisher=Cambridge University Press |isbn=9781316425190 |page=62 |url=https://www.cambridge.org/core/books/ecological-climatology/D146443B007985BC366B2512345692C0 |accessdate=13 November 2019}}</ref>{{TOC right}} Solar zenith angle is normally used in combination with the [[solar azimuth angle]] to determine the [[position of the Sun]] as observed from a given location on the surface of the Earth. |
||
==Formula== |
==Formula== |
||
<math display="block"> \cos \theta_s = \sin \alpha_s = \sin \Phi \sin \delta + \cos \Phi \cos \delta \cos h</math> |
|||
where |
where |
||
* <math>\theta_s</math> is the ''solar zenith angle'' |
* <math>\theta_s</math> is the ''solar zenith angle'' |
||
* <math>\alpha_s</math> is the ''solar altitude angle'', <math>\alpha_s |
* <math>\alpha_s</math> is the ''solar altitude angle'', <math>\alpha_s = 90^\circ - \theta_s</math> |
||
* <math>h</math> is the [[hour angle]], in the local [[solar time]]. |
* <math>h</math> is the [[hour angle]], in the local [[solar time]]. |
||
* <math>\delta</math> is the current [[declination of the Sun]] |
* <math>\delta</math> is the current [[declination of the Sun]] |
||
| Line 21: | Line 21: | ||
In the Earth-Centered Earth-Fixed ([[ECEF]]) geocentric Cartesian coordinate system, let <math>(\phi_{s}, \lambda_{s})</math> and <math>(\phi_{o}, \lambda_{o})</math> be the latitudes and longitudes, or coordinates, of the [[subsolar point]] and the observer's point, then the upward-pointing unit vectors at the two points, <math>\mathbf{S}</math> and <math>\mathbf{V}_{oz}</math>, are |
In the Earth-Centered Earth-Fixed ([[ECEF]]) geocentric Cartesian coordinate system, let <math>(\phi_{s}, \lambda_{s})</math> and <math>(\phi_{o}, \lambda_{o})</math> be the latitudes and longitudes, or coordinates, of the [[subsolar point]] and the observer's point, then the upward-pointing unit vectors at the two points, <math>\mathbf{S}</math> and <math>\mathbf{V}_{oz}</math>, are |
||
<math display="block">\mathbf{S}=\cos\phi_{s}\cos\lambda_{s}{\mathbf i}+\cos\phi_{s}\sin\lambda_{s}{\mathbf j}+\sin\phi_{s}{\mathbf k},</math> |
|||
<math display="block">\mathbf{V}_{oz}=\cos\phi_{o}\cos\lambda_{o}{\mathbf i}+\cos\phi_{o}\sin\lambda_{o}{\mathbf j}+\sin\phi_{o}{\mathbf k}.</math> |
|||
where <math>{\mathbf i}</math>, <math>{\mathbf j}</math> and <math>{\mathbf k}</math> are the basis vectors in the ECEF coordinate system. |
where <math>{\mathbf i}</math>, <math>{\mathbf j}</math> and <math>{\mathbf k}</math> are the basis vectors in the ECEF coordinate system. |
||
| Line 28: | Line 28: | ||
Now the cosine of the solar zenith angle, <math>\theta_{s}</math>, is simply the [[dot product]] of the above two vectors |
Now the cosine of the solar zenith angle, <math>\theta_{s}</math>, is simply the [[dot product]] of the above two vectors |
||
<math display="block">\cos\theta_{s} = \mathbf{S}\cdot\mathbf{V}_{oz} = \sin\phi_{o}\sin\phi_{s} + \cos\phi_{o}\cos\phi_{s}\cos(\lambda_{s}-\lambda_{o}).</math> |
|||
Note that <math>\phi_{s}</math> is the same as <math>\delta</math>, the declination of the Sun, and <math>\lambda_{s}-\lambda_{o}</math> is equivalent to <math>-h</math>, where <math>h</math> is the hour angle defined earlier. So the above format is mathematically identical to the one given earlier. |
Note that <math>\phi_{s}</math> is the same as <math>\delta</math>, the declination of the Sun, and <math>\lambda_{s}-\lambda_{o}</math> is equivalent to <math>-h</math>, where <math>h</math> is the hour angle defined earlier. So the above format is mathematically identical to the one given earlier. |
||
| Line 35: | Line 35: | ||
=== Minimum and Maximum === |
=== Minimum and Maximum === |
||
[[File: |
[[File:Solar Zenith Angle min.png|thumb|The daily minimum of the solar zenith angle as a function of latitude and day of year for the year 2020.]] |
||
[[File: |
[[File:Solar Zenith Angle max.png|thumb|The daily maximum of the solar zenith angle as a function of latitude and day of year for the year 2020.]] |
||
At any given location on any given day, the solar zenith angle, <math>\theta_{s}</math>, reaches its minimum, <math>\theta_{min}</math>, at local solar noon when the hour angle <math>h=0</math>, or <math>\lambda_{s}-\lambda_{o}=0</math>, namely, <math>\cos\theta_{min}=\cos(|\phi_{o}-\phi_{s}|)</math>, or <math>\theta_{min}=|\phi_{o}-\phi_{s}|</math>. If <math>\theta_{min}>90^{\circ}</math>, it is polar night. |
At any given location on any given day, the solar zenith angle, <math>\theta_{s}</math>, reaches its minimum, <math>\theta_\text{min}</math>, at local solar noon when the hour angle <math>h = 0</math>, or <math>\lambda_{s}-\lambda_{o}=0</math>, namely, <math>\cos\theta_\text{min} = \cos(|\phi_{o}-\phi_{s}|)</math>, or <math>\theta_\text{min} = |\phi_{o}-\phi_{s}|</math>. If <math>\theta_\text{min} > 90^{\circ}</math>, it is polar night. |
||
And at any given location on any given day, the solar zenith angle, <math>\theta_{s}</math>, reaches its maximum, <math>\theta_{max}</math>, at local midnight when the hour angle <math>h=-180^{\circ}</math>, or <math>\lambda_{s}-\lambda_{o}=-180^{\circ}</math>, namely, <math>\cos\theta_{max}=\cos(180^{\circ}-|\phi_{o}+\phi_{s}|)</math>, or <math>\theta_{max}=180^{\circ}-|\phi_{o}+\phi_{s}|</math>. If <math>\theta_{max}<90^{\circ}</math>, it is polar day. |
And at any given location on any given day, the solar zenith angle, <math>\theta_{s}</math>, reaches its maximum, <math>\theta_\text{max}</math>, at local midnight when the hour angle <math>h = -180^{\circ}</math>, or <math>\lambda_{s}-\lambda_{o}=-180^{\circ}</math>, namely, <math>\cos\theta_\text{max} = \cos(180^{\circ}-|\phi_{o}+\phi_{s}|)</math>, or <math>\theta_\text{max} = 180^{\circ}-|\phi_{o}+\phi_{s}|</math>. If <math>\theta_\text{max} < 90^{\circ}</math>, it is polar day. |
||
===Caveats=== |
===Caveats=== |
||
| Line 53: | Line 53: | ||
{{Main articles|Sunrise equation}} |
{{Main articles|Sunrise equation}} |
||
Sunset and sunrise occur (approximately) when the zenith angle is 90°, where the hour angle ''h''<sub>0</sub> satisfies<ref name="hartmann" /> |
Sunset and sunrise occur (approximately) when the zenith angle is 90°, where the hour angle ''h''<sub>0</sub> satisfies<ref name="hartmann" /> |
||
<math display="block">\cos h_0 = -\tan \Phi \tan \delta.</math> |
|||
Precise times of sunset and [[Sunrise#Angle|sunrise]] occur when the upper limb of the Sun appears, as refracted by the atmosphere, to be on the horizon. |
Precise times of sunset and [[Sunrise#Angle|sunrise]] occur when the upper limb of the Sun appears, as refracted by the atmosphere, to be on the horizon. |
||
| Line 59: | Line 59: | ||
===Albedo=== |
===Albedo=== |
||
A weighted daily average zenith angle, used in computing the local [[albedo of the Earth]], is given by |
A weighted daily average zenith angle, used in computing the local [[albedo of the Earth]], is given by |
||
<math display="block">\overline{\cos \theta_s} = \frac{\displaystyle \int_{-h_0}^{h_0} Q \cos \theta_s \, \text{d}h}{\displaystyle \int_{-h_0}^{h_0} Q \, \text{d}h}</math> |
|||
where ''Q'' is the instantaneous [[irradiance]].<ref name="hartmann" /> |
where ''Q'' is the instantaneous [[irradiance]].<ref name="hartmann" /> |
||
| Line 66: | Line 66: | ||
* 90° if you are on the equator, a day of equinox, at a solar hour of twelve |
* 90° if you are on the equator, a day of equinox, at a solar hour of twelve |
||
* near 0° at the sunset or at the sunrise |
* near 0° at the sunset or at the sunrise |
||
* between |
* between −90° and 0° during the night (midnight) |
||
An exact calculation is given in [[position of the Sun]]. Other approximations exist elsewhere.<ref>{{cite web|last=livioflores-ga|url=http://answers.google.com/answers/threadview/id/782886.html|title=Equation to know where the Sun is at a given place at a given date-time|accessdate=9 March 2013}}</ref> |
An exact calculation is given in [[position of the Sun]]. Other approximations exist elsewhere.<ref>{{cite web|last=livioflores-ga|url=http://answers.google.com/answers/threadview/id/782886.html|title=Equation to know where the Sun is at a given place at a given date-time|accessdate=9 March 2013}}</ref> |
||
{{ |
{{subsolar point date graph.svg}} |
||
==See also== |
==See also== |
||
| Line 76: | Line 76: | ||
* [[Horizontal coordinate system]] |
* [[Horizontal coordinate system]] |
||
* [[List of orbits]] |
* [[List of orbits]] |
||
* {{slink|Photovoltaic mounting system#Orientation and inclination}} |
|||
* [[Position of the Sun]] |
* [[Position of the Sun]] |
||
* [[Sun path]] |
* [[Sun path]] |
||
Latest revision as of 07:15, 9 June 2023
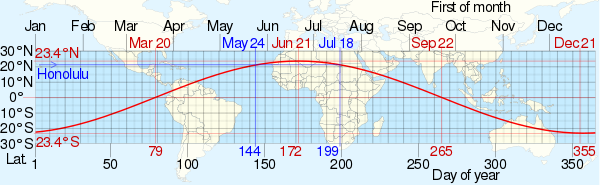
The solar zenith angle is the zenith angle of the sun, i.e., the angle between the sun’s rays and the vertical direction. It is the complement to the solar altitude or solar elevation, which is the altitude angle or elevation angle between the sun’s rays and a horizontal plane.[1][2] At solar noon, the zenith angle is at a minimum and is equal to latitude minus solar declination angle. This is the basis by which ancient mariners navigated the oceans.[3]
Solar zenith angle is normally used in combination with the solar azimuth angle to determine the position of the Sun as observed from a given location on the surface of the Earth.
Formula
[edit]
where
- is the solar zenith angle
- is the solar altitude angle,
- is the hour angle, in the local solar time.
- is the current declination of the Sun
- is the local latitude.
Derivation of the formula using the subsolar point and vector analysis
[edit]While the formula can be derived by applying the cosine law to the zenith-pole-Sun spherical triangle, the spherical trigonometry is a relatively esoteric subject.
By introducing the coordinates of the subsolar point and using vector analysis, the formula can be obtained straightforward without incurring the use of spherical trigonometry.[4]
In the Earth-Centered Earth-Fixed (ECEF) geocentric Cartesian coordinate system, let and be the latitudes and longitudes, or coordinates, of the subsolar point and the observer's point, then the upward-pointing unit vectors at the two points, and , are
where , and are the basis vectors in the ECEF coordinate system.
Now the cosine of the solar zenith angle, , is simply the dot product of the above two vectors
Note that is the same as , the declination of the Sun, and is equivalent to , where is the hour angle defined earlier. So the above format is mathematically identical to the one given earlier.
Additionally, Ref. [4] also derived the formula for solar azimuth angle in a similar fashion without using spherical trigonometry.
Minimum and Maximum
[edit]

At any given location on any given day, the solar zenith angle, , reaches its minimum, , at local solar noon when the hour angle , or , namely, , or . If , it is polar night.
And at any given location on any given day, the solar zenith angle, , reaches its maximum, , at local midnight when the hour angle , or , namely, , or . If , it is polar day.
Caveats
[edit]The calculated values are approximations due to the distinction between common/geodetic latitude and geocentric latitude. However, the two values differ by less than 12 minutes of arc, which is less than the apparent angular radius of the sun.
The formula also neglects the effect of atmospheric refraction.[5]
Applications
[edit]Sunrise/Sunset
[edit]Sunset and sunrise occur (approximately) when the zenith angle is 90°, where the hour angle h0 satisfies[2]
Precise times of sunset and sunrise occur when the upper limb of the Sun appears, as refracted by the atmosphere, to be on the horizon.
Albedo
[edit]A weighted daily average zenith angle, used in computing the local albedo of the Earth, is given by where Q is the instantaneous irradiance.[2]
Summary of special angles
[edit]For example, the solar elevation angle is :
- 90° if you are on the equator, a day of equinox, at a solar hour of twelve
- near 0° at the sunset or at the sunrise
- between −90° and 0° during the night (midnight)
An exact calculation is given in position of the Sun. Other approximations exist elsewhere.[6]
See also
[edit]- Azimuth
- Solar azimuth angle
- Horizontal coordinate system
- List of orbits
- Photovoltaic mounting system § Orientation and inclination
- Position of the Sun
- Sun path
- Sunrise
- Sunset
- Sun transit time
References
[edit]- ^ Jacobson, Mark Z. (2005). Fundamentals of Atmospheric Modeling (2nd ed.). Cambridge University Press. p. 317. ISBN 0521548659.
- ^ a b c Hartmann, Dennis L. (1994). Global Physical Climatology. Academic Press. p. 30. ISBN 0080571638.
- ^ Bonan, Gordon (2005). Ecological climatology: concepts and applications. Cambridge University Press. p. 62. ISBN 9781316425190. Retrieved 13 November 2019.
- ^ a b Zhang, T., Stackhouse, P.W., Macpherson, B., and Mikovitz, J.C., 2021. A solar azimuth formula that renders circumstantial treatment unnecessary without compromising mathematical rigor: Mathematical setup, application and extension of a formula based on the subsolar point and atan2 function. Renewable Energy, 172, 1333-1340. DOI: https://doi.org/10.1016/j.renene.2021.03.047
- ^ Woolf, Harold M. (1968). "On the computation of solar elevation angles and the determination of sunrise and sunset times". NASA Technical Memorandu, X-1646. Washington, D.C.: 3.
- ^ livioflores-ga. "Equation to know where the Sun is at a given place at a given date-time". Retrieved 9 March 2013.