Log-Cauchy distribution: Difference between revisions
m moved TheAdminsAreGay to Log-Cauchy distribution over redirect: rvv |
→Characterization: All other formulas in the article distinguish the levels of parentheses according to American Physical Society style. |
||
| (47 intermediate revisions by 28 users not shown) | |||
| Line 3: | Line 3: | ||
| type =density |
| type =density |
||
| box_width =300px |
| box_width =300px |
||
| pdf_image = [[File:Logcauchypdf.svg|275px|Log-Cauchy density function for values of <math>(\mu, \sigma)</math>]] |
|||
| pdf_image = |
|||
| cdf_image = [[File:Logcauchycdf.svg|275px|Log-Cauchy cumulative distribution function for values of <math>(\mu, \sigma)</math>]] |
|||
| cdf_image = |
|||
| parameters =<math>\mu</math> ([[real number|real]])<br><math>\displaystyle \sigma > 0\!</math> (real) |
| parameters =<math>\mu</math> ([[real number|real]])<br/><math>\displaystyle \sigma > 0\!</math> (real) |
||
| support =<math>\displaystyle x \in (0, +\infty)\!</math> |
| support =<math>\displaystyle x \in (0, +\infty)\!</math> |
||
| pdf =<math>{ 1 \over x\pi } \left[ { \sigma \over (\ln x - \mu)^2 + \sigma^2 } \right], \ \ x>0</math> |
| pdf =<math>{ 1 \over x\pi } \left[ { \sigma \over (\ln x - \mu)^2 + \sigma^2 } \right], \ \ x>0</math> |
||
| Line 11: | Line 11: | ||
| qf = |
| qf = |
||
| qdf = |
| qdf = |
||
| mean = |
| mean =infinite |
||
| median =<math>e^{\mu}\,</math> |
| median =<math>e^{\mu}\,</math> |
||
| mode = |
| mode = |
||
| Line 22: | Line 22: | ||
}} |
}} |
||
In probability theory, a '''log-Cauchy distribution''' is a [[probability distribution]] of a [[random variable]] whose [[logarithm]] is |
In probability theory, a '''log-Cauchy distribution''' is a [[probability distribution]] of a [[random variable]] whose [[logarithm]] is distributed in accordance with a [[Cauchy distribution]]. If ''X'' is a random variable with a Cauchy distribution, then ''Y'' = [[exponential function|exp(''X'')]] has a log-Cauchy distribution; likewise, if ''Y'' has a log-Cauchy distribution, then ''X'' = log(''Y'') has a Cauchy distribution.<ref name=robust/> |
||
==Characterization== |
==Characterization== |
||
The log-Cauchy distribution is a special case of the [[log-t distribution]] where the [[degrees of freedom]] parameter is equal to 1.<ref name=logt>{{cite journal|journal=Revista Colombiana de Estadística - Applied Statistics|accessdate=2022-04-01|date=January 2022|volume=45|issue=1|pages=209–229|title=Some Inferential Problems from Log Student's T-distribution and its Multivariate Extension|author=Olosunde, Akinlolu & Olofintuade, Sylvester|doi=10.15446/rce.v45n1.90672|url=https://www.proquest.com/openview/70d41b2007ad2f9ade89ed9ef6eba775/1?pq-origsite=gscholar&cbl=2035762|doi-access=free}}</ref> |
|||
===Probability density function=== |
===Probability density function=== |
||
The log-Cauchy distribution has the [[probability density function]]: |
The log-Cauchy distribution has the [[probability density function]]: |
||
:<math>\begin{align} |
|||
| ⚫ | |||
f(x; \mu,\sigma) |
|||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
\end{align}</math> |
|||
where <math> \mu</math> is a [[real number]] and <math> \sigma >0</math>.<ref name=robust>{{cite web|title=Applied Robust Statistics|url=http://www.math.siu.edu/olive/run.pdf|author=Olive, D.J.|date=June 23, 2008|publisher=Southern Illinois University|page=86| |
where <math> \mu</math> is a [[real number]] and <math> \sigma >0</math>.<ref name=robust>{{cite web|title=Applied Robust Statistics|url=http://www.math.siu.edu/olive/run.pdf|author=Olive, D.J.|date=June 23, 2008|publisher=Southern Illinois University|page=86|access-date=2011-10-18|url-status=dead|archive-url=https://web.archive.org/web/20110928191222/http://www.math.siu.edu/olive/run.pdf|archive-date=September 28, 2011}}</ref><ref name=stochastic>{{cite book|title=Statistical analysis of stochastic processes in time|url=https://archive.org/details/statisticalanaly00lind|url-access=limited|author=Lindsey, J.K.|pages=[https://archive.org/details/statisticalanaly00lind/page/n48 33], 50, 56, 62, 145|year=2004|publisher=Cambridge University Press|isbn=978-0-521-83741-5}}</ref> If <math>\sigma</math> is known, the [[scale parameter]] is <math>e^{\mu}</math>.<ref name=robust/> <math> \mu</math> and <math> \sigma</math> correspond to the [[location parameter]] and [[scale parameter]] of the associated Cauchy distribution.<ref name=robust/><ref name=hiv>{{cite book|title=Stochastic processes in epidemiology: HIV/AIDS, other infectious diseases|url=https://archive.org/details/stochasticproces00mode|url-access=limited|author1=Mode, C.J. |author2=Sleeman, C.K. |name-list-style=amp |pages=[https://archive.org/details/stochasticproces00mode/page/n51 29]–37|year=2000|publisher=World Scientific|isbn=978-981-02-4097-4}}</ref> Some authors define <math> \mu</math> and <math> \sigma</math> as the [[location parameter|location]] and scale parameters, respectively, of the log-Cauchy distribution.<ref name=hiv/> |
||
For <math>\mu = 0</math> and <math>\sigma =1</math>, corresponding to a standard Cauchy distribution, the probability density function reduces to:<ref name=life/> |
For <math>\mu = 0</math> and <math>\sigma =1</math>, corresponding to a standard Cauchy distribution, the probability density function reduces to:<ref name=life/> |
||
:<math> f(x; 0,1) = \frac{1}{x\pi |
:<math> f(x; 0,1) = \frac{1}{x\pi [1 + (\ln x)^2]}, \ \ x>0</math> |
||
===Cumulative distribution function=== |
===Cumulative distribution function=== |
||
The cumulative distribution function ([[cdf]]) when <math>\mu = 0</math> and <math>\sigma =1</math> is:<ref name=life/> |
The cumulative distribution function ([[Cumulative distribution function|cdf]]) when <math>\mu = 0</math> and <math>\sigma =1</math> is:<ref name=life/> |
||
:<math>F(x; 0, 1)=\frac{1}{2} + \frac{1}{\pi} \arctan(\ln x), \ \ x>0</math> |
:<math>F(x; 0, 1)=\frac{1}{2} + \frac{1}{\pi} \arctan(\ln x), \ \ x>0</math> |
||
===Survival function=== |
===Survival function=== |
||
| Line 47: | Line 51: | ||
===Hazard rate=== |
===Hazard rate=== |
||
The [[hazard rate]] when <math>\mu = 0</math> and <math>\sigma =1</math> is:<ref name=life/> |
The [[hazard rate]] when <math>\mu = 0</math> and <math>\sigma =1</math> is:<ref name=life/> |
||
:<math> \lambda(x; 0,1) = |
:<math> \lambda(x; 0,1) = \left\{\frac{1}{x\pi \left[1 + \left(\ln x\right)^2\right]} \left[\frac{1}{2} - \frac{1}{\pi} \arctan(\ln x)\right]\right\}^{-1}, \ \ x>0</math> |
||
The hazard rate |
The hazard rate decreases at the beginning and at the end of the distribution, but there may be an interval over which the hazard rate increases.<ref name=life/> |
||
==Properties== |
==Properties== |
||
The log-Cauchy distribution is an example of a [[heavy-tailed distribution]].<ref name=small>{{cite |
The log-Cauchy distribution is an example of a [[heavy-tailed distribution]].<ref name=small>{{cite book|title=Laws of Small Numbers: Extremes and Rare Events|url=https://archive.org/details/lawssmallnumbers00falk|url-access=limited|author=Falk, M.|author2=Hüsler, J.|author3=Reiss, R.|name-list-style=amp|page=[https://archive.org/details/lawssmallnumbers00falk/page/n96 80]|year=2010|publisher=Springer|isbn=978-3-0348-0008-2}}</ref> Some authors regard it as a "super-heavy tailed" distribution, because it has a heavier tail than a [[Pareto distribution]]-type heavy tail, i.e., it has a [[logarithmic growth|logarithmically decaying]] tail.<ref name=small/><ref>{{cite web |
||
|title=Statistical inference for heavy and super-heavy tailed distributions |
|||
|url=http://docentes.deio.fc.ul.pt/fragaalves/SuperHeavy.pdf |
|||
|archive-url=https://web.archive.org/web/20070623175435/http://docentes.deio.fc.ul.pt/fragaalves/SuperHeavy.pdf |
|||
| ⚫ | |||
|url-status=dead |
|||
Trade, Human Capital and Technology Spillovers: An Industry Level Analysis|author=Wang, Y.|page=14|publisher=Carleton University|accessdate=2011-10-19}}</ref> |
|||
|archive-date=June 23, 2007 |
|||
|author=Alves, M.I.F. |
|||
|author2=de Haan, L. |
|||
|author3=Neves, C. |
|||
|name-list-style=amp |
|||
|date=March 10, 2006 |
|||
| ⚫ | }}</ref> As with the Cauchy distribution, none of the non-trivial [[moment (mathematics)|moments]] of the log-Cauchy distribution are finite.<ref name=life>{{cite book|title=Life distributions: structure of nonparametric, semiparametric, and parametric families|url=https://archive.org/details/lifedistribution00mars|url-access=limited|author1=Marshall, A.W. |author2=Olkin, I. |name-list-style=amp |pages=[https://archive.org/details/lifedistribution00mars/page/n451 443]–444|year=2007|publisher=Springer|isbn=978-0-387-20333-1}}</ref> The [[mean]] is a moment so the log-Cauchy distribution does not have a defined mean or [[standard deviation]].<ref>{{cite web|title=Moment|url=http://mathworld.wolfram.com/Moment.html|publisher=[[Mathworld]]|access-date=2011-10-19}}</ref><ref>{{cite journal|title=Trade, Human Capital and Technology Spillovers: An Industry Level Analysis|author=Wang, Y.|page=14|publisher=Carleton University}}</ref> |
||
The |
The log-Cauchy distribution is [[Infinite divisibility (probability)|infinitely divisible]] for some parameters but not for others.<ref>{{cite journal|title=On the Lévy Measure of the Lognormal and LogCauchy Distributions|url=http://resources.metapress.com/pdf-preview.axd?code=gn16hw202rxh4q1g&size=largest|access-date=2011-10-18|author=Bondesson, L.|journal=Methodology and Computing in Applied Probability|year=2003|pages=243–256|url-status=dead|archive-url=https://web.archive.org/web/20120425064706/http://resources.metapress.com/pdf-preview.axd?code=gn16hw202rxh4q1g&size=largest|archive-date=2012-04-25}}</ref> Like the [[lognormal distribution]], [[log-t distribution|log-t or log-Student distribution]] and [[Weibull distribution]], the log-Cauchy distribution is a special case of the [[Generalized beta distribution#Generalized beta of the second kind .28GB2.29|generalized beta distribution of the second kind]].<ref>{{cite book|title=Return distributions in finance|url=https://archive.org/details/returndistributi00satc_172|url-access=limited|author1=Knight, J. |author2=Satchell, S. |name-list-style=amp |page=[https://archive.org/details/returndistributi00satc_172/page/n167 153]|year=2001|publisher=Butterworth-Heinemann|isbn=978-0-7506-4751-9}}</ref><ref>{{cite book|title=Market consistency: model calibration in imperfect markets|author=Kemp, M.|year=2009|publisher=Wiley|isbn=978-0-470-77088-7}}</ref> The log-Cauchy is actually a special case of the log-t distribution, similar to the Cauchy distribution being a special case of the [[Student's t distribution]] with 1 degree of freedom.<ref>{{cite book|title=Statistical distributions in scientific work: proceedings of the NATO Advanced Study Institute|author=MacDonald, J.B.|chapter=Measuring Income Inequality|page=169|editor=Taillie, C. |editor2=Patil, G.P. |editor3=Baldessari, B.|year=1981|publisher=Springer|isbn=978-90-277-1334-6}}</ref><ref name=kleiber>{{cite book|title=Statistical Size Distributions in Economics and Actuarial Science|url=https://archive.org/details/statisticalsized0000unse|url-access=registration|author1=Kleiber, C. |author2=Kotz, S. |name-list-style=amp |pages=[https://archive.org/details/statisticalsized0000unse/page/101 101]–102, 110|year=2003|publisher=Wiley|isbn=978-0-471-15064-0}}</ref> |
||
Since the Cauchy distribution is a [[stable distribution]], the log-Cauchy distribution is a logstable distribution.<ref>{{cite journal|title=Distribution function values for logstable distributions |
Since the Cauchy distribution is a [[stable distribution]], the log-Cauchy distribution is a logstable distribution.<ref>{{cite journal|title=Distribution function values for logstable distributions|doi=10.1016/0898-1221(93)90128-I|author=Panton, D.B.|date=May 1993|pages=17–24|volume=25|issue=9|journal=Computers & Mathematics with Applications|doi-access=free}}</ref> Logstable distributions have [[pole (complex analysis)|poles]] at x=0.<ref name=kleiber/> |
||
==Estimating parameters== |
==Estimating parameters== |
||
| Line 65: | Line 78: | ||
==Uses== |
==Uses== |
||
In [[Bayesian statistics]], the log-Cauchy distribution can be used to approximate the [[improper prior|improper]] [[Harold Jeffreys|Jeffreys]]-Haldane density, 1/k, which is sometimes suggested as the [[prior distribution]] for k where k is a positive parameter being estimated.<ref>{{cite book|title=Good thinking: the foundations of probability and its applications|author=Good, I.J.|page=102|year=1983|publisher=University of Minnesota Press|isbn= |
In [[Bayesian statistics]], the log-Cauchy distribution can be used to approximate the [[improper prior|improper]] [[Harold Jeffreys|Jeffreys]]-Haldane density, 1/k, which is sometimes suggested as the [[prior distribution]] for k where k is a positive parameter being estimated.<ref>{{cite book|title=Good thinking: the foundations of probability and its applications|author=Good, I.J.|page=102|year=1983|publisher=University of Minnesota Press|isbn=978-0-8166-1142-3}}</ref><ref>{{cite book|title=Frontiers of Statistical Decision Making and Bayesian Analysis|page=12|author=Chen, M.|year=2010|publisher=Springer|isbn=978-1-4419-6943-9}}</ref> The log-Cauchy distribution can be used to model certain survival processes where significant [[outlier]]s or extreme results may occur.<ref name=stochastic/><ref name=hiv/><ref>{{cite journal|title=Some statistical issues in modelling pharmacokinetic data|author=Lindsey, J.K.|author2=Jones, B.|author3=Jarvis, P.|name-list-style=amp|journal=Statistics in Medicine|date=September 2001|volume=20|issue=17–18|pages=2775–278|doi=10.1002/sim.742|pmid=11523082|s2cid=41887351 }}</ref> An example of a process where a log-Cauchy distribution may be an appropriate model is the time between someone becoming infected with [[HIV]] and showing symptoms of the disease, which may be very long for some people.<ref name=hiv/> It has also been proposed as a model for [[species abundance]] patterns.<ref>{{cite journal|title=LogCauchy, log-sech and lognormal distributions of species abundances in forest communities|journal=Ecological Modelling|volume=184|issue=2–4|doi=10.1016/j.ecolmodel.2004.10.011|date=June 2005|pages=329–340|author=Zuo-Yun, Y.|display-authors=etal }}</ref> |
||
==References== |
==References== |
||
{{Reflist|colwidth=33em}} |
|||
{{reflist}} |
|||
{{ProbDistributions|continuous-semi-infinite}} |
{{ProbDistributions|continuous-semi-infinite}} |
||
[[Category:Continuous distributions]] |
[[Category:Continuous distributions]] |
||
Latest revision as of 08:30, 26 June 2023
|
Probability density function 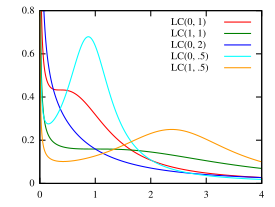 | |||
|
Cumulative distribution function 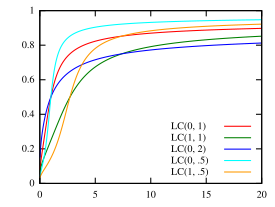 | |||
| Parameters |
(real) (real) | ||
|---|---|---|---|
| Support | |||
| CDF | |||
| Mean | infinite | ||
| Median | |||
| Variance | infinite | ||
| Skewness | does not exist | ||
| Excess kurtosis | does not exist | ||
| MGF | does not exist | ||
In probability theory, a log-Cauchy distribution is a probability distribution of a random variable whose logarithm is distributed in accordance with a Cauchy distribution. If X is a random variable with a Cauchy distribution, then Y = exp(X) has a log-Cauchy distribution; likewise, if Y has a log-Cauchy distribution, then X = log(Y) has a Cauchy distribution.[1]
Characterization
[edit]The log-Cauchy distribution is a special case of the log-t distribution where the degrees of freedom parameter is equal to 1.[2]
Probability density function
[edit]The log-Cauchy distribution has the probability density function:
where is a real number and .[1][3] If is known, the scale parameter is .[1] and correspond to the location parameter and scale parameter of the associated Cauchy distribution.[1][4] Some authors define and as the location and scale parameters, respectively, of the log-Cauchy distribution.[4]
For and , corresponding to a standard Cauchy distribution, the probability density function reduces to:[5]
Cumulative distribution function
[edit]The cumulative distribution function (cdf) when and is:[5]
Survival function
[edit]The survival function when and is:[5]
Hazard rate
[edit]The hazard rate when and is:[5]
The hazard rate decreases at the beginning and at the end of the distribution, but there may be an interval over which the hazard rate increases.[5]
Properties
[edit]The log-Cauchy distribution is an example of a heavy-tailed distribution.[6] Some authors regard it as a "super-heavy tailed" distribution, because it has a heavier tail than a Pareto distribution-type heavy tail, i.e., it has a logarithmically decaying tail.[6][7] As with the Cauchy distribution, none of the non-trivial moments of the log-Cauchy distribution are finite.[5] The mean is a moment so the log-Cauchy distribution does not have a defined mean or standard deviation.[8][9]
The log-Cauchy distribution is infinitely divisible for some parameters but not for others.[10] Like the lognormal distribution, log-t or log-Student distribution and Weibull distribution, the log-Cauchy distribution is a special case of the generalized beta distribution of the second kind.[11][12] The log-Cauchy is actually a special case of the log-t distribution, similar to the Cauchy distribution being a special case of the Student's t distribution with 1 degree of freedom.[13][14]
Since the Cauchy distribution is a stable distribution, the log-Cauchy distribution is a logstable distribution.[15] Logstable distributions have poles at x=0.[14]
Estimating parameters
[edit]The median of the natural logarithms of a sample is a robust estimator of .[1] The median absolute deviation of the natural logarithms of a sample is a robust estimator of .[1]
Uses
[edit]In Bayesian statistics, the log-Cauchy distribution can be used to approximate the improper Jeffreys-Haldane density, 1/k, which is sometimes suggested as the prior distribution for k where k is a positive parameter being estimated.[16][17] The log-Cauchy distribution can be used to model certain survival processes where significant outliers or extreme results may occur.[3][4][18] An example of a process where a log-Cauchy distribution may be an appropriate model is the time between someone becoming infected with HIV and showing symptoms of the disease, which may be very long for some people.[4] It has also been proposed as a model for species abundance patterns.[19]
References
[edit]- ^ a b c d e f Olive, D.J. (June 23, 2008). "Applied Robust Statistics" (PDF). Southern Illinois University. p. 86. Archived from the original (PDF) on September 28, 2011. Retrieved 2011-10-18.
- ^ Olosunde, Akinlolu & Olofintuade, Sylvester (January 2022). "Some Inferential Problems from Log Student's T-distribution and its Multivariate Extension". Revista Colombiana de Estadística - Applied Statistics. 45 (1): 209–229. doi:10.15446/rce.v45n1.90672. Retrieved 2022-04-01.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ^ a b Lindsey, J.K. (2004). Statistical analysis of stochastic processes in time. Cambridge University Press. pp. 33, 50, 56, 62, 145. ISBN 978-0-521-83741-5.
- ^ a b c d Mode, C.J. & Sleeman, C.K. (2000). Stochastic processes in epidemiology: HIV/AIDS, other infectious diseases. World Scientific. pp. 29–37. ISBN 978-981-02-4097-4.
- ^ a b c d e f Marshall, A.W. & Olkin, I. (2007). Life distributions: structure of nonparametric, semiparametric, and parametric families. Springer. pp. 443–444. ISBN 978-0-387-20333-1.
- ^ a b Falk, M.; Hüsler, J. & Reiss, R. (2010). Laws of Small Numbers: Extremes and Rare Events. Springer. p. 80. ISBN 978-3-0348-0008-2.
- ^ Alves, M.I.F.; de Haan, L. & Neves, C. (March 10, 2006). "Statistical inference for heavy and super-heavy tailed distributions" (PDF). Archived from the original (PDF) on June 23, 2007.
- ^ "Moment". Mathworld. Retrieved 2011-10-19.
- ^ Wang, Y. "Trade, Human Capital and Technology Spillovers: An Industry Level Analysis". Carleton University: 14.
{{cite journal}}: Cite journal requires|journal=(help) - ^ Bondesson, L. (2003). "On the Lévy Measure of the Lognormal and LogCauchy Distributions". Methodology and Computing in Applied Probability: 243–256. Archived from the original on 2012-04-25. Retrieved 2011-10-18.
- ^ Knight, J. & Satchell, S. (2001). Return distributions in finance. Butterworth-Heinemann. p. 153. ISBN 978-0-7506-4751-9.
- ^ Kemp, M. (2009). Market consistency: model calibration in imperfect markets. Wiley. ISBN 978-0-470-77088-7.
- ^ MacDonald, J.B. (1981). "Measuring Income Inequality". In Taillie, C.; Patil, G.P.; Baldessari, B. (eds.). Statistical distributions in scientific work: proceedings of the NATO Advanced Study Institute. Springer. p. 169. ISBN 978-90-277-1334-6.
- ^ a b Kleiber, C. & Kotz, S. (2003). Statistical Size Distributions in Economics and Actuarial Science. Wiley. pp. 101–102, 110. ISBN 978-0-471-15064-0.
- ^ Panton, D.B. (May 1993). "Distribution function values for logstable distributions". Computers & Mathematics with Applications. 25 (9): 17–24. doi:10.1016/0898-1221(93)90128-I.
- ^ Good, I.J. (1983). Good thinking: the foundations of probability and its applications. University of Minnesota Press. p. 102. ISBN 978-0-8166-1142-3.
- ^ Chen, M. (2010). Frontiers of Statistical Decision Making and Bayesian Analysis. Springer. p. 12. ISBN 978-1-4419-6943-9.
- ^ Lindsey, J.K.; Jones, B. & Jarvis, P. (September 2001). "Some statistical issues in modelling pharmacokinetic data". Statistics in Medicine. 20 (17–18): 2775–278. doi:10.1002/sim.742. PMID 11523082. S2CID 41887351.
- ^ Zuo-Yun, Y.; et al. (June 2005). "LogCauchy, log-sech and lognormal distributions of species abundances in forest communities". Ecological Modelling. 184 (2–4): 329–340. doi:10.1016/j.ecolmodel.2004.10.011.




![{\displaystyle {1 \over x\pi }\left[{\sigma \over (\ln x-\mu )^{2}+\sigma ^{2}}\right],\ \ x>0}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/8ac7d87d9737a9d396f445dfeb9b4cff6c3d0a12)


![{\displaystyle {\begin{aligned}f(x;\mu ,\sigma )&={\frac {1}{x\pi \sigma \left[1+\left({\frac {\ln x-\mu }{\sigma }}\right)^{2}\right]}},\ \ x>0\\&={1 \over x\pi }\left[{\sigma \over (\ln x-\mu )^{2}+\sigma ^{2}}\right],\ \ x>0\end{aligned}}}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/a188fc444184e191f4e0325b64a2fb201546adfe)





![{\displaystyle f(x;0,1)={\frac {1}{x\pi [1+(\ln x)^{2}]}},\ \ x>0}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/c949bf99e759a9ba26dc5577f0925c93778fbc56)


![{\displaystyle \lambda (x;0,1)=\left\{{\frac {1}{x\pi \left[1+\left(\ln x\right)^{2}\right]}}\left[{\frac {1}{2}}-{\frac {1}{\pi }}\arctan(\ln x)\right]\right\}^{-1},\ \ x>0}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/517de41276551270538d7c0ed002e4419828ee45)