Logarithmic resistor ladder: Difference between revisions
Em3rgent0rdr (talk | contribs) →Background: emphasize "linear" for R-2R, so readers are clear that is not logarithmic. |
|||
| (25 intermediate revisions by 12 users not shown) | |||
| Line 1: | Line 1: | ||
A '''logarithmic resistor ladder''' is an [[electronic circuit]] composed of a series of [[resistor]]s and [[switch]]es, designed to create an attenuation from an input to an output signal, where the [[logarithm]] of the attenuation ratio is proportional to a |
A '''logarithmic resistor ladder''' is an [[electronic circuit]], composed of a series of [[resistor]]s and [[switch]]es, designed to create an [[attenuation]] from an input to an output signal, where the [[logarithm]] of the attenuation ratio is proportional to a [[binary number]] that represents the state of the switches. |
||
The logarithmic behavior of the circuit is its main differentiator in comparison with [[digital-to-analog converter]]s in general, and traditional [[Resistor ladder|R-2R Ladder]] networks specifically. Logarithmic attenuation is desired in situations where a large [[dynamic range]] needs to be handled. The circuit described in this article is applied in [[Preamplifier|audio devices]], since human [[dynamic range#Audio|perception of sound level]] is properly expressed on a logarithmic scale. |
The logarithmic behavior of the circuit is its main differentiator in comparison with [[digital-to-analog converter]]s (DACs) in general, and traditional [[Resistor ladder|R-2R Ladder]] networks specifically. Logarithmic attenuation is desired in situations where a large [[dynamic range]] needs to be handled. The circuit described in this article is applied in [[Preamplifier|audio devices]], since human [[dynamic range#Audio|perception of sound level]] is properly expressed on a logarithmic scale. |
||
== Logarithmic input/output behavior == |
== Logarithmic input/output behavior == |
||
As in [[digital-to-analog converter]]s, a |
As in [[digital-to-analog converter]]s, a binary number is applied to the ladder network, whose ''N'' bits are treated as representing an integer value: |
||
:<math>\mathrm{CodeValue} = \sum_{i=1}^N s_i \cdot 2^{i-1}</math> |
:<math>\mathrm{CodeValue} = \sum_{i=1}^N s_i \cdot 2^{i-1}</math> |
||
where <math>s_i</math> is 0 or 1 depending on the state of the ''i<sup>th</sup>'' switch. |
|||
| ⚫ | |||
:<math>V_{out} = a \cdot (\mathrm{CodeValue} + b ) \cdot V_{in}</math> where <math>a</math> and <math>b</math> are design constants and where <math>V_{in}</math> typically is a '''constant reference''' voltage. |
|||
| ⚫ | |||
(DA-converters that are designed to handle a '''variable''' input voltage are |
|||
:<math>V_{out} = V_{in} \cdot c \cdot (\mathrm{CodeValue} + d )</math> |
|||
where <math>c</math> and <math>d</math> are design constants and where <math>V_{in}</math> typically is a '''constant reference''' voltage (or is a '''variable''' input voltage for a '''multiplying DAC'''.<ref>{{cite web |url=http://www.analog.com/enwiki/static/imported-files/overviews/AnalogMultiplyingDACs.pdf |title=Multiplying DACs, flexible building blocks |year=2010 |publisher=Analog Devices inc. |accessdate=29 March 2012}}</ref>) |
|||
In contrast, the logarithmic ladder network discussed in this article creates a behavior as: |
In contrast, the logarithmic ladder network discussed in this article creates a behavior as: |
||
:<math>\log (V_{out} / V_{in}) = |
:<math>\log (V_{out} / V_{in}) = c \cdot \mathrm{CodeValue}</math> |
||
which can also be expressed as <math>V_{in}</math> multiplied by some base <math>\alpha</math> [[raised to the power of]] the code value: |
|||
:<math>V_{out} = V_{in} \cdot \alpha ^ \mathrm{CodeValue}</math> |
|||
| ⚫ | |||
== Circuit implementation == |
== Circuit implementation == |
||
[[File: |
[[File:Circuit_diagram_of_logarithmic_ladder_DA_converter,_Mar_2012.png|alt=Schematic diagram|Circuit diagram]] |
||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
:<math>Ratio_i = \text{if}\; sw_i \;\text{then}\; \alpha^{2^{i-1}} \;\text{else}\; 1</math> |
:<math>Ratio_i = \text{if}\; sw_i \;\text{then}\; \alpha^{2^{i-1}} \;\text{else}\; 1</math> |
||
For logarithmic scaled attenuators, it is common practice to express their attenuation in [[decibel]]s: |
For logarithmic scaled attenuators, it is common practice to equivalently express their attenuation in [[decibel]]s: |
||
:<math>dB(Ratio_i) = 20 \log_{10} \alpha^{2^{i-1}} = 2^{i-1} \cdot 20 \cdot \log_{10} \alpha</math> for <math>i = 1 .. N</math> and <math>sw_i = 1</math> |
:<math>dB(Ratio_i) = 20 \log_{10} \alpha^{2^{i-1}} = 2^{i-1} \cdot 20 \cdot \log_{10} \alpha</math> for <math>i = 1 .. N</math> and <math>sw_i = 1</math> |
||
| Line 28: | Line 34: | ||
To show that this <math>Ratio_i</math> satisfies the overall intention: |
To show that this <math>Ratio_i</math> satisfies the overall intention: |
||
:<math>\log (V_{out}/V_{in}) = \log (\prod_{i=1}^N Ratio_i) = \sum_{i=1}^N \log (Ratio_i) = |
:<math>\log (V_{out}/V_{in}) = \log (\prod_{i=1}^N Ratio_i) = \sum_{i=1}^N \log (Ratio_i) = \log (\alpha) \cdot CodeValue = c \cdot CodeValue</math> |
||
| ⚫ | |||
The different stages 1 .. N should function independently of each other, as to obtain 2<sup>N</sup> different states with a composable behavior. To achieve an attenuation of each stage that is independent of its surrounding stages, either one of two design choices is to be implemented: constant input resistance or constant output resistance. |
The different stages 1 .. N should function independently of each other, as to obtain 2<sup>N</sup> different states with a composable behavior. To achieve an attenuation of each stage that is independent of its surrounding stages, either one of two design choices is to be implemented: constant input resistance or constant output resistance. Because the stages operate independently, they can be inserted in the chain in any order. |
||
=== Constant input resistance === |
=== Constant input resistance === |
||
| Line 55: | Line 60: | ||
\end{cases}</math> |
\end{cases}</math> |
||
Again, all resistor values of the circuit diagram follow easily after choosing values for N, <math>\alpha</math> and R<sub>source</sub>. (The value of R<sub>load</sub> does not influence the logarithmic behavior) |
Again, all resistor values of the circuit diagram follow easily after choosing values for N, <math>\alpha</math> and R<sub>source</sub>. (The value of R<sub>load</sub> does not influence the logarithmic behavior). |
||
For example, with a R<sub>load</sub> of 1 kΩ, and 1 dB attenuation, the resistor values would be: |
|||
R<sub>a</sub> = 108.7 Ω, |
|||
R<sub>b</sub> = 8195.5 Ω. |
|||
The next step (2 dB) would use: R<sub>a</sub> = 369.0 Ω, |
|||
R<sub>b</sub> = 1709.7 Ω. |
|||
== Circuit variations == |
== Circuit variations == |
||
* The circuit as depicted above, can also be applied in reverse direction. That correspondingly reverses the role of constant-input and constant-output resistance equations. |
* The circuit as depicted above, can also be applied in reverse direction. That correspondingly reverses the role of constant-input and constant-output resistance equations. |
||
* Since the stages do not influence each other's attenuation, the stage order can be chosen arbitrarily. Such reordering can have a significant effect on the ''input'' resistance of the ''constant output resistance'' attenuator and vice versa. |
* Since the stages do not significantly influence each other's attenuation, the stage order can be chosen arbitrarily. Such reordering can have a significant effect on the ''input'' resistance of the ''constant output resistance'' attenuator and vice versa. |
||
== Background == |
== Background == |
||
R-2R ladder networks used for |
R-2R ladder networks used for ''linear'' digital-to-analog conversion are old ({{Slink|Resistor ladder|History}} mentions a 1953 article and a 1955 patent). |
||
Multiplying |
Multiplying DACs with logarithmic behavior were not known for a long time after that. An initial approach was to map the logarithmic code to a much longer code word, which could be applied to the classical (linear) R-2R based DAC. Lengthening the codeword is needed in that approach to achieve sufficient dynamic range. This approach was implemented in a device from Analog Devices Inc.,<ref>{{cite web |
||
| url = http://www.analog.com/media/en/technical-documentation/obsolete-data-sheets/1257410AD7118.pdf |
|||
| ⚫ | |||
| title = LOGDAC CMOS Logarithmic D/A Converter AD7118 |
|||
| publisher = Analog Devices Inc. |
|||
| archive-url = https://web.archive.org/web/20150825062826/http://www.analog.com/media/en/technical-documentation/obsolete-data-sheets/1257410AD7118.pdf |
|||
| archive-date = 25 August 2015 |
|||
| access-date = 25 August 2015 |
|||
| ⚫ | |||
== See also == |
== See also == |
||
| Line 78: | Line 96: | ||
* [http://www.vaneijndhoven.net/jos/attenuator-calculator/index.html Online calculator] to configure logarithmic ladder networks |
* [http://www.vaneijndhoven.net/jos/attenuator-calculator/index.html Online calculator] to configure logarithmic ladder networks |
||
[[Category: |
[[Category:Analog circuits]] |
||
[[Category:Electrical components]] |
|||
[[Category:Resistive components]] |
|||
Latest revision as of 01:56, 28 June 2023
A logarithmic resistor ladder is an electronic circuit, composed of a series of resistors and switches, designed to create an attenuation from an input to an output signal, where the logarithm of the attenuation ratio is proportional to a binary number that represents the state of the switches.
The logarithmic behavior of the circuit is its main differentiator in comparison with digital-to-analog converters (DACs) in general, and traditional R-2R Ladder networks specifically. Logarithmic attenuation is desired in situations where a large dynamic range needs to be handled. The circuit described in this article is applied in audio devices, since human perception of sound level is properly expressed on a logarithmic scale.
Logarithmic input/output behavior
[edit]As in digital-to-analog converters, a binary number is applied to the ladder network, whose N bits are treated as representing an integer value:
where is 0 or 1 depending on the state of the ith switch.
For comparison, recall a conventional linear DAC or R-2R network produces an output voltage signal of:
where and are design constants and where typically is a constant reference voltage (or is a variable input voltage for a multiplying DAC.[1])
In contrast, the logarithmic ladder network discussed in this article creates a behavior as:
which can also be expressed as multiplied by some base raised to the power of the code value:
where
Circuit implementation
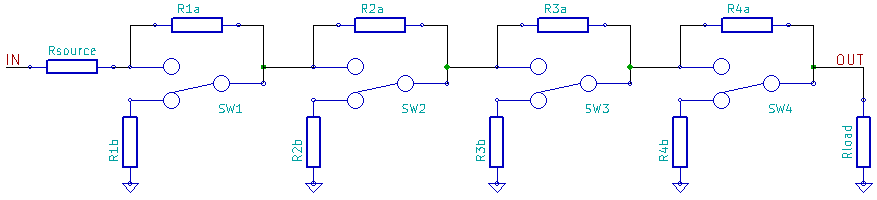
[edit]This example circuit is composed of 4 stages, numbered 1 to 4, and includes a source resistance Rsource and load resistance Rload.
Each stage i has a designed input-to-output voltage attenuation Ratioi as:
For logarithmic scaled attenuators, it is common practice to equivalently express their attenuation in decibels:
- for and
This reveals a basic property:
To show that this satisfies the overall intention:
The different stages 1 .. N should function independently of each other, as to obtain 2N different states with a composable behavior. To achieve an attenuation of each stage that is independent of its surrounding stages, either one of two design choices is to be implemented: constant input resistance or constant output resistance. Because the stages operate independently, they can be inserted in the chain in any order.
Constant input resistance
[edit]The input resistance of any stage shall be independent of its on/off switch position, and must be equal to Rload.
This leads to:
With these equations, all resistor values of the circuit diagram follow easily after choosing values for N, and Rload. (The value of Rsource does not influence the logarithmic behavior)
Constant output resistance
[edit]The output resistance of any stage shall be independent of its on/off switch position, and must be equal to Rsource.
This leads to:
Again, all resistor values of the circuit diagram follow easily after choosing values for N, and Rsource. (The value of Rload does not influence the logarithmic behavior).
For example, with a Rload of 1 kΩ, and 1 dB attenuation, the resistor values would be: Ra = 108.7 Ω, Rb = 8195.5 Ω.
The next step (2 dB) would use: Ra = 369.0 Ω, Rb = 1709.7 Ω.
Circuit variations
[edit]- The circuit as depicted above, can also be applied in reverse direction. That correspondingly reverses the role of constant-input and constant-output resistance equations.
- Since the stages do not significantly influence each other's attenuation, the stage order can be chosen arbitrarily. Such reordering can have a significant effect on the input resistance of the constant output resistance attenuator and vice versa.
Background
[edit]R-2R ladder networks used for linear digital-to-analog conversion are old (Resistor ladder § History mentions a 1953 article and a 1955 patent).
Multiplying DACs with logarithmic behavior were not known for a long time after that. An initial approach was to map the logarithmic code to a much longer code word, which could be applied to the classical (linear) R-2R based DAC. Lengthening the codeword is needed in that approach to achieve sufficient dynamic range. This approach was implemented in a device from Analog Devices Inc.,[2] protected through a 1981 patent filing.[3]
See also
[edit]References
[edit]- ^ "Multiplying DACs, flexible building blocks" (PDF). Analog Devices inc. 2010. Retrieved 29 March 2012.
- ^ "LOGDAC CMOS Logarithmic D/A Converter AD7118" (PDF). Analog Devices Inc. Archived from the original (PDF) on 25 August 2015. Retrieved 25 August 2015.
- ^ US patent 4521764, Burton, David P., "Signal-controllable attenuator employing a digital-to-analog converter", issued 4 June 1985
External links
[edit]- Online calculator to configure logarithmic ladder networks