Savart: Difference between revisions
→top: ({{audio|Jot on C.mid|play}}) |
Fgnievinski (talk | contribs) removed Category:Units of measurement; added Category:Units of level using HotCat |
||
| (20 intermediate revisions by 10 users not shown) | |||
| Line 1: | Line 1: | ||
{{For|the French physicist from whom the savart takes its name|Félix Savart}} |
{{Short description|Unit of measurement for musical pitch intervals}}{{For|the French physicist from whom the savart takes its name|Félix Savart}} |
||
[[Image:Five decades visualization.svg|thumb|1/100 heptaméride (jot), 1/10 heptaméride (decameride), 1 heptamérides, 10 heptamérides, 100 heptamérides, 1,000 heptamérides (decade).]] |
[[Image:Five decades visualization.svg|thumb|1/100 heptaméride (jot), 1/10 heptaméride (decameride), 1 heptamérides, 10 heptamérides, 100 heptamérides, 1,000 heptamérides (decade).]] |
||
The '''savart''' {{IPAc-en|s|ə|ˈ|v|ɑr}} is a unit of measurement for musical [[list of pitch intervals|pitch intervals]] ({{Audio|Savart on C.mid|play}}). One savart is equal to one thousandth of a [[decade (log scale)|decade]] ([[just major third|10/1]]: 3,986.313714 cents): 3.9863 cents. Musically, in just intonation, the interval of a decade is precisely a just major twenty-fourth, or, in other words, three octaves and a just major third. Today the savart has largely been replaced by the [[cent (music)|cent]] and the [[millioctave]]. The savart is practically the same as the earlier '''heptameride''' (eptameride), one seventh of a '''meride'''. [[ |
The '''savart''' {{IPAc-en|s|ə|ˈ|v|ɑr}} is a unit of measurement for musical [[list of pitch intervals|pitch intervals]] ({{Audio|Savart on C.mid|play}}). One savart is equal to one thousandth of a [[decade (log scale)|decade]] ([[just major third|10/1]]: 3,986.313714 cents): 3.9863 cents. Musically, in just intonation, the interval of a decade is precisely a just major twenty-fourth, or, in other words, three octaves and a just major third. Today, musical use of the savart has largely been replaced by the [[cent (music)|cent]] and the [[millioctave]]. The savart is practically the same as the earlier '''heptameride''' (eptameride), one seventh of a '''meride''' ({{audio|Meride on C.mid|play}}). [[Power of 10|One tenth]] of an heptameride is a '''decameride''' ({{audio|Decameride on C.mid|play}}) and a hundredth of an heptameride (thousandth of a decade) is approximately one '''jot''' ({{audio|Jot on C.mid|play}}). |
||
==Definition== |
==Definition== |
||
| Line 14: | Line 14: | ||
<math>\frac{f_1}{f_2} = 10^{s/1000}</math> |
<math>\frac{f_1}{f_2} = 10^{s/1000}</math> |
||
Like the more common cent, the savart is a [[logarithm]]ic measure, and thus intervals can be added by simply adding their savart values, instead of multiplying them as you would frequencies. The number of savarts in an octave is 1000 times the base-10 logarithm of 2, or nearly 301.03. Sometimes this is rounded to 300, which makes the unit more useful for [[equal temperament]].<ref name="hf">{{cite web|url=http://www.huygens-fokker.org/docs/measures.html|title=Logarithmic Interval Measures|author=Huygens-Fokker Foundation| |
Like the more common cent, the savart is a [[logarithm]]ic measure, and thus intervals can be added by simply adding their savart values, instead of multiplying them as you would frequencies. The number of savarts in an octave is 1000 times the base-10 logarithm of 2, or nearly 301.03. Sometimes this is rounded to 300, which makes the unit more useful for [[equal temperament]].<ref name="hf">{{cite web|url=http://www.huygens-fokker.org/docs/measures.html|title=Logarithmic Interval Measures|author=Huygens-Fokker Foundation|author-link=Huygens-Fokker Foundation|access-date=2007-06-13 <!-- archiveurl = https://web.archive.org/web/20070214012515/http://www.xs4all.nl/~huygensf/doc/measures.html --> <!-- Bot retrieved archive |archive-date = 2007-02-14 -->}}</ref> |
||
==Conversion== |
==Conversion== |
||
The conversion from savarts into cents or |
The conversion from savarts into cents, millioctaves or [[millidecade]]s is: |
||
<math>1\ \mathrm{savart} = \frac{1.2}{\log_{10}{2}}\ \mathrm{cent} \approx 3.9863\ \mathrm{cent}</math> |
<math>1\ \mathrm{savart} = \frac{1.2}{\log_{10}{2}}\ \mathrm{cent} \approx 3.9863\ \mathrm{cent}</math> |
||
<math>1\ \mathrm{savart} = \frac{1}{\log_{10}{2}}\ \mathrm{millioctave} \approx 3.3219\ \mathrm{millioctave}</math> |
<math>1\ \mathrm{savart} = \frac{1}{\log_{10}{2}}\ \mathrm{millioctave} \approx 3.3219\ \mathrm{millioctave}</math> |
||
1 savart = 0.001 decade = 1 millidecade<ref>Martin, S. B., Gaudet, B. J., Klinck, H., Dugan, P. J., Miksis-Olds, J. L., Mellinger, D. K., ... & Moors-Murphy, H. (2021). Hybrid millidecade spectra: A practical format for exchange of long-term ambient sound data. JASA Express Letters, 1(1), 011203.</ref> |
|||
==History== |
==History== |
||
| Line 28: | Line 30: | ||
The savart is named after the French physicist and doctor [[Félix Savart]] (1791–1841) who advocated the earlier similar interval of the French acoustician [[Joseph Sauveur]] (1653–1716). Sauveur proposed the ''méride'', ''eptaméride'' (or ''heptaméride''), and ''decaméride''. In English these are meride, heptameride, and decameride respectively. The octave is divided into 43 merides, the meride is divided into seven heptamerides, and the heptameride is divided into ten decamerides. There are thus {{nowrap|43 × 7 {{=}} 301}} heptamerides in an octave.<ref>Hermann von Helmholtz (1912). ''On the sensations of tone as a physiological basis for the theory of music'', p.437. Longmans, Green.</ref> The attraction of this scheme to Sauveur was that log<sub>10</sub>(2) is very close to .301, and thus the number of heptamerides in a given ratio is found to a high degree of accuracy from simply its log times 1000. This is equivalent to assuming 1000 heptamerides in a decade rather than 301 in an octave, the same as Savart's definition. The unit was given the name ''savart'' sometime in the 20th century.<ref name="hf"/> A disadvantage of this scheme is that there are not an exact number of heptamerides/savarts in an [[equal tempered]] semitone. For this reason Alexander Wood used a modified definition of the savart, with 300 savarts in an octave, and hence 25 savarts in a semitone.<ref>Alexander Wood, ''The Physics of Music'', pages 53-54, Read Books, 2007 {{ISBN|140674493X}} (first published Methuen, 1944 {{OCLC|220112916}}.</ref> |
The savart is named after the French physicist and doctor [[Félix Savart]] (1791–1841) who advocated the earlier similar interval of the French acoustician [[Joseph Sauveur]] (1653–1716). Sauveur proposed the ''méride'', ''eptaméride'' (or ''heptaméride''), and ''decaméride''. In English these are meride, heptameride, and decameride respectively. The octave is divided into 43 merides, the meride is divided into seven heptamerides, and the heptameride is divided into ten decamerides. There are thus {{nowrap|43 × 7 {{=}} 301}} heptamerides in an octave.<ref>Hermann von Helmholtz (1912). ''On the sensations of tone as a physiological basis for the theory of music'', p.437. Longmans, Green.</ref> The attraction of this scheme to Sauveur was that log<sub>10</sub>(2) is very close to .301, and thus the number of heptamerides in a given ratio is found to a high degree of accuracy from simply its log times 1000. This is equivalent to assuming 1000 heptamerides in a decade rather than 301 in an octave, the same as Savart's definition. The unit was given the name ''savart'' sometime in the 20th century.<ref name="hf"/> A disadvantage of this scheme is that there are not an exact number of heptamerides/savarts in an [[equal tempered]] semitone. For this reason Alexander Wood used a modified definition of the savart, with 300 savarts in an octave, and hence 25 savarts in a semitone.<ref>Alexander Wood, ''The Physics of Music'', pages 53-54, Read Books, 2007 {{ISBN|140674493X}} (first published Methuen, 1944 {{OCLC|220112916}}.</ref> |
||
A related unit is the jot, of which there are 30103 in an octave, or approximately 100,000 in a decade. The jot is defined in a similar way to the savart, but has a more accurate rounding of log<sub>10</sub>(2) because more digits are used.<ref>Joe Monzo, [http://tonalsoft.com/enc/h/heptameride.aspx "Heptaméride"] and [http://tonalsoft.com/enc/j/jot.aspx "Jot"], ''Tonalsoft Encyclopedia of Microtonal Music Theory'', retrieved and [https:// |
A related unit is the jot, of which there are 30103 in an octave, or approximately 100,000 in a decade. The jot is defined in a similar way to the savart, but has a more accurate rounding of log<sub>10</sub>(2) because more digits are used.<ref>Joe Monzo, [http://tonalsoft.com/enc/h/heptameride.aspx "Heptaméride"] and [http://tonalsoft.com/enc/j/jot.aspx "Jot"], ''Tonalsoft Encyclopedia of Microtonal Music Theory'', retrieved and [https://web.archive.org/web/20120904225147/http://tonalsoft.com/enc/s/savart.aspx archived][https://web.archive.org/web/20120905112525/http://tonalsoft.com/enc/j/jot.aspx] 11 October 2012.</ref> There are approximately 100 jots in a savart. The jot was first described by [[Augustus De Morgan]] (1806-1871) which he called an ''atom''. The name ''jot'' was coined by [[John Curwen]] (1816-1880) at the suggestion of [[Hermann von Helmholtz]].<ref>Hermann von Helmholtz, (trans. A. J. Ellis), ''On the Sensations of Tone as a Physiological Basis for the Theory of Music'', page 654, Longmans, 1875 {{OCLC|8101251}}.</ref> |
||
==Comparison== |
==Comparison== |
||
| Line 47: | Line 49: | ||
| Jot || 30,103 || 0.0398631 || 1/30,103 octave || 2<sup>1/30,103</sup> || 1.000023 || {{audio|Jot on C.mid|Play}} |
| Jot || 30,103 || 0.0398631 || 1/30,103 octave || 2<sup>1/30,103</sup> || 1.000023 || {{audio|Jot on C.mid|Play}} |
||
|} |
|} |
||
==Other uses== |
|||
The unit is used for acoustical engineering analysis, especially in [[underwater acoustics]], where it is known as a millidecade. |
|||
==See also== |
==See also== |
||
| Line 61: | Line 66: | ||
[[Category:Equal temperaments]] |
[[Category:Equal temperaments]] |
||
[[Category:Intervals (music)]] |
[[Category:Intervals (music)]] |
||
[[Category:Units of |
[[Category:Units of level]] |
||
[[Category:1000 (number)]] |
[[Category:1000 (number)]] |
||
Latest revision as of 02:26, 16 October 2023
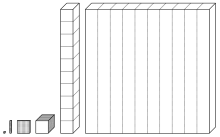
The savart /səˈvɑːr/ is a unit of measurement for musical pitch intervals (ⓘ). One savart is equal to one thousandth of a decade (10/1: 3,986.313714 cents): 3.9863 cents. Musically, in just intonation, the interval of a decade is precisely a just major twenty-fourth, or, in other words, three octaves and a just major third. Today, musical use of the savart has largely been replaced by the cent and the millioctave. The savart is practically the same as the earlier heptameride (eptameride), one seventh of a meride (ⓘ). One tenth of an heptameride is a decameride (ⓘ) and a hundredth of an heptameride (thousandth of a decade) is approximately one jot (ⓘ).
Definition
[edit]If is the ratio of frequencies of a given interval, the corresponding measure in savarts is given by:
or
Like the more common cent, the savart is a logarithmic measure, and thus intervals can be added by simply adding their savart values, instead of multiplying them as you would frequencies. The number of savarts in an octave is 1000 times the base-10 logarithm of 2, or nearly 301.03. Sometimes this is rounded to 300, which makes the unit more useful for equal temperament.[1]
Conversion
[edit]The conversion from savarts into cents, millioctaves or millidecades is:
1 savart = 0.001 decade = 1 millidecade[2]
History
[edit]The savart is named after the French physicist and doctor Félix Savart (1791–1841) who advocated the earlier similar interval of the French acoustician Joseph Sauveur (1653–1716). Sauveur proposed the méride, eptaméride (or heptaméride), and decaméride. In English these are meride, heptameride, and decameride respectively. The octave is divided into 43 merides, the meride is divided into seven heptamerides, and the heptameride is divided into ten decamerides. There are thus 43 × 7 = 301 heptamerides in an octave.[3] The attraction of this scheme to Sauveur was that log10(2) is very close to .301, and thus the number of heptamerides in a given ratio is found to a high degree of accuracy from simply its log times 1000. This is equivalent to assuming 1000 heptamerides in a decade rather than 301 in an octave, the same as Savart's definition. The unit was given the name savart sometime in the 20th century.[1] A disadvantage of this scheme is that there are not an exact number of heptamerides/savarts in an equal tempered semitone. For this reason Alexander Wood used a modified definition of the savart, with 300 savarts in an octave, and hence 25 savarts in a semitone.[4]
A related unit is the jot, of which there are 30103 in an octave, or approximately 100,000 in a decade. The jot is defined in a similar way to the savart, but has a more accurate rounding of log10(2) because more digits are used.[5] There are approximately 100 jots in a savart. The jot was first described by Augustus De Morgan (1806-1871) which he called an atom. The name jot was coined by John Curwen (1816-1880) at the suggestion of Hermann von Helmholtz.[6]
Comparison
[edit]| Name | Steps per octave | Cents | Relative | Interval | Ratio | Audio |
|---|---|---|---|---|---|---|
| Decade | 0.301030 | 3,986.313714 | 1,000 heptamérides | 101/1 | 10.000000 | ⓘ |
| Méride | 43.004285 | 27.904196 | 7 heptamérides | 107/1,000 | 1.016249 | ⓘ |
| Heptaméride | 301.029996 | 3.986314 | 1/1,000 decade, 1/7 méride, 10 decamérides, or 100 jots | 101/1,000 | 1.002305 | ⓘ |
| Demi-heptaméride | 602.059991 | 1.993157 | 1/2 heptaméride | 101/2,000 | 1.001152 | ⓘ |
| Decaméride | 3,010.299957 | 0.398631 | 1/10 heptaméride | 101/10,000 | 1.000230 | ⓘ |
| Jot | 30,103 | 0.0398631 | 1/30,103 octave | 21/30,103 | 1.000023 | ⓘ |
Other uses
[edit]The unit is used for acoustical engineering analysis, especially in underwater acoustics, where it is known as a millidecade.
See also
[edit]Notes
[edit]- ^ a b Huygens-Fokker Foundation. "Logarithmic Interval Measures". Retrieved 2007-06-13.
- ^ Martin, S. B., Gaudet, B. J., Klinck, H., Dugan, P. J., Miksis-Olds, J. L., Mellinger, D. K., ... & Moors-Murphy, H. (2021). Hybrid millidecade spectra: A practical format for exchange of long-term ambient sound data. JASA Express Letters, 1(1), 011203.
- ^ Hermann von Helmholtz (1912). On the sensations of tone as a physiological basis for the theory of music, p.437. Longmans, Green.
- ^ Alexander Wood, The Physics of Music, pages 53-54, Read Books, 2007 ISBN 140674493X (first published Methuen, 1944 OCLC 220112916.
- ^ Joe Monzo, "Heptaméride" and "Jot", Tonalsoft Encyclopedia of Microtonal Music Theory, retrieved and archived[1] 11 October 2012.
- ^ Hermann von Helmholtz, (trans. A. J. Ellis), On the Sensations of Tone as a Physiological Basis for the Theory of Music, page 654, Longmans, 1875 OCLC 8101251.





