Conway puzzle: Difference between revisions
Appearance
Content deleted Content added
m →Solution: horizintal → horizontal ; removing undue italics |
-cat |
||
| (18 intermediate revisions by 14 users not shown) | |||
| Line 1: | Line 1: | ||
{{Short description|Three-dimensional packing problem}} |
|||
[[Image: |
[[Image:Conway_puzzle_pieces.svg|thumb|Pieces used in the Conway puzzle]] |
||
'''Conway's puzzle''' is a [[packing problem]] using rectangular blocks, named after its inventor, mathematician [[John Horton Conway|John Conway]]. It calls for packing thirteen 1 × 2 × 4 blocks, one 2 × 2 × 2 block, one 1 × 2 × 2 block, and three 1 × 1 × 3 blocks into a 5 × 5 × 5 box.<ref>{{ |
'''Conway's puzzle''', or '''blocks-in-a-box''', is a [[packing problem]] using rectangular blocks, named after its inventor, mathematician [[John Horton Conway|John Conway]]. It calls for packing thirteen 1 × 2 × 4 blocks, one 2 × 2 × 2 block, one 1 × 2 × 2 block, and three 1 × 1 × 3 blocks into a 5 × 5 × 5 box.<ref>{{MathWorld | urlname=ConwayPuzzle | title=Conway Puzzle}}</ref> |
||
==Solution== |
==Solution== |
||
[[Image:Conway |
[[Image:Conway puzzle_hint.svg|thumb|upright|A possible placement for the three 1×1×3 blocks – {{nowrap|the vertical}} block has corners touching corners of the two horizontal blocks]] |
||
The solution of the Conway puzzle is straightforward |
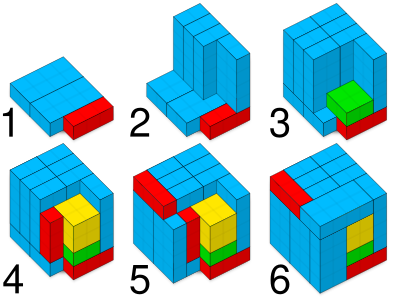
The solution of the Conway puzzle is straightforward once one realizes, based on [[parity (mathematics)|parity]] considerations, that the three 1 × 1 × 3 blocks need to be placed so that precisely one of them appears in each 5 × 5 × 1 slice of the cube.<ref>Elwyn R. Berlekamp, John H. Conway and Richard K. Guy: winning ways for your mathematical plays, 2nd ed, vol. 4, 2004.</ref> This is analogous to similar insight that facilitates the solution of the simpler [[Slothouber–Graatsma puzzle]].[[File:conway_puzzle_solution.svg|thumb|none|400px|A step-by-step solution to the Conway puzzle]] |
||
==See also== |
==See also== |
||
| ⚫ | |||
*[[Slothouber–Graatsma puzzle]] |
|||
| ⚫ | |||
| ⚫ | |||
{{reflist}} |
|||
==External links== |
==External links== |
||
*[http://www.johnrausch.com/PuzzlingWorld/ |
* [http://www.johnrausch.com/PuzzlingWorld/chap03.htm#p6 The Conway puzzle in Stewart Coffin's "The Puzzling World of Polyhedral Dissections"] |
||
| ⚫ | |||
<references/> |
|||
{{Packing problem}} |
{{Packing problem}} |
||
[[Category: |
[[Category:Packing problems]] |
||
| ⚫ | |||
[[Category:Recreational mathematics]] |
|||
[[Category:Tiling puzzles]] |
[[Category:Tiling puzzles]] |
||
[[Category:Mechanical puzzle cubes]] |
|||
| ⚫ | |||
{{Mathapplied-stub}} |
|||
[[eo:Enigmo de Conway]] |
|||
[[zh:康威立方]] |
|||
Latest revision as of 19:58, 22 October 2023

Conway's puzzle, or blocks-in-a-box, is a packing problem using rectangular blocks, named after its inventor, mathematician John Conway. It calls for packing thirteen 1 × 2 × 4 blocks, one 2 × 2 × 2 block, one 1 × 2 × 2 block, and three 1 × 1 × 3 blocks into a 5 × 5 × 5 box.[1]
Solution
[edit]
The solution of the Conway puzzle is straightforward once one realizes, based on parity considerations, that the three 1 × 1 × 3 blocks need to be placed so that precisely one of them appears in each 5 × 5 × 1 slice of the cube.[2] This is analogous to similar insight that facilitates the solution of the simpler Slothouber–Graatsma puzzle.
See also
[edit]References
[edit]- ^ Weisstein, Eric W. "Conway Puzzle". MathWorld.
- ^ Elwyn R. Berlekamp, John H. Conway and Richard K. Guy: winning ways for your mathematical plays, 2nd ed, vol. 4, 2004.
