Nerve complex: Difference between revisions
Erel Segal (talk | contribs) m Erel Segal moved page Nerve of a covering to Nerve complex over redirect: A nerve is a more general term; it relates not only to a covering |
m Open access bot: arxiv updated in citation with #oabot. |
||
| (17 intermediate revisions by 10 users not shown) | |||
| Line 1: | Line 1: | ||
[[File:Constructing nerve.png|thumb|Constructing the nerve of an open good cover containing 3 sets in the plane.]] |
[[File:Constructing nerve.png|thumb|Constructing the nerve of an [[Good_cover_(algebraic_topology)|open good cover]] containing 3 sets in the plane.]] |
||
In [[topology]], the '''nerve |
In [[topology]], the '''nerve complex''' of a [[set family]] is an [[abstract simplicial complex|abstract complex]] that records the pattern of intersections between the sets in the family. It was introduced by [[Pavel Alexandrov]]<ref>{{cite journal |last=Aleksandroff |first=P. S. |author-link=Pavel Alexandrov |year=1928 |title=Über den allgemeinen Dimensionsbegriff und seine Beziehungen zur elementaren geometrischen Anschauung |journal=[[Mathematische Annalen]] |volume=98 |pages=617–635 |doi=10.1007/BF01451612 |s2cid=119590045}}</ref> and now has many variants and generalisations, among them the '''Čech nerve''' of a cover, which in turn is generalised by [[hypercovering|hypercoverings]]. It captures many of the interesting topological properties in an algorithmic or combinatorial way.<ref>{{Cite book |last1=Eilenberg |first1=Samuel |title=Foundations of Algebraic Topology |last2=Steenrod |first2=Norman |date=1952-12-31 |publisher=[[Princeton University Press]] |isbn=978-1-4008-7749-2 |location=Princeton |doi=10.1515/9781400877492 |author1-link=Samuel Eilenberg |author2-link=Norman Steenrod}}</ref> |
||
== |
==Basic definition== |
||
Let <math> |
Let <math>I</math> be a set of indices and <math>C</math> be a family of sets <math>(U_i)_{i\in I}</math>. The '''nerve''' of <math>C</math> is a set of finite subsets of the index set ''<math>I</math>''. It contains all finite subsets <math>J\subseteq I</math> such that the intersection of the <math>U_i</math> whose subindices are in <math>J</math> is non-empty:''<ref name=":0">{{Cite Matousek 2007}}, Section 4.3</ref>{{Rp|page=81|location=}}'' |
||
:<math>N(C) := \bigg\{J\subseteq I: \bigcap_{j\in J}U_j \neq \varnothing, J \text{ finite set} \bigg\}.</math> |
:<math>N(C) := \bigg\{J\subseteq I: \bigcap_{j\in J}U_j \neq \varnothing, J \text{ finite set} \bigg\}.</math> |
||
The set <math>N(C)</math> may contain singletons (elements <math>i \in I</math> such that <math>U_i</math> is non-empty), pairs (pairs of elements <math>i,j \in I</math> such that <math>U_i \cap U_j \neq \emptyset</math>), triplets, and so on. If <math>J \in N(C)</math>, then any subset of <math>J</math> is also in <math>N(C)</math>, making <math>N(C)</math> an [[abstract simplicial complex]] |
In Alexandrov's original definition, the sets <math>(U_i)_{i\in I}</math> are [[Open set|open subsets]] of some topological space <math>X</math>. |
||
The set <math>N(C)</math> may contain singletons (elements <math>i \in I</math> such that <math>U_i</math> is non-empty), pairs (pairs of elements <math>i,j \in I</math> such that <math>U_i \cap U_j \neq \emptyset</math>), triplets, and so on. If <math>J \in N(C)</math>, then any subset of <math>J</math> is also in <math>N(C)</math>, making <math>N(C)</math> an [[abstract simplicial complex]]. Hence N(C) is often called the '''nerve complex''' of <math>C</math>. |
|||
==Examples== |
==Examples== |
||
# Let ''X'' be the circle <math>S^1</math> and <math>C = \{U_1, U_2\}</math>, where <math>U_1</math> is an arc covering the upper half of <math>S^1</math> and <math>U_2</math> is an arc covering its lower half, with some overlap at both sides (they must overlap at both sides in order to cover all of <math>S^1</math>). Then <math>N(C) = \{ \{1\}, \{2\}, \{1,2\} \}</math>, which is an abstract 1-simplex. |
# Let ''X'' be the circle <math>S^1</math> and <math>C = \{U_1, U_2\}</math>, where <math>U_1</math> is an arc covering the upper half of <math>S^1</math> and <math>U_2</math> is an arc covering its lower half, with some overlap at both sides (they must overlap at both sides in order to cover all of <math>S^1</math>). Then <math>N(C) = \{ \{1\}, \{2\}, \{1,2\} \}</math>, which is an abstract 1-simplex. |
||
# Let ''X'' be the circle <math>S^1</math> and <math>C = \{U_1, U_2, U_3\}</math>, where each <math>U_i</math> is an arc covering one third of <math>S^1</math>, with some overlap with the adjacent <math>U_i</math>. Then <math>N(C) = \{ \{1\}, \{2\}, \{3\}, \{1,2\}, \{2,3\}, \{3,1\} \}</math>. Note that {1,2,3} is not in <math>N(C)</math> since the common intersection of all three sets is empty. |
# Let ''X'' be the circle <math>S^1</math> and <math>C = \{U_1, U_2, U_3\}</math>, where each <math>U_i</math> is an arc covering one third of <math>S^1</math>, with some overlap with the adjacent <math>U_i</math>. Then <math>N(C) = \{ \{1\}, \{2\}, \{3\}, \{1,2\}, \{2,3\}, \{3,1\} \}</math>. Note that {1,2,3} is not in <math>N(C)</math> since the common intersection of all three sets is empty; so <math>N(C)</math> is an unfilled triangle. |
||
==The Čech nerve== |
==The Čech nerve== |
||
| Line 19: | Line 22: | ||
==Nerve theorems== |
==Nerve theorems== |
||
The nerve complex <math>N(C)</math> is a simple combinatorial object. Often, it is much simpler than the underlying topological space (the union of the sets in <math>C</math>). Therefore, a natural question is whether the topology of <math>N(C)</math> is equivalent to the topology of <math>\bigcup C</math>. |
|||
In general, this need not be the case. For example, one can cover any [[N-sphere|''n''-sphere]] with two contractible sets <math>U_1</math> and <math>U_2</math> that have a non-empty intersection, as in example 1 above. In this case, <math>N(C)</math> is an abstract 1-simplex, which is similar to a line but not to a sphere. |
|||
| ⚫ | However, in some cases <math>N(C)</math> does reflect the topology of ''X''. For example, if a circle is covered by three open arcs, intersecting in pairs as in Example 2 above, then <math>N(C)</math> is a 2-simplex (without its interior) and it is [[homotopy-equivalent]] to the original circle.<ref>{{Cite book|last1=Artin|first1=Michael|author1-link=Michael Artin|last2=Mazur|first2=Barry|author2-link=Barry Mazur|date=1969|title=Etale Homotopy|series=[[Lecture Notes in Mathematics]]|volume=100| doi=10.1007/bfb0080957|isbn=978-3-540-04619-6|issn=0075-8434}}</ref> |
||
A '''nerve theorem''' (or '''nerve lemma''') is a theorem that gives sufficient conditions on ''C'' guaranteeing that <math>N(C)</math> reflects, in some sense, the topology of ''<math>\bigcup C</math>''. A '''functorial nerve theorem''' is a nerve theorem that is functorial in an approriate sense, which is, for example, crucial in [[topological data analysis]].<ref>{{Cite journal|last1=Bauer|first1=Ulrich|last2=Kerber|first2=Michael|last3=Roll|first3=Fabian|last4=Rolle|first4=Alexander|date=2023|title=A unified view on the functorial nerve theorem and its variations|journal=[[Expositiones Mathematicae]]| language=en|doi=10.1016/j.exmath.2023.04.005|arxiv=2203.03571}}</ref> |
|||
=== Leray's nerve theorem === |
|||
| ⚫ | The basic nerve theorem of [[Jean Leray]] says that, if any intersection of sets in <math>N(C)</math> is [[Contractible space|contractible]] (equivalently: for each finite <math>J\subset I</math> the set <math>\bigcap_{i\in J} U_i</math> is either empty or contractible; equivalently: ''C'' is a [[good cover|good open cover]]), then <math>N(C)</math> is [[homotopy-equivalent]] to ''<math>\bigcup C</math>''. |
||
=== Borsuk's nerve theorem === |
|||
| ⚫ | However, in some cases <math>N(C)</math> does reflect the topology of ''X''. For example, if a circle is covered by three open arcs, intersecting in pairs as in Example 2 above, then <math>N(C)</math> is a 2-simplex (without its interior) and it is [[homotopy-equivalent]] to the original circle.<ref>{{Cite |
||
There is a discrete version, which is attributed to [[Karol Borsuk|Borsuk]].<ref>{{Cite journal |last=Borsuk |first=Karol |date=1948 |title=On the imbedding of systems of compacta in simplicial complexes |url=https://eudml.org/doc/213158 |journal=Fundamenta Mathematicae |volume=35 |issue=1 |pages=217–234 |doi=10.4064/fm-35-1-217-234 |issn=0016-2736|doi-access=free }}</ref>''<ref name=":0" />{{Rp|page=81|location=Thm.4.4.4}}'' Let ''K<sub>1</sub>,...,K<sub>n</sub>'' be [[Abstract simplicial complex|abstract simplicial complexes]], and denote their union by ''K''. Let ''U<sub>i</sub>'' = ||''K<sub>i</sub>||'' = the [[Abstract simplicial complex|geometric realization]] of ''K<sub>i</sub>'', and denote the nerve of {''U<sub>1</sub>'', ... , ''U<sub>n</sub>'' } by ''N''. |
|||
If, for each nonempty <math>J\subset I</math>, the intersection <math>\bigcap_{i\in J} U_i</math> is either empty or contractible, then ''N'' is [[homotopy-equivalent]] to ''K''. |
|||
A '''nerve theorem''' (or '''nerve lemma''') is a theorem that gives sufficient conditions on ''C'' guaranteeing that <math>N(C)</math> reflects, in some sense, the topology of ''X''. |
|||
A stronger theorem was proved by [[Anders Björner|Anders Bjorner]].<ref>{{Cite journal |last=Björner |first=Anders |authorlink=Anders Björner|date=2003-04-01 |title=Nerves, fibers and homotopy groups |journal=[[Journal of Combinatorial Theory]]|series=Series A |language=en |volume=102 |issue=1 |pages=88–93 |doi=10.1016/S0097-3165(03)00015-3 |doi-access=free |issn=0097-3165}}</ref> if, for each nonempty <math>J\subset I</math>, the intersection <math>\bigcap_{i\in J} U_i</math> is either empty or [[N-connected space|(k-|J|+1)-connected]], then for every ''j'' ≤ ''k'', the ''j''-th [[homotopy group]] of ''N'' is isomorphic to the ''j''-th [[homotopy group]] of ''K''. In particular, ''N'' is ''k''-connected if-and-only-if ''K'' is ''k''-connected. |
|||
| ⚫ | The basic nerve theorem of [[Jean Leray]] says that, if any intersection of sets in <math>N(C)</math> is [[Contractible space|contractible]] (equivalently: for each finite <math>J\subset I</math> the set <math>\bigcap_{i\in J} U_i</math> is either empty or contractible; equivalently: ''C'' is a [[good cover|good open cover]]), then <math>N(C)</math> is [[homotopy-equivalent]] to '' |
||
=== Čech nerve theorem === |
|||
Another nerve theorem relates to the Čech nerve above: if <math>X</math> is compact and all intersections of sets in ''C'' are contractible or empty, then the space <math>|S(\pi_0(C))|</math> is [[homotopy-equivalent]] to <math>X</math>.<ref>{{nlab|id=nerve+theorem|title=Nerve theorem}}</ref> |
Another nerve theorem relates to the Čech nerve above: if <math>X</math> is compact and all intersections of sets in ''C'' are contractible or empty, then the space <math>|S(\pi_0(C))|</math> is [[homotopy-equivalent]] to <math>X</math>.<ref>{{nlab|id=nerve+theorem|title=Nerve theorem}}</ref> |
||
| Line 46: | Line 60: | ||
[[Category:Topology]] |
[[Category:Topology]] |
||
[[Category:Simplicial sets]] |
[[Category:Simplicial sets]] |
||
[[Category: |
[[Category:Families of sets]] |
||
Latest revision as of 13:29, 7 November 2023
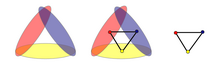
In topology, the nerve complex of a set family is an abstract complex that records the pattern of intersections between the sets in the family. It was introduced by Pavel Alexandrov[1] and now has many variants and generalisations, among them the Čech nerve of a cover, which in turn is generalised by hypercoverings. It captures many of the interesting topological properties in an algorithmic or combinatorial way.[2]
Basic definition
[edit]Let be a set of indices and be a family of sets . The nerve of is a set of finite subsets of the index set . It contains all finite subsets such that the intersection of the whose subindices are in is non-empty:[3]: 81
In Alexandrov's original definition, the sets are open subsets of some topological space .
The set may contain singletons (elements such that is non-empty), pairs (pairs of elements such that ), triplets, and so on. If , then any subset of is also in , making an abstract simplicial complex. Hence N(C) is often called the nerve complex of .
Examples
[edit]- Let X be the circle and , where is an arc covering the upper half of and is an arc covering its lower half, with some overlap at both sides (they must overlap at both sides in order to cover all of ). Then , which is an abstract 1-simplex.
- Let X be the circle and , where each is an arc covering one third of , with some overlap with the adjacent . Then . Note that {1,2,3} is not in since the common intersection of all three sets is empty; so is an unfilled triangle.
The Čech nerve
[edit]Given an open cover of a topological space , or more generally a cover in a site, we can consider the pairwise fibre products , which in the case of a topological space are precisely the intersections . The collection of all such intersections can be referred to as and the triple intersections as .
By considering the natural maps and , we can construct a simplicial object defined by , n-fold fibre product. This is the Čech nerve.[4]
By taking connected components we get a simplicial set, which we can realise topologically: .
Nerve theorems
[edit]The nerve complex is a simple combinatorial object. Often, it is much simpler than the underlying topological space (the union of the sets in ). Therefore, a natural question is whether the topology of is equivalent to the topology of .
In general, this need not be the case. For example, one can cover any n-sphere with two contractible sets and that have a non-empty intersection, as in example 1 above. In this case, is an abstract 1-simplex, which is similar to a line but not to a sphere.
However, in some cases does reflect the topology of X. For example, if a circle is covered by three open arcs, intersecting in pairs as in Example 2 above, then is a 2-simplex (without its interior) and it is homotopy-equivalent to the original circle.[5]
A nerve theorem (or nerve lemma) is a theorem that gives sufficient conditions on C guaranteeing that reflects, in some sense, the topology of . A functorial nerve theorem is a nerve theorem that is functorial in an approriate sense, which is, for example, crucial in topological data analysis.[6]
Leray's nerve theorem
[edit]The basic nerve theorem of Jean Leray says that, if any intersection of sets in is contractible (equivalently: for each finite the set is either empty or contractible; equivalently: C is a good open cover), then is homotopy-equivalent to .
Borsuk's nerve theorem
[edit]There is a discrete version, which is attributed to Borsuk.[7][3]: 81, Thm.4.4.4 Let K1,...,Kn be abstract simplicial complexes, and denote their union by K. Let Ui = ||Ki|| = the geometric realization of Ki, and denote the nerve of {U1, ... , Un } by N.
If, for each nonempty , the intersection is either empty or contractible, then N is homotopy-equivalent to K.
A stronger theorem was proved by Anders Bjorner.[8] if, for each nonempty , the intersection is either empty or (k-|J|+1)-connected, then for every j ≤ k, the j-th homotopy group of N is isomorphic to the j-th homotopy group of K. In particular, N is k-connected if-and-only-if K is k-connected.
Čech nerve theorem
[edit]Another nerve theorem relates to the Čech nerve above: if is compact and all intersections of sets in C are contractible or empty, then the space is homotopy-equivalent to .[9]
Homological nerve theorem
[edit]The following nerve theorem uses the homology groups of intersections of sets in the cover.[10] For each finite , denote the j-th reduced homology group of .
If HJ,j is the trivial group for all J in the k-skeleton of N(C) and for all j in {0, ..., k-dim(J)}, then N(C) is "homology-equivalent" to X in the following sense:
- for all j in {0, ..., k};
- if then .
See also
[edit]References
[edit]- ^ Aleksandroff, P. S. (1928). "Über den allgemeinen Dimensionsbegriff und seine Beziehungen zur elementaren geometrischen Anschauung". Mathematische Annalen. 98: 617–635. doi:10.1007/BF01451612. S2CID 119590045.
- ^ Eilenberg, Samuel; Steenrod, Norman (1952-12-31). Foundations of Algebraic Topology. Princeton: Princeton University Press. doi:10.1515/9781400877492. ISBN 978-1-4008-7749-2.
- ^ a b Matoušek, Jiří (2007). Using the Borsuk-Ulam Theorem: Lectures on Topological Methods in Combinatorics and Geometry (2nd ed.). Berlin-Heidelberg: Springer-Verlag. ISBN 978-3-540-00362-5.
Written in cooperation with Anders Björner and Günter M. Ziegler
, Section 4.3 - ^ "Čech nerve in nLab". ncatlab.org. Retrieved 2020-08-07.
- ^ Artin, Michael; Mazur, Barry (1969). Etale Homotopy. Lecture Notes in Mathematics. Vol. 100. doi:10.1007/bfb0080957. ISBN 978-3-540-04619-6. ISSN 0075-8434.
- ^ Bauer, Ulrich; Kerber, Michael; Roll, Fabian; Rolle, Alexander (2023). "A unified view on the functorial nerve theorem and its variations". Expositiones Mathematicae. arXiv:2203.03571. doi:10.1016/j.exmath.2023.04.005.
- ^ Borsuk, Karol (1948). "On the imbedding of systems of compacta in simplicial complexes". Fundamenta Mathematicae. 35 (1): 217–234. doi:10.4064/fm-35-1-217-234. ISSN 0016-2736.
- ^ Björner, Anders (2003-04-01). "Nerves, fibers and homotopy groups". Journal of Combinatorial Theory. Series A. 102 (1): 88–93. doi:10.1016/S0097-3165(03)00015-3. ISSN 0097-3165.
- ^ Nerve theorem at the nLab
- ^ Meshulam, Roy (2001-01-01). "The Clique Complex and Hypergraph Matching". Combinatorica. 21 (1): 89–94. doi:10.1007/s004930170006. ISSN 1439-6912. S2CID 207006642.





































