Jump to content

Truncated order-6 square tiling: Difference between revisions

From Wikipedia, the free encyclopedia
Browse history interactively
← Previous edit
Content deleted Content added
VisualWikitext
m →References: fix author's name, replaced: Chaim Goodman-Strass → Chaim Goodman-Strauss
 
(31 intermediate revisions by 5 users not shown)
Line 1: Line 1:
{{Uniform hyperbolic tiles db|Uniform hyperbolic tiling stat table|U64_12}}
{{Uniform hyperbolic tiles db|Uniform hyperbolic tiling stat table|U64_12}}
In [[geometry]], the '''truncated order-6 square tiling''' is a uniform tiling of the [[Hyperbolic geometry|hyperbolic plane]]. It has [[Schläfli symbol]] of t<sub>0,1</sub>{4,6}.
In [[geometry]], the '''truncated order-6 square tiling''' is a uniform tiling of the [[Hyperbolic geometry|hyperbolic plane]]. It has [[Schläfli symbol]] of t{4,6}.


== Uniform colorings ==
== Uniform colorings ==


{| class=wikitable
{| class=wikitable width=240
|- valign=top
|- valign=top
|width=120|[[File:Uniform_tiling_443-t012.png|120px]]<BR>The half symmetry [1<sup>+</sup>,6,4] = [(4,4,3)] can be shown with alternating two colors of octagons.
|[[File:Uniform_tiling_443-t012.png|240px]]<BR>The half symmetry [1<sup>+</sup>,6,4] = [(4,4,3)] can be shown with alternating two colors of octagons, with as [[Coxeter diagram]] {{CDD|branch_11|split2-44|node_1}}.
|width=240|[[File:Order4 hexakis hexagonal til.png|120px]][[File:Hyperbolic domains 443.png|120px]]<BR>The dual tiling represents the fundamental domains of the *443 orbifold, shown in two different centers here.
|}
|}


== Symmetry ==
== Symmetry ==
[[File:Truncated_order-6_square_tiling_with_mirrors.png|thumb|left|Truncated order-6 square tiling with *443 symmetry mirror lines]]
⚫
The dual tiling represents the fundamental domains of the *443 orbifold symmetry. There are two reflective subgroup kaleidoscopic constructed from [(4,4,3)] by removing one or two of three mirrors. In these images fundamental domains are alternately colored black and cyan, and mirrors exist on the boundaries between colors.


A larger subgroup is constructed [(4,4,3*)], index 6, as (3*22) with gyration points removed, becomes (*222222).
⚫
The dual tiling represents the fundamental domains of the *443 orbifold symmetry. There are two reflective subgroup kaleidoscopic constructed from [(4,4,3)] by removing one or two of three mirrors. In these images fundamental domains are alternately colored black and white, and mirrors exist on the boundaries between colors. The symmetry can be doubled as [[642 symmetry]] by adding a mirror bisecting the fundamental domain.


The symmetry can be doubled as [[642 symmetry]] by adding a mirror bisecting the fundamental domain.
⚫
{| class=wikitable
{{-}}
⚫
|+ Small index subgroup symmetries of [(4,4,3)] (*443)
⚫
{| class="wikitable collapsible collapsed"
⚫
!colspan=12| Small index subgroups of [(4,4,3)] (*443)
|- align=center
|- align=center
⚫
![[Subgroup index|Index]]
!Fundamental<BR>domains
|[[File:443 symmetry mirrors.png|120px]]
|[[File:H2chess 344d.png|120px]][[File:H2chess 344a.png|120px]]
⚫
|- align=center
⚫
!Subgroup index
!1
!1
!colspan=2|2
!2
!6
|-
⚫
!rowspan=2|[[Coxeter notation|Coxeter]]<BR>([[Orbifold notation|orbifold]])
!rowspan=2|[(4,4,3)]<BR>(*443)
![(4,1<sup>+</sup>,4,3)]<BR>([[3232 symmetry|*3232]])
|- align=center
|- align=center
!Diagram
⚫
![(4,4,3<sup>+</sup>)]<BR>(3*22)
|[[File:443_symmetry_000.png|150px]]
|[[File:443_symmetry_0a0.png|150px]]
|[[File:443_symmetry_a0a.png|150px]]
|[[File:443_symmetry_z0z.png|150px]]
⚫
|- align=center
⚫
![[Coxeter notation|Coxeter]]<BR>([[Orbifold notation|orbifold]])
|[(4,4,3)] = {{CDD|node_c1|split1-44|branch_c2}}<BR>(*443)
|[(4,1<sup>+</sup>,4,3)] = {{CDD|labelh|node|split1-44|branch_c2}} = {{CDD|branch_c2|2a2b-cross|branch_c2}}<BR>([[3232 symmetry|*3232]])
⚫
|[(4,4,3<sup>+</sup>)] = {{CDD|node_c1|split1-44|branch_h2h2}}<BR>(3*22)
|[(4,4,3*)] = {{CDD|node_c1|split1-44|branch|labels}}<BR>([[222222 symmetry|*222222]])
|-
|-
!colspan=3|Rotation subgroups
!colspan=5|Direct subgroups
|- align=center
|- align=center
!Index
!Subgroup index
!2
!2
!colspan=2|4
!colspan=2|4
!12
|-
|- align=center
⚫
!Rotation subgroup<BR>Coxeter<BR>(orbifold)
!Diagram
⚫
![(4,4,3)]<sup>+</sup><BR>(443)
|[[File:443_symmetry_aaa.png|150px]]
!colspan=2|[(4,1<sup>+</sup>,4,3<sup>+</sup>)]<BR>(3232)
|colspan=2|[[File:443_symmetry_abc.png|150px]]
|[[File:443_symmetry_zaz.png|150px]]
|- align=center
⚫
!Coxeter<BR>(orbifold)
⚫
|[(4,4,3)]<sup>+</sup> = {{CDD|node_h2|split1-44|branch_h2h2}}<BR>(443)
|colspan=2|[(4,4,3<sup>+</sup>)]<sup>+</sup> = {{CDD|labelh|node|split1-44|branch_h2h2}} = {{CDD|branch_h2h2|2xa2xb-cross|branch_h2h2}}<BR>(3232)
|[(4,4,3*)]<sup>+</sup> = {{CDD|node_h2|split1-44|branch|labels}}<BR>(222222)
|}
|}


== Related polyhedra and tiling ==
== Related polyhedra and tilings ==
From a [[Wythoff construction]] there are eight hyperbolic [[Uniform tilings in hyperbolic plane|uniform tilings]] that can be based from the regular order-4 hexagonal tiling.
From a [[Wythoff construction]] there are eight hyperbolic [[Uniform tilings in hyperbolic plane|uniform tilings]] that can be based from the regular order-4 hexagonal tiling.


Line 52: Line 65:


{{Truncated figure4 table}}
{{Truncated figure4 table}}
{{Omnitruncated34 table}}


==See also==
==See also==
{{Commonscat|Uniform tiling 6-8-8}}
*[[Square tiling]]
*[[Square tiling]]
*[[Tilings of regular polygons]]
*[[Tilings of regular polygons]]
Line 60: Line 75:


==References==
==References==
* [[John Horton Conway|John H. Conway]], Heidi Burgiel, Chaim Goodman-Strass, ''The Symmetries of Things'' 2008, ISBN 978-1-56881-220-5 (Chapter 19, The Hyperbolic Archimedean Tessellations)
* [[John Horton Conway|John H. Conway]], Heidi Burgiel, Chaim Goodman-Strauss, ''The Symmetries of Things'' 2008, {{isbn|978-1-56881-220-5}} (Chapter 19, The Hyperbolic Archimedean Tessellations)
* {{Cite book|title=The Beauty of Geometry: Twelve Essays|year=1999|publisher=Dover Publications|lccn=99035678|isbn=0-486-40919-8|chapter=Chapter 10: Regular honeycombs in hyperbolic space}}
* {{Cite book|title=The Beauty of Geometry: Twelve Essays|year=1999|publisher=Dover Publications|lccn=99035678|isbn=0-486-40919-8|chapter=Chapter 10: Regular honeycombs in hyperbolic space}}


Line 70: Line 85:
* [http://www.plunk.org/~hatch/HyperbolicTesselations Hyperbolic Planar Tessellations, Don Hatch]
* [http://www.plunk.org/~hatch/HyperbolicTesselations Hyperbolic Planar Tessellations, Don Hatch]


[[Category:Tessellation]]
{{Tessellation}}

[[Category:Hyperbolic tilings]]
[[Category:Isogonal tilings]]
[[Category:Order-6 tilings]]
[[Category:Square tilings]]
[[Category:Truncated tilings]]
[[Category:Uniform tilings]]

Latest revision as of 21:58, 12 December 2023

Truncated order-6 square tiling
Truncated order-6 square tiling
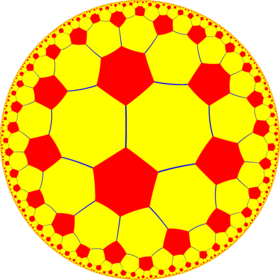Poincaré disk model of the hyperbolic plane
Type Hyperbolic uniform tiling
Vertex configuration 8.8.6
Schläfli symbol t{4,6}
Wythoff symbol 2 6 | 4
Coxeter diagram
Symmetry group [6,4], (*642)
[(3,3,4)], (*334)
Dual Order-4 hexakis hexagonal tiling
Properties Vertex-transitive

In geometry, the truncated order-6 square tiling is a uniform tiling of the hyperbolic plane. It has Schläfli symbol of t{4,6}.

Uniform colorings

[edit]

The half symmetry [1+,6,4] = [(4,4,3)] can be shown with alternating two colors of octagons, with as Coxeter diagram .

Symmetry

[edit]
Truncated order-6 square tiling with *443 symmetry mirror lines

The dual tiling represents the fundamental domains of the *443 orbifold symmetry. There are two reflective subgroup kaleidoscopic constructed from [(4,4,3)] by removing one or two of three mirrors. In these images fundamental domains are alternately colored black and cyan, and mirrors exist on the boundaries between colors.

A larger subgroup is constructed [(4,4,3*)], index 6, as (3*22) with gyration points removed, becomes (*222222).

The symmetry can be doubled as 642 symmetry by adding a mirror bisecting the fundamental domain.

[edit]

From a Wythoff construction there are eight hyperbolic uniform tilings that can be based from the regular order-4 hexagonal tiling.

Drawing the tiles colored as red on the original faces, yellow at the original vertices, and blue along the original edges, there are 8 forms.

Uniform tetrahexagonal tilings
Symmetry: [6,4], (*642)
(with [6,6] (*662), [(4,3,3)] (*443) , [∞,3,∞] (*3222) index 2 subsymmetries)
(And [(∞,3,∞,3)] (*3232) index 4 subsymmetry)

=

=
=
=
=
=

=

=

=
=
=


=
{6,4} t{6,4} r{6,4} t{4,6} {4,6} rr{6,4} tr{6,4}
Uniform duals
V64 V4.12.12 V(4.6)2 V6.8.8 V46 V4.4.4.6 V4.8.12
Alternations
[1+,6,4]
(*443) 		[6+,4]
(6*2) 		[6,1+,4]
(*3222) 		[6,4+]
(4*3) 		[6,4,1+]
(*662) 		[(6,4,2+)]
(2*32) 		[6,4]+
(642)

=
=
=
=
=
=
h{6,4} s{6,4} hr{6,4} s{4,6} h{4,6} hrr{6,4} sr{6,4}

It can also be generated from the (4 4 3) hyperbolic tilings:

Uniform (4,4,3) tilings
Symmetry: [(4,4,3)] (*443) [(4,4,3)]+
(443) 		[(4,4,3+)]
(3*22) 		[(4,1+,4,3)]
(*3232)
h{6,4}
t0(4,4,3) 		h2{6,4}
t0,1(4,4,3) 		{4,6}1/2
t1(4,4,3) 		h2{6,4}
t1,2(4,4,3) 		h{6,4}
t2(4,4,3) 		r{6,4}1/2
t0,2(4,4,3) 		t{4,6}1/2
t0,1,2(4,4,3) 		s{4,6}1/2
s(4,4,3) 		hr{4,6}1/2
hr(4,3,4) 		h{4,6}1/2
h(4,3,4) 		q{4,6}
h1(4,3,4)
Uniform duals
V(3.4)4 V3.8.4.8 V(4.4)3 V3.8.4.8 V(3.4)4 V4.6.4.6 V6.8.8 V3.3.3.4.3.4 V(4.4.3)2 V66 V4.3.4.6.6
*n42 symmetry mutation of truncated tilings: n.8.8
Symmetry
*n42
[n,4] 		Spherical Euclidean Compact hyperbolic Paracompact
*242
[2,4] 		*342
[3,4] 		*442
[4,4] 		*542
[5,4] 		*642
[6,4] 		*742
[7,4] 		*842
[8,4]... 		*∞42
[∞,4]
Truncated
figures
Config. 2.8.8 3.8.8 4.8.8 5.8.8 6.8.8 7.8.8 8.8.8 ∞.8.8
n-kis
figures
Config. V2.8.8 V3.8.8 V4.8.8 V5.8.8 V6.8.8 V7.8.8 V8.8.8 V∞.8.8
*n32 symmetry mutation of omnitruncated tilings: 6.8.2n
Sym.
*n43
[(n,4,3)] 		Spherical Compact hyperbolic Paraco.
*243
[4,3] 		*343
[(3,4,3)] 		*443
[(4,4,3)] 		*543
[(5,4,3)] 		*643
[(6,4,3)] 		*743
[(7,4,3)] 		*843
[(8,4,3)] 		*∞43
[(∞,4,3)]
Figures
Config. 4.8.6 6.8.6 8.8.6 10.8.6 12.8.6 14.8.6 16.8.6 ∞.8.6
Duals
Config. V4.8.6 V6.8.6 V8.8.6 V10.8.6 V12.8.6 V14.8.6 V16.8.6 V6.8.∞

See also

[edit]
Wikimedia Commons has media related to Uniform tiling 6-8-8.

References

[edit]
  • John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 19, The Hyperbolic Archimedean Tessellations)
  • "Chapter 10: Regular honeycombs in hyperbolic space". The Beauty of Geometry: Twelve Essays. Dover Publications. 1999. ISBN 0-486-40919-8. LCCN 99035678.
[edit]
Retrieved from "https://en.wikipedia.org/enwiki/w/index.php?title=Truncated_order-6_square_tiling&oldid=1189602105"