Truncated order-6 square tiling: Difference between revisions
m →References: fix author's name, replaced: Chaim Goodman-Strass → Chaim Goodman-Strauss |
|||
| (9 intermediate revisions by 4 users not shown) | |||
| Line 4: | Line 4: | ||
== Uniform colorings == |
== Uniform colorings == |
||
{| class=wikitable |
{| class=wikitable width=240 |
||
|- valign=top |
|- valign=top |
||
|[[File:Uniform_tiling_443-t012.png|240px]]<BR>The half symmetry [1<sup>+</sup>,6,4] = [(4,4,3)] can be shown with alternating two colors of octagons, with as [[Coxeter diagram]] {{CDD|branch_11|split2-44|node_1}}. |
|||
|width=240|[[File:Order4 hexakis hexagonal til.png|120px]][[File:Hyperbolic domains 443.png|120px]]<BR>The dual tiling represents the fundamental domains of the *443 orbifold, shown in two different centers here. |
|||
|} |
|} |
||
== Symmetry == |
== Symmetry == |
||
[[File:Truncated_order-6_square_tiling_with_mirrors.png|thumb|left|Truncated order-6 square tiling with *443 symmetry mirror lines]] |
[[File:Truncated_order-6_square_tiling_with_mirrors.png|thumb|left|Truncated order-6 square tiling with *443 symmetry mirror lines]] |
||
The dual tiling represents the fundamental domains of the *443 orbifold symmetry. There are two reflective subgroup kaleidoscopic constructed from [(4,4,3)] by removing one or two of three mirrors. In these images fundamental domains are alternately colored black and cyan, and mirrors exist on the boundaries between colors. |
The dual tiling represents the fundamental domains of the *443 orbifold symmetry. There are two reflective subgroup kaleidoscopic constructed from [(4,4,3)] by removing one or two of three mirrors. In these images fundamental domains are alternately colored black and cyan, and mirrors exist on the boundaries between colors. |
||
A larger subgroup is constructed [(4,4,3*)], index 6, as (3*22) with gyration points removed, becomes (*222222). |
A larger subgroup is constructed [(4,4,3*)], index 6, as (3*22) with gyration points removed, becomes (*222222). |
||
The symmetry can be doubled as [[642 symmetry]] by adding a mirror bisecting the fundamental domain. |
|||
{{-}} |
{{-}} |
||
{| class=wikitable |
{| class="wikitable collapsible collapsed" |
||
| |
!colspan=12| Small index subgroups of [(4,4,3)] (*443) |
||
|- align=center |
|- align=center |
||
![[Subgroup index|Index]] |
![[Subgroup index|Index]] |
||
| Line 31: | Line 32: | ||
|- align=center |
|- align=center |
||
![[Coxeter notation|Coxeter]]<BR>([[Orbifold notation|orbifold]]) |
![[Coxeter notation|Coxeter]]<BR>([[Orbifold notation|orbifold]]) |
||
|[(4,4,3)] |
|[(4,4,3)] = {{CDD|node_c1|split1-44|branch_c2}}<BR>(*443) |
||
|[(4,1<sup>+</sup>,4,3)] |
|[(4,1<sup>+</sup>,4,3)] = {{CDD|labelh|node|split1-44|branch_c2}} = {{CDD|branch_c2|2a2b-cross|branch_c2}}<BR>([[3232 symmetry|*3232]]) |
||
|[(4,4,3<sup>+</sup>)] |
|[(4,4,3<sup>+</sup>)] = {{CDD|node_c1|split1-44|branch_h2h2}}<BR>(3*22) |
||
|[(4,4,3*)] |
|[(4,4,3*)] = {{CDD|node_c1|split1-44|branch|labels}}<BR>([[222222 symmetry|*222222]]) |
||
|- |
|- |
||
!colspan=5|Direct subgroups |
!colspan=5|Direct subgroups |
||
| Line 49: | Line 50: | ||
|- align=center |
|- align=center |
||
!Coxeter<BR>(orbifold) |
!Coxeter<BR>(orbifold) |
||
|[(4,4,3)]<sup>+</sup> |
|[(4,4,3)]<sup>+</sup> = {{CDD|node_h2|split1-44|branch_h2h2}}<BR>(443) |
||
|colspan=2|[(4,4,3<sup>+</sup>)]<sup>+</sup> |
|colspan=2|[(4,4,3<sup>+</sup>)]<sup>+</sup> = {{CDD|labelh|node|split1-44|branch_h2h2}} = {{CDD|branch_h2h2|2xa2xb-cross|branch_h2h2}}<BR>(3232) |
||
|[(4,4,3*)]<sup>+</sup> |
|[(4,4,3*)]<sup>+</sup> = {{CDD|node_h2|split1-44|branch|labels}}<BR>(222222) |
||
|} |
|} |
||
== Related polyhedra and |
== Related polyhedra and tilings == |
||
From a [[Wythoff construction]] there are eight hyperbolic [[Uniform tilings in hyperbolic plane|uniform tilings]] that can be based from the regular order-4 hexagonal tiling. |
From a [[Wythoff construction]] there are eight hyperbolic [[Uniform tilings in hyperbolic plane|uniform tilings]] that can be based from the regular order-4 hexagonal tiling. |
||
| Line 64: | Line 65: | ||
{{Truncated figure4 table}} |
{{Truncated figure4 table}} |
||
{{Omnitruncated34 table}} |
|||
==See also== |
==See also== |
||
| Line 73: | Line 75: | ||
==References== |
==References== |
||
* [[John Horton Conway|John H. Conway]], Heidi Burgiel, Chaim Goodman- |
* [[John Horton Conway|John H. Conway]], Heidi Burgiel, Chaim Goodman-Strauss, ''The Symmetries of Things'' 2008, {{isbn|978-1-56881-220-5}} (Chapter 19, The Hyperbolic Archimedean Tessellations) |
||
* {{Cite book|title=The Beauty of Geometry: Twelve Essays|year=1999|publisher=Dover Publications|lccn=99035678|isbn=0-486-40919-8|chapter=Chapter 10: Regular honeycombs in hyperbolic space}} |
* {{Cite book|title=The Beauty of Geometry: Twelve Essays|year=1999|publisher=Dover Publications|lccn=99035678|isbn=0-486-40919-8|chapter=Chapter 10: Regular honeycombs in hyperbolic space}} |
||
| Line 88: | Line 90: | ||
[[Category:Isogonal tilings]] |
[[Category:Isogonal tilings]] |
||
[[Category:Order-6 tilings]] |
[[Category:Order-6 tilings]] |
||
[[Category:Square tilings]] |
|||
[[Category:Truncated tilings]] |
[[Category:Truncated tilings]] |
||
[[Category:Uniform tilings]] |
[[Category:Uniform tilings]] |
||
Latest revision as of 21:58, 12 December 2023
| Truncated order-6 square tiling | |
|---|---|
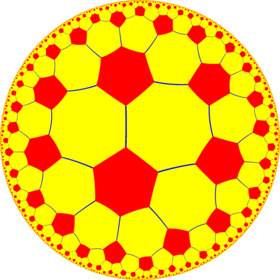 Poincaré disk model of the hyperbolic plane | |
| Type | Hyperbolic uniform tiling |
| Vertex configuration | 8.8.6 |
| Schläfli symbol | t{4,6} |
| Wythoff symbol | 2 6 | 4 |
| Coxeter diagram | |
| Symmetry group | [6,4], (*642) [(3,3,4)], (*334) |
| Dual | Order-4 hexakis hexagonal tiling |
| Properties | Vertex-transitive |
In geometry, the truncated order-6 square tiling is a uniform tiling of the hyperbolic plane. It has Schläfli symbol of t{4,6}.
Uniform colorings
[edit] The half symmetry [1+,6,4] = [(4,4,3)] can be shown with alternating two colors of octagons, with as Coxeter diagram |
Symmetry
[edit]
The dual tiling represents the fundamental domains of the *443 orbifold symmetry. There are two reflective subgroup kaleidoscopic constructed from [(4,4,3)] by removing one or two of three mirrors. In these images fundamental domains are alternately colored black and cyan, and mirrors exist on the boundaries between colors.
A larger subgroup is constructed [(4,4,3*)], index 6, as (3*22) with gyration points removed, becomes (*222222).
The symmetry can be doubled as 642 symmetry by adding a mirror bisecting the fundamental domain.
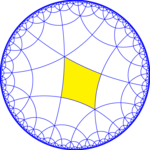
| Small index subgroups of [(4,4,3)] (*443) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Index | 1 | 2 | 6 | ||||||||
| Diagram | 
|
|

|

| |||||||
| Coxeter (orbifold) |
[(4,4,3)] = (*443) |
[(4,1+,4,3)] = (*3232) |
[(4,4,3+)] = (3*22) |
[(4,4,3*)] = (*222222) | |||||||
| Direct subgroups | |||||||||||
| Index | 2 | 4 | 12 | ||||||||
| Diagram | 
|

|

| ||||||||
| Coxeter (orbifold) |
[(4,4,3)]+ = (443) |
[(4,4,3+)]+ = (3232) |
[(4,4,3*)]+ = (222222) | ||||||||
Related polyhedra and tilings
[edit]From a Wythoff construction there are eight hyperbolic uniform tilings that can be based from the regular order-4 hexagonal tiling.
Drawing the tiles colored as red on the original faces, yellow at the original vertices, and blue along the original edges, there are 8 forms.
| Uniform tetrahexagonal tilings | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry: [6,4], (*642) (with [6,6] (*662), [(4,3,3)] (*443) , [∞,3,∞] (*3222) index 2 subsymmetries) (And [(∞,3,∞,3)] (*3232) index 4 subsymmetry) | |||||||||||
= = = |
= |
= = = |
= |
= = = |
= |
||||||

|

|

|
|

|

|

| |||||
| {6,4} | t{6,4} | r{6,4} | t{4,6} | {4,6} | rr{6,4} | tr{6,4} | |||||
| Uniform duals | |||||||||||

|

|

|

|

|

|

| |||||
| V64 | V4.12.12 | V(4.6)2 | V6.8.8 | V46 | V4.4.4.6 | V4.8.12 | |||||
| Alternations | |||||||||||
| [1+,6,4] (*443) |
[6+,4] (6*2) |
[6,1+,4] (*3222) |
[6,4+] (4*3) |
[6,4,1+] (*662) |
[(6,4,2+)] (2*32) |
[6,4]+ (642) | |||||
= |
= |
= |
= |
= |
= |
||||||

|

|

|

|

|

|

| |||||
| h{6,4} | s{6,4} | hr{6,4} | s{4,6} | h{4,6} | hrr{6,4} | sr{6,4} | |||||
It can also be generated from the (4 4 3) hyperbolic tilings:
| Uniform (4,4,3) tilings | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry: [(4,4,3)] (*443) | [(4,4,3)]+ (443) |
[(4,4,3+)] (3*22) |
[(4,1+,4,3)] (*3232) | |||||||

|

|

|

|

|

|

|

|

|

|

|
| h{6,4} t0(4,4,3) |
h2{6,4} t0,1(4,4,3) |
{4,6}1/2 t1(4,4,3) |
h2{6,4} t1,2(4,4,3) |
h{6,4} t2(4,4,3) |
r{6,4}1/2 t0,2(4,4,3) |
t{4,6}1/2 t0,1,2(4,4,3) |
s{4,6}1/2 s(4,4,3) |
hr{4,6}1/2 hr(4,3,4) |
h{4,6}1/2 h(4,3,4) |
q{4,6} h1(4,3,4) |
| Uniform duals | ||||||||||

|

|

|

|
|||||||
| V(3.4)4 | V3.8.4.8 | V(4.4)3 | V3.8.4.8 | V(3.4)4 | V4.6.4.6 | V6.8.8 | V3.3.3.4.3.4 | V(4.4.3)2 | V66 | V4.3.4.6.6 |
| *n42 symmetry mutation of truncated tilings: n.8.8 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry *n42 [n,4] |
Spherical | Euclidean | Compact hyperbolic | Paracompact | |||||||
| *242 [2,4] |
*342 [3,4] |
*442 [4,4] |
*542 [5,4] |
*642 [6,4] |
*742 [7,4] |
*842 [8,4]... |
*∞42 [∞,4] | ||||
| Truncated figures |

|

|

|

|

|

|

|

| |||
| Config. | 2.8.8 | 3.8.8 | 4.8.8 | 5.8.8 | 6.8.8 | 7.8.8 | 8.8.8 | ∞.8.8 | |||
| n-kis figures |

|

|

|

|

|

|

|

| |||
| Config. | V2.8.8 | V3.8.8 | V4.8.8 | V5.8.8 | V6.8.8 | V7.8.8 | V8.8.8 | V∞.8.8 | |||
| *n32 symmetry mutation of omnitruncated tilings: 6.8.2n | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sym. *n43 [(n,4,3)] |
Spherical | Compact hyperbolic | Paraco. | |||||||||
| *243 [4,3] |
*343 [(3,4,3)] |
*443 [(4,4,3)] |
*543 [(5,4,3)] |
*643 [(6,4,3)] |
*743 [(7,4,3)] |
*843 [(8,4,3)] |
*∞43 [(∞,4,3)] | |||||
| Figures | 
|

|

|

|

|

|

|

| ||||
| Config. | 4.8.6 | 6.8.6 | 8.8.6 | 10.8.6 | 12.8.6 | 14.8.6 | 16.8.6 | ∞.8.6 | ||||
| Duals | 
|

|

|

|

|

|

|

| ||||
| Config. | V4.8.6 | V6.8.6 | V8.8.6 | V10.8.6 | V12.8.6 | V14.8.6 | V16.8.6 | V6.8.∞ | ||||
See also
[edit]References
[edit]- John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 19, The Hyperbolic Archimedean Tessellations)
- "Chapter 10: Regular honeycombs in hyperbolic space". The Beauty of Geometry: Twelve Essays. Dover Publications. 1999. ISBN 0-486-40919-8. LCCN 99035678.


