Deferred measurement principle: Difference between revisions
image now vector graphic |
m derp |
||
| (14 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| ⚫ | |||
{{multiple image |
|||
{{Orphan|date=August 2017}} |
|||
|direction=vertical |
|||
| width = 400 |
|||
| footer = '''Example:''' Two variants of the [[Quantum_teleportation#Alternative_notations|teleportation circuit]]. The 2-[[qubit]] [[quantum state|state]]s <math>|\Phi^{+}\rangle</math> and <math>|\beta_{00}\rangle</math> refer to the same [[Bell state]]. |
|||
| image1 = Quantum_teleportation_circuit.svg |
|||
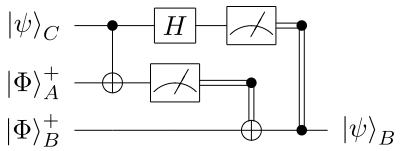
| caption1 = Measurement is performed early and the resulting classical bits are sent. The classical bits control if the 1-qubit [[quantum logic gate#X|X]] and [[quantum logic gate#Z|Z]] gates are executed, allowing teleportation.<ref>{{Cite book|title=Quantum Computation and Quantum Information|last1=Nielsen|first1=Michael A.|last2=Chuang|first2=Isaac|date=2010|publisher=[[Cambridge University Press]]|isbn=978-1-10700-217-3|location=Cambridge|oclc=43641333|author-link=Michael Nielsen|author-link2=Isaac Chuang|url=https://www.cambridge.org/9781107002173|pages=26–28}}</ref> |
|||
| image2 = AltTeleport.jpg |
|||
| caption2 = By moving the measurement to the end, the 2-qubit [[quantum logic gate#Controlled gates|controlled]]-X and -Z gates need to be applied, which requires both qubits to be near (i.e. at a distance where 2-qubit quantum effects can be controlled), and thus limits the distance of the teleportion. While logically equivalent, deferring the measurement have physical implications. |
|||
}} |
|||
| ⚫ | The '''deferred measurement principle''' is a result in [[quantum computing]] which states that delaying measurements until the end of a quantum computation doesn't affect the [[probability distribution]] of outcomes.<ref name="NielsenChuang2010">{{cite book|author1=Michael A. Nielsen|author2=Isaac L. Chuang|title=Quantum Computation and Quantum Information: 10th Anniversary Edition|url=https://books.google.com/books?id=-s4DEy7o-a0C|date=9 December 2010|publisher=Cambridge University Press|isbn=978-1-139-49548-6 |page=186 |section=4.4 Measurement}}</ref><ref name="Cross2012">{{cite book|author=Odel A. Cross|title=Topics in Quantum Computing|url=https://books.google.com/books?id=b_D9flK2h8QC&pg=PA348|date=5 November 2012|publisher=O. A. Cross|isbn=978-1-4800-2749-7|page=348 |section=5.2.2 Deferred Measurement}}</ref> |
||
| ⚫ | |||
| ⚫ | The ''' |
||
A consequence of the deferred measurement principle is that measuring commutes with conditioning. |
A consequence of the deferred measurement principle is that measuring commutes with conditioning. |
||
| Line 18: | Line 24: | ||
[[Category:Quantum information science]] |
[[Category:Quantum information science]] |
||
{{quantum-stub}} |
{{quantum-stub}} |
||
Latest revision as of 19:31, 6 February 2024

The deferred measurement principle is a result in quantum computing which states that delaying measurements until the end of a quantum computation doesn't affect the probability distribution of outcomes.[2][3]
A consequence of the deferred measurement principle is that measuring commutes with conditioning. The choice of whether to measure a qubit before, after, or during an operation conditioned on that qubit will have no observable effect on a circuit's final expected results.
Thanks to the deferred measurement principle, measurements in a quantum circuit can often be shifted around so they happen at better times. For example, measuring qubits as early as possible can reduce the maximum number of simultaneously stored qubits; potentially enabling an algorithm to be run on a smaller quantum computer or to be simulated more efficiently. Alternatively, deferring all measurements until the end of circuits allows them to be analyzed using only pure states.
References
[edit]- ^ Nielsen, Michael A.; Chuang, Isaac (2010). Quantum Computation and Quantum Information. Cambridge: Cambridge University Press. pp. 26–28. ISBN 978-1-10700-217-3. OCLC 43641333.
- ^ Michael A. Nielsen; Isaac L. Chuang (9 December 2010). "4.4 Measurement". Quantum Computation and Quantum Information: 10th Anniversary Edition. Cambridge University Press. p. 186. ISBN 978-1-139-49548-6.
- ^ Odel A. Cross (5 November 2012). "5.2.2 Deferred Measurement". Topics in Quantum Computing. O. A. Cross. p. 348. ISBN 978-1-4800-2749-7.