Talk:Section formula: Difference between revisions
Appearance
Content deleted Content added
No edit summary Tags: Mobile edit Mobile web edit Advanced mobile edit |
m Maintain {{WPBS}}: 2 WikiProject templates. Remove 1 deprecated parameter: field. Tag: |
||
| (8 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
{{WikiProject |
{{WikiProject banner shell|class=Stub| |
||
{{WikiProject Mathematics|importance=low}} |
|||
{{maths rating}} |
|||
{{WikiProject Articles for creation|ts=20201004055349|reviewer=Buidhe|oldid=974134955}} |
|||
}} |
|||
== Someone Deleted this == |
|||
===Coordinates of centroid=== |
|||
[[File:Mediane.JPG|thumb|Centroid of a triangle]] |
|||
The centroid of a triangle is the intersection of the [[Medians of a triangle|medians]] and divides each median in the ratio <math display="inline">2:1</math>. Let the vertices of the triangle be <math>A(x_1, y_1)</math>, <math display="inline">B(x_2, y_2)</math> and <math display="inline">C(x_3, y_3)</math>. So, a median from point A will intersect BC at <math display="inline">\left(\frac{x_2 + x_3}{2}, \frac{y_2 + y_3}{2}\right)</math>. Using the section formula, the centroid becomes: |
|||
<math display="block"> |
|||
G = \left(\frac{x_1 + x_2 + x_3}{3}, \frac{y_1 + y_2 + y_3}{3} \right) |
|||
</math> |
|||
=== Coordinates of incenter === |
|||
[[File:Inner center triangle proof.svg]] |
|||
Let the sides of a triangle be <math display="inline">a</math>, <math display="inline">b</math> and <math display="inline">c</math> its vertices are <math display="inline">A(x_1, y_1)</math>, <math display="inline">B(x_2, y_2)</math> and <math display="inline">C(x_3, y_3)</math>. The [[Incenter|Incentre]] (intersection of the [[angle bisectors]]) divides the angle bisectors in the ratio <math display="inline">(b+c):a</math>, <math display="inline">(a+c):b</math> and <math display="inline">(a+b):c</math>. An angle bisector also divides the opposite side in the ratio of the adjacent sides ([[Angle bisector theorem]]). So they meet at <math display="inline">\left(\frac{bx_2+cx_3}{b+c}, \frac{by_2+cy_3}{b+c}\right)</math>. Thus, the incenter is |
|||
<math display="block"> |
|||
I = \left(\frac{ax_1 + bx_2 + cx_3}{a+b+c}, \frac{ay_1 + by_2 + cy_3}{a+b+c} \right) |
|||
</math> |
|||
This is essentially the weighted average of the vertices. |
|||
[[User:Shubhrajit Sadhukhan|Shubhrajit Sadhukhan]] ([[User talk:Shubhrajit Sadhukhan|talk]]) 13:25, 7 November 2020 (UTC) |
|||
Latest revision as of 04:37, 9 March 2024
| This article is rated Stub-class on Wikipedia's content assessment scale. It is of interest to the following WikiProjects: | |||||||||||||||||||||
| |||||||||||||||||||||
Someone Deleted this
[edit]Coordinates of centroid
[edit]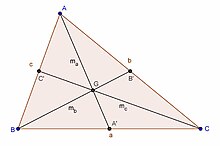
The centroid of a triangle is the intersection of the medians and divides each median in the ratio . Let the vertices of the triangle be , and . So, a median from point A will intersect BC at . Using the section formula, the centroid becomes:
Coordinates of incenter
[edit]Let the sides of a triangle be , and its vertices are , and . The Incentre (intersection of the angle bisectors) divides the angle bisectors in the ratio , and . An angle bisector also divides the opposite side in the ratio of the adjacent sides (Angle bisector theorem). So they meet at . Thus, the incenter is
This is essentially the weighted average of the vertices.



















