Ionian mode: Difference between revisions
Reverted 1 edit by 68.116.207.182 (talk): Unnecessary |
|||
| (52 intermediate revisions by 36 users not shown) | |||
| Line 1: | Line 1: | ||
{{Short description|Musical mode}} |
|||
[[Image:Ionian mode C.png|thumb|right|300px|Ionian mode on C {{audio|Ionian mode C.mid|Play}}.]] |
|||
{{Thumb|content=<score sound="1"> { |
|||
\override Score.TimeSignature #'stencil = ##f |
|||
\relative c' { |
|||
\clef treble \time 7/4 |
|||
c4^\markup { C Ionian scale } d e f g a b c |
|||
} } |
|||
</score>}} |
|||
The '''Ionian mode''' is a [[Mode (music)|musical mode]] or, in modern usage, a [[diatonic scale]] also called the [[major scale]]. It is named after the [[Ionians|Ionian Greeks]]. |
|||
It is the name assigned by [[Heinrich Glarean]] in 1547 to his new [[Gregorian mode#Authentic mode|authentic mode]] on C (mode 11 in his numbering scheme), which uses the [[diatonic]] [[octave species]] from C to the C an octave higher, divided at G (as its dominant, [[reciting tone]]/reciting note or ''tenor'') into a fourth species of [[perfect fifth]] (tone–tone–semitone–tone) plus a third species of [[perfect fourth]] (tone–tone–semitone): C D E F G + G A B C.<ref>{{harv|Powers|2001a}}</ref> This octave species is essentially the same as the [[Major scale|major mode]] of [[tonal music]].<ref>{{harv|Jones|1974|loc=42}}</ref> |
|||
Church music |
Church music had been explained by theorists as being organised in eight [[Mode (music)|musical modes]]: the scales on D, E, F, and G in the "greater perfect system" of "musica recta,"<ref>{{harv|Powers|2001b|loc=§II: "Medieval Modal Theory"}}</ref> each with their [[authentic mode|authentic]] and [[plagal mode|plagal]] counterparts. |
||
Glarean's twelfth mode was the plagal version of the Ionian mode, called [[Hypoionian mode|Hypoionian]] (under Ionian), based on the same relative scale, but with the [[major third]] as its ''tenor'', and having a melodic range from a [[perfect fourth]] below the tonic, to a [[perfect fifth]] above it |
Glarean's twelfth mode was the plagal version of the Ionian mode, called [[Hypoionian mode|Hypoionian]] (under Ionian), based on the same relative scale, but with the [[major third]] as its ''tenor'', and having a melodic range from a [[perfect fourth]] below the tonic, to a [[perfect fifth]] above it.<ref>{{harv|Powers|2001c}}</ref> |
||
== |
==See also== |
||
*[[Bilawal]], the equivalent scale ([[thaat]]) in [[Hindustani music]] |
|||
| ⚫ | * |
||
*[[Sankarabharanam (raga)|Shankarabharanam]], the equivalent scale ([[melakarta]]) in [[Carnatic music]] |
|||
| ⚫ | * Powers, Harold S. 2001a. "Ionian". ''The New Grove Dictionary of Music and Musicians'', |
||
| ⚫ | |||
==Notes== |
|||
| ⚫ | |||
{{reflist|22em}} |
|||
===References=== |
|||
| ⚫ | *{{wikicite|ref={{harvid|Jones|1974}}|reference=Jones, George Thaddeus. 1974. "Medieval Church Modes", in his ''Music Theory: The Fundamental Concepts of Tonal Music, Including Notation, Terminology, and Harmony'', 42–43. Barnes & Noble Outline Series 137. New York, Hagerstown, San Francisco, London: Barnes & Noble Books; Toronto: Fitzhenry & Whiteside. {{ISBN|0-06-460137-4|0-06-467168-2}} {{OCLC|834716}}}} |
||
| ⚫ | * {{wikicite|ref={{harvid|Powers|2001a}}|reference=[[Harold Powers|Powers, Harold S.]] 2001a. "Ionian". ''[[The New Grove Dictionary of Music and Musicians]]'', 2nd edition, 29 vols., edited by [[Stanley Sadie]] and [[John Tyrrell (musicologist)|John Tyrrell]], 12:{{Page needed|date=June 2009}}. London: Macmillan; New York: Grove's Dictionaries of Music. {{ISBN|978-1-56159-239-5}}.}} |
||
| ⚫ | * {{wikicite|ref={{harvid|Powers|2001b}}|reference=Powers, Harold S. 2001b. "Mode". ''The New Grove Dictionary of Music and Musicians'', 2nd edition, 29 vols., edited by Stanley Sadie and John Tyrrell, 16:{{Page needed|date=June 2009}}. London: Macmillan; New York: Grove's Dictionaries of Music. {{ISBN|978-1-56159-239-5}}.}} |
||
| ⚫ | * {{wikicite|ref={{harvid|Powers|2001c}}|reference=Powers, Harold S. 2001c. "Hypoionian". ''The New Grove Dictionary of Music and Musicians'', 2nd edition, 29 vols., edited by Stanley Sadie and John Tyrrell, 12:37–38. London: Macmillan; New York: Grove's Dictionaries of Music. {{ISBN|978-1-56159-239-5}}.}} |
||
==External links== |
==External links== |
||
* [ |
* [https://gosk.com/scales/major-scale-for-guitar.php Ionian mode for guitar] at GOSK.com |
||
* [http://gosk.com/scales/major-scale-for-guitar.php Ionian mode for guitar] at GOSK.com |
|||
{{Modes}} |
{{Modes}} |
||
{{Authority control}} |
|||
{{DEFAULTSORT:Ionian Mode}} |
{{DEFAULTSORT:Ionian Mode}} |
||
[[Category:Modes]] |
[[Category:Modes (music)]] |
||
[[Category:Diatonic set theory]] |
|||
[[ |
[[Category:Major scales]] |
||
[[da:Ionisk (toneart)]] |
|||
[[de:Ionischer Modus]] |
|||
[[et:Joonia helilaad]] |
|||
[[nl:Ionisch (toonladder)]] |
|||
[[no:Jonisk skala]] |
|||
[[oc:Mòde ionian]] |
|||
[[pt:Modo jônio]] |
|||
[[uk:Іонійський лад]] |
|||
Latest revision as of 00:34, 7 May 2024
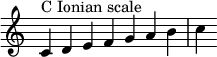
The Ionian mode is a musical mode or, in modern usage, a diatonic scale also called the major scale. It is named after the Ionian Greeks.
It is the name assigned by Heinrich Glarean in 1547 to his new authentic mode on C (mode 11 in his numbering scheme), which uses the diatonic octave species from C to the C an octave higher, divided at G (as its dominant, reciting tone/reciting note or tenor) into a fourth species of perfect fifth (tone–tone–semitone–tone) plus a third species of perfect fourth (tone–tone–semitone): C D E F G + G A B C.[1] This octave species is essentially the same as the major mode of tonal music.[2]
Church music had been explained by theorists as being organised in eight musical modes: the scales on D, E, F, and G in the "greater perfect system" of "musica recta,"[3] each with their authentic and plagal counterparts.
Glarean's twelfth mode was the plagal version of the Ionian mode, called Hypoionian (under Ionian), based on the same relative scale, but with the major third as its tenor, and having a melodic range from a perfect fourth below the tonic, to a perfect fifth above it.[4]
See also
[edit]- Bilawal, the equivalent scale (thaat) in Hindustani music
- Shankarabharanam, the equivalent scale (melakarta) in Carnatic music
Notes
[edit]- ^ (Powers 2001a)
- ^ (Jones 1974, 42)
- ^ (Powers 2001b, §II: "Medieval Modal Theory")
- ^ (Powers 2001c)
References
[edit]- Jones, George Thaddeus. 1974. "Medieval Church Modes", in his Music Theory: The Fundamental Concepts of Tonal Music, Including Notation, Terminology, and Harmony, 42–43. Barnes & Noble Outline Series 137. New York, Hagerstown, San Francisco, London: Barnes & Noble Books; Toronto: Fitzhenry & Whiteside. ISBN 0-06-460137-4, 0-06-467168-2 OCLC 834716
- Powers, Harold S. 2001a. "Ionian". The New Grove Dictionary of Music and Musicians, 2nd edition, 29 vols., edited by Stanley Sadie and John Tyrrell, 12:[page needed]. London: Macmillan; New York: Grove's Dictionaries of Music. ISBN 978-1-56159-239-5.
- Powers, Harold S. 2001b. "Mode". The New Grove Dictionary of Music and Musicians, 2nd edition, 29 vols., edited by Stanley Sadie and John Tyrrell, 16:[page needed]. London: Macmillan; New York: Grove's Dictionaries of Music. ISBN 978-1-56159-239-5.
- Powers, Harold S. 2001c. "Hypoionian". The New Grove Dictionary of Music and Musicians, 2nd edition, 29 vols., edited by Stanley Sadie and John Tyrrell, 12:37–38. London: Macmillan; New York: Grove's Dictionaries of Music. ISBN 978-1-56159-239-5.
External links
[edit]- Ionian mode for guitar at GOSK.com
