Transport length: Difference between revisions

Content deleted Content added

Inline

Latest revision as of 18:11, 17 May 2024

The transport length in a strongly diffusing medium (noted l*) is the length over which the direction of propagation of the photon is randomized. It is related to the mean free path l by the relation:^[1]

$l^{*}={\frac {l}{1-g}}$

with g: the asymmetry coefficient. $g=\langle cos(\theta )\rangle$ or averaging of the scattering angle θ over a high number of scattering events.

g can be evaluated with the Mie theory.
If g=0, l=l*. A single scattering is already isotropic.
If g→1, l*→infinite. A single scattering doesn't deviate the photons. Then the scattering never gets isotropic.

This length is useful for renormalizing a non-isotropic scattering problem into an isotropic one in order to use classical diffusion laws (Fick law and Brownian motion). The transport length might be measured by transmission experiments and backscattering experiments.^[2]^[3]

Mean free path simple scheme

References

^ Ishimaru, A. (1978). Wave Propagation and Scattering in Random Media. New York: Academic Press.
^ Mengual, O.; Meunier, G.; Cayré, I.; Puech, K.; Snabre, P. (1999). "TURBISCAN MA 2000: Multiple light scattering measurement for concentrated emulsion and suspension instability analysis". Talanta. 50 (2): 445–456. doi:10.1016/S0039-9140(99)00129-0. PMID 18967735.
^ Snabre, Patrick; Arhaliass, Abdellah (1998). "Anisotropic scattering of light in random media: Incoherent backscattered spotlight". Applied Optics. 37 (18): 4017–26. Bibcode:1998ApOpt..37.4017S. doi:10.1364/AO.37.004017. PMID 18273374.

External links

Illustrated description (movies) of multiple light scattering and application to colloid stability^{[permanent dead link‍]}

This scattering–related article is a stub. You can help Wikipedia by expanding it.

[1] Ishimaru, A. (1978). Wave Propagation and Scattering in Random Media. New York: Academic Press.

[2] Mengual, O.; Meunier, G.; Cayré, I.; Puech, K.; Snabre, P. (1999). "TURBISCAN MA 2000: Multiple light scattering measurement for concentrated emulsion and suspension instability analysis". Talanta. 50 (2): 445–456. doi:10.1016/S0039-9140(99)00129-0. PMID 18967735.

[3] Snabre, Patrick; Arhaliass, Abdellah (1998). "Anisotropic scattering of light in random media: Incoherent backscattered spotlight". Applied Optics. 37 (18): 4017–26. Bibcode:1998ApOpt..37.4017S. doi:10.1364/AO.37.004017. PMID 18273374.

[1]

[2]

[3]

@@ Line 1: / Line 1: @@
+{{Short description|Measurement of photon propagation}}
-The '''transport length''' in a strongly diffusing medium (noted l*) is the length over which the direction of propagation of the photon is randomized. It is related to the [[mean free path]] l by the relation<ref>A. Ishimaru, Wave Propagation and Scattering in Random Media, Academic Press, New York, 1978.</ref>    : <br />
+The '''transport length''' in a strongly diffusing medium (noted l*) is the length over which the direction of propagation of the [[photon]] is randomized. It is related to the [[mean free path]] l by the relation:<ref>{{cite book |first=A. |last=Ishimaru |year=1978 |title=Wave Propagation and Scattering in Random Media |publisher=Academic Press |location=New York}}</ref>
-<math>l^*=\frac{l}{1-g}</math><br />
-with:
+<math>l^*=\frac{l}{1-g}</math>
-g: the assymetry coefficient. <math>g=  <cos (\theta) > </math> or averaging of the scattering angle θ over a high number of scattering events.<br />
+with g: the asymmetry coefficient. <math>g=  \langle cos (\theta) \rangle </math> or averaging of the scattering angle θ over a high number of [[scattering event]]s.
 g can be evaluated with the [[Mie theory]].<br />
 If g=0, l=l*. A single scattering is already isotropic.<br />
-If g→1, l*→infinite. A single scattering doesn't deviate the photons. Then the scattering never gets isotropic.<br /><br />
+If g→1, l*→infinite. A single scattering doesn't deviate the photons. Then the scattering never gets isotropic.
-This length is usefull for renormalizing a non isotropic scattering problem into an isotropic one in order to use classical diffusion laws ([[Fick_law]], [[Brownian_motion]]). The transport length might be measured by transmission experiments of backscattering experiments <ref>Talanta, Volume 50, Issue 2, 13 September 1999, Pages 445-456 </ref>   <ref>P. Snabre, A. Arhaliass, Anisotropic scattering of light in random media. Incoherent backscattered spot light,Appl. Optics 37 (18) (1998) 211 – 225.</ref>
+This length is useful for renormalizing a non-isotropic scattering problem into an isotropic one in order to use classical diffusion laws ([[Fick law]] and [[Brownian motion]]). The transport length might be measured by transmission experiments and backscattering experiments.<ref>{{Cite journal | doi=10.1016/S0039-9140(99)00129-0| pmid=18967735| title=TURBISCAN MA 2000: Multiple light scattering measurement for concentrated emulsion and suspension instability analysis| year=1999| last1=Mengual| first1=O.| last2=Meunier| first2=G.| last3=Cayré| first3=I.| last4=Puech| first4=K.| last5=Snabre| first5=P.| journal=Talanta| volume=50| issue=2| pages=445–456}}</ref><ref>{{Cite journal | doi=10.1364/AO.37.004017| pmid=18273374| bibcode=1998ApOpt..37.4017S| title=Anisotropic scattering of light in random media: Incoherent backscattered spotlight| year=1998| last1=Snabre| first1=Patrick| last2=Arhaliass| first2=Abdellah| journal=Applied Optics| volume=37| issue=18| pages=4017–26}}</ref>
 <gallery>
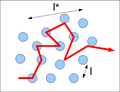
 Image:figure_mean_free_path.png|Mean free path simple scheme
 </gallery>
 ==References==
 <references/>
 ==External links==
-* [http://www.formulaction.com/tech_mls_gb.html  Illustrated description (movies) of multiple light scattering and application to colloid stability]
+* [http://www.formulaction.com/MLS_video.html  Illustrated description (movies) of multiple light scattering and application to colloid stability]{{Dead link|date=July 2018 |bot=InternetArchiveBot |fix-attempted=no }}
+[[Category:Scattering, absorption and radiative transfer (optics)]]
+[[Category:Colloids]]
+{{scattering-stub}}
-[[Category:optics]]
-[[Category:colloids]]