Complex multiplication: Difference between revisions
Initial page |
→Sample consequence: references taken from Heegner_number, see that article for attribution |
||
| (136 intermediate revisions by 72 users not shown) | |||
| Line 1: | Line 1: | ||
{{Short description|Theory of a class of elliptic curves}} |
|||
In [[mathematics]], '''complex multiplication''' is the theory of [[elliptic curve]]s ''E'' that have an [[endomorphism ring]] larger than the [[integer]]s; and also the theory in higher dimensions of [[abelian variety|abelian varieties]] ''A'' having ''enough'' endomorphisms in a certain precise sense (it roughly means that the action on the [[tangent space]] at the [[identity element]] of ''A'' is a [[direct sum]] of one-dimensional [[module (mathematics)|modules]]. [[David Hilbert]] is said to have remarked that ''the theory of complex multiplication is the most beautiful part of mathematics''. |
|||
{{about|a topic in the theory of [[elliptic curves]]|information about multiplication of complex numbers|complex numbers}} |
|||
In [[mathematics]], '''complex multiplication''' ('''CM''') is the theory of [[elliptic curve]]s ''E'' that have an [[endomorphism ring]] larger than the [[integer]]s.{{sfn|Silverman|2009|p=69|loc=Remark 4.3}} Put another way, it contains the theory of [[elliptic function]]s with extra symmetries, such as are visible when the [[period lattice]] is the [[Gaussian integer]] [[Lattice (group)|lattice]] or [[Eisenstein integer]] lattice. |
|||
It has an aspect belonging to the theory of [[special function]]s, because such elliptic functions, or [[abelian function]]s of [[several complex variables]], are then 'very special' functions satisfying extra identities and taking explicitly calculable special values at particular points. It has also turned out to be a central theme in [[algebraic number theory]], allowing some features of the theory of [[cyclotomic field]]s to be carried over to wider areas of application. [[David Hilbert]] is said to have remarked that the theory of complex multiplication of elliptic curves was not only the most beautiful part of mathematics but of all science.<ref>{{Citation |
|||
An example of an elliptic curve with complex multiplication is |
|||
| last=Reid |
|||
| first=Constance |
|||
| author-link=Constance Reid |
|||
| title=Hilbert |
|||
| publisher=Springer |
|||
| isbn=978-0-387-94674-0 |
|||
| year=1996 |
|||
| page=[https://archive.org/details/hilbert0000reid/page/200 200] |
|||
| url=https://archive.org/details/hilbert0000reid/page/200 |
|||
}}</ref> |
|||
There is also the [[Complex multiplication of abelian varieties|higher-dimensional complex multiplication theory]] of [[abelian variety|abelian varieties]] ''A'' having ''enough'' endomorphisms in a certain precise sense, roughly that the action on the [[tangent space]] at the [[identity element]] of ''A'' is a [[direct sum of modules|direct sum]] of one-dimensional [[module (mathematics)|modules]]. |
|||
:'''C'''/'''Z'''[''i'']θ |
|||
==Example of the imaginary quadratic field extension== |
|||
where '''Z'''[''i''] is the [[Gaussian integer]] ring, and θ is any non-zero complex number. Any such complex [[torus]] has the Gaussian integers as endomorphism ring. It is known that the corresponding curves can all be written as |
|||
[[Image:Lattice torsion points.svg|right|thumb|300px|An elliptic curve over the complex numbers is obtained as a quotient of the complex plane by a lattice Λ, here spanned by two fundamental periods ''ω''<sub>1</sub> and ''ω''<sub>2</sub>. The four-torsion is also shown, corresponding to the lattice 1/4 Λ containing Λ. |
|||
: ''Y<sup>2</sup> = 4X<sup>3</sup> − aX'', |
|||
The example of an elliptic curve corresponding to the Gaussian integers occurs when ω<sub>2</sub> = ''i'' ''ω''<sub>1</sub>.]] |
|||
having an order 4 automorphism sending |
|||
Consider an imaginary quadratic field <math display="inline">K = \Q\left(\sqrt{-d}\right) , \, d \in \Z, d > 0</math>. |
|||
: ''Y'' → −''iY'', ''X'' → −''X'' |
|||
An elliptic function <math>f</math> is said to have '''complex multiplication''' if there is an algebraic relation between <math>f(z)</math> and <math>f(\lambda z)</math> for all <math>\lambda</math> in <math>K</math>. |
|||
Conversely, Kronecker conjectured – in what became known as the ''[[Kronecker Jugendtraum]]'' – that every abelian extension of <math>K</math> '''could be obtained''' by the (roots of the) equation of a suitable elliptic curve with complex multiplication. To this day this remains one of the few cases of [[Hilbert's twelfth problem]] which has actually been solved. |
|||
in line with the action of ''i'' on the [[Weierstrass elliptic function]]s. This is a typical elliptic curve with complex multiplication, in the sense that over the complex number field they are all found as such quotients, in which some [[order (ring theory)|order]] in the [[ring of integers]] in an imaginary [[quadratic field]] takes the place of the Gaussian integers. |
|||
An example of an elliptic curve with complex multiplication is |
|||
When the base field is a [[finite field]], there are always non-trivial endomorphisms of an elliptic curve; so the ''complex multiplication'' case is in a sense typical (and the terminology isn't often applied). But when the base field is a [[number field]], complex multiplication is the exception. It is known that, in a general sense, the case of complex multiplication is the hardest to resolve for the [[Hodge conjecture]]. |
|||
:<math>\mathbb{C}/ (\theta \mathbb{Z}[i])</math> |
|||
[[Kronecker]] first postulated that the values of [[elliptic function]]s at torsion points should be enough to generate all [[abelian extension]]s for imaginary quadratic fields, an idea that went back to [[Eisenstein]] in some cases, and even to [[Gauss]]. This became as the [[Kronecker Jugendtraum]]; and was certainly what would have prompted Hilbert's remark above, since it makes explicit [[class field theory]] in the way the [[roots of unity]] do for abelian extensions of the [[rational number]] field. Many generalisations have been sought of Kronecker's ideas; they do however lie somewhat obliquely to the main thrust of the [[Langlands philosophy]], and there is no definitive statement currently known. |
|||
where '''Z'''[''i''] is the [[Gaussian integer]] ring, and ''θ'' is any non-zero complex number. Any such complex [[torus]] has the Gaussian integers as endomorphism ring. It is known that the corresponding curves can all be written as |
|||
See also: [[abelian variety of CM-type]]. |
|||
:<math>Y^2 = 4X^3 - aX</math> |
|||
for some <math>a \in \mathbb{C} </math>, which demonstrably has two conjugate order-4 [[automorphism]]s sending |
|||
:<math>Y \to \pm iY,\quad X \to -X</math> |
|||
in line with the action of ''i'' on the [[Weierstrass elliptic function]]s. |
|||
More generally, consider the lattice Λ, an additive group in the complex plane, generated by <math>\omega_1,\omega_2</math>. Then we define the Weierstrass function of the variable <math>z</math> in <math>\mathbb{C}</math> as follows: |
|||
:<math>\wp(z;\Lambda) = \wp(z;\omega_1,\omega_2) = \frac{1}{z^2} + \sum_{(m,n)\ne (0,0)} \left\{\frac{1}{(z+m\omega_1+n\omega_2)^2} - \frac{1}{\left(m\omega_1+n\omega_2\right)^2}\right\},</math> |
|||
and |
|||
:<math>g_2 = 60\sum_{(m,n) \neq (0,0)} (m\omega_1+n\omega_2)^{-4}</math> |
|||
:<math>g_3 =140\sum_{(m,n) \neq (0,0)} (m\omega_1+n\omega_2)^{-6}.</math> |
|||
Let <math>\wp'</math> be the derivative of <math>\wp</math>. Then we obtain an isomorphism of complex Lie groups: |
|||
:<math>w\mapsto(\wp(w):\wp'(w):1) \in \mathbb{P}^2(\mathbb{C}) </math> |
|||
from the complex torus group <math>\mathbb{C}/\Lambda</math> to the projective elliptic curve defined in homogeneous coordinates by |
|||
:<math>E = \left\{ (x:y:z) \in \mathbb{C}^3 \mid y^2z = 4x^3 - g_2xz^2 - g_3 z^3 \right\} </math> |
|||
and where the point at infinity, the zero element of the group law of the elliptic curve, is by convention taken to be <math>(0:1:0)</math>. |
|||
If the lattice defining the elliptic curve is actually preserved under multiplication by (possibly a proper subring of) the ring of integers <math>\mathfrak{o}_K</math> of <math>K</math>, then the ring of analytic automorphisms of <math> E = \mathbb{C}/\Lambda</math> turns out to be isomorphic to this (sub)ring. |
|||
If we rewrite <math>\tau = \omega_1/\omega_2</math> where <math>\operatorname{Im}\tau > 0</math> and <math>\Delta(\Lambda) = g_2(\Lambda)^3 - 27g_3(\Lambda)^2</math>, then |
|||
:<math> j(\tau)=j(E)=j(\Lambda)=2^63^3g_2(\Lambda)^3/\Delta(\Lambda)\ .</math> |
|||
This means that the [[j-invariant]] of <math>E</math> is an [[algebraic number]] – lying in <math>K</math> – if <math>E</math> has complex multiplication. |
|||
==Abstract theory of endomorphisms== |
|||
The ring of endomorphisms of an elliptic curve can be of one of three forms: the integers '''Z'''; an [[Order (ring theory)|order]] in an [[imaginary quadratic number field]]; or an order in a definite [[quaternion algebra]] over '''Q'''.{{sfn|Silverman|1986|p=102}} |
|||
When the field of definition is a [[finite field]], there are always non-trivial endomorphisms of an elliptic curve, coming from the [[Frobenius map]], so every such curve has ''complex multiplication'' (and the terminology is not often applied). But when the base field is a number field, complex multiplication is the exception. It is known that, in a general sense, the case of complex multiplication is the hardest to resolve for the [[Hodge conjecture]]. |
|||
==Kronecker and abelian extensions== |
|||
{{further|Hilbert's twelfth problem}} |
|||
[[Leopold Kronecker|Kronecker]] first postulated that the values of [[elliptic function]]s at torsion points should be enough to generate all [[abelian extension]]s for imaginary quadratic fields, an idea that went back to [[Gotthold Eisenstein|Eisenstein]] in some cases, and even to [[Carl Friedrich Gauss|Gauss]]. This became known as the ''[[Kronecker Jugendtraum]]''; and was certainly what had prompted Hilbert's remark above, since it makes explicit [[class field theory]] in the way the [[roots of unity]] do for abelian extensions of the [[rational number|rational number field]], via [[Shimura's reciprocity law]]. |
|||
Indeed, let ''K'' be an imaginary quadratic field with class field ''H''. Let ''E'' be an elliptic curve with complex multiplication by the integers of ''K'', defined over ''H''. Then the [[maximal abelian extension]] of ''K'' is generated by the ''x''-coordinates of the points of finite order on some Weierstrass model for ''E'' over ''H''.{{sfn|Serre|1967|p=295}} |
|||
Many generalisations have been sought of Kronecker's ideas; they do however lie somewhat obliquely to the main thrust of the [[Langlands philosophy]], and there is no definitive statement currently known. |
|||
==Sample consequence== |
|||
It is no accident that [[Ramanujan's constant]], the [[transcendental number]]<ref>{{MathWorld|title=Transcendental Number|urlname=TranscendentalNumber}} gives <math>e^{\pi\sqrt{d}}, d \in Z^*</math>, based on |
|||
Nesterenko, Yu. V. "On Algebraic Independence of the Components of Solutions of a System of Linear Differential Equations." Izv. Akad. Nauk SSSR, Ser. Mat. 38, 495–512, 1974. English translation in Math. USSR 8, 501–518, 1974.</ref> |
|||
: <math>e^{\pi \sqrt{163}} = 262537412640768743.99999999999925007\dots\,</math> |
|||
or equivalently, |
|||
: <math>e^{\pi \sqrt{163}} = 640320^3+743.99999999999925007\dots\,</math> |
|||
is an [[almost integer]], in that it is [[Mathematical coincidence#Containing pi or e and number 163|very close]] to an [[integer]].<ref>[http://mathworld.wolfram.com/RamanujanConstant.html Ramanujan Constant – from Wolfram MathWorld<!-- Bot-generated title -->]</ref> This remarkable fact is explained by the theory of complex multiplication, together with some knowledge of [[modular forms]], and the fact that |
|||
: <math>\mathbf{Z}\left[ \frac{1+\sqrt{-163}}{2}\right]</math> |
|||
is a [[unique factorization domain]]. |
|||
Here <math>(1+\sqrt{-163})/2</math> satisfies {{nowrap|1=''α''<sup>2</sup> = ''α'' − 41}}. In general, ''S''[''α''] denotes the set of all [[polynomial]] expressions in α with coefficients in ''S'', which is the smallest ring containing ''α'' and ''S''. Because α satisfies this quadratic equation, the required polynomials can be limited to degree one. |
|||
Alternatively, |
|||
: <math>e^{\pi \sqrt{163}} = 12^3(231^2-1)^3+743.99999999999925007\dots\,</math> |
|||
an internal structure due to certain [[Eisenstein series]], and with similar simple expressions for the other [[Heegner number]]s. |
|||
==Singular moduli== |
|||
The points of the upper half-plane ''τ'' which correspond to the period ratios of elliptic curves over the complex numbers with complex multiplication are precisely the imaginary quadratic numbers.{{sfn|Silverman|1986|p=339}} The corresponding [[Elliptic modular function|modular invariant]]s ''j''(''τ'') are the '''singular moduli''', coming from an older terminology in which "singular" referred to the property of having non-trivial endomorphisms rather than referring to a [[singular curve]].{{sfn|Silverman|1994|p=104}} |
|||
The [[modular function]] ''j''(''τ'') is algebraic on imaginary quadratic numbers ''τ'':{{sfn|Serre|1967|p=293}} these are the only algebraic numbers in the upper half-plane for which ''j'' is algebraic.<ref>{{cite book | first=Alan | last=Baker | author-link=Alan Baker (mathematician) | title=Transcendental Number Theory | publisher=[[Cambridge University Press]] | year=1975 | isbn=0-521-20461-5 | zbl=0297.10013 | page=56 }}</ref> |
|||
If Λ is a lattice with period ratio ''τ'' then we write ''j''(Λ) for ''j''(''τ''). If further Λ is an ideal '''a''' in the ring of integers ''O<sub>K</sub>'' of a quadratic imaginary field ''K'' then we write ''j''('''a''') for the corresponding singular modulus. The values ''j''('''a''') are then real algebraic integers, and generate the [[Hilbert class field]] ''H'' of ''K'': the [[field extension]] degree [''H'':''K''] = ''h'' is the class number of ''K'' and the ''H''/''K'' is a [[Galois extension]] with [[Galois group]] isomorphic to the [[ideal class group]] of ''K''. The class group acts on the values ''j''('''a''') by ['''b'''] : ''j''('''a''') → ''j''('''ab'''). |
|||
In particular, if ''K'' has class number one, then ''j''('''a''') = ''j''(''O'') is a rational integer: for example, ''j''('''Z'''[i]) = ''j''(i) = 1728. |
|||
==See also== |
|||
* [[Algebraic Hecke character]] |
|||
* [[Heegner point]] |
|||
* [[Hilbert's twelfth problem]] |
|||
* [[Lubin–Tate formal group]], [[local field]]s |
|||
* [[Drinfeld shtuka]], [[global function field]] case |
|||
* [[Wiles's proof of Fermat's Last Theorem]] |
|||
==Citations== |
|||
{{reflist}} |
|||
==References== |
|||
{{refbegin|2}} |
|||
* Borel, A.; Chowla, S.; Herz, C. S.; Iwasawa, K.; Serre, J.-P. ''Seminar on complex multiplication''. Seminar held at the Institute for Advanced Study, Princeton, N.J., 1957–58. Lecture Notes in Mathematics, No. 21 Springer-Verlag, Berlin-New York, 1966 |
|||
* {{cite book | last=Husemöller | first=Dale H. | title=Elliptic curves | others=With an appendix by Ruth Lawrence | series=Graduate Texts in Mathematics | volume=111 |publisher=[[Springer-Verlag]] | year=1987 | isbn=0-387-96371-5 | zbl=0605.14032 }} |
|||
* {{cite book | last=Lang | first=Serge | author-link=Serge Lang | title=Complex multiplication | series=Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences] | volume=255 | publisher=[[Springer-Verlag]] | location=New York | year=1983 | isbn=0-387-90786-6 | zbl=0536.14029 | url-access=registration | url=https://archive.org/details/complexmultiplic0000lang }} |
|||
* {{cite book | last=Serre | first=J.-P. | author-link=Jean-Pierre Serre | chapter=XIII. Complex multiplication | pages=292–296 | editor1-first=J.W.S. | editor1-last=Cassels | editor1-link=J. W. S. Cassels | editor2-first=Albrecht | editor2-last=Fröhlich | editor2-link=Albrecht Fröhlich | title=Algebraic Number Theory | year=1967 | publisher=Academic Press }} |
|||
*{{cite book | last=Shimura | first=Goro | author-link=Goro Shimura | title=Introduction to the arithmetic theory of automorphic functions | publisher=Iwanami Shoten | location=Tokyo | series=Publications of the Mathematical Society of Japan | year=1971 | volume=11 | zbl=0221.10029 }} |
|||
* {{cite book | last=Shimura | first=Goro | author-link=Goro Shimura | title=Abelian varieties with complex multiplication and modular functions | series=Princeton Mathematical Series | volume=46 | publisher=[[Princeton University Press]] | location=Princeton, NJ | year=1998 | isbn=0-691-01656-9 | zbl=0908.11023 }} |
|||
* {{cite book | first=Joseph H. | last=Silverman | author-link=Joseph H. Silverman | title=The Arithmetic of Elliptic Curves | series=[[Graduate Texts in Mathematics]] | publisher=[[Springer-Verlag]] | volume=106 | year=1986 | isbn=0-387-96203-4 | zbl=0585.14026 }} |
|||
* {{cite book | last=Silverman | first=Joseph H. | author-link=Joseph H. Silverman| title = The Arithmetic of Elliptic Curves | series=Graduate Texts in Mathematics | year=2009 | volume=106 | edition=2nd | publisher=[[Springer Science+Business Media|Springer Science]] | doi=10.1007/978-0-387-09494-6 | url=https://link.springer.com/book/10.1007/978-0-387-09494-6 | isbn=978-0-387-09493-9}} |
|||
* {{cite book | first=Joseph H. | last=Silverman | author-link=Joseph H. Silverman | title=Advanced Topics in the Arithmetic of Elliptic Curves | series=[[Graduate Texts in Mathematics]] | publisher=[[Springer-Verlag]] | volume=151 | year=1994 | isbn=0-387-94328-5 | zbl=0911.14015 }} |
|||
{{refend}} |
|||
==External links== |
|||
* [http://planetmath.org/ComplexMultiplication Complex multiplication] from [[PlanetMath|PlanetMath.org]] |
|||
* [http://planetmath.org/ExamplesOfEllipticCurvesWithComplexMultiplication Examples of elliptic curves with complex multiplication] from [[PlanetMath|PlanetMath.org]] |
|||
* {{cite journal | title = Galois Representations and Modular Forms | citeseerx = 10.1.1.125.6114 | author-link = Kenneth Alan Ribet | first = Kenneth A. | last = Ribet | journal = [[Bulletin of the American Mathematical Society]] | volume = 32 | issue = 4 |date=October 1995 | pages = 375–402 | doi=10.1090/s0273-0979-1995-00616-6| arxiv = math/9503219 | s2cid = 16786407 }} |
|||
{{DEFAULTSORT:Complex Multiplication}} |
|||
[[Category:Abelian varieties]] |
|||
[[Category:Elliptic functions]] |
|||
[[Category:Class field theory]] |
|||
Latest revision as of 23:40, 18 June 2024
In mathematics, complex multiplication (CM) is the theory of elliptic curves E that have an endomorphism ring larger than the integers.[1] Put another way, it contains the theory of elliptic functions with extra symmetries, such as are visible when the period lattice is the Gaussian integer lattice or Eisenstein integer lattice.
It has an aspect belonging to the theory of special functions, because such elliptic functions, or abelian functions of several complex variables, are then 'very special' functions satisfying extra identities and taking explicitly calculable special values at particular points. It has also turned out to be a central theme in algebraic number theory, allowing some features of the theory of cyclotomic fields to be carried over to wider areas of application. David Hilbert is said to have remarked that the theory of complex multiplication of elliptic curves was not only the most beautiful part of mathematics but of all science.[2]
There is also the higher-dimensional complex multiplication theory of abelian varieties A having enough endomorphisms in a certain precise sense, roughly that the action on the tangent space at the identity element of A is a direct sum of one-dimensional modules.
Example of the imaginary quadratic field extension
[edit]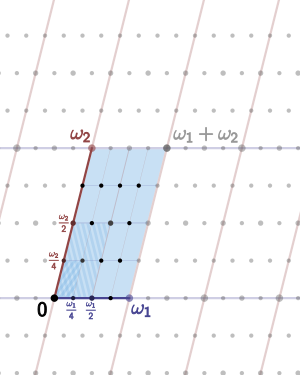
Consider an imaginary quadratic field . An elliptic function is said to have complex multiplication if there is an algebraic relation between and for all in .
Conversely, Kronecker conjectured – in what became known as the Kronecker Jugendtraum – that every abelian extension of could be obtained by the (roots of the) equation of a suitable elliptic curve with complex multiplication. To this day this remains one of the few cases of Hilbert's twelfth problem which has actually been solved.
An example of an elliptic curve with complex multiplication is
where Z[i] is the Gaussian integer ring, and θ is any non-zero complex number. Any such complex torus has the Gaussian integers as endomorphism ring. It is known that the corresponding curves can all be written as
for some , which demonstrably has two conjugate order-4 automorphisms sending
in line with the action of i on the Weierstrass elliptic functions.
More generally, consider the lattice Λ, an additive group in the complex plane, generated by . Then we define the Weierstrass function of the variable in as follows:
and
Let be the derivative of . Then we obtain an isomorphism of complex Lie groups:
from the complex torus group to the projective elliptic curve defined in homogeneous coordinates by
and where the point at infinity, the zero element of the group law of the elliptic curve, is by convention taken to be . If the lattice defining the elliptic curve is actually preserved under multiplication by (possibly a proper subring of) the ring of integers of , then the ring of analytic automorphisms of turns out to be isomorphic to this (sub)ring.
If we rewrite where and , then
This means that the j-invariant of is an algebraic number – lying in – if has complex multiplication.
Abstract theory of endomorphisms
[edit]The ring of endomorphisms of an elliptic curve can be of one of three forms: the integers Z; an order in an imaginary quadratic number field; or an order in a definite quaternion algebra over Q.[3]
When the field of definition is a finite field, there are always non-trivial endomorphisms of an elliptic curve, coming from the Frobenius map, so every such curve has complex multiplication (and the terminology is not often applied). But when the base field is a number field, complex multiplication is the exception. It is known that, in a general sense, the case of complex multiplication is the hardest to resolve for the Hodge conjecture.
Kronecker and abelian extensions
[edit]Kronecker first postulated that the values of elliptic functions at torsion points should be enough to generate all abelian extensions for imaginary quadratic fields, an idea that went back to Eisenstein in some cases, and even to Gauss. This became known as the Kronecker Jugendtraum; and was certainly what had prompted Hilbert's remark above, since it makes explicit class field theory in the way the roots of unity do for abelian extensions of the rational number field, via Shimura's reciprocity law.
Indeed, let K be an imaginary quadratic field with class field H. Let E be an elliptic curve with complex multiplication by the integers of K, defined over H. Then the maximal abelian extension of K is generated by the x-coordinates of the points of finite order on some Weierstrass model for E over H.[4]
Many generalisations have been sought of Kronecker's ideas; they do however lie somewhat obliquely to the main thrust of the Langlands philosophy, and there is no definitive statement currently known.
Sample consequence
[edit]It is no accident that Ramanujan's constant, the transcendental number[5]
or equivalently,
is an almost integer, in that it is very close to an integer.[6] This remarkable fact is explained by the theory of complex multiplication, together with some knowledge of modular forms, and the fact that
is a unique factorization domain.
Here satisfies α2 = α − 41. In general, S[α] denotes the set of all polynomial expressions in α with coefficients in S, which is the smallest ring containing α and S. Because α satisfies this quadratic equation, the required polynomials can be limited to degree one.
Alternatively,
an internal structure due to certain Eisenstein series, and with similar simple expressions for the other Heegner numbers.
Singular moduli
[edit]The points of the upper half-plane τ which correspond to the period ratios of elliptic curves over the complex numbers with complex multiplication are precisely the imaginary quadratic numbers.[7] The corresponding modular invariants j(τ) are the singular moduli, coming from an older terminology in which "singular" referred to the property of having non-trivial endomorphisms rather than referring to a singular curve.[8]
The modular function j(τ) is algebraic on imaginary quadratic numbers τ:[9] these are the only algebraic numbers in the upper half-plane for which j is algebraic.[10]
If Λ is a lattice with period ratio τ then we write j(Λ) for j(τ). If further Λ is an ideal a in the ring of integers OK of a quadratic imaginary field K then we write j(a) for the corresponding singular modulus. The values j(a) are then real algebraic integers, and generate the Hilbert class field H of K: the field extension degree [H:K] = h is the class number of K and the H/K is a Galois extension with Galois group isomorphic to the ideal class group of K. The class group acts on the values j(a) by [b] : j(a) → j(ab).
In particular, if K has class number one, then j(a) = j(O) is a rational integer: for example, j(Z[i]) = j(i) = 1728.
See also
[edit]- Algebraic Hecke character
- Heegner point
- Hilbert's twelfth problem
- Lubin–Tate formal group, local fields
- Drinfeld shtuka, global function field case
- Wiles's proof of Fermat's Last Theorem
Citations
[edit]- ^ Silverman 2009, p. 69, Remark 4.3.
- ^ Reid, Constance (1996), Hilbert, Springer, p. 200, ISBN 978-0-387-94674-0
- ^ Silverman 1986, p. 102.
- ^ Serre 1967, p. 295.
- ^ Weisstein, Eric W. "Transcendental Number". MathWorld. gives , based on Nesterenko, Yu. V. "On Algebraic Independence of the Components of Solutions of a System of Linear Differential Equations." Izv. Akad. Nauk SSSR, Ser. Mat. 38, 495–512, 1974. English translation in Math. USSR 8, 501–518, 1974.
- ^ Ramanujan Constant – from Wolfram MathWorld
- ^ Silverman 1986, p. 339.
- ^ Silverman 1994, p. 104.
- ^ Serre 1967, p. 293.
- ^ Baker, Alan (1975). Transcendental Number Theory. Cambridge University Press. p. 56. ISBN 0-521-20461-5. Zbl 0297.10013.
References
[edit]- Borel, A.; Chowla, S.; Herz, C. S.; Iwasawa, K.; Serre, J.-P. Seminar on complex multiplication. Seminar held at the Institute for Advanced Study, Princeton, N.J., 1957–58. Lecture Notes in Mathematics, No. 21 Springer-Verlag, Berlin-New York, 1966
- Husemöller, Dale H. (1987). Elliptic curves. Graduate Texts in Mathematics. Vol. 111. With an appendix by Ruth Lawrence. Springer-Verlag. ISBN 0-387-96371-5. Zbl 0605.14032.
- Lang, Serge (1983). Complex multiplication. Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences]. Vol. 255. New York: Springer-Verlag. ISBN 0-387-90786-6. Zbl 0536.14029.
- Serre, J.-P. (1967). "XIII. Complex multiplication". In Cassels, J.W.S.; Fröhlich, Albrecht (eds.). Algebraic Number Theory. Academic Press. pp. 292–296.
- Shimura, Goro (1971). Introduction to the arithmetic theory of automorphic functions. Publications of the Mathematical Society of Japan. Vol. 11. Tokyo: Iwanami Shoten. Zbl 0221.10029.
- Shimura, Goro (1998). Abelian varieties with complex multiplication and modular functions. Princeton Mathematical Series. Vol. 46. Princeton, NJ: Princeton University Press. ISBN 0-691-01656-9. Zbl 0908.11023.
- Silverman, Joseph H. (1986). The Arithmetic of Elliptic Curves. Graduate Texts in Mathematics. Vol. 106. Springer-Verlag. ISBN 0-387-96203-4. Zbl 0585.14026.
- Silverman, Joseph H. (2009). The Arithmetic of Elliptic Curves. Graduate Texts in Mathematics. Vol. 106 (2nd ed.). Springer Science. doi:10.1007/978-0-387-09494-6. ISBN 978-0-387-09493-9.
- Silverman, Joseph H. (1994). Advanced Topics in the Arithmetic of Elliptic Curves. Graduate Texts in Mathematics. Vol. 151. Springer-Verlag. ISBN 0-387-94328-5. Zbl 0911.14015.
External links
[edit]- Complex multiplication from PlanetMath.org
- Examples of elliptic curves with complex multiplication from PlanetMath.org
- Ribet, Kenneth A. (October 1995). "Galois Representations and Modular Forms". Bulletin of the American Mathematical Society. 32 (4): 375–402. arXiv:math/9503219. CiteSeerX 10.1.1.125.6114. doi:10.1090/s0273-0979-1995-00616-6. S2CID 16786407.







![{\displaystyle \mathbb {C} /(\theta \mathbb {Z} [i])}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/106250e91ece2bf71ea951e37a08f3933391f97e)
























![{\displaystyle \mathbf {Z} \left[{\frac {1+{\sqrt {-163}}}{2}}\right]}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/21c4f31f477f4a26d3756410c565fd0bd7d75108)


