Semiregular polytope: Difference between revisions
Double sharp (talk | contribs) mNo edit summary |
Removing from Category:Polytopes using Cat-a-lot |
||
| (47 intermediate revisions by 9 users not shown) | |||
| Line 1: | Line 1: | ||
{{Short description|Isogonal polytope with regular facets}} |
|||
{| class="wikitable" align=right |
|||
{| class=wikitable align=right width=450 |
|||
|+ Convex semiregular polychora |
|||
|+ Gosset's figures |
|||
|- align="center" |
|||
!colspan=3|3D honeycombs |
|||
| [[File:Schlegel half-solid rectified 5-cell.png|100px]]<br>[[Rectified 5-cell]] |
|||
|- |
|||
| [[File:Schlegel half-solid alternated cantitruncated 16-cell.png|100px]]<br>[[Snub 24-cell]] |
|||
|[[File:HC P1-P3.png|150px]]<BR>[[Tetrahedral-octahedral honeycomb|Simple tetroctahedric check]] |
|||
| [[File:Rectified 600-cell schlegel halfsolid.png|100px]]<br>[[Rectified 600-cell]] |
|||
|[[File:Gyrated alternated cubic honeycomb.png|150px]]<BR>[[Gyrated alternated cubic honeycomb|Complex tetroctahedric check]] |
|||
|- |
|||
!colspan=3|4D polytopes |
|||
|- |
|||
|[[File:Schlegel half-solid rectified 5-cell.png|150px]]<BR>[[Rectified 5-cell|Tetroctahedric]] |
|||
|[[File:Rectified 600-cell schlegel halfsolid.png|150px]]<BR>[[Rectified 600-cell|Octicosahedric]] |
|||
|[[File:Ortho solid 969-uniform polychoron 343-snub.png|150px]]<BR>[[Snub 24-cell|Tetricosahedric]] |
|||
|} |
|} |
||
In [[geometry]], a '''semiregular [[polytope]]''' is usually taken to be a [[polytope]] that is [[vertex-uniform]] and has all its [[facet (geometry)|facets]] being [[regular polytope]]s. |
|||
In [[ |
In [[geometry]], by [[Thorold Gosset]]'s definition a '''semiregular polytope''' is usually taken to be a [[polytope]] that is [[isogonal figure|vertex-transitive]] and has all its [[facet (geometry)|facets]] being [[regular polytope]]s. [[E.L. Elte]] compiled a [[Emanuel_Lodewijk_Elte#Elte's semiregular polytopes of the first kind|longer list in 1912]] as ''The Semiregular Polytopes of the Hyperspaces'' which included a wider definition. |
||
== Gosset's list == |
|||
The three convex semiregular [[polychoron|polychora]] (4-polytopes) are the [[rectified 5-cell]], [[snub 24-cell]] and [[rectified 600-cell]]. The only semiregular polytopes in higher dimensions are the [[uniform k 21 polytope|''k''<sub>21</sub> polytopes]], where the rectified 5-cell is the special case of ''k'' = 0. |
|||
In [[three-dimensional space]] and below, the terms ''semiregular polytope'' and ''[[uniform polytope]]'' have identical meanings, because all uniform [[polygon]]s must be [[regular polygon|regular]]. However, since not all [[uniform polyhedra]] are [[regular polyhedra|regular]], the number of semiregular polytopes in dimensions higher than three is much smaller than the number of uniform polytopes in the same number of dimensions. |
|||
The three convex semiregular [[4-polytope]]s are the [[rectified 5-cell]], [[snub 24-cell]] and [[rectified 600-cell]]. The only semiregular polytopes in higher dimensions are the [[uniform k 21 polytope|''k''<sub>21</sub> polytopes]], where the rectified 5-cell is the special case of ''k'' = 0. These were all listed by Gosset, but a proof of the completeness of this list was not published until the work of {{harvtxt|Makarov|1988}} for four dimensions, and {{harvtxt|Blind|Blind|1991}} for higher dimensions. |
|||
;Gosset's 4-polytopes (with his names in parentheses): |
|||
:[[Rectified 5-cell]] (Tetroctahedric), {{CDD|node|3|node_1|3|node|3|node}} |
|||
:[[Rectified 600-cell]] (Octicosahedric), {{CDD|node|3|node_1|3|node|5|node}} |
|||
:[[Snub 24-cell]] (Tetricosahedric), {{CDD|node_h|3|node_h|4|node|3|node}}, {{CDD|node_h|3|node_h|3|node_h|4|node}} or {{CDD|node_h|3|node_h|split1|nodes_hh}} |
|||
;[[Semiregular E-polytope]]s in higher dimensions: |
|||
:[[5-demicube]] (5-ic semi-regular), a [[5-polytope]], {{CDD|node_h1|4|node|3|node|3|node|3|node}} ↔ {{CDD|nodes_10ru|split2|node|3|node|3|node}} |
|||
:[[2 21 polytope|2<sub>21</sub> polytope]] (6-ic semi-regular), a [[6-polytope]], {{CDD|nodea_1|3a|nodea|3a|branch|3a|nodea|3a|nodea}} or {{CDD|nodes_10r|3ab|nodes|split2|node|3|node}} |
|||
:[[3 21 polytope|3<sub>21</sub> polytope]] (7-ic semi-regular), a [[7-polytope]], {{CDD|nodea_1|3a|nodea|3a|nodea|3a|branch|3a|nodea|3a|nodea}} |
|||
:[[4 21 polytope|4<sub>21</sub> polytope]] (8-ic semi-regular), an [[8-polytope]], {{CDD|nodea_1|3a|nodea|3a|nodea|3a|nodea|3a|branch|3a|nodea|3a|nodea}} |
|||
==Euclidean honeycombs== |
|||
[[File:HC P1-P3.png|185px|thumb|The [[tetrahedral-octahedral honeycomb]] in Euclidean 3-space has alternating tetrahedral and octahedral cells.]] |
|||
Semiregular polytopes can be extended to semiregular [[honeycomb (geometry)|honeycombs]]. The semiregular Euclidean honeycombs are the [[tetrahedral-octahedral honeycomb]] (3D), [[gyrated alternated cubic honeycomb]] (3D) and the [[5 21 honeycomb|5<sub>21</sub> honeycomb]] (8D). |
Semiregular polytopes can be extended to semiregular [[honeycomb (geometry)|honeycombs]]. The semiregular Euclidean honeycombs are the [[tetrahedral-octahedral honeycomb]] (3D), [[gyrated alternated cubic honeycomb]] (3D) and the [[5 21 honeycomb|5<sub>21</sub> honeycomb]] (8D). |
||
Gosset [[Convex uniform honeycomb|honeycombs]]: |
|||
#[[Tetrahedral-octahedral honeycomb]] or [[alternated cubic honeycomb]] (Simple tetroctahedric check), {{CDD|node_h1|4|node|3|node|4|node}} ↔ {{CDD|nodes_10ru|split2|node|4|node}} (Also [[quasiregular polytope]]) |
|||
#[[Gyrated alternated cubic honeycomb]] (Complex tetroctahedric check), {{CDD|node|3|node|6|node_h|2x|node_h|infin|node}} |
|||
Semiregular E-honeycomb: |
|||
*[[5 21 honeycomb|5<sub>21</sub> honeycomb]] (9-ic check) (8D Euclidean honeycomb), {{CDD|nodea_1|3a|nodea|3a|nodea|3a|nodea|3a|nodea|3a|branch|3a|nodea|3a|nodea}} |
|||
{{harvtxt|Gosset|1900}} additionally allowed Euclidean honeycombs as facets of higher-dimensional Euclidean honeycombs, giving the following additional figures: |
|||
#Hypercubic honeycomb prism, named by Gosset as the (''n'' – 1)-ic semi-check (analogous to a single rank or file of a chessboard) |
|||
#[[Convex uniform honeycomb#Frieze forms|Alternated hexagonal slab honeycomb]] (tetroctahedric semi-check), {{CDD|node_h|2x|node_h|6|node|3|node}} |
|||
==Hyperbolic honeycombs== |
|||
[[File:H3 4333-0100 center ultrawide.png|thumb|The [[hyperbolic tetrahedral-octahedral honeycomb]] has tetrahedral and two types of octahedral cells.]] |
|||
There are also hyperbolic uniform honeycombs composed of only regular cells {{harv|Coxeter|Whitrow|1950}}, including: |
|||
*[[Hyperbolic uniform honeycomb]]s, 3D honeycombs: |
|||
*# [[Alternated order-5 cubic honeycomb]], {{CDD|node_h1|4|node|3|node|5|node}} ↔ {{CDD|nodes_10ru|split2|node|5|node}} (Also [[quasiregular polytope]]) |
|||
*# [[Hyperbolic tetrahedral-octahedral honeycomb|Tetrahedral-octahedral honeycomb]], {{CDD|label4|branch|3ab|branch_10l}} |
|||
*# [[Tetrahedron-icosahedron honeycomb]], {{CDD|label5|branch|3ab|branch_10l}} |
|||
*[[Paracompact uniform honeycomb]]s, 3D honeycombs, which include uniform tilings as cells: |
|||
*# [[Rectified order-6 tetrahedral honeycomb]], {{CDD|node|3|node_1|3|node|6|node}} |
|||
*# [[Rectified square tiling honeycomb]], {{CDD|node|4|node_1|4|node|3|node}} |
|||
*# [[Rectified order-4 square tiling honeycomb]], {{CDD|node|4|node_1|4|node|3|node}} ↔ {{CDD|node_1|4|node|4|node|3|node}} |
|||
*# [[Alternated order-6 cubic honeycomb]], {{CDD|node_h1|4|node|3|node|6|node}} ↔ {{CDD|nodes_10ru|split2|node|6|node}} (Also quasiregular) |
|||
*# [[Alternated hexagonal tiling honeycomb]], {{CDD||node_h1|6|node|3|node|3|node}} ↔ {{CDD|branch_10ru|split2|node|3|node}} |
|||
*# [[Alternated order-4 hexagonal tiling honeycomb]], {{CDD||node_h1|6|node|3|node|4|node}} ↔ {{CDD|branch_10ru|split2|node|4|node}} |
|||
*# [[Alternated order-5 hexagonal tiling honeycomb]], {{CDD||node_h1|6|node|3|node|5|node}} ↔ {{CDD|branch_10ru|split2|node|5|node}} |
|||
*# [[Alternated order-6 hexagonal tiling honeycomb]], {{CDD||node_h1|6|node|3|node|6|node}} ↔ {{CDD|branch_10ru|split2|node|6|node}} |
|||
*# [[Alternated square tiling honeycomb]], {{CDD|node_h1|4|node|4|node|3|node}} ↔ {{CDD|nodes_10ru|split2-44|node|3|node}} (Also quasiregular) |
|||
*# [[Cubic-square tiling honeycomb]], {{CDD|label4|branch_10r|4a4b|branch}} |
|||
*# [[Order-4 square tiling honeycomb]], {{CDD|label4|branch_10r|4a4b|branch|label4}} = {{CDD|node_1|4|node|4|node|4|node}} |
|||
*# [[Tetrahedral-triangular tiling honeycomb]], {{CDD|label6|branch|3ab|branch_10l}} |
|||
*9D hyperbolic paracompact honeycomb: |
|||
*# [[6 21 honeycomb|6<sub>21</sub> honeycomb]] (10-ic check), {{CDD|nodea_1|3a|nodea|3a|nodea|3a|nodea|3a|nodea|3a|nodea|3a|branch|3a|nodea|3a|nodea}} |
|||
==See also== |
==See also== |
||
*[[Semiregular polyhedron]] |
*[[Semiregular polyhedron]] |
||
{{geometry-stub}} |
|||
== References == |
|||
[[Category:Polytopes]] |
|||
*{{cite journal |
|||
| last1 = Blind | first1 = G. |
|||
| last2 = Blind | first2 = R. | author2-link = Roswitha Blind |
|||
| doi = 10.1007/BF02566640 |
|||
| issue = 1 |
|||
| journal = [[Commentarii Mathematici Helvetici]] |
|||
| mr = 1090169 |
|||
| pages = 150–154 |
|||
| title = The semiregular polytopes |
|||
| volume = 66 |
|||
| year = 1991 |
|||
| s2cid = 119695696 |
|||
}} |
|||
* {{cite book | first = H. S. M. | last = Coxeter | authorlink = Harold Scott MacDonald Coxeter | year = 1973 | title = [[Regular Polytopes (book)|Regular Polytopes]] | edition = 3rd | publisher = Dover Publications | location = New York | isbn = 0-486-61480-8}} |
|||
* {{cite journal |
|||
| last1 = Coxeter | first1 = H. S. M. | author1-link = Harold Scott MacDonald Coxeter |
|||
| last2 = Whitrow | first2 = G. J. |
|||
| doi = 10.1098/rspa.1950.0070 |
|||
| journal = [[Proceedings of the Royal Society]] |
|||
| mr = 0041576 |
|||
| pages = 417–437 |
|||
| title = World-structure and non-Euclidean honeycombs |
|||
| volume = 201 |
|||
| year = 1950 |
|||
| issue = 1066 | bibcode = 1950RSPSA.201..417C | s2cid = 120322123 }} |
|||
* {{Cite book | last = Elte | first = E. L. | authorlink = Emanuel Lodewijk Elte | title = The Semiregular Polytopes of the Hyperspaces | publisher = University of Groningen | location = Groningen | year = 1912 | isbn = 1-4181-7968-X}} |
|||
* {{cite journal | last=Gosset | first=Thorold | authorlink = Thorold Gosset | title = On the regular and semi-regular figures in space of ''n'' dimensions | journal = [[Messenger of Mathematics]] | volume = 29 | pages = 43–48 | year = 1900}} |
|||
* {{cite journal |
|||
| last = Makarov | first = P. V. |
|||
| department = Voprosy Diskret. Geom. |
|||
| journal = Mat. Issled. Akad. Nauk. Mold. |
|||
| mr = 958024 |
|||
| pages = 139–150, 177 |
|||
| title = On the derivation of four-dimensional semi-regular polytopes |
|||
| volume = 103 |
|||
| year = 1988 |
|||
}} |
|||
[[Category:Uniform polytopes]] |
|||
Latest revision as of 03:30, 24 July 2024
| 3D honeycombs | ||
|---|---|---|
 Simple tetroctahedric check |
 Complex tetroctahedric check | |
| 4D polytopes | ||
 Tetroctahedric |
 Octicosahedric |
 Tetricosahedric |
In geometry, by Thorold Gosset's definition a semiregular polytope is usually taken to be a polytope that is vertex-transitive and has all its facets being regular polytopes. E.L. Elte compiled a longer list in 1912 as The Semiregular Polytopes of the Hyperspaces which included a wider definition.
Gosset's list
[edit]In three-dimensional space and below, the terms semiregular polytope and uniform polytope have identical meanings, because all uniform polygons must be regular. However, since not all uniform polyhedra are regular, the number of semiregular polytopes in dimensions higher than three is much smaller than the number of uniform polytopes in the same number of dimensions.
The three convex semiregular 4-polytopes are the rectified 5-cell, snub 24-cell and rectified 600-cell. The only semiregular polytopes in higher dimensions are the k21 polytopes, where the rectified 5-cell is the special case of k = 0. These were all listed by Gosset, but a proof of the completeness of this list was not published until the work of Makarov (1988) for four dimensions, and Blind & Blind (1991) for higher dimensions.
- Gosset's 4-polytopes (with his names in parentheses)
- Rectified 5-cell (Tetroctahedric),







- Rectified 600-cell (Octicosahedric),







- Snub 24-cell (Tetricosahedric),






 ,
, 





 or
or 



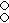
- Semiregular E-polytopes in higher dimensions
- 5-demicube (5-ic semi-regular), a 5-polytope,








 ↔
↔ 






- 221 polytope (6-ic semi-regular), a 6-polytope,








 or
or 






- 321 polytope (7-ic semi-regular), a 7-polytope,











- 421 polytope (8-ic semi-regular), an 8-polytope,













Euclidean honeycombs
[edit]
Semiregular polytopes can be extended to semiregular honeycombs. The semiregular Euclidean honeycombs are the tetrahedral-octahedral honeycomb (3D), gyrated alternated cubic honeycomb (3D) and the 521 honeycomb (8D).
Gosset honeycombs:
- Tetrahedral-octahedral honeycomb or alternated cubic honeycomb (Simple tetroctahedric check),






 ↔
↔ 



 (Also quasiregular polytope)
(Also quasiregular polytope) - Gyrated alternated cubic honeycomb (Complex tetroctahedric check),









Semiregular E-honeycomb:
- 521 honeycomb (9-ic check) (8D Euclidean honeycomb),















Gosset (1900) additionally allowed Euclidean honeycombs as facets of higher-dimensional Euclidean honeycombs, giving the following additional figures:
- Hypercubic honeycomb prism, named by Gosset as the (n – 1)-ic semi-check (analogous to a single rank or file of a chessboard)
- Alternated hexagonal slab honeycomb (tetroctahedric semi-check),







Hyperbolic honeycombs
[edit]
There are also hyperbolic uniform honeycombs composed of only regular cells (Coxeter & Whitrow 1950), including:
- Hyperbolic uniform honeycombs, 3D honeycombs:
- Paracompact uniform honeycombs, 3D honeycombs, which include uniform tilings as cells:
- Rectified order-6 tetrahedral honeycomb,







- Rectified square tiling honeycomb,







- Rectified order-4 square tiling honeycomb,






 ↔
↔ 






- Alternated order-6 cubic honeycomb,






 ↔
↔ 



 (Also quasiregular)
(Also quasiregular) - Alternated hexagonal tiling honeycomb,






 ↔
↔ 




- Alternated order-4 hexagonal tiling honeycomb,






 ↔
↔ 




- Alternated order-5 hexagonal tiling honeycomb,






 ↔
↔ 




- Alternated order-6 hexagonal tiling honeycomb,






 ↔
↔ 




- Alternated square tiling honeycomb,






 ↔
↔ 



 (Also quasiregular)
(Also quasiregular) - Cubic-square tiling honeycomb,




- Order-4 square tiling honeycomb,




 =
= 






- Tetrahedral-triangular tiling honeycomb,




- Rectified order-6 tetrahedral honeycomb,
- 9D hyperbolic paracompact honeycomb:
- 621 honeycomb (10-ic check),

















- 621 honeycomb (10-ic check),
See also
[edit]References
[edit]- Blind, G.; Blind, R. (1991). "The semiregular polytopes". Commentarii Mathematici Helvetici. 66 (1): 150–154. doi:10.1007/BF02566640. MR 1090169. S2CID 119695696.
- Coxeter, H. S. M. (1973). Regular Polytopes (3rd ed.). New York: Dover Publications. ISBN 0-486-61480-8.
- Coxeter, H. S. M.; Whitrow, G. J. (1950). "World-structure and non-Euclidean honeycombs". Proceedings of the Royal Society. 201 (1066): 417–437. Bibcode:1950RSPSA.201..417C. doi:10.1098/rspa.1950.0070. MR 0041576. S2CID 120322123.
- Elte, E. L. (1912). The Semiregular Polytopes of the Hyperspaces. Groningen: University of Groningen. ISBN 1-4181-7968-X.
- Gosset, Thorold (1900). "On the regular and semi-regular figures in space of n dimensions". Messenger of Mathematics. 29: 43–48.
- Makarov, P. V. (1988). "On the derivation of four-dimensional semi-regular polytopes". Voprosy Diskret. Geom. Mat. Issled. Akad. Nauk. Mold. 103: 139–150, 177. MR 0958024.
