Root locus analysis: Difference between revisions

Content deleted Content added

Inline

Latest revision as of 04:52, 31 July 2024

In control theory and stability theory, root locus analysis is a graphical method for examining how the roots of a system change with variation of a certain system parameter, commonly a gain within a feedback system. This is a technique used as a stability criterion in the field of classical control theory developed by Walter R. Evans which can determine stability of the system. The root locus plots the poles of the closed loop transfer function in the complex s-plane as a function of a gain parameter (see pole–zero plot).

Evans also invented in 1948 an analog computer to compute root loci, called a "Spirule" (after "spiral" and "slide rule"); it found wide use before the advent of digital computers.^[1]^[2]^[3]^[4]^[5]^[6]^[7]^[8]^[9]

Uses

In addition to determining the stability of the system, the root locus can be used to design the damping ratio (ζ) and natural frequency (ω_n) of a feedback system. Lines of constant damping ratio can be drawn radially from the origin and lines of constant natural frequency can be drawn as arccosine whose center points coincide with the origin. By selecting a point along the root locus that coincides with a desired damping ratio and natural frequency, a gain K can be calculated and implemented in the controller. More elaborate techniques of controller design using the root locus are available in most control textbooks: for instance, lag, lead, PI, PD and PID controllers can be designed approximately with this technique.

The definition of the damping ratio and natural frequency presumes that the overall feedback system is well approximated by a second order system; i.e. the system has a dominant pair of poles. This is often not the case, so it is good practice to simulate the final design to check if the project goals are satisfied.

Definition

The root locus of a feedback system is the graphical representation in the complex s-plane of the possible locations of its closed-loop poles for varying values of a certain system parameter. The points that are part of the root locus satisfy the angle condition. The value of the parameter for a certain point of the root locus can be obtained using the magnitude condition.

Suppose there is a feedback system with input signal $X(s)$ and output signal $Y(s)$ . The forward path transfer function is $G(s)$ ; the feedback path transfer function is $H(s)$ .

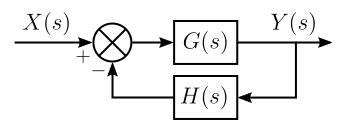
For this system, the closed-loop transfer function is given by^[10]

T(s)={\frac {Y(s)}{X(s)}}={\frac {G(s)}{1+G(s)H(s)}}

Thus, the closed-loop poles of the closed-loop transfer function are the roots of the characteristic equation $1+G(s)H(s)=0$ . The roots of this equation may be found wherever $1+G(s)H(s)=0$ .

In systems without pure delay, the product $G(s)H(s)$ is a rational polynomial function and may be expressed as^[11]

G(s)H(s)=K{\frac {(s+z_{1})(s+z_{2})\cdots (s+z_{m})}{(s+p_{1})(s+p_{2})\cdots (s+p_{n})}}

where $-z_{i}$ are the $m$ zeros, $-p_{i}$ are the $n$ poles, and $K$ is a scalar gain. Typically, a root locus diagram will indicate the transfer function's pole locations for varying values of the parameter $K$ . A root locus plot will be all those points in the s-plane where $G(s)H(s)=-1$ for any value of $K$ .

The factoring of $K$ and the use of simple monomials means the evaluation of the rational polynomial can be done with vector techniques that add or subtract angles and multiply or divide magnitudes. The vector formulation arises from the fact that each monomial term $(s-a)$ in the factored $G(s)H(s)$ represents the vector from $a$ to $s$ in the s-plane. The polynomial can be evaluated by considering the magnitudes and angles of each of these vectors.

According to vector mathematics, the angle of the result of the rational polynomial is the sum of all the angles in the numerator minus the sum of all the angles in the denominator. So to test whether a point in the s-plane is on the root locus, only the angles to all the open loop poles and zeros need be considered. This is known as the angle condition.

Similarly, the magnitude of the result of the rational polynomial is the product of all the magnitudes in the numerator divided by the product of all the magnitudes in the denominator. It turns out that the calculation of the magnitude is not needed to determine if a point in the s-plane is part of the root locus because $K$ varies and can take an arbitrary real value. For each point of the root locus a value of $K$ can be calculated. This is known as the magnitude condition.

The root locus only gives the location of closed loop poles as the gain $K$ is varied. The value of $K$ does not affect the location of the zeros. The open-loop zeros are the same as the closed-loop zeros.

Angle condition

A point $s$ of the complex s-plane satisfies the angle condition if

\angle (G(s)H(s))=\pi

which is the same as saying that

\sum _{i=1}^{m}\angle (s+z_{i})-\sum _{i=1}^{n}\angle (s+p_{i})=\pi

that is, the sum of the angles from the open-loop zeros to the point $s$ (measured per zero w.r.t. a horizontal running through that zero) minus the angles from the open-loop poles to the point $s$ (measured per pole w.r.t. a horizontal running through that pole) has to be equal to $\pi$ , or 180 degrees. Note that these interpretations should not be mistaken for the angle differences between the point $s$ and the zeros/poles.

Magnitude condition

A value of $K$ satisfies the magnitude condition for a given $s$ point of the root locus if

|G(s)H(s)|=1

which is the same as saying that

K{\frac {|s+z_{1}||s+z_{2}|\cdots |s+z_{m}|}{|s+p_{1}||s+p_{2}|\cdots |s+p_{n}|}}=1

.

Sketching root locus

Using a few basic rules, the root locus method can plot the overall shape of the path (locus) traversed by the roots as the value of $K$ varies. The plot of the root locus then gives an idea of the stability and dynamics of this feedback system for different values of $K$ .^[12]^[13] The rules are the following:

Mark open-loop poles and zeros
Mark real axis portion to the left of an odd number of poles and zeros
Find asymptotes

Let P be the number of poles and Z be the number of zeros:

P-Z={\text{number of asymptotes}}\,

The asymptotes intersect the real axis at $\alpha$ (which is called the centroid) and depart at angle $\phi$ given by:

\phi _{l}={\frac {180^{\circ }+(l-1)360^{\circ }}{P-Z}},l=1,2,\ldots ,P-Z

\alpha ={\frac {\operatorname {Re} \left(\sum _{P}-\sum _{Z}\right)}{P-Z}}

where $\sum _{P}$ is the sum of all the locations of the poles, $\sum _{Z}$ is the sum of all the locations of the explicit zeros and $\operatorname {Re} ()$ denotes that we are only interested in the real part.

Phase condition on test point to find angle of departure
Compute breakaway/break-in points

The breakaway points are located at the roots of the following equation:

{\frac {dG(s)H(s)}{ds}}=0{\text{ or }}{\frac {d{\overline {GH}}(z)}{dz}}=0

Once you solve for z, the real roots give you the breakaway/reentry points. Complex roots correspond to a lack of breakaway/reentry.

Plotting root locus

Given the general closed-loop denominator rational polynomial

1+G(s)H(s)=1+K{\frac {b_{m}s^{m}+\ldots +b_{1}s+b_{0}}{s^{n}+a_{n-1}s^{n-1}+\ldots +a_{1}s+a_{0}}},

the characteristic equation can be simplified to

s^{n}+a_{n-1}s^{n-1}+\ldots +(a_{m}+Kb_{m})s^{m}+\ldots +(a_{1}+Kb_{1})s+(a_{0}+Kb_{0})=0.

The solutions of $s$ to this equation are the root loci of the closed-loop transfer function.

Example

Given

1+G(s)H(s)=1+K{\frac {s+3}{s^{3}+3s^{2}+5s+1}},

we will have the characteristic equation

s^{3}+3s^{2}+(5+K)s+(1+3K)=0.

The following MATLAB code will plot the root locus of the closed-loop transfer function as $K$ varies using the described manual method as well as the rlocus built-in function:

% Manual method
K_array = (0:0.1:220).'; % .' is a transpose. Looking up in Matlab documentation.
NK = length(K_array);
x_array = zeros(NK, 3);
y_array = zeros(NK, 3);

for nK = 1:NK
   K = K_array(nK);
   C = [1, 3, (5 + K), (1 + 3*K)];
   r = roots(C).';
   x_array(nK,:) = real(r);
   y_array(nK,:) = imag(r);
end

figure();
plot(x_array, y_array);
grid on;

% Built-in method
sys = tf([1, 3], [1, 3, 5, 1]);
figure();
rlocus(sys);

The following Python code can also be used to calculate and plot the root locus of the closed-loop transfer function using the Python Control Systems Library^[14] and Matplotlib^[15].

import control as ct
import matplotlib.pyplot as plt

# Define the transfer function
sys = ct.TransferFunction([1, 3], [1, 3, 5, 1])

# Calculate and plot the root locus
roots, gains = ct.root_locus(sys, plot=True)
plt.show()

z-plane versus s-plane

The root locus method can also be used for the analysis of sampled data systems by computing the root locus in the z-plane, the discrete counterpart of the s-plane. The equation $z = e sT$ maps continuous s-plane poles (not zeros) into the z-domain, where $T$ is the sampling period. The stable, left half s-plane maps into the interior of the unit circle of the z-plane, with the s-plane origin equating to |z| = 1 (because e⁰ = 1). A diagonal line of constant damping in the s-plane maps around a spiral from (1,0) in the z plane as it curves in toward the origin. The Nyquist aliasing criteria is expressed graphically in the z-plane by the x-axis, where $ωnT = π$ . The line of constant damping just described spirals in indefinitely but in sampled data systems, frequency content is aliased down to lower frequencies by integral multiples of the Nyquist frequency. That is, the sampled response appears as a lower frequency and better damped as well since the root in the z-plane maps equally well to the first loop of a different, better damped spiral curve of constant damping. Many other interesting and relevant mapping properties can be described, not least that z-plane controllers, having the property that they may be directly implemented from the z-plane transfer function (zero/pole ratio of polynomials), can be imagined graphically on a z-plane plot of the open loop transfer function, and immediately analyzed utilizing root locus.

Since root locus is a graphical angle technique, root locus rules work the same in the $z$ and $s$ planes.

The idea of a root locus can be applied to many systems where a single parameter $K$ is varied. For example, it is useful to sweep any system parameter for which the exact value is uncertain in order to determine its behavior.

References

^ "1990". McKelvey School of Engineering at Washington University in St. Louis. Retrieved 2023-03-12.
^ Evans, Walter R. (1965), Spirule Instructions, Whittier, CA: The Spirule Company
^ Robert H., J.C. (2012). Dynamics of Physical Systems. Dover Civil and Mechanical Engineering. Dover Publications. p. 727. ISBN 978-0-486-13969-2. Retrieved 2023-03-12.
^ Doebelin, E.O. (1985). Control System Principles and Design. Wiley. p. 312. ISBN 978-0-471-08815-8. Retrieved 2023-03-12.
^ Savant, C.J. (1958). Basic Feedback Control System Design. Engineering special collection. McGraw-Hill. Retrieved 2023-03-12.
^ Harris, L.D. (1961). Introduction to Feedback Systems. Wiley. ISBN 978-0-598-48455-0. Retrieved 2023-03-12.
^ D'Azzo, J.J.; Houpis, C.H. (1968). Principles of Electrical Engineering: Electric Circuits, Electronics, Instrumentation, Energy Conversion, Control Systems, Computers. C. E. Merrill Publishing Company. Retrieved 2023-03-12.
^ Gupta, S.C.; Hasdorff, L. (1983). Fundamentals of Automatic Control. Krieger. ISBN 978-0-89874-578-8. Retrieved 2023-03-12.
^ Dransfield, P. (1968). Engineering Systems and Automatic Control. Prentice-Hall. Retrieved 2023-03-12.
^ Kuo 1967, p. 331.
^ Kuo 1967, p. 332.
^ Evans, W. R. (January 1948), "Graphical Analysis of Control Systems", Trans. AIEE, 67 (1): 547–551, doi:10.1109/T-AIEE.1948.5059708, ISSN 0096-3860, S2CID 51634121
^ Evans, W. R. (January 1950), "Control Systems Synthesis by Root Locus Method", Trans. AIEE, 69 (1): 66–69, doi:10.1109/T-AIEE.1950.5060121, ISSN 0096-3860, S2CID 51633514
^ The Python Control Systems Library, Control Systems Library for Python, 2023-12-19, retrieved 2023-12-19
^ "Matplotlib — Visualization with Python". matplotlib.org. Retrieved 2023-12-19.

Kuo, Benjamin C. (1967). "Root Locus Technique". Automatic Control Systems (second ed.). Englewood Cliffs, NJ: Prentice-Hall. pp. 329–388. ASIN B000KPT04C. LCCN 67016388. OCLC 3805225.

External links

Wikibooks: Control Systems/Root Locus
Carnegie Mellon / University of Michigan Tutorial
Excellent examples. Start with example 5 and proceed backwards through 4 to 1. Also visit the main page
The root-locus method: Drawing by hand techniques
"RootLocs": A free multi-featured root-locus plotter for Mac and Windows platforms
"Root Locus": A free root-locus plotter/analyzer for Windows
Root Locus at ControlTheoryPro.com
Root Locus Analysis of Control Systems
MATLAB function for computing root locus of a SISO open-loop model
Wechsler, E. R. (January–March 1983), "Root Locus Algorithms for Programmable Pocket Calculators" (PDF), Telecommunications and Data Acquisition Progress Report, 73, NASA: 60–64, Bibcode:1983TDAPR..73...60W
Mathematica function for plotting the root locus
Šekara, Tomislav B.; Rapaić, Milan R. (1 October 2015). "A revision of root locus method with applications". Journal of Process Control. 34: 26–34. doi:10.1016/j.jprocont.2015.07.007.

[McKelvey_School_of_Engineering_at_Washington_University_in_St._Louis-1] "1990". McKelvey School of Engineering at Washington University in St. Louis. Retrieved 2023-03-12.

[2] Evans, Walter R. (1965), Spirule Instructions, Whittier, CA: The Spirule Company

[Robert_H._2012_p._727-3] Robert H., J.C. (2012). Dynamics of Physical Systems. Dover Civil and Mechanical Engineering. Dover Publications. p. 727. ISBN 978-0-486-13969-2. Retrieved 2023-03-12.

[Doebelin_1985_p._312-4] Doebelin, E.O. (1985). Control System Principles and Design. Wiley. p. 312. ISBN 978-0-471-08815-8. Retrieved 2023-03-12.

[Savant_1958_p.-5] Savant, C.J. (1958). Basic Feedback Control System Design. Engineering special collection. McGraw-Hill. Retrieved 2023-03-12.

[Harris_1961_p.-6] Harris, L.D. (1961). Introduction to Feedback Systems. Wiley. ISBN 978-0-598-48455-0. Retrieved 2023-03-12.

[DAzzo_Houpis_1968_p.-7] D'Azzo, J.J.; Houpis, C.H. (1968). Principles of Electrical Engineering: Electric Circuits, Electronics, Instrumentation, Energy Conversion, Control Systems, Computers. C. E. Merrill Publishing Company. Retrieved 2023-03-12.

[Gupta_Hasdorff_1983_p.-8] Gupta, S.C.; Hasdorff, L. (1983). Fundamentals of Automatic Control. Krieger. ISBN 978-0-89874-578-8. Retrieved 2023-03-12.

[Dransfield_1968_p.-9] Dransfield, P. (1968). Engineering Systems and Automatic Control. Prentice-Hall. Retrieved 2023-03-12.

[FOOTNOTEKuo1967331-10] Kuo 1967, p. 331.

[FOOTNOTEKuo1967332-11] Kuo 1967, p. 332.

[12] Evans, W. R. (January 1948), "Graphical Analysis of Control Systems", Trans. AIEE, 67 (1): 547–551, doi:10.1109/T-AIEE.1948.5059708, ISSN 0096-3860, S2CID 51634121

[13] Evans, W. R. (January 1950), "Control Systems Synthesis by Root Locus Method", Trans. AIEE, 69 (1): 66–69, doi:10.1109/T-AIEE.1950.5060121, ISSN 0096-3860, S2CID 51633514

[14] The Python Control Systems Library, Control Systems Library for Python, 2023-12-19, retrieved 2023-12-19

[15] "Matplotlib — Visualization with Python". matplotlib.org. Retrieved 2023-12-19.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]