Lambert series

For generalized Lambert series, see Appell–Lerch sum.

Function ${\textstyle S(q)=\sum _{n=1}^{\infty }{\frac {q^{n}}{1-q^{n}}}}$, represented as a Matplotlib plot, using a version of the domain coloring method

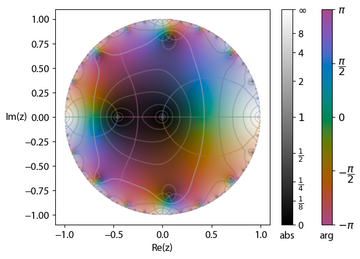
In mathematics, a Lambert series, named for Johann Heinrich Lambert, is a series taking the form

$S(q)=\sum _{n=1}^{\infty }a_{n}{\frac {q^{n}}{1-q^{n}}}.$

It can be resummed formally by expanding the denominator:

$S(q)=\sum _{n=1}^{\infty }a_{n}\sum _{k=1}^{\infty }q^{nk}=\sum _{m=1}^{\infty }b_{m}q^{m}$

where the coefficients of the new series are given by the Dirichlet convolution of a_n with the constant function 1(n) = 1:

$b_{m}=(a*1)(m)=\sum _{n\mid m}a_{n}.\,$

This series may be inverted by means of the Möbius inversion formula, and is an example of a Möbius transform.

Examples

Since this last sum is a typical number-theoretic sum, almost any natural multiplicative function will be exactly summable when used in a Lambert series. Thus, for example, one has

$\sum _{n=1}^{\infty }q^{n}\sigma _{0}(n)=\sum _{n=1}^{\infty }{\frac {q^{n}}{1-q^{n}}}$

where $\sigma _{0}(n)=d(n)$ is the number of positive divisors of the number n.

For the higher order sum-of-divisor functions, one has

$\sum _{n=1}^{\infty }q^{n}\sigma _{\alpha }(n)=\sum _{n=1}^{\infty }{\frac {n^{\alpha }q^{n}}{1-q^{n}}}$

where $\alpha$ is any complex number and

$\sigma _{\alpha }(n)=({\textrm {Id}}_{\alpha }*1)(n)=\sum _{d\mid n}d^{\alpha }\,$

is the divisor function. In particular, for $\alpha =1$, the Lambert series one gets is

$q{\frac {F'(q)}{F(q)}}$

which is (up to the factor of $q$) the logarithmic derivative of the usual generating function for partition numbers

$F(q):={\frac {1}{\phi (q)}}=\sum _{k=0}^{\infty }p(k)q^{k}=\prod _{n=1}^{\infty }{\frac {1}{1-q^{n}}}.$

Additional Lambert series related to the previous identity include those for the variants of the Möbius function given below $\mu (n)$

$\sum _{n=1}^{\infty }\mu (n)\,{\frac {q^{n}}{1-q^{n}}}=q.$

Related Lambert series over the Möbius function include the following identities for any prime $\alpha \in \mathbb {Z} ^{+}$:

$\sum _{n\geq 1}{\frac {\mu (n)q^{n}}{1+q^{n}}}=q-2q^{2}$

$\sum _{n\geq 1}{\frac {\mu (\alpha n)q^{n}}{1-q^{n}}}=-\sum _{n\geq 0}q^{\alpha ^{n}}.$

The proof of the first identity above follows from a multi-section (or bisection) identity of these Lambert series generating functions in the following form where we denote $L_{f}(q):=q$ to be the Lambert series generating function of the arithmetic function f:

${\begin{aligned}\sum _{n\geq 1}{\frac {f(n)q^{n}}{1+q^{n}}}&=\sum _{n\geq 1}{\frac {f(n)q^{n}}{1-q^{n}}}-\sum _{n\geq 1}{\frac {2f(n)q^{2n}}{1-q^{2n}}}\\&=L_{f}(q)-2\cdot L_{f}(q^{2}).\end{aligned}}$

For Euler's totient function $\varphi (n)$:

$\sum _{n=1}^{\infty }\varphi (n)\,{\frac {q^{n}}{1-q^{n}}}={\frac {q}{(1-q)^{2}}}.$

For Von Mangoldt function $\Lambda (n)$:

$\sum _{n=1}^{\infty }\Lambda (n)\,{\frac {q^{n}}{1-q^{n}}}=\sum _{n=1}^{\infty }\log(n)q^{n}$

For Liouville's function $\lambda (n)$:

$\sum _{n=1}^{\infty }\lambda (n)\,{\frac {q^{n}}{1-q^{n}}}=\sum _{n=1}^{\infty }q^{n^{2}}$

with the sum on the right similar to the Ramanujan theta function, or Jacobi theta function $\vartheta _{3}(q)$. Note that Lambert series in which the a_n are trigonometric functions, for example, a_n = sin(2n x), can be evaluated by various combinations of the logarithmic derivatives of Jacobi theta functions.

Generally speaking, we can extend the previous generating function expansion by letting $\chi _{m}(n)$ denote the characteristic function of the $m^{th}$ powers, $n=k^{m}\in \mathbb {Z} ^{+}$, for positive natural numbers $m>2$ and defining the generalized m-Liouville lambda function to be the arithmetic function satisfying $\chi _{m}(n):=(1\ast \lambda _{m})(n)$. This definition of $\lambda _{m}(n)$ clearly implies that $\lambda _{m}(n)=\sum _{d^{m}|n}\mu \left({\frac {n}{d^{m}}}\right)$, which in turn shows that

$\sum _{n\geq 1}{\frac {\lambda _{m}(n)q^{n}}{1-q^{n}}}=\sum _{n\geq 1}q^{n^{m}},\ {\text{ for }}m\geq 2.$

We also have a slightly more generalized Lambert series expansion generating the sum of squares function $r_{2}(n)$ in the form of

$\sum _{n=1}^{\infty }{\frac {4\cdot (-1)^{n+1}q^{2n+1}}{1-q^{2n+1}}}=\sum _{m=1}^{\infty }r_{2}(m)q^{m}.$

In general, if we write the Lambert series over $f(n)$ which generates the arithmetic functions $g(m)=(f\ast 1)(m)$, the next pairs of functions correspond to other well-known convolutions expressed by their Lambert series generating functions in the forms of

$(f,g)=(\mu ,\varepsilon ),(\varphi ,\operatorname {Id} _{1}),(\lambda ,\chi _{\operatorname {sq} }),(\Lambda ,\log ),(|\mu |,2^{\omega }),(J_{t},\operatorname {Id} _{t}),(d^{3},(d\ast 1)^{2}),$

where $\varepsilon (n)=\delta _{n,1}$ is the multiplicative identity for Dirichlet convolutions, $\operatorname {Id} _{k}(n)=n^{k}$ is the identity function for $k^{th}$ powers, $\chi _{\operatorname {sq} }$ denotes the characteristic function for the squares, $\omega (n)$ which counts the number of distinct prime factors of $n$ (see prime omega function), $J_{t}$ is Jordan's totient function, and $d(n)=\sigma _{0}(n)$ is the divisor function (see Dirichlet convolutions).

The conventional use of the letter q in the summations is a historical usage, referring to its origins in the theory of elliptic curves and theta functions, as the nome.

Alternate form

Substituting $q=e^{-z}$ one obtains another common form for the series, as

$\sum _{n=1}^{\infty }{\frac {a_{n}}{e^{zn}-1}}=\sum _{m=1}^{\infty }b_{m}e^{-mz}$

where

$b_{m}=(a*1)(m)=\sum _{d\mid m}a_{d}\,$

as before. Examples of Lambert series in this form, with $z=2\pi$, occur in expressions for the Riemann zeta function for odd integer values; see Zeta constants for details.

Current usage

In the literature we find Lambert series applied to a wide variety of sums. For example, since $q^{n}/(1-q^{n})=\mathrm {Li} _{0}(q^{n})$ is a polylogarithm function, we may refer to any sum of the form

$\sum _{n=1}^{\infty }{\frac {\xi ^{n}\,\mathrm {Li} _{u}(\alpha q^{n})}{n^{s}}}=\sum _{n=1}^{\infty }{\frac {\alpha ^{n}\,\mathrm {Li} _{s}(\xi q^{n})}{n^{u}}}$

as a Lambert series, assuming that the parameters are suitably restricted. Thus

$12\left(\sum _{n=1}^{\infty }n^{2}\,\mathrm {Li} _{-1}(q^{n})\right)^{\!2}=\sum _{n=1}^{\infty }n^{2}\,\mathrm {Li} _{-5}(q^{n})-\sum _{n=1}^{\infty }n^{4}\,\mathrm {Li} _{-3}(q^{n}),$

which holds for all complex q not on the unit circle, would be considered a Lambert series identity. This identity follows in a straightforward fashion from some identities published by the Indian mathematician S. Ramanujan. A very thorough exploration of Ramanujan's works can be found in the works by Bruce Berndt.

Factorization theorems

A somewhat newer construction recently published over 2017–2018 relates to so-termed Lambert series factorization theorems of the form

$\sum _{n\geq 1}{\frac {a_{n}q^{n}}{1\pm q^{n}}}={\frac {1}{(\mp q;q)_{\infty }}}\sum _{n\geq 1}\left((s_{o}(n,k)\pm s_{e}(n,k))a_{k}\right)q^{n},$

where $s_{o}(n,k)\pm s_{e}(n,k)=[q^{n}](\mp q;q)_{\infty }{\frac {q^{k}}{1\pm q^{k}}}$ is the respective sum or difference of the restricted partition functions $s_{e/o}(n,k)$ which denote the number of $k$'s in all partitions of $n$ into an even (respectively, odd) number of distinct parts. Let $s_{n,k}:=s_{e}(n,k)-s_{o}(n,k)=[q^{n}](q;q)_{\infty }{\frac {q^{k}}{1-q^{k}}}$ denote the invertible lower triangular sequence whose first few values are shown in the table below.

n \ k	1	2	3	4	5	6	7	8
1	1	0	0	0	0	0	0	0
2	0	1	0	0	0	0	0	0
3	-1	-1	1	0	0	0	0	0
4	-1	0	-1	1	0	0	0	0
5	-1	-1	-1	-1	1	0	0	0
6	0	0	1	-1	-1	1	0	0
7	0	0	-1	0	-1	-1	1	0
8	1	0	0	1	0	-1	-1	1

Another characteristic form of the Lambert series factorization theorem expansions is given by

$L_{f}(q):=\sum _{n\geq 1}{\frac {f(n)q^{n}}{1-q^{n}}}={\frac {1}{(q;q)_{\infty }}}\sum _{n\geq 1}\left(s_{n,k}f(k)\right)q^{n},$

where $(q;q)_{\infty }$ is the (infinite) q-Pochhammer symbol. The invertible matrix products on the right-hand-side of the previous equation correspond to inverse matrix products whose lower triangular entries are given in terms of the partition function and the Möbius function by the divisor sums

$s_{n,k}^{(-1)}=\sum _{d|n}p(d-k)\mu \left({\frac {n}{d}}\right)$

The next table lists the first several rows of these corresponding inverse matrices.

n \ k	1	2	3	4	5	6	7	8
1	1	0	0	0	0	0	0	0
2	0	1	0	0	0	0	0	0
3	1	1	1	0	0	0	0	0
4	2	1	1	1	0	0	0	0
5	4	3	2	1	1	0	0	0
6	5	3	2	2	1	1	0	0
7	10	7	5	3	2	1	1	0
8	12	9	6	4	3	2	1	1

We let $G_{j}:={\frac {1}{2}}\left\lceil {\frac {j}{2}}\right\rceil \left\lceil {\frac {3j+1}{2}}\right\rceil$ denote the sequence of interleaved pentagonal numbers, i.e., so that the pentagonal number theorem is expanded in the form of

$(q;q)_{\infty }=\sum _{n\geq 0}(-1)^{\left\lceil {\frac {n}{2}}\right\rceil }q^{G_{n}}.$

Then for any Lambert series $L_{f}(q)$ generating the sequence of $g(n)=(f\ast 1)(n)$, we have the corresponding inversion relation of the factorization theorem expanded above given by

$f(n)=\sum _{k=1}^{n}\sum _{d|n}p(d-k)\mu (n/d)\times \sum _{j:k-G_{j}>0}(-1)^{\left\lceil {\frac {j}{2}}\right\rceil }b(k-G_{j}).$

This work on Lambert series factorization theorems is extended in to more general expansions of the form

$\sum _{n\geq 1}{\frac {a_{n}q^{n}}{1-q^{n}}}={\frac {1}{C(q)}}\sum _{n\geq 1}\left(\sum _{k=1}^{n}s_{n,k}(\gamma ){\widetilde {a}}_{k}(\gamma )\right)q^{n},$

where $C(q)$ is any (partition-related) reciprocal generating function, $\gamma (n)$ is any arithmetic function, and where the modified coefficients are expanded by

${\widetilde {a}}_{k}(\gamma )=\sum _{d|k}\sum _{r|{\frac {k}{d}}}a_{d}\gamma (r).$

The corresponding inverse matrices in the above expansion satisfy

$s_{n,k}^{(-1)}(\gamma )=\sum _{d|n}[q^{d-k}]{\frac {1}{C(q)}}\gamma \left({\frac {n}{d}}\right),$

so that as in the first variant of the Lambert factorization theorem above we obtain an inversion relation for the right-hand-side coefficients of the form

${\widetilde {a}}_{k}(\gamma )=\sum _{k=1}^{n}s_{n,k}^{(-1)}(\gamma )\times [q^{k}]\left(\sum _{d=1}^{k}{\frac {a_{d}q^{d}}{1-q^{d}}}C(q)\right).$

Recurrence relations

Within this section we define the following functions for natural numbers $n,x\geq 1$:

$g_{f}(n):=(f\ast 1)(n),$

$\Sigma _{f}(x):=\sum _{1\leq n\leq x}g_{f}(n).$

We also adopt the notation from the previous section that

$s_{n,k}=[q^{n}](q;q)_{\infty }{\frac {q^{k}}{1-q^{k}}},$

where $(q;q)_{\infty }$ is the infinite q-Pochhammer symbol. Then we have the following recurrence relations for involving these functions and the pentagonal numbers proved in:

$g_{f}(n+1)=\sum _{b=\pm 1}\sum _{k=1}^{\left\lfloor {\frac {{\sqrt {24n+1}}-b}{6}}\right\rfloor }(-1)^{k+1}g_{f}\left(n+1-{\frac {k(3k+b)}{2}}\right)+\sum _{k=1}^{n+1}s_{n+1,k}f(k),$

$\Sigma _{f}(x+1)=\sum _{b=\pm 1}\sum _{k=1}^{\left\lfloor {\frac {{\sqrt {24x+1}}-b}{6}}\right\rfloor }(-1)^{k+1}\Sigma _{f}\left(n+1-{\frac {k(3k+b)}{2}}\right)+\sum _{n=0}^{x}\sum _{k=1}^{n+1}s_{n+1,k}f(k).$

Derivatives

Derivatives of a Lambert series can be obtained by differentiation of the series termwise with respect to $q$. We have the following identities for the termwise $s^{th}$ derivatives of a Lambert series for any $s\geq 1$

$q^{s}\cdot D^{(s)}\left[{\frac {q^{i}}{1-q^{i}}}\right]=\sum _{m=0}^{s}\sum _{k=0}^{m}\left[{\begin{matrix}s\\m\end{matrix}}\right]\left\{{\begin{matrix}m\\k\end{matrix}}\right\}{\frac {(-1)^{s-k}k!i^{m}}{(1-q^{i})^{k+1}}}$

$q^{s}\cdot D^{(s)}\left[{\frac {q^{i}}{1-q^{i}}}\right]=\sum _{r=0}^{s}\left[\sum _{m=0}^{s}\sum _{k=0}^{m}\left[{\begin{matrix}s\\m\end{matrix}}\right]\left\{{\begin{matrix}m\\k\end{matrix}}\right\}{\binom {s-k}{r}}{\frac {(-1)^{s-k-r}k!i^{m}}{(1-q^{i})^{k+1}}}\right]q^{(r+1)i},$

where the bracketed triangular coefficients in the previous equations denote the Stirling numbers of the first and second kinds. We also have the next identity for extracting the individual coefficients of the terms implicit to the previous expansions given in the form of

$[q^{n}]\left(\sum _{i\geq t}{\frac {a_{i}q^{mi}}{(1-q^{i})^{k+1}}}\right)=\sum _{\begin{matrix}d|n\\t\leq d\leq \left\lfloor {\frac {n}{m}}\right\rfloor \end{matrix}}{\binom {{\frac {n}{d}}-m+k}{k}}a_{d}.$

Now if we define the functions $A_{t}(n)$ for any $n,t\geq 1$ by

$A_{t}(n):=\sum _{\begin{matrix}0\leq k\leq m\leq t\\0\leq r\leq t\end{matrix}}\sum _{d|n}\left[{\begin{matrix}t\\m\end{matrix}}\right]\left\{{\begin{matrix}m\\k\end{matrix}}\right\}{\binom {t-k}{r}}{\binom {{\frac {n}{d}}-1-r+k}{k}}(-1)^{t-k-r}k!d^{m}\cdot a_{d}\cdot \left[t\leq d\leq \left\lfloor {\frac {n}{r+1}}\right\rfloor \right]_{\delta },$

where $[\cdot ]_{\delta }$ denotes Iverson's convention, then we have the coefficients for the $t^{th}$ derivatives of a Lambert series given by

${\begin{aligned}A_{t}(n)&=[q^{n}]\left(q^{t}\cdot D^{(t)}\left[\sum _{i\geq t}{\frac {a_{i}q^{i}}{1-q^{i}}}\right]\right)\\&=[q^{n}]\left(\sum _{n\geq 1}{\frac {(A_{t}\ast \mu )(n)q^{n}}{1-q^{n}}}\right).\end{aligned}}$

Of course, by a typical argument purely by operations on formal power series we also have that

$[q^{n}]\left(q^{t}\cdot D^{(t)}\left[\sum _{i\geq 1}{\frac {f(i)q^{i}}{1-q^{i}}}\right]\right)={\frac {n!}{(n-t)!}}\cdot (f\ast 1)(n).$

See also

• Erdős–Borwein constant
• Arithmetic function
• Dirichlet convolution

References

• Berry, Michael V. (2010). Functions of Number Theory. CAMBRIDGE UNIVERSITY PRESS. pp. 637–641. ISBN 978-0-521-19225-5.
• Lambert, Preston A. (1904). "Expansions of algebraic functions at singular points". Proc. Am. Philos. Soc. 43 (176): 164–172. JSTOR 983503.
• Apostol, Tom M. (1976), Introduction to analytic number theory, Undergraduate Texts in Mathematics, New York-Heidelberg: Springer-Verlag, ISBN 978-0-387-90163-3, MR 0434929, Zbl 0335.10001
• "Lambert series", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• Weisstein, Eric W. "Lambert Series". MathWorld.
• Schmidt, Maxie Dion (2020-04-06). "A catalog of interesting and useful Lambert series identities". arXiv:2004.02976 [math.NT].