Maximum spacing estimation: Difference between revisions
Marcocapelle (talk | contribs) removed Category:Estimation theory; added Category:Estimation methods using HotCat |
swap out deadlink |
||
| (23 intermediate revisions by 20 users not shown) | |||
| Line 1: | Line 1: | ||
{{Short description|Method of estimating a statistical model's parameters}} |
|||
[[Image:Spacings.svg|thumb|right|260px|The maximum spacing method tries to find a distribution function such that the spacings, ''D''<sub>(''i'')</sub>, are all approximately of the same length. This is done by maximizing their [[geometric mean]].]] |
|||
[[File:Spacings.svg|thumb|260px|The maximum spacing method tries to find a distribution function such that the spacings, ''D''<sub>(''i'')</sub>, are all approximately of the same length. This is done by maximizing their [[geometric mean]].]] |
|||
In [[statistics]], '''maximum spacing estimation''' ('''MSE''' or '''MSP'''), or '''maximum product of spacing estimation (MPS)''', is a method for estimating the parameters of a univariate [[parametric model|statistical model]].<ref name="CA83">{{harvtxt|Cheng|Amin|1983}}</ref> The method requires maximization of the [[geometric mean]] of ''spacings'' in the data, which are the differences between the values of the [[cumulative distribution function]] at neighbouring data points. |
In [[statistics]], '''maximum spacing estimation''' ('''MSE''' or '''MSP'''), or '''maximum product of spacing estimation (MPS)''', is a method for estimating the parameters of a univariate [[parametric model|statistical model]].<ref name="CA83">{{harvtxt|Cheng|Amin|1983}}</ref> The method requires maximization of the [[geometric mean]] of ''spacings'' in the data, which are the differences between the values of the [[cumulative distribution function]] at neighbouring data points. |
||
| Line 5: | Line 6: | ||
The concept underlying the method is based on the [[probability integral transform]], in that a set of independent random samples derived from any random variable should on average be uniformly distributed with respect to the cumulative distribution function of the random variable. The MPS method chooses the parameter values that make the observed data as uniform as possible, according to a specific quantitative measure of uniformity. |
The concept underlying the method is based on the [[probability integral transform]], in that a set of independent random samples derived from any random variable should on average be uniformly distributed with respect to the cumulative distribution function of the random variable. The MPS method chooses the parameter values that make the observed data as uniform as possible, according to a specific quantitative measure of uniformity. |
||
One of the most common methods for estimating the parameters of a distribution from data, the method of [[maximum likelihood]] (MLE), can break down in various cases, such as involving certain mixtures of continuous distributions.<ref name |
One of the most common methods for estimating the parameters of a distribution from data, the method of [[maximum likelihood]] (MLE), can break down in various cases, such as involving certain mixtures of continuous distributions.<ref name="R84">{{harvtxt|Ranneby|1984}}</ref> In these cases the method of maximum spacing estimation may be successful. |
||
Apart from its use in pure mathematics and statistics, the trial applications of the method have been reported using data from fields such as [[hydrology]],<ref>{{harvtxt|Hall|al.|2004}}</ref> [[econometrics]],<ref>{{harvtxt|Anatolyev|Kosenok|2004}}</ref> [[magnetic resonance imaging]],<ref>{{harvtxt|Pieciak|2014}}</ref> and others.<ref>{{harvtxt|Wong|Li|2006}}</ref> |
Apart from its use in pure mathematics and statistics, the trial applications of the method have been reported using data from fields such as [[hydrology]],<ref>{{harvtxt|Hall|al.|2004}}</ref> [[econometrics]],<ref>{{harvtxt|Anatolyev|Kosenok|2004}}</ref> [[magnetic resonance imaging]],<ref>{{harvtxt|Pieciak|2014}}</ref> and others.<ref>{{harvtxt|Wong|Li|2006}}</ref> |
||
==History and usage== |
== History and usage == |
||
The MSE method was derived independently by Russel Cheng and Nik Amin at the [[Cardiff University|University of Wales Institute of Science and Technology]], and Bo Ranneby at the [[Swedish University of Agricultural Sciences]].<ref name |
The MSE method was derived independently by Russel Cheng and Nik Amin at the [[Cardiff University|University of Wales Institute of Science and Technology]], and Bo Ranneby at the [[Swedish University of Agricultural Sciences]].<ref name="R84" /> The authors explained that due to the [[probability integral transform]] at the true parameter, the “spacing” between each observation should be uniformly distributed. This would imply that the difference between the values of the [[cumulative distribution function]] at consecutive observations should be equal. This is the case that maximizes the [[geometric mean]] of such spacings, so solving for the parameters that maximize the geometric mean would achieve the “best” fit as defined this way. {{harvtxt|Ranneby|1984}} justified the method by demonstrating that it is an estimator of the [[Kullback–Leibler divergence]], similar to [[maximum likelihood estimation]], but with more robust properties for some classes of problems. |
||
There are certain distributions, especially those with three or more parameters, whose [[Likelihood# |
There are certain distributions, especially those with three or more parameters, whose [[Likelihood#Relationship between the likelihood and probability density functions|likelihoods]] may become infinite along certain paths in the [[parameter space]]. Using maximum likelihood to estimate these parameters often breaks down, with one parameter tending to the specific value that causes the likelihood to be infinite, rendering the other parameters inconsistent. The method of maximum spacings, however, being dependent on the difference between points on the cumulative distribution function and not individual likelihood points, does not have this issue, and will return valid results over a much wider array of distributions.<ref name="CA83" /> |
||
The distributions that tend to have likelihood issues are often those used to model physical phenomena. {{harvtxt|Hall|al.|2004}} seek to analyze flood alleviation methods, which requires accurate models of river flood effects. The distributions that better model these effects are all three-parameter models, which suffer from the infinite likelihood issue described above, leading to |
The distributions that tend to have likelihood issues are often those used to model physical phenomena. {{harvtxt|Hall|al.|2004}} seek to analyze flood alleviation methods, which requires accurate models of river flood effects. The distributions that better model these effects are all three-parameter models, which suffer from the infinite likelihood issue described above, leading to Hall's investigation of the maximum spacing procedure. {{harvtxt|Wong|Li|2006}}, when comparing the method to maximum likelihood, use various data sets ranging from a set on the oldest ages at death in Sweden between 1905 and 1958 to a set containing annual maximum wind speeds. |
||
==Definition== |
== Definition == |
||
Given an [[iid]] [[random sample]] {''x''<sub>1</sub>, |
Given an [[iid]] [[random sample]] {''x''<sub>1</sub>, ..., ''x''<sub>''n''</sub>} of size ''n'' from a [[univariate distribution]] with continuous cumulative distribution function ''F''(''x'';''θ''<sub>0</sub>), where ''θ''<sub>0</sub> ∈ Θ is an unknown parameter to be [[estimation|estimated]], let {''x''<sub>(1)</sub>, ..., ''x''<sub>(''n'')</sub>} be the corresponding [[order statistic|ordered]] sample, that is the result of sorting of all observations from smallest to largest. For convenience also denote ''x''<sub>(0)</sub> = −∞ and ''x''<sub>(''n''+1)</sub> = +∞. |
||
Define the ''spacings'' as the “gaps” between the values of the distribution function at adjacent ordered points:<ref name |
Define the ''spacings'' as the “gaps” between the values of the distribution function at adjacent ordered points:<ref name="Pyke65">{{harvtxt|Pyke|1965}}</ref> |
||
<math display="block"> |
|||
D_i(\theta) = F(x_{(i)};\,\theta) - F(x_{(i-1)};\,\theta), \quad i=1,\ldots,n+1. |
D_i(\theta) = F(x_{(i)};\,\theta) - F(x_{(i-1)};\,\theta), \quad i=1,\ldots,n+1. |
||
</math> |
</math> |
||
Then the '''maximum spacing estimator''' of ''θ''<sub>0</sub> is defined as a value that maximizes the [[natural logarithm|logarithm]] of the [[geometric mean]] of sample spacings: |
Then the '''maximum spacing estimator''' of ''θ''<sub>0</sub> is defined as a value that maximizes the [[natural logarithm|logarithm]] of the [[geometric mean]] of sample spacings: |
||
<math display="block"> |
|||
\hat{\theta} = \underset{\theta\in\Theta}{\operatorname{arg\,max}} \; S_n(\theta), |
\hat{\theta} = \underset{\theta\in\Theta}{\operatorname{arg\,max}} \; S_n(\theta), |
||
\quad\text{where }\ |
\quad\text{where }\ |
||
| Line 36: | Line 37: | ||
Note that some authors define the function ''S''<sub>''n''</sub>(''θ'') somewhat differently. In particular, {{harvtxt|Ranneby|1984}} multiplies each ''D''<sub>''i''</sub> by a factor of (''n''+1), whereas {{harvtxt|Cheng|Stephens|1989}} omit the {{frac|''n''+1}} factor in front of the sum and add the “−” sign in order to turn the maximization into minimization. As these are constants with respect to ''θ'', the modifications do not alter the location of the maximum of the function ''S''<sub>''n''</sub>. |
Note that some authors define the function ''S''<sub>''n''</sub>(''θ'') somewhat differently. In particular, {{harvtxt|Ranneby|1984}} multiplies each ''D''<sub>''i''</sub> by a factor of (''n''+1), whereas {{harvtxt|Cheng|Stephens|1989}} omit the {{frac|''n''+1}} factor in front of the sum and add the “−” sign in order to turn the maximization into minimization. As these are constants with respect to ''θ'', the modifications do not alter the location of the maximum of the function ''S''<sub>''n''</sub>. |
||
==Examples== |
== Examples == |
||
This section presents two examples of calculating the maximum spacing estimator. |
This section presents two examples of calculating the maximum spacing estimator. |
||
===Example 1=== |
=== Example 1 === |
||
[[ |
[[File:Spacing Estimation plot for MSE example.svg|thumb|350px|alt=A box containing the graph of two offset concave functions with different peaks, vertical lines bisecting the peaks, and labeled arrows pointing to where the vertical lines intersect the bottom of the box.|Plots of the [[Natural logarithm|log]] value of ''λ'' for the simplistic example under both likelihood and spacing estimation. The values for which both likelihood and spacing are maximized, the maximum likelihood and maximum spacing estimates, are identified.]] |
||
Suppose two values ''x''<sub>(1)</sub> = 2, ''x''<sub>(2)</sub> = 4 were sampled from the [[exponential distribution]] ''F''(''x'';''λ'') = 1 − e<sup>−''xλ''</sup>, ''x'' ≥ 0 with unknown parameter ''λ'' > 0. In order to construct the MSE we have to first find the spacings: |
Suppose two values ''x''<sub>(1)</sub> = 2, ''x''<sub>(2)</sub> = 4 were sampled from the [[exponential distribution]] ''F''(''x'';''λ'') = 1 − e<sup>−''xλ''</sup>, ''x'' ≥ 0 with unknown parameter ''λ'' > 0. In order to construct the MSE we have to first find the spacings: |
||
{| class="wikitable" style="margin:1em auto;" |
|||
<center> |
|||
{| class="wikitable" |
|||
|- |
|||
! ''i'' !! ''F''(''x''<sub>(''i'')</sub>) !! ''F''(''x''<sub>(''i''−1)</sub>) !! ''D''<sub>''i''</sub> = ''F''(''x''<sub>(''i'')</sub>) − ''F''(''x''<sub>(''i''−1)</sub>) |
! ''i'' !! ''F''(''x''<sub>(''i'')</sub>) !! ''F''(''x''<sub>(''i''−1)</sub>) !! ''D''<sub>''i''</sub> = ''F''(''x''<sub>(''i'')</sub>) − ''F''(''x''<sub>(''i''−1)</sub>) |
||
|- |
|- |
||
| 1 || 1 − e<sup>−2''λ''</sup> || 0 || 1 − e<sup>−2''λ''</sup> |
| 1 || 1 − e<sup>−2''λ''</sup> || 0 || 1 − e<sup>−2''λ''</sup> |
||
|- |
|- |
||
| 2 || 1 − e<sup>−4''λ''</sup> || 1 − e<sup>−2''λ''</sup> || e<sup>−2''λ''</sup> − e<sup>−4''λ''</sup> |
| 2 || 1 − e<sup>−4''λ''</sup> || 1 − e<sup>−2''λ''</sup> || e<sup>−2''λ''</sup> − e<sup>−4''λ''</sup> |
||
|- |
|- |
||
| 3 || 1 || 1 − e<sup>−4''λ''</sup> || e<sup>−4''λ''</sup> |
| 3 || 1 || 1 − e<sup>−4''λ''</sup> || e<sup>−4''λ''</sup> |
||
|} |
|} |
||
</center> |
|||
The process continues by finding the ''λ'' that maximizes the geometric mean of the “difference” column. Using the convention that ignores taking the (''n''+1)st root, this turns into the maximization of the following product: (1 − e<sup>−2''λ''</sup>) · (e<sup>−2''λ''</sup> − e<sup>−4''λ''</sup>) · (e<sup>−4''λ''</sup>). Letting ''μ'' = e<sup>−2''λ''</sup>, the problem becomes finding the maximum of ''μ''<sup>5</sup>−2''μ''<sup>4</sup>+''μ''<sup>3</sup>. Differentiating, the ''μ'' has to satisfy 5''μ''<sup>4</sup>−8''μ''<sup>3</sup>+3''μ''<sup>2</sup> = 0. This equation has roots 0, 0.6, and 1. As ''μ'' is actually e<sup>−2''λ''</sup>, it has to be greater than zero but less than one. Therefore, the only acceptable solution is |
The process continues by finding the ''λ'' that maximizes the geometric mean of the “difference” column. Using the convention that ignores taking the (''n''+1)st root, this turns into the maximization of the following product: (1 − e<sup>−2''λ''</sup>) · (e<sup>−2''λ''</sup> − e<sup>−4''λ''</sup>) · (e<sup>−4''λ''</sup>). Letting ''μ'' = e<sup>−2''λ''</sup>, the problem becomes finding the maximum of ''μ''<sup>5</sup>−2''μ''<sup>4</sup>+''μ''<sup>3</sup>. Differentiating, the ''μ'' has to satisfy 5''μ''<sup>4</sup>−8''μ''<sup>3</sup>+3''μ''<sup>2</sup> = 0. This equation has roots 0, 0.6, and 1. As ''μ'' is actually e<sup>−2''λ''</sup>, it has to be greater than zero but less than one. Therefore, the only acceptable solution is |
||
<math display="block"> |
|||
\mu=0.6 \quad \Rightarrow \quad \lambda_{\text{MSE}} = \frac{\ln 0.6}{-2} \approx 0.255, |
\mu=0.6 \quad \Rightarrow \quad \lambda_{\text{MSE}} = \frac{\ln 0.6}{-2} \approx 0.255, |
||
</math> |
</math> |
||
which corresponds to an exponential distribution with a mean of {{frac|''λ''}} ≈ 3.915. For comparison, the maximum likelihood estimate of λ is the inverse of the sample mean, 3, so ''λ''<sub>MLE</sub> = ⅓ ≈ 0.333. |
which corresponds to an exponential distribution with a mean of {{frac|''λ''}} ≈ 3.915. For comparison, the maximum likelihood estimate of λ is the inverse of the sample mean, 3, so ''λ''<sub>MLE</sub> = ⅓ ≈ 0.333. |
||
===Example 2=== |
=== Example 2 === |
||
Suppose {''x''<sub>(1)</sub>, |
Suppose {''x''<sub>(1)</sub>, ..., ''x''<sub>(''n'')</sub>} is the ordered sample from a [[Uniform distribution (continuous)|uniform distribution]] ''U''(''a'',''b'') with unknown endpoints ''a'' and ''b''. The cumulative distribution function is ''F''(''x'';''a'',''b'') = (''x''−''a'')/(''b''−''a'') when ''x''∈[''a'',''b'']. Therefore, individual spacings are given by |
||
<math display="block"> |
|||
D_1 = \frac{x_{(1)}-a}{b-a}, \ \ |
D_1 = \frac{x_{(1)}-a}{b-a}, \ \ |
||
D_i = \frac{x_{(i)}-x_{(i-1)}}{b-a}\ \text{for } i = 2, \ldots, n, \ \ |
D_i = \frac{x_{(i)}-x_{(i-1)}}{b-a}\ \text{for } i = 2, \ldots, n, \ \ |
||
| Line 71: | Line 69: | ||
Calculating the geometric mean and then taking the logarithm, statistic ''S''<sub>''n''</sub> will be equal to |
Calculating the geometric mean and then taking the logarithm, statistic ''S''<sub>''n''</sub> will be equal to |
||
<math display="block"> |
|||
S_n(a,b) = \tfrac{ |
S_n(a,b) = \tfrac{\ln(x_{(1)}-a)}{n+1} + \tfrac{\sum_{i=2}^n \ln(x_{(i)}-x_{(i-1)})}{n+1} + \tfrac{\ln(b-x_{(n)})}{n+1} - \ln(b-a) |
||
</math> |
</math> |
||
Here only |
Here only three terms depend on the parameters ''a'' and ''b''. Differentiating with respect to those parameters and solving the resulting linear system, the maximum spacing estimates will be |
||
: <math alt="MS estimator of a is the minimal x minus the sample range divided by n−1; MS estimator of b is the maximal x plus the sample range divided by n−1"> |
: <math alt="MS estimator of a is the minimal x minus the sample range divided by n−1; MS estimator of b is the maximal x plus the sample range divided by n−1"> |
||
\hat{a} = \frac{nx_{(1)} - x_{(n)}}{n-1},\ \ \hat{b} = \frac{nx_{(n)}-x_{(1)}}{n-1}. |
\hat{a} = \frac{nx_{(1)} - x_{(n)}}{n-1},\ \ \hat{b} = \frac{nx_{(n)}-x_{(1)}}{n-1}. |
||
</math> |
</math> |
||
These are known to be the [[uniformly minimum variance unbiased]] (UMVU) estimators for the continuous uniform distribution.<ref name="CA83"/> In comparison, the maximum likelihood estimates for this problem <math alt="ML estimate of a is the smallest of x’s">\scriptstyle\hat{a}=x_{(1)}</math> and <math alt="ML estimate of b is the largest of x’s">\scriptstyle\hat{b}=x_{(n)}</math> are biased and have higher [[mean-squared error]]. |
These are known to be the [[uniformly minimum variance unbiased]] (UMVU) estimators for the continuous uniform distribution.<ref name="CA83" /> In comparison, the maximum likelihood estimates for this problem <math alt="ML estimate of a is the smallest of x’s">\scriptstyle\hat{a}=x_{(1)}</math> and <math alt="ML estimate of b is the largest of x’s">\scriptstyle\hat{b}=x_{(n)}</math> are biased and have higher [[mean-squared error]]. |
||
==Properties== |
== Properties == |
||
=== Consistency and efficiency === |
|||
===Consistency and efficiency=== |
|||
{{Expand section|date=May 2010}} |
|||
{{multiple image |
{{multiple image |
||
| width = 200 |
| width = 200 |
||
| Line 95: | Line 93: | ||
}} |
}} |
||
The maximum spacing estimator is a [[consistent estimator]] in that it [[convergence in probability|converges in probability]] to the true value of the parameter, ''θ''<sub>0</sub>, as the sample size increases to infinity.<ref name |
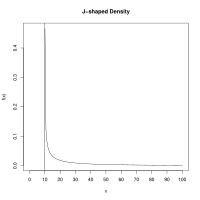
The maximum spacing estimator is a [[consistent estimator]] in that it [[convergence in probability|converges in probability]] to the true value of the parameter, ''θ''<sub>0</sub>, as the sample size increases to infinity.<ref name="R84" /> The consistency of maximum spacing estimation holds under much more general conditions than for [[maximum likelihood]] estimators. In particular, in cases where the underlying distribution is J-shaped, maximum likelihood will fail where MSE succeeds.<ref name="CA83" /> An example of a J-shaped density is the [[Weibull distribution]], specifically a [[Weibull distribution#Related distributions|shifted Weibull]], with a [[shape parameter]] less than 1. The density will tend to infinity as ''x'' approaches the [[location parameter]] rendering estimates of the other parameters inconsistent. |
||
Maximum spacing estimators are also at least as [[Efficiency (statistics)#Asymptotic efficiency|asymptotically efficient]] as maximum likelihood estimators, where the latter exist. However, MSEs may exist in cases where MLEs do not.<ref name |
Maximum spacing estimators are also at least as [[Efficiency (statistics)#Asymptotic efficiency|asymptotically efficient]] as maximum likelihood estimators, where the latter exist. However, MSEs may exist in cases where MLEs do not.<ref name="CA83" /> |
||
===Sensitivity=== |
=== Sensitivity === |
||
Maximum spacing estimators are sensitive to closely spaced observations, and especially ties.<ref name |
Maximum spacing estimators are sensitive to closely spaced observations, and especially ties.<ref name="CS89">{{harvtxt|Cheng|Stephens|1989}}</ref> Given |
||
<math display="block"> |
|||
X_{i+k} = X_{i+k-1}=\cdots=X_i, \, |
X_{i+k} = X_{i+k-1}=\cdots=X_i, \, |
||
</math> |
</math> |
||
we get |
we get |
||
<math display="block"> |
|||
D_{i+k}(\theta) = D_{i+k-1}(\theta) = \cdots = D_{i+1}(\theta) = 0. \, |
D_{i+k}(\theta) = D_{i+k-1}(\theta) = \cdots = D_{i+1}(\theta) = 0. \, |
||
</math> |
</math> |
||
When the ties are due to multiple observations, the repeated spacings (those that would otherwise be zero) should be replaced by the corresponding likelihood.<ref name |
When the ties are due to multiple observations, the repeated spacings (those that would otherwise be zero) should be replaced by the corresponding likelihood.<ref name="CA83" /> That is, one should substitute <math>f_{i}(\theta)</math> for <math>D_i(\theta)</math>, as |
||
<math display="block"> |
|||
\lim_{x_i \to x_{i-1}}\frac{\int_{x_{i-1}}^{x_i}f(t;\theta)\,dt}{x_i-x_{i-1}} = f(x_{i-1},\theta) = f(x_{i},\theta), |
\lim_{x_i \to x_{i-1}}\frac{\int_{x_{i-1}}^{x_i}f(t;\theta)\,dt}{x_i-x_{i-1}} = f(x_{i-1},\theta) = f(x_{i},\theta), |
||
</math> |
</math> |
||
since <math>x_{i} = x_{i-1}</math>. |
since <math>x_{i} = x_{i-1}</math>. |
||
When ties are due to rounding error, {{harvtxt|Cheng|Stephens|1989}} suggest another method to remove the effects. |
When ties are due to rounding error, {{harvtxt|Cheng|Stephens|1989}} suggest another method to remove the effects.{{NoteTag|There appear to be some minor typographical errors in the paper. For example, in section 4.2, equation (4.1), the rounding replacement for <math>D_j</math>, should not have the log term. In section 1, equation (1.2), <math>D_j</math> is defined to be the spacing itself, and <math>M(\theta)</math> is the negative sum of the logs of <math>D_j</math>. If <math>D_j</math> is logged at this step, the result is always ≤ 0, as the difference between two adjacent points on a cumulative distribution is always ≤ 1, and strictly < 1 unless there are only two points at the bookends. Also, in section 4.3, on page 392, calculation shows that it is the variance <math>\textstyle\tilde{\sigma^2}</math> which has MPS estimate of 6.87, not the standard deviation <math>\textstyle\tilde{\sigma}</math>. – ''Editor''}} |
||
Given ''r'' tied observations from ''x''<sub>''i''</sub> to ''x''<sub>''i''+''r''−1</sub>, let ''δ'' represent the [[round-off error]]. All of the true values should then fall in the range <math>x \pm \delta</math>. The corresponding points on the distribution should now fall between <math>y_L = F(x-\delta, \hat\theta)</math> and <math>y_U = F(x+\delta, \hat\theta)</math>. Cheng and Stephens suggest assuming that the rounded values are [[Uniform distribution (continuous)|uniformly spaced]] in this interval, by defining |
Given ''r'' tied observations from ''x''<sub>''i''</sub> to ''x''<sub>''i''+''r''−1</sub>, let ''δ'' represent the [[round-off error]]. All of the true values should then fall in the range <math>x \pm \delta</math>. The corresponding points on the distribution should now fall between <math>y_L = F(x-\delta, \hat\theta)</math> and <math>y_U = F(x+\delta, \hat\theta)</math>. Cheng and Stephens suggest assuming that the rounded values are [[Uniform distribution (continuous)|uniformly spaced]] in this interval, by defining |
||
<math display="block"> |
|||
D_j = \frac{y_U-y_L}{r-1} \quad (j=i+1,\ldots,i+r-1). |
D_j = \frac{y_U-y_L}{r-1} \quad (j=i+1,\ldots,i+r-1). |
||
</math> |
</math> |
||
The MSE method is also sensitive to secondary clustering.<ref name |
The MSE method is also sensitive to secondary clustering.<ref name="CS89" /> One example of this phenomenon is when a set of observations is thought to come from a single [[normal distribution]], but in fact comes from a [[Mixture (probability)|mixture]] normals with different means. A second example is when the data is thought to come from an [[exponential distribution]], but actually comes from a [[gamma distribution]]. In the latter case, smaller spacings may occur in the lower tail. A high value of ''M''(''θ'') would indicate this secondary clustering effect, and suggesting a closer look at the data is required.<ref name="CS89" /> |
||
== |
== Moran test == |
||
The statistic ''S<sub>n</sub>''(''θ'') is also a form of [[Pat Moran (statistician)|Moran]] or Moran-Darling statistic, ''M''(''θ''), which can be used to test [[goodness of fit]]. |
The statistic ''S<sub>n</sub>''(''θ'') is also a form of [[Pat Moran (statistician)|Moran]] or Moran-Darling statistic, ''M''(''θ''), which can be used to test [[goodness of fit]].{{NoteTag|The literature refers to related statistics as Moran or Moran-Darling statistics. For example, {{harvtxt|Cheng|Stephens|1989}} analyze the form <math>\scriptstyle M(\theta)= -\sum_{j=1}^{n+1}\log{D_i(\theta)}</math> where <math>\scriptstyle D_i(\theta)</math> is defined as above. {{harvtxt|Wong|Li|2006}} use the same form as well. However, {{harvtxt|Beirlant|al.|2001}} uses the form <math>\scriptstyle M_n= -\sum_{j=0}^{n}\ln{((n + 1)(X_{n,i+1} - X_{n,i}))}</math>, with the additional factor of <math>(n+1)</math> inside the logged summation. The extra factors will make a difference in terms of the expected mean and variance of the statistic. For consistency, this article will continue to use the Cheng & Amin/Wong & Li form. -- ''Editor''}} |
||
It has been shown that the statistic, when defined as |
It has been shown that the statistic, when defined as |
||
<math display="block"> |
|||
S_n(\theta) = M_n(\theta)= -\sum_{j=1}^{n+1}\ln{D_j(\theta)}, |
S_n(\theta) = M_n(\theta)= -\sum_{j=1}^{n+1}\ln{D_j(\theta)}, |
||
</math> |
</math> |
||
is [[Estimator#Asymptotic normality|asymptotically normal]], and that a chi-squared approximation exists for small samples.<ref name |
is [[Estimator#Asymptotic normality|asymptotically normal]], and that a chi-squared approximation exists for small samples.<ref name="CS89" /> In the case where we know the true parameter <math>\theta^0</math>, {{harvtxt|Cheng|Stephens|1989}} show that the statistic <math>\scriptstyle M_n(\theta)</math> has a [[normal distribution]] with |
||
<math display="block">\begin{align} |
|||
\mu_M & \approx (n+1)(\ln(n+1)+\gamma)-\frac{1}{2}-\frac{1}{12(n+1)},\\ |
\mu_M & \approx (n+1)(\ln(n+1)+\gamma)-\frac{1}{2}-\frac{1}{12(n+1)},\\ |
||
\sigma^2_M & \approx (n+1)\left ( \frac{\pi^2}{6} -1 \right ) -\frac{1}{2}-\frac{1}{6(n+1)}, |
\sigma^2_M & \approx (n+1)\left ( \frac{\pi^2}{6} -1 \right ) -\frac{1}{2}-\frac{1}{6(n+1)}, |
||
\end{align}</math> |
\end{align}</math> |
||
where ''γ'' is the [[Euler–Mascheroni constant]] which is approximately 0.57722. |
where ''γ'' is the [[Euler–Mascheroni constant]] which is approximately 0.57722.{{NoteTag|{{harvtxt|Wong|Li|2006}} leave out the [[Euler–Mascheroni constant]] from their description. -- ''Editor''}} |
||
The distribution can also be approximated by that of <math>A</math>, where |
The distribution can also be approximated by that of <math>A</math>, where |
||
<math display="block"> |
|||
A = C_1 + C_2\chi^2_n \, |
A = C_1 + C_2\chi^2_n \, |
||
</math>, |
</math>, |
||
in which |
in which |
||
<math display="block">\begin{align} |
|||
C_1 &= \mu_M - \sqrt{\frac{\sigma^2_Mn}{2}},\\ |
C_1 &= \mu_M - \sqrt{\frac{\sigma^2_Mn}{2}},\\ |
||
C_2 &= {\sqrt\frac{\sigma^2_M}{2n}},\\ |
C_2 &= {\sqrt\frac{\sigma^2_M}{2n}},\\ |
||
\end{align}</math> |
\end{align}</math> |
||
and where <math>\chi^2_n</math> follows a [[chi-squared distribution]] with <math>n</math> [[Degrees of freedom (statistics)|degrees of freedom]]. Therefore, to test the hypothesis <math>H_0</math> that a random sample of <math>n</math> values comes from the distribution <math>F(x,\theta)</math>, the statistic <math>T(\theta)= \frac{M(\theta)-C_1}{C_2}</math> can be calculated. Then <math>H_0</math> should be rejected with [[Statistical significance|significance]] <math>\alpha</math> if the value is greater than the [[critical value]] of the appropriate chi-squared distribution.<ref name |
and where <math>\chi^2_n</math> follows a [[chi-squared distribution]] with <math>n</math> [[Degrees of freedom (statistics)|degrees of freedom]]. Therefore, to test the hypothesis <math>H_0</math> that a random sample of <math>n</math> values comes from the distribution <math>F(x,\theta)</math>, the statistic <math>T(\theta)= \frac{M(\theta)-C_1}{C_2}</math> can be calculated. Then <math>H_0</math> should be rejected with [[Statistical significance|significance]] <math>\alpha</math> if the value is greater than the [[critical value (statistics)|critical value]] of the appropriate chi-squared distribution.<ref name="CS89" /> |
||
Where ''θ''<sub>0</sub> is being estimated by <math>\hat\theta</math>, {{harvtxt|Cheng|Stephens|1989}} showed that <math>S_n(\hat\theta) = M_n(\hat\theta)</math> has the same asymptotic mean and variance as in the known case. However, the test statistic to be used requires the addition of a bias correction term and is: |
Where ''θ''<sub>0</sub> is being estimated by <math>\hat\theta</math>, {{harvtxt|Cheng|Stephens|1989}} showed that <math>S_n(\hat\theta) = M_n(\hat\theta)</math> has the same asymptotic mean and variance as in the known case. However, the test statistic to be used requires the addition of a bias correction term and is: |
||
<math display="block"> |
|||
T(\hat\theta) = \frac{M(\hat\theta)+\frac{k}{2}-C_1}{C_2}, |
T(\hat\theta) = \frac{M(\hat\theta)+\frac{k}{2}-C_1}{C_2}, |
||
</math> |
</math> |
||
where <math>k</math> is the number of parameters in the estimate. |
where <math>k</math> is the number of parameters in the estimate. |
||
==Generalized maximum spacing== |
== Generalized maximum spacing == |
||
===Alternate measures and spacings=== |
=== Alternate measures and spacings === |
||
{{harvtxt|Ranneby|Ekström|1997}} generalized the MSE method to approximate other [[F-divergence|measures]] besides the |
{{harvtxt|Ranneby|Ekström|1997}} generalized the MSE method to approximate other [[F-divergence|measures]] besides the Kullback–Leibler measure. {{harvtxt|Ekström|1997}} further expanded the method to investigate properties of estimators using higher order spacings, where an ''m''-order spacing would be defined as <math>F(X_{j+m}) - F(X_{j})</math>. |
||
===Multivariate distributions=== |
=== Multivariate distributions === |
||
{{harvtxt|Ranneby|al.|2005}} discuss extended maximum spacing methods to the [[Joint probability distribution|multivariate]] case. As there is no natural order for <math>\mathbb{R}^k (k>1)</math>, they discuss two alternative approaches: a geometric approach based on [[Dirichlet cell]]s and a probabilistic approach based on a “nearest neighbor ball” metric. |
{{harvtxt|Ranneby|al.|2005}} discuss extended maximum spacing methods to the [[Joint probability distribution|multivariate]] case. As there is no natural order for <math>\mathbb{R}^k (k>1)</math>, they discuss two alternative approaches: a geometric approach based on [[Dirichlet cell]]s and a probabilistic approach based on a “nearest neighbor ball” metric. |
||
==See also== |
== See also == |
||
* [[Kullback–Leibler divergence]] |
* [[Kullback–Leibler divergence]] |
||
* [[Maximum likelihood]] |
* [[Maximum likelihood]] |
||
* [[Probability distribution]] |
* [[Probability distribution]] |
||
==Notes== |
== Notes == |
||
{{NoteFoot}} |
|||
{{Reflist|group="note"}} |
|||
==References== |
== References == |
||
=== Citations === |
|||
{{Reflist|3}} |
|||
{{Reflist|20em}} |
|||
===Works cited=== |
=== Works cited === |
||
{{refbegin}} |
{{refbegin}} |
||
* {{cite journal |
* {{cite journal |
||
| last1 = Anatolyev |
| last1 = Anatolyev |
||
| first1 = Stanislav |
|||
| last2 = Kosenok |
| last2 = Kosenok |
||
| first2 = Grigory |
|||
| year |
| year = 2005 |
||
| title = An alternative to maximum likelihood based on spacings |
| title = An alternative to maximum likelihood based on spacings |
||
| journal = Econometric Theory |
| journal = Econometric Theory |
||
| volume = 21 |
| volume = 21 |
||
| issue = 2 |
|||
| pages = 472–476 |
|||
| doi = 10.1017/S0266466605050255 |
| doi = 10.1017/S0266466605050255 |
||
| url = http://fir.nes.ru/~gkosenok/MPS.pdf |
| url = http://fir.nes.ru/~gkosenok/MPS.pdf |
||
| |
| access-date = 2009-01-21 |
||
| ref = CITEREFAnatolyevKosenok2004 |
| ref = CITEREFAnatolyevKosenok2004 |
||
| citeseerx = 10.1.1.494.7340 |
|||
| s2cid = 123004317 |
|||
| archive-date = 2011-08-16 |
|||
| archive-url = https://web.archive.org/web/20110816101736/http://fir.nes.ru/~gkosenok/MPS.pdf |
|||
| url-status = dead |
|||
}} |
}} |
||
* {{cite journal |
* {{cite journal |
||
| |
|last1 = Beirlant |
||
| |
|first1 = J. |
||
| |
|last2 = Dudewicz |
||
| |
|first2 = E.J. |
||
| |
|last3 = Györfi |
||
|first3 = L. |
|||
| title = Nonparametric entropy estimation: an overview |
|||
|last4 = van der Meulen |
|||
| journal = International Journal of Mathematical and Statistical Sciences |
|||
| |
|first4 = E.C. |
||
|year = 1997 |
|||
| issn = 1055-7490 |
|||
|title = Nonparametric entropy estimation: an overview |
|||
| url = http://www.menem.com/ilya/digital_library/entropy/beirlant_etal_97.pdf |
|||
|journal = International Journal of Mathematical and Statistical Sciences |
|||
| accessdate = 2008-12-31 |
|||
|volume = 6 |
|||
| ref = CITEREFBeirlantal.2001 |
|||
|issue = 1 |
|||
|archiveurl = https://web.archive.org/web/20050505044534/http://www.menem.com/ilya/digital_library/entropy/beirlant_etal_97.pdf |archivedate = May 5, 2005}} <small>''Note: linked paper is an updated 2001 version.''</small> |
|||
|pages = 17–40 |
|||
|issn = 1055-7490 |
|||
|url = http://www.menem.com/ilya/digital_library/entropy/beirlant_etal_97.pdf |
|||
|access-date = 2008-12-31 |
|||
|ref = CITEREFBeirlantal.2001 |
|||
|archive-url = https://web.archive.org/web/20050505044534/http://www.menem.com/ilya/digital_library/entropy/beirlant_etal_97.pdf |
|||
|archive-date = May 5, 2005 |
|||
}} <small>''Note: linked paper is an updated 2001 version.''</small> |
|||
* {{cite journal |
* {{cite journal |
||
| last1 = Cheng | first1 = R.C.H. |
| last1 = Cheng | first1 = R.C.H. |
||
| Line 209: | Line 225: | ||
| issn = 0035-9246 |
| issn = 0035-9246 |
||
| jstor = 2345411 |
| jstor = 2345411 |
||
| doi = 10.1111/j.2517-6161.1983.tb01268.x |
|||
| ref = harv |
|||
}} |
}} |
||
* {{cite journal |
* {{cite journal |
||
| Line 215: | Line 231: | ||
| last2 = Stephens | first2 = M. A. |
| last2 = Stephens | first2 = M. A. |
||
| year = 1989 |
| year = 1989 |
||
| title = A goodness-of-fit test using |
| title = A goodness-of-fit test using Moran's statistic with estimated parameters |
||
| journal = Biometrika |
| journal = Biometrika |
||
| volume = 76 | issue = 2 | pages = 386–392 |
| volume = 76 | issue = 2 | pages = 386–392 |
||
| doi = 10.1093/biomet/76.2.385 |
| doi = 10.1093/biomet/76.2.385 |
||
| ref = harv |
|||
}} |
}} |
||
* {{cite journal |
* {{cite journal |
||
| last |
| last = Ekström |
||
| first = Magnus |
| first = Magnus |
||
| year |
| year = 1997 |
||
| title = Generalized maximum spacing estimates |
| title = Generalized maximum spacing estimates |
||
| journal = University of Umeå, Department of Mathematics |
| journal = University of Umeå, Department of Mathematics |
||
| Line 230: | Line 245: | ||
| issn = 0345-3928 |
| issn = 0345-3928 |
||
| url = http://www.matstat.umu.se/varia/reports/rep9706.ps.gz |
| url = http://www.matstat.umu.se/varia/reports/rep9706.ps.gz |
||
| |
| access-date = 2008-12-30 |
||
| archive-url = https://web.archive.org/web/20070214143052/http://www.matstat.umu.se/varia/reports/rep9706.ps.gz |
|||
| ref = harv |
|||
| |
| archive-date = February 14, 2007 |
||
* {{cite journal |
|||
| last1 = Hall | first1 = M.J. |
|||
| last2 = van den Boogaard | first2 = H.F.P. |
|||
| last3 = Fernando | first3 = R.C. |
|||
| last4 = Mynett | first4 = A.E. |
|||
| year = 2004 |
|||
| title = The construction of confidence intervals for frequency analysis using resampling techniques |
|||
| journal = Hydrology and Earth System Sciences |
|||
| volume = 8 | issue = 2 | pages = 235–246 |
|||
| issn = 1027-5606 |
|||
| url = http://www.hydrol-earth-syst-sci.net/8/235/2004/hess-8-235-2004.pdf |
|||
| accessdate = 2009-01-21 |
|||
| ref = CITEREFHallal.2004 | doi=10.5194/hess-8-235-2004 |
|||
}} |
}} |
||
* {{cite journal |
|||
|last1 = Hall |
|||
|first1 = M.J. |
|||
|last2 = van den Boogaard |
|||
|first2 = H.F.P. |
|||
|last3 = Fernando |
|||
|first3 = R.C. |
|||
|last4 = Mynett |
|||
|first4 = A.E. |
|||
|year = 2004 |
|||
|title = The construction of confidence intervals for frequency analysis using resampling techniques |
|||
|journal = Hydrology and Earth System Sciences |
|||
|volume = 8 |
|||
|issue = 2 |
|||
|pages = 235–246 |
|||
|issn = 1027-5606 |
|||
|ref = CITEREFHallal.2004 |
|||
|doi = 10.5194/hess-8-235-2004 |
|||
|url = https://hal.archives-ouvertes.fr/hal-00304907/document |
|||
|doi-access = free |
|||
}} |
|||
* {{cite conference |
* {{cite conference |
||
| last1 = Pieciak |
| last1 = Pieciak |
||
| first1 = Tomasz |
|||
| year |
| year = 2014 |
||
| title = The maximum spacing noise estimation in single-coil background MRI data |
| title = The maximum spacing noise estimation in single-coil background MRI data |
||
| conference = IEEE International Conference on Image Processing |
| conference = IEEE International Conference on Image Processing |
||
| pages = |
| pages = 1743–1747 |
||
| location = Paris |
| location = Paris |
||
| doi = 10.1109/icip.2014.7025349 |
|||
| url = http://home.agh.edu.pl/pieciak/publikacje_pieciak/2014_ICIP_Pieciak.pdf |
|||
| url = https://scholar.archive.org/work/e2l3rb6s3va7pd3kf6oioymgza |
|||
| accessdate = 2015-07-07 |
|||
| ref = CITEREFPieciak2014 |
|||
}} |
}} |
||
* {{cite journal |
* {{cite journal |
||
| Line 266: | Line 289: | ||
| issn = 0035-9246 |
| issn = 0035-9246 |
||
| jstor = 2345793 |
| jstor = 2345793 |
||
| ref = harv |
|||
| issue = 3 |
| issue = 3 |
||
| doi = 10.1111/j.2517-6161.1965.tb00602.x |
|||
}} |
}} |
||
* {{cite journal |
* {{cite journal |
||
| Line 277: | Line 300: | ||
| issn = 0303-6898 |
| issn = 0303-6898 |
||
| jstor = 4615946 |
| jstor = 4615946 |
||
| ref = harv |
|||
}} |
}} |
||
* {{cite journal |
* {{cite journal |
||
| |
|last1 = Ranneby |
||
|first1 = Bo |
|||
| |
|last2 = Ekström |
||
|first2 = Magnus |
|||
| |
|year = 1997 |
||
| |
|title = Maximum spacing estimates based on different metrics |
||
| |
|journal = University of Umeå, Department of Mathematics |
||
| |
|volume = 5 |
||
| |
|issn = 0345-3928 |
||
| |
|url = http://www.matstat.umu.se/varia/reports/rep9705.ps.gz |
||
| |
|access-date = 2008-12-30 |
||
|archive-url = https://web.archive.org/web/20070214143042/http://www.matstat.umu.se/varia/reports/rep9705.ps.gz |
|||
| ref = harv |
|||
|archive-date = February 14, 2007 |
|||
|archiveurl = https://web.archive.org/web/20070214143042/http://www.matstat.umu.se/varia/reports/rep9705.ps.gz |archivedate = February 14, 2007}} |
|||
}} |
|||
* {{cite journal |
* {{cite journal |
||
| |
|last1 = Ranneby |
||
| |
|first1 = Bo |
||
|last2 = Jammalamadakab |
|||
| last3 = Teterukovskiy | first3 = Alex |
|||
| |
|first2 = S. Rao |
||
|last3 = Teterukovskiy |
|||
| title = The maximum spacing estimation for multivariate observations |
|||
|first3 = Alex |
|||
| journal = Journal of Statistical Planning and Inference |
|||
| |
|year = 2005 |
||
|title = The maximum spacing estimation for multivariate observations |
|||
| doi = 10.1016/j.jspi.2004.06.059 |
|||
|journal = Journal of Statistical Planning and Inference |
|||
| url = http://www.pstat.ucsb.edu/faculty/jammalam/html/research%20publication_files/MSP2.pdf |
|||
|volume = 129 |
|||
| accessdate = 2008-12-31 |
|||
|issue = 1–2 |
|||
| ref = CITEREFRannebyal.2005 |
|||
|pages = 427–446 |
|||
}} |
|||
|doi = 10.1016/j.jspi.2004.06.059 |
|||
|url = http://www.pstat.ucsb.edu/faculty/jammalam/html/research%20publication_files/MSP2.pdf |
|||
|access-date = 2008-12-31 |
|||
|ref = CITEREFRannebyal.2005 |
|||
}} |
|||
* {{cite book |
* {{cite book |
||
| last1 = Wong | first1 = T.S.T |
| last1 = Wong | first1 = T.S.T |
||
| Line 313: | Line 343: | ||
| pages = 272–283 |
| pages = 272–283 |
||
| doi = 10.1214/074921706000001102 |
| doi = 10.1214/074921706000001102 |
||
| arxiv = math/0702830v1 |
| arxiv = math/0702830v1 |
||
| series = Institute of Mathematical Statistics Lecture Notes – Monograph Series |
|||
| ref = harv |
|||
| isbn = 978-0-940600-68-3 |
|||
| s2cid = 88516426 |
|||
}} |
}} |
||
{{refend}} |
{{refend}} |
||
{{-}} |
|||
{{Statistics}} |
{{Statistics}} |
||
[[Category:Estimation methods]] |
|||
[[Category:Probability distribution fitting]] |
|||
{{good article}} |
{{good article}} |
||
{{DEFAULTSORT:Maximum Spacing Estimation}} |
|||
[[Category:Estimation methods]] |
|||
[[Category:Fitting probability distributions]] |
|||
Latest revision as of 06:40, 15 September 2024

In statistics, maximum spacing estimation (MSE or MSP), or maximum product of spacing estimation (MPS), is a method for estimating the parameters of a univariate statistical model.[1] The method requires maximization of the geometric mean of spacings in the data, which are the differences between the values of the cumulative distribution function at neighbouring data points.
The concept underlying the method is based on the probability integral transform, in that a set of independent random samples derived from any random variable should on average be uniformly distributed with respect to the cumulative distribution function of the random variable. The MPS method chooses the parameter values that make the observed data as uniform as possible, according to a specific quantitative measure of uniformity.
One of the most common methods for estimating the parameters of a distribution from data, the method of maximum likelihood (MLE), can break down in various cases, such as involving certain mixtures of continuous distributions.[2] In these cases the method of maximum spacing estimation may be successful.
Apart from its use in pure mathematics and statistics, the trial applications of the method have been reported using data from fields such as hydrology,[3] econometrics,[4] magnetic resonance imaging,[5] and others.[6]
History and usage
[edit]The MSE method was derived independently by Russel Cheng and Nik Amin at the University of Wales Institute of Science and Technology, and Bo Ranneby at the Swedish University of Agricultural Sciences.[2] The authors explained that due to the probability integral transform at the true parameter, the “spacing” between each observation should be uniformly distributed. This would imply that the difference between the values of the cumulative distribution function at consecutive observations should be equal. This is the case that maximizes the geometric mean of such spacings, so solving for the parameters that maximize the geometric mean would achieve the “best” fit as defined this way. Ranneby (1984) justified the method by demonstrating that it is an estimator of the Kullback–Leibler divergence, similar to maximum likelihood estimation, but with more robust properties for some classes of problems.
There are certain distributions, especially those with three or more parameters, whose likelihoods may become infinite along certain paths in the parameter space. Using maximum likelihood to estimate these parameters often breaks down, with one parameter tending to the specific value that causes the likelihood to be infinite, rendering the other parameters inconsistent. The method of maximum spacings, however, being dependent on the difference between points on the cumulative distribution function and not individual likelihood points, does not have this issue, and will return valid results over a much wider array of distributions.[1]
The distributions that tend to have likelihood issues are often those used to model physical phenomena. Hall & al. (2004) seek to analyze flood alleviation methods, which requires accurate models of river flood effects. The distributions that better model these effects are all three-parameter models, which suffer from the infinite likelihood issue described above, leading to Hall's investigation of the maximum spacing procedure. Wong & Li (2006), when comparing the method to maximum likelihood, use various data sets ranging from a set on the oldest ages at death in Sweden between 1905 and 1958 to a set containing annual maximum wind speeds.
Definition
[edit]Given an iid random sample {x1, ..., xn} of size n from a univariate distribution with continuous cumulative distribution function F(x;θ0), where θ0 ∈ Θ is an unknown parameter to be estimated, let {x(1), ..., x(n)} be the corresponding ordered sample, that is the result of sorting of all observations from smallest to largest. For convenience also denote x(0) = −∞ and x(n+1) = +∞.
Define the spacings as the “gaps” between the values of the distribution function at adjacent ordered points:[7]
Then the maximum spacing estimator of θ0 is defined as a value that maximizes the logarithm of the geometric mean of sample spacings:
By the inequality of arithmetic and geometric means, function Sn(θ) is bounded from above by −ln(n+1), and thus the maximum has to exist at least in the supremum sense.
Note that some authors define the function Sn(θ) somewhat differently. In particular, Ranneby (1984) multiplies each Di by a factor of (n+1), whereas Cheng & Stephens (1989) omit the 1⁄n+1 factor in front of the sum and add the “−” sign in order to turn the maximization into minimization. As these are constants with respect to θ, the modifications do not alter the location of the maximum of the function Sn.
Examples
[edit]This section presents two examples of calculating the maximum spacing estimator.
Example 1
[edit]
Suppose two values x(1) = 2, x(2) = 4 were sampled from the exponential distribution F(x;λ) = 1 − e−xλ, x ≥ 0 with unknown parameter λ > 0. In order to construct the MSE we have to first find the spacings:
| i | F(x(i)) | F(x(i−1)) | Di = F(x(i)) − F(x(i−1)) |
|---|---|---|---|
| 1 | 1 − e−2λ | 0 | 1 − e−2λ |
| 2 | 1 − e−4λ | 1 − e−2λ | e−2λ − e−4λ |
| 3 | 1 | 1 − e−4λ | e−4λ |
The process continues by finding the λ that maximizes the geometric mean of the “difference” column. Using the convention that ignores taking the (n+1)st root, this turns into the maximization of the following product: (1 − e−2λ) · (e−2λ − e−4λ) · (e−4λ). Letting μ = e−2λ, the problem becomes finding the maximum of μ5−2μ4+μ3. Differentiating, the μ has to satisfy 5μ4−8μ3+3μ2 = 0. This equation has roots 0, 0.6, and 1. As μ is actually e−2λ, it has to be greater than zero but less than one. Therefore, the only acceptable solution is which corresponds to an exponential distribution with a mean of 1⁄λ ≈ 3.915. For comparison, the maximum likelihood estimate of λ is the inverse of the sample mean, 3, so λMLE = ⅓ ≈ 0.333.
Example 2
[edit]Suppose {x(1), ..., x(n)} is the ordered sample from a uniform distribution U(a,b) with unknown endpoints a and b. The cumulative distribution function is F(x;a,b) = (x−a)/(b−a) when x∈[a,b]. Therefore, individual spacings are given by
Calculating the geometric mean and then taking the logarithm, statistic Sn will be equal to Here only three terms depend on the parameters a and b. Differentiating with respect to those parameters and solving the resulting linear system, the maximum spacing estimates will be
These are known to be the uniformly minimum variance unbiased (UMVU) estimators for the continuous uniform distribution.[1] In comparison, the maximum likelihood estimates for this problem and are biased and have higher mean-squared error.
Properties
[edit]Consistency and efficiency
[edit]The maximum spacing estimator is a consistent estimator in that it converges in probability to the true value of the parameter, θ0, as the sample size increases to infinity.[2] The consistency of maximum spacing estimation holds under much more general conditions than for maximum likelihood estimators. In particular, in cases where the underlying distribution is J-shaped, maximum likelihood will fail where MSE succeeds.[1] An example of a J-shaped density is the Weibull distribution, specifically a shifted Weibull, with a shape parameter less than 1. The density will tend to infinity as x approaches the location parameter rendering estimates of the other parameters inconsistent.
Maximum spacing estimators are also at least as asymptotically efficient as maximum likelihood estimators, where the latter exist. However, MSEs may exist in cases where MLEs do not.[1]
Sensitivity
[edit]Maximum spacing estimators are sensitive to closely spaced observations, and especially ties.[8] Given we get
When the ties are due to multiple observations, the repeated spacings (those that would otherwise be zero) should be replaced by the corresponding likelihood.[1] That is, one should substitute for , as since .
When ties are due to rounding error, Cheng & Stephens (1989) suggest another method to remove the effects.[note 1] Given r tied observations from xi to xi+r−1, let δ represent the round-off error. All of the true values should then fall in the range . The corresponding points on the distribution should now fall between and . Cheng and Stephens suggest assuming that the rounded values are uniformly spaced in this interval, by defining
The MSE method is also sensitive to secondary clustering.[8] One example of this phenomenon is when a set of observations is thought to come from a single normal distribution, but in fact comes from a mixture normals with different means. A second example is when the data is thought to come from an exponential distribution, but actually comes from a gamma distribution. In the latter case, smaller spacings may occur in the lower tail. A high value of M(θ) would indicate this secondary clustering effect, and suggesting a closer look at the data is required.[8]
Moran test
[edit]The statistic Sn(θ) is also a form of Moran or Moran-Darling statistic, M(θ), which can be used to test goodness of fit.[note 2] It has been shown that the statistic, when defined as is asymptotically normal, and that a chi-squared approximation exists for small samples.[8] In the case where we know the true parameter , Cheng & Stephens (1989) show that the statistic has a normal distribution with where γ is the Euler–Mascheroni constant which is approximately 0.57722.[note 3]
The distribution can also be approximated by that of , where , in which and where follows a chi-squared distribution with degrees of freedom. Therefore, to test the hypothesis that a random sample of values comes from the distribution , the statistic can be calculated. Then should be rejected with significance if the value is greater than the critical value of the appropriate chi-squared distribution.[8]
Where θ0 is being estimated by , Cheng & Stephens (1989) showed that has the same asymptotic mean and variance as in the known case. However, the test statistic to be used requires the addition of a bias correction term and is: where is the number of parameters in the estimate.
Generalized maximum spacing
[edit]Alternate measures and spacings
[edit]Ranneby & Ekström (1997) generalized the MSE method to approximate other measures besides the Kullback–Leibler measure. Ekström (1997) further expanded the method to investigate properties of estimators using higher order spacings, where an m-order spacing would be defined as .
Multivariate distributions
[edit]Ranneby & al. (2005) discuss extended maximum spacing methods to the multivariate case. As there is no natural order for , they discuss two alternative approaches: a geometric approach based on Dirichlet cells and a probabilistic approach based on a “nearest neighbor ball” metric.
See also
[edit]Notes
[edit]- ^ There appear to be some minor typographical errors in the paper. For example, in section 4.2, equation (4.1), the rounding replacement for , should not have the log term. In section 1, equation (1.2), is defined to be the spacing itself, and is the negative sum of the logs of . If is logged at this step, the result is always ≤ 0, as the difference between two adjacent points on a cumulative distribution is always ≤ 1, and strictly < 1 unless there are only two points at the bookends. Also, in section 4.3, on page 392, calculation shows that it is the variance which has MPS estimate of 6.87, not the standard deviation . – Editor
- ^ The literature refers to related statistics as Moran or Moran-Darling statistics. For example, Cheng & Stephens (1989) analyze the form where is defined as above. Wong & Li (2006) use the same form as well. However, Beirlant & al. (2001) uses the form , with the additional factor of inside the logged summation. The extra factors will make a difference in terms of the expected mean and variance of the statistic. For consistency, this article will continue to use the Cheng & Amin/Wong & Li form. -- Editor
- ^ Wong & Li (2006) leave out the Euler–Mascheroni constant from their description. -- Editor
References
[edit]Citations
[edit]Works cited
[edit]- Anatolyev, Stanislav; Kosenok, Grigory (2005). "An alternative to maximum likelihood based on spacings" (PDF). Econometric Theory. 21 (2): 472–476. CiteSeerX 10.1.1.494.7340. doi:10.1017/S0266466605050255. S2CID 123004317. Archived from the original (PDF) on 2011-08-16. Retrieved 2009-01-21.
- Beirlant, J.; Dudewicz, E.J.; Györfi, L.; van der Meulen, E.C. (1997). "Nonparametric entropy estimation: an overview" (PDF). International Journal of Mathematical and Statistical Sciences. 6 (1): 17–40. ISSN 1055-7490. Archived from the original (PDF) on May 5, 2005. Retrieved 2008-12-31. Note: linked paper is an updated 2001 version.
- Cheng, R.C.H.; Amin, N.A.K. (1983). "Estimating parameters in continuous univariate distributions with a shifted origin". Journal of the Royal Statistical Society, Series B. 45 (3): 394–403. doi:10.1111/j.2517-6161.1983.tb01268.x. ISSN 0035-9246. JSTOR 2345411.
- Cheng, R.C.H; Stephens, M. A. (1989). "A goodness-of-fit test using Moran's statistic with estimated parameters". Biometrika. 76 (2): 386–392. doi:10.1093/biomet/76.2.385.
- Ekström, Magnus (1997). "Generalized maximum spacing estimates". University of Umeå, Department of Mathematics. 6. ISSN 0345-3928. Archived from the original on February 14, 2007. Retrieved 2008-12-30.
- Hall, M.J.; van den Boogaard, H.F.P.; Fernando, R.C.; Mynett, A.E. (2004). "The construction of confidence intervals for frequency analysis using resampling techniques". Hydrology and Earth System Sciences. 8 (2): 235–246. doi:10.5194/hess-8-235-2004. ISSN 1027-5606.
- Pieciak, Tomasz (2014). The maximum spacing noise estimation in single-coil background MRI data. IEEE International Conference on Image Processing. Paris. pp. 1743–1747. doi:10.1109/icip.2014.7025349.
- Pyke, Ronald (1965). "Spacings". Journal of the Royal Statistical Society, Series B. 27 (3): 395–449. doi:10.1111/j.2517-6161.1965.tb00602.x. ISSN 0035-9246. JSTOR 2345793.
- Ranneby, Bo (1984). "The maximum spacing method. An estimation method related to the maximum likelihood method". Scandinavian Journal of Statistics. 11 (2): 93–112. ISSN 0303-6898. JSTOR 4615946.
- Ranneby, Bo; Ekström, Magnus (1997). "Maximum spacing estimates based on different metrics". University of Umeå, Department of Mathematics. 5. ISSN 0345-3928. Archived from the original on February 14, 2007. Retrieved 2008-12-30.
- Ranneby, Bo; Jammalamadakab, S. Rao; Teterukovskiy, Alex (2005). "The maximum spacing estimation for multivariate observations" (PDF). Journal of Statistical Planning and Inference. 129 (1–2): 427–446. doi:10.1016/j.jspi.2004.06.059. Retrieved 2008-12-31.
- Wong, T.S.T; Li, W.K. (2006). "A note on the estimation of extreme value distributions using maximum product of spacings". Time series and related topics: in memory of Ching-Zong Wei. Institute of Mathematical Statistics Lecture Notes – Monograph Series. Beachwood, Ohio: Institute of Mathematical Statistic. pp. 272–283. arXiv:math/0702830v1. doi:10.1214/074921706000001102. ISBN 978-0-940600-68-3. S2CID 88516426.


![{\displaystyle {\hat {\theta }}={\underset {\theta \in \Theta }{\operatorname {arg\,max} }}\;S_{n}(\theta ),\quad {\text{where }}\ S_{n}(\theta )=\ln \!\!{\sqrt[{n+1}]{D_{1}D_{2}\cdots D_{n+1}}}={\frac {1}{n+1}}\sum _{i=1}^{n+1}\ln {D_{i}}(\theta ).}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/9a31b5ecd6b17eba0ab4543bd2d844d706d1f573)