Wild arc: Difference between revisions
reconstructing title of citation after search for rest of cite |
m Split the first paragraph so that the definition is in the first portion and the history is in the second portion. |
||
| (30 intermediate revisions by 13 users not shown) | |||
| Line 1: | Line 1: | ||
{{Short description|Embedding of the unit interval into 3-space ambient isotopy inequivalent to a line segment}} |
|||
| ⚫ | |||
{{About|a mathematical object|animal rehabilitation|Wild Animal Rehabilitation Center}} |
|||
[[File:Wild3.png|400px|thumb|Fox-Artin arc Example 1.1]] |
|||
In [[geometric topology]], a '''wild arc''' is an [[embedding]] of the [[unit interval]] into 3-dimensional space not equivalent to the usual one in the sense that there does not exist an [[ambient isotopy]] taking the [[Path_(topology)#Arc|arc]] to a straight line segment. |
|||
{{harvtxt|Antoine|1920}} found the first example of a wild arc. {{harvtxt|Fox|Artin|1948}} found another example, called the '''Fox-Artin arc''', whose [[Complement (set theory)|complement]] is not [[simply connected]]. |
|||
==Fox-Artin arcs== |
|||
Two very similar wild arcs appear in the {{harvtxt|Fox|Artin|1948}} article. Example 1.1 (page 981) is most generally referred to as the Fox-Artin wild arc. The crossings have the regular sequence over/over/under/over/under/under when following the curve from left to right. |
|||
The left end-point 0 of the closed unit interval <math>[0,1]</math> is mapped by the arc to the left limit point of the curve, and 1 is mapped to the right limit point. The range of the arc lies in the [[Euclidean space]] <math>\mathbb{R}^3</math> or the [[3-sphere]] <math>S^3</math>. |
|||
===Fox-Artin arc variant=== |
|||
[[File:Wild1.png|400px|thumb|Fox-Artin arc Example 1.1*]] |
|||
Example 1.1* has the crossing sequence over/under/over/under/over/under. According to {{harvtxt|Fox|Artin|1948}}, page 982: "This is just the [[chain stitch]] of [[knitting]] extended indefinitely in both directions." |
|||
This arc cannot be continuously deformed to produce Example 1.1 in <math>\mathbb{R}^3</math> or <math>S^3</math>, despite its similar appearance. |
|||
| ⚫ | |||
Also shown here is an alternative style of diagram for the arc in Example 1.1*. |
|||
==See also== |
==See also== |
||
*[[Wild knot]] |
*[[Wild knot]] |
||
*[[Alexander horned sphere]] |
|||
==Further reading== |
==Further reading== |
||
*{{citation|first=L.|last=Antoine|title=Sur la possibilité d'étendre l'homéomorphie de deux figures à leurs voisinages|journal=C.R. Acad. Sci. Paris|year=1920|volume=171|page=661}} |
*{{citation|first=L.|last=Antoine|title=Sur la possibilité d'étendre l'homéomorphie de deux figures à leurs voisinages|journal=C. R. Acad. Sci. Paris|year=1920|volume=171|page=661|lang=fr}} |
||
*{{Citation | last1=Fox | first1=Ralph H. | last2=Harrold | first2=O. G. | title=Topology of 3-manifolds and related topics (Proc. The Univ. of Georgia Institute, 1961) | publisher=[[Prentice Hall]] | mr=0140096 | year=1962 | chapter=The Wilder arcs | pages=184–187}} |
*{{Citation | last1=Fox | first1=Ralph H. | last2=Harrold | first2=O. G. | title=Topology of 3-manifolds and related topics (Proc. The Univ. of Georgia Institute, 1961) | publisher=[[Prentice Hall]] | mr=0140096 | year=1962 | chapter=The Wilder arcs | pages=184–187}} |
||
*{{Citation | last1=Fox | first1=Ralph H. |author1-link=Ralph Fox| last2=Artin | first2=Emil | author2-link=Emil Artin | title=Some wild cells and spheres in three-dimensional space | jstor=1969408 | mr=0027512 | year=1948 | journal=[[Annals of Mathematics |
*{{Citation | last1=Fox | first1=Ralph H. |author1-link=Ralph Fox| last2=Artin | first2=Emil | author2-link=Emil Artin | title=Some wild cells and spheres in three-dimensional space | jstor=1969408 | mr=0027512 | year=1948 | journal=[[Annals of Mathematics]] |series=Second Series | issn=0003-486X | volume=49 | issue=4 | pages=979–990 | doi=10.2307/1969408}} |
||
* {{cite book |
* {{cite book|first1=John Gilbert|last1=Hocking|first2=Gail Sellers|last2=Young|title=Topology|year=1988|orig-year=1961|publisher=Dover|isbn=0-486-65676-4|pages=[https://archive.org/details/topology00hock_0/page/176 176–177]|url-access=registration|url=https://archive.org/details/topology00hock_0/page/176}} |
||
*{{Citation | last1=McPherson | first1=James M. | title=Wild arcs in three-space. I. Families of Fox–Artin arcs | url=http://projecteuclid.org/euclid.pjm/1102947540 | mr=0343276 | year=1973 | journal=[[Pacific Journal of Mathematics]] | issn=0030-8730 | volume=45 | pages=585–598 | doi=10.2140/pjm.1973.45.585}} |
*{{Citation | last1=McPherson | first1=James M. | title=Wild arcs in three-space. I. Families of Fox–Artin arcs | url=http://projecteuclid.org/euclid.pjm/1102947540 | mr=0343276 | year=1973 | journal=[[Pacific Journal of Mathematics]] | issn=0030-8730 | volume=45 | issue=2 | pages=585–598 | doi=10.2140/pjm.1973.45.585| doi-access=free }} |
||
{{Topology}} |
|||
[[Category:Geometric topology]] |
[[Category:Geometric topology]] |
||
Latest revision as of 15:51, 22 September 2024
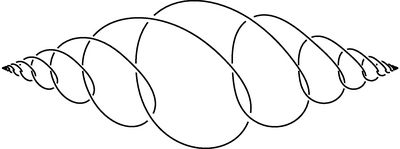
In geometric topology, a wild arc is an embedding of the unit interval into 3-dimensional space not equivalent to the usual one in the sense that there does not exist an ambient isotopy taking the arc to a straight line segment.
Antoine (1920) found the first example of a wild arc. Fox & Artin (1948) found another example, called the Fox-Artin arc, whose complement is not simply connected.
Fox-Artin arcs
[edit]Two very similar wild arcs appear in the Fox & Artin (1948) article. Example 1.1 (page 981) is most generally referred to as the Fox-Artin wild arc. The crossings have the regular sequence over/over/under/over/under/under when following the curve from left to right.
The left end-point 0 of the closed unit interval is mapped by the arc to the left limit point of the curve, and 1 is mapped to the right limit point. The range of the arc lies in the Euclidean space or the 3-sphere .
Fox-Artin arc variant
[edit]
Example 1.1* has the crossing sequence over/under/over/under/over/under. According to Fox & Artin (1948), page 982: "This is just the chain stitch of knitting extended indefinitely in both directions."
This arc cannot be continuously deformed to produce Example 1.1 in or , despite its similar appearance.

Also shown here is an alternative style of diagram for the arc in Example 1.1*.
See also
[edit]Further reading
[edit]- Antoine, L. (1920), "Sur la possibilité d'étendre l'homéomorphie de deux figures à leurs voisinages", C. R. Acad. Sci. Paris (in French), 171: 661
- Fox, Ralph H.; Harrold, O. G. (1962), "The Wilder arcs", Topology of 3-manifolds and related topics (Proc. The Univ. of Georgia Institute, 1961), Prentice Hall, pp. 184–187, MR 0140096
- Fox, Ralph H.; Artin, Emil (1948), "Some wild cells and spheres in three-dimensional space", Annals of Mathematics, Second Series, 49 (4): 979–990, doi:10.2307/1969408, ISSN 0003-486X, JSTOR 1969408, MR 0027512
- Hocking, John Gilbert; Young, Gail Sellers (1988) [1961]. Topology. Dover. pp. 176–177. ISBN 0-486-65676-4.
- McPherson, James M. (1973), "Wild arcs in three-space. I. Families of Fox–Artin arcs", Pacific Journal of Mathematics, 45 (2): 585–598, doi:10.2140/pjm.1973.45.585, ISSN 0030-8730, MR 0343276

![{\displaystyle [0,1]}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)


