5-cell honeycomb: Difference between revisions
m Replace magic links with templates per local RfC and MediaWiki RfC |
img |
||
| (30 intermediate revisions by 12 users not shown) | |||
| Line 1: | Line 1: | ||
{{short description|Geometric figure}} |
|||
{| class="wikitable" align="right" style="margin-left:10px" |
{| class="wikitable" align="right" style="margin-left:10px" |
||
!bgcolor=#e7dcc3 colspan=2|4-simplex honeycomb |
!bgcolor=#e7dcc3 colspan=2|4-simplex honeycomb |
||
| Line 8: | Line 9: | ||
|bgcolor=#e7dcc3|Family||[[Simplectic honeycomb]] |
|bgcolor=#e7dcc3|Family||[[Simplectic honeycomb]] |
||
|- |
|- |
||
|bgcolor=#e7dcc3|[[Schläfli symbol]]||{3<sup>[5]</sup>} |
|bgcolor=#e7dcc3|[[Schläfli symbol]]||{3<sup>[5]</sup>} = 0<sub>[5]</sub> |
||
|- |
|- |
||
|bgcolor=#e7dcc3|[[Coxeter diagram]]||{{CDD|node_1|split1|nodes|3ab|branch}} |
|bgcolor=#e7dcc3|[[Coxeter diagram]]||{{CDD|node_1|split1|nodes|3ab|branch}} |
||
| Line 14: | Line 15: | ||
|bgcolor=#e7dcc3|4-face types||[[5-cell|{3,3,3}]][[File:Schlegel wireframe 5-cell.png|40px]]<BR>[[Rectified 5-cell|t<sub>1</sub>{3,3,3}]] [[File:Schlegel half-solid rectified 5-cell.png|40px]] |
|bgcolor=#e7dcc3|4-face types||[[5-cell|{3,3,3}]][[File:Schlegel wireframe 5-cell.png|40px]]<BR>[[Rectified 5-cell|t<sub>1</sub>{3,3,3}]] [[File:Schlegel half-solid rectified 5-cell.png|40px]] |
||
|- |
|- |
||
|bgcolor=#e7dcc3|Cell types||[[tetrahedron|{3,3}]] [[File:Uniform polyhedron-33-t0.png|20px]]<BR>[[Octahedron|t<sub>1</sub>{3,3}]] [[File:Uniform polyhedron-33-t1. |
|bgcolor=#e7dcc3|Cell types||[[tetrahedron|{3,3}]] [[File:Uniform polyhedron-33-t0.png|20px]]<BR>[[Octahedron|t<sub>1</sub>{3,3}]] [[File:Uniform polyhedron-33-t1.svg|20px]] |
||
|- |
|- |
||
|bgcolor=#e7dcc3|Face types||[[triangle|{3}]] |
|bgcolor=#e7dcc3|Face types||[[triangle|{3}]] |
||
| Line 20: | Line 21: | ||
|bgcolor=#e7dcc3|Vertex figure||[[File:4-simplex_honeycomb_verf.png|80px]]<BR>[[Runcinated 5-cell|t<sub>0,3</sub>{3,3,3}]] |
|bgcolor=#e7dcc3|Vertex figure||[[File:4-simplex_honeycomb_verf.png|80px]]<BR>[[Runcinated 5-cell|t<sub>0,3</sub>{3,3,3}]] |
||
|- |
|- |
||
|bgcolor=#e7dcc3|[[Coxeter notation|Symmetry]]||<math>{\tilde{A}}_4</math>×2 |
|bgcolor=#e7dcc3|[[Coxeter notation|Symmetry]]||<math>{\tilde{A}}_4</math>×2<BR>[3<sup>[5]</sup>] |
||
|- |
|- |
||
|bgcolor=#e7dcc3|Properties||[[vertex-transitive]] |
|bgcolor=#e7dcc3|Properties||[[vertex-transitive]] |
||
| Line 26: | Line 27: | ||
In [[Four-dimensional space|four-dimensional]] [[Euclidean geometry]], the '''4-simplex honeycomb''', '''5-cell honeycomb''' or '''pentachoric-dispentachoric honeycomb''' is a space-filling [[tessellation]] [[honeycomb (geometry)|honeycomb]]. It is composed of [[5-cell]]s and [[rectified 5-cell]]s facets in a ratio of 1:1. |
In [[Four-dimensional space|four-dimensional]] [[Euclidean geometry]], the '''4-simplex honeycomb''', '''5-cell honeycomb''' or '''pentachoric-dispentachoric honeycomb''' is a space-filling [[tessellation]] [[honeycomb (geometry)|honeycomb]]. It is composed of [[5-cell]]s and [[rectified 5-cell]]s facets in a ratio of 1:1. |
||
== Structure== |
|||
Cells of the [[vertex figure]] are ten [[tetrahedron]]s and 20 [[triangular prism]]s, corresponding to the ten [[5-cell]]s and 20 [[rectified 5-cell]]s that meet at each vertex. All the vertices lie in parallel realms in which they form [[alternated cubic honeycomb]]s, the tetrahedra being either tops of the rectified 5-cell or the bases of the 5-cell, and the octahedra being the bottoms of the rectified 5-cell.<ref>Olshevsky (2006), Model 134</ref> |
Cells of the [[vertex figure]] are ten [[tetrahedron]]s and 20 [[triangular prism]]s, corresponding to the ten [[5-cell]]s and 20 [[rectified 5-cell]]s that meet at each vertex. All the vertices lie in parallel realms in which they form [[alternated cubic honeycomb]]s, the tetrahedra being either tops of the rectified 5-cell or the bases of the 5-cell, and the octahedra being the bottoms of the rectified 5-cell.<ref>Olshevsky (2006), Model 134</ref> |
||
| Line 45: | Line 46: | ||
|{{CDD|node_1|4|node|4|node}} |
|{{CDD|node_1|4|node|4|node}} |
||
|} |
|} |
||
Two different [[aperiodic tiling]]s with 5-fold symmetry can be obtained by projecting two-dimensional slices of the honeycomb: the [[Penrose tiling]] composed of rhombi, and the [[Tübingen triangle]] tiling composed of isosceles triangles.<ref>{{cite journal |last1=Baake |first1=M. |last2=Kramer |first2=P. |last3=Schlottmann |first3=M. |last4=Zeidler |first4=D. |title=PLANAR PATTERNS WITH FIVEFOLD SYMMETRY AS SECTIONS OF PERIODIC STRUCTURES IN 4-SPACE |journal=International Journal of Modern Physics B |date=December 1990 |volume=04 |issue=15n16 |pages=2217–2268 |doi=10.1142/S0217979290001054}}</ref> |
|||
== A4 lattice == |
== A4 lattice == |
||
The [[vertex arrangement]] of the ''5-cell honeycomb'' is called the '''A4 lattice''', or '''4-simplex lattice'''. The 20 vertices of its [[vertex figure]], the [[runcinated 5-cell]] represent the 20 roots of the <math>{\tilde{A}}_4</math> Coxeter group.<ref>{{Cite web|url=http://www.math.rwth-aachen.de/~Gabriele.Nebe/LATTICES/A4.html|title = The Lattice A4}}</ref><ref>{{Cite web|url=https://m.wolframalpha.com/input/?i=A4+root+lattice&lk=3|title = A4 root lattice - Wolfram|Alpha}}</ref> It is the 4-dimensional case of a [[simplectic honeycomb]]. |
|||
The A{{sup sub|*|4}} lattice is the union of five A<sub>4</sub> lattices, and is the dual to the [[omnitruncated 5-simplex honeycomb]], and therefore the [[Voronoi cell]] of this lattice is an [[omnitruncated 5-cell]] |
The A{{sup sub|*|4}} lattice<ref>{{Cite web|url=http://www.math.rwth-aachen.de/~Gabriele.Nebe/LATTICES/As4.html|title=The Lattice A4}}</ref> is the union of five A<sub>4</sub> lattices, and is the dual to the [[omnitruncated 5-simplex honeycomb]], and therefore the [[Voronoi cell]] of this lattice is an [[omnitruncated 5-cell]] |
||
: {{CDD|node_1|split1|nodes|3ab|branch}} ∪ {{CDD|node|split1| |
: {{CDD|node_1|split1|nodes|3ab|branch}} ∪ {{CDD|node|split1|nodes_10lur|3ab|branch}} ∪ {{CDD|node|split1|nodes_01lr|3ab|branch}} ∪ {{CDD|node|split1|nodes|3ab|branch_10l}} ∪ {{CDD|node|split1|nodes|3ab|branch_01l}} = dual of {{CDD|node_1|split1|nodes_11|3ab|branch_11}} |
||
== Related polytopes and honeycombs == |
== Related polytopes and honeycombs == |
||
| Line 76: | Line 79: | ||
|bgcolor=#e7dcc3|Vertex figure||triangular elongated-antiprismatic prism |
|bgcolor=#e7dcc3|Vertex figure||triangular elongated-antiprismatic prism |
||
|- |
|- |
||
|bgcolor=#e7dcc3|[[Coxeter notation|Symmetry]]||<math>{\tilde{A}}_4</math>×2 |
|bgcolor=#e7dcc3|[[Coxeter notation|Symmetry]]||<math>{\tilde{A}}_4</math>×2<BR>[3<sup>[5]</sup>] |
||
|- |
|- |
||
|bgcolor=#e7dcc3|Properties||[[vertex-transitive]] |
|bgcolor=#e7dcc3|Properties||[[vertex-transitive]] |
||
| Line 108: | Line 111: | ||
|bgcolor=#e7dcc3|Face types||[[Triangle]] {3}<BR>[[Hexagon]] {6} |
|bgcolor=#e7dcc3|Face types||[[Triangle]] {3}<BR>[[Hexagon]] {6} |
||
|- |
|- |
||
|bgcolor=#e7dcc3|Vertex figure||[[File:Truncated_5-cell_honeycomb_verf.png|100px]]<BR> |
|bgcolor=#e7dcc3|Vertex figure||[[File:Truncated_5-cell_honeycomb_verf.png|100px]]<BR>[[Tetrahedral antiprism]]<BR>[3,4,2<sup>+</sup>], order 48 |
||
|- |
|- |
||
|bgcolor=#e7dcc3|[[Coxeter notation|Symmetry]]||<math>{\tilde{A}}_4</math>×2 |
|bgcolor=#e7dcc3|[[Coxeter notation|Symmetry]]||<math>{\tilde{A}}_4</math>×2<BR>[3<sup>[5]</sup>] |
||
|- |
|- |
||
|bgcolor=#e7dcc3|Properties||[[vertex-transitive]] |
|bgcolor=#e7dcc3|Properties||[[vertex-transitive]] |
||
| Line 116: | Line 119: | ||
The '''cyclotruncated 4-simplex honeycomb''' or '''cyclotruncated 5-cell honeycomb''' is a space-filling [[tessellation]] [[honeycomb (geometry)|honeycomb]]. It can also be seen as a '''birectified 5-cell honeycomb'''. |
The '''cyclotruncated 4-simplex honeycomb''' or '''cyclotruncated 5-cell honeycomb''' is a space-filling [[tessellation]] [[honeycomb (geometry)|honeycomb]]. It can also be seen as a '''birectified 5-cell honeycomb'''. |
||
It is composed of [[5-cell]]s, [[truncated 5-cell]]s, and [[bitruncated 5-cell]]s facets in a ratio of 2:2:1. Its [[vertex figure]] is |
It is composed of [[5-cell]]s, [[truncated 5-cell]]s, and [[bitruncated 5-cell]]s facets in a ratio of 2:2:1. Its [[vertex figure]] is a [[tetrahedral antiprism]], with 2 [[regular tetrahedron]], 8 [[triangular pyramid]], and 6 [[tetragonal disphenoid]] cells, defining 2 [[5-cell]], 8 [[truncated 5-cell]], and 6 [[bitruncated 5-cell]] facets around a vertex. |
||
It can be constructed as five sets of parallel [[hyperplane]]s that divide space into two half-spaces. The 3-space hyperplanes contain [[quarter cubic honeycomb]]s as a collection facets.<ref>Olshevsky, (2006) Model 135</ref> |
It can be constructed as five sets of parallel [[hyperplane]]s that divide space into two half-spaces. The 3-space hyperplanes contain [[quarter cubic honeycomb]]s as a collection facets.<ref>Olshevsky, (2006) Model 135</ref> |
||
| Line 125: | Line 128: | ||
{{-}} |
{{-}} |
||
=== Truncated 5-cell honeycomb=== |
=== Truncated 5-cell honeycomb=== |
||
{| class="wikitable" align="right" style="margin-left:10px" width="360" |
{| class="wikitable" align="right" style="margin-left:10px" width="360" |
||
!bgcolor=#e7dcc3 colspan=2|Truncated 4-simplex honeycomb |
!bgcolor=#e7dcc3 colspan=2|Truncated 4-simplex honeycomb |
||
| Line 143: | Line 146: | ||
|bgcolor=#e7dcc3|Vertex figure||triangular elongated-antiprismatic pyramid |
|bgcolor=#e7dcc3|Vertex figure||triangular elongated-antiprismatic pyramid |
||
|- |
|- |
||
|bgcolor=#e7dcc3|[[Coxeter notation|Symmetry]]||<math>{\tilde{A}}_4</math>×2 |
|bgcolor=#e7dcc3|[[Coxeter notation|Symmetry]]||<math>{\tilde{A}}_4</math>×2<BR>[3<sup>[5]</sup>] |
||
|- |
|- |
||
|bgcolor=#e7dcc3|Properties||[[vertex-transitive]] |
|bgcolor=#e7dcc3|Properties||[[vertex-transitive]] |
||
| Line 170: | Line 173: | ||
|bgcolor=#e7dcc3|Cell types||[[Truncated tetrahedron]] [[File:Truncated tetrahedron.png|20px]]<BR>[[Octahedron]] [[File:Octahedron.png|20px]]<BR>[[Cuboctahedron]] [[File:Cuboctahedron.png|20px]]<BR>[[Triangular prism]] [[File:Triangular prism.png|20px]]<BR>[[Hexagonal prism]] [[File:Hexagonal prism.png|20px]] |
|bgcolor=#e7dcc3|Cell types||[[Truncated tetrahedron]] [[File:Truncated tetrahedron.png|20px]]<BR>[[Octahedron]] [[File:Octahedron.png|20px]]<BR>[[Cuboctahedron]] [[File:Cuboctahedron.png|20px]]<BR>[[Triangular prism]] [[File:Triangular prism.png|20px]]<BR>[[Hexagonal prism]] [[File:Hexagonal prism.png|20px]] |
||
|- |
|- |
||
|bgcolor=#e7dcc3|Vertex figure|| |
|bgcolor=#e7dcc3|Vertex figure||Bidiminished rectified pentachoron |
||
|- |
|- |
||
|bgcolor=#e7dcc3|[[Coxeter notation|Symmetry]]||<math>{\tilde{A}}_4</math>×2 |
|bgcolor=#e7dcc3|[[Coxeter notation|Symmetry]]||<math>{\tilde{A}}_4</math>×2<BR>[3<sup>[5]</sup>] |
||
|- |
|- |
||
|bgcolor=#e7dcc3|Properties||[[vertex-transitive]] |
|bgcolor=#e7dcc3|Properties||[[vertex-transitive]] |
||
| Line 207: | Line 210: | ||
|bgcolor=#e7dcc3|Vertex figure||tilted rectangular [[duopyramid]] |
|bgcolor=#e7dcc3|Vertex figure||tilted rectangular [[duopyramid]] |
||
|- |
|- |
||
|bgcolor=#e7dcc3|[[Coxeter notation|Symmetry]]||<math>{\tilde{A}}_4</math>×2 |
|bgcolor=#e7dcc3|[[Coxeter notation|Symmetry]]||<math>{\tilde{A}}_4</math>×2<BR>[3<sup>[5]</sup>] |
||
|- |
|- |
||
|bgcolor=#e7dcc3|Properties||[[vertex-transitive]] |
|bgcolor=#e7dcc3|Properties||[[vertex-transitive]] |
||
| Line 246: | Line 249: | ||
|} |
|} |
||
The '''omnitruncated 4-simplex honeycomb''' or '''omnitruncated 5-cell honeycomb''' is a space-filling [[tessellation]] [[honeycomb (geometry)|honeycomb]]. It can also be seen as |
The '''omnitruncated 4-simplex honeycomb''' or '''omnitruncated 5-cell honeycomb''' is a space-filling [[tessellation]] [[honeycomb (geometry)|honeycomb]]. It can also be seen as a '''cyclosteriruncicantitruncated 5-cell honeycomb'''. |
||
. |
. |
||
| Line 253: | Line 256: | ||
[[Coxeter]] calls this '''Hinton's honeycomb''' after [[Charles Howard Hinton|C. H. Hinton]], who described it in his book ''The Fourth Dimension'' in 1906.<ref name=cox>{{cite book|title=The Beauty of Geometry: Twelve Essays|year= 1999|publisher= Dover Publications|lccn=99035678|isbn= 0-486-40919-8 }} (The classification of Zonohededra, page 73)</ref> |
[[Coxeter]] calls this '''Hinton's honeycomb''' after [[Charles Howard Hinton|C. H. Hinton]], who described it in his book ''The Fourth Dimension'' in 1906.<ref name=cox>{{cite book|title=The Beauty of Geometry: Twelve Essays|year= 1999|publisher= Dover Publications|lccn=99035678|isbn= 0-486-40919-8 }} (The classification of Zonohededra, page 73)</ref> |
||
The facets of all [[omnitruncated simplectic honeycomb]]s are called [[ |
The facets of all [[omnitruncated simplectic honeycomb]]s are called [[permutohedron|permutohedra]] and can be positioned in ''n+1'' space with integral coordinates, permutations of the whole numbers (0,1,..,n). |
||
==== Alternate names==== |
==== Alternate names==== |
||
| Line 261: | Line 264: | ||
==== A<sub>4</sub><sup>*</sup> lattice ==== |
==== A<sub>4</sub><sup>*</sup> lattice ==== |
||
The A{{sup sub|*|4}} lattice is the union of five A<sub>4</sub> lattices, and is the dual to the |
The A{{sup sub|*|4}} lattice is the union of five A<sub>4</sub> lattices, and is the dual to the omnitruncated 5-cell honeycomb, and therefore the [[Voronoi cell]] of this lattice is an [[omnitruncated 5-cell]].<ref>[http://www.math.rwth-aachen.de/~Gabriele.Nebe/LATTICES/As4.html The Lattice A4*]</ref> |
||
: {{CDD|node_1|split1|nodes|3ab|branch}} ∪ {{CDD|node|split1|nodes_10lur|3ab|branch}} ∪ {{CDD|node|split1|nodes_01lr|3ab|branch}} ∪ {{CDD|node|split1|nodes|3ab|branch_10l}} ∪ {{CDD|node|split1|nodes|3ab|branch_01l}} = dual of {{CDD|node_1|split1|nodes_11|3ab|branch_11}} |
: {{CDD|node_1|split1|nodes|3ab|branch}} ∪ {{CDD|node|split1|nodes_10lur|3ab|branch}} ∪ {{CDD|node|split1|nodes_01lr|3ab|branch}} ∪ {{CDD|node|split1|nodes|3ab|branch_10l}} ∪ {{CDD|node|split1|nodes|3ab|branch_01l}} = dual of {{CDD|node_1|split1|nodes_11|3ab|branch_11}} |
||
{{-}} |
{{-}} |
||
== Alternated form == |
|||
This honeycomb can be [[Alternation (geometry)|alternated]], creating [[Runcinated 5-cell#Full snub 5-cell|omnisnub 5-cells]] with irregular [[5-cell]]s created at the deleted vertices. Although it is not uniform, the 5-cells have a symmetry of order 10. |
|||
==See also== |
==See also== |
||
| Line 279: | Line 286: | ||
* [[Norman Johnson (mathematician)|Norman Johnson]] ''Uniform Polytopes'', Manuscript (1991) |
* [[Norman Johnson (mathematician)|Norman Johnson]] ''Uniform Polytopes'', Manuscript (1991) |
||
* ''Kaleidoscopes: Selected Writings of H.S.M. Coxeter'', edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, {{ISBN|978-0-471-01003-6}} [http://www.wiley.com/WileyCDA/WileyTitle/productCd-0471010030.html] |
* ''Kaleidoscopes: Selected Writings of H.S.M. Coxeter'', edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, {{ISBN|978-0-471-01003-6}} [http://www.wiley.com/WileyCDA/WileyTitle/productCd-0471010030.html] |
||
** (Paper 22) H.S.M. Coxeter, ''Regular and Semi Regular Polytopes I'', [Math. Zeit. 46 (1940) |
** (Paper 22) H.S.M. Coxeter, ''Regular and Semi Regular Polytopes I'', [Math. Zeit. 46 (1940) 380–407, MR 2,10] (1.9 Uniform space-fillings) |
||
** (Paper 24) H.S.M. Coxeter, ''Regular and Semi-Regular Polytopes III'', [Math. Zeit. 200 (1988) 3-45] |
** (Paper 24) H.S.M. Coxeter, ''Regular and Semi-Regular Polytopes III'', [Math. Zeit. 200 (1988) 3-45] |
||
* |
* George Olshevsky, ''Uniform Panoploid Tetracombs'', Manuscript (2006) ''(Complete list of 11 convex uniform tilings, 28 convex uniform honeycombs, and 143 convex uniform tetracombs)'' Model 134 |
||
* {{KlitzingPolytopes|flat.htm|4D|Euclidean tesselations}}, x3o3o3o3o3*a - cypit - O134, x3x3x3x3x3*a - otcypit - 135, x3x3x3o3o3*a - gocyropit - O137, x3x3o3x3o3*a - cypropit - O138, x3x3x3x3o3*a - gocypapit - O139, x3x3x3x3x3*a - otcypit - 140 |
* {{KlitzingPolytopes|flat.htm|4D|Euclidean tesselations}}, x3o3o3o3o3*a - cypit - O134, x3x3x3x3x3*a - otcypit - 135, x3x3x3o3o3*a - gocyropit - O137, x3x3o3x3o3*a - cypropit - O138, x3x3x3x3o3*a - gocypapit - O139, x3x3x3x3x3*a - otcypit - 140 |
||
* |
* Affine Coxeter group Wa(A4), Quaternions, and Decagonal Quasicrystals, Mehmet Koca, Nazife O. Koca, Ramazan Koc (2013) {{ArXiv|1209.1878}} |
||
{{Honeycombs}} |
{{Honeycombs}} |
||
Latest revision as of 10:01, 24 September 2024
| 4-simplex honeycomb | |
|---|---|
| (No image) | |
| Type | Uniform 4-honeycomb |
| Family | Simplectic honeycomb |
| Schläfli symbol | {3[5]} = 0[5] |
| Coxeter diagram | |
| 4-face types | {3,3,3} t1{3,3,3} |
| Cell types | {3,3} t1{3,3} |
| Face types | {3} |
| Vertex figure |  t0,3{3,3,3} |
| Symmetry | ×2 [3[5]] |
| Properties | vertex-transitive |
In four-dimensional Euclidean geometry, the 4-simplex honeycomb, 5-cell honeycomb or pentachoric-dispentachoric honeycomb is a space-filling tessellation honeycomb. It is composed of 5-cells and rectified 5-cells facets in a ratio of 1:1.
Structure
[edit]Cells of the vertex figure are ten tetrahedrons and 20 triangular prisms, corresponding to the ten 5-cells and 20 rectified 5-cells that meet at each vertex. All the vertices lie in parallel realms in which they form alternated cubic honeycombs, the tetrahedra being either tops of the rectified 5-cell or the bases of the 5-cell, and the octahedra being the bottoms of the rectified 5-cell.[1]
Alternate names
[edit]- Cyclopentachoric tetracomb
- Pentachoric-dispentachoric tetracomb
Projection by folding
[edit]The 5-cell honeycomb can be projected into the 2-dimensional square tiling by a geometric folding operation that maps two pairs of mirrors into each other, sharing the same vertex arrangement:
Two different aperiodic tilings with 5-fold symmetry can be obtained by projecting two-dimensional slices of the honeycomb: the Penrose tiling composed of rhombi, and the Tübingen triangle tiling composed of isosceles triangles.[2]
A4 lattice
[edit]The vertex arrangement of the 5-cell honeycomb is called the A4 lattice, or 4-simplex lattice. The 20 vertices of its vertex figure, the runcinated 5-cell represent the 20 roots of the Coxeter group.[3][4] It is the 4-dimensional case of a simplectic honeycomb.
The A*
4 lattice[5] is the union of five A4 lattices, and is the dual to the omnitruncated 5-simplex honeycomb, and therefore the Voronoi cell of this lattice is an omnitruncated 5-cell




 ∪
∪ 



 ∪
∪ 



 ∪
∪ 



 ∪
∪ 



 = dual of
= dual of 

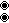


Related polytopes and honeycombs
[edit]The tops of the 5-cells in this honeycomb adjoin the bases of the 5-cells, and vice versa, in adjacent laminae (or layers); but alternating laminae may be inverted so that the tops of the rectified 5-cells adjoin the tops of the rectified 5-cells and the bases of the 5-cells adjoin the bases of other 5-cells. This inversion results in another non-Wythoffian uniform convex honeycomb. Octahedral prisms and tetrahedral prisms may be inserted in between alternated laminae as well, resulting in two more non-Wythoffian elongated uniform honeycombs.[6]
This honeycomb is one of seven unique uniform honeycombs[7] constructed by the Coxeter group. The symmetry can be multiplied by the symmetry of rings in the Coxeter–Dynkin diagrams:
| A4 honeycombs | ||||
|---|---|---|---|---|
| Pentagon symmetry |
Extended symmetry |
Extended diagram |
Extended group |
Honeycomb diagrams |
| a1 | [3[5]] | (None) | ||
| i2 | [[3[5]]] | ×2 | ||
| r10 | [5[3[5]]] | ×10 | ||
Rectified 5-cell honeycomb
[edit]| Rectified 5-cell honeycomb | |
|---|---|
| (No image) | |
| Type | Uniform 4-honeycomb |
| Schläfli symbol | t0,2{3[5]} or r{3[5]} |
| Coxeter diagram | |
| 4-face types | t1{33} t0,2{33} t0,3{33} |
| Cell types | Tetrahedron Octahedron Cuboctahedron Triangular prism |
| Vertex figure | triangular elongated-antiprismatic prism |
| Symmetry | ×2 [3[5]] |
| Properties | vertex-transitive |
The rectified 4-simplex honeycomb or rectified 5-cell honeycomb is a space-filling tessellation honeycomb.
Alternate names
[edit]- small cyclorhombated pentachoric tetracomb
- small prismatodispentachoric tetracomb
Cyclotruncated 5-cell honeycomb
[edit]| Cyclotruncated 5-cell honeycomb | |
|---|---|
| (No image) | |
| Type | Uniform 4-honeycomb |
| Family | Truncated simplectic honeycomb |
| Schläfli symbol | t0,1{3[5]} |
| Coxeter diagram | |
| 4-face types | {3,3,3} t{3,3,3} 2t{3,3,3} |
| Cell types | {3,3} t{3,3} |
| Face types | Triangle {3} Hexagon {6} |
| Vertex figure |  Tetrahedral antiprism [3,4,2+], order 48 |
| Symmetry | ×2 [3[5]] |
| Properties | vertex-transitive |
The cyclotruncated 4-simplex honeycomb or cyclotruncated 5-cell honeycomb is a space-filling tessellation honeycomb. It can also be seen as a birectified 5-cell honeycomb.
It is composed of 5-cells, truncated 5-cells, and bitruncated 5-cells facets in a ratio of 2:2:1. Its vertex figure is a tetrahedral antiprism, with 2 regular tetrahedron, 8 triangular pyramid, and 6 tetragonal disphenoid cells, defining 2 5-cell, 8 truncated 5-cell, and 6 bitruncated 5-cell facets around a vertex.
It can be constructed as five sets of parallel hyperplanes that divide space into two half-spaces. The 3-space hyperplanes contain quarter cubic honeycombs as a collection facets.[8]
Alternate names
[edit]- Cyclotruncated pentachoric tetracomb
- Small truncated-pentachoric tetracomb
Truncated 5-cell honeycomb
[edit]| Truncated 4-simplex honeycomb | |
|---|---|
| (No image) | |
| Type | Uniform 4-honeycomb |
| Schläfli symbol | t0,1,2{3[5]} or t{3[5]} |
| Coxeter diagram | |
| 4-face types | t0,1{33} t0,1,2{33} t0,3{33} |
| Cell types | Tetrahedron Truncated tetrahedron Truncated octahedron Triangular prism |
| Vertex figure | triangular elongated-antiprismatic pyramid |
| Symmetry | ×2 [3[5]] |
| Properties | vertex-transitive |
The truncated 4-simplex honeycomb or truncated 5-cell honeycomb is a space-filling tessellation honeycomb. It can also be called a cyclocantitruncated 5-cell honeycomb.
Alaternate names
[edit]- Great cyclorhombated pentachoric tetracomb
- Great truncated-pentachoric tetracomb
Cantellated 5-cell honeycomb
[edit]| Cantellated 5-cell honeycomb | |
|---|---|
| (No image) | |
| Type | Uniform 4-honeycomb |
| Schläfli symbol | t0,1,3{3[5]} or rr{3[5]} |
| Coxeter diagram | |
| 4-face types | t0,2{33} t1,2{33} t0,1,3{33} |
| Cell types | Truncated tetrahedron Octahedron Cuboctahedron Triangular prism Hexagonal prism |
| Vertex figure | Bidiminished rectified pentachoron |
| Symmetry | ×2 [3[5]] |
| Properties | vertex-transitive |
The cantellated 4-simplex honeycomb or cantellated 5-cell honeycomb is a space-filling tessellation honeycomb. It can also be called a cycloruncitruncated 5-cell honeycomb.
Alternate names
[edit]- Cycloprismatorhombated pentachoric tetracomb
- Great prismatodispentachoric tetracomb
Bitruncated 5-cell honeycomb
[edit]| Bitruncated 5-cell honeycomb | |
|---|---|
| (No image) | |
| Type | Uniform 4-honeycomb |
| Schläfli symbol | t0,1,2,3{3[5]} or 2t{3[5]} |
| Coxeter diagram | |
| 4-face types | t0,1,3{33} t0,1,2{33} t0,1,2,3{33} |
| Cell types | Cuboctahedron Truncated octahedron |
| Vertex figure | tilted rectangular duopyramid |
| Symmetry | ×2 [3[5]] |
| Properties | vertex-transitive |
The bitruncated 4-simplex honeycomb or bitruncated 5-cell honeycomb is a space-filling tessellation honeycomb. It can also be called a cycloruncicantitruncated 5-cell honeycomb.
Alternate names
[edit]- Great cycloprismated pentachoric tetracomb
- Grand prismatodispentachoric tetracomb
Omnitruncated 5-cell honeycomb
[edit]| Omnitruncated 4-simplex honeycomb | |
|---|---|
| (No image) | |
| Type | Uniform 4-honeycomb |
| Family | Omnitruncated simplectic honeycomb |
| Schläfli symbol | t0,1,2,3,4{3[5]} or tr{3[5]} |
| Coxeter diagram | |
| 4-face types | t0,1,2,3{3,3,3} |
| Cell types | t0,1,2{3,3} {6}x{} |
| Face types | {4} {6} |
| Vertex figure |  Irr. 5-cell |
| Symmetry | ×10, [5[3[5]]] |
| Properties | vertex-transitive, cell-transitive |
The omnitruncated 4-simplex honeycomb or omnitruncated 5-cell honeycomb is a space-filling tessellation honeycomb. It can also be seen as a cyclosteriruncicantitruncated 5-cell honeycomb. .
It is composed entirely of omnitruncated 5-cell (omnitruncated 4-simplex) facets.
Coxeter calls this Hinton's honeycomb after C. H. Hinton, who described it in his book The Fourth Dimension in 1906.[9]
The facets of all omnitruncated simplectic honeycombs are called permutohedra and can be positioned in n+1 space with integral coordinates, permutations of the whole numbers (0,1,..,n).
Alternate names
[edit]- Omnitruncated cyclopentachoric tetracomb
- Great-prismatodecachoric tetracomb
A4* lattice
[edit]The A*
4 lattice is the union of five A4 lattices, and is the dual to the omnitruncated 5-cell honeycomb, and therefore the Voronoi cell of this lattice is an omnitruncated 5-cell.[10]




 ∪
∪ 



 ∪
∪ 



 ∪
∪ 



 ∪
∪ 



 = dual of
= dual of 

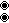


Alternated form
[edit]This honeycomb can be alternated, creating omnisnub 5-cells with irregular 5-cells created at the deleted vertices. Although it is not uniform, the 5-cells have a symmetry of order 10.
See also
[edit]Regular and uniform honeycombs in 4-space:
- Tesseractic honeycomb
- 16-cell honeycomb
- 24-cell honeycomb
- Truncated 24-cell honeycomb
- Snub 24-cell honeycomb
Notes
[edit]- ^ Olshevsky (2006), Model 134
- ^ Baake, M.; Kramer, P.; Schlottmann, M.; Zeidler, D. (December 1990). "PLANAR PATTERNS WITH FIVEFOLD SYMMETRY AS SECTIONS OF PERIODIC STRUCTURES IN 4-SPACE". International Journal of Modern Physics B. 04 (15n16): 2217–2268. doi:10.1142/S0217979290001054.
- ^ "The Lattice A4".
- ^ "A4 root lattice - Wolfram|Alpha".
- ^ "The Lattice A4".
- ^ Olshevsky (2006), Klitzing, elong( x3o3o3o3o3*a ) - ecypit - O141, schmo( x3o3o3o3o3*a ) - zucypit - O142, elongschmo( x3o3o3o3o3*a ) - ezucypit - O143
- ^ mathworld: Necklace, OEIS sequence A000029 8-1 cases, skipping one with zero marks
- ^ Olshevsky, (2006) Model 135
- ^ The Beauty of Geometry: Twelve Essays. Dover Publications. 1999. ISBN 0-486-40919-8. LCCN 99035678. (The classification of Zonohededra, page 73)
- ^ The Lattice A4*
References
[edit]- Norman Johnson Uniform Polytopes, Manuscript (1991)
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380–407, MR 2,10] (1.9 Uniform space-fillings)
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
- George Olshevsky, Uniform Panoploid Tetracombs, Manuscript (2006) (Complete list of 11 convex uniform tilings, 28 convex uniform honeycombs, and 143 convex uniform tetracombs) Model 134
- Klitzing, Richard. "4D Euclidean tesselations"., x3o3o3o3o3*a - cypit - O134, x3x3x3x3x3*a - otcypit - 135, x3x3x3o3o3*a - gocyropit - O137, x3x3o3x3o3*a - cypropit - O138, x3x3x3x3o3*a - gocypapit - O139, x3x3x3x3x3*a - otcypit - 140
- Affine Coxeter group Wa(A4), Quaternions, and Decagonal Quasicrystals, Mehmet Koca, Nazife O. Koca, Ramazan Koc (2013) arXiv:1209.1878
| Space | Family | / / | ||||
|---|---|---|---|---|---|---|
| E2 | Uniform tiling | 0[3] | δ3 | hδ3 | qδ3 | Hexagonal |
| E3 | Uniform convex honeycomb | 0[4] | δ4 | hδ4 | qδ4 | |
| E4 | Uniform 4-honeycomb | 0[5] | δ5 | hδ5 | qδ5 | 24-cell honeycomb |
| E5 | Uniform 5-honeycomb | 0[6] | δ6 | hδ6 | qδ6 | |
| E6 | Uniform 6-honeycomb | 0[7] | δ7 | hδ7 | qδ7 | 222 |
| E7 | Uniform 7-honeycomb | 0[8] | δ8 | hδ8 | qδ8 | 133 • 331 |
| E8 | Uniform 8-honeycomb | 0[9] | δ9 | hδ9 | qδ9 | 152 • 251 • 521 |
| E9 | Uniform 9-honeycomb | 0[10] | δ10 | hδ10 | qδ10 | |
| E10 | Uniform 10-honeycomb | 0[11] | δ11 | hδ11 | qδ11 | |
| En-1 | Uniform (n-1)-honeycomb | 0[n] | δn | hδn | qδn | 1k2 • 2k1 • k21 |










