Tricolorability: Difference between revisions
VectorPosse (talk | contribs) →Properties: Added a little about counting 3-colorings. |
Citation bot (talk | contribs) Altered pages. Formatted dashes. | Use this bot. Report bugs. | Suggested by ΘΘεοχάρης | Category:Graph coloring | #UCB_Category 45/82 |
||
| (28 intermediate revisions by 18 users not shown) | |||
| Line 1: | Line 1: | ||
{{short description|Property in knot theory}} |
|||
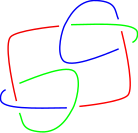
[[Image:Tricoloring.png|thumb|right|A tricolored [[trefoil knot]].]]In the [[mathematics|mathematical]] field of [[knot theory]], the '''tricolorability''' of a [[knot]] is the ability of a knot to be colored with three colors subject to certain rules. Tricolorability is an [[Knot invariant|isotopy invariant]], and hence can be used to distinguish between two different (non-[[Regular isotopy|isotopic]]) knots. In particular, since the [[unknot]] is not tricolorable, any tricolorable knot is necessarily nontrivial. |
[[Image:Tricoloring.png|thumb|right|A tricolored [[trefoil knot]].]]In the [[mathematics|mathematical]] field of [[knot theory]], the '''tricolorability''' of a [[knot (mathematics)|knot]] is the ability of a knot to be colored with three colors subject to certain rules. Tricolorability is an [[Knot invariant|isotopy invariant]], and hence can be used to distinguish between two different (non-[[Regular isotopy|isotopic]]) knots. In particular, since the [[unknot]] is not tricolorable, any tricolorable knot is necessarily nontrivial. |
||
==Rules of tricolorability== |
==Rules of tricolorability== |
||
A knot is tricolorable if each strand of the |
In these rules a '''strand''' in a [[knot diagram]] will be a piece of the string that goes from one undercrossing to the next.<ref>Xaoyu Qiao, E. L., [http://web.math.ucsb.edu/~padraic/ucsb_2014_15/ccs_problem_solving_w2015/Tricolorability.pdf Knot Theory Week 2: Tricolorability] (January 20, 2015), Section 3.</ref> A knot is '''tricolorable''' if each strand of the knot diagram can be colored one of three colors, subject to the following rules:<ref name="Weisstein">Weisstein, Eric W. (2010). ''CRC Concise Encyclopedia of Mathematics'', Second Edition, p.3045. {{isbn|9781420035223}}. quoted at {{MathWorld|title=Tricolorable|id=Tricolorable}} Accessed: May 5, 2013.</ref> |
||
:1. At least two colors must be used, and |
:1. At least two colors must be used, and |
||
:2. At each crossing, the three incident strands are either all the same color or all different colors. |
:2. At each crossing, the three incident strands are either all the same color or all different colors. |
||
Some references state instead that all three colors must be used.<ref name="GP">Gilbert, N.D. and Porter, T. (1994) ''Knots and Surfaces'', p. 8</ref> For a knot, this is equivalent to the definition above; however, for a link it is not. |
|||
| ⚫ | "The trefoil knot and trivial 2-link are tricolorable, but the unknot, [[Whitehead link]], and [[Figure |
||
| ⚫ | "The trefoil knot and trivial 2-link are tricolorable, but the unknot, [[Whitehead link]], and [[Figure-eight knot (mathematics)|figure-eight knot]] are not. If the projection of a knot is tricolorable, then [[Reidemeister moves]] on the knot preserve tricolorability, so either every projection of a knot is tricolorable or none is."<ref name="Weisstein"/> |
||
==Examples== |
==Examples== |
||
| Line 12: | Line 15: | ||
===Example of a tricolorable knot=== |
===Example of a tricolorable knot=== |
||
[[Image: |
[[Image:TricoloredGrannyKnot.svg]] |
||
The [[granny knot (mathematics)|granny knot]] is tricolorable. In this coloring the three strands at every crossing have three different colors. Coloring one but not both of the [[trefoil knot]]s all red would also give an admissible coloring. The true lover's knot is also tricolorable.<ref>[[Mladen Bestvina|Bestvina, Mladen]] (February 2003). "[http://www.math.utah.edu/~bestvina/HS07/knots-hs07.pdf Knots: a handout for mathcircles]", ''Math.Utah.edu''.</ref> |
The [[granny knot (mathematics)|granny knot]] is tricolorable. In this coloring the three strands at every crossing have three different colors. Coloring one but not both of the [[trefoil knot]]s all red would also give an admissible coloring. The true lover's knot is also tricolorable.<ref>[[Mladen Bestvina|Bestvina, Mladen]] (February 2003). "[http://www.math.utah.edu/~bestvina/HS07/knots-hs07.pdf Knots: a handout for mathcircles]", ''Math.Utah.edu''.</ref> |
||
Tricolorable knots with less than nine crossings include 6<sub>1</sub>, 7<sub>4</sub>, 7<sub>7</sub>, 8<sub>5</sub>, 8<sub>10</sub>, 8<sub>11</sub>, 8<sub>15</sub>, 8<sub>18</sub>, 8<sub>19</sub>, 8<sub>20</sub>, and 8<sub>21</sub>. |
|||
===Example of a non-tricolorable knot=== |
===Example of a non-tricolorable knot=== |
||
[[File:Failed_Tricoloring_of_Figure_8.svg]] |
|||
[[Image:Figure8Knot4.png]] |
|||
The [[figure-eight knot (mathematics)|figure-eight knot]] is not tricolorable. In the diagram shown, it has four strands with each pair of strands meeting at some crossing. If three of the strands had the same color, then all strands would be forced to be the same color. Otherwise each of these four strands must have a distinct color. Since tricolorability is a knot invariant, none of its other |
The [[figure-eight knot (mathematics)|figure-eight knot]] is not tricolorable. In the diagram shown, it has four strands with each pair of strands meeting at some crossing. If three of the strands had the same color, then all strands would be forced to be the same color. Otherwise each of these four strands must have a distinct color. Since tricolorability is a knot invariant, none of its other diagrams can be tricolored either. |
||
==Isotopy invariant== |
==Isotopy invariant== |
||
Tricolorability is an [[Knot invariant|isotopy invariant]], which is a property of a knot or [[Link (knot theory)|link]] that remains constant regardless of any [[ambient isotopy]]. This can be proven by examining [[Reidemeister move]]s. Since each Reidemeister move can be made without affecting tricolorability, tricolorability is an isotopy invariant. |
Tricolorability is an [[Knot invariant|isotopy invariant]], which is a property of a knot or [[Link (knot theory)|link]] that remains constant regardless of any [[ambient isotopy]]. This can be proven for tame knots by examining [[Reidemeister move]]s. Since each Reidemeister move can be made without affecting tricolorability, tricolorability is an isotopy invariant of tame knots.<ref>{{Cite book |last=Adams |first=Colin |url=https://www.worldcat.org/title/ocm55633800 |title=The knot book: an elementary introduction to the mathematical theory of knots |date=2004 |publisher=American Mathematical Society |isbn=978-0-8218-3678-1 |location=Providence, R.I |pages=22–27 |oclc=ocm55633800}}</ref> |
||
{| border=1 style="border-collapse: collapse;" cellspacing=10 cellpadding=5 align="center" |
{| border=1 style="border-collapse: collapse;" cellspacing=10 cellpadding=5 align="center" |
||
!Reidemeister Move I is tricolorable.!!Reidemeister Move II is tricolorable.!!Reidemeister Move III is tricolorable. |
!Reidemeister Move I is tricolorable.!!Reidemeister Move II is tricolorable.!!Reidemeister Move III is tricolorable. |
||
|- |
|- |
||
|[[Image: |
|[[Image:Tricolor Invariance on Reidemeister I.svg|center|x100px]]||[[Image:Tricolor Invariance on Reidemeister II.svg|center|x100px]]||[[Image:Tricolor Invariance on Reidemeister III.svg|center|x100px]] |
||
|} |
|} |
||
==Properties== |
==Properties== |
||
Because tricolorability is a binary classification (a link is either tricolorable or not), it is a relatively weak invariant. The composition of a tricolorable knot with another knot is always tricolorable. A way to strengthen the invariant is to count the number of possible 3-colorings. In this case, the rule that at least two colors are used is relaxed and now every link has at least three 3-colorings (just color every arc the same color). In this case, a link is 3-colorable if it has more than three 3-colorings. |
Because tricolorability is a binary classification (a link is either tricolorable or not*), it is a relatively weak invariant. The composition of a tricolorable knot with another knot is always tricolorable. A way to strengthen the invariant is to count the number of possible 3-colorings. In this case, the rule that at least two colors are used is relaxed and now every link has at least three 3-colorings (just color every arc the same color). In this case, a link is 3-colorable if it has more than three 3-colorings. |
||
Any separable link with a tricolorable separable component is also tricolorable. |
Any separable link with a tricolorable separable component is also tricolorable. |
||
| Line 55: | Line 60: | ||
[[Category:Graph coloring]] |
[[Category:Graph coloring]] |
||
[[Category:Tricolorable knots and links| ]] |
[[Category:Tricolorable knots and links| ]] |
||
[[Category:Knot invariants]] |
|||
Latest revision as of 18:42, 25 September 2024

In the mathematical field of knot theory, the tricolorability of a knot is the ability of a knot to be colored with three colors subject to certain rules. Tricolorability is an isotopy invariant, and hence can be used to distinguish between two different (non-isotopic) knots. In particular, since the unknot is not tricolorable, any tricolorable knot is necessarily nontrivial.
Rules of tricolorability
[edit]In these rules a strand in a knot diagram will be a piece of the string that goes from one undercrossing to the next.[1] A knot is tricolorable if each strand of the knot diagram can be colored one of three colors, subject to the following rules:[2]
- 1. At least two colors must be used, and
- 2. At each crossing, the three incident strands are either all the same color or all different colors.
Some references state instead that all three colors must be used.[3] For a knot, this is equivalent to the definition above; however, for a link it is not.
"The trefoil knot and trivial 2-link are tricolorable, but the unknot, Whitehead link, and figure-eight knot are not. If the projection of a knot is tricolorable, then Reidemeister moves on the knot preserve tricolorability, so either every projection of a knot is tricolorable or none is."[2]
Examples
[edit]Here is an example of how to color a knot in accordance of the rules of tricolorability. By convention, knot theorists use the colors red, green, and blue.
Example of a tricolorable knot
[edit]The granny knot is tricolorable. In this coloring the three strands at every crossing have three different colors. Coloring one but not both of the trefoil knots all red would also give an admissible coloring. The true lover's knot is also tricolorable.[4]
Tricolorable knots with less than nine crossings include 61, 74, 77, 85, 810, 811, 815, 818, 819, 820, and 821.
Example of a non-tricolorable knot
[edit]The figure-eight knot is not tricolorable. In the diagram shown, it has four strands with each pair of strands meeting at some crossing. If three of the strands had the same color, then all strands would be forced to be the same color. Otherwise each of these four strands must have a distinct color. Since tricolorability is a knot invariant, none of its other diagrams can be tricolored either.
Isotopy invariant
[edit]Tricolorability is an isotopy invariant, which is a property of a knot or link that remains constant regardless of any ambient isotopy. This can be proven for tame knots by examining Reidemeister moves. Since each Reidemeister move can be made without affecting tricolorability, tricolorability is an isotopy invariant of tame knots.[5]
| Reidemeister Move I is tricolorable. | Reidemeister Move II is tricolorable. | Reidemeister Move III is tricolorable. |
|---|---|---|
 |
 |
 |
Properties
[edit]Because tricolorability is a binary classification (a link is either tricolorable or not*), it is a relatively weak invariant. The composition of a tricolorable knot with another knot is always tricolorable. A way to strengthen the invariant is to count the number of possible 3-colorings. In this case, the rule that at least two colors are used is relaxed and now every link has at least three 3-colorings (just color every arc the same color). In this case, a link is 3-colorable if it has more than three 3-colorings.
Any separable link with a tricolorable separable component is also tricolorable.
In torus knots
[edit]If the torus knot/link denoted by (m,n) is tricolorable, then so are (j*m,i*n) and (i*n,j*m) for any natural numbers i and j.
See also
[edit]Sources
[edit]- ^ Xaoyu Qiao, E. L., Knot Theory Week 2: Tricolorability (January 20, 2015), Section 3.
- ^ a b Weisstein, Eric W. (2010). CRC Concise Encyclopedia of Mathematics, Second Edition, p.3045. ISBN 9781420035223. quoted at Weisstein, Eric W. "Tricolorable". MathWorld. Accessed: May 5, 2013.
- ^ Gilbert, N.D. and Porter, T. (1994) Knots and Surfaces, p. 8
- ^ Bestvina, Mladen (February 2003). "Knots: a handout for mathcircles", Math.Utah.edu.
- ^ Adams, Colin (2004). The knot book: an elementary introduction to the mathematical theory of knots. Providence, R.I: American Mathematical Society. pp. 22–27. ISBN 978-0-8218-3678-1. OCLC 55633800.
Further reading
[edit]- Weisstein, Eric W. "Three-Colorable Knot". MathWorld. Accessed: May 5, 2013.