Freeform surface modelling: Difference between revisions
No edit summary |
Anachronist (talk | contribs) Undid revision 1251821164 by 2A02:1210:4C65:1A00:B85D:61F3:E43D:E63 (talk) - that isn't software |
||
| (62 intermediate revisions by 42 users not shown) | |||
| Line 1: | Line 1: | ||
{{Short description|Techniques for creating complex surfaces in 3D graphics software}} |
|||
{{dablink|For other uses of the term 'freeform,' see [[Freeform (disambiguation)|Freeform]].}} |
|||
{{Multiple issues|section=| |
|||
{{More citations needed|date=April 2017}} |
|||
{{Lead rewrite|date=April 2017}} |
|||
}} |
|||
| ⚫ | |||
{{unreferenced|date=October 2011}} |
|||
| ⚫ | |||
The technology has encompassed two main fields. Either creating aesthetic ([[class A surfaces]]) that also perform a function; for example, car bodies and consumer product outer forms, or technical surfaces for components such as gas turbine blades and other fluid dynamic engineering components. |
The technology has encompassed two main fields. Either creating aesthetic surfaces ([[class A surfaces]]) that also perform a function; for example, car bodies and consumer product outer forms, or technical surfaces for components such as gas turbine blades and other fluid dynamic engineering components. |
||
CAD software packages use two basic methods for the creation of surfaces. The first begins with construction curves ([[Spline (mathematics)|splines]]) from which the 3D surface is then swept (section along guide rail) or meshed (lofted) through. |
CAD software packages use two basic methods for the creation of surfaces. The first begins with construction curves ([[Spline (mathematics)|splines]]) from which the 3D surface is then swept (section along guide rail) or meshed (lofted) through. |
||
[[ |
[[File:Ff surface3 t.png|thumb|A surface being created from curves]] |
||
The second method is direct creation of the surface with manipulation of the surface poles/control points. |
The second method is direct creation of the surface with manipulation of the surface poles/control points. |
||
[[ |
[[File:Freeform1.gif|thumb|Surface edit by poles]] |
||
From these initially created surfaces, other surfaces are constructed using either derived methods such as offset or angled extensions from surfaces; or via bridging and blending between groups of surfaces. |
From these initially created surfaces, other surfaces are constructed using either derived methods such as offset or angled extensions from surfaces; or via bridging and blending between groups of surfaces. |
||
[[ |
[[File:blend1.png|thumb|Variable smooth blend between surfaces<br/>([[:File:blend1a.gif|animated version]])]] |
||
== Surfaces == |
== Surfaces == |
||
'''Freeform surface''', or '''freeform surfacing''', is used in [[CAD]] and other [[computer graphics]] software to describe the skin of a 3D geometric element. Freeform surfaces do not have rigid radial dimensions, unlike regular surfaces such as [[Plane (mathematics)|plane]]s, [[cylinder (geometry)|cylinder]]s and [[conic]] surfaces. They are used to describe forms such as [[turbine]] blades, car bodies and boat [[Hull (watercraft)|hull]]s. Initially developed for the automotive and [[aerospace]] industries, freeform surfacing is now widely used in all [[engineering]] design disciplines from consumer goods products to ships. Most systems today use [[nonuniform rational B-spline]] (NURBS) mathematics to describe the surface forms; however, there are other methods such as [[ |
'''Freeform surface''', or '''freeform surfacing''', is used in [[Computer-aided design|CAD]] and other [[computer graphics]] software to describe the skin of a 3D geometric element. Freeform surfaces do not have rigid radial dimensions, unlike regular surfaces such as [[Plane (mathematics)|plane]]s, [[cylinder (geometry)|cylinder]]s and [[conic]] surfaces. They are used to describe forms such as [[turbine]] blades, car bodies and boat [[Hull (watercraft)|hull]]s. Initially developed for the automotive and [[aerospace]] industries, freeform surfacing is now widely used in all [[engineering]] design disciplines from consumer goods products to ships. Most systems today use [[nonuniform rational B-spline]] (NURBS) mathematics<ref name="hp.com">{{cite web|last1=Metzger|first1=Michael|last2=Eismann|first2=Sabine|title=Freeform Surface Modeling|url=http://www.hpl.hp.com/hpjournal/95oct/oct95a6.pdf|website=hp.com|access-date=April 15, 2017}}</ref> to describe the surface forms; however, there are other methods such as [[Gordon surface]]s or [[Coons patch|Coons surface]]s . |
||
The forms of freeform surfaces (and curves) are not stored or defined in [[Computer-aided design|CAD]] software in terms of [[polynomial equation]]s, but by their poles, [[Degree (angle)|degree]], and number of patches (segments with spline curves). The degree of a surface determines its mathematical properties, and can be seen as representing the shape by a polynomial with variables to the power of the degree value. For example, a surface with a degree of 1 would be a flat [[cross section (geometry)|cross section]] surface. A surface with degree 2 would be curved in one direction, while a degree 3 surface could (but does not necessarily) change once from [[wikt:concave|concave]] to [[wikt:convex|convex]] curvature. Some CAD systems use the term ''order'' instead of ''degree''. The order of a polynomial is one greater than the degree, and gives the number of [[coefficient]]s rather than the greatest [[exponent]]. |
The forms of freeform surfaces (and curves) are not stored or defined in [[Computer-aided design|CAD]] software in terms of [[polynomial equation]]s, but by their poles, [[Degree (angle)|degree]], and number of patches (segments with spline curves). The degree of a surface determines its mathematical properties, and can be seen as representing the shape by a polynomial with variables to the power of the degree value. For example, a surface with a degree of 1 would be a flat [[cross section (geometry)|cross section]] surface. A surface with degree 2 would be curved in one direction, while a degree 3 surface could (but does not necessarily) change once from [[wikt:concave|concave]] to [[wikt:convex|convex]] curvature. Some CAD systems use the term ''order'' instead of ''degree''. The order of a polynomial is one greater than the degree, and gives the number of [[coefficient]]s rather than the greatest [[exponent]]. |
||
[[ |
[[File:Surface modelling.svg|thumb|Example surface pole map]] |
||
The poles (sometimes known as ''[[Control point (mathematics)|control point]]s'') of a surface define its shape. The natural surface edges are defined by the positions of the first and last poles. (Note that a surface can have trimmed boundaries.) The intermediate poles act like magnets drawing the surface in their direction. The surface does not, however, go through these points. The second and third poles as well as defining shape, respectively determine the start and [[tangent]] angles and the [[curvature]]. In a single patch surface ([[Bézier surface]]), there is one more pole than the degree values of the surface. |
The poles (sometimes known as ''[[Control point (mathematics)|control point]]s'') of a surface define its shape. The natural surface edges are defined by the positions of the first and last poles. (Note that a surface can have trimmed boundaries.) The intermediate poles act like magnets drawing the surface in their direction. The surface does not, however, go through these points. The second and third poles as well as defining shape, respectively determine the start and [[tangent]] angles and the [[curvature]]. In a single patch surface ([[Bézier surface]]), there is one more pole than the degree values of the surface. Surface patches can be merged into a single NURBS surface; at these points are knot lines. The number of knots will determine the influence of the poles on either side and how smooth the transition is. The smoothness between patches, known as ''continuity'', is often referred to in terms of a ''C value'': |
||
* C0: just touching, could have a nick |
|||
Surface patches can be merged into a single NURBS surface; at these points are knot lines. The number of knots will determine the influence of the poles on either side and how smooth the transition is. The smoothness between patches, known as ''continuity'', is often referred to in terms of a ''C value'': |
|||
* |
* C1: tangent, but could have sudden change in curvature |
||
| ⚫ | |||
*C1: tangent, but could have sudden change in curvature |
|||
| ⚫ | |||
Two more important aspects are the U and V parameters. These are values on the surface ranging from 0 to 1, used in the mathematical definition of the surface and for defining paths on the surface: for example, a trimmed boundary edge. Note that they are not proportionally spaced along the surface. A curve of constant U or constant V is known as an isoperimetric curve, or U (V) line. In CAD systems, surfaces are often displayed with their poles of constant U or constant V values connected together by lines; these are known as ''control polygons''. |
Two more important aspects are the U and V parameters. These are values on the surface ranging from 0 to 1, used in the mathematical definition of the surface and for defining paths on the surface: for example, a trimmed boundary edge. Note that they are not proportionally spaced along the surface. A curve of constant U or constant V is known as an isoperimetric curve, or U (V) line. In CAD systems, surfaces are often displayed with their poles of constant U or constant V values connected together by lines; these are known as ''control polygons''. |
||
| Line 36: | Line 40: | ||
One example of where surfacing excels is automotive body panels. Just blending two curved areas of the panel with different radii of curvature together, maintaining tangential continuity (meaning that the blended surface doesn't change direction suddenly, but smoothly) won't be enough. They need to have a continuous rate of curvature change between the two sections, or else their reflections will appear disconnected. |
One example of where surfacing excels is automotive body panels. Just blending two curved areas of the panel with different radii of curvature together, maintaining tangential continuity (meaning that the blended surface doesn't change direction suddenly, but smoothly) won't be enough. They need to have a continuous rate of curvature change between the two sections, or else their reflections will appear disconnected. |
||
The continuity is defined using the terms |
The continuity is defined using the terms: |
||
*G0 – position (touching) |
* G0 – position (touching) |
||
*G1 – tangent (angle) |
* G1 – tangent (angle) |
||
*G2 – curvature (radius) |
* G2 – curvature (radius) |
||
*G3 – acceleration (rate of change of curvature) |
* G3 – acceleration (rate of change of curvature) |
||
[[File:Geometric continuity.png|alt=Geometric continuity|none|thumb|Curve and line G0, G1, G2 and G3 continuity]] |
|||
To achieve a high quality [[NURBS]] or Bézier surface, degrees of 5 or greater are generally used |
To achieve a high quality [[NURBS]] or Bézier surface, degrees of 5 or greater are generally used. |
||
== History of terms == |
|||
The term lofting originally came from the shipbuilding industry where loftsmen worked on "barn loft" type structures to create the keel and bulkhead forms out of wood. This was then passed on to the aircraft then automotive industries who also required streamline shapes. |
|||
The term spline also has nautical origins coming from East Anglian dialect word for a thin long strip of wood (probably from old English and Germanic word splint). |
|||
== Freeform surface modelling software == |
== Freeform surface modelling software == |
||
<!-- Please only list software that is notable enough to have a Wikipedia article (read: no red links).--> |
|||
| ⚫ | |||
{{Div col|colwidth=20em}} |
|||
| ⚫ | |||
*[[ |
* [[Autodesk Alias]] |
||
* [[Autodesk Inventor]] |
|||
*[[Cobalt (CAD program)|Cobalt]] ([http://www.ashlar.com/sections/products/cobalt/cobalt.html Ashlar-Vellum]) |
|||
* [[Blender (software)|Blender]] |
|||
*[[form-Z|form•Z]] ([http://www.formz.com form-Z]) |
|||
* [[CATIA]] (FreeStyle) |
|||
*[[PowerSHAPE]] ([http://www.powershape.com/ PowerSHAPE]) |
|||
* [[Cobalt (CAD program)|Cobalt]] |
|||
*[[Solidworks]] |
|||
*[[ |
* [[form-Z|form•Z]] |
||
*[[ |
* [[Fusion 360]] (Autodesk) |
||
*[[ |
* [[ICEMSurf]] |
||
| ⚫ | |||
*ProEngineer ISDX ([http://www.ptc.com/products/creo/interactive-surface-design-extension]) |
|||
*[[ |
* [[Onshape]] |
||
*[[ |
* [[Siemens NX]] |
||
*[[ |
* [[PowerSHAPE]] |
||
* [[PTC Creo]], formerly ProEngineer ISDX |
|||
* VSR Shape Modeling ([http://www.virtualshape.com/en/products/shape-modeling]) |
|||
* [[PTC Creo Elements/Pro]] |
|||
*[[FreeForm Modeling Plus]] from [[SensAble Technologies]] ([http://www.sensable.com/ Sensable.com]) Now part of Geomagic Design. |
|||
*[[ |
* [[Rhinoceros 3D]] |
||
* |
* [[SolidWorks]] |
||
* [[SolidThinking]] |
|||
*FreeSHIP ([http://www.freeship.org FreeSHIP]) Link broken as of Jan 2014. |
|||
| ⚫ | |||
*GenesisIOD ([http://www.right-toolbox.com.ar/genesis/index.html GenesisIOD]) |
|||
{{Div col end}} |
|||
*OmniCAD ([http://www.omnicad.com OmniCAD]) |
|||
*Thinkdesign ([http://www.superfici3d.com Thinkdesign]) |
|||
*MicroStation ([http://www.Bentley.com Bentley Systems Inc]) |
|||
*Shark FX ([http://punchcad.com/index_pro.htm Punch!]) |
|||
*'''Moi''' Moment of Inspiration 3D modeling for designers and artists ([http://moi3d.com/ Moi3d]) |
|||
*[[Blender (software)|Blender]] Free 3D Modelling Software from [[Blender Foundation]] |
|||
== See also == |
== See also == |
||
{{Div col|colwidth=20em}} |
|||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
* [[Parametric surface]] |
|||
| ⚫ | |||
| ⚫ | |||
{{Div col end}} |
|||
==References== |
|||
| ⚫ | |||
{{Reflist}} |
|||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
== External links == |
|||
* [http://www.kodg-3d.com/en/tutorials/alias-tutorials.html Autodesk Alias Tutorials] |
|||
| ⚫ | |||
[[Category:Computer-aided design]] |
[[Category:Computer-aided design]] |
||
| ⚫ | |||
[[Category:Surfaces]] |
[[Category:Surfaces]] |
||
Latest revision as of 01:44, 19 October 2024
This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these messages)
|
Freeform surface modelling is a technique for engineering freeform surfaces with a CAD or CAID system.
The technology has encompassed two main fields. Either creating aesthetic surfaces (class A surfaces) that also perform a function; for example, car bodies and consumer product outer forms, or technical surfaces for components such as gas turbine blades and other fluid dynamic engineering components.
CAD software packages use two basic methods for the creation of surfaces. The first begins with construction curves (splines) from which the 3D surface is then swept (section along guide rail) or meshed (lofted) through.

The second method is direct creation of the surface with manipulation of the surface poles/control points.

From these initially created surfaces, other surfaces are constructed using either derived methods such as offset or angled extensions from surfaces; or via bridging and blending between groups of surfaces.

(animated version)
Surfaces
[edit]Freeform surface, or freeform surfacing, is used in CAD and other computer graphics software to describe the skin of a 3D geometric element. Freeform surfaces do not have rigid radial dimensions, unlike regular surfaces such as planes, cylinders and conic surfaces. They are used to describe forms such as turbine blades, car bodies and boat hulls. Initially developed for the automotive and aerospace industries, freeform surfacing is now widely used in all engineering design disciplines from consumer goods products to ships. Most systems today use nonuniform rational B-spline (NURBS) mathematics[1] to describe the surface forms; however, there are other methods such as Gordon surfaces or Coons surfaces .
The forms of freeform surfaces (and curves) are not stored or defined in CAD software in terms of polynomial equations, but by their poles, degree, and number of patches (segments with spline curves). The degree of a surface determines its mathematical properties, and can be seen as representing the shape by a polynomial with variables to the power of the degree value. For example, a surface with a degree of 1 would be a flat cross section surface. A surface with degree 2 would be curved in one direction, while a degree 3 surface could (but does not necessarily) change once from concave to convex curvature. Some CAD systems use the term order instead of degree. The order of a polynomial is one greater than the degree, and gives the number of coefficients rather than the greatest exponent.

The poles (sometimes known as control points) of a surface define its shape. The natural surface edges are defined by the positions of the first and last poles. (Note that a surface can have trimmed boundaries.) The intermediate poles act like magnets drawing the surface in their direction. The surface does not, however, go through these points. The second and third poles as well as defining shape, respectively determine the start and tangent angles and the curvature. In a single patch surface (Bézier surface), there is one more pole than the degree values of the surface. Surface patches can be merged into a single NURBS surface; at these points are knot lines. The number of knots will determine the influence of the poles on either side and how smooth the transition is. The smoothness between patches, known as continuity, is often referred to in terms of a C value:
- C0: just touching, could have a nick
- C1: tangent, but could have sudden change in curvature
- C2: the patches are curvature continuous to one another
Two more important aspects are the U and V parameters. These are values on the surface ranging from 0 to 1, used in the mathematical definition of the surface and for defining paths on the surface: for example, a trimmed boundary edge. Note that they are not proportionally spaced along the surface. A curve of constant U or constant V is known as an isoperimetric curve, or U (V) line. In CAD systems, surfaces are often displayed with their poles of constant U or constant V values connected together by lines; these are known as control polygons.
Modelling
[edit]When defining a form, an important factor is the continuity between surfaces - how smoothly they connect to one another.
One example of where surfacing excels is automotive body panels. Just blending two curved areas of the panel with different radii of curvature together, maintaining tangential continuity (meaning that the blended surface doesn't change direction suddenly, but smoothly) won't be enough. They need to have a continuous rate of curvature change between the two sections, or else their reflections will appear disconnected.
The continuity is defined using the terms:
- G0 – position (touching)
- G1 – tangent (angle)
- G2 – curvature (radius)
- G3 – acceleration (rate of change of curvature)
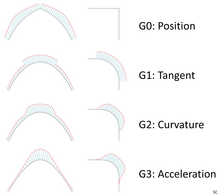
To achieve a high quality NURBS or Bézier surface, degrees of 5 or greater are generally used.
Freeform surface modelling software
[edit]- Autodesk Alias
- Autodesk Inventor
- Blender
- CATIA (FreeStyle)
- Cobalt
- form•Z
- Fusion 360 (Autodesk)
- ICEMSurf
- KeyCreator
- Onshape
- Siemens NX
- PowerSHAPE
- PTC Creo, formerly ProEngineer ISDX
- PTC Creo Elements/Pro
- Rhinoceros 3D
- SolidWorks
- SolidThinking
- Tebis
See also
[edit]References
[edit]- ^ Metzger, Michael; Eismann, Sabine. "Freeform Surface Modeling" (PDF). hp.com. Retrieved April 15, 2017.
