Malfatti circles: Difference between revisions
Inserted the paper proving for the first time in a rigorous and complete manner the solution of the Malfatti Problem and thus concluding such solution. |
Dedhert.Jr (talk | contribs) Undid revision 1252877767 by 95.1.79.102 (talk) |
||
| (26 intermediate revisions by 9 users not shown) | |||
| Line 31: | Line 31: | ||
Malfatti's assumption that the two problems are equivalent is incorrect. {{harvs|last1=Lob|last2=Richmond|year=1930|txt}}, who went back to the original Italian text, observed that for some triangles a larger area can be achieved by a [[greedy algorithm]] that inscribes a single circle of maximal radius within the triangle, inscribes a second circle within one of the three remaining corners of the triangle, the one with the smallest angle, and inscribes a third circle within the largest of the five remaining pieces. The difference in area for an equilateral triangle is small, just over 1%,{{sfnp|Wells|1991}} but as {{harvs|first=Howard|last=Eves|authorlink=Howard Eves|year=1946|txt}} pointed out, for an [[isosceles triangle]] with a very sharp apex, the optimal circles (stacked one atop each other above the base of the triangle) have nearly twice the area of the Malfatti circles.<ref>See also {{harvtxt|Ogilvy|1990}}.</ref> |
Malfatti's assumption that the two problems are equivalent is incorrect. {{harvs|last1=Lob|last2=Richmond|year=1930|txt}}, who went back to the original Italian text, observed that for some triangles a larger area can be achieved by a [[greedy algorithm]] that inscribes a single circle of maximal radius within the triangle, inscribes a second circle within one of the three remaining corners of the triangle, the one with the smallest angle, and inscribes a third circle within the largest of the five remaining pieces. The difference in area for an equilateral triangle is small, just over 1%,{{sfnp|Wells|1991}} but as {{harvs|first=Howard|last=Eves|authorlink=Howard Eves|year=1946|txt}} pointed out, for an [[isosceles triangle]] with a very sharp apex, the optimal circles (stacked one atop each other above the base of the triangle) have nearly twice the area of the Malfatti circles.<ref>See also {{harvtxt|Ogilvy|1990}}.</ref> |
||
In fact, the Malfatti circles are never optimal. It was discovered through numerical computations in the 1960s, and later proven rigorously, that the Lob–Richmond procedure always produces the three circles with largest area, and that these are always larger than the Malfatti circles.<ref>{{harvtxt|Goldberg|1967}}; {{harvtxt|Gabai|Liban|1968}}; {{harvtxt|Zalgaller|1994}}; {{harvtxt|Zalgaller|Los'|1994}}; {{harvtxt|Lombardi|2022}}.</ref> {{harvtxt|Melissen|1997}} conjectured more generally that, for any integer {{mvar|n}}, the greedy algorithm finds the area-maximizing set of {{mvar|n}} circles within a given triangle; the conjecture is known to be true for {{math|''n'' ≤ 3}}.{{sfnp|Andreatta|Bezdek|Boroński|2010}} |
|||
==History== |
==History== |
||
| Line 82: | Line 82: | ||
| title = Das Malfattische Problem |
| title = Das Malfattische Problem |
||
| url = https://archive.org/details/abv4116.0001.001.umich.edu |
| url = https://archive.org/details/abv4116.0001.001.umich.edu |
||
| year = 1846 |
| year = 1846| hdl = 2027/miun.abv4116.0001.001 |
||
| hdl-access = free |
|||
}}. |
|||
*{{citation |
*{{citation |
||
| last = Adams | first = C. | author-link = Karl Adams (mathematician) |
| last = Adams | first = C. | author-link = Karl Adams (mathematician) |
||
| Line 199: | Line 201: | ||
| title = Analytical researches connected with Steiner's extension of Malfatti's problem |
| title = Analytical researches connected with Steiner's extension of Malfatti's problem |
||
| volume = 142 |
| volume = 142 |
||
| year = 1854| doi-access = |
| year = 1854| doi-access = |
||
}}. Reprinted in {{citation |
}}. Reprinted in {{citation |
||
| last = Cayley | first = A. | author-link = Arthur Cayley |
| last = Cayley | first = A. | author-link = Arthur Cayley |
||
| Line 402: | Line 404: | ||
| url = https://eudml.org/doc/204672 |
| url = https://eudml.org/doc/204672 |
||
| year = 1914}}. See also {{mathgenealogy|id=37715|title=Kurt Loeber}}. |
| year = 1914}}. See also {{mathgenealogy|id=37715|title=Kurt Loeber}}. |
||
*{{citation |
|||
| last = Lombardi | first = Giancarlo |
|||
| date = June 2022 |
|||
| doi = 10.1007/s12215-022-00759-2 |
|||
| journal = Rendiconti del Circolo Matematico di Palermo | series = Series 2 |
|||
| title = Proving the solution of Malfatti's marble problem| volume = 72 |
|||
| issue = 3 |
|||
| pages = 1751–1782 |
|||
| s2cid = 249915691 |
|||
}}. |
|||
*{{citation |
*{{citation |
||
| last = Malfatti | first = Gianfrancesco | author-link = Gian Francesco Malfatti |
| last = Malfatti | first = Gianfrancesco | author-link = Gian Francesco Malfatti |
||
| Line 542: | Line 554: | ||
| pages = 143 | journal = [[The Mathematical Gazette]] |
| pages = 143 | journal = [[The Mathematical Gazette]] |
||
| title = 899. A trigonometrical solution of Malfatti's problem of describing three circles mutually in contact, each of which touches two sides of a triangle |
| title = 899. A trigonometrical solution of Malfatti's problem of describing three circles mutually in contact, each of which touches two sides of a triangle |
||
| volume = 14| jstor = 3602652 }}. |
| volume = 14| jstor = 3602652 | s2cid = 188799431 }}. |
||
*{{citation |
*{{citation |
||
| last = Scardapane | first = N. M. |
| last = Scardapane | first = N. M. |
||
| Line 634: | Line 646: | ||
| url = https://archive.org/stream/transactionsofro24roya#page/126/mode/2up |
| url = https://archive.org/stream/transactionsofro24roya#page/126/mode/2up |
||
| volume = 24 |
| volume = 24 |
||
| year = 1867| doi = 10.1017/S0080456800031689 }}. |
| year = 1867| doi = 10.1017/S0080456800031689 | s2cid = 122494700 }}. |
||
*{{citation |
*{{citation |
||
| last1 = Takeshima | first1 = Taku |
| last1 = Takeshima | first1 = Taku |
||
| Line 681: | Line 693: | ||
| url = https://archive.org/details/bub_gb_WxuznK28XmMC |
| url = https://archive.org/details/bub_gb_WxuznK28XmMC |
||
| year = 1871}}. See also {{mathgenealogy|id=206882|title=Armin Wittstein}}. |
| year = 1871}}. See also {{mathgenealogy|id=206882|title=Armin Wittstein}}. |
||
*{{citation |
|||
<ref>{{cite journal |last1=Zalgaller |first1=V. A. |title=An inequality for acute triangles |journal=Journal of Mathematical Sciences |date=1994 |issue=72, No. 4 |page=3160–3162}}</ref> |
|||
| last = Zalgaller | first = V. A. |
|||
| doi = 10.1007/BF01249513 |
|||
| issue = 4 |
|||
| journal = Journal of Mathematical Sciences |
|||
| mr = 1267527 |
|||
| pages = 3160–3162 |
|||
| title = An inequality for acute triangles |
|||
| volume = 72 |
|||
| year = 1994| s2cid = 121622126 |
|||
| doi-access = free |
|||
}}. |
|||
*{{citation |
*{{citation |
||
| last1 = Zalgaller | first1 = V. A. | author1-link = Victor Zalgaller |
| last1 = Zalgaller | first1 = V. A. | author1-link = Victor Zalgaller |
||
Latest revision as of 10:18, 23 October 2024

In geometry, the Malfatti circles are three circles inside a given triangle such that each circle is tangent to the other two and to two sides of the triangle. They are named after Gian Francesco Malfatti, who made early studies of the problem of constructing these circles in the mistaken belief that they would have the largest possible total area of any three disjoint circles within the triangle.
Malfatti's problem has been used to refer both to the problem of constructing the Malfatti circles and to the problem of finding three area-maximizing circles within a triangle. A simple construction of the Malfatti circles was given by Steiner (1826), and many mathematicians have since studied the problem. Malfatti himself supplied a formula for the radii of the three circles, and they may also be used to define two triangle centers, the Ajima–Malfatti points of a triangle.
The problem of maximizing the total area of three circles in a triangle is never solved by the Malfatti circles. Instead, the optimal solution can always be found by a greedy algorithm that finds the largest circle within the given triangle, the largest circle within the three connected subsets of the triangle outside of the first circle, and the largest circle within the five connected subsets of the triangle outside of the first two circles. Although this procedure was first formulated in 1930, its correctness was not proven until 1994.
Malfatti's problem
[edit]
Gian Francesco Malfatti (1803) posed the problem of cutting three cylindrical columns out of a triangular prism of marble, maximizing the total volume of the columns. He assumed that the solution to this problem was given by three tangent circles within the triangular cross-section of the wedge. That is, more abstractly, he conjectured that the three Malfatti circles have the maximum total area of any three disjoint circles within a given triangle.[1] Malfatti's work was popularized for a wider readership in French by Joseph Diaz Gergonne in the first volume of his Annales (1811), with further discussion in the second and tenth. However, Gergonne only stated the circle-tangency problem, not the area-maximizing one.
Malfatti's assumption that the two problems are equivalent is incorrect. Lob and Richmond (1930), who went back to the original Italian text, observed that for some triangles a larger area can be achieved by a greedy algorithm that inscribes a single circle of maximal radius within the triangle, inscribes a second circle within one of the three remaining corners of the triangle, the one with the smallest angle, and inscribes a third circle within the largest of the five remaining pieces. The difference in area for an equilateral triangle is small, just over 1%,[2] but as Howard Eves (1946) pointed out, for an isosceles triangle with a very sharp apex, the optimal circles (stacked one atop each other above the base of the triangle) have nearly twice the area of the Malfatti circles.[3]
In fact, the Malfatti circles are never optimal. It was discovered through numerical computations in the 1960s, and later proven rigorously, that the Lob–Richmond procedure always produces the three circles with largest area, and that these are always larger than the Malfatti circles.[4] Melissen (1997) conjectured more generally that, for any integer n, the greedy algorithm finds the area-maximizing set of n circles within a given triangle; the conjecture is known to be true for n ≤ 3.[5]
History
[edit]The problem of constructing three circles tangent to each other within a triangle was posed by the 18th-century Japanese mathematician Ajima Naonobu prior to the work of Malfatti, and included in an unpublished collection of Ajima's works made a year after Ajima's death by his student Kusaka Makoto.[5][6] Even earlier, the same problem was considered in a 1384 manuscript by Gilio di Cecco da Montepulciano, now in the Municipal Library of Siena, Italy.[7] Jacob Bernoulli (1744) studied a special case of the problem, for a specific isosceles triangle.
Since the work of Malfatti, there has been a significant amount of work on methods for constructing Malfatti's three tangent circles; Richard K. Guy writes that the literature on the problem is "extensive, widely scattered, and not always aware of itself".[8] Notably, Jakob Steiner (1826) presented a simple geometric construction based on bitangents; other authors have since claimed that Steiner's presentation lacked a proof, which was later supplied by Andrew Hart (1856), but Guy points to the proof scattered within two of Steiner's own papers from that time. Solutions based on algebraic formulations of the problem include those by C. L. Lehmus (1819), E. C. Catalan (1846), C. Adams (1846, 1849), J. Derousseau (1895), and Andreas Pampuch (1904). The algebraic solutions do not distinguish between internal and external tangencies among the circles and the given triangle; if the problem is generalized to allow tangencies of either kind, then a given triangle will have 32 different solutions and conversely a triple of mutually tangent circles will be a solution for eight different triangles.[8] Bottema (2001) credits the enumeration of these solutions to Pampuch (1904), but Cajori (1893) notes that this count of the number of solutions was already given in a remark by Steiner (1826). The problem and its generalizations were the subject of many other 19th-century mathematical publications,[9] and its history and mathematics have been the subject of ongoing study since then.[10] It has also been a frequent topic in books on geometry.[11]
Gatto (2000) and Mazzotti (1998) recount an episode in 19th-century Neapolitan mathematics related to the Malfatti circles. In 1839, Vincenzo Flauti, a synthetic geometer, posed a challenge involving the solution of three geometry problems, one of which was the construction of Malfatti's circles; his intention in doing so was to show the superiority of synthetic to analytic techniques. Despite a solution being given by Fortunato Padula, a student in a rival school of analytic geometry, Flauti awarded the prize to his own student, Nicola Trudi, whose solutions Flauti had known of when he posed his challenge. More recently, the problem of constructing the Malfatti circles has been used as a test problem for computer algebra systems.[12]
Steiner's construction
[edit]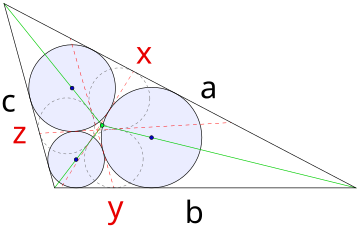
Although much of the early work on the Malfatti circles used analytic geometry, Steiner (1826) provided the following simple synthetic construction.
A circle that is tangent to two sides of a triangle, as the Malfatti circles are, must be centered on one of the angle bisectors of the triangle (green in the figure). These bisectors partition the triangle into three smaller triangles, and Steiner's construction of the Malfatti circles begins by drawing a different triple of circles (shown dashed in the figure) inscribed within each of these three smaller triangles. In general these circles are disjoint, so each pair of two circles has four bitangents (lines touching both). Two of these bitangents pass between their circles: one is an angle bisector, and the second is shown as a red dashed line in the figure. Label the three sides of the given triangle as a, b, and c, and label the three bitangents that are not angle bisectors as x, y, and z, where x is the bitangent to the two circles that do not touch side a, y is the bitangent to the two circles that do not touch side b, and z is the bitangent to the two circles that do not touch side c. Then the three Malfatti circles are the inscribed circles to the three tangential quadrilaterals abyx, aczx, and bczy.[13] In case of symmetry two of the dashed circles may touch in a point on a bisector, making two bitangents coincide there, but still setting up the relevant quadrilaterals for Malfatti's circles.
The three bitangents x, y, and z cross the triangle sides at the point of tangency with the third inscribed circle, and may also be found as the reflections of the angle bisectors across the lines connecting pairs of centers of these incircles.[8]
Radius formula
[edit]The radius of each of the three Malfatti circles may be determined as a formula involving the three side lengths a, b, and c of the triangle, the inradius r, the semiperimeter , and the three distances d, e, and f from the incenter of the triangle to the vertices opposite sides a, b, and c respectively. The formulae for the three radii are:[14]
Related formulae may be used to find examples of triangles whose side lengths, inradii, and Malfatti radii are all rational numbers or all integers. For instance, the triangle with side lengths 28392, 21000, and 25872 has inradius 6930 and Malfatti radii 3969, 4900, and 4356. As another example, the triangle with side lengths 152460, 165000, and 190740 has inradius 47520 and Malfatti radii 27225, 30976, and 32400.[15]
Ajima–Malfatti points
[edit]
Given a triangle ABC and its three Malfatti circles, let D, E, and F be the points where two of the circles touch each other, opposite vertices A, B, and C respectively. Then the three lines AD, BE, and CF meet in a single triangle center known as the first Ajima–Malfatti point after the contributions of Ajima and Malfatti to the circle problem. The second Ajima–Malfatti point is the meeting point of three lines connecting the tangencies of the Malfatti circles with the centers of the excircles of the triangle.[16][17] Other triangle centers also associated with the Malfatti circles include the Yff–Malfatti point, formed in the same way as the first Malfatti point from three mutually tangent circles that are all tangent to the lines through the sides of the given triangle, but that lie partially outside the triangle,[18] and the radical center of the three Malfatti circles (the point where the three bitangents used in their construction meet).[19]
See also
[edit]- Circle packing in an equilateral triangle
- Circle packing in an isosceles right triangle
- Six circles theorem
Notes
[edit]- ^ Ogilvy (1990).
- ^ Wells (1991).
- ^ See also Ogilvy (1990).
- ^ Goldberg (1967); Gabai & Liban (1968); Zalgaller (1994); Zalgaller & Los' (1994); Lombardi (2022).
- ^ a b Andreatta, Bezdek & Boroński (2010).
- ^ Fukagawa & Rothman (2008).
- ^ Simi & Toti Rigatelli (1993).
- ^ a b c Guy (2007).
- ^ Paucker (1831); Zornow (1833); Plücker (1834a, 1834b); Terquem (1847); Quidde (1850); Sylvester (1850); Scheffler (1851); Schellbach (1853); Cayley (1849, 1854, 1857, 1875–1876); Clebsch (1857); Talbot (1867); Wittstein (1871); Affolter (1873); Mertens (1873); Baker (1874); Schröter (1874); Simons (1874); Miller (1875); Seitz (1875); Godt (1877); Lebon (1889); Bellacchi (1895); Wedell (1897).
- ^ Hagge (1908); Loeber (1914); Danielsson (1926); Rogers (1928); Scardapane (1931); Procissi (1932); Eves (1946); Naitō (1975); Fiocca (1980); Hitotumatu (1995); Takeshima & Anai (1996); Gatto (2000); Bottema (2001); Andreatta, Bezdek & Boroński (2010); Horváth (2014).
- ^ Casey (1882); Rouché & de Comberousse (1891); Coolidge (1916); Baker (1925); Dörrie (1965); Ogilvy (1990); Wells (1991); Martin (1998); Andreescu, Mushkarov & Stoyanov (2006).
- ^ Hitotumatu (1995); Takeshima & Anai (1996).
- ^ Martin (1998), exercise 5.20, p. 96.
- ^ According to Stevanović (2003), these formulae were discovered by Malfatti and published posthumously by him in 1811. However, the 1811 publication, "Résolues", Annales de Mathématiques Pures et Appliquées, 1: 347–348, 1811, is an unsigned letter (likely from journal editor Joseph Diez Gergonne) giving this formula as equivalent to the results in Malfatti (1803).
- ^ Miller (1875).
- ^ Weisstein, Eric W., "Ajima-Malfatti Points", MathWorld.
- ^ C. Kimberling, Encyclopedia of Triangle Centers Archived 2012-04-19 at the Wayback Machine, X(179) and X(180).
- ^ Encyclopedia of Triangle Centers, X(400).
- ^ Stevanović (2003).
References
[edit]- Adams, C. (1846), Das Malfattische Problem, Winterthür: Druck und Verlag der Steiner'schen Buchhandlung, hdl:2027/miun.abv4116.0001.001.
- Adams, C. (1849), "Lemmes sur les cercles inscrits à un triangle, et solution algébrique du problème de Malfatti", Nouvelles Annales de Mathématiques, 8: 62–63.
- Affolter, Fr. G. (1873), "Ueber das Malfatti'sche Problem", Mathematische Annalen, 6 (4): 597–602, doi:10.1007/BF01443199, MR 1509836, S2CID 120293529.
- Andreatta, Marco; Bezdek, András; Boroński, Jan P. (2010), "The problem of Malfatti: two centuries of debate" (PDF), The Mathematical Intelligencer, 33 (1): 72–76, doi:10.1007/s00283-010-9154-7, S2CID 55185397.
- Andreescu, Titu; Mushkarov, Oleg; Stoyanov, Luchezar N. (2006), "2.3 Malfatti's Problems", Geometric Problems on Maxima and Minima, Birkhäuser, pp. 80–87, doi:10.1007/0-8176-4473-3, ISBN 978-0-8176-3517-6.
- Baker, H. F. (1925), "II.Ex.8: Solution of Malfatti's Problem", Principles of Geometry, Vol. IV: Higher Geometry, Cambridge University Press, pp. 68–69.
- Baker, Marcus (1874), "The history of Malfatti's problem", Bulletin of the Philosophical Society of Washington, 2: 113–123.
- Bellacchi, G. (1895), "Nota sul problema del Malfatti", Periodico di Matematica per l'Insegnamento Secondario, 10: 25–26, 93–96, 156–163. Continued in vol. 11 (1896), pp. 25–27.
- Bernoulli, Jacob (1744), "Solutio Tergemini Problematis: Lemma II", Opera, vol. I, Geneva: Cramer & Philibert, pp. 303–305
- Bottema, Oene (2001), "The Malfatti problem" (PDF), Forum Geometricorum, 1: 43–50, MR 1891514.
- Cajori, Florian (1893), A history of mathematics, Macmillan & Co., p. 296.
- Casey, John (1882), "VI.61 Malfatti's Problem", A Sequel to the First Six Books of the Elements of Euclid (2nd ed.), London: Longmans, Green, & Co, pp. 152–153.
- Catalan, E. (1846), "Note sur le problème de Malfatti", Nouvelles Annales de Mathématiques, 5: 60–64.
- Cayley, A. (1849), "On system of equations connected with Malfatti's problem, and on another algebraical system", The Cambridge and Dublin Mathematical Journal, 4: 270–275. Reprinted in Cayley, A. (1889a), The collected mathematical papers of Arthur Cayley, Vol. I, Cambridge University Press, pp. 465–470.
- Cayley, A. (1854), "Analytical researches connected with Steiner's extension of Malfatti's problem", Philosophical Transactions of the Royal Society of London, 142: 253–278, doi:10.1098/rspl.1850.0072. Reprinted in Cayley, A. (1889b), The collected mathematical papers of Arthur Cayley, Vol. II, Cambridge University Press, pp. 57–86.
- Cayley, A. (1857), "On Schellbach's solution of Malfatti's problem", The Quarterly Journal of Pure and Applied Mathematics, 1: 222–226. Reprinted in Cayley, A. (1890), The collected mathematical papers of Arthur Cayley, Vol. III, Cambridge University Press, pp. 44–47.
- Cayley, A. (1875–1876), "On a system of equations connected with Malfatti's problem", Proceedings of the London Mathematical Society, 7: 38–42, doi:10.1112/plms/s1-7.1.38. Reprinted in Cayley, A. (1896), The collected mathematical papers of Arthur Cayley, Vol. IX, Cambridge University Press, pp. 546–550.
- Clebsch, A. (1857), "Anwendung der elliptischen Funktionen auf ein Problem der Geometrie des Raumes", Journal für die reine und angewandte Mathematik, 1857 (53): 292–308, doi:10.1515/crll.1857.53.292, S2CID 122806088.
- Coolidge, Julian Lowell (1916), A Treatise on the Circle and the Sphere, Oxford: Clarendon Press, pp. 174–183.
- Danielsson, Ólafur (1926), "En Løsning af Malfattis Problem", Matematisk Tidsskrift A: 29–32, JSTOR 24534655.
- Derousseau, J. (1895), "Historique et résolution analytique complète du problème de Malfatti", Mémoires de la Société Royale des Sciences de Liège, 2nd ser., 18: 1–52.
- Dörrie, H. (1965), "§30. Malfatti's Problem", 100 Great Problems of Elementary Mathematics: Their History and Solutions, New York: Dover, pp. 147–151, ISBN 978-0-486-61348-2.
- Eves, Howard (1946), "Malfatti Problem (problem 4145)", Problems and Solutions, American Mathematical Monthly, 53 (5): 285–286, doi:10.2307/2305117, JSTOR 2305117.
- Fiocca, Alessandra (1980), "Il problema di Malfatti nella letteratura matematica dell'800", Annali dell'Università di Ferrara, 26 (1): 173–202, doi:10.1007/BF02825179, S2CID 118548931.
- Fukagawa, Hidetoshi; Rothman, Tony (2008), Sacred Mathematics: Japanese Temple Geometry, Princeton University Press, p. 79, ISBN 978-0-691-12745-3.
- Gabai, Hyman; Liban, Eric (1968), "On Goldberg's inequality associated with the Malfatti problem", Mathematics Magazine, 41 (5): 251–252, doi:10.1080/0025570x.1968.11975890, JSTOR 2688807
- Gatto, Romano (2000), "The debate about methods and Vincenzo Flauti's challenge to the mathematicians of the Kingdom of Naples", Società Nazionale di Scienze, Lettere e Arti in Napoli. Rendiconto dell'Accademia delle Scienze Fisiche e Matematiche, Serie IV, 67: 181–233, MR 1834240.
- Godt, W. (1877), "Ueber die Steinersche Verallgemeinerung des Malfattischen Problems", Journal für die reine und angewandte Mathematik, 84: 259–263.
- Goldberg, M. (1967), "On the Original Malfatti Problem", Mathematics Magazine, 40 (5): 241–247, doi:10.2307/2688277, JSTOR 2688277, MR 1571715.
- Guy, Richard K. (2007), "The lighthouse theorem, Morley & Malfatti—a budget of paradoxes", American Mathematical Monthly, 114 (2): 97–141, doi:10.1080/00029890.2007.11920398, JSTOR 27642143, MR 2290364, S2CID 46275242.
- Hagge, K. (1908), "Zur Konstruktion der Malfattischen Kreise", Zeitschrift für Mathematischen und Naturwissenschaftlichen Unterricht, 39: 580–588.
- Hart, Andrew S. (1856), "Geometrical investigation of Steiner's construction for Malfatti's problem", The Quarterly Journal of Pure and Applied Mathematics, 1: 219–221.
- Hitotumatu, Sin (1995), "The Malfatti problem", The state of the art of scientific computing and its prospects, II, Sūrikaisekikenkyūsho Kōkyūroku (in Japanese), vol. 915, pp. 167–170, MR 1385273.
- Horváth, Ákos G. (2014), "Malfatti's problem on the hyperbolic plane", Studia Scientiarum Mathematicarum Hungarica, 51 (2): 201–212, arXiv:1204.5014, doi:10.1556/SScMath.51.2014.2.1276, MR 3238131.
- Lebon, Ernest (1889), "Solution du problème de Malfatti", Rendiconti del Circolo Matematico di Palermo, 3 (1): 120–130, doi:10.1007/bf03011513, S2CID 120020307.
- Lechmütz, C. L. (1819), "Solution nouvelle du problème où il s'agit d'inscrire à un triangle donne quelconque trois cercles tels que chacun d'eux touche les deux autres et deux côtés du triangle", Géométrie mixte, Annales de Mathématiques Pures et Appliquées, 10: 289–298.
- Lob, H.; Richmond, H. W. (1930), "On the Solutions of Malfatti's Problem for a Triangle", Proceedings of the London Mathematical Society, 2nd ser., 30 (1): 287–304, doi:10.1112/plms/s2-30.1.287.
- Loeber, Kurt (1914), Beiträge zur Lösung und Geschichte des Malfattischen Problems und Seiner Erweiterungen, Doctoral dissertation, Martin-Luther-Universität Halle-Wittenberg. See also Kurt Loeber at the Mathematics Genealogy Project.
- Lombardi, Giancarlo (June 2022), "Proving the solution of Malfatti's marble problem", Rendiconti del Circolo Matematico di Palermo, Series 2, 72 (3): 1751–1782, doi:10.1007/s12215-022-00759-2, S2CID 249915691.
- Malfatti, Gianfrancesco (1803), "Memoria sopra un problema stereotomico", Memorie di Matematica e di Fisica della Società Italiana delle Scienze, 10: 235–244.
- Martin, George Edward (1998), "Malfatti's Problem", Geometric Constructions, Undergraduate Texts in Mathematics, Springer-Verlag, pp. 92–95, ISBN 978-0-387-98276-2. The cover of Martin's book features an illustration of the Malfatti circles.
- Mazzotti, Massimo (1998), "The geometers of God: mathematics and reaction in the kingdom of Naples" (PDF), Isis, 89 (4): 674–701, doi:10.1086/384160, hdl:10036/31212, MR 1670633, S2CID 143956681, archived from the original (PDF) on 2016-04-14, retrieved 2011-06-10.
- Melissen, J. B. M. (1997), Packing and Covering with Circles, PhD thesis, Utrecht University
{{citation}}: CS1 maint: location missing publisher (link). - Mertens, F. (1873), "Ueber die Malfattische Aufgabe für das sphärische Dreieck.", Journal für die reine und angewandte Mathematik, 1873 (76): 92–96, doi:10.1515/crll.1873.76.92, S2CID 124307093.
- Miller, W. J. C., ed. (1875), "Problem 4331", Mathematical questions with their solutions, from the "Educational times" (PDF), vol. 16, Hodgson, pp. 70–71, Bibcode:1877Natur..16..417., doi:10.1038/016417a0, S2CID 45983078. Proposed by Artemas Martin; solved by the proposer and by Asher B. Evans; compare Martin's Question 4401, also in this volume, pp. 102–103, again solved by Evans and Martin. Note further that Martin had asked for a geometrical solution in The Lady's and Gentleman's Diary for 1869 (so appearing in late 1868), with solution in the LDG for the following year, pp. 89–90. Versions of the problem then appear from 1879 in The Mathematical Visitor, edited by Martin.
- Naitō, Jun (1975), "A generalization of Malfatti's problem", Science Reports of the Faculty of Education, Gifu University: Natural Science, 5 (4): 277–286, MR 0394416
- Ogilvy, C. Stanley (1990), "Malfatti's problem", Excursions in Geometry, Dover, pp. 145–147, ISBN 978-0-486-26530-8.
- Paucker, M. G. (1831), "Memoire sur une question de géométrie relative aux tactions des cercles", Mémoires Présentés à l'Académie Impériale des Sciences de Saint-Pétersbourg par Divers Savans, 1: 503–586.
- Pampuch, A. (1904), "Die 32 Lösungen des Malfatisschen Problems", Archiv der Mathematik und Physik, 3rd ser., 8 (1): 36–49.
- Plücker, J. (1834a), "Das Malfattische Problem", Journal für die reine und angewandte Mathematik, 11: 117–129, doi:10.1515/crll.1834.11.117, S2CID 199547169.
- Plücker, J. (1834b), "Über die Steinersche Verallgemeinerung der Malfattischen Aufgabe", Journal für die reine und angewandte Mathematik, 11: 356–360, doi:10.1515/crll.1834.11.356, S2CID 199546776.
- Procissi, Angiolo (1932), "Questioni connesse col problema di Malfatti e bibliografia", Periodico di Matematiche: Storia, Didattica, Filosofia, 12: 189–205. As cited by Guy (2007) and Fiocca (1980).
- Rouché, Eugène; de Comberousse, Charles (1891), "Problème de Malfatti", Traité de Géométrie, Première Partie: Géométrie Plane (6th ed.), Paris: Gauthier-Villars, pp. 295–298.
- Quidde, A. (1850), "Das Malfattische Problem. Beweis der Steinerschen Construction", Archiv der Mathematik und Physik, 15: 197–204.
- Rogers, L. J. (1928), "899. A trigonometrical solution of Malfatti's problem of describing three circles mutually in contact, each of which touches two sides of a triangle", The Mathematical Gazette, 14 (194): 143, doi:10.2307/3602652, JSTOR 3602652, S2CID 188799431.
- Scardapane, N. M. (1931), "Il problema di Malfatti", Periodico di Matematiche: Storia, Didattica, Filosofia, 11: 281–292. As cited by Fiocca (1980).
- Scheffler, H. (1851), "Auflösung des Malfatti'schen Problems", Archiv der Mathematik und Physik, 16: 424–430.
- Schellbach, K. H. (1853), "Solution du problème de Malfatti, dans le triangle rectiligne et sphérique", Nouvelles Annales de Mathématiques, 12: 131–136.
- Schröter, H. (1874), "Die Steinersche Auflösung der Malfattischen Aufgabe", Journal für die reine und angewandte Mathematik, 77: 230–244.
- Seitz, E. B. (1875), "Solution of a problem", The Analyst, 2 (3): 74–76, doi:10.2307/2635869, JSTOR 2635869.
- Simi, A.; Toti Rigatelli, L. (1993), "Some 14th- and 15th-century texts on practical geometry", Vestigia mathematica, Amsterdam: Rodopi, pp. 453–470, MR 1258835.
- Simons, P. A. (1874), "Quelques réflexions sur le problème de Malfatti", Bulletins de l'Académie Royale des Sciences, des Lettres et des Beaux-Arts de Belgique, 2nd Ser., 38: 88–108.
- Steiner, Jacob (1826), "Einige geometrische Betrachtungen", Journal für die reine und angewandte Mathematik, 1: 161–184, 252–288, doi:10.1515/crll.1826.1.161, S2CID 122065577. Reprinted in Steiner, Jacob (1881), Weierstrass, K. (ed.), Gesammelte Werke, Berlin: Druck und Verlag von G. Reimer, pp. 17–76 and separately as Steiner, Jacob (1901), Stern, Rudolf (ed.), Einige geometrische Betrachtungen, Leipzig: Verlag von Wilhelm Engelmann. See in particular section 14, pp. 25–27 of the Engelmann reprint.
- Stevanović, Milorad R. (2003), "Triangle centers associated with the Malfatti circles" (PDF), Forum Geometricorum, 3: 83–93, MR 2004112.
- Sylvester, J.J. (1850), "XLVIII. On the solution of a system of equations in which three homogeneous quadratic functions of three unknown quantities are respectively equaled to numerical multiples of a fourth non-homogeneous function of the same", The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 37 (251): 370–373, doi:10.1080/14786445008646630.
- Talbot, H. F. (1867), "Researches on Malfatti's problem", Transactions of the Royal Society of Edinburgh, 24: 127–138, doi:10.1017/S0080456800031689, S2CID 122494700.
- Takeshima, Taku; Anai, Hirokazu (1996), "Computer algebra applied to Malfatti's problem of constructing three tangent circles inside a triangle—the construction of towers over the field of rational functions", Studies in the theory of computer algebra and its applications, Sūrikaisekikenkyūsho Kōkyūroku (in Japanese), vol. 941, pp. 15–24, MR 1410316.
- Terquem, O. (1847), "Problème de Malfatti. Solution géométrique", Nouvelles Annales de Mathématiques, 6: 346–350.
- Wedell, Charlotte (1897), Application de la théorie des fonctions elliptiques à la solution du problème de Malfatti, Doctoral dissertation, University of Lausanne.
- Wells, David (1991), "Malfatti's problem", The Penguin Dictionary of Curious and Interesting Geometry, New York: Penguin Books, pp. 145–146, ISBN 978-0-14-011813-1.
- Wittstein, Armin (1871), Geschichte des Malfatti'schen Problems, Doctoral dissertation, Munich: University of Erlangen. See also Armin Wittstein at the Mathematics Genealogy Project.
- Zalgaller, V. A. (1994), "An inequality for acute triangles", Journal of Mathematical Sciences, 72 (4): 3160–3162, doi:10.1007/BF01249513, MR 1267527, S2CID 121622126.
- Zalgaller, V. A.; Los', G. A. (1994), "The solution of Malfatti's problem", Journal of Mathematical Sciences, 72 (4): 3163–3177, doi:10.1007/BF01249514, S2CID 120731663.
- Zornow, A. (1833), "Démonstration de la solution du problème de Malfatti, donnée par Mr. Steiner p. 178. du tome I. cah. 2", Journal für die Reine und Angewandte Mathematik, 1833 (10): 300–302, doi:10.1515/crll.1833.10.300, MR 1577950, S2CID 123031698.




