Cauchy distribution: Difference between revisions
Citation bot (talk | contribs) Alter: template type, pages. Add: issue, eprint, class. Removed parameters. Formatted dashes. Some additions/deletions were parameter name changes. | Use this bot. Report bugs. | Suggested by Spinixster | Category:Articles with bare URLs for citations from June 2023 | #UCB_Category 3/3 |
m →History: undid truncation of Maria Gaetana Agnesi’s name |
||
| (39 intermediate revisions by 29 users not shown) | |||
| Line 1: | Line 1: | ||
{{short description|Probability distribution}} |
{{short description|Probability distribution}} |
||
{{ |
{{redirect-distinguish|Lorentz distribution|Lorenz curve|Lorenz system}} |
||
{{Probability distribution |
{{Probability distribution |
||
| name =Cauchy |
| name =Cauchy |
||
| Line 25: | Line 25: | ||
| fisher = <math>\frac{1}{2\gamma^2}</math> |
| fisher = <math>\frac{1}{2\gamma^2}</math> |
||
}} |
}} |
||
The '''Cauchy distribution''', named after [[Augustin Cauchy]], is a [[continuous probability distribution]]. It is also known, especially among [[physicist]]s, as the '''Lorentz distribution''' (after [[Hendrik Lorentz]]), '''Cauchy–Lorentz distribution''', '''Lorentz(ian) function''', or '''Breit–Wigner distribution'''. The Cauchy distribution <math>f(x; x_0,\gamma)</math> is the distribution of the {{mvar|x}}-intercept of a ray issuing from <math>(x_0,\gamma)</math> with a uniformly distributed angle. It is also the distribution of the [[Ratio distribution|ratio of two |
The '''Cauchy distribution''', named after [[Augustin-Louis Cauchy]], is a [[continuous probability distribution]]. It is also known, especially among [[physicist]]s, as the '''Lorentz distribution''' (after [[Hendrik Lorentz]]), '''Cauchy–Lorentz distribution''', '''Lorentz(ian) function''', or '''Breit–Wigner distribution'''. The Cauchy distribution <math>f(x; x_0,\gamma)</math> is the distribution of the {{mvar|x}}-intercept of a ray issuing from <math>(x_0,\gamma)</math> with a uniformly distributed angle. It is also the distribution of the [[Ratio distribution|ratio]] of two independent [[Normal distribution|normally distributed]] random variables with mean zero. |
||
The Cauchy distribution is often used in statistics as the canonical example of a "[[pathological (mathematics)|pathological]]" distribution since both its [[expected value]] and its [[variance]] are undefined (but see {{slink||Moments}} below). The Cauchy distribution does not have finite [[moment (mathematics)|moment]]s of order greater than or equal to one; only fractional absolute moments exist.<ref name=jkb1>{{cite book|author1=N. L. Johnson |author2=S. Kotz |author3=N. Balakrishnan |title=Continuous Univariate Distributions, Volume 1|publisher=Wiley|location=New York|year=1994}}, Chapter 16.</ref> The Cauchy distribution has no [[moment generating function]]. |
The Cauchy distribution is often used in statistics as the canonical example of a "[[pathological (mathematics)|pathological]]" distribution since both its [[expected value]] and its [[variance]] are undefined (but see {{slink||Moments}} below). The Cauchy distribution does not have finite [[moment (mathematics)|moment]]s of order greater than or equal to one; only fractional absolute moments exist.<ref name=jkb1>{{cite book|author1=N. L. Johnson |author2=S. Kotz |author3=N. Balakrishnan |title=Continuous Univariate Distributions, Volume 1|publisher=Wiley|location=New York|year=1994}}, Chapter 16.</ref> The Cauchy distribution has no [[moment generating function]]. |
||
| Line 31: | Line 31: | ||
In [[mathematics]], it is closely related to the [[Poisson kernel]], which is the [[fundamental solution]] for the [[Laplace equation]] in the [[upper half-plane]]. |
In [[mathematics]], it is closely related to the [[Poisson kernel]], which is the [[fundamental solution]] for the [[Laplace equation]] in the [[upper half-plane]]. |
||
It is one of the few |
It is one of the few [[stable distribution]]s with a probability density function that can be expressed analytically, the others being the [[normal distribution]] and the [[Lévy distribution]]. |
||
==History== |
==History== |
||
[[File:Mean estimator consistency.gif|thumb|upright=1.35|right|Estimating the mean and standard deviation through |
[[File:Mean estimator consistency.gif|thumb|upright=1.35|right|Estimating the mean and standard deviation through a sample from a Cauchy distribution (bottom) does not converge as the size of the sample grows, as in the [[normal distribution]] (top). There can be arbitrarily large jumps in the estimates, as seen in the graphs on the bottom. (Click to expand)]] |
||
A function with the form of the density function of the Cauchy distribution was studied geometrically by [[Pierre de Fermat|Fermat]] in 1659, and later was known as the [[witch of Agnesi]], after [[Maria Gaetana |
A function with the form of the density function of the Cauchy distribution was studied geometrically by [[Pierre de Fermat|Fermat]] in 1659, and later was known as the [[witch of Agnesi]], after [[Maria Gaetana Agnesi]] included it as an example in her 1748 calculus textbook. Despite its name, the first explicit analysis of the properties of the Cauchy distribution was published by the French mathematician [[Siméon Denis Poisson|Poisson]] in 1824, with Cauchy only becoming associated with it during an academic controversy in 1853.<ref>Cauchy and the Witch of Agnesi in ''Statistics on the Table'', S M Stigler Harvard 1999 Chapter 18</ref> Poisson noted that if the mean of observations following such a distribution were taken, the [[standard deviation]] did not converge to any finite number. As such, [[Pierre-Simon Laplace|Laplace]]'s use of the [[central limit theorem]] with such a distribution was inappropriate, as it assumed a finite mean and variance. Despite this, Poisson did not regard the issue as important, in contrast to [[Irénée-Jules Bienaymé|Bienaymé]], who was to engage Cauchy in a long dispute over the matter. |
||
==Constructions== |
==Constructions== |
||
Here are the most important constructions. |
|||
=== Rotational symmetry === |
=== Rotational symmetry === |
||
If |
If one stands in front of a line and kicks a ball with a direction (more precisely, an angle) uniformly at random towards the line, then the distribution of the point where the ball hits the line is a Cauchy distribution. |
||
More formally, consider a point at <math>(x_0, \gamma)</math> in the x-y plane, and select a line passing the point, with its direction chosen uniformly at random. The intersection of the line with the x-axis is the Cauchy distribution with location <math>x_0</math> and scale <math>\gamma</math>. |
More formally, consider a point at <math>(x_0, \gamma)</math> in the x-y plane, and select a line passing the point, with its direction (angle with the <math>x</math>-axis) chosen uniformly (between -90° and +90°) at random. The intersection of the line with the x-axis is the Cauchy distribution with location <math>x_0</math> and scale <math>\gamma</math>. |
||
This definition gives a simple way to sample from the standard Cauchy distribution. Let <math> u </math> be a sample from a uniform distribution from <math>[0,1]</math>, then we can generate a sample, <math>x</math> from the standard Cauchy distribution using |
This definition gives a simple way to sample from the standard Cauchy distribution. Let <math> u </math> be a sample from a uniform distribution from <math>[0,1]</math>, then we can generate a sample, <math>x</math> from the standard Cauchy distribution using |
||
:<math> x = \tan\left(\pi(u-\frac{1}{2})\right) </math> |
:<math> x = \tan\left(\pi(u-\frac{1}{2})\right) </math> |
||
When <math>U</math> and <math>V</math> are two independent [[normal distribution|normally distributed]] [[random variable]]s with [[expected value]] 0 and [[variance]] 1, then the ratio <math>U/V</math> has the standard Cauchy distribution. |
When <math>U</math> and <math>V</math> are two independent [[normal distribution|normally distributed]] [[random variable]]s with [[expected value]] 0 and [[variance]] 1, then the ratio <math>U/V</math> has the standard Cauchy distribution. |
||
More generally, if <math>(U, V)</math> is a rotationally symmetric distribution on the plane, then the ratio <math>U/V</math> has the standard Cauchy distribution. |
More generally, if <math>(U, V)</math> is a rotationally symmetric distribution on the plane, then the ratio <math>U/V</math> has the standard Cauchy distribution. |
||
| Line 56: | Line 56: | ||
:<math>f(x; x_0,\gamma) = \frac{1}{\pi\gamma \left[1 + \left(\frac{x - x_0}{\gamma}\right)^2\right]} = { 1 \over \pi } \left[ { \gamma \over (x - x_0)^2 + \gamma^2 } \right], </math> |
:<math>f(x; x_0,\gamma) = \frac{1}{\pi\gamma \left[1 + \left(\frac{x - x_0}{\gamma}\right)^2\right]} = { 1 \over \pi } \left[ { \gamma \over (x - x_0)^2 + \gamma^2 } \right], </math> |
||
where <math>x_0</math> is the [[location parameter]], specifying the location of the peak of the distribution, and <math>\gamma</math> is the [[scale parameter]] which specifies the half-width at half-maximum (HWHM), alternatively <math>2\gamma</math> is [[full width at half maximum]] (FWHM). <math>\gamma</math> is also equal to half the [[interquartile range]] and is sometimes called the [[probable error]]. [[Augustin-Louis Cauchy]] exploited such a density function in 1827 with an [[infinitesimal]] scale parameter, defining |
where <math>x_0</math> is the [[location parameter]], specifying the location of the peak of the distribution, and <math>\gamma</math> is the [[scale parameter]] which specifies the half-width at half-maximum (HWHM), alternatively <math>2\gamma</math> is [[full width at half maximum]] (FWHM). <math>\gamma</math> is also equal to half the [[interquartile range]] and is sometimes called the [[probable error]]. This function is also known as a [[Lorentzian function]],<ref>{{cite web |title=Lorentzian Function |url=https://mathworld.wolfram.com/LorentzianFunction.html |website=MathWorld |publisher=Wolfram Research |accessdate=27 October 2024}}</ref> and an example of a [[nascent delta function]], and therefore approaches a [[Dirac delta function]] in the limit as <math>\gamma \to 0</math>. [[Augustin-Louis Cauchy]] exploited such a density function in 1827 with an [[infinitesimal]] scale parameter, defining this [[Dirac delta function]]. |
||
==== Properties of PDF ==== |
==== Properties of PDF ==== |
||
| Line 86: | Line 86: | ||
=== Other constructions === |
=== Other constructions === |
||
The standard Cauchy distribution is the [[Student's t-distribution|Student's ''t''-distribution]] with one degree of freedom, and so it may be constructed by any method that constructs the Student's t-distribution. |
The standard Cauchy distribution is the [[Student's t-distribution|Student's ''t''-distribution]] with one degree of freedom, and so it may be constructed by any method that constructs the Student's t-distribution.<ref>{{Cite journal |last=Li |first=Rui |last2=Nadarajah |first2=Saralees |date=2020-03-01 |title=A review of Student’s t distribution and its generalizations |url=https://link.springer.com/article/10.1007/s00181-018-1570-0 |journal=Empirical Economics |language=en |volume=58 |issue=3 |pages=1461–1490 |doi=10.1007/s00181-018-1570-0 |issn=1435-8921}}</ref> |
||
If <math>\Sigma</math> is a <math>p\times p</math> positive-semidefinite covariance matrix with strictly positive diagonal entries, then for [[Independent and identically distributed random variables|independent and identically distributed]] <math>X,Y\sim N(0,\Sigma)</math> and any random <math>p</math>-vector <math>w</math> independent of <math>X</math> and <math>Y</math> such that <math>w_1+\cdots+w_p=1</math> and <math>w_i\geq 0, i=1,\ldots,p,</math> (defining a [[categorical distribution]]) it holds that |
If <math>\Sigma</math> is a <math>p\times p</math> positive-semidefinite covariance matrix with strictly positive diagonal entries, then for [[Independent and identically distributed random variables|independent and identically distributed]] <math>X,Y\sim N(0,\Sigma)</math> and any random <math>p</math>-vector <math>w</math> independent of <math>X</math> and <math>Y</math> such that <math>w_1+\cdots+w_p=1</math> and <math>w_i\geq 0, i=1,\ldots,p,</math> (defining a [[categorical distribution]]) it holds that |
||
| Line 97: | Line 96: | ||
The Cauchy distribution is an [[infinitely divisible probability distribution]]. It is also a strictly [[stability (probability)|stable]] distribution.<ref>{{cite book |author1=Campbell B. Read |author2=N. Balakrishnan |author3=Brani Vidakovic |author4=Samuel Kotz |year=2006 |title=Encyclopedia of Statistical Sciences |page=778 |edition=2nd |publisher=[[John Wiley & Sons]] |isbn=978-0-471-15044-2|title-link=Encyclopedia of Statistical Sciences }}</ref> |
The Cauchy distribution is an [[infinitely divisible probability distribution]]. It is also a strictly [[stability (probability)|stable]] distribution.<ref>{{cite book |author1=Campbell B. Read |author2=N. Balakrishnan |author3=Brani Vidakovic |author4=Samuel Kotz |year=2006 |title=Encyclopedia of Statistical Sciences |page=778 |edition=2nd |publisher=[[John Wiley & Sons]] |isbn=978-0-471-15044-2|title-link=Encyclopedia of Statistical Sciences }}</ref> |
||
Like all stable distributions, the [[location-scale family]] to which the Cauchy distribution belongs is closed under [[linear transformations]] with [[real number|real]] coefficients. In addition, the Cauchy |
Like all stable distributions, the [[location-scale family]] to which the Cauchy distribution belongs is closed under [[linear transformations]] with [[real number|real]] coefficients. In addition, the family of Cauchy-distributed random variables is closed under [[Möbius transformation|linear fractional transformations]] with real coefficients.<ref>{{cite journal|first1=Franck B. | last1=Knight|title=A characterization of the Cauchy type|journal=[[Proceedings of the American Mathematical Society]]|volume = 55|issue=1|year = 1976|pages= 130–135|doi=10.2307/2041858|jstor=2041858|doi-access=free}}</ref> In this connection, see also [[McCullagh's parametrization of the Cauchy distributions]]. |
||
=== Sum of Cauchy |
=== Sum of Cauchy-distributed random variables === |
||
If <math>X_1, X_2, |
If <math>X_1, X_2, \ldots, X_n</math> are an [[Independent and identically distributed random variables|IID]] sample from the standard Cauchy distribution, then their [[sample mean]] <math>\bar X = \frac 1n \sum_i X_i</math> is also standard Cauchy distributed. In particular, the average does not converge to the mean, and so the standard Cauchy distribution does not follow the law of large numbers. |
||
This can be proved by repeated integration with the PDF, or more conveniently, by using the [[Characteristic function (probability theory)|characteristic function]] of standard Cauchy distribution (see below):<math display="block">\varphi_X(t) = \operatorname{E}\left[e^{iXt} \right ] = e^{- |
This can be proved by repeated integration with the PDF, or more conveniently, by using the [[Characteristic function (probability theory)|characteristic function]] of the standard Cauchy distribution (see below):<math display="block">\varphi_X(t) = \operatorname{E}\left[e^{iXt} \right ] = e^{-|t|}.</math>With this, we have <math>\varphi_{\sum_i X_i}(t) = e^{-n |t|} </math>, and so <math>\bar X</math> has a standard Cauchy distribution. |
||
More generally, if <math>X_1, X_2, |
More generally, if <math>X_1, X_2, \ldots, X_n</math> are independent and Cauchy distributed with location parameters <math>x_1, \ldots, x_n</math> and scales <math>\gamma_1, \ldots, \gamma_n</math>, and <math>a_1, \ldots, a_n</math> are real numbers, then <math>\sum_i a_iX_i</math> is Cauchy distributed with location <math>\sum_i a_ix_i</math> and scale<math>\sum_i |a_i|\gamma_i</math>. We see that there is no law of large numbers for any weighted sum of independent Cauchy distributions. |
||
This shows that the condition of finite variance in the [[central limit theorem]] cannot be dropped. It is also an example of a more generalized version of the central limit theorem that is characteristic of all [[stable distribution]]s, of which the Cauchy distribution is a special case. |
This shows that the condition of finite variance in the [[central limit theorem]] cannot be dropped. It is also an example of a more generalized version of the central limit theorem that is characteristic of all [[stable distribution]]s, of which the Cauchy distribution is a special case. |
||
=== Central limit theorem === |
=== Central limit theorem === |
||
If <math>X_1, X_2, |
If <math>X_1, X_2, \ldots </math> are and IID sample with PDF <math>\rho</math> such that <math>\lim_{c \to \infty}\frac{1}{c} \int_{-c}^c x^2\rho(x) \, dx = \frac{2\gamma}{\pi} </math> is finite, but nonzero, then <math>\frac 1n \sum_{i=1}^n X_i</math> converges in distribution to a Cauchy distribution with scale <math>\gamma</math>.<ref>{{cite web | title=Updates to the Cauchy Central Limit | website=Quantum Calculus | date=13 November 2022 | url=https://www.quantumcalculus.org/updates-to-the-cauchy-central-limit/ | access-date=21 June 2023}}</ref> |
||
===Characteristic function=== |
===Characteristic function=== |
||
| Line 122: | Line 121: | ||
The ''n''th moment of a distribution is the ''n''th derivative of the characteristic function evaluated at <math>t=0</math>. Observe that the characteristic function is not [[Differentiable function|differentiable]] at the origin: this corresponds to the fact that the Cauchy distribution does not have well-defined moments higher than the zeroth moment. |
The ''n''th moment of a distribution is the ''n''th derivative of the characteristic function evaluated at <math>t=0</math>. Observe that the characteristic function is not [[Differentiable function|differentiable]] at the origin: this corresponds to the fact that the Cauchy distribution does not have well-defined moments higher than the zeroth moment. |
||
=== |
=== Kullback–Leibler divergence === |
||
The [[Kullback–Leibler divergence]] between two Cauchy distributions has the following symmetric closed-form formula:<ref>{{cite arXiv |last1=Frederic |first1=Chyzak |last2=Nielsen |first2=Frank |year=2019 |title=A closed-form formula for the Kullback-Leibler divergence between Cauchy distributions |class=cs.IT |eprint=1905.10965}}</ref> |
The [[Kullback–Leibler divergence]] between two Cauchy distributions has the following symmetric closed-form formula:<ref>{{cite arXiv |last1=Frederic |first1=Chyzak |last2=Nielsen |first2=Frank |year=2019 |title=A closed-form formula for the Kullback-Leibler divergence between Cauchy distributions |class=cs.IT |eprint=1905.10965}}</ref> |
||
:<math> |
:<math> |
||
| Line 129: | Line 128: | ||
Any [[f-divergence]] between two Cauchy distributions is symmetric and can be expressed as a function of the chi-squared divergence.<ref>{{cite journal |last1=Nielsen |first1=Frank |last2=Okamura |first2=Kazuki |year=2023 |title=On f-Divergences Between Cauchy Distributions |journal=IEEE Transactions on Information Theory |volume=69 |issue=5 |pages=3150–3171 |doi=10.1109/TIT.2022.3231645 |arxiv=2101.12459|s2cid=231728407 }}</ref> |
Any [[f-divergence]] between two Cauchy distributions is symmetric and can be expressed as a function of the chi-squared divergence.<ref>{{cite journal |last1=Nielsen |first1=Frank |last2=Okamura |first2=Kazuki |year=2023 |title=On f-Divergences Between Cauchy Distributions |journal=IEEE Transactions on Information Theory |volume=69 |issue=5 |pages=3150–3171 |doi=10.1109/TIT.2022.3231645 |arxiv=2101.12459|s2cid=231728407 }}</ref> |
||
Closed-form expression for the [[total variation]], [[Jensen–Shannon divergence]], [[Hellinger distance]], etc are available. |
Closed-form expression for the [[total variation]], [[Jensen–Shannon divergence]], [[Hellinger distance]], etc. are available. |
||
===Comparison with the normal distribution=== |
|||
Compared to the normal distribution, the Cauchy density function has a higher peak and lower tails. |
|||
An example is shown in the two figures added here |
|||
[[File:Cauchy density.png|thumb|left|Observed histogram and best fitting Cauchy density function.<ref name="cumfreq">{{cite web |title=CumFreq, free software for cumulative frequency analysis and probability distribution fitting |url=https://www.waterlog.info/cumfreq.htm |url-status=live |archive-url=https://web.archive.org/web/20180221100105/https://www.waterlog.info/cumfreq.htm|archive-date=2018-02-21}}</ref>]] |
|||
[[File:Normal best density.png|thumb|right|Observed histogram and best fitting normal density function.<ref name="cumfreq" />]] |
|||
The figure to the left shows the ''Cauchy probability density function'' fitted to an observed [[histogram]]. The peak of the function is higher than the peak of the histogram while the tails are lower than those of the histogram.<br> |
|||
The figure to the right shows the ''normal probability density function'' fitted to ''the same'' observed histogram. The peak of the function is lower than the peak of the histogram.<br> |
|||
This illustrates the above statement. |
|||
=== Entropy === |
=== Entropy === |
||
| Line 156: | Line 145: | ||
:<math>Q'(p; \gamma) = \gamma\,\pi\,{\sec}^2\left[\pi\left(p-\tfrac 1 2 \right)\right].\!</math> |
:<math>Q'(p; \gamma) = \gamma\,\pi\,{\sec}^2\left[\pi\left(p-\tfrac 1 2 \right)\right].\!</math> |
||
The [[differential entropy]] of a distribution can be defined in terms of its quantile density,<ref>{{cite journal |last1=Vasicek |first1=Oldrich |year=1976 |title=A Test for Normality Based on Sample Entropy |journal=Journal of the Royal Statistical Society, Series B |volume=38 |issue=1 |pages=54–59}}</ref> specifically: |
The [[differential entropy]] of a distribution can be defined in terms of its quantile density,<ref>{{cite journal |last1=Vasicek |first1=Oldrich |year=1976 |title=A Test for Normality Based on Sample Entropy |journal=Journal of the Royal Statistical Society, Series B |volume=38 |issue=1 |pages=54–59|doi=10.1111/j.2517-6161.1976.tb01566.x }}</ref> specifically: |
||
:<math>H(\gamma) = \int_0^1 \log\,(Q'(p; \gamma))\,\mathrm dp = \log(4\pi\gamma)</math> |
:<math>H(\gamma) = \int_0^1 \log\,(Q'(p; \gamma))\,\mathrm dp = \log(4\pi\gamma)</math> |
||
| ⚫ | The Cauchy distribution is the [[maximum entropy probability distribution]] for a random variate <math>X</math> for which<ref>{{cite journal |last1=Park |first1=Sung Y. |last2=Bera |first2=Anil K. |year=2009 |title=Maximum entropy autoregressive conditional heteroskedasticity model |url=http://www.econ.yorku.ca/cesg/papers/berapark.pdf |url-status=dead |journal=Journal of Econometrics |publisher=Elsevier |volume=150 |issue=2 |pages=219–230 |doi=10.1016/j.jeconom.2008.12.014 |archive-url=https://web.archive.org/web/20110930062639/http://www.econ.yorku.ca/cesg/papers/berapark.pdf |archive-date=2011-09-30 |access-date=2011-06-02}}</ref> |
||
The Cauchy distribution is the [[maximum entropy probability distribution]] for a random variate <math>X</math> for which |
|||
:<math>\operatorname{E}[\log(1+(X-x_0)^2/\gamma^2)]=\log 4</math> |
:<math>\operatorname{E}[\log(1+(X-x_0)^2/\gamma^2)]=\log 4</math> |
||
or, alternatively, for a random variate <math>X</math> for which |
|||
:<math>\operatorname{E}[\log(1+(X-x_0)^2)]=2\log(1+\gamma).</math> |
|||
| ⚫ | |||
:<math>\operatorname{E}\!\left[\ln(1+X^2) \right]=\ln 4.</math> |
|||
==Moments== |
==Moments== |
||
| Line 176: | Line 157: | ||
=== Sample moments === |
=== Sample moments === |
||
If we take IID |
If we take an IID sample <math>X_1, X_2, \ldots </math> from the standard Cauchy distribution, then the sequence of their sample mean is <math>S_n = \frac 1n \sum_{i=1}^n X_i</math>, which also has the standard Cauchy distribution. Consequently, no matter how many terms we take, the sample average does not converge. |
||
Similarly, the sample variance <math>V_n = \frac 1n \sum_{i=1}^n (X_i - S_n)^2</math> also does not converge. |
Similarly, the sample variance <math>V_n = \frac 1n \sum_{i=1}^n (X_i - S_n)^2</math> also does not converge. |
||
| Line 182: | Line 163: | ||
A typical trajectory of <math>S_1, S_2, ...</math> looks like long periods of slow convergence to zero, punctuated by large jumps away from zero, but never getting too far away. A typical trajectory of <math>V_1, V_2, ...</math> looks similar, but the jumps accumulate faster than the decay, diverging to infinity. These two kinds of trajectories are plotted in the figure. |
A typical trajectory of <math>S_1, S_2, ...</math> looks like long periods of slow convergence to zero, punctuated by large jumps away from zero, but never getting too far away. A typical trajectory of <math>V_1, V_2, ...</math> looks similar, but the jumps accumulate faster than the decay, diverging to infinity. These two kinds of trajectories are plotted in the figure. |
||
Moments of sample lower than order 1 would converge to zero. Moments of sample higher than order 2 would diverge to infinity even faster than sample variance. |
Moments of sample lower than order 1 would converge to zero. Moments of sample higher than order 2 would diverge to infinity even faster than sample variance. |
||
===Mean=== |
===Mean=== |
||
| Line 192: | Line 173: | ||
for an arbitrary real number <math>a</math>. |
for an arbitrary real number <math>a</math>. |
||
For the integral to exist (even as an infinite value), at least one of the terms in this sum should be finite, or both should be infinite and have the same sign. But in the case of the Cauchy distribution, both the terms in this sum ({{EquationNote|2}}) are infinite and have opposite sign. Hence ({{EquationNote|1}}) is undefined, and thus so is the mean.<ref name="uah">{{cite web | url=http://www.randomservices.org/random/special/Cauchy.html | title=Cauchy Distribution | author=Kyle Siegrist | work=Random | access-date=5 July 2021 | archive-date=9 July 2021 | archive-url=https://web.archive.org/web/20210709183100/http://www.randomservices.org/random/special/Cauchy.html | url-status=live }}</ref> |
For the integral to exist (even as an infinite value), at least one of the terms in this sum should be finite, or both should be infinite and have the same sign. But in the case of the Cauchy distribution, both the terms in this sum ({{EquationNote|2}}) are infinite and have opposite sign. Hence ({{EquationNote|1}}) is undefined, and thus so is the mean.<ref name="uah">{{cite web | url=http://www.randomservices.org/random/special/Cauchy.html | title=Cauchy Distribution | author=Kyle Siegrist | work=Random | access-date=5 July 2021 | archive-date=9 July 2021 | archive-url=https://web.archive.org/web/20210709183100/http://www.randomservices.org/random/special/Cauchy.html | url-status=live }}</ref> When the mean of a probability distribution function (PDF) is undefined, no one can compute a reliable average over the experimental data points, regardless of the sample's size. |
||
Note that the [[Cauchy principal value]] of the mean of the Cauchy distribution is |
Note that the [[Cauchy principal value]] of the mean of the Cauchy distribution is |
||
| Line 253: | Line 234: | ||
Solving just for <math>x_0</math> requires solving a polynomial of degree <math>2n-1</math>,<ref name=ferguson/> and solving just for <math>\,\!\gamma</math> requires solving a polynomial of degree <math>2n</math>. Therefore, whether solving for one parameter or for both parameters simultaneously, a [[numerical analysis|numerical]] solution on a computer is typically required. The benefit of maximum likelihood estimation is asymptotic efficiency; estimating <math>x_0</math> using the sample median is only about 81% as asymptotically efficient as estimating <math>x_0</math> by maximum likelihood.<ref name=bloch/><ref>{{cite journal|last1=Barnett|first1=V. D.|year=1966|journal=Journal of the American Statistical Association |volume=61|issue=316|pages=1205–1218|title=Order Statistics Estimators of the Location of the Cauchy Distribution|jstor=2283210|doi=10.1080/01621459.1966.10482205}}</ref> The truncated sample mean using the middle 24% order statistics is about 88% as asymptotically efficient an estimator of <math>x_0</math> as the maximum likelihood estimate.<ref name=bloch/> When [[Newton's method]] is used to find the solution for the maximum likelihood estimate, the middle 24% order statistics can be used as an initial solution for <math>x_0</math>. |
Solving just for <math>x_0</math> requires solving a polynomial of degree <math>2n-1</math>,<ref name=ferguson/> and solving just for <math>\,\!\gamma</math> requires solving a polynomial of degree <math>2n</math>. Therefore, whether solving for one parameter or for both parameters simultaneously, a [[numerical analysis|numerical]] solution on a computer is typically required. The benefit of maximum likelihood estimation is asymptotic efficiency; estimating <math>x_0</math> using the sample median is only about 81% as asymptotically efficient as estimating <math>x_0</math> by maximum likelihood.<ref name=bloch/><ref>{{cite journal|last1=Barnett|first1=V. D.|year=1966|journal=Journal of the American Statistical Association |volume=61|issue=316|pages=1205–1218|title=Order Statistics Estimators of the Location of the Cauchy Distribution|jstor=2283210|doi=10.1080/01621459.1966.10482205}}</ref> The truncated sample mean using the middle 24% order statistics is about 88% as asymptotically efficient an estimator of <math>x_0</math> as the maximum likelihood estimate.<ref name=bloch/> When [[Newton's method]] is used to find the solution for the maximum likelihood estimate, the middle 24% order statistics can be used as an initial solution for <math>x_0</math>. |
||
The shape can be estimated using the median of absolute values, since for location 0 Cauchy variables <math>X\sim\mathrm{Cauchy}(0,\gamma)</math>, the <math>\ |
The shape can be estimated using the median of absolute values, since for location 0 Cauchy variables <math>X\sim\mathrm{Cauchy}(0,\gamma)</math>, the <math>\operatorname{median}(|X|) = \gamma</math> the shape parameter. |
||
==Multivariate Cauchy distribution== |
==Multivariate Cauchy distribution== |
||
| Line 298: | Line 279: | ||
*If <math>X \sim \operatorname{Cauchy}(x_0, \gamma_0)</math> and <math>Y \sim \operatorname{Cauchy}(x_1,\gamma_1)</math> are independent, then <math> X+Y \sim \operatorname{Cauchy}(x_0+x_1,\gamma_0 +\gamma_1)</math> and <math> X-Y \sim \operatorname{Cauchy}(x_0-x_1, \gamma_0+\gamma_1)</math> |
*If <math>X \sim \operatorname{Cauchy}(x_0, \gamma_0)</math> and <math>Y \sim \operatorname{Cauchy}(x_1,\gamma_1)</math> are independent, then <math> X+Y \sim \operatorname{Cauchy}(x_0+x_1,\gamma_0 +\gamma_1)</math> and <math> X-Y \sim \operatorname{Cauchy}(x_0-x_1, \gamma_0+\gamma_1)</math> |
||
*If <math>X \sim \operatorname{Cauchy}(0,\gamma)</math> then <math> \tfrac{1}{X} \sim \operatorname{Cauchy}(0, \tfrac{1}{\gamma})</math> |
*If <math>X \sim \operatorname{Cauchy}(0,\gamma)</math> then <math> \tfrac{1}{X} \sim \operatorname{Cauchy}(0, \tfrac{1}{\gamma})</math> |
||
*[[McCullagh's parametrization of the Cauchy distributions]]:<ref name="McCullagh1992">[[Peter McCullagh|McCullagh, P.]], [https://archive.today/ |
*[[McCullagh's parametrization of the Cauchy distributions]]:<ref name="McCullagh1992">[[Peter McCullagh|McCullagh, P.]], [https://archive.today/20120707071014/http://biomet.oxfordjournals.org/cgi/content/abstract/79/2/247 "Conditional inference and Cauchy models"], ''[[Biometrika]]'', volume 79 (1992), pages 247–259. [http://www.stat.uchicago.edu/~pmcc/pubs/paper18.pdf PDF] {{Webarchive |url=https://web.archive.org/web/20100610000327/http://www.stat.uchicago.edu/~pmcc/pubs/paper18.pdf |date=2010-06-10 }} from McCullagh's homepage.</ref> Expressing a Cauchy distribution in terms of one complex parameter <math>\psi = x_0+i\gamma</math>, define <math>X \sim \operatorname{Cauchy}(\psi)</math> to mean <math>X \sim \operatorname{Cauchy}(x_0,|\gamma|)</math>. If <math>X \sim \operatorname{Cauchy}(\psi)</math> then: <math display="block">\frac{aX+b}{cX+d} \sim \operatorname{Cauchy}\left(\frac{a\psi+b}{c\psi+d}\right)</math> where <math>a</math>, <math>b</math>, <math>c</math> and <math>d</math> are real numbers. |
||
* Using the same convention as above, if <math>X \sim \operatorname{Cauchy}(\psi)</math> then:<ref name="McCullagh1992"/> <math display="block">\frac{X-i}{X+i} \sim \operatorname{CCauchy}\left(\frac{\psi-i}{\psi+i}\right)</math>where <math>\operatorname{CCauchy}</math> is the [[circular Cauchy distribution]]. |
* Using the same convention as above, if <math>X \sim \operatorname{Cauchy}(\psi)</math> then:<ref name="McCullagh1992"/> <math display="block">\frac{X-i}{X+i} \sim \operatorname{CCauchy}\left(\frac{\psi-i}{\psi+i}\right)</math>where <math>\operatorname{CCauchy}</math> is the [[circular Cauchy distribution]]. |
||
| Line 315: | Line 296: | ||
This last representation is a consequence of the formula |
This last representation is a consequence of the formula |
||
: <math>\pi |x| = \operatorname{PV }\int_{\mathbb{R} \ |
: <math>\pi |x| = \operatorname{PV }\int_{\mathbb{R} \smallsetminus\lbrace 0 \rbrace} (1 - e^{ixy}) \, \frac{dy}{y^2} </math> |
||
==Related distributions== |
==Related distributions== |
||
*<math>\operatorname{Cauchy}(0,1) \sim \textrm{t}(\mathrm{df}=1)\,</math> [[Student's t distribution|Student's ''t'' distribution]] |
*<math>\operatorname{Cauchy}(0,1) \sim \textrm{t}(\mathrm{df}=1)\,</math> [[Student's t distribution|Student's ''t'' distribution]] |
||
*<math>\operatorname{Cauchy}(\mu,\sigma) \sim \textrm{t}_{(\mathrm{df}=1)}(\mu,\sigma)\,</math> [[Student's t distribution# |
*<math>\operatorname{Cauchy}(\mu,\sigma) \sim \textrm{t}_{(\mathrm{df}=1)}(\mu,\sigma)\,</math> [[Student's t distribution#location-scale|non-standardized Student's ''t'' distribution]] |
||
*If <math>X, Y \sim \textrm{N}(0,1)\, X, Y</math> independent, then <math> \tfrac X Y\sim \textrm{Cauchy}(0,1)\,</math> |
*If <math>X, Y \sim \textrm{N}(0,1)\, X, Y</math> independent, then <math> \tfrac X Y\sim \textrm{Cauchy}(0,1)\,</math> |
||
*If <math>X \sim \textrm{U}(0,1)\,</math> then <math> \tan \left( \pi \left(X-\tfrac{1}{2}\right) \right) \sim \textrm{Cauchy}(0,1)\,</math> |
*If <math>X \sim \textrm{U}(0,1)\,</math> then <math> \tan \left( \pi \left(X-\tfrac{1}{2}\right) \right) \sim \textrm{Cauchy}(0,1)\,</math> |
||
| Line 329: | Line 310: | ||
*The Cauchy distribution is a singular limit of a [[hyperbolic distribution]]{{Citation needed|date=April 2011}} |
*The Cauchy distribution is a singular limit of a [[hyperbolic distribution]]{{Citation needed|date=April 2011}} |
||
*The [[wrapped Cauchy distribution]], taking values on a circle, is derived from the Cauchy distribution by wrapping it around the circle. |
*The [[wrapped Cauchy distribution]], taking values on a circle, is derived from the Cauchy distribution by wrapping it around the circle. |
||
*If <math>X \sim \textrm{N}(0,1)</math>, <math>Z \sim \operatorname{Inverse-Gamma}(1/2, s^2/2)</math>, then <math>Y = \mu + X \sqrt Z \sim \operatorname{Cauchy}(\mu,s)</math>. For half-Cauchy distributions, the relation holds by setting <math>X \sim \textrm{N}(0,1) I\{X |
*If <math>X \sim \textrm{N}(0,1)</math>, <math>Z \sim \operatorname{Inverse-Gamma}(1/2, s^2/2)</math>, then <math>Y = \mu + X \sqrt Z \sim \operatorname{Cauchy}(\mu,s)</math>. For half-Cauchy distributions, the relation holds by setting <math>X \sim \textrm{N}(0,1) I\{X\ge0\}</math>. |
||
==Relativistic Breit–Wigner distribution== |
==Relativistic Breit–Wigner distribution== |
||
| Line 338: | Line 319: | ||
*In [[spectroscopy]], the Cauchy distribution describes the shape of [[spectral line]]s which are subject to [[homogeneous broadening]] in which all atoms interact in the same way with the frequency range contained in the line shape. Many mechanisms cause homogeneous broadening, most notably [[Line broadening#Pressure broadening|collision broadening]].<ref>{{cite book |author=E. Hecht |year=1987 |title=Optics |page=603 |edition=2nd |publisher=[[Addison-Wesley]] }}</ref> [[Spectral line#Natural broadening|Lifetime or natural broadening]] also gives rise to a line shape described by the Cauchy distribution. |
*In [[spectroscopy]], the Cauchy distribution describes the shape of [[spectral line]]s which are subject to [[homogeneous broadening]] in which all atoms interact in the same way with the frequency range contained in the line shape. Many mechanisms cause homogeneous broadening, most notably [[Line broadening#Pressure broadening|collision broadening]].<ref>{{cite book |author=E. Hecht |year=1987 |title=Optics |page=603 |edition=2nd |publisher=[[Addison-Wesley]] }}</ref> [[Spectral line#Natural broadening|Lifetime or natural broadening]] also gives rise to a line shape described by the Cauchy distribution. |
||
*Applications of the Cauchy distribution or its transformation can be found in fields working with exponential growth. A 1958 paper by White <ref>{{cite journal |author=White, J.S. |date=December 1958 |title=The Limiting Distribution of the Serial Correlation Coefficient in the Explosive Case |journal=The Annals of Mathematical Statistics |volume=29 |issue=4 |pages=1188–1197 |doi=10.1214/aoms/1177706450 |doi-access=free}}</ref> derived the test statistic for estimators of <math>\hat{\beta}</math> for the equation <math>x_{t+1}=\beta{x}_t+\varepsilon_{t+1},\beta>1</math> and where the maximum likelihood estimator is found using ordinary least squares showed the sampling distribution of the statistic is the Cauchy distribution. |
*Applications of the Cauchy distribution or its transformation can be found in fields working with [[exponential growth]]. A 1958 paper by White <ref>{{cite journal |author=White, J.S. |date=December 1958 |title=The Limiting Distribution of the Serial Correlation Coefficient in the Explosive Case |journal=The Annals of Mathematical Statistics |volume=29 |issue=4 |pages=1188–1197 |doi=10.1214/aoms/1177706450 |doi-access=free}}</ref> derived the test statistic for estimators of <math>\hat{\beta}</math> for the equation <math>x_{t+1}=\beta{x}_t+\varepsilon_{t+1},\beta>1</math> and where the maximum likelihood estimator is found using ordinary least squares showed the sampling distribution of the statistic is the Cauchy distribution. |
||
[[File:Cauchy distribution.png|thumb|upright=1.15|Fitted cumulative Cauchy distribution to maximum one-day rainfalls using [[CumFreq]], see also [[distribution fitting]]<ref name=cumfreq/>]] |
[[File:Cauchy distribution.png|thumb|upright=1.15|Fitted cumulative Cauchy distribution to maximum one-day rainfalls using [[CumFreq]], see also [[distribution fitting]]<ref name="cumfreq">{{cite web |title=CumFreq, free software for cumulative frequency analysis and probability distribution fitting |url=https://www.waterlog.info/cumfreq.htm |url-status=live |archive-url=https://web.archive.org/web/20180221100105/https://www.waterlog.info/cumfreq.htm|archive-date=2018-02-21}}</ref>]] |
||
*The Cauchy distribution is often the distribution of observations for objects that are spinning. The classic reference for this is called the Gull's lighthouse problem<ref>Gull, S.F. (1988) Bayesian Inductive Inference and Maximum Entropy. Kluwer Academic Publishers, Berlin. https://doi.org/10.1007/978-94-009-3049-0_4 {{Webarchive|url=https://web.archive.org/web/20220125125834/https://link.springer.com/chapter/10.1007%2F978-94-009-3049-0_4 |date=2022-01-25 }}</ref> and as in the above section as the Breit–Wigner distribution in particle physics. |
*The Cauchy distribution is often the distribution of observations for objects that are spinning. The classic reference for this is called the Gull's lighthouse problem<ref>Gull, S.F. (1988) Bayesian Inductive Inference and Maximum Entropy. Kluwer Academic Publishers, Berlin. https://doi.org/10.1007/978-94-009-3049-0_4 {{Webarchive|url=https://web.archive.org/web/20220125125834/https://link.springer.com/chapter/10.1007%2F978-94-009-3049-0_4 |date=2022-01-25 }}</ref> and as in the above section as the Breit–Wigner distribution in particle physics. |
||
*In [[hydrology]] the Cauchy distribution is applied to extreme events such as annual maximum one-day rainfalls and river discharges. The blue picture illustrates an example of fitting the Cauchy distribution to ranked monthly maximum one-day rainfalls showing also the 90% [[confidence belt]] based on the [[binomial distribution]]. The rainfall data are represented by [[plotting position]]s as part of the [[cumulative frequency analysis]]. |
*In [[hydrology]] the Cauchy distribution is applied to extreme events such as annual maximum one-day rainfalls and river discharges. The blue picture illustrates an example of fitting the Cauchy distribution to ranked monthly maximum one-day rainfalls showing also the 90% [[confidence belt]] based on the [[binomial distribution]]. The rainfall data are represented by [[plotting position]]s as part of the [[cumulative frequency analysis]]. |
||
*The expression for imaginary part of complex [[Permittivity|electrical permittivity]] according to Lorentz model is a model VAR ([[value at risk]]) producing a much larger probability of extreme risk than [[Gaussian Distribution]].<ref>Tong Liu (2012), An intermediate distribution between Gaussian and Cauchy distributions. https://arxiv.org/pdf/1208.5109.pdf {{Webarchive|url=https://web.archive.org/web/20200624234315/https://arxiv.org/pdf/1208.5109.pdf |date=2020-06-24 }}</ref> |
*The expression for the imaginary part of complex [[Permittivity|electrical permittivity]], according to the Lorentz model, is a Cauchy distribution. |
||
*As an additional distribution to model [[fat tails]] in [[computational finance]], Cauchy distributions can be used to model VAR ([[value at risk]]) producing a much larger probability of extreme risk than [[Gaussian Distribution]].<ref>Tong Liu (2012), An intermediate distribution between Gaussian and Cauchy distributions. https://arxiv.org/pdf/1208.5109.pdf {{Webarchive|url=https://web.archive.org/web/20200624234315/https://arxiv.org/pdf/1208.5109.pdf |date=2020-06-24 }}</ref> |
|||
==See also== |
==See also== |
||
Latest revision as of 10:58, 19 November 2024
|
Probability density function 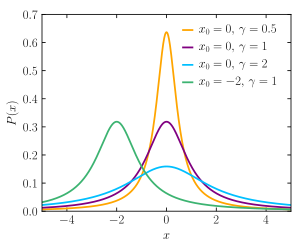 The purple curve is the standard Cauchy distribution | |||
|
Cumulative distribution function  | |||
| Parameters |
location (real) scale (real) | ||
|---|---|---|---|
| Support | |||
| CDF | |||
| Quantile | |||
| Mean | undefined | ||
| Median | |||
| Mode | |||
| Variance | undefined | ||
| MAD | |||
| Skewness | undefined | ||
| Excess kurtosis | undefined | ||
| Entropy | |||
| MGF | does not exist | ||
| CF | |||
| Fisher information | |||
The Cauchy distribution, named after Augustin-Louis Cauchy, is a continuous probability distribution. It is also known, especially among physicists, as the Lorentz distribution (after Hendrik Lorentz), Cauchy–Lorentz distribution, Lorentz(ian) function, or Breit–Wigner distribution. The Cauchy distribution is the distribution of the x-intercept of a ray issuing from with a uniformly distributed angle. It is also the distribution of the ratio of two independent normally distributed random variables with mean zero.
The Cauchy distribution is often used in statistics as the canonical example of a "pathological" distribution since both its expected value and its variance are undefined (but see § Moments below). The Cauchy distribution does not have finite moments of order greater than or equal to one; only fractional absolute moments exist.[1] The Cauchy distribution has no moment generating function.
In mathematics, it is closely related to the Poisson kernel, which is the fundamental solution for the Laplace equation in the upper half-plane.
It is one of the few stable distributions with a probability density function that can be expressed analytically, the others being the normal distribution and the Lévy distribution.
History
[edit]
A function with the form of the density function of the Cauchy distribution was studied geometrically by Fermat in 1659, and later was known as the witch of Agnesi, after Maria Gaetana Agnesi included it as an example in her 1748 calculus textbook. Despite its name, the first explicit analysis of the properties of the Cauchy distribution was published by the French mathematician Poisson in 1824, with Cauchy only becoming associated with it during an academic controversy in 1853.[2] Poisson noted that if the mean of observations following such a distribution were taken, the standard deviation did not converge to any finite number. As such, Laplace's use of the central limit theorem with such a distribution was inappropriate, as it assumed a finite mean and variance. Despite this, Poisson did not regard the issue as important, in contrast to Bienaymé, who was to engage Cauchy in a long dispute over the matter.
Constructions
[edit]Here are the most important constructions.
Rotational symmetry
[edit]If one stands in front of a line and kicks a ball with a direction (more precisely, an angle) uniformly at random towards the line, then the distribution of the point where the ball hits the line is a Cauchy distribution.
More formally, consider a point at in the x-y plane, and select a line passing the point, with its direction (angle with the -axis) chosen uniformly (between -90° and +90°) at random. The intersection of the line with the x-axis is the Cauchy distribution with location and scale .
This definition gives a simple way to sample from the standard Cauchy distribution. Let be a sample from a uniform distribution from , then we can generate a sample, from the standard Cauchy distribution using
When and are two independent normally distributed random variables with expected value 0 and variance 1, then the ratio has the standard Cauchy distribution.
More generally, if is a rotationally symmetric distribution on the plane, then the ratio has the standard Cauchy distribution.
Probability density function (PDF)
[edit]The Cauchy distribution is the probability distribution with the following probability density function (PDF)[1][3]
where is the location parameter, specifying the location of the peak of the distribution, and is the scale parameter which specifies the half-width at half-maximum (HWHM), alternatively is full width at half maximum (FWHM). is also equal to half the interquartile range and is sometimes called the probable error. This function is also known as a Lorentzian function,[4] and an example of a nascent delta function, and therefore approaches a Dirac delta function in the limit as . Augustin-Louis Cauchy exploited such a density function in 1827 with an infinitesimal scale parameter, defining this Dirac delta function.
Properties of PDF
[edit]The maximum value or amplitude of the Cauchy PDF is , located at .
It is sometimes convenient to express the PDF in terms of the complex parameter
The special case when and is called the standard Cauchy distribution with the probability density function[5][6]
In physics, a three-parameter Lorentzian function is often used:
where is the height of the peak. The three-parameter Lorentzian function indicated is not, in general, a probability density function, since it does not integrate to 1, except in the special case where
Cumulative distribution function (CDF)
[edit]The Cauchy distribution is the probability distribution with the following cumulative distribution function (CDF):
and the quantile function (inverse cdf) of the Cauchy distribution is
It follows that the first and third quartiles are , and hence the interquartile range is .
For the standard distribution, the cumulative distribution function simplifies to arctangent function :
Other constructions
[edit]The standard Cauchy distribution is the Student's t-distribution with one degree of freedom, and so it may be constructed by any method that constructs the Student's t-distribution.[7]
If is a positive-semidefinite covariance matrix with strictly positive diagonal entries, then for independent and identically distributed and any random -vector independent of and such that and (defining a categorical distribution) it holds that
Properties
[edit]The Cauchy distribution is an example of a distribution which has no mean, variance or higher moments defined. Its mode and median are well defined and are both equal to .
The Cauchy distribution is an infinitely divisible probability distribution. It is also a strictly stable distribution.[9]
Like all stable distributions, the location-scale family to which the Cauchy distribution belongs is closed under linear transformations with real coefficients. In addition, the family of Cauchy-distributed random variables is closed under linear fractional transformations with real coefficients.[10] In this connection, see also McCullagh's parametrization of the Cauchy distributions.
Sum of Cauchy-distributed random variables
[edit]If are an IID sample from the standard Cauchy distribution, then their sample mean is also standard Cauchy distributed. In particular, the average does not converge to the mean, and so the standard Cauchy distribution does not follow the law of large numbers.
This can be proved by repeated integration with the PDF, or more conveniently, by using the characteristic function of the standard Cauchy distribution (see below):With this, we have , and so has a standard Cauchy distribution.
More generally, if are independent and Cauchy distributed with location parameters and scales , and are real numbers, then is Cauchy distributed with location and scale. We see that there is no law of large numbers for any weighted sum of independent Cauchy distributions.
This shows that the condition of finite variance in the central limit theorem cannot be dropped. It is also an example of a more generalized version of the central limit theorem that is characteristic of all stable distributions, of which the Cauchy distribution is a special case.
Central limit theorem
[edit]If are and IID sample with PDF such that is finite, but nonzero, then converges in distribution to a Cauchy distribution with scale .[11]
Characteristic function
[edit]Let denote a Cauchy distributed random variable. The characteristic function of the Cauchy distribution is given by
which is just the Fourier transform of the probability density. The original probability density may be expressed in terms of the characteristic function, essentially by using the inverse Fourier transform:
The nth moment of a distribution is the nth derivative of the characteristic function evaluated at . Observe that the characteristic function is not differentiable at the origin: this corresponds to the fact that the Cauchy distribution does not have well-defined moments higher than the zeroth moment.
Kullback–Leibler divergence
[edit]The Kullback–Leibler divergence between two Cauchy distributions has the following symmetric closed-form formula:[12]
Any f-divergence between two Cauchy distributions is symmetric and can be expressed as a function of the chi-squared divergence.[13] Closed-form expression for the total variation, Jensen–Shannon divergence, Hellinger distance, etc. are available.
Entropy
[edit]The entropy of the Cauchy distribution is given by:
The derivative of the quantile function, the quantile density function, for the Cauchy distribution is:
The differential entropy of a distribution can be defined in terms of its quantile density,[14] specifically:
The Cauchy distribution is the maximum entropy probability distribution for a random variate for which[15]
Moments
[edit]The Cauchy distribution is usually used as an illustrative counterexample in elementary probability courses, as a distribution with no well-defined (or "indefinite") moments.
Sample moments
[edit]If we take an IID sample from the standard Cauchy distribution, then the sequence of their sample mean is , which also has the standard Cauchy distribution. Consequently, no matter how many terms we take, the sample average does not converge.
Similarly, the sample variance also does not converge.

A typical trajectory of looks like long periods of slow convergence to zero, punctuated by large jumps away from zero, but never getting too far away. A typical trajectory of looks similar, but the jumps accumulate faster than the decay, diverging to infinity. These two kinds of trajectories are plotted in the figure.
Moments of sample lower than order 1 would converge to zero. Moments of sample higher than order 2 would diverge to infinity even faster than sample variance.
Mean
[edit]If a probability distribution has a density function , then the mean, if it exists, is given by
| (1) |
We may evaluate this two-sided improper integral by computing the sum of two one-sided improper integrals. That is,
| (2) |
for an arbitrary real number .
For the integral to exist (even as an infinite value), at least one of the terms in this sum should be finite, or both should be infinite and have the same sign. But in the case of the Cauchy distribution, both the terms in this sum (2) are infinite and have opposite sign. Hence (1) is undefined, and thus so is the mean.[16] When the mean of a probability distribution function (PDF) is undefined, no one can compute a reliable average over the experimental data points, regardless of the sample's size.
Note that the Cauchy principal value of the mean of the Cauchy distribution is which is zero. On the other hand, the related integral is not zero, as can be seen by computing the integral. This again shows that the mean (1) cannot exist.
Various results in probability theory about expected values, such as the strong law of large numbers, fail to hold for the Cauchy distribution.[16]
Smaller moments
[edit]The absolute moments for are defined. For we have
Higher moments
[edit]The Cauchy distribution does not have finite moments of any order. Some of the higher raw moments do exist and have a value of infinity, for example, the raw second moment:
By re-arranging the formula, one can see that the second moment is essentially the infinite integral of a constant (here 1). Higher even-powered raw moments will also evaluate to infinity. Odd-powered raw moments, however, are undefined, which is distinctly different from existing with the value of infinity. The odd-powered raw moments are undefined because their values are essentially equivalent to since the two halves of the integral both diverge and have opposite signs. The first raw moment is the mean, which, being odd, does not exist. (See also the discussion above about this.) This in turn means that all of the central moments and standardized moments are undefined since they are all based on the mean. The variance—which is the second central moment—is likewise non-existent (despite the fact that the raw second moment exists with the value infinity).
The results for higher moments follow from Hölder's inequality, which implies that higher moments (or halves of moments) diverge if lower ones do.
Moments of truncated distributions
[edit]Consider the truncated distribution defined by restricting the standard Cauchy distribution to the interval [−10100, 10100]. Such a truncated distribution has all moments (and the central limit theorem applies for i.i.d. observations from it); yet for almost all practical purposes it behaves like a Cauchy distribution.[17]
Estimation of parameters
[edit]Because the parameters of the Cauchy distribution do not correspond to a mean and variance, attempting to estimate the parameters of the Cauchy distribution by using a sample mean and a sample variance will not succeed.[18] For example, if an i.i.d. sample of size n is taken from a Cauchy distribution, one may calculate the sample mean as:
Although the sample values will be concentrated about the central value , the sample mean will become increasingly variable as more observations are taken, because of the increased probability of encountering sample points with a large absolute value. In fact, the distribution of the sample mean will be equal to the distribution of the observations themselves; i.e., the sample mean of a large sample is no better (or worse) an estimator of than any single observation from the sample. Similarly, calculating the sample variance will result in values that grow larger as more observations are taken.
Therefore, more robust means of estimating the central value and the scaling parameter are needed. One simple method is to take the median value of the sample as an estimator of and half the sample interquartile range as an estimator of . Other, more precise and robust methods have been developed [19][20] For example, the truncated mean of the middle 24% of the sample order statistics produces an estimate for that is more efficient than using either the sample median or the full sample mean.[21][22] However, because of the fat tails of the Cauchy distribution, the efficiency of the estimator decreases if more than 24% of the sample is used.[21][22]
Maximum likelihood can also be used to estimate the parameters and . However, this tends to be complicated by the fact that this requires finding the roots of a high degree polynomial, and there can be multiple roots that represent local maxima.[23] Also, while the maximum likelihood estimator is asymptotically efficient, it is relatively inefficient for small samples.[24][25] The log-likelihood function for the Cauchy distribution for sample size is:
Maximizing the log likelihood function with respect to and by taking the first derivative produces the following system of equations:
Note that
is a monotone function in and that the solution must satisfy
Solving just for requires solving a polynomial of degree ,[23] and solving just for requires solving a polynomial of degree . Therefore, whether solving for one parameter or for both parameters simultaneously, a numerical solution on a computer is typically required. The benefit of maximum likelihood estimation is asymptotic efficiency; estimating using the sample median is only about 81% as asymptotically efficient as estimating by maximum likelihood.[22][26] The truncated sample mean using the middle 24% order statistics is about 88% as asymptotically efficient an estimator of as the maximum likelihood estimate.[22] When Newton's method is used to find the solution for the maximum likelihood estimate, the middle 24% order statistics can be used as an initial solution for .
The shape can be estimated using the median of absolute values, since for location 0 Cauchy variables , the the shape parameter.
Multivariate Cauchy distribution
[edit]A random vector is said to have the multivariate Cauchy distribution if every linear combination of its components has a Cauchy distribution. That is, for any constant vector , the random variable should have a univariate Cauchy distribution.[27] The characteristic function of a multivariate Cauchy distribution is given by:
where and are real functions with a homogeneous function of degree one and a positive homogeneous function of degree one.[27] More formally:[27]
for all .
An example of a bivariate Cauchy distribution can be given by:[28]
Note that in this example, even though the covariance between and is 0, and are not statistically independent.[28]
We also can write this formula for complex variable. Then the probability density function of complex cauchy is :
Like how the standard Cauchy distribution is the Student t-distribution with one degree of freedom, the multidimensional Cauchy density is the multivariate Student distribution with one degree of freedom. The density of a dimension Student distribution with one degree of freedom is:
The properties of multidimensional Cauchy distribution are then special cases of the multivariate Student distribution.
Transformation properties
[edit]- If then [29]
- If and are independent, then and
- If then
- McCullagh's parametrization of the Cauchy distributions:[30] Expressing a Cauchy distribution in terms of one complex parameter , define to mean . If then: where , , and are real numbers.
- Using the same convention as above, if then:[30] where is the circular Cauchy distribution.
Lévy measure
[edit]The Cauchy distribution is the stable distribution of index 1. The Lévy–Khintchine representation of such a stable distribution of parameter is given, for by:
where
and can be expressed explicitly.[31] In the case of the Cauchy distribution, one has .
This last representation is a consequence of the formula
Related distributions
[edit]- Student's t distribution
- non-standardized Student's t distribution
- If independent, then
- If then
- If then
- If then
- The Cauchy distribution is a limiting case of a Pearson distribution of type 4[citation needed]
- The Cauchy distribution is a special case of a Pearson distribution of type 7.[1]
- The Cauchy distribution is a stable distribution: if , then .
- The Cauchy distribution is a singular limit of a hyperbolic distribution[citation needed]
- The wrapped Cauchy distribution, taking values on a circle, is derived from the Cauchy distribution by wrapping it around the circle.
- If , , then . For half-Cauchy distributions, the relation holds by setting .
Relativistic Breit–Wigner distribution
[edit]In nuclear and particle physics, the energy profile of a resonance is described by the relativistic Breit–Wigner distribution, while the Cauchy distribution is the (non-relativistic) Breit–Wigner distribution.[citation needed]
Occurrence and applications
[edit]- In spectroscopy, the Cauchy distribution describes the shape of spectral lines which are subject to homogeneous broadening in which all atoms interact in the same way with the frequency range contained in the line shape. Many mechanisms cause homogeneous broadening, most notably collision broadening.[32] Lifetime or natural broadening also gives rise to a line shape described by the Cauchy distribution.
- Applications of the Cauchy distribution or its transformation can be found in fields working with exponential growth. A 1958 paper by White [33] derived the test statistic for estimators of for the equation and where the maximum likelihood estimator is found using ordinary least squares showed the sampling distribution of the statistic is the Cauchy distribution.

- The Cauchy distribution is often the distribution of observations for objects that are spinning. The classic reference for this is called the Gull's lighthouse problem[35] and as in the above section as the Breit–Wigner distribution in particle physics.
- In hydrology the Cauchy distribution is applied to extreme events such as annual maximum one-day rainfalls and river discharges. The blue picture illustrates an example of fitting the Cauchy distribution to ranked monthly maximum one-day rainfalls showing also the 90% confidence belt based on the binomial distribution. The rainfall data are represented by plotting positions as part of the cumulative frequency analysis.
- The expression for the imaginary part of complex electrical permittivity, according to the Lorentz model, is a Cauchy distribution.
- As an additional distribution to model fat tails in computational finance, Cauchy distributions can be used to model VAR (value at risk) producing a much larger probability of extreme risk than Gaussian Distribution.[36]
See also
[edit]- Lévy flight and Lévy process
- Laplace distribution, the Fourier transform of the Cauchy distribution
- Cauchy process
- Stable process
- Slash distribution
References
[edit]- ^ a b c N. L. Johnson; S. Kotz; N. Balakrishnan (1994). Continuous Univariate Distributions, Volume 1. New York: Wiley., Chapter 16.
- ^ Cauchy and the Witch of Agnesi in Statistics on the Table, S M Stigler Harvard 1999 Chapter 18
- ^ Feller, William (1971). An Introduction to Probability Theory and Its Applications, Volume II (2 ed.). New York: John Wiley & Sons Inc. pp. 704. ISBN 978-0-471-25709-7.
- ^ "Lorentzian Function". MathWorld. Wolfram Research. Retrieved 27 October 2024.
- ^ Riley, Ken F.; Hobson, Michael P.; Bence, Stephen J. (2006). Mathematical Methods for Physics and Engineering (3 ed.). Cambridge, UK: Cambridge University Press. pp. 1333. ISBN 978-0-511-16842-0.
- ^ Balakrishnan, N.; Nevrozov, V. B. (2003). A Primer on Statistical Distributions (1 ed.). Hoboken, New Jersey: John Wiley & Sons Inc. pp. 305. ISBN 0-471-42798-5.
- ^ Li, Rui; Nadarajah, Saralees (2020-03-01). "A review of Student's t distribution and its generalizations". Empirical Economics. 58 (3): 1461–1490. doi:10.1007/s00181-018-1570-0. ISSN 1435-8921.
- ^ Pillai N.; Meng, X.L. (2016). "An unexpected encounter with Cauchy and Lévy". The Annals of Statistics. 44 (5): 2089–2097. arXiv:1505.01957. doi:10.1214/15-AOS1407. S2CID 31582370.
- ^ Campbell B. Read; N. Balakrishnan; Brani Vidakovic; Samuel Kotz (2006). Encyclopedia of Statistical Sciences (2nd ed.). John Wiley & Sons. p. 778. ISBN 978-0-471-15044-2.
- ^ Knight, Franck B. (1976). "A characterization of the Cauchy type". Proceedings of the American Mathematical Society. 55 (1): 130–135. doi:10.2307/2041858. JSTOR 2041858.
- ^ "Updates to the Cauchy Central Limit". Quantum Calculus. 13 November 2022. Retrieved 21 June 2023.
- ^ Frederic, Chyzak; Nielsen, Frank (2019). "A closed-form formula for the Kullback-Leibler divergence between Cauchy distributions". arXiv:1905.10965 [cs.IT].
- ^ Nielsen, Frank; Okamura, Kazuki (2023). "On f-Divergences Between Cauchy Distributions". IEEE Transactions on Information Theory. 69 (5): 3150–3171. arXiv:2101.12459. doi:10.1109/TIT.2022.3231645. S2CID 231728407.
- ^ Vasicek, Oldrich (1976). "A Test for Normality Based on Sample Entropy". Journal of the Royal Statistical Society, Series B. 38 (1): 54–59. doi:10.1111/j.2517-6161.1976.tb01566.x.
- ^ Park, Sung Y.; Bera, Anil K. (2009). "Maximum entropy autoregressive conditional heteroskedasticity model" (PDF). Journal of Econometrics. 150 (2). Elsevier: 219–230. doi:10.1016/j.jeconom.2008.12.014. Archived from the original (PDF) on 2011-09-30. Retrieved 2011-06-02.
- ^ a b Kyle Siegrist. "Cauchy Distribution". Random. Archived from the original on 9 July 2021. Retrieved 5 July 2021.
- ^ Hampel, Frank (1998), "Is statistics too difficult?" (PDF), Canadian Journal of Statistics, 26 (3): 497–513, doi:10.2307/3315772, hdl:20.500.11850/145503, JSTOR 3315772, S2CID 53117661, archived from the original on 2022-01-25, retrieved 2019-09-25.
- ^ "Illustration of instability of sample means". Archived from the original on 2017-03-24. Retrieved 2014-11-22.
- ^ Cane, Gwenda J. (1974). "Linear Estimation of Parameters of the Cauchy Distribution Based on Sample Quantiles". Journal of the American Statistical Association. 69 (345): 243–245. doi:10.1080/01621459.1974.10480163. JSTOR 2285535.
- ^ Zhang, Jin (2010). "A Highly Efficient L-estimator for the Location Parameter of the Cauchy Distribution". Computational Statistics. 25 (1): 97–105. doi:10.1007/s00180-009-0163-y. S2CID 123586208.
- ^ a b Rothenberg, Thomas J.; Fisher, Franklin, M.; Tilanus, C.B. (1964). "A note on estimation from a Cauchy sample". Journal of the American Statistical Association. 59 (306): 460–463. doi:10.1080/01621459.1964.10482170.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ^ a b c d Bloch, Daniel (1966). "A note on the estimation of the location parameters of the Cauchy distribution". Journal of the American Statistical Association. 61 (316): 852–855. doi:10.1080/01621459.1966.10480912. JSTOR 2282794.
- ^ a b Ferguson, Thomas S. (1978). "Maximum Likelihood Estimates of the Parameters of the Cauchy Distribution for Samples of Size 3 and 4". Journal of the American Statistical Association. 73 (361): 211–213. doi:10.1080/01621459.1978.10480031. JSTOR 2286549.
- ^ Cohen Freue, Gabriella V. (2007). "The Pitman estimator of the Cauchy location parameter" (PDF). Journal of Statistical Planning and Inference. 137 (6): 1901. doi:10.1016/j.jspi.2006.05.002. Archived from the original (PDF) on 2011-08-16.
- ^ Wilcox, Rand (2012). Introduction to Robust Estimation & Hypothesis Testing. Elsevier.
- ^ Barnett, V. D. (1966). "Order Statistics Estimators of the Location of the Cauchy Distribution". Journal of the American Statistical Association. 61 (316): 1205–1218. doi:10.1080/01621459.1966.10482205. JSTOR 2283210.
- ^ a b c Ferguson, Thomas S. (1962). "A Representation of the Symmetric Bivariate Cauchy Distribution". The Annals of Mathematical Statistics. 33 (4): 1256–1266. doi:10.1214/aoms/1177704357. JSTOR 2237984. Retrieved 2017-01-07.
- ^ a b Molenberghs, Geert; Lesaffre, Emmanuel (1997). "Non-linear Integral Equations to Approximate Bivariate Densities with Given Marginals and Dependence Function" (PDF). Statistica Sinica. 7: 713–738. Archived from the original (PDF) on 2009-09-14.
- ^ Lemons, Don S. (2002), "An Introduction to Stochastic Processes in Physics", American Journal of Physics, 71 (2), The Johns Hopkins University Press: 35, Bibcode:2003AmJPh..71..191L, doi:10.1119/1.1526134, ISBN 0-8018-6866-1
- ^ a b McCullagh, P., "Conditional inference and Cauchy models", Biometrika, volume 79 (1992), pages 247–259. PDF Archived 2010-06-10 at the Wayback Machine from McCullagh's homepage.
- ^ Kyprianou, Andreas (2009). Lévy processes and continuous-state branching processes:part I (PDF). p. 11. Archived (PDF) from the original on 2016-03-03. Retrieved 2016-05-04.
- ^ E. Hecht (1987). Optics (2nd ed.). Addison-Wesley. p. 603.
- ^ White, J.S. (December 1958). "The Limiting Distribution of the Serial Correlation Coefficient in the Explosive Case". The Annals of Mathematical Statistics. 29 (4): 1188–1197. doi:10.1214/aoms/1177706450.
- ^ "CumFreq, free software for cumulative frequency analysis and probability distribution fitting". Archived from the original on 2018-02-21.
- ^ Gull, S.F. (1988) Bayesian Inductive Inference and Maximum Entropy. Kluwer Academic Publishers, Berlin. https://doi.org/10.1007/978-94-009-3049-0_4 Archived 2022-01-25 at the Wayback Machine
- ^ Tong Liu (2012), An intermediate distribution between Gaussian and Cauchy distributions. https://arxiv.org/pdf/1208.5109.pdf Archived 2020-06-24 at the Wayback Machine




![{\displaystyle {\frac {1}{\pi \gamma \,\left[1+\left({\frac {x-x_{0}}{\gamma }}\right)^{2}\right]}}\!}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/2fa7448ba911130c1e33621f1859393d3f00af5c)

![{\displaystyle x_{0}+\gamma \,\tan[\pi (p-{\tfrac {1}{2}})]}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/6b28bd2a0c25cb1d212b29f0fc22baf6f84e3e0f)









![{\displaystyle [0,1]}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)





![{\displaystyle f(x;x_{0},\gamma )={\frac {1}{\pi \gamma \left[1+\left({\frac {x-x_{0}}{\gamma }}\right)^{2}\right]}}={1 \over \pi }\left[{\gamma \over (x-x_{0})^{2}+\gamma ^{2}}\right],}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/2026aa2c40888a5189ad754d4bc21731a032575a)









![{\displaystyle f(x;x_{0},\gamma ,I)={\frac {I}{\left[1+\left({\frac {x-x_{0}}{\gamma }}\right)^{2}\right]}}=I\left[{\gamma ^{2} \over (x-x_{0})^{2}+\gamma ^{2}}\right],}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/ef75c5f31667a907f64963eb478d03f33f8374d2)



![{\displaystyle Q(p;x_{0},\gamma )=x_{0}+\gamma \,\tan \left[\pi \left(p-{\tfrac {1}{2}}\right)\right].}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/42c17241be79f1edbb111b82fc9a86ad55c9fd37)















![{\displaystyle \varphi _{X}(t)=\operatorname {E} \left[e^{iXt}\right]=e^{-|t|}.}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/57686177a5992b93dece0dba15fd1f64758dfb0d)












![{\displaystyle \varphi _{X}(t)=\operatorname {E} \left[e^{iXt}\right]=\int _{-\infty }^{\infty }f(x;x_{0},\gamma )e^{ixt}\,dx=e^{ix_{0}t-\gamma |t|}.}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/90a76888a502d3e9959365d896466e4dee540d17)



![{\displaystyle {\begin{aligned}H(\gamma )&=-\int _{-\infty }^{\infty }f(x;x_{0},\gamma )\log(f(x;x_{0},\gamma ))\,dx\\[6pt]&=\log(4\pi \gamma )\end{aligned}}}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/d648f0a9098d95824886093f233fb0681578a4eb)
![{\displaystyle Q'(p;\gamma )=\gamma \,\pi \,{\sec }^{2}\left[\pi \left(p-{\tfrac {1}{2}}\right)\right].\!}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/c98f59acfc3b417126a88a731035e87a4deaa16b)

![{\displaystyle \operatorname {E} [\log(1+(X-x_{0})^{2}/\gamma ^{2})]=\log 4}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/a7f6982d1d9f8690a4cd034887fe55c659e005b0)












![{\displaystyle \operatorname {E} [|X|^{p}]=\gamma ^{p}\mathrm {sec} (\pi p/2).}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/34e2a867bc2b1f3c8c5fe805aa71577f466e948c)
![{\displaystyle {\begin{aligned}\operatorname {E} [X^{2}]&\propto \int _{-\infty }^{\infty }{\frac {x^{2}}{1+x^{2}}}\,dx=\int _{-\infty }^{\infty }1-{\frac {1}{1+x^{2}}}\,dx\\[8pt]&=\int _{-\infty }^{\infty }dx-\int _{-\infty }^{\infty }{\frac {1}{1+x^{2}}}\,dx=\int _{-\infty }^{\infty }dx-\pi =\infty .\end{aligned}}}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/b821427592463519bb2fe3f38a52f61183af76cd)























![{\displaystyle f(x,y;x_{0},y_{0},\gamma )={1 \over 2\pi }\left[{\gamma \over ((x-x_{0})^{2}+(y-y_{0})^{2}+\gamma ^{2})^{3/2}}\right].}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/6d8819f3c50d69b56d61fe3055c18b1b53d37e50)

![{\displaystyle f(z;z_{0},\gamma )={1 \over 2\pi }\left[{\gamma \over (|z-z_{0}|^{2}+\gamma ^{2})^{3/2}}\right].}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/de0257adbd6a9a7b9216baf7a6837e0da6255390)

![{\displaystyle f({\mathbf {x} };{\mathbf {\mu } },{\mathbf {\Sigma } },k)={\frac {\Gamma \left({\frac {1+k}{2}}\right)}{\Gamma ({\frac {1}{2}})\pi ^{\frac {k}{2}}\left|{\mathbf {\Sigma } }\right|^{\frac {1}{2}}\left[1+({\mathbf {x} }-{\mathbf {\mu } })^{T}{\mathbf {\Sigma } }^{-1}({\mathbf {x} }-{\mathbf {\mu } })\right]^{\frac {1+k}{2}}}}.}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/d9e1b5b8a0ffbbba9a4478b2acb4da449c1006d5)






































