Nusselt number: Difference between revisions
Formatted citations and added Winterton 1998 |
Undid revision 1225744662 by Davidem88 (talk) rv old linkspamming |
||
| (21 intermediate revisions by 13 users not shown) | |||
| Line 1: | Line 1: | ||
{{Short description|Ratio of a fluid's rates of convective and conductive heat transfer}} |
|||
{{Use dmy dates|date=April 2020}} |
{{Use dmy dates|date=April 2020}} |
||
| ⚫ | In [[fluid dynamics]], the '''Nusselt number''' ('''Nu''') is the ratio of [[ |
||
| ⚫ | In [[Thermal fluids|thermal fluid dynamics]], the '''Nusselt number''' ({{math|'''Nu'''}}, after [[Wilhelm Nusselt]]{{r|çengel|p=336}}) is the ratio of total [[heat transfer]] to [[heat conduction|conductive]] heat transfer at a [[boundary (thermodynamic)|boundary]] in a [[fluid]]. Total heat transfer combines conduction and [[convection]]. Convection includes both [[advection]] (fluid motion) and [[diffusion]] (conduction). The conductive component is measured under the same conditions as the convective but for a hypothetically motionless fluid. It is a [[dimensionless number]], closely related to the fluid's [[Rayleigh number]].<ref name="çengel">{{cite book |last1=Çengel |first1=Yunus A. |title=Heat and Mass Transfer |url=https://archive.org/details/HeatAndMassTransferByCengel2ndEdition |date=2002 |publisher=McGraw-Hill |edition=2nd}}</ref>{{rp|466}} |
||
| ⚫ | A Nusselt number of |
||
| ⚫ | A Nusselt number of order one represents heat transfer by pure conduction.{{r|çengel|p=336}} A value between one and 10 is characteristic of [[slug flow]] or [[laminar flow]].<ref name=whiting>{{cite web |title=The Nusselt Number |url=http://pages.jh.edu/~virtlab/heat/nusselt/nusselt.htm |website=Whiting School of Engineering |access-date=3 April 2019}}</ref> A larger Nusselt number corresponds to more active convection, with [[turbulent flow]] typically in the 100–1000 range.<ref name=whiting/> |
||
| ⚫ | |||
| ⚫ | |||
==Definition== |
==Definition== |
||
The Nusselt number is the ratio of |
The Nusselt number is the ratio of total heat transfer (convection + conduction) to conductive heat transfer across a boundary. The convection and conduction heat flows are [[Parallel (geometry)|parallel]] to each other and to the surface normal of the boundary surface, and are all [[perpendicular]] to the [[mean]] fluid flow in the simple case. |
||
:<math>\mathrm{Nu}_L = \frac{\mbox{ |
:<math>\mathrm{Nu}_L = \frac{\mbox{Total heat transfer }}{\mbox{Conductive heat transfer }} = \frac{h}{k/L} = \frac{hL}{k}</math> |
||
where ''h'' is the [[convective]] [[heat transfer coefficient]] of the flow, ''L'' is the [[characteristic length]], and ''k'' is the [[thermal conductivity]] of the fluid. |
where ''h'' is the [[convective]] [[heat transfer coefficient]] of the flow, ''L'' is the [[characteristic length]], and ''k'' is the [[thermal conductivity]] of the fluid. |
||
| Line 25: | Line 27: | ||
==Context== |
==Context== |
||
An understanding of convection boundary layers is necessary to |
An understanding of convection boundary layers is necessary to understand convective heat transfer between a surface and a fluid flowing past it. A thermal boundary layer develops if the fluid free stream temperature and the surface temperatures differ. A temperature profile exists due to the energy exchange resulting from this temperature difference. |
||
[[Image:Thermal Boundary Layer.jpg|frame|right|Thermal Boundary Layer]] |
[[Image:Thermal Boundary Layer.jpg|frame|right|Thermal Boundary Layer]] |
||
| Line 86: | Line 88: | ||
[[Wiktionary:empirical|Empirical]] correlations for a wide variety of geometries are available that express the Nusselt number in the aforementioned forms. |
[[Wiktionary:empirical|Empirical]] correlations for a wide variety of geometries are available that express the Nusselt number in the aforementioned forms. |
||
See also [[Heat transfer coefficient#Convective_heat_transfer_correlations]]. |
|||
=== Free convection === |
=== Free convection === |
||
| Line 111: | Line 114: | ||
:<math>\overline{\mathrm{Nu}}_L \ = 0.52\, \mathrm{Ra}_L^{1/5} \, \quad 10^5 \le \mathrm{Ra}_L \le 10^{10}</math> |
:<math>\overline{\mathrm{Nu}}_L \ = 0.52\, \mathrm{Ra}_L^{1/5} \, \quad 10^5 \le \mathrm{Ra}_L \le 10^{10}</math> |
||
====Free convection from enclosure heated from below==== |
|||
Cited<ref name="bejanauth">{{cite book |author-link=Adrian Bejan |last1=Bejan |first1=Adrian|title=Convection Heat Transfer |url=https://www.researchgate.net/profile/Gamal-Abdelaziz-2/post/How_to_calculate_Nusselt_number_if_an_enclosure_is_heated_from_two_sides_horizontally_and_vertically/attachment/5f511b80ed60840001ca5842/AS%3A931720878649344%401599150976439/download/Adrian+Bejan%28auth.%29-Convection+Heat+Transfer%2C+Fourth+Edition+%282013%29.pdf?_tp=eyJjb250ZXh0Ijp7ImZpcnN0UGFnZSI6InB1YmxpY2F0aW9uIiwicGFnZSI6InF1ZXN0aW9uIn19 |url-access=limited |edition=4th |publisher=Wiley |year=2013 |isbn=978-0-470-90037-6 }}</ref> as coming from Bejan: |
|||
:<math>\overline{\mathrm{Nu}}_L \ = 0.069\, \mathrm{Ra}_L^{1/3}Pr^{0.074} \, \quad 3 * 10^5 \le \mathrm{Ra}_L \le 7 * 10^{9}</math> |
|||
This equation <i>"holds when the |
|||
horizontal layer is sufficiently wide so that the effect of the short vertical sides |
|||
is minimal."</i> |
|||
It was empirically determined by Globe and Dropkin in 1959:<ref>{{Cite journal |last1=Globe |first1=Samuel |last2=Dropkin |first2=David |date=1959 |title=Natural-Convection Heat Transfer in Liquids Confined by Two Horizontal Plates and Heated From Below |url=https://asmedigitalcollection.asme.org/heattransfer/article-abstract/81/1/24/397579/Natural-Convection-Heat-Transfer-in-Liquids?redirectedFrom=fulltext |journal=Journal of Heat Transfer |volume=81 |issue=1 |pages=24–28 |doi=10.1115/1.4008124 |via=ASME Digital Collection}}</ref> <i>"Tests were made in cylindrical containers having copper tops and bottoms and insulating walls."</i> The containers used were around 5" in diameter and 2" high. |
|||
===Flat plate in laminar flow=== |
===Flat plate in laminar flow=== |
||
| Line 145: | Line 157: | ||
====Dittus–Boelter equation==== |
====Dittus–Boelter equation==== |
||
The Dittus–Boelter equation (for turbulent flow) as introduced by W.H. McAdams<ref>{{cite journal |last1=Winterton |first1=R.H.S. |title=Where did the Dittus and Boelter equation come from? |journal=International Journal of Heat and Mass Transfer |date=February 1998 |volume=41 |issue= |
The Dittus–Boelter equation (for turbulent flow) as introduced by W.H. McAdams<ref>{{cite journal |last1=Winterton |first1=R.H.S. |title=Where did the Dittus and Boelter equation come from? |journal=International Journal of Heat and Mass Transfer |date=February 1998 |volume=41 |issue=4–5 |pages=809–810 |doi=10.1016/S0017-9310(97)00177-4 |publisher=Elsevier|bibcode=1998IJHMT..41..809W |url=http://herve.lemonnier.sci.free.fr/TPF/NE/Winterton.pdf}}</ref> is an [[explicit function]] for calculating the Nusselt number. It is easy to solve but is less accurate when there is a large temperature difference across the fluid. It is tailored to smooth tubes, so use for rough tubes (most commercial applications) is cautioned. The Dittus–Boelter equation is: |
||
:<math>\mathrm{Nu}_D = 0.023\, \mathrm{Re}_D^{4/5}\, \mathrm{Pr}^{n}</math> |
:<math>\mathrm{Nu}_D = 0.023\, \mathrm{Re}_D^{4/5}\, \mathrm{Pr}^{n}</math> |
||
Latest revision as of 21:01, 19 November 2024
In thermal fluid dynamics, the Nusselt number (Nu, after Wilhelm Nusselt[1]: 336 ) is the ratio of total heat transfer to conductive heat transfer at a boundary in a fluid. Total heat transfer combines conduction and convection. Convection includes both advection (fluid motion) and diffusion (conduction). The conductive component is measured under the same conditions as the convective but for a hypothetically motionless fluid. It is a dimensionless number, closely related to the fluid's Rayleigh number.[1]: 466
A Nusselt number of order one represents heat transfer by pure conduction.[1]: 336 A value between one and 10 is characteristic of slug flow or laminar flow.[2] A larger Nusselt number corresponds to more active convection, with turbulent flow typically in the 100–1000 range.[2]
A similar non-dimensional property is the Biot number, which concerns thermal conductivity for a solid body rather than a fluid. The mass transfer analogue of the Nusselt number is the Sherwood number.
Definition
[edit]The Nusselt number is the ratio of total heat transfer (convection + conduction) to conductive heat transfer across a boundary. The convection and conduction heat flows are parallel to each other and to the surface normal of the boundary surface, and are all perpendicular to the mean fluid flow in the simple case.
where h is the convective heat transfer coefficient of the flow, L is the characteristic length, and k is the thermal conductivity of the fluid.
- Selection of the characteristic length should be in the direction of growth (or thickness) of the boundary layer; some examples of characteristic length are: the outer diameter of a cylinder in (external) cross flow (perpendicular to the cylinder axis), the length of a vertical plate undergoing natural convection, or the diameter of a sphere. For complex shapes, the length may be defined as the volume of the fluid body divided by the surface area.
- The thermal conductivity of the fluid is typically (but not always) evaluated at the film temperature, which for engineering purposes may be calculated as the mean-average of the bulk fluid temperature and wall surface temperature.
In contrast to the definition given above, known as average Nusselt number, the local Nusselt number is defined by taking the length to be the distance from the surface boundary[1][page needed] to the local point of interest.
The mean, or average, number is obtained by integrating the expression over the range of interest, such as:[3]
Context
[edit]An understanding of convection boundary layers is necessary to understand convective heat transfer between a surface and a fluid flowing past it. A thermal boundary layer develops if the fluid free stream temperature and the surface temperatures differ. A temperature profile exists due to the energy exchange resulting from this temperature difference.
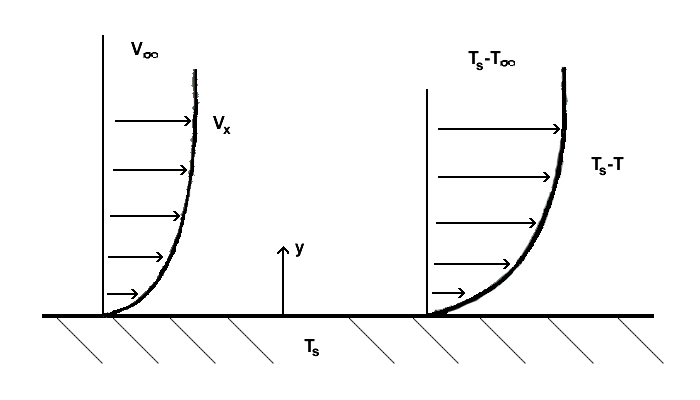
The heat transfer rate can be written using Newton's law of cooling as
- ,
where h is the heat transfer coefficient and A is the heat transfer surface area. Because heat transfer at the surface is by conduction, the same quantity can be expressed in terms of the thermal conductivity k:
- .
These two terms are equal; thus
- .
Rearranging,
- .
Multiplying by a representative length L gives a dimensionless expression:
- .
The right-hand side is now the ratio of the temperature gradient at the surface to the reference temperature gradient, while the left-hand side is similar to the Biot modulus. This becomes the ratio of conductive thermal resistance to the convective thermal resistance of the fluid, otherwise known as the Nusselt number, Nu.
- .
Derivation
[edit]The Nusselt number may be obtained by a non-dimensional analysis of Fourier's law since it is equal to the dimensionless temperature gradient at the surface:
- , where q is the heat transfer rate, k is the constant thermal conductivity and T the fluid temperature.
Indeed, if: and
we arrive at
then we define
so the equation becomes
By integrating over the surface of the body:
,
where .
Empirical correlations
[edit]Typically, for free convection, the average Nusselt number is expressed as a function of the Rayleigh number and the Prandtl number, written as:
Otherwise, for forced convection, the Nusselt number is generally a function of the Reynolds number and the Prandtl number, or
Empirical correlations for a wide variety of geometries are available that express the Nusselt number in the aforementioned forms. See also Heat transfer coefficient#Convective_heat_transfer_correlations.
Free convection
[edit]Free convection at a vertical wall
[edit]Cited[4]: 493 as coming from Churchill and Chu:
Free convection from horizontal plates
[edit]If the characteristic length is defined
where is the surface area of the plate and is its perimeter.
Then for the top surface of a hot object in a colder environment or bottom surface of a cold object in a hotter environment[4]: 493
And for the bottom surface of a hot object in a colder environment or top surface of a cold object in a hotter environment[4]: 493
Free convection from enclosure heated from below
[edit]Cited[5] as coming from Bejan:
This equation "holds when the horizontal layer is sufficiently wide so that the effect of the short vertical sides is minimal."
It was empirically determined by Globe and Dropkin in 1959:[6] "Tests were made in cylindrical containers having copper tops and bottoms and insulating walls." The containers used were around 5" in diameter and 2" high.
Flat plate in laminar flow
[edit]The local Nusselt number for laminar flow over a flat plate, at a distance downstream from the edge of the plate, is given by[4]: 490
The average Nusselt number for laminar flow over a flat plate, from the edge of the plate to a downstream distance , is given by[4]: 490
Sphere in convective flow
[edit]In some applications, such as the evaporation of spherical liquid droplets in air, the following correlation is used:[7]
Forced convection in turbulent pipe flow
[edit]Gnielinski correlation
[edit]Gnielinski's correlation for turbulent flow in tubes:[4]: 490, 515 [8]
where f is the Darcy friction factor that can either be obtained from the Moody chart or for smooth tubes from correlation developed by Petukhov:[4]: 490
The Gnielinski Correlation is valid for:[4]: 490
Dittus–Boelter equation
[edit]The Dittus–Boelter equation (for turbulent flow) as introduced by W.H. McAdams[9] is an explicit function for calculating the Nusselt number. It is easy to solve but is less accurate when there is a large temperature difference across the fluid. It is tailored to smooth tubes, so use for rough tubes (most commercial applications) is cautioned. The Dittus–Boelter equation is:
where:
- is the inside diameter of the circular duct
- is the Prandtl number
- for the fluid being heated, and for the fluid being cooled.[4]: 493
The Dittus–Boelter equation is valid for[4]: 514
The Dittus–Boelter equation is a good approximation where temperature differences between bulk fluid and heat transfer surface are minimal, avoiding equation complexity and iterative solving. Taking water with a bulk fluid average temperature of 20 °C (68 °F), viscosity 10.07×10−4 Pa.s and a heat transfer surface temperature of 40 °C (104 °F) (viscosity 6.96×10−4 Pa.s, a viscosity correction factor for can be obtained as 1.45. This increases to 3.57 with a heat transfer surface temperature of 100 °C (212 °F) (viscosity 2.82×10−4 Pa.s), making a significant difference to the Nusselt number and the heat transfer coefficient.
Sieder–Tate correlation
[edit]The Sieder–Tate correlation for turbulent flow is an implicit function, as it analyzes the system as a nonlinear boundary value problem. The Sieder–Tate result can be more accurate as it takes into account the change in viscosity ( and ) due to temperature change between the bulk fluid average temperature and the heat transfer surface temperature, respectively. The Sieder–Tate correlation is normally solved by an iterative process, as the viscosity factor will change as the Nusselt number changes.[10]
- [4]: 493
where:
- is the fluid viscosity at the bulk fluid temperature
- is the fluid viscosity at the heat-transfer boundary surface temperature
The Sieder–Tate correlation is valid for[4]: 493
Forced convection in fully developed laminar pipe flow
[edit]For fully developed internal laminar flow, the Nusselt numbers tend towards a constant value for long pipes.
For internal flow:
where:
- Dh = Hydraulic diameter
- kf = thermal conductivity of the fluid
- h = convective heat transfer coefficient
Convection with uniform temperature for circular tubes
[edit]From Incropera & DeWitt,[4]: 486–487
OEIS sequence A282581 gives this value as .
Convection with uniform heat flux for circular tubes
[edit]For the case of constant surface heat flux,[4]: 486–487
See also
[edit]- Sherwood number (mass transfer Nusselt number)
- Churchill–Bernstein equation
- Biot number
- Reynolds number
- Convective heat transfer
- Heat transfer coefficient
- Thermal conductivity
References
[edit]- ^ a b c d Çengel, Yunus A. (2002). Heat and Mass Transfer (2nd ed.). McGraw-Hill.
- ^ a b "The Nusselt Number". Whiting School of Engineering. Retrieved 3 April 2019.
- ^ E. Sanvicente; et al. (2012). "Transitional natural convection flow and heat transfer in an open channel". International Journal of Thermal Sciences. 63: 87–104. doi:10.1016/j.ijthermalsci.2012.07.004.
- ^ a b c d e f g h i j k l m n Incropera, Frank P.; DeWitt, David P. (2007). Fundamentals of Heat and Mass Transfer (6th ed.). Hoboken: Wiley. ISBN 978-0-471-45728-2.
- ^ Bejan, Adrian (2013). Convection Heat Transfer (PDF) (4th ed.). Wiley. ISBN 978-0-470-90037-6.
- ^ Globe, Samuel; Dropkin, David (1959). "Natural-Convection Heat Transfer in Liquids Confined by Two Horizontal Plates and Heated From Below". Journal of Heat Transfer. 81 (1): 24–28. doi:10.1115/1.4008124 – via ASME Digital Collection.
- ^ McAllister, Sara; Chen, Jyh-Yuan; Fernández Pello, Carlos (2011). "Droplet Vaporization in Convective Flow". Fundamentals of combustion processes. Mechanical Engineering. New York: Springer. p. 159. doi:10.1007/978-1-4419-7943-8. ISBN 978-1-4419-7942-1. LCCN 2011925371.
- ^ Gnielinski, Volker (1975). "Neue Gleichungen für den Wärme- und den Stoffübergang in turbulent durchströmten Rohren und Kanälen". Forsch. Ing.-Wes. 41 (1): 8–16. doi:10.1007/BF02559682. S2CID 124105274.
- ^ Winterton, R.H.S. (February 1998). "Where did the Dittus and Boelter equation come from?" (PDF). International Journal of Heat and Mass Transfer. 41 (4–5). Elsevier: 809–810. Bibcode:1998IJHMT..41..809W. doi:10.1016/S0017-9310(97)00177-4.
- ^ "Temperature Profile in Steam Generator Tube Metal" (PDF). Archived from the original (PDF) on 3 March 2016. Retrieved 23 September 2009.
External links
[edit]- Simple derivation of the Nusselt number from Newton's law of cooling (Accessed 23 September 2009)




















![{\displaystyle {\overline {\mathrm {Nu} }}_{L}\ =0.68+{\frac {0.663\,\mathrm {Ra} _{L}^{1/4}}{\left[1+(0.492/\mathrm {Pr} )^{9/16}\,\right]^{4/9}\,}}\quad \mathrm {Ra} _{L}\leq 10^{8}}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/899edee66f93581df2ff942e4ada9d3bc4b7b452)
































