Longest common substring: Difference between revisions
FlaxenHobbit (talk | contribs) Hyphenated adjectival phrase in hatnote per MOS:HYPHEN and MOS:REDIRECT. Tags: Mobile edit Mobile web edit Advanced mobile edit |
m →Algorithms: remove a redundant link to the "Dynamic programming" programming article (in two sentences close to each other) |
||
| (25 intermediate revisions by 14 users not shown) | |||
| Line 1: | Line 1: | ||
{{Short description|Computer science problem}} |
|||
{{Wikibooks |Algorithm Implementation/Strings/Longest common substring}} |
{{Wikibooks |Algorithm Implementation/Strings/Longest common substring}} |
||
{{Distinguish|longest |
{{Distinguish|longest common subsequence}} |
||
In [[computer science]], |
In [[computer science]], a '''longest common substring''' of two or more strings is a longest [[string (computer science)|string]] that is a [[substring]] of all of them. There may be more than one longest common substring. Applications include [[data deduplication]] and [[plagiarism detection]]. |
||
Applications include [[data deduplication]] and [[plagiarism detection]]. |
|||
==Examples== |
==Examples== |
||
[[File:LongestSubstring svg.svg|thumb|The strings "BADANAT" and "CANADAS" share the maximal-length substrings "ADA" and "ANA".]] |
[[File:LongestSubstring svg.svg|thumb|The strings "BADANAT" and "CANADAS" share the maximal-length substrings "ADA" and "ANA".]] |
||
The picture shows two strings where the problem has multiple solutions. Although the substring occurrences always overlap, |
The picture shows two strings where the problem has multiple solutions. Although the substring occurrences always overlap, it is impossible to obtain a longer common substring by "uniting" them. |
||
The strings "ABABC", "BABCA" |
The strings "ABABC", "BABCA" and "ABCBA" have only one longest common substring, viz. "ABC" of length 3. Other common substrings are "A", "AB", "B", "BA", "BC" and "C". |
||
ABABC |
ABABC |
||
| Line 19: | Line 19: | ||
Given two strings, <math>S</math> of length <math>m</math> and <math>T</math> of length <math>n</math>, find a longest string which is substring of both <math>S</math> and <math>T</math>. |
Given two strings, <math>S</math> of length <math>m</math> and <math>T</math> of length <math>n</math>, find a longest string which is substring of both <math>S</math> and <math>T</math>. |
||
A generalization is the |
A generalization is the ''k''-'''common substring problem'''. Given the set of strings <math>S = \{S_1, \ldots, S_K\}</math>, where <math>|S_i|=n_i</math> and <math display=inline>\sum n_i = N</math>. Find for each <math>2 \leq k \leq K</math>, a longest string which occurs as substring of at least <math>k</math> strings. |
||
==Algorithms== |
==Algorithms== |
||
One can find the lengths and starting positions of the longest common substrings of <math>S</math> and <math>T</math> in [[Big O notation#Family of Bachmann–Landau notations|<math>\Theta</math>]]<math>(n+m)</math> time with the help of a [[generalized suffix tree]]. A faster algorithm can be achieved in the [[word RAM]] model of computation if the size <math>\sigma</math> of the input alphabet is in <math>2^{o(\sqrt{\log(n+m)})}</math>. In particular, this algorithm runs in <math>O((n+m)\log\sigma/\sqrt{\log (n+m)})</math> time using <math>O((n+m)\log\sigma/\log (n+m))</math> space.<ref name="CKPR21">{{cite conference | last1 = Charalampopoulos | first1 = Panagiotis | last2 = Kociumaka | first2 = Tomasz | last3 = Pissis | first3 = Solon P. | last4 = Radoszewski | first4 = Jakub | date = Aug 2021 | title = Faster Algorithms for Longest Common Substring | conference = European Symposium on Algorithms | editor1-last=Mutzel|editor1-first=Petra|editor2-last=Pagh|editor2-first=Rasmus|editor3-last=Herman|editor3-first=Grzegorz | publisher=Schloss Dagstuhl | series=Leibniz International Proceedings in Informatics (LIPIcs) | volume=204 | doi = 10.4230/LIPIcs.ESA.2021.30 }} Here: Theorem 1, p.30:2.</ref> Solving the problem by [[dynamic programming]] costs <math>\Theta(nm)</math>. The solutions to the generalized problem take <math>\Theta(n_1 + |
One can find the lengths and starting positions of the longest common substrings of <math>S</math> and <math>T</math> in [[Big O notation#Family of Bachmann–Landau notations|<math>\Theta</math>]]<math>(n+m)</math> time with the help of a [[generalized suffix tree]]. A faster algorithm can be achieved in the [[word RAM]] model of computation if the size <math>\sigma</math> of the input alphabet is in <math>2^{o \left( \sqrt{\log(n+m)} \right) }</math>. In particular, this algorithm runs in <math display=inline>O\left( (n+m) \log \sigma/\sqrt{\log (n+m)} \right) </math> time using <math>O\left((n+m)\log\sigma/\log (n+m) \right)</math> space.<ref name="CKPR21">{{cite conference | last1 = Charalampopoulos | first1 = Panagiotis | last2 = Kociumaka | first2 = Tomasz | last3 = Pissis | first3 = Solon P. | last4 = Radoszewski | first4 = Jakub | date = Aug 2021 | title = Faster Algorithms for Longest Common Substring | conference = European Symposium on Algorithms | editor1-last=Mutzel|editor1-first=Petra|editor2-last=Pagh|editor2-first=Rasmus|editor3-last=Herman|editor3-first=Grzegorz | publisher=Schloss Dagstuhl | series=Leibniz International Proceedings in Informatics (LIPIcs) | volume=204 | doi = 10.4230/LIPIcs.ESA.2021.30 | doi-access = free }} Here: Theorem 1, p.30:2.</ref> Solving the problem by [[dynamic programming]] costs <math>\Theta(nm)</math>. The solutions to the generalized problem take <math>\Theta(n_1 + \cdots + n_K)</math> space and <math>\Theta(n_1 \cdots n_K)</math> time with dynamic programming and take <math>\Theta(n_1 + \cdots + n_K)</math> time with a [[generalized suffix tree]]. |
||
===Suffix tree=== |
===Suffix tree=== |
||
| Line 33: | Line 33: | ||
The following pseudocode finds the set of longest common substrings between two strings with dynamic programming: |
The following pseudocode finds the set of longest common substrings between two strings with dynamic programming: |
||
'''function''' |
'''function''' LongestCommonSubstring(S[1..r], T[1..n]) |
||
L := '''array'''(1..r, 1..n) |
L := '''array'''(1..r, 1..n) |
||
z := 0 |
z := 0 |
||
| Line 54: | Line 54: | ||
'''return''' ret |
'''return''' ret |
||
This algorithm runs in <math>O(n r)</math> time. The array <code>L</code> stores the longest common |
This algorithm runs in <math>O(n r)</math> time. The array <code>L</code> stores the length of the longest common suffix of the prefixes <code>S[1..i]</code> and <code>T[1..j]</code> which ''end at position'' <code>i</code> and <code>j</code>, respectively. The variable <code>z</code> is used to hold the length of the longest common substring found so far. The set <code>ret</code> is used to hold the set of strings which are of length <code>z</code>. The set <code>ret</code> can be saved efficiently by just storing the index <code>i</code>, which is the last character of the longest common substring (of size z) instead of <code>S[i-z+1..i]</code>. Thus all the longest common substrings would be, for each i in <code>ret</code>, <code>S[(ret[i]-z)..(ret[i])]</code>. |
||
The following tricks can be used to reduce the memory usage of an implementation: |
The following tricks can be used to reduce the memory usage of an implementation: |
||
* Keep only the last and current row of the DP table to save memory (<math>O(\min(r, n))</math> instead of <math>O(n r)</math>) |
* Keep only the last and current row of the DP table to save memory (<math>O(\min(r, n))</math> instead of <math>O(n r)</math>) |
||
** The last and current row can be stored on the same 1D array by traversing the inner loop backwards |
|||
* Store only non-zero values in the rows. This can be done using hash-tables instead of arrays. This is useful for large alphabets. |
* Store only non-zero values in the rows. This can be done using hash-tables instead of arrays. This is useful for large alphabets. |
||
Latest revision as of 13:30, 22 November 2024
In computer science, a longest common substring of two or more strings is a longest string that is a substring of all of them. There may be more than one longest common substring. Applications include data deduplication and plagiarism detection.
Examples
[edit]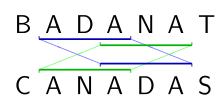
The picture shows two strings where the problem has multiple solutions. Although the substring occurrences always overlap, it is impossible to obtain a longer common substring by "uniting" them.
The strings "ABABC", "BABCA" and "ABCBA" have only one longest common substring, viz. "ABC" of length 3. Other common substrings are "A", "AB", "B", "BA", "BC" and "C".
ABABC
|||
BABCA
|||
ABCBA
Problem definition
[edit]Given two strings, of length and of length , find a longest string which is substring of both and .
A generalization is the k-common substring problem. Given the set of strings , where and . Find for each , a longest string which occurs as substring of at least strings.
Algorithms
[edit]One can find the lengths and starting positions of the longest common substrings of and in time with the help of a generalized suffix tree. A faster algorithm can be achieved in the word RAM model of computation if the size of the input alphabet is in . In particular, this algorithm runs in time using space.[1] Solving the problem by dynamic programming costs . The solutions to the generalized problem take space and time with dynamic programming and take time with a generalized suffix tree.
Suffix tree
[edit]
The longest common substrings of a set of strings can be found by building a generalized suffix tree for the strings, and then finding the deepest internal nodes which have leaf nodes from all the strings in the subtree below it. The figure on the right is the suffix tree for the strings "ABAB", "BABA" and "ABBA", padded with unique string terminators, to become "ABAB$0", "BABA$1" and "ABBA$2". The nodes representing "A", "B", "AB" and "BA" all have descendant leaves from all of the strings, numbered 0, 1 and 2.
Building the suffix tree takes time (if the size of the alphabet is constant). If the tree is traversed from the bottom up with a bit vector telling which strings are seen below each node, the k-common substring problem can be solved in time. If the suffix tree is prepared for constant time lowest common ancestor retrieval, it can be solved in time.[2]
Dynamic programming
[edit]The following pseudocode finds the set of longest common substrings between two strings with dynamic programming:
function LongestCommonSubstring(S[1..r], T[1..n])
L := array(1..r, 1..n)
z := 0
ret := {}
for i := 1..r
for j := 1..n
if S[i] = T[j]
if i = 1 or j = 1
L[i, j] := 1
else
L[i, j] := L[i − 1, j − 1] + 1
if L[i, j] > z
z := L[i, j]
ret := {S[i − z + 1..i]}
else if L[i, j] = z
ret := ret ∪ {S[i − z + 1..i]}
else
L[i, j] := 0
return ret
This algorithm runs in time. The array L stores the length of the longest common suffix of the prefixes S[1..i] and T[1..j] which end at position i and j, respectively. The variable z is used to hold the length of the longest common substring found so far. The set ret is used to hold the set of strings which are of length z. The set ret can be saved efficiently by just storing the index i, which is the last character of the longest common substring (of size z) instead of S[i-z+1..i]. Thus all the longest common substrings would be, for each i in ret, S[(ret[i]-z)..(ret[i])].
The following tricks can be used to reduce the memory usage of an implementation:
- Keep only the last and current row of the DP table to save memory ( instead of )
- The last and current row can be stored on the same 1D array by traversing the inner loop backwards
- Store only non-zero values in the rows. This can be done using hash-tables instead of arrays. This is useful for large alphabets.
See also
[edit]- Longest palindromic substring
- n-gram, all the possible substrings of length n that are contained in a string
References
[edit]- ^ Charalampopoulos, Panagiotis; Kociumaka, Tomasz; Pissis, Solon P.; Radoszewski, Jakub (Aug 2021). Mutzel, Petra; Pagh, Rasmus; Herman, Grzegorz (eds.). Faster Algorithms for Longest Common Substring. European Symposium on Algorithms. Leibniz International Proceedings in Informatics (LIPIcs). Vol. 204. Schloss Dagstuhl. doi:10.4230/LIPIcs.ESA.2021.30. Here: Theorem 1, p.30:2.
- ^ Gusfield, Dan (1999) [1997]. Algorithms on Strings, Trees and Sequences: Computer Science and Computational Biology. USA: Cambridge University Press. ISBN 0-521-58519-8.
External links
[edit]- Dictionary of Algorithms and Data Structures: longest common substring
- Perl/XS implementation of the dynamic programming algorithm
- Perl/XS implementation of the suffix tree algorithm
- Dynamic programming implementations in various languages on wikibooks
- working AS3 implementation of the dynamic programming algorithm
- Suffix Tree based C implementation of Longest common substring for two strings






















