Lurie–Houghton telescope: Difference between revisions
Typo fixed (schimdt->schmidt) Tags: Mobile edit Mobile web edit |
Added short description Tags: Mobile edit Mobile app edit Android app edit App description add |
||
| (8 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
{{Short description|Type of telescope}} |
|||
{{use dmy dates|date=February 2023}} |
|||
[[Image:lh scope front closeup 600x430.jpg|right|thumb|250px|A Lurie–Houghton telescope]] |
[[Image:lh scope front closeup 600x430.jpg|right|thumb|250px|A Lurie–Houghton telescope]] |
||
The '''Houghton telescope''' or '''Lurie–Houghton telescope''' is a [[catadioptric]] [[telescope]]. Houghton's original design |
The '''Houghton telescope''' or '''Lurie–Houghton telescope''' is a [[catadioptric]] [[telescope]]. Houghton's original design uses a two-lens corrector at the front of the telescope and a spherical mirror at the back; it was patented in 1944.<ref name=patent-1944/> Instead of the hard to make intricately shaped compound curve [[Schmidt corrector plate]], or the heavy [[meniscus corrector|Maksutov-type meniscus corrector lens]], the Houghton double-lens corrector is relatively easy to make. |
||
It consists of two lenses: A positive and a negative, set at the front of the telescope which fixes the telescope's aperture. All lens and mirror surfaces are [[spherical mirror|spherical]], which eases construction. These lenses are relatively thin, though not as thin as the [[Schmidt corrector plate|Schmidt corrector]]. Light loss and "ghost" reflections, troublesome in the past, are minimal with modern [[anti-reflective coating]]s. |
|||
Lurie slightly modified Houghton's original design by adding a diagonal mirror to direct the focused light outside the telescope tube in the same way as a [[Newtonian telescope]].<ref>{{cite book |last1=Rutten |first1=Harrie |last2=van Venrooij |first2=Martin |year=1988 |title=Telescope Optics - Evaluation and Design |page=127 |publisher=Willmann-Bell, Inc. |location=Richmond, VA |ISBN=0-943396-18-2}}</ref> |
|||
Lurie's modification of Houghton's original design places a diagonal mirror on the corrector, to direct the focused light outside the telescope tube in the same way as a [[Newtonian telescope]]; doing so allows a shorter focal length and wider field of view.<ref name=Rutten-vanVenrooij-1988/> |
|||
== The corrector == |
== The corrector == |
||
Each surface of the lenses in the corrector{{efn| |
|||
| ⚫ | |||
By definition, a "corrector lens" has total power 1, or a magnification ratio of 1:1. |
|||
}} |
|||
| ⚫ | creates a degree of freedom to correct optical aberrations. There are enough degrees of freedom to correct for [[spherical aberration]], [[Coma (optics)|coma]], and field curvature. It is placed in the path of the incoming light rays, which are parallel, so the residual [[chromatic aberration]] is very nearly zero. The Houghton corrector can be made of the same type of glass (usually [[BK7 glass|BK7]]) which reduces cost. The design tolerances are very relaxed, compared to the similar [[Maksutov telescope]]s. |
||
There are two types of correctors: symmetric and asymmetric. In the symmetric version |
There are two types of correctors: symmetric and asymmetric. In the symmetric version {{nobr| {{mvar|r}}{{sub|1}} {{=}} −{{mvar|r}}{{sub|3}} }} and {{nobr| {{mvar|r}}{{sub|2}} {{=}} −{{mvar|r}}{{sub|4}} }} which allows for [[interferometry]] testing of the surfaces against each other. However, the correction is not quite as good as with the asymmetric corrector, which has four different radii. |
||
The following figure shows the equations necessary to design the symmetric-form of the corrector. |
The following figure shows the equations necessary to design the symmetric-form of the corrector.{{efn| |
||
Note that in these equations {{mvar|D}} is not the diameter of the primary mirror; rather, it is the distance from the mirror to the corrector as a fraction of the focal length of the mirror. |
|||
}} |
|||
[[Image:lh design equations s.gif|center|Houghton doublet corrector design equations – special case symmetric design.]] |
[[Image:lh design equations s.gif|center|Houghton doublet corrector design equations – special case symmetric design.]] |
||
== The mirrors == |
== The mirrors == |
||
Unlike the |
Unlike the paraboloidal mirror used in the Newtonian telescope, the Houghton uses a spheroidal primary mirror. A spheroidal mirror is much easier to make because the entire surface appears to uniformly "black out" when checked with a [[Foucault test]]. In the Houghton and the Lurie–Houghton, the radius of curvature of the primary mirror is slightly less than that of the total system. The diameter of the primary mirror should be larger than the aperture set by the corrector, to reduce [[vignetting]]. |
||
The secondary mirror in the Lurie–Houghton is identical to the secondary mirror in a Newtonian telescope. An advantage of the Lurie–Houghton over the Newtonian is that the secondary mirror can be mounted to one of the corrector lenses, thus eliminating the spider mount. This eliminates star image [[diffraction spike]]s, caused by the vanes of the spider mount. |
The secondary mirror in the Lurie–Houghton is identical to the secondary mirror in a Newtonian telescope. An advantage of the Lurie–Houghton over the Newtonian is that the secondary mirror can be mounted to one of the corrector lenses, thus eliminating the spider mount. This eliminates star image [[diffraction spike]]s, caused by the [[spider vane|vanes of the spider]] mount. |
||
==Notes== |
==Notes== |
||
| Line 21: | Line 30: | ||
==References== |
==References== |
||
{{reflist |
{{reflist|25em |refs= |
||
<ref name=patent-1944> |
|||
{{cite patent |
|||
|country=US |
|||
|number=2350112 |
|||
|inventor=Houghton, James Leonard |
|||
|assign1=[[Eastman Kodak]] Co., Rochester, NY |
|||
|gdate=30 May 1944 |
|||
|fdate=2 March 1942 |
|||
}} |
|||
</ref> |
|||
<ref name=Rutten-vanVenrooij-1988> |
|||
{{cite book |
|||
|last1=Rutten |first1=Harrie |
|||
|last2=van Venrooij |first2=Martin |
|||
|year=1988 |
|||
|title=Telescope Optics – Evaluation and Design |
|||
|page=127 |
|||
|publisher=Willmann-Bell |
|||
|location=Richmond, VA |
|||
|isbn=0-943396-18-2 |
|||
}} |
|||
</ref> |
|||
}} <!-- end "refs=" --> |
|||
==See also== |
==See also== |
||
| Line 28: | Line 63: | ||
==External links== |
==External links== |
||
* |
* {{cite web |title=Image gallery of a Lurie–Houghton telescope amateur construction project |website=Natural Images Gallery |url=http://naturalimagesgallery.com/atm/lh_scope |access-date=2023-02-28}} |
||
{{DEFAULTSORT:Lurie-Houghton telescope}} |
{{DEFAULTSORT:Lurie-Houghton telescope}} |
||
Latest revision as of 13:20, 23 November 2024

The Houghton telescope or Lurie–Houghton telescope is a catadioptric telescope. Houghton's original design uses a two-lens corrector at the front of the telescope and a spherical mirror at the back; it was patented in 1944.[1] Instead of the hard to make intricately shaped compound curve Schmidt corrector plate, or the heavy Maksutov-type meniscus corrector lens, the Houghton double-lens corrector is relatively easy to make.
It consists of two lenses: A positive and a negative, set at the front of the telescope which fixes the telescope's aperture. All lens and mirror surfaces are spherical, which eases construction. These lenses are relatively thin, though not as thin as the Schmidt corrector. Light loss and "ghost" reflections, troublesome in the past, are minimal with modern anti-reflective coatings.
Lurie's modification of Houghton's original design places a diagonal mirror on the corrector, to direct the focused light outside the telescope tube in the same way as a Newtonian telescope; doing so allows a shorter focal length and wider field of view.[2]
The corrector
[edit]Each surface of the lenses in the corrector[a] creates a degree of freedom to correct optical aberrations. There are enough degrees of freedom to correct for spherical aberration, coma, and field curvature. It is placed in the path of the incoming light rays, which are parallel, so the residual chromatic aberration is very nearly zero. The Houghton corrector can be made of the same type of glass (usually BK7) which reduces cost. The design tolerances are very relaxed, compared to the similar Maksutov telescopes.
There are two types of correctors: symmetric and asymmetric. In the symmetric version r1 = −r3 and r2 = −r4 which allows for interferometry testing of the surfaces against each other. However, the correction is not quite as good as with the asymmetric corrector, which has four different radii.
The following figure shows the equations necessary to design the symmetric-form of the corrector.[b]
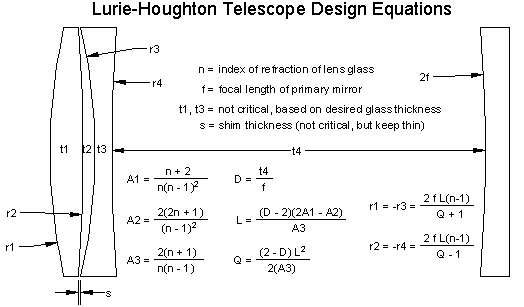
The mirrors
[edit]Unlike the paraboloidal mirror used in the Newtonian telescope, the Houghton uses a spheroidal primary mirror. A spheroidal mirror is much easier to make because the entire surface appears to uniformly "black out" when checked with a Foucault test. In the Houghton and the Lurie–Houghton, the radius of curvature of the primary mirror is slightly less than that of the total system. The diameter of the primary mirror should be larger than the aperture set by the corrector, to reduce vignetting.
The secondary mirror in the Lurie–Houghton is identical to the secondary mirror in a Newtonian telescope. An advantage of the Lurie–Houghton over the Newtonian is that the secondary mirror can be mounted to one of the corrector lenses, thus eliminating the spider mount. This eliminates star image diffraction spikes, caused by the vanes of the spider mount.
Notes
[edit]References
[edit]- ^ US 2350112, Houghton, James Leonard, issued 30 May 1944, assigned to Eastman Kodak Co., Rochester, NY
- ^ Rutten, Harrie; van Venrooij, Martin (1988). Telescope Optics – Evaluation and Design. Richmond, VA: Willmann-Bell. p. 127. ISBN 0-943396-18-2.
See also
[edit]External links
[edit]- "Image gallery of a Lurie–Houghton telescope amateur construction project". Natural Images Gallery. Retrieved 28 February 2023.
