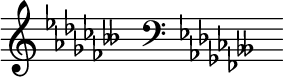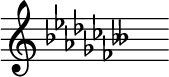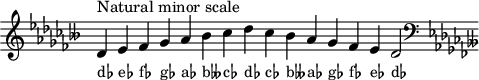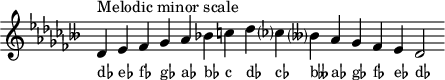Jump to content

D-flat minor: Difference between revisions

From Wikipedia, the free encyclopedia
Browse history interactively
← Previous edit
Content deleted Content added
VisualWikitext
No edit summary
Converted unformatted section links via script.
 
(41 intermediate revisions by 15 users not shown)
Line 1: Line 1:
{{Short description|Minor key based on D-flat}}
{{See also|C-sharp minor}}
{{Infobox musical scale
{{Infobox musical scale
| name=D-flat minor<score>{ \new Staff \with{ \magnifyStaff #3/2 } << \time 2/16 \override Score.TimeSignature #'stencil = ##f { \clef treble \key des \minor s16 \clef bass \key des \minor s16 } >> }</score>
| name=D-flat minor<br><score>{ \magnifyStaff #3/2 \omit Score.TimeSignature \key des \minor s16 \clef F \key des \minor s^"" }</score><br>{{nobold|Alternative notation}}<score>{ \magnifyStaff #3/2 \omit Score.TimeSignature \set Staff.keyAlterations = #`((6 . ,FLAT)(2 . ,FLAT)(5 . ,FLAT)(1 . ,FLAT)(4 . ,FLAT)(0 . ,FLAT)(3 . ,FLAT)(6 . ,DOUBLE-FLAT)) s^"" }</score>
| relative=[[F-flat major]] (theoretical)<br>→enharmonic: [[E major]]
| relative=[[F-flat major]] (theoretical)<br>→[[Enharmonic key|enharmonic]]: [[E major]]
| parallel=[[D-flat major]]
| parallel=[[D-flat major]]
| dominant=[[A-flat minor]]<br>→enharmonic: [[G-sharp minor]] or [[A-flat major]] (only [[harmonic minor]])
| dominant=[[A-flat minor]]
| subdominant=G-flat minor (theoretical)<br>→enharmonic: [[F-sharp minor]]
| subdominant=[[G-flat minor]] (theoretical)<br>→[[Enharmonic key|enharmonic]]: [[F-sharp minor]]
| enharmonic=[[C-sharp minor]]
| enharmonic=[[C-sharp minor]]
| first_pitch=D{{music|flat}}
| first_pitch=D{{music|flat}}
Line 16: Line 16:
}}
}}


'''D-flat minor''' is a [[theoretical key]] based on [[D♭ (musical note)|D{{music|flat}}]], consisting of the pitches D{{music|flat}}, [[E♭ (musical note)|E{{music|flat}}]], [[F♭ (musical note)|F{{music|flat}}]], [[G♭ (musical note)|G{{music|flat}}]], [[A♭ (musical note)|A{{music|flat}}]], [[B-double flat|B{{music|flat}}{{music|flat}}]], and [[C♭ (musical note)|C{{music|flat}}]]. Its [[key signature]] has six [[Flat (music)|flats]] and one [[Double-flat|double flat]]. Its [[Relative key|relative major]] is [[F-flat major]], which is usually replaced by [[E major]]. Its [[Parallel key|parallel major]] is [[D-flat major]], and its direct enharmonic equivalent, [[C-sharp minor]], is normally used.
'''D-flat minor''' is a [[theoretical key]] based on [[D♭ (musical note)|D{{music|flat}}]], consisting of the pitches D{{music|flat}}, [[E♭ (musical note)|E{{music|flat}}]], [[F♭ (musical note)|F{{music|flat}}]], [[G♭ (musical note)|G{{music|flat}}]], [[A♭ (musical note)|A{{music|flat}}]], [[B-double flat|B]]{{music|doubleflat}}, and [[C♭ (musical note)|C{{music|flat}}]]. Its [[key signature]] has eight [[Flat (music)|flats]], requiring one [[double flat]] and six single flats. Its [[Relative key|relative major]] is [[F-flat major]], which is usually replaced by [[E major]]. Its [[Parallel key|parallel major]] is [[D-flat major]]. Its direct [[enharmonic]] equivalent, [[C-sharp minor]], is normally used.


The D-flat [[natural minor scale]] is:
The D-flat [[natural minor scale]] is:


:<score sound="1"> {
:<score sound raw>
\header { tagline = ##f }
\override Score.TimeSignature #'stencil = ##f
\relative c' {
scale = \relative c' { \key des \minor \omit Score.TimeSignature
\clef treble \key des \minor \time 7/4 des4^\markup { Natural minor scale } es fes ges aes beses ces des ces beses aes ges fes es des2
des^"Natural minor scale" es fes ges aes beses ces des ces beses aes ges fes es des2 \clef F \key des \minor }
\score { { << \cadenzaOn \scale \context NoteNames \scale >> } \layout { } \midi { } }
\clef bass \key des \minor
} }
</score>
</score>


Changes needed for the melodic and harmonic versions of the scale are written in with accidentals as necessary. The D-flat [[Harmonic minor scale|harmonic minor]] and [[Melodic minor scale|melodic minor scales]] are:
Changes needed for the melodic and harmonic versions of the scale are written in with accidentals as necessary. The D-flat [[Harmonic minor scale|harmonic minor]] and [[Melodic minor scale|melodic minor scales]] are:


:<score sound="1"> {
:<score sound raw>
\header { tagline = ##f }
\override Score.TimeSignature #'stencil = ##f
\relative c' {
scale = \relative c' { \key des \minor \omit Score.TimeSignature
\clef treble \key des \minor \time 7/4 des4^\markup { Harmonic minor scale } es fes ges aes beses c des c beses aes ges fes es des2
des^"Harmonic minor scale" es fes ges aes beses c des c beses aes ges fes es des2 }
\score { { << \cadenzaOn \scale \context NoteNames \scale >> } \layout { } \midi { } }
} }
</score>
</score>


:<score sound="1"> {
:<score sound raw>\header { tagline = ##f }
scale = \relative c' { \accidentalStyle modern \key des \minor \omit Score.TimeSignature
\override Score.TimeSignature #'stencil = ##f
⚫
des^"Melodic minor scale" es fes ges aes bes c des ces? beses? aes ges fes es des2 }
\relative c' {
\score { { << \cadenzaOn \scale \context NoteNames \scale >> } \layout { } \midi { } }</score>
⚫
\clef treble \key des \minor \time 7/4 des4^\markup { Melodic minor scale } es fes ges aes bes c des ces! beses! aes ges fes es des2

} }
⚫
D-flat minor is usually notated as the enharmonic key of [[C-sharp minor]], as in the second and third measures of [[Amy Beach]]'s ''[[Canticle of the Sun]]''.<ref>{{cite book|title=The Canticle of the Sun|author=Amy Beach|author2=Betty Buchanan|name-list-style=amp|date=2006|publisher=A-R Editions, Inc.|isbn=0-89579-583-3|page=xiii}}</ref> However, unusually, two of [[Giuseppe Verdi|Verdi]]'s most well-known operas, ''[[La traviata]]'' and ''[[Rigoletto]]'', both end in D-flat minor (although written with the five-flat key signature of the parallel major). [[Gustav Mahler|Mahler]]'s thematic motif "der kleine Appell" ("call to order") from his [[Symphony No. 4 (Mahler)|Fourth]] and [[Symphony No. 5 (Mahler)|Fifth Symphonies]] uses both notations: in his Symphony No. 4 (first movement) it is in D-flat minor, but in his Symphony No. 5 it is in C-sharp minor. In the Adagio of his [[Symphony No. 9 (Mahler)|Symphony No. 9]], a solo bassoon interpolation following the main theme appears first in D-flat minor, returning twice more notated in C-sharp minor. Likewise, in the Adagio of [[Anton Bruckner|Bruckner]]'s [[Symphony No. 8 (Bruckner)|Symphony No. 8]], phrases that are tonally in D-flat minor are notated as C-sharp minor.<ref>{{cite book|title=A Theory of Harmony|author=Ernst Levy|date=1985|publisher=SUNY Press|isbn=0-87395-993-0|page=62}}</ref><ref>{{cite book|chapter=Structural Considerations|title=Mahler's Fourth Symphony|author=James L. Zychowicz|date=2005|publisher=Oxford University Press|isbn=0-19-816206-5|page=28}}</ref><ref>{{cite book|title=Musical Semiotics in Growth|editor=Eero Tarasti|editor2=Paul Forsell|editor3=Richard Littlefield|pages=14&ndash;15|chapter=Music history revisited|author=Eero Tarasti|author-link=Eero Tarasti|date=1996|publisher=Indiana University Press|isbn=0-253-32949-3}}</ref><ref>{{cite book|title=Mahler: A Musical Physiognomy|url=https://archive.org/details/mahlermusicalphy0000ador|url-access=registration|author=Theodor W. Adorno|author-link=Theodor W. Adorno|translator=Edmund Jephcott|pages=[https://archive.org/details/mahlermusicalphy0000ador/page/165 165]&ndash;166|date=1992|publisher=University of Chicago Press|isbn=0-226-00769-3}}</ref>
</score>

⚫
D-flat minor is usually notated as the enharmonic key of [[C-sharp minor]], as in the second and third measures of [[Amy Beach]]'s ''[[Canticle of the Sun]]''.<ref>{{cite book|title=The Canticle of the Sun|author=Amy Beach|author2=Betty Buchanan|name-list-style=amp|date=2006|publisher=A-R Editions, Inc.|isbn=0-89579-583-3|page=xiii}}</ref> However, unusually, two of [[Giuseppe Verdi|Verdi]]'s most well-known operas, ''[[La traviata]]'' and ''[[Rigoletto]]'', both end in D-flat minor (although written with the five-flat key signature of the parallel major). [[Gustav Mahler|Mahler]]'s thematic motif "der kleine Appell" ("call to order") from his [[Symphony No. 4 (Mahler)|Fourth]] and [[Symphony No. 5 (Mahler)|Fifth Symphonies]] uses both notations: in his Symphony No. 4 (first movement) it is in D-flat minor, but in his Symphony No. 5 it is in C-sharp minor. In the Adagio of his [[Symphony No. 9 (Mahler)|Symphony No. 9]] a solo bassoon interpolation following the main theme appears first in D-flat minor, returning twice more notated in C-sharp minor. Likewise, in the Adagio of [[Anton Bruckner|Bruckner]]'s [[Symphony No. 8 (Bruckner)|Symphony No. 8]], phrases that are tonally in D-flat minor are notated as C-sharp minor.<ref>{{cite book|title=A Theory of Harmony|author=Ernst Levy|date=1985|publisher=SUNY Press|isbn=0-87395-993-0|page=62}}</ref><ref>{{cite book|chapter=Structural Considerations|title=Mahler's Fourth Symphony|author=James L. Zychowicz|date=2005|publisher=Oxford University Press|isbn=0-19-816206-5|page=28}}</ref><ref>{{cite book|title=Musical Semiotics in Growth|editor=Eero Tarasti|editor2=Paul Forsell|editor3=Richard Littlefield|pages=14&ndash;15|chapter=Music history revisited|author=Eero Tarasti|author-link=Eero Tarasti|date=1996|publisher=Indiana University Press|isbn=0-253-32949-3}}</ref><ref>{{cite book|title=Mahler: A Musical Physiognomy|url=https://archive.org/details/mahlermusicalphy0000ador|url-access=registration|author=Theodor W. Adorno|author-link=Theodor W. Adorno|translator=Edmund Jephcott|pages=[https://archive.org/details/mahlermusicalphy0000ador/page/165 165]&ndash;166|date=1992|publisher=University of Chicago Press|isbn=0-226-00769-3}}</ref>
However, D-flat minor is used on [[Max Reger]]'s ''On the Theory of Modulation'' on pp. 42–45, using the key signature.<ref>{{cite book |author=Max Reger |title=Supplement to the Theory of Modulation |publisher=C. F. Kahnt Nachfolger |year=1904 |location=Leipzig |pages=[https://archive.org/details/supplementtotheo00rege/page/42/mode/2up 42–45] |translator=John Bernhoff}}</ref>

== Scale degree chords ==
The [[scale-degree]] chords of D-flat minor are:
* [[Tonic (music)|Tonic]] – D-flat minor
* [[Supertonic]] – [[Diminished triad|E-flat diminished]]
* [[Mediant]] – [[F-flat major]]
* [[Subdominant]] – [[G-flat minor]]
* [[Dominant (music)|Dominant]] – [[A-flat minor]]
* [[Submediant]] – [[B double flat major|B-double-flat major]]
* [[Subtonic]] – [[C-flat major]]

== See also ==

* [[Key (music)]]
* [[Major and minor]]
* [[Chord (music)]]
* [[Chord notation]]
* {{Section link|Key signature#Double flats and sharps}}


==References==
==References==

Latest revision as of 02:46, 25 November 2024

D-flat minor
{ \magnifyStaff #3/2 \omit Score.TimeSignature \key des \minor s16 \clef F \key des \minor s^"" }

Alternative notation
{ \magnifyStaff #3/2 \omit Score.TimeSignature \set Staff.keyAlterations = #`((6 . ,FLAT)(2 . ,FLAT)(5 . ,FLAT)(1 . ,FLAT)(4 . ,FLAT)(0 . ,FLAT)(3 . ,FLAT)(6 . ,DOUBLE-FLAT)) s^"" }
Relative keyF-flat major (theoretical)
→enharmonic: E major
Parallel keyD-flat major
Dominant keyA-flat minor
SubdominantG-flat minor (theoretical)
→enharmonic: F-sharp minor
EnharmonicC-sharp minor
Component pitches
D♭, E♭, F♭, G♭, A♭, Bdouble flat, C♭

D-flat minor is a theoretical key based on D♭, consisting of the pitches D♭, E♭, F♭, G♭, A♭, Bdouble flat, and C♭. Its key signature has eight flats, requiring one double flat and six single flats. Its relative major is F-flat major, which is usually replaced by E major. Its parallel major is D-flat major. Its direct enharmonic equivalent, C-sharp minor, is normally used.

The D-flat natural minor scale is:

\header { tagline = ##f } scale = \relative c' { \key des \minor \omit Score.TimeSignature des^"Natural minor scale" es fes ges aes beses ces des ces beses aes ges fes es des2 \clef F \key des \minor } \score { { << \cadenzaOn \scale \context NoteNames \scale >> } \layout { } \midi { } }

Changes needed for the melodic and harmonic versions of the scale are written in with accidentals as necessary. The D-flat harmonic minor and melodic minor scales are:

\header { tagline = ##f } scale = \relative c' { \key des \minor \omit Score.TimeSignature des^"Harmonic minor scale" es fes ges aes beses c des c beses aes ges fes es des2 } \score { { << \cadenzaOn \scale \context NoteNames \scale >> } \layout { } \midi { } }
\header { tagline = ##f } scale = \relative c' { \accidentalStyle modern \key des \minor \omit Score.TimeSignature des^"Melodic minor scale" es fes ges aes bes c des ces? beses? aes ges fes es des2 } \score { { << \cadenzaOn \scale \context NoteNames \scale >> } \layout { } \midi { } }

D-flat minor is usually notated as the enharmonic key of C-sharp minor, as in the second and third measures of Amy Beach's Canticle of the Sun.[1] However, unusually, two of Verdi's most well-known operas, La traviata and Rigoletto, both end in D-flat minor (although written with the five-flat key signature of the parallel major). Mahler's thematic motif "der kleine Appell" ("call to order") from his Fourth and Fifth Symphonies uses both notations: in his Symphony No. 4 (first movement) it is in D-flat minor, but in his Symphony No. 5 it is in C-sharp minor. In the Adagio of his Symphony No. 9, a solo bassoon interpolation following the main theme appears first in D-flat minor, returning twice more notated in C-sharp minor. Likewise, in the Adagio of Bruckner's Symphony No. 8, phrases that are tonally in D-flat minor are notated as C-sharp minor.[2][3][4][5]

However, D-flat minor is used on Max Reger's On the Theory of Modulation on pp. 42–45, using the key signature.[6]

Scale degree chords

[edit]

The scale-degree chords of D-flat minor are:

See also

[edit]

References

[edit]
  1. ^ Amy Beach & Betty Buchanan (2006). The Canticle of the Sun. A-R Editions, Inc. p. xiii. ISBN 0-89579-583-3.
  2. ^ Ernst Levy (1985). A Theory of Harmony. SUNY Press. p. 62. ISBN 0-87395-993-0.
  3. ^ James L. Zychowicz (2005). "Structural Considerations". Mahler's Fourth Symphony. Oxford University Press. p. 28. ISBN 0-19-816206-5.
  4. ^ Eero Tarasti (1996). "Music history revisited". In Eero Tarasti; Paul Forsell; Richard Littlefield (eds.). Musical Semiotics in Growth. Indiana University Press. pp. 14–15. ISBN 0-253-32949-3.
  5. ^ Theodor W. Adorno (1992). Mahler: A Musical Physiognomy. Translated by Edmund Jephcott. University of Chicago Press. pp. 165–166. ISBN 0-226-00769-3.
  6. ^ Max Reger (1904). Supplement to the Theory of Modulation. Translated by John Bernhoff. Leipzig: C. F. Kahnt Nachfolger. pp. 42–45.
Retrieved from "https://en.wikipedia.org/enwiki/w/index.php?title=D-flat_minor&oldid=1259428321"