Liénard–Wiechert potential: Difference between revisions
| (42 intermediate revisions by 22 users not shown) | |||
| Line 1: | Line 1: | ||
{{Short description| |
{{Short description|Electromagnetic effect of point charges}} |
||
{{Electromagnetism|cTopic=Electrodynamics}} |
{{Electromagnetism|cTopic=Electrodynamics}} |
||
The '''Liénard–Wiechert potentials''' describe the classical [[electromagnetism|electromagnetic]] effect of a moving [[electric charge|electric point charge]] in terms of a [[vector potential]] and a [[scalar potential]] in the [[Lorenz gauge]]. Stemming directly from [[Maxwell's equations]], these describe the complete, [[Special relativity|relativistically]] correct, time-varying [[electromagnetic field]] for a [[point charge]] in arbitrary motion, but are not corrected for [[Quantum mechanics|quantum mechanical]] effects. [[Electromagnetic radiation]] in the form of [[wave (physics)|waves]] can be obtained from these potentials. These expressions were developed in part by [[Alfred-Marie Liénard]] in 1898<ref> |
The '''Liénard–Wiechert potentials''' describe the classical [[electromagnetism|electromagnetic]] effect of a moving [[electric charge|electric point charge]] in terms of a [[vector potential]] and a [[scalar potential]] in the [[Lorenz gauge]]. Stemming directly from [[Maxwell's equations]], these describe the complete, [[Special relativity|relativistically]] correct, time-varying [[electromagnetic field]] for a [[point charge]] in arbitrary motion, but are not corrected for [[Quantum mechanics|quantum mechanical]] effects. [[Electromagnetic radiation]] in the form of [[wave (physics)|waves]] can be obtained from these potentials. These expressions were developed in part by [[Alfred-Marie Liénard]] in 1898<ref>{{Cite journal |title=Champ électrique et magnétique produit par une charge concentrée en un point et animée d'un mouvement quelconque|journal=L'Éclairage Électrique|volume=16|issue=27,28,29| pages=5–14,53–59,106–112|year = 1898|last1 = Liénard|first1 = A.|url=http://cnum.cnam.fr/CGI/fpage.cgi?P91.16/0006/80/694/0/0}}</ref> and independently by [[Emil Wiechert]] in 1900.<ref>{{Cite journal | doi=10.1002/andp.19013090403|title = Elektrodynamische Elementargesetze| journal=Annalen der Physik| volume=309| issue=4| pages=667–689|year = 1901|last1 = Wiechert|first1 = E.| bibcode=1901AnP...309..667W|url = https://zenodo.org/record/2502302}}</ref><ref>[http://verplant.org/history-geophysics/Wiechert.htm Some Aspects in Emil Wiechert<!-- Bot generated title -->]</ref> |
||
==Equations== |
==Equations== |
||
| Line 8: | Line 8: | ||
{{see also|retarded potential}} |
{{see also|retarded potential}} |
||
The retarded time is defined, in the context of distributions of charges and currents, as |
|||
| ⚫ | |||
:<math>t_r(\mathbf{r},\mathbf{r_s}, t) = t - \frac{1}{c}|\mathbf{r} - \mathbf{r}_s|,</math> |
|||
where <math> \mathbf{r} </math> is the observation point, and <math>\mathbf{r}_s</math> is the observed point subject to the variations of source charges and currents. |
|||
For a moving point charge <math>q</math> whose given trajectory is <math>\mathbf{r_s}(t)</math>, <math>\mathbf{r_s}</math> |
|||
is no more fixed, but becomes a function of the retarded time itself. In other words, following the trajectory |
|||
of <math>q</math> yields the implicit equation |
|||
:<math>t_r = t - \frac{1}{c}|\mathbf{r} - \mathbf{r}_s(t_r)|,</math> |
|||
which provides the retarded time <math>t_r</math> as a function of the current time (and of the given trajectory): |
|||
:<math>t_r = t_r(\mathbf{r},t)</math>. |
|||
| ⚫ | |||
:<math>\varphi(\mathbf{r}, t) = \frac{1}{4 \pi \epsilon_0} \left(\frac{q}{(1 - \mathbf{n}_s \cdot \boldsymbol{\beta}_s)|\mathbf{r} - \mathbf{r}_s|} \right)_{t_r}</math> |
:<math>\varphi(\mathbf{r}, t) = \frac{1}{4 \pi \epsilon_0} \left(\frac{q}{(1 - \mathbf{n}_s \cdot \boldsymbol{\beta}_s)|\mathbf{r} - \mathbf{r}_s|} \right)_{t_r}</math> |
||
| Line 19: | Line 29: | ||
* <math>\boldsymbol{\beta}_s(t) = \frac{\mathbf{v}_s(t)}{c}</math> is the velocity of the source expressed as a fraction of the speed of light; |
* <math>\boldsymbol{\beta}_s(t) = \frac{\mathbf{v}_s(t)}{c}</math> is the velocity of the source expressed as a fraction of the speed of light; |
||
* <math>{|\mathbf{r} - \mathbf{r}_s|}</math> is the distance from the source; |
* <math>{|\mathbf{r} - \mathbf{r}_s|}</math> is the distance from the source; |
||
* <math>\mathbf{n}_s = \frac{\mathbf{r} - \mathbf{r}_s}{|\mathbf{r} - \mathbf{r}_s|}</math> is the unit vector pointing in the direction from the source and, |
* <math>\mathbf{n}_s = \frac{\mathbf{r} - \mathbf{r}_s}{|\mathbf{r} - \mathbf{r}_s|}</math> is the unit vector pointing in the direction from the source and, |
||
| ⚫ | |||
| ⚫ | This can also be written in a [[Lorentz covariance|covariant way]], where the [[electromagnetic four-potential]] at <math>X^{\mu}=(t,x,y,z)</math> is:<ref>[http://www.damtp.cam.ac.uk/user/tong/em.html David Tong: Lectures on Electromagnetism], Lecture 5: 4.Electromagnetism and Relativity, University of Cambridge</ref> |
||
| ⚫ | |||
| ⚫ | This can also be written in a [[Lorentz covariance|covariant way]], where the [[electromagnetic four-potential]] at <math>X^{\mu}=(t,x,y,z) |
||
:<math>A^{\mu}(X)= -\frac{\mu_0 q c}{4 \pi} \left(\frac{U^{\mu}}{R_{\nu}U^{\nu}} \right)_{t_r} </math> |
:<math>A^{\mu}(X)= -\frac{\mu_0 q c}{4 \pi} \left(\frac{U^{\mu}}{R_{\nu}U^{\nu}} \right)_{t_r} </math> |
||
where <math>R^{\mu}=X^{\mu}-R_{\rm s}^{\mu}</math> and <math>R_{\rm s}^{\mu}</math> is the position of the source and <math>U^{\mu}=dX^{\mu}/d\tau</math> is its four velocity. |
where <math>R^{\mu}=X^{\mu}-R_{\rm s}^{\mu}</math> and <math>R_{\rm s}^{\mu}</math> is the position of the source and <math>U^{\mu}=dX^{\mu}/d\tau</math> is its four velocity. |
||
===Field computation=== |
===Field computation=== |
||
[[File:Em static field.png|thumb|Electromagnetic field (arbitrary unit) of a positive point charge moving at constant speed. When <math>v=0</math>, the electromagnetic field reduces to electrostatic field (in blue). Due to its insignificance at large distance, this field is ignored in high energy physics when computing electromagnetic radiation power. However, it is used for wakefield modeling. The Coulomb field is also known as pancake field when <math>\beta \approx 1</math>. <ref>{{cite book|first1=R.P.|language=en|last1=Walker|title=CERN Accelerator School: Synchrotron radiation|url=https://cds.cern.ch/record/398429/files/p437.pdf}}</ref> <ref>{{cite book|first1=P.B.|language=en|last1=Wilson|title=INTRODUCTION TO WAKEFIELDS AND WAKE POTENTIALS|url=https://inspirehep.net/files/044458b0b7d1c825e9c7ab8e9acf5c9a}}</ref>]] |
|||
| ⚫ | |||
[[File:Em parallel field.png|thumb|Electromagnetic field (arbitrary unit) of a positive accelerated point charge (far from the source). Acceleration is parallel to velocity. When the particle decelerates, this leads to [[Bremsstrahlung|braking radiations]] which can be strong when particles collide.]] |
|||
| ⚫ | |||
[[File:Em perp field.png|thumb|Electromagnetic field (arbitrary unit) of a positive accelerated point charge (far from the source). Acceleration is perpendicular to velocity. It is the [[synchrotron radiation]].]] |
|||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | <math display="block">\mathbf{E}(\mathbf{r}, t) = \frac{1}{4 \pi \varepsilon_0} \left(\frac{q(\mathbf{n}_s - \boldsymbol{\beta}_s)}{\gamma^2 (1 - \mathbf{n}_s \cdot \boldsymbol{\beta}_s)^3 |\mathbf{r} - \mathbf{r}_s|^2} + \frac{q \mathbf{n}_s \times \big((\mathbf{n}_s - \boldsymbol{\beta}_s) \times \dot{\boldsymbol{\beta}_s}\big)}{c(1 - \mathbf{n}_s \cdot \boldsymbol{\beta}_s)^3 |\mathbf{r} - \mathbf{r}_s|} \right)_{t_r}</math> |
||
and |
and |
||
<math display="block">\mathbf{B}(\mathbf{r}, t) = \frac{\mu_0}{4 \pi} \left(\frac{q c(\boldsymbol{\beta}_s \times \mathbf{n}_s)}{\gamma^2 (1-\mathbf{n}_s \cdot \boldsymbol{\beta}_s)^3 |\mathbf{r} - \mathbf{r}_s|^2} + \frac{q \mathbf{n}_s \times \Big(\mathbf{n}_s \times \big((\mathbf{n}_s - \boldsymbol{\beta}_s) \times \dot{\boldsymbol{\beta}_s}\big) \Big)}{(1 - \mathbf{n}_s \cdot \boldsymbol{\beta}_s)^3 |\mathbf{r} - \mathbf{r}_s|} \right)_{t_r}</math> |
|||
<math display="block">\mathbf{B}(\mathbf{r}, t) = \frac{\mathbf{n}_s(t_r)}{c} \times \mathbf{E}(\mathbf{r}, t)</math> |
|||
where <math display="inline"> \boldsymbol{\beta}_s(t) = \frac{\mathbf{v}_s(t)}{c}</math>, <math display="inline">\mathbf{n}_s(t) = \frac{\mathbf{r} - \mathbf{r}_s(t)}{|\mathbf{r} - \mathbf{r}_s(t)|}</math> and <math display="inline">\gamma(t) = \frac{1}{\sqrt{1 - |\boldsymbol{\beta}_s(t)|^2}}</math> (the [[Lorentz factor]]). |
|||
The first term is link to the static field of the charge when it moves at a constant velocity. |
|||
where <math>\boldsymbol{\beta}_s(t) = \frac{\mathbf{v}_s(t)}{c}</math>, <math>\mathbf{n}_s(t) = \frac{\mathbf{r} - \mathbf{r}_s(t)}{|\mathbf{r} - \mathbf{r}_s(t)|}</math> and <math>\gamma(t) = \frac{1}{\sqrt{1 - |\boldsymbol{\beta}_s(t)|^2}}</math> (the [[Lorentz factor]]). |
|||
Note that the <math>\mathbf{n}_s - \boldsymbol{\beta}_s</math> part of the first term updates the direction of the field toward the instantaneous position of the charge, if it continues to move with constant velocity <math>c\boldsymbol{\beta}_s</math>. This term is connected with the "static" part of the electromagnetic field of the charge. |
|||
The second term, which is connected with [[electromagnetic radiation]] by the moving charge, requires charge acceleration <math>\dot{\boldsymbol{\beta}}_s</math> and if this is zero, the value of this term is zero, and the charge does not radiate (emit electromagnetic radiation). This term requires additionally that a component of the charge acceleration be in a direction transverse to the line which connects the charge <math>q</math> and the observer of the field <math>\mathbf{E}(\mathbf{r}, t)</math>. The direction of the field associated with this radiative term is toward the fully time-retarded position of the charge (i.e. where the charge was when it was accelerated). |
The second term, which is connected with [[electromagnetic radiation]] by the moving charge, requires charge acceleration <math>\dot{\boldsymbol{\beta}}_s</math> and if this is zero, the value of this term is zero, and the charge does not radiate (emit electromagnetic radiation). This term requires additionally that a component of the charge acceleration be in a direction transverse to the line which connects the charge <math>q</math> and the observer of the field <math>\mathbf{E}(\mathbf{r}, t)</math>. The direction of the field associated with this radiative term is toward the fully time-retarded position of the charge (i.e. where the charge was when it was accelerated). |
||
====Static field==== |
|||
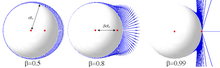
The <math>\mathbf{n}_s - \boldsymbol{\beta}_s</math> part of the first term of the electric field updates the direction of the field toward the instantaneous position of the charge, if it continues to move with constant velocity <math>c \boldsymbol{\beta}_s</math>. This term is connected with the "static" part of the electromagnetic field of the charge. On the illustration, we observe an event that happened in the center of the sphere and that propagated at the speed of light. The problem is that when the speed of the particle is very close to the speed of light, the particle is then almost on the wave front which explains this strong electrostatic field on the front as we are now very close to the particle. Note that outside the propagation sphere, the electric field has its initial state (no connection with the event we observe). When the speed is very close to the speed of light, we consider that the electric field becomes almost flat in the transverse plane, a bit like a "pancake", with an opening angle on <math>1/\gamma</math>. |
|||
[[File:Em static field2.png|thumb|Electrostatic field of a positive charge moving at a constant velocity. See Note.]] |
|||
==Derivation== |
==Derivation== |
||
The <math>\varphi(\mathbf{r}, t)</math> scalar and <math>\mathbf{A}(\mathbf{r}, t)</math> vector potentials satisfy the [[nonhomogeneous electromagnetic wave equation]] where the sources are expressed with the charge and current densities <math>\rho(\mathbf{r}, t)</math> and <math>\mathbf{J}(\mathbf{r}, t)</math> |
The <math>\varphi(\mathbf{r}, t)</math> scalar and <math>\mathbf{A}(\mathbf{r}, t)</math> vector potentials satisfy the [[nonhomogeneous electromagnetic wave equation]] where the sources are expressed with the charge and current densities <math>\rho(\mathbf{r}, t)</math> and <math>\mathbf{J}(\mathbf{r}, t)</math> |
||
<math display="block"> |
|||
\nabla^2 \varphi + {{\partial } \over \partial t} \left ( \nabla \cdot \mathbf{A} \right ) = - {\rho \over \varepsilon_0} \,, </math> |
\nabla^2 \varphi + {{\partial } \over \partial t} \left ( \nabla \cdot \mathbf{A} \right ) = - {\rho \over \varepsilon_0} \,, </math> |
||
and the Ampère-Maxwell law is: |
and the Ampère-Maxwell law is: |
||
| ⚫ | |||
:<math> |
|||
| ⚫ | |||
Since the potentials are not unique, but have [[Gauge theory#Classical gauge theory|gauge]] freedom, these equations can be simplified by [[gauge fixing]]. A common choice is the [[Lorenz gauge condition]]: |
Since the potentials are not unique, but have [[Gauge theory#Classical gauge theory|gauge]] freedom, these equations can be simplified by [[gauge fixing]]. A common choice is the [[Lorenz gauge condition]]: |
||
| ⚫ | |||
| ⚫ | |||
Then the nonhomogeneous wave equations become uncoupled and symmetric in the potentials: |
Then the nonhomogeneous wave equations become uncoupled and symmetric in the potentials: |
||
<math display="block"> |
|||
:<math> |
|||
\nabla^2 \varphi - {1 \over c^2} {\partial^2 \varphi \over \partial t^2} = - {\rho \over \varepsilon_0} \,,</math> |
\nabla^2 \varphi - {1 \over c^2} {\partial^2 \varphi \over \partial t^2} = - {\rho \over \varepsilon_0} \,,</math> |
||
<math display="block"> |
|||
:<math> |
|||
\nabla^2 \mathbf{A} - {1 \over c^2} {\partial^2 \mathbf{A} \over \partial t^2} = - \mu_0 \mathbf{J} \,. </math> |
\nabla^2 \mathbf{A} - {1 \over c^2} {\partial^2 \mathbf{A} \over \partial t^2} = - \mu_0 \mathbf{J} \,. </math> |
||
Generally, the retarded solutions for the scalar and vector potentials (SI units) are |
Generally, the retarded solutions for the scalar and vector potentials (SI units) are |
||
<math display="block"> |
|||
\varphi(\mathbf{r}, t) = \frac{1}{4\pi \ |
\varphi(\mathbf{r}, t) = \frac{1}{4\pi \varepsilon_0}\int \frac{\rho(\mathbf{r}', t_r')}{|\mathbf{r} - \mathbf{r}'|} d^3\mathbf{r}' + \varphi_0(\mathbf{r}, t) |
||
</math> |
</math> |
||
and |
and |
||
<math display="block"> |
|||
:<math> |
|||
\mathbf{A}(\mathbf{r}, t) = \frac{\mu_0}{4\pi} \int \frac{\mathbf{J}(\mathbf{r}', t_r')}{|\mathbf{r} - \mathbf{r}'|} d^3\mathbf{r}' + \mathbf{A}_0(\mathbf{r}, t) |
\mathbf{A}(\mathbf{r}, t) = \frac{\mu_0}{4\pi} \int \frac{\mathbf{J}(\mathbf{r}', t_r')}{|\mathbf{r} - \mathbf{r}'|} d^3\mathbf{r}' + \mathbf{A}_0(\mathbf{r}, t) |
||
</math> |
</math> |
||
where <math>t_r' = t - \frac{1}{c}|\mathbf{r} - \mathbf{r}'|</math> is the retarded time and <math>\varphi_0(\mathbf{r}, t)</math> and <math>\mathbf{A}_0(\mathbf{r}, t)</math> |
where <math display="inline">t_r' = t - \frac{1}{c} |\mathbf{r} - \mathbf{r}'|</math> is the retarded time and <math>\varphi_0(\mathbf{r}, t)</math> and <math>\mathbf{A}_0(\mathbf{r}, t)</math> |
||
satisfy the homogeneous wave equation with no sources and |
satisfy the homogeneous wave equation with no sources and boundary conditions. In the case that there are no boundaries surrounding the sources then |
||
<math>\varphi_0(\mathbf{r}, t)=0</math> and <math>\mathbf{A}_0(\mathbf{r}, t)=0</math>. |
<math>\varphi_0(\mathbf{r}, t) = 0</math> and <math>\mathbf{A}_0(\mathbf{r}, t) = 0</math>. |
||
For a moving point charge whose trajectory is given as a function of time by <math>\mathbf{r}_s(t')</math>, the charge and current densities are as follows: |
For a moving point charge whose trajectory is given as a function of time by <math>\mathbf{r}_s(t')</math>, the charge and current densities are as follows: |
||
<math display="block"> |
|||
\rho(\mathbf{r}', t') = q \delta^3(\mathbf{r'} - \mathbf{r}_s(t')) |
\rho(\mathbf{r}', t') = q \delta^3(\mathbf{r'} - \mathbf{r}_s(t')) |
||
</math> |
</math> |
||
<math display="block"> |
|||
\mathbf{J}(\mathbf{r}', t') = q\mathbf{v}_s(t') \delta^3(\mathbf{r'} - \mathbf{r}_s(t')) |
\mathbf{J}(\mathbf{r}', t') = q\mathbf{v}_s(t') \delta^3(\mathbf{r'} - \mathbf{r}_s(t')) |
||
</math> |
</math> |
||
| Line 99: | Line 107: | ||
Substituting into the expressions for the potential gives |
Substituting into the expressions for the potential gives |
||
<math display="block"> |
|||
\varphi(\mathbf{r}, t) = \frac{1}{4\pi\epsilon_0} \int \frac{q \delta^3(\mathbf{r'} - \mathbf{r}_s(t_r'))}{|\mathbf{r} - \mathbf{r}'|} d^3\mathbf{r}' |
\varphi(\mathbf{r}, t) = \frac{1}{4\pi\epsilon_0} \int \frac{q \delta^3(\mathbf{r'} - \mathbf{r}_s(t_r'))}{|\mathbf{r} - \mathbf{r}'|} d^3\mathbf{r}' |
||
</math> |
</math> |
||
<math display="block"> |
|||
\mathbf{A}(\mathbf{r}, t) = \frac{\mu_0}{4\pi} \int \frac{q\mathbf{v}_s(t_r') \delta^3(\mathbf{r'} - \mathbf{r}_s(t_r'))}{|\mathbf{r} - \mathbf{r}'|} d^3\mathbf{r}' |
\mathbf{A}(\mathbf{r}, t) = \frac{\mu_0}{4\pi} \int \frac{q\mathbf{v}_s(t_r') \delta^3(\mathbf{r'} - \mathbf{r}_s(t_r'))}{|\mathbf{r} - \mathbf{r}'|} d^3\mathbf{r}' |
||
</math> |
</math> |
||
These integrals are difficult to evaluate in their present form, so we will rewrite them by replacing <math>t_r'</math> with <math>t'</math> and integrating over the delta distribution <math>\delta(t' - t_r')</math>: |
These integrals are difficult to evaluate in their present form, so we will rewrite them by replacing <math>t_r'</math> with <math>t'</math> and integrating over the delta distribution <math>\delta(t' - t_r')</math>: |
||
<math display="block"> |
|||
\varphi(\mathbf{r}, t) = \frac{1}{4\pi \epsilon_0} \iint \frac{q\delta^3(\mathbf{r'} - \mathbf{r}_s(t'))}{|\mathbf{r} - \mathbf{r}'|} \delta(t' - t_r') \, dt' \, d^3\mathbf{r}' |
\varphi(\mathbf{r}, t) = \frac{1}{4\pi \epsilon_0} \iint \frac{q\delta^3(\mathbf{r'} - \mathbf{r}_s(t'))}{|\mathbf{r} - \mathbf{r}'|} \delta(t' - t_r') \, dt' \, d^3\mathbf{r}' |
||
</math> |
</math> |
||
<math display="block"> |
|||
\mathbf{A}(\mathbf{r}, t) = \frac{\mu_0}{4\pi} \iint \frac{q\mathbf{v}_s(t') \delta^3(\mathbf{r'} - \mathbf{r}_s(t'))}{|\mathbf{r} - \mathbf{r}'|} \delta(t' - t_r') \, dt' \, d^3\mathbf{r}' |
\mathbf{A}(\mathbf{r}, t) = \frac{\mu_0}{4\pi} \iint \frac{q\mathbf{v}_s(t') \delta^3(\mathbf{r'} - \mathbf{r}_s(t'))}{|\mathbf{r} - \mathbf{r}'|} \delta(t' - t_r') \, dt' \, d^3\mathbf{r}' |
||
</math> |
</math> |
||
We exchange the order of integration: |
We exchange the order of integration: |
||
<math display="block"> |
|||
\varphi(\mathbf{r}, t) = \frac{1}{4\pi \epsilon_0} \iint \frac{\delta(t' - t_r')}{|\mathbf{r} - \mathbf{r}'|} q\delta^3(\mathbf{r'} - \mathbf{r}_s(t')) \, d^3\mathbf{r}' dt' |
\varphi(\mathbf{r}, t) = \frac{1}{4\pi \epsilon_0} \iint \frac{\delta(t' - t_r')}{|\mathbf{r} - \mathbf{r}'|} q\delta^3(\mathbf{r'} - \mathbf{r}_s(t')) \, d^3\mathbf{r}' dt' |
||
</math> |
</math> |
||
<math display="block"> |
|||
\mathbf{A}(\mathbf{r}, t) = \frac{\mu_0}{4\pi} \iint \frac{\delta(t' - t_r')}{|\mathbf{r} - \mathbf{r}'|} q\mathbf{v}_s(t') \delta^3(\mathbf{r'} - \mathbf{r}_s(t')) \, d^3\mathbf{r}' dt' |
\mathbf{A}(\mathbf{r}, t) = \frac{\mu_0}{4\pi} \iint \frac{\delta(t' - t_r')}{|\mathbf{r} - \mathbf{r}'|} q\mathbf{v}_s(t') \delta^3(\mathbf{r'} - \mathbf{r}_s(t')) \, d^3\mathbf{r}' dt' |
||
</math> |
</math> |
||
The delta function picks out <math>\mathbf{r}' = \mathbf{r}_s(t')</math> which allows us to perform the inner integration with ease. Note that <math>t_r'</math> is a function of <math>\mathbf{r}'</math>, so this integration also fixes <math>t_r' = t - \frac{1}{c}|\mathbf{r} - \mathbf{r}_s(t')|</math>. |
The delta function picks out <math>\mathbf{r}' = \mathbf{r}_s(t')</math> which allows us to perform the inner integration with ease. Note that <math>t_r'</math> is a function of <math>\mathbf{r}'</math>, so this integration also fixes <math display="inline">t_r' = t - \frac{1}{c} |\mathbf{r} - \mathbf{r}_s(t')|</math>. |
||
<math display="block"> |
|||
\varphi(\mathbf{r}, t) = \frac{1}{4\pi \epsilon_0} \int q\frac{\delta(t' - t_r')}{|\mathbf{r} - \mathbf{r}_s(t')|} dt' |
\varphi(\mathbf{r}, t) = \frac{1}{4\pi \epsilon_0} \int q\frac{\delta(t' - t_r')}{|\mathbf{r} - \mathbf{r}_s(t')|} dt' |
||
</math> |
</math> |
||
<math display="block"> |
|||
\mathbf{A}(\mathbf{r}, t) = \frac{\mu_0}{4\pi} \int q\mathbf{v}_s(t') \frac{\delta(t' - t_r')}{|\mathbf{r} - \mathbf{r}_s(t')|} \, dt' |
\mathbf{A}(\mathbf{r}, t) = \frac{\mu_0}{4\pi} \int q\mathbf{v}_s(t') \frac{\delta(t' - t_r')}{|\mathbf{r} - \mathbf{r}_s(t')|} \, dt' |
||
</math> |
</math> |
||
The retarded time <math>t_r'</math> is a function of the field point <math>(\mathbf{r}, t)</math> and the source trajectory <math>\mathbf{r}_s(t')</math>, and hence depends on <math>t'</math>. To evaluate this integral, therefore, we need the identity |
The retarded time <math>t_r'</math> is a function of the field point <math>(\mathbf{r}, t)</math> and the source trajectory <math>\mathbf{r}_s(t')</math>, and hence depends on <math>t'</math>. To evaluate this integral, therefore, we need the [[Dirac delta function#Composition with a function|identity]] |
||
| ⚫ | |||
| ⚫ | |||
where each <math>t_i</math> is a zero of <math>f</math>. Because there is only one retarded time <math>t_r</math> for any given space-time coordinates <math>(\mathbf{r}, t)</math> and source trajectory <math>\mathbf{r}_s(t')</math>, this reduces to: |
where each <math>t_i</math> is a zero of <math>f</math>. Because there is only one retarded time <math>t_r</math> for any given space-time coordinates <math>(\mathbf{r}, t)</math> and source trajectory <math>\mathbf{r}_s(t')</math>, this reduces to: |
||
<math display="block">\begin{align}\delta(t' - t_r') |
|||
=& \frac{\delta(t' - t_r)}{\frac{\partial}{\partial t'}(t' - t_r')|_{t' = t_r}} |
|||
= \frac{\delta(t' - t_r)}{\frac{\partial}{\partial t'}(t' - |
= \frac{\delta(t' - t_r)}{\frac{\partial}{\partial t'}(t' - (t - \frac{1}{c} |\mathbf{r} - \mathbf{r}_s(t')|))|_{t' = t_r}} \\ |
||
&= \frac{\delta(t' - t_r)}{1 + \frac{1}{c} (\mathbf{r} - \mathbf{r}_s(t'))/|\mathbf{r} - \mathbf{r}_s(t')|\cdot (-\mathbf{v}_s(t')) |_{t' = t_r}}\\ |
|||
&= \frac{\delta(t' - t_r)}{1 +\frac{1}{c}(\mathbf{r} - \mathbf{r}_s(t'))/|\mathbf{r} - \mathbf{r}_s(t')|\cdot (-\mathbf{v}_s(t')) |_{t' = t_r}}\\ |
|||
&= \frac{\delta(t' - t_r)}{1 - \boldsymbol{\beta}_s \cdot (\mathbf{r}-\mathbf{r}_s)/|\mathbf{r}-\mathbf{r}_s|}\end{align}</math> |
&= \frac{\delta(t' - t_r)}{1 - \boldsymbol{\beta}_s \cdot (\mathbf{r}-\mathbf{r}_s)/|\mathbf{r}-\mathbf{r}_s|}\end{align}</math> |
||
| ⚫ | where <math>\boldsymbol{\beta}_s = \mathbf{v}_s/c</math> and <math>\mathbf{r}_s</math> are evaluated at the retarded time <math>t_r</math>, and we have used the identity <math>|\mathbf{x}|' = \hat{\mathbf{x}} \cdot \mathbf{v}</math> with <math>\mathbf{v} = \mathbf{x}'</math>. Notice that the retarded time <math>t_r</math> is the solution of the equation <math display="inline">t_r = t - \frac{1}{c} |\mathbf{r} - \mathbf{r}_s(t_r)|</math>. Finally, the delta function picks out <math>t' = t_r</math>, and |
||
<math display="block"> |
|||
| ⚫ | where <math>\boldsymbol{\beta}_s = \mathbf{v}_s/c</math> and <math>\mathbf{r}_s</math> are evaluated at the retarded time <math>t_r</math>, and we have used the identity <math>|\mathbf{x}|' = \hat{\mathbf{x}} \cdot \mathbf{v}</math> with <math>\mathbf{v} = \mathbf{x}'</math>. Notice that the retarded time <math>t_r</math> is the solution of the equation <math>t_r = t - \frac{1}{c}|\mathbf{r} - \mathbf{r}_s(t_r)|</math>. Finally, the delta function picks out <math>t' = t_r</math>, and |
||
:<math> |
|||
\varphi(\mathbf{r}, t) = \frac{1}{4\pi \epsilon_0} \left(\frac{q}{|\mathbf{r}-\mathbf{r}_s| (1 - \boldsymbol{\beta}_s \cdot (\mathbf{r}-\mathbf{r}_s)/|\mathbf{r}-\mathbf{r}_s|)}\right)_{t_r} = \frac{1}{4\pi \epsilon_0} \left(\frac{q}{(1-\mathbf{n}_s\cdot \boldsymbol{\beta}_s)|\mathbf{r}-\mathbf{r}_s|}\right)_{t_r} |
\varphi(\mathbf{r}, t) = \frac{1}{4\pi \epsilon_0} \left(\frac{q}{|\mathbf{r}-\mathbf{r}_s| (1 - \boldsymbol{\beta}_s \cdot (\mathbf{r}-\mathbf{r}_s)/|\mathbf{r}-\mathbf{r}_s|)}\right)_{t_r} = \frac{1}{4\pi \epsilon_0} \left(\frac{q}{(1-\mathbf{n}_s\cdot \boldsymbol{\beta}_s)|\mathbf{r}-\mathbf{r}_s|}\right)_{t_r} |
||
</math> |
</math> |
||
<math display="block"> |
|||
\mathbf{A}(\mathbf{r}, t) = \frac{\mu_0}{4\pi} \left(\frac{q\mathbf{v}}{|\mathbf{r}-\mathbf{r}_s| (1 - \boldsymbol{\beta}_s \cdot (\mathbf{r}-\mathbf{r}_s)/|\mathbf{r}-\mathbf{r}_s|)}\right)_{t_r} = \frac{\mu_0 c}{4\pi} \left(\frac{q\boldsymbol{\beta}_s}{(1-\mathbf{n}_s\cdot \boldsymbol{\beta}_s)|\mathbf{r}-\mathbf{r}_s|}\right)_{t_r} |
\mathbf{A}(\mathbf{r}, t) = \frac{\mu_0}{4\pi} \left(\frac{q\mathbf{v}}{|\mathbf{r}-\mathbf{r}_s| (1 - \boldsymbol{\beta}_s \cdot (\mathbf{r}-\mathbf{r}_s)/|\mathbf{r}-\mathbf{r}_s|)}\right)_{t_r} = \frac{\mu_0 c}{4\pi} \left(\frac{q\boldsymbol{\beta}_s}{(1-\mathbf{n}_s\cdot \boldsymbol{\beta}_s)|\mathbf{r}-\mathbf{r}_s|}\right)_{t_r} |
||
</math> |
</math> |
||
which are the Liénard–Wiechert potentials. |
which are the Liénard–Wiechert potentials. |
||
| Line 156: | Line 158: | ||
In order to calculate the derivatives of <math>\varphi</math> and <math>\mathbf{A}</math> it is convenient to first compute the derivatives of the retarded time. Taking the derivatives of both sides of its defining equation (remembering that <math>\mathbf{r_s} = \mathbf{r_s}(t_r)</math>): |
In order to calculate the derivatives of <math>\varphi</math> and <math>\mathbf{A}</math> it is convenient to first compute the derivatives of the retarded time. Taking the derivatives of both sides of its defining equation (remembering that <math>\mathbf{r_s} = \mathbf{r_s}(t_r)</math>): |
||
<math display="block">t_r + \frac{1}{c} |\mathbf{r}-\mathbf{r_s}|= t </math> |
|||
Differentiating with respect to t, |
Differentiating with respect to t, |
||
<math display="block">\frac{d t_r}{d t} + \frac{1}{c}\frac{d t_r}{d t}\frac{d |\mathbf{r}-\mathbf{r_s}|}{d t_r}= 1 </math> |
|||
<math display="block">\frac{d t_r}{d t} \left(1 - \mathbf{n}_s\cdot{\boldsymbol \beta}_s\right) = 1 </math> |
|||
<math display="block">\frac{d t_r}{d t} = \frac{1}{\left(1 - \mathbf{n}_s\cdot{\boldsymbol \beta}_s\right)} </math> |
|||
Similarly, taking the gradient with respect to <math>\mathbf{r}</math> gives |
Similarly, taking the gradient with respect to <math>\mathbf{r}</math> and using the multivariable [[chain rule]] gives |
||
<math display="block">{\boldsymbol \nabla} t_r + \frac{1}{c}{\boldsymbol \nabla} |\mathbf{r}-\mathbf{r_s}| = 0 </math> |
|||
<math display="block">{\boldsymbol \nabla} t_r + \frac{1}{c} \left({\boldsymbol \nabla} t_r \frac{d |\mathbf{r}-\mathbf{r_s}|}{d t_r} + \mathbf{n}_s\right) = 0 </math> |
|||
<math display="block">{\boldsymbol \nabla} t_r \left(1 - \mathbf{n}_s\cdot{\boldsymbol \beta}_s\right) = -\mathbf{n}_s/c </math> |
|||
<math display="block">{\boldsymbol \nabla} t_r = -\frac{\mathbf{n}_s/c}{\left(1 - \mathbf{n}_s\cdot{\boldsymbol \beta}_s\right)} </math> |
|||
It follows that |
It follows that |
||
<math display="block">\frac{d |\mathbf{r}-\mathbf{r_s}|}{d t} = \frac{d t_r}{d t}\frac{d |\mathbf{r}-\mathbf{r_s}|}{d t_r} = \frac{- \mathbf{n}_s\cdot{\boldsymbol \beta}_s c}{\left(1 - \mathbf{n}_s\cdot{\boldsymbol \beta}_s\right)}</math> |
|||
<math display="block">{\boldsymbol \nabla} |\mathbf{r}-\mathbf{r_s}| = {\boldsymbol \nabla} t_r \frac{d |\mathbf{r}-\mathbf{r_s}|}{d t_r} + \mathbf{n}_s = \frac{\mathbf{n}_s}{\left(1 - \mathbf{n}_s\cdot{\boldsymbol \beta}_s\right)}</math> |
|||
These can be used in calculating the derivatives of the vector potential and the resulting expressions are |
These can be used in calculating the derivatives of the vector potential and the resulting expressions are |
||
<math display="block">\begin{align} |
|||
\frac{d \varphi}{d t} =& |
|||
-\frac{q}{4\pi\epsilon_0}\frac{1}{|\mathbf{r}-\mathbf{r_s}|^2\left(1-\mathbf{n}_s\cdot{\boldsymbol \beta}_s\right)^2}\frac{d}{d t}\left[(|\mathbf{r}-\mathbf{r_s}|(1-\mathbf{n}_s\cdot{\boldsymbol \beta}_s)\right]\\ |
-\frac{q}{4\pi\epsilon_0}\frac{1}{|\mathbf{r}-\mathbf{r_s}|^2\left(1-\mathbf{n}_s\cdot{\boldsymbol \beta}_s\right)^2}\frac{d}{d t}\left[(|\mathbf{r}-\mathbf{r_s}|(1-\mathbf{n}_s\cdot{\boldsymbol \beta}_s)\right]\\ |
||
=& -\frac{q}{4\pi\epsilon_0}\frac{1}{|\mathbf{r}-\mathbf{r_s}|^2\left(1-\mathbf{n}_s\cdot{\boldsymbol \beta}_s\right)^2}\frac{d}{d t}\left[|\mathbf{r}-\mathbf{r_s}|-(\mathbf{r}-\mathbf{r_s})\cdot{\boldsymbol \beta}_s\right]\\ |
=& -\frac{q}{4\pi\epsilon_0}\frac{1}{|\mathbf{r}-\mathbf{r_s}|^2\left(1-\mathbf{n}_s\cdot{\boldsymbol \beta}_s\right)^2}\frac{d}{d t}\left[|\mathbf{r}-\mathbf{r_s}|-(\mathbf{r}-\mathbf{r_s})\cdot{\boldsymbol \beta}_s\right]\\ |
||
=& -\frac{q c}{4\pi\epsilon_0}\frac{1}{|\mathbf{r}-\mathbf{r_s}|^2\left(1-\mathbf{n}_s\cdot{\boldsymbol \beta}_s\right)^3}\left[- \mathbf{n}_s\cdot{\boldsymbol \beta}_s + {\beta_s}^2 - (\mathbf{r}-\mathbf{r_s})\cdot \dot {\boldsymbol \beta}_s /c \right]\end{align}</math> |
=& -\frac{q c}{4\pi\epsilon_0}\frac{1}{|\mathbf{r}-\mathbf{r_s}|^2\left(1-\mathbf{n}_s\cdot{\boldsymbol \beta}_s\right)^3}\left[- \mathbf{n}_s\cdot{\boldsymbol \beta}_s + {\beta_s}^2 - (\mathbf{r}-\mathbf{r_s})\cdot \dot {\boldsymbol \beta}_s /c \right]\end{align}</math> |
||
<math display="block">\begin{align}{\boldsymbol \nabla}\cdot\mathbf{A} =& |
|||
-\frac{q}{4\pi\epsilon_0 c}\frac{1}{|\mathbf{r}-\mathbf{r_s}|^2\left(1-\mathbf{n}_s\cdot{\boldsymbol \beta}_s\right)^2}\big({\boldsymbol \nabla} \left[\left(|\mathbf{r}-\mathbf{r_s}|-(\mathbf{r}-\mathbf{r_s})\cdot{\boldsymbol \beta}_s\right)\right]\cdot{\boldsymbol \beta}_s - \left[\left(|\mathbf{r}-\mathbf{r_s}|-(\mathbf{r}-\mathbf{r_s})\cdot{\boldsymbol \beta}_s\right)\right]{\boldsymbol \nabla}\cdot{\boldsymbol \beta}_s\big)\\ |
-\frac{q}{4\pi\epsilon_0 c}\frac{1}{|\mathbf{r}-\mathbf{r_s}|^2\left(1-\mathbf{n}_s\cdot{\boldsymbol \beta}_s\right)^2} \big({\boldsymbol \nabla} \left[\left(|\mathbf{r}-\mathbf{r_s}|-(\mathbf{r}-\mathbf{r_s})\cdot{\boldsymbol \beta}_s\right)\right]\cdot{\boldsymbol \beta}_s - \left[\left(|\mathbf{r}-\mathbf{r_s}|-(\mathbf{r}-\mathbf{r_s})\cdot{\boldsymbol \beta}_s\right)\right]{\boldsymbol \nabla}\cdot{\boldsymbol \beta}_s\big)\\ |
||
=& - \frac{q}{4\pi\epsilon_0 c}\frac{1}{|\mathbf{r}-\mathbf{r_s}|^2\left(1-\mathbf{n}_s\cdot{\boldsymbol \beta}_s\right)^3}\cdot\\ |
=& - \frac{q}{4\pi\epsilon_0 c}\frac{1}{|\mathbf{r}-\mathbf{r_s}|^2\left(1-\mathbf{n}_s\cdot{\boldsymbol \beta}_s\right)^3}\cdot\\ |
||
&\left[(\mathbf{n}_s\cdot {\boldsymbol \beta}_s) - {\beta}_s^2(1-\mathbf{n}_s\cdot {\boldsymbol \beta}_s) - {\beta}_s^2\mathbf{n}_s\cdot {\boldsymbol \beta}_s + \left((\mathbf{r}-\mathbf{r_s})\cdot \dot {\boldsymbol \beta}_s/c\right)(\mathbf{n}_s\cdot {\boldsymbol \beta}_s) + \big(|\mathbf{r}-\mathbf{r_s}|-(\mathbf{r}-\mathbf{r_s})\cdot{\boldsymbol \beta}_s\big)(\mathbf{n}_s\cdot \dot {\boldsymbol \beta}_s/c)\right] |
&\left[(\mathbf{n}_s\cdot {\boldsymbol \beta}_s) - {\beta}_s^2(1-\mathbf{n}_s\cdot {\boldsymbol \beta}_s) - {\beta}_s^2\mathbf{n}_s\cdot {\boldsymbol \beta}_s + \left((\mathbf{r}-\mathbf{r_s})\cdot \dot {\boldsymbol \beta}_s/c\right)(\mathbf{n}_s\cdot {\boldsymbol \beta}_s) + \big(|\mathbf{r}-\mathbf{r_s}|-(\mathbf{r}-\mathbf{r_s})\cdot{\boldsymbol \beta}_s\big)(\mathbf{n}_s\cdot \dot {\boldsymbol \beta}_s/c)\right] |
||
\\=&\frac{q}{4\pi\epsilon_0 c}\frac{1}{|\mathbf{r}-\mathbf{r_s}|^2\left(1-\mathbf{n}_s\cdot{\boldsymbol \beta}_s\right)^3}\left[\beta_s^2 - \mathbf{n}_s\cdot{\boldsymbol \beta}_s - (\mathbf{r}-\mathbf{r_s})\cdot \dot {\boldsymbol \beta}_s/c\right]\end{align}</math> |
\\=&\frac{q}{4\pi\epsilon_0 c}\frac{1}{|\mathbf{r}-\mathbf{r_s}|^2\left(1-\mathbf{n}_s\cdot{\boldsymbol \beta}_s\right)^3}\left[\beta_s^2 - \mathbf{n}_s\cdot{\boldsymbol \beta}_s - (\mathbf{r}-\mathbf{r_s})\cdot \dot {\boldsymbol \beta}_s/c\right]\end{align}</math> |
||
These show that the Lorenz gauge is satisfied, namely that <math>\frac{d \varphi}{d t} + c^2 {\boldsymbol \nabla}\cdot\mathbf{A} = 0 </math>. |
These show that the Lorenz gauge is satisfied, namely that <math display="inline">\frac{d \varphi}{d t} + c^2 {\boldsymbol \nabla}\cdot\mathbf{A} = 0 </math>. |
||
Similarly one calculates: |
Similarly one calculates: |
||
<math display="block">{\boldsymbol \nabla}\varphi = -\frac{q}{4\pi\epsilon_0}\frac{1}{|\mathbf{r}-\mathbf{r_s}|^2\left(1-\mathbf{n}_s\cdot{\boldsymbol \beta}_s\right)^3}\left[\mathbf{n}_s\left(1-{\beta_s}^2 + (\mathbf{r}-\mathbf{r_s})\cdot \dot {\boldsymbol \beta}_s/c\right) - {\boldsymbol \beta}_s(1-\mathbf{n}_s\cdot{\boldsymbol \beta}_s)\right]</math> |
|||
<math display="block">\frac{d\mathbf{A}}{dt} = \frac{q}{4\pi\epsilon_0}\frac{1}{|\mathbf{r}-\mathbf{r_s}|^2\left(1-\mathbf{n}_s\cdot{\boldsymbol \beta}_s\right)^3}\left[{\boldsymbol \beta}_s\left(\mathbf{n}_s\cdot{\boldsymbol \beta}_s-{\beta_s}^2 + (\mathbf{r}-\mathbf{r_s})\cdot \dot {\boldsymbol \beta}_s/c\right) + |\mathbf{r}-\mathbf{r_s}|\dot {\boldsymbol \beta}_s (1-\mathbf{n}_s\cdot{\boldsymbol \beta}_s)/c\right]</math> |
|||
By noting that for any vectors <math>\mathbf{u}</math>, <math>\mathbf{v}</math>, <math>\mathbf{w}</math>: |
By noting that for any vectors <math>\mathbf{u}</math>, <math>\mathbf{v}</math>, <math>\mathbf{w}</math>: |
||
<math display="block">\mathbf{u}\times(\mathbf{v}\times\mathbf{w}) = (\mathbf{u}\cdot\mathbf{w})\mathbf{v}- (\mathbf{u}\cdot \mathbf{v})\mathbf{w}</math> |
|||
The expression for the electric field mentioned above becomes |
The expression for the electric field mentioned above becomes |
||
<math display="block">\begin{align}\mathbf{E}(\mathbf{r}, t) =& \frac{q}{4 \pi \epsilon_0} \frac{1}{|\mathbf{r} - \mathbf{r}_s|^2(1 - \mathbf{n}_s \cdot {\boldsymbol \beta}_s)^3}\cdot \\ |
|||
&\left[\left(\mathbf{n}_s - {\boldsymbol \beta}_s\right)(1-{\beta_s}^2) + |\mathbf{r} - \mathbf{r}_s|(\mathbf{n}_s \cdot \dot{\boldsymbol \beta}_s/c) (\mathbf{n}_s - {\boldsymbol \beta}_s) - |\mathbf{r} - \mathbf{r}_s|\big(\mathbf{n}_s \cdot (\mathbf{n}_s - {\boldsymbol \beta}_s)\big) \dot{\boldsymbol \beta}_s/c \right]\end{align} |
&\left[\left(\mathbf{n}_s - {\boldsymbol \beta}_s\right)(1-{\beta_s}^2) + |\mathbf{r} - \mathbf{r}_s|(\mathbf{n}_s \cdot \dot{\boldsymbol \beta}_s/c) (\mathbf{n}_s - {\boldsymbol \beta}_s) - |\mathbf{r} - \mathbf{r}_s|\big(\mathbf{n}_s \cdot (\mathbf{n}_s - {\boldsymbol \beta}_s)\big) \dot{\boldsymbol \beta}_s/c \right]\end{align} |
||
</math> |
</math> |
||
| Line 210: | Line 213: | ||
Similarly <math>{\boldsymbol \nabla}\times\mathbf{A}</math> gives the expression of the magnetic field mentioned above: |
Similarly <math>{\boldsymbol \nabla}\times\mathbf{A}</math> gives the expression of the magnetic field mentioned above: |
||
<math display="block">\begin{align}{\mathbf{B}} =& {\boldsymbol \nabla}\times\mathbf{A} \\[1ex] |
|||
=& |
|||
-\frac{q}{4\pi\epsilon_0 c}\frac{1}{|\mathbf{r}-\mathbf{r_s}|^2\left(1-\mathbf{n}_s\cdot{\boldsymbol \beta}_s\right)^2}\big({\boldsymbol \nabla} \left[\left(|\mathbf{r}-\mathbf{r_s}|-(\mathbf{r}-\mathbf{r_s})\cdot{\boldsymbol \beta}_s\right)\right]\times{\boldsymbol \beta}_s - \left[\left(|\mathbf{r}-\mathbf{r_s}|-(\mathbf{r}-\mathbf{r_s})\cdot{\boldsymbol \beta}_s\right)\right]{\boldsymbol \nabla}\times{\boldsymbol \beta}_s\big)\\ |
-\frac{q}{4\pi\epsilon_0 c}\frac{1}{|\mathbf{r}-\mathbf{r_s}|^2\left(1-\mathbf{n}_s\cdot{\boldsymbol \beta}_s\right)^2}\big({\boldsymbol \nabla} \left[\left(|\mathbf{r}-\mathbf{r_s}|-(\mathbf{r}-\mathbf{r_s})\cdot{\boldsymbol \beta}_s\right)\right]\times{\boldsymbol \beta}_s - \left[\left(|\mathbf{r}-\mathbf{r_s}|-(\mathbf{r}-\mathbf{r_s})\cdot{\boldsymbol \beta}_s\right)\right]{\boldsymbol \nabla}\times{\boldsymbol \beta}_s\big)\\ |
||
=& - \frac{q}{4\pi\epsilon_0 c}\frac{1}{|\mathbf{r}-\mathbf{r_s}|^2\left(1-\mathbf{n}_s\cdot{\boldsymbol \beta}_s\right)^3}\cdot\\ |
=& - \frac{q}{4\pi\epsilon_0 c}\frac{1}{|\mathbf{r}-\mathbf{r_s}|^2\left(1-\mathbf{n}_s\cdot{\boldsymbol \beta}_s\right)^3}\cdot\\ |
||
&\left[(\mathbf{n}_s\times {\boldsymbol \beta}_s) - ({\boldsymbol \beta}_s\times {\boldsymbol \beta}_s)(1-\mathbf{n}_s\cdot {\boldsymbol \beta}_s) - {\beta}_s^2\mathbf{n}_s\times {\boldsymbol \beta}_s + \left((\mathbf{r}-\mathbf{r_s})\cdot \dot {\boldsymbol \beta}_s/c\right)(\mathbf{n}_s\times {\boldsymbol \beta}_s) + \big(|\mathbf{r}-\mathbf{r_s}|-(\mathbf{r}-\mathbf{r_s})\cdot{\boldsymbol \beta}_s\big)(\mathbf{n}_s\times \dot {\boldsymbol \beta}_s/c)\right] |
&\qquad \left[(\mathbf{n}_s\times {\boldsymbol \beta}_s) - ({\boldsymbol \beta}_s\times {\boldsymbol \beta}_s)(1-\mathbf{n}_s\cdot {\boldsymbol \beta}_s) - {\beta}_s^2\mathbf{n}_s\times {\boldsymbol \beta}_s + \left((\mathbf{r}-\mathbf{r_s})\cdot \dot {\boldsymbol \beta}_s/c\right)(\mathbf{n}_s\times {\boldsymbol \beta}_s) + \big(|\mathbf{r}-\mathbf{r_s}|-(\mathbf{r}-\mathbf{r_s})\cdot{\boldsymbol \beta}_s\big)(\mathbf{n}_s\times \dot {\boldsymbol \beta}_s/c)\right] |
||
\\=& |
\\=& |
||
-\frac{q}{4 \pi \epsilon_0 c} \frac{1}{|\mathbf{r} - \mathbf{r}_s|^2(1 - \mathbf{n}_s \cdot {\boldsymbol \beta}_s)^3}\cdot \\ |
-\frac{q}{4 \pi \epsilon_0 c} \frac{1}{|\mathbf{r} - \mathbf{r}_s|^2(1 - \mathbf{n}_s \cdot {\boldsymbol \beta}_s)^3}\cdot \\ |
||
&\left[\left(\mathbf{n}_s\times{\boldsymbol \beta}_s\right)(1-{\beta_s}^2) + |\mathbf{r} - \mathbf{r}_s|(\mathbf{n}_s \cdot \dot{\boldsymbol \beta}_s/c) (\mathbf{n}_s\times {\boldsymbol \beta}_s) + |\mathbf{r} - \mathbf{r}_s|\big(\mathbf{n}_s \cdot (\mathbf{n}_s - {\boldsymbol \beta}_s)\big) \mathbf{n}_s\times\dot{\boldsymbol \beta}_s/c \right] = \frac{\mathbf{n}_s}{c}\times\mathbf{E} |
&\qquad \left[\left(\mathbf{n}_s\times{\boldsymbol \beta}_s\right)(1-{\beta_s}^2) + |\mathbf{r} - \mathbf{r}_s|(\mathbf{n}_s \cdot \dot{\boldsymbol \beta}_s/c) (\mathbf{n}_s\times {\boldsymbol \beta}_s) + |\mathbf{r} - \mathbf{r}_s|\big(\mathbf{n}_s \cdot (\mathbf{n}_s - {\boldsymbol \beta}_s)\big) \mathbf{n}_s\times\dot{\boldsymbol \beta}_s/c \right] \\[1ex] |
||
=& \frac{\mathbf{n}_s}{c}\times\mathbf{E} |
|||
\end{align}</math> |
\end{align}</math> |
||
The source terms <math>\mathbf{r}_s</math>, <math>\mathbf{n}_s</math>, and <math>\mathbf{\beta}_s</math> are to be evaluated at the retarded time. |
The source terms <math>\mathbf{r}_s</math>, <math>\mathbf{n}_s</math>, and <math>\mathbf{\beta}_s</math> are to be evaluated at the retarded time. |
||
| Line 226: | Line 231: | ||
The Liénard–Wiechert description is accurate for a large, independently moving particle (i.e. the treatment is "classical" and the acceleration of the charge is due to a force independent of the electromagnetic field). The Liénard–Wiechert formulation always provides two sets of solutions: Advanced fields are absorbed by the charges and retarded fields are emitted. Schwarzschild and Fokker considered the advanced field of a system of moving charges, and the retarded field of a system of charges having the same geometry and opposite charges. Linearity of Maxwell's equations in vacuum allows one to add both systems, so that the charges disappear: This trick allows Maxwell's equations to become linear in matter. |
The Liénard–Wiechert description is accurate for a large, independently moving particle (i.e. the treatment is "classical" and the acceleration of the charge is due to a force independent of the electromagnetic field). The Liénard–Wiechert formulation always provides two sets of solutions: Advanced fields are absorbed by the charges and retarded fields are emitted. Schwarzschild and Fokker considered the advanced field of a system of moving charges, and the retarded field of a system of charges having the same geometry and opposite charges. Linearity of Maxwell's equations in vacuum allows one to add both systems, so that the charges disappear: This trick allows Maxwell's equations to become linear in matter. |
||
Multiplying electric parameters of both problems by arbitrary real constants produces a coherent interaction of light with matter which generalizes Einstein's theory<ref>{{cite journal|last=Einstein|first=A.|author-link=Albert Einstein|title=Zur Quantentheorie der Strahlung|journal=Physikalische Zeitschrift|volume=18 |pages=121–128|year=1917|bibcode=1917PhyZ...18..121E|url=https://babel.hathitrust.org/cgi/pt?id=mdp.39015009220800&view=1up&seq=141|language=de}}</ref> which is now considered as founding theory of lasers: it is not necessary to study a large set of identical molecules to get coherent amplification in the mode obtained by arbitrary multiplications of advanced and retarded fields. |
Multiplying electric parameters of both problems by arbitrary real constants produces a coherent interaction of light with matter which generalizes Einstein's theory<ref>{{cite journal|last=Einstein|first=A.|author-link=Albert Einstein|title=Zur Quantentheorie der Strahlung|journal=Physikalische Zeitschrift|volume=18 |pages=121–128|year=1917|bibcode=1917PhyZ...18..121E|url=https://babel.hathitrust.org/cgi/pt?id=mdp.39015009220800&view=1up&seq=141|language=de}}</ref> which is now considered as founding theory of lasers: it is not necessary to study a large set of identical molecules to get coherent amplification in the mode obtained by arbitrary multiplications of advanced and retarded fields. |
||
To compute energy, it is necessary to use the absolute fields which |
To compute energy, it is necessary to use the absolute fields which include the zero point field; otherwise, an error appears, for instance in photon counting. |
||
It is important to take into account the zero point field discovered by Planck.<ref>{{cite journal|last=Planck|first=M.|author-link=Max Planck|title=Eine neue Strahlungshypothese|journal=Verhandlungen der Deutschen Physikalischen Gesellschaft|volume=13|year=1911|pages=138–175|language=de|url=https://babel.hathitrust.org/cgi/pt?id=coo.31924056113495&view=1up&seq=154}}</ref> It replaces Einstein's "A" coefficient and explains that the classical electron is stable on Rydberg's classical orbits. Moreover, introducing the fluctuations of the zero point field produces Willis E. Lamb's correction of levels of H atom. |
It is important to take into account the zero point field discovered by Planck.<ref>{{cite journal|last=Planck|first=M.|author-link=Max Planck|title=Eine neue Strahlungshypothese|journal=Verhandlungen der Deutschen Physikalischen Gesellschaft|volume=13|year=1911|pages=138–175|language=de|url=https://babel.hathitrust.org/cgi/pt?id=coo.31924056113495&view=1up&seq=154}}</ref> It replaces Einstein's "A" coefficient and explains that the classical electron is stable on Rydberg's classical orbits. Moreover, introducing the fluctuations of the zero point field produces Willis E. Lamb's correction of levels of H atom. |
||
| Line 256: | Line 261: | ||
====Uniqueness==== |
====Uniqueness==== |
||
For a given point <math>(\mathbf{r}, t)</math> and trajectory of the point source <math>\mathbf{r}_s(t')</math>, there is at most one value of the retarded time <math>t_r</math>, ''i.e.'', one value <math>t_r</math> such that <math>|\mathbf{r} - \mathbf{r}_s(t_r)| = c(t - t_r)</math>. This can be realized by assuming that there are two retarded times <math>t_1</math> and <math>t_2</math>, with <math>t_1 \leq t_2</math>. Then, <math>|\mathbf{r} - \mathbf{r}_s(t_1)| = c(t - t_1)</math> and <math>|\mathbf{r} - \mathbf{r}_s(t_2)| = c(t - t_2)</math>. Subtracting gives <math> c(t_2 - t_1) = |\mathbf{r} - \mathbf{r}_s(t_1)| - |\mathbf{r} - \mathbf{r}_s(t_2)| \leq |\mathbf{r}_s(t_2) - \mathbf{r}_s(t_1)|</math> by the [[triangle inequality]]. Unless <math>t_2 = t_1</math>, this then implies that the average velocity of the charge between <math>t_1</math> and <math>t_2</math> is <math>|\mathbf{r}_s(t_2) - \mathbf{r}_s(t_1)|/(t_2 - t_1) \geq c</math>, which is impossible. The intuitive interpretation is that one can only ever "see" the point source at one location/time at once unless it travels at least at the speed of light to another location. As the source moves forward in time, the cross section of its light cone at present time contracts faster than the source can approach, so it can never intersect the point <math>\mathbf{r}</math> again. |
For a given point <math>(\mathbf{r}, t)</math> and trajectory of the point source <math>\mathbf{r}_s(t')</math>, there is at most one value of the retarded time <math>t_r</math>, ''i.e.'', one value <math>t_r</math> such that <math>|\mathbf{r} - \mathbf{r}_s(t_r)| = c(t - t_r)</math>. This can be realized by assuming that there are two retarded times <math>t_1</math> and <math>t_2</math>, with <math>t_1 \leq t_2</math>. Then, <math>|\mathbf{r} - \mathbf{r}_s(t_1)| = c(t - t_1)</math> and <math>|\mathbf{r} - \mathbf{r}_s(t_2)| = c(t - t_2)</math>. Subtracting gives <math display="block"> c(t_2 - t_1) = |\mathbf{r} - \mathbf{r}_s(t_1)| - |\mathbf{r} - \mathbf{r}_s(t_2)| \leq |\mathbf{r}_s(t_2) - \mathbf{r}_s(t_1)|</math> by the [[triangle inequality]]. Unless <math>t_2 = t_1</math>, this then implies that the average velocity of the charge between <math>t_1</math> and <math>t_2</math> is <math>|\mathbf{r}_s(t_2) - \mathbf{r}_s(t_1)|/(t_2 - t_1) \geq c</math>, which is impossible. The intuitive interpretation is that one can only ever "see" the point source at one location/time at once unless it travels at least at the speed of light to another location. As the source moves forward in time, the cross section of its light cone at present time contracts faster than the source can approach, so it can never intersect the point <math>\mathbf{r}</math> again. |
||
The conclusion is that, under certain conditions, the retarded time exists and is unique. |
The conclusion is that, under certain conditions, the retarded time exists and is unique. |
||
| Line 276: | Line 281: | ||
==References== |
==References== |
||
<references /> |
<references /> |
||
*Griffiths, David. Introduction to Electrodynamics. Prentice Hall, 1999. {{ISBN|0-13-805326-X}}. |
|||
==External links== |
|||
*[https://feynmanlectures.caltech.edu/II_21.html The Feynman Lectures on Physics Vol. II Ch. 21: Solutions of Maxwell’s Equations with Currents and Charges] |
|||
{{DEFAULTSORT:Lienard-Wiechert potential}} |
{{DEFAULTSORT:Lienard-Wiechert potential}} |
||
Latest revision as of 07:41, 26 November 2024
| Articles about |
| Electromagnetism |
|---|
 |
The Liénard–Wiechert potentials describe the classical electromagnetic effect of a moving electric point charge in terms of a vector potential and a scalar potential in the Lorenz gauge. Stemming directly from Maxwell's equations, these describe the complete, relativistically correct, time-varying electromagnetic field for a point charge in arbitrary motion, but are not corrected for quantum mechanical effects. Electromagnetic radiation in the form of waves can be obtained from these potentials. These expressions were developed in part by Alfred-Marie Liénard in 1898[1] and independently by Emil Wiechert in 1900.[2][3]
Equations
[edit]Definition of Liénard–Wiechert potentials
[edit]The retarded time is defined, in the context of distributions of charges and currents, as
where is the observation point, and is the observed point subject to the variations of source charges and currents. For a moving point charge whose given trajectory is , is no more fixed, but becomes a function of the retarded time itself. In other words, following the trajectory of yields the implicit equation
which provides the retarded time as a function of the current time (and of the given trajectory):
- .
The Liénard–Wiechert potentials (scalar potential field) and (vector potential field) are, for a source point charge at position traveling with velocity :
and
where:
- is the velocity of the source expressed as a fraction of the speed of light;
- is the distance from the source;
- is the unit vector pointing in the direction from the source and,
- The symbol means that the quantities inside the parenthesis should be evaluated at the retarded time .
This can also be written in a covariant way, where the electromagnetic four-potential at is:[4]
where and is the position of the source and is its four velocity.
Field computation
[edit]


We can calculate the electric and magnetic fields directly from the potentials using the definitions: and
The calculation is nontrivial and requires a number of steps. The electric and magnetic fields are (in non-covariant form): and
where , and (the Lorentz factor).
The first term is link to the static field of the charge when it moves at a constant velocity.
The second term, which is connected with electromagnetic radiation by the moving charge, requires charge acceleration and if this is zero, the value of this term is zero, and the charge does not radiate (emit electromagnetic radiation). This term requires additionally that a component of the charge acceleration be in a direction transverse to the line which connects the charge and the observer of the field . The direction of the field associated with this radiative term is toward the fully time-retarded position of the charge (i.e. where the charge was when it was accelerated).
Static field
[edit]The part of the first term of the electric field updates the direction of the field toward the instantaneous position of the charge, if it continues to move with constant velocity . This term is connected with the "static" part of the electromagnetic field of the charge. On the illustration, we observe an event that happened in the center of the sphere and that propagated at the speed of light. The problem is that when the speed of the particle is very close to the speed of light, the particle is then almost on the wave front which explains this strong electrostatic field on the front as we are now very close to the particle. Note that outside the propagation sphere, the electric field has its initial state (no connection with the event we observe). When the speed is very close to the speed of light, we consider that the electric field becomes almost flat in the transverse plane, a bit like a "pancake", with an opening angle on .
Derivation
[edit]The scalar and vector potentials satisfy the nonhomogeneous electromagnetic wave equation where the sources are expressed with the charge and current densities and and the Ampère-Maxwell law is:
Since the potentials are not unique, but have gauge freedom, these equations can be simplified by gauge fixing. A common choice is the Lorenz gauge condition:
Then the nonhomogeneous wave equations become uncoupled and symmetric in the potentials:
Generally, the retarded solutions for the scalar and vector potentials (SI units) are and
where is the retarded time and and satisfy the homogeneous wave equation with no sources and boundary conditions. In the case that there are no boundaries surrounding the sources then and .
For a moving point charge whose trajectory is given as a function of time by , the charge and current densities are as follows:
where is the three-dimensional Dirac delta function and is the velocity of the point charge.
Substituting into the expressions for the potential gives
These integrals are difficult to evaluate in their present form, so we will rewrite them by replacing with and integrating over the delta distribution :
We exchange the order of integration:
The delta function picks out which allows us to perform the inner integration with ease. Note that is a function of , so this integration also fixes .
The retarded time is a function of the field point and the source trajectory , and hence depends on . To evaluate this integral, therefore, we need the identity where each is a zero of . Because there is only one retarded time for any given space-time coordinates and source trajectory , this reduces to: where and are evaluated at the retarded time , and we have used the identity with . Notice that the retarded time is the solution of the equation . Finally, the delta function picks out , and which are the Liénard–Wiechert potentials.
Lorenz gauge, electric and magnetic fields
[edit]In order to calculate the derivatives of and it is convenient to first compute the derivatives of the retarded time. Taking the derivatives of both sides of its defining equation (remembering that ): Differentiating with respect to t,
Similarly, taking the gradient with respect to and using the multivariable chain rule gives
It follows that
These can be used in calculating the derivatives of the vector potential and the resulting expressions are
These show that the Lorenz gauge is satisfied, namely that .
Similarly one calculates:
By noting that for any vectors , , : The expression for the electric field mentioned above becomes which is easily seen to be equal to
Similarly gives the expression of the magnetic field mentioned above: The source terms , , and are to be evaluated at the retarded time.
Implications
[edit]This section's factual accuracy is disputed. (November 2019) |
The study of classical electrodynamics was instrumental in Albert Einstein's development of the theory of relativity. Analysis of the motion and propagation of electromagnetic waves led to the special relativity description of space and time. The Liénard–Wiechert formulation is an important launchpad into a deeper analysis of relativistic moving particles.
The Liénard–Wiechert description is accurate for a large, independently moving particle (i.e. the treatment is "classical" and the acceleration of the charge is due to a force independent of the electromagnetic field). The Liénard–Wiechert formulation always provides two sets of solutions: Advanced fields are absorbed by the charges and retarded fields are emitted. Schwarzschild and Fokker considered the advanced field of a system of moving charges, and the retarded field of a system of charges having the same geometry and opposite charges. Linearity of Maxwell's equations in vacuum allows one to add both systems, so that the charges disappear: This trick allows Maxwell's equations to become linear in matter. Multiplying electric parameters of both problems by arbitrary real constants produces a coherent interaction of light with matter which generalizes Einstein's theory[7] which is now considered as founding theory of lasers: it is not necessary to study a large set of identical molecules to get coherent amplification in the mode obtained by arbitrary multiplications of advanced and retarded fields. To compute energy, it is necessary to use the absolute fields which include the zero point field; otherwise, an error appears, for instance in photon counting.
It is important to take into account the zero point field discovered by Planck.[8] It replaces Einstein's "A" coefficient and explains that the classical electron is stable on Rydberg's classical orbits. Moreover, introducing the fluctuations of the zero point field produces Willis E. Lamb's correction of levels of H atom.
Quantum electrodynamics helped bring together the radiative behavior with the quantum constraints. It introduces quantization of normal modes of the electromagnetic field in assumed perfect optical resonators.
Universal speed limit
[edit]The force on a particle at a given location r and time t depends in a complicated way on the position of the source particles at an earlier time tr due to the finite speed, c, at which electromagnetic information travels. A particle on Earth 'sees' a charged particle accelerate on the Moon as this acceleration happened 1.5 seconds ago, and a charged particle's acceleration on the Sun as happened 500 seconds ago. This earlier time in which an event happens such that a particle at location r 'sees' this event at a later time t is called the retarded time, tr. The retarded time varies with position; for example the retarded time at the Moon is 1.5 seconds before the current time and the retarded time on the Sun is 500 s before the current time on the Earth. The retarded time tr=tr(r,t) is defined implicitly by
where is the distance of the particle from the source at the retarded time. Only electromagnetic wave effects depend fully on the retarded time.
A novel feature in the Liénard–Wiechert potential is seen in the breakup of its terms into two types of field terms (see below), only one of which depends fully on the retarded time. The first of these is the static electric (or magnetic) field term that depends only on the distance to the moving charge, and does not depend on the retarded time at all, if the velocity of the source is constant. The other term is dynamic, in that it requires that the moving charge be accelerating with a component perpendicular to the line connecting the charge and the observer and does not appear unless the source changes velocity. This second term is connected with electromagnetic radiation.
The first term describes near field effects from the charge, and its direction in space is updated with a term that corrects for any constant-velocity motion of the charge on its distant static field, so that the distant static field appears at distance from the charge, with no aberration of light or light-time correction. This term, which corrects for time-retardation delays in the direction of the static field, is required by Lorentz invariance. A charge moving with a constant velocity must appear to a distant observer in exactly the same way as a static charge appears to a moving observer, and in the latter case, the direction of the static field must change instantaneously, with no time-delay. Thus, static fields (the first term) point exactly at the true instantaneous (non-retarded) position of the charged object if its velocity has not changed over the retarded time delay. This is true over any distance separating objects.
The second term, however, which contains information about the acceleration and other unique behavior of the charge that cannot be removed by changing the Lorentz frame (inertial reference frame of the observer), is fully dependent for direction on the time-retarded position of the source. Thus, electromagnetic radiation (described by the second term) always appears to come from the direction of the position of the emitting charge at the retarded time. Only this second term describes information transfer about the behavior of the charge, which transfer occurs (radiates from the charge) at the speed of light. At "far" distances (longer than several wavelengths of radiation), the 1/R dependence of this term makes electromagnetic field effects (the value of this field term) more powerful than "static" field effects, which are described by the 1/R2 field of the first (static) term and thus decay more rapidly with distance from the charge.
Existence and uniqueness of the retarded time
[edit]Existence
[edit]The retarded time is not guaranteed to exist in general. For example, if, in a given frame of reference, an electron has just been created, then at this very moment another electron does not yet feel its electromagnetic force at all. However, under certain conditions, there always exists a retarded time. For example, if the source charge has existed for an unlimited amount of time, during which it has always travelled at a speed not exceeding , then there exists a valid retarded time . This can be seen by considering the function . At the present time ; . The derivative is given by
By the mean value theorem, . By making sufficiently large, this can become negative, i.e., at some point in the past, . By the intermediate value theorem, there exists an intermediate with , the defining equation of the retarded time. Intuitively, as the source charge moves back in time, the cross section of its light cone at present time expands faster than it can recede, so eventually it must reach the point . This is not necessarily true if the source charge's speed is allowed to be arbitrarily close to , i.e., if for any given speed there was some time in the past when the charge was moving at this speed. In this case the cross section of the light cone at present time approaches the point as the observer travels back in time but does not necessarily ever reach it.
Uniqueness
[edit]For a given point and trajectory of the point source , there is at most one value of the retarded time , i.e., one value such that . This can be realized by assuming that there are two retarded times and , with . Then, and . Subtracting gives by the triangle inequality. Unless , this then implies that the average velocity of the charge between and is , which is impossible. The intuitive interpretation is that one can only ever "see" the point source at one location/time at once unless it travels at least at the speed of light to another location. As the source moves forward in time, the cross section of its light cone at present time contracts faster than the source can approach, so it can never intersect the point again.
The conclusion is that, under certain conditions, the retarded time exists and is unique.
See also
[edit]- Maxwell's equations which govern classical electromagnetism
- Classical electromagnetism for the larger theory surrounding this analysis
- Relativistic electromagnetism
- Special relativity, which was a direct consequence of these analyses
- Rydberg formula for quantum description of the EM radiation due to atomic orbital electrons
- Jefimenko's equations
- Larmor formula
- Abraham–Lorentz force
- Inhomogeneous electromagnetic wave equation
- Wheeler–Feynman absorber theory also known as the Wheeler–Feynman time-symmetric theory
- Paradox of a charge in a gravitational field
- Whitehead's theory of gravitation
References
[edit]- ^ Liénard, A. (1898). "Champ électrique et magnétique produit par une charge concentrée en un point et animée d'un mouvement quelconque". L'Éclairage Électrique. 16 (27, 28, 29): 5–14, 53–59, 106–112.
- ^ Wiechert, E. (1901). "Elektrodynamische Elementargesetze". Annalen der Physik. 309 (4): 667–689. Bibcode:1901AnP...309..667W. doi:10.1002/andp.19013090403.
- ^ Some Aspects in Emil Wiechert
- ^ David Tong: Lectures on Electromagnetism, Lecture 5: 4.Electromagnetism and Relativity, University of Cambridge
- ^ Walker, R.P. CERN Accelerator School: Synchrotron radiation (PDF).
- ^ Wilson, P.B. INTRODUCTION TO WAKEFIELDS AND WAKE POTENTIALS.
- ^ Einstein, A. (1917). "Zur Quantentheorie der Strahlung". Physikalische Zeitschrift (in German). 18: 121–128. Bibcode:1917PhyZ...18..121E.
- ^ Planck, M. (1911). "Eine neue Strahlungshypothese". Verhandlungen der Deutschen Physikalischen Gesellschaft (in German). 13: 138–175.

































































































![{\displaystyle {\begin{aligned}{\frac {d\varphi }{dt}}=&-{\frac {q}{4\pi \epsilon _{0}}}{\frac {1}{|\mathbf {r} -\mathbf {r_{s}} |^{2}\left(1-\mathbf {n} _{s}\cdot {\boldsymbol {\beta }}_{s}\right)^{2}}}{\frac {d}{dt}}\left[(|\mathbf {r} -\mathbf {r_{s}} |(1-\mathbf {n} _{s}\cdot {\boldsymbol {\beta }}_{s})\right]\\=&-{\frac {q}{4\pi \epsilon _{0}}}{\frac {1}{|\mathbf {r} -\mathbf {r_{s}} |^{2}\left(1-\mathbf {n} _{s}\cdot {\boldsymbol {\beta }}_{s}\right)^{2}}}{\frac {d}{dt}}\left[|\mathbf {r} -\mathbf {r_{s}} |-(\mathbf {r} -\mathbf {r_{s}} )\cdot {\boldsymbol {\beta }}_{s}\right]\\=&-{\frac {qc}{4\pi \epsilon _{0}}}{\frac {1}{|\mathbf {r} -\mathbf {r_{s}} |^{2}\left(1-\mathbf {n} _{s}\cdot {\boldsymbol {\beta }}_{s}\right)^{3}}}\left[-\mathbf {n} _{s}\cdot {\boldsymbol {\beta }}_{s}+{\beta _{s}}^{2}-(\mathbf {r} -\mathbf {r_{s}} )\cdot {\dot {\boldsymbol {\beta }}}_{s}/c\right]\end{aligned}}}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/bf0cb7d22ad7cb62421732d7a761c15bf2544a66)
![{\displaystyle {\begin{aligned}{\boldsymbol {\nabla }}\cdot \mathbf {A} =&-{\frac {q}{4\pi \epsilon _{0}c}}{\frac {1}{|\mathbf {r} -\mathbf {r_{s}} |^{2}\left(1-\mathbf {n} _{s}\cdot {\boldsymbol {\beta }}_{s}\right)^{2}}}{\big (}{\boldsymbol {\nabla }}\left[\left(|\mathbf {r} -\mathbf {r_{s}} |-(\mathbf {r} -\mathbf {r_{s}} )\cdot {\boldsymbol {\beta }}_{s}\right)\right]\cdot {\boldsymbol {\beta }}_{s}-\left[\left(|\mathbf {r} -\mathbf {r_{s}} |-(\mathbf {r} -\mathbf {r_{s}} )\cdot {\boldsymbol {\beta }}_{s}\right)\right]{\boldsymbol {\nabla }}\cdot {\boldsymbol {\beta }}_{s}{\big )}\\=&-{\frac {q}{4\pi \epsilon _{0}c}}{\frac {1}{|\mathbf {r} -\mathbf {r_{s}} |^{2}\left(1-\mathbf {n} _{s}\cdot {\boldsymbol {\beta }}_{s}\right)^{3}}}\cdot \\&\left[(\mathbf {n} _{s}\cdot {\boldsymbol {\beta }}_{s})-{\beta }_{s}^{2}(1-\mathbf {n} _{s}\cdot {\boldsymbol {\beta }}_{s})-{\beta }_{s}^{2}\mathbf {n} _{s}\cdot {\boldsymbol {\beta }}_{s}+\left((\mathbf {r} -\mathbf {r_{s}} )\cdot {\dot {\boldsymbol {\beta }}}_{s}/c\right)(\mathbf {n} _{s}\cdot {\boldsymbol {\beta }}_{s})+{\big (}|\mathbf {r} -\mathbf {r_{s}} |-(\mathbf {r} -\mathbf {r_{s}} )\cdot {\boldsymbol {\beta }}_{s}{\big )}(\mathbf {n} _{s}\cdot {\dot {\boldsymbol {\beta }}}_{s}/c)\right]\\=&{\frac {q}{4\pi \epsilon _{0}c}}{\frac {1}{|\mathbf {r} -\mathbf {r_{s}} |^{2}\left(1-\mathbf {n} _{s}\cdot {\boldsymbol {\beta }}_{s}\right)^{3}}}\left[\beta _{s}^{2}-\mathbf {n} _{s}\cdot {\boldsymbol {\beta }}_{s}-(\mathbf {r} -\mathbf {r_{s}} )\cdot {\dot {\boldsymbol {\beta }}}_{s}/c\right]\end{aligned}}}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/ae3bf7a74f6df3e27466f521f55f644fd46ce15b)

![{\displaystyle {\boldsymbol {\nabla }}\varphi =-{\frac {q}{4\pi \epsilon _{0}}}{\frac {1}{|\mathbf {r} -\mathbf {r_{s}} |^{2}\left(1-\mathbf {n} _{s}\cdot {\boldsymbol {\beta }}_{s}\right)^{3}}}\left[\mathbf {n} _{s}\left(1-{\beta _{s}}^{2}+(\mathbf {r} -\mathbf {r_{s}} )\cdot {\dot {\boldsymbol {\beta }}}_{s}/c\right)-{\boldsymbol {\beta }}_{s}(1-\mathbf {n} _{s}\cdot {\boldsymbol {\beta }}_{s})\right]}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/738d03d16e4ab07494a35a4c1e9476639c3808bd)
![{\displaystyle {\frac {d\mathbf {A} }{dt}}={\frac {q}{4\pi \epsilon _{0}}}{\frac {1}{|\mathbf {r} -\mathbf {r_{s}} |^{2}\left(1-\mathbf {n} _{s}\cdot {\boldsymbol {\beta }}_{s}\right)^{3}}}\left[{\boldsymbol {\beta }}_{s}\left(\mathbf {n} _{s}\cdot {\boldsymbol {\beta }}_{s}-{\beta _{s}}^{2}+(\mathbf {r} -\mathbf {r_{s}} )\cdot {\dot {\boldsymbol {\beta }}}_{s}/c\right)+|\mathbf {r} -\mathbf {r_{s}} |{\dot {\boldsymbol {\beta }}}_{s}(1-\mathbf {n} _{s}\cdot {\boldsymbol {\beta }}_{s})/c\right]}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/df4575676f035df4925a1fd52060b32035fe476f)




![{\displaystyle {\begin{aligned}\mathbf {E} (\mathbf {r} ,t)=&{\frac {q}{4\pi \epsilon _{0}}}{\frac {1}{|\mathbf {r} -\mathbf {r} _{s}|^{2}(1-\mathbf {n} _{s}\cdot {\boldsymbol {\beta }}_{s})^{3}}}\cdot \\&\left[\left(\mathbf {n} _{s}-{\boldsymbol {\beta }}_{s}\right)(1-{\beta _{s}}^{2})+|\mathbf {r} -\mathbf {r} _{s}|(\mathbf {n} _{s}\cdot {\dot {\boldsymbol {\beta }}}_{s}/c)(\mathbf {n} _{s}-{\boldsymbol {\beta }}_{s})-|\mathbf {r} -\mathbf {r} _{s}|{\big (}\mathbf {n} _{s}\cdot (\mathbf {n} _{s}-{\boldsymbol {\beta }}_{s}){\big )}{\dot {\boldsymbol {\beta }}}_{s}/c\right]\end{aligned}}}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/aed73cb808e33e4e5aae57ee0683dcd226db158a)


![{\displaystyle {\begin{aligned}{\mathbf {B} }=&{\boldsymbol {\nabla }}\times \mathbf {A} \\[1ex]=&-{\frac {q}{4\pi \epsilon _{0}c}}{\frac {1}{|\mathbf {r} -\mathbf {r_{s}} |^{2}\left(1-\mathbf {n} _{s}\cdot {\boldsymbol {\beta }}_{s}\right)^{2}}}{\big (}{\boldsymbol {\nabla }}\left[\left(|\mathbf {r} -\mathbf {r_{s}} |-(\mathbf {r} -\mathbf {r_{s}} )\cdot {\boldsymbol {\beta }}_{s}\right)\right]\times {\boldsymbol {\beta }}_{s}-\left[\left(|\mathbf {r} -\mathbf {r_{s}} |-(\mathbf {r} -\mathbf {r_{s}} )\cdot {\boldsymbol {\beta }}_{s}\right)\right]{\boldsymbol {\nabla }}\times {\boldsymbol {\beta }}_{s}{\big )}\\=&-{\frac {q}{4\pi \epsilon _{0}c}}{\frac {1}{|\mathbf {r} -\mathbf {r_{s}} |^{2}\left(1-\mathbf {n} _{s}\cdot {\boldsymbol {\beta }}_{s}\right)^{3}}}\cdot \\&\qquad \left[(\mathbf {n} _{s}\times {\boldsymbol {\beta }}_{s})-({\boldsymbol {\beta }}_{s}\times {\boldsymbol {\beta }}_{s})(1-\mathbf {n} _{s}\cdot {\boldsymbol {\beta }}_{s})-{\beta }_{s}^{2}\mathbf {n} _{s}\times {\boldsymbol {\beta }}_{s}+\left((\mathbf {r} -\mathbf {r_{s}} )\cdot {\dot {\boldsymbol {\beta }}}_{s}/c\right)(\mathbf {n} _{s}\times {\boldsymbol {\beta }}_{s})+{\big (}|\mathbf {r} -\mathbf {r_{s}} |-(\mathbf {r} -\mathbf {r_{s}} )\cdot {\boldsymbol {\beta }}_{s}{\big )}(\mathbf {n} _{s}\times {\dot {\boldsymbol {\beta }}}_{s}/c)\right]\\=&-{\frac {q}{4\pi \epsilon _{0}c}}{\frac {1}{|\mathbf {r} -\mathbf {r} _{s}|^{2}(1-\mathbf {n} _{s}\cdot {\boldsymbol {\beta }}_{s})^{3}}}\cdot \\&\qquad \left[\left(\mathbf {n} _{s}\times {\boldsymbol {\beta }}_{s}\right)(1-{\beta _{s}}^{2})+|\mathbf {r} -\mathbf {r} _{s}|(\mathbf {n} _{s}\cdot {\dot {\boldsymbol {\beta }}}_{s}/c)(\mathbf {n} _{s}\times {\boldsymbol {\beta }}_{s})+|\mathbf {r} -\mathbf {r} _{s}|{\big (}\mathbf {n} _{s}\cdot (\mathbf {n} _{s}-{\boldsymbol {\beta }}_{s}){\big )}\mathbf {n} _{s}\times {\dot {\boldsymbol {\beta }}}_{s}/c\right]\\[1ex]=&{\frac {\mathbf {n} _{s}}{c}}\times \mathbf {E} \end{aligned}}}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/ee7977d3db2afe694b584a0e152229d9773e2226)
























