Floorplan (microelectronics): Difference between revisions
No edit summary |
m lc per MOS:EXPABBR Tags: Visual edit Mobile edit Mobile web edit Advanced mobile edit |
||
| (31 intermediate revisions by 28 users not shown) | |||
| Line 1: | Line 1: | ||
{{Short description|Layout of major electronic circuit blocks}} |
|||
| ⚫ | |||
{{cleanup images |date=May 2024}} |
|||
{{Use American English|date = April 2019}} |
|||
| ⚫ | |||
In [[electronic design automation]], a '''floorplan''' of an [[integrated circuit]] is a schematic representation of tentative [[placement (EDA)|placement]] of its major functional blocks. |
In [[electronic design automation]], a '''floorplan''' of an [[integrated circuit]] is a schematic representation of tentative [[placement (EDA)|placement]] of its major functional blocks. |
||
In modern electronic design process floorplans are created during the |
In modern electronic design process floorplans are created during the '''floorplanning''' design stage, an early stage in the hierarchical approach to [[integrated circuit design]]. |
||
Depending on the design methodology, the actual |
Depending on the design methodology being followed, the actual definition of a floorplan may differ. |
||
==Floorplanning== |
==Floorplanning== |
||
Floorplanning takes in some of the geometrical constraints in a design. Here are some examples: |
|||
* bonding |
* [[bonding pad]]s for off-chip connections (often using [[wire bonding]]) are normally located along the periphery of the chip; |
||
* line |
* [[line driver]]s often have to be located as close to bonding pads as possible; |
||
* chip area is therefore in some cases given a minimum area in order to fit in the required number of pads; |
* chip area is therefore in some cases given a minimum area in order to fit in the required number of pads; |
||
* areas are clustered in order to limit data paths thus frequently featuring defined structures such as [[cache]] [[RAM]], [[multiplier]], [[barrel shifter]], [[line driver]] and [[arithmetic logic unit]]; |
* areas are clustered in order to limit data paths thus frequently featuring defined structures such as [[CPU cache|cache]] [[Random-access memory|RAM]], [[Multiplication|multiplier]], [[barrel shifter]], [[line driver]] and [[arithmetic logic unit]]; |
||
* purchased intellectual property blocks (such as a processor core |
* purchased intellectual property blocks ([[Semiconductor intellectual property core|IP-blocks]]), such as a [[processor core]], come in predefined area blocks; |
||
* some IP-blocks come with legal limitations such as permitting no routing of signals directly above the block. |
* some IP-blocks come with legal limitations such as permitting no routing of signals directly above the block. |
||
==Mathematical models and optimization problems== |
==Mathematical models and optimization problems== |
||
| ⚫ | |||
| ⚫ | |||
In some approaches the floorplan may be a partition of the whole chip area into [[axis aligned rectangle]]s to be occupied by IC blocks. This partition is subject to various constraints and requirements of optimization: block area, [[aspect ratio]]s, estimated total measure of interconnects, etc. |
In some approaches the floorplan may be a partition of the whole chip area into [[axis aligned rectangle]]s to be occupied by IC blocks. This partition is subject to various constraints and requirements of optimization: block area, [[aspect ratio]]s, estimated total measure of interconnects, etc. |
||
Finding good floorplans has been a research area in [[combinatorial optimization]]. Most of problems related to finding optimal floorplans are [[NP-hard]], i.e., require vast computational resources. Therefore the most common approach is to use various optimization heuristics for finding good solutions. |
Finding good floorplans has been a research area in [[combinatorial optimization]]. Most of the problems related to finding optimal floorplans are [[NP-hard]], i.e., require vast computational resources. Therefore, the most common approach is to use various optimization heuristics for finding good solutions. |
||
Another approach is to restrict design methodology to certain classes of floorplans, such as sliceable floorplans |
Another approach is to restrict design methodology to certain classes of floorplans, such as sliceable floorplans. |
||
===Sliceable floorplans=== |
===Sliceable floorplans=== |
||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
*A floorplan that consists of a single rectangular block is sliceable. |
*A floorplan that consists of a single rectangular block is sliceable. |
||
*If a block from a sliceable floorplan is cut ("sliced") in two by a vertical or horizontal line, the resulting floorplan is sliceable. |
*If a block from a sliceable floorplan is cut ("sliced") in two by a vertical or horizontal line, the resulting floorplan is sliceable. |
||
Sliceable floorplans have been used in a number of early [[ |
Sliceable floorplans have been used in a number of early [[electronic design automation]] tools<ref name=dorf/> for a number of reasons. Sliceable floorplans may be conveniently represented by [[binary tree]]s (more specifically, [[k-d tree|''k''-d trees]]), which correspond to the order of slicing. More importantly, a number of NP-hard problems with floorplans have [[polynomial time]] algorithms when restricted to sliceable floorplans.<ref>Sarrafzadeh, M, "[https://ieeexplore.ieee.org/abstract/document/580085/ Transforming an arbitrary floorplan into a sliceable one]", Proc. 1993 IEEE/ACM International Conference on Computer-Aided Design (ICCAD-93), pp. 386-389. </ref> |
||
==Further |
==Further reading== |
||
* [http://www.schoelzke.info/mirror/galway/projects/ChipPlanner-Description.htm The Chip Planner of the PLAYOUT System] |
* [http://www.schoelzke.info/mirror/galway/projects/ChipPlanner-Description.htm The Chip Planner of the PLAYOUT System] |
||
* [https://www.ifte.de/books/eda/index.html ''VLSI Physical Design: From Graph Partitioning to Timing Closure''], by Kahng, Lienig, Markov and Hu, {{doi|10.1007/978-3-030-96415-3}}{{ISBN|978-3-030-96414-6}}, 2022 |
|||
* [http://vlsisystemdesign.com/Physical-Design-Forum.php Floorplanning the blocks inside IC - VLSI SYSTEM DESIGN] |
|||
* [https://www.ifte.de/books/pd/index.html ''Fundamentals of Layout Design for Electronic Circuits''], by Lienig, Scheible, Springer, {{doi|10.1007/978-3-030-39284-0}}{{ISBN|978-3-030-39284-0}}, 2020 |
|||
==References== |
==References== |
||
{{reflist}} |
{{reflist}} |
||
| Line 42: | Line 47: | ||
[[Category:Electronics optimization]] |
[[Category:Electronics optimization]] |
||
[[Category:Combinatorial optimization]] |
[[Category:Combinatorial optimization]] |
||
[[Category: |
[[Category:Rectangular subdivisions]] |
||
[[de:Floorplanning]] |
|||
[[ko:평면 배치 기법]] |
|||
Latest revision as of 05:36, 1 December 2024
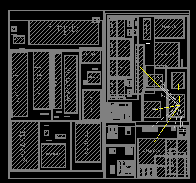
In electronic design automation, a floorplan of an integrated circuit is a schematic representation of tentative placement of its major functional blocks.
In modern electronic design process floorplans are created during the floorplanning design stage, an early stage in the hierarchical approach to integrated circuit design.
Depending on the design methodology being followed, the actual definition of a floorplan may differ.
Floorplanning
[edit]Floorplanning takes in some of the geometrical constraints in a design. Here are some examples:
- bonding pads for off-chip connections (often using wire bonding) are normally located along the periphery of the chip;
- line drivers often have to be located as close to bonding pads as possible;
- chip area is therefore in some cases given a minimum area in order to fit in the required number of pads;
- areas are clustered in order to limit data paths thus frequently featuring defined structures such as cache RAM, multiplier, barrel shifter, line driver and arithmetic logic unit;
- purchased intellectual property blocks (IP-blocks), such as a processor core, come in predefined area blocks;
- some IP-blocks come with legal limitations such as permitting no routing of signals directly above the block.
Mathematical models and optimization problems
[edit]

In some approaches the floorplan may be a partition of the whole chip area into axis aligned rectangles to be occupied by IC blocks. This partition is subject to various constraints and requirements of optimization: block area, aspect ratios, estimated total measure of interconnects, etc.
Finding good floorplans has been a research area in combinatorial optimization. Most of the problems related to finding optimal floorplans are NP-hard, i.e., require vast computational resources. Therefore, the most common approach is to use various optimization heuristics for finding good solutions.
Another approach is to restrict design methodology to certain classes of floorplans, such as sliceable floorplans.
Sliceable floorplans
[edit]A sliceable floorplan is a floorplan that may be defined recursively as described below. [1]
- A floorplan that consists of a single rectangular block is sliceable.
- If a block from a sliceable floorplan is cut ("sliced") in two by a vertical or horizontal line, the resulting floorplan is sliceable.
Sliceable floorplans have been used in a number of early electronic design automation tools[1] for a number of reasons. Sliceable floorplans may be conveniently represented by binary trees (more specifically, k-d trees), which correspond to the order of slicing. More importantly, a number of NP-hard problems with floorplans have polynomial time algorithms when restricted to sliceable floorplans.[2]
Further reading
[edit]- The Chip Planner of the PLAYOUT System
- VLSI Physical Design: From Graph Partitioning to Timing Closure, by Kahng, Lienig, Markov and Hu, doi:10.1007/978-3-030-96415-3ISBN 978-3-030-96414-6, 2022
- Fundamentals of Layout Design for Electronic Circuits, by Lienig, Scheible, Springer, doi:10.1007/978-3-030-39284-0ISBN 978-3-030-39284-0, 2020
References
[edit]- ^ a b "The Electrical Engineering Handbook", Richard C. Dorf (1997) ISBN 0-8493-8574-1
- ^ Sarrafzadeh, M, "Transforming an arbitrary floorplan into a sliceable one", Proc. 1993 IEEE/ACM International Conference on Computer-Aided Design (ICCAD-93), pp. 386-389.

