RF chain: Difference between revisions
m cite repair; |
Citation bot (talk | contribs) Added doi-broken-date. | Use this bot. Report bugs. | #UCB_CommandLine |
||
| (3 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
An '''RF chain''' is a cascade of electronic components and sub-units which may include [[RF power amplifier|amplifiers]], [[RF and microwave filter|filters]], [[Frequency mixer|mixers]], [[Attenuator (electronics)|attenuators]] and [[Detector (radio)|detectors]].<ref name = Steer>Steer M., "Microwave and RF Design", Scitech Publ., Inc., N.C., 2010, also from Yes Dee Publ., India, 2016</ref> It can take many forms, for example, as a wide-band receiver-detector for [[electronic warfare]] (EW) applications, as a tunable narrow-band receiver for communications purposes, as a [[repeater]] in signal distribution systems, or as an amplifier and [[Block upconverter|up-converters]] for a transmitter-driver. In this article, the term RF (radio frequency) covers the frequency range " |
An '''RF chain''' is a cascade of electronic components and sub-units which may include [[RF power amplifier|amplifiers]], [[RF and microwave filter|filters]], [[Frequency mixer|mixers]], [[Attenuator (electronics)|attenuators]] and [[Detector (radio)|detectors]].<ref name = Steer>Steer M., "Microwave and RF Design", Scitech Publ., Inc., N.C., 2010, also from Yes Dee Publ., India, 2016</ref> It can take many forms, for example, as a wide-band receiver-detector for [[electronic warfare]] (EW) applications, as a tunable narrow-band receiver for communications purposes, as a [[repeater]] in signal distribution systems, or as an amplifier and [[Block upconverter|up-converters]] for a transmitter-driver. In this article, the term RF (radio frequency) covers the frequency range "medium Frequencies" up to "microwave Frequencies", i.e. from 100 kHz to 20 GHz.<ref name = Frenzel>Frenzel L.E. "Principles of Electronic Communication Systems", 3rd Ed., McGraw Hill, 2008</ref>{{rp|15}} |
||
The key electrical parameters for an RF chain are system gain, [[noise figure]] (or [[noise factor]]) and overload level.<ref name = Egan>Egan W.F., "Practical RF System Design", Wiley, 2003</ref>{{rp|2}} Other important parameters, related to these properties, are sensitivity (the minimum signal level which can be resolved at the output of the chain); dynamic range (the total range of signals that the chain can handle from a maximum level down to smallest level that can be reliably processed) and spurious signal levels (unwanted signals produced by devices such as mixers and non-linear amplifiers). In addition, there may be concerns regarding the immunity to incoming interference or, conversely, the amount of undesirable radiation emanating from the chain. The tolerance of a system to mechanical vibration may be important too. Furthermore, the physical properties of the chain, such as size, weight and power consumption may also be important considerations. |
The key electrical parameters for an RF chain are system gain, [[noise figure]] (or [[noise factor]]) and overload level.<ref name = Egan>Egan W.F., "Practical RF System Design", Wiley, 2003</ref>{{rp|2}} Other important parameters, related to these properties, are sensitivity (the minimum signal level which can be resolved at the output of the chain); dynamic range (the total range of signals that the chain can handle from a maximum level down to smallest level that can be reliably processed) and spurious signal levels (unwanted signals produced by devices such as mixers and non-linear amplifiers). In addition, there may be concerns regarding the immunity to incoming interference or, conversely, the amount of undesirable radiation emanating from the chain. The tolerance of a system to mechanical vibration may be important too. Furthermore, the physical properties of the chain, such as size, weight and power consumption may also be important considerations. |
||
| Line 5: | Line 5: | ||
An addition to considering the performance of the RF chain, the signal and signal-to-noise requirements of the various signal processing components, which may follow it, are discussed because they often determine the target figures for a chain. |
An addition to considering the performance of the RF chain, the signal and signal-to-noise requirements of the various signal processing components, which may follow it, are discussed because they often determine the target figures for a chain. |
||
==Parameter sets== |
== Parameter sets == |
||
Each two-port network in an RF chain can be described by a parameter set, which relates the voltages and currents appearing at the terminals of that network.<ref name = Matthaei>Matthaei G., Young L., Jones E.M.T., " |
Each two-port network in an RF chain can be described by a parameter set, which relates the voltages and currents appearing at the terminals of that network.<ref name = Matthaei>Matthaei G., Young L., Jones E.M.T., "Microwave Filters, Impedance-Matching Networks, and Coupling Structures", McGraw Hill 1964, Artech House 1980</ref>{{rp|29}} Examples are: [[impedance parameters]], i.e. [[z-parameters]]; [[admittance parameters]], i.e. [[y-parameters]] or, for high frequency situations, [[scattering parameters]], i.e. S-parameters.<ref>Agilent Technologies Inc., "s-Parameter Design", Application note AN154, 2006. Find at: http://sss-mag.com/pdf/AN154.pdf</ref><ref name = Orfanidis>Orfanidis S.J., "Electromagnetic Waves and Antennas", Rutgers University, 1999</ref>{{rp|663}} Scattering parameters avoid the need for ports to be open or short-circuited, which are difficult requirements to achieve at microwave frequencies. |
||
[[File: Two-port network(2).png|thumb|right|Two-port network]] |
[[File: Two-port network(2).png|thumb|right|Two-port network]] |
||
In theory, if the parameter set is known for each of the components in an RF chain, then the response of the chain can be calculated precisely, whatever the configuration. Unfortunately, acquiring the detailed information required to carry out this procedure is usually an onerous task, especially when more than two or three components are in cascade. A simpler approach is to assume the chain is a cascade of impedance matched components and then, subsequently, to apply a tolerance spread for mismatch effects (see later). |
In theory, if the parameter set is known for each of the components in an RF chain, then the response of the chain can be calculated precisely, whatever the configuration. Unfortunately, acquiring the detailed information required to carry out this procedure is usually an onerous task, especially when more than two or three components are in cascade. A simpler approach is to assume the chain is a cascade of impedance matched components and then, subsequently, to apply a tolerance spread for mismatch effects (see later). |
||
{{-}} |
|||
==A system spreadsheet== |
== A system spreadsheet == |
||
A system spreadsheet has been a popular way of displaying the important parameters of a chain, in a stage-by-stage manner, for the frequency range of interest.<ref name = Egan /> It has the advantage of highlighting key performance figures and also pin-pointing where possible problem areas may occur within the chain, which are not always apparent from a consideration of overall results. Such a chart can be compiled manually<ref name = Egan />{{rp|139}} or, more conveniently, by means of a computer program<ref>Analog Devices, " |
A system spreadsheet has been a popular way of displaying the important parameters of a chain, in a stage-by-stage manner, for the frequency range of interest.<ref name = Egan /> It has the advantage of highlighting key performance figures and also pin-pointing where possible problem areas may occur within the chain, which are not always apparent from a consideration of overall results. Such a chart can be compiled manually<ref name = Egan />{{rp|139}} or, more conveniently, by means of a computer program.<ref>Analog Devices, "ADIsimRF Signal Chain Calculator". Find at: www.analog.com/en/design-center/adisimrf.</ref><ref>RFdude System Tools. Find at: http://tools.rfdude.com/rfsyscalc/cascade.html</ref><ref>RF Cafe, RF Cafe Calculator Workbook, v.7.7. Find at: www.rfcafe.com/business/software/rf-cafe-calculator-workbook/</ref><ref>Kelley R., RF Chain Calculator, Atmospheric Radar Research Center. Find at: https://arrc.ou.edu/tools/RF%20Chain%20Calculator%20(8-6-2012%20Release).xlsx</ref> |
||
In addition, 'tookits' are available which provide aids to the system designer.<ref>Teledyne Inc. " |
In addition, 'tookits' are available which provide aids to the system designer.<ref>Teledyne Inc. "Teledyne Toolbox" Find at: www.softpedia.com/get/Science-CAD/Teledyne-Microelectronics-RF-Toolbox.shtml |
||
</ref><ref>Avago Technologies, AppCAD v. 4.0.0 (previously Agilent v. 3.02), Find at: www.hp.woodshot.comwww.hp.woodshot.com</ref><ref>Mathworks, "Four Steps for Building Smarter RF Systems with MATLAB"</ref> |
</ref><ref>Avago Technologies, AppCAD v. 4.0.0 (previously Agilent v. 3.02), Find at: www.hp.woodshot.comwww.hp.woodshot.com</ref><ref>Mathworks, "Four Steps for Building Smarter RF Systems with MATLAB"</ref> |
||
Some routines, useful for spreadsheet development, are given next. |
Some routines, useful for spreadsheet development, are given next. |
||
==Key spreadsheet topics== |
== Key spreadsheet topics == |
||
For the parameters considered below, the chain is assumed to contain a cascade of devices, which are (nominally) impedance matched. The procedures given here allow all calculations to be displayed in the spreadsheet in sequence and no macros are used. Although this makes for a longer spreadsheet, no calculations are hidden from the user. |
For the parameters considered below, the chain is assumed to contain a cascade of devices, which are (nominally) impedance matched. The procedures given here allow all calculations to be displayed in the spreadsheet in sequence and no macros are used. Although this makes for a longer spreadsheet, no calculations are hidden from the user. |
||
For convenience, the spread sheet columns, show the frequency in sub-bands, with bandwidths sufficiently narrow to ensure that any gain ripple is sufficiently characterized. |
For convenience, the spread sheet columns, show the frequency in sub-bands, with bandwidths sufficiently narrow to ensure that any gain ripple is sufficiently characterized. |
||
[[File:Combined_data.png|thumb|right|Adding |
[[File:Combined_data.png|thumb|right|Adding stage ''n'' to the cascade]] |
||
Consider the n |
Consider the ''n''th stage in a chain of RF devices. The cumulative [[Gain (electronics)|gain]], [[noise figure]], 1 dB compression point<ref name = Frenzel(2)>Frenzel L., "What's the difference between the third order intercept and the 1-dB compression points?" Find at: |
||
http://electronicdesign.com/what-s-difference-between-third-order-intercept-and-1-db-compression-point</ref><ref name = Egan />{{rp|119}} and output [[thermal noise]] power for the preceding |
http://electronicdesign.com/what-s-difference-between-third-order-intercept-and-1-db-compression-point</ref><ref name = Egan />{{rp|119}} and output [[thermal noise]] power for the preceding {{nowrap|''n'' − 1}} devices are given by Gcum<sub>''n''−1</sub>, Fcum<sub>''n''−1</sub>, Pcum<sub>''n''−1</sub> and Ncum<sub>''n''−1</sub>, respectively. We wish to determine the new cumulative figures, when the n<sup>th</sup> stage is included, i.e. the values of Gcum<sub>''n''</sub>, Fcum<sub>''n''</sub>, Pcum<sub>''n''</sub> and Ncum<sub>''n''</sub>, given that the ''n''th stage has values of ''G''<sub>''n''</sub>, ''F''<sub>''n''</sub>, P1<sub>''n''</sub> for its gain, noise figure and 1 dB compression point, respectively. |
||
===Cumulative gain=== |
=== Cumulative gain === |
||
The cumulative gain, Gcum<sub>n</sub> after n stages, is given by |
The cumulative gain, Gcum<sub>''n''</sub> after ''n'' stages, is given by |
||
:<math> |
: <math>\mathrm{Gcum}_n = \mathrm{Gcum}_{n-1} \times G_n</math> |
||
and Gcum<sub>n</sub>(dB) is given by |
and Gcum<sub>''n''</sub>(dB) is given by |
||
:<math> |
: <math>\mathrm{Gcum}_n(dB) = \mathrm{Gcum}_{n - 1}(dB) + G_n(dB)</math> |
||
where Gcum<sub>n |
where Gcum<sub>''n''−1</sub> [dB] is the total gain of the first {{nowrap|''n'' − 1}} stages and ''G''<sub>''n''</sub> [dB] is the gain of the ''n''th stage. |
||
Conversion equations between |
Conversion equations between logarithmic and linear terms are: |
||
:<math>G = 10^{G(dB)/10} = \exp \big (0.23026 \times G(dB) \big )</math> |
: <math>G = 10^{G(dB)/10} = \exp \big (0.23026 \times G(dB) \big )</math> |
||
and |
and |
||
: <math>G(dB) = 10 \times \log_{10}G = 4.6429 \times \ln(G) </math> |
: <math>G(dB) = 10 \times \log_{10}G = 4.6429 \times \ln(G) </math> |
||
===Cumulative noise factor ( |
=== Cumulative noise factor (noise Figure) === |
||
The cumulative [[noise factor]], after n stages of the overall cascade, Fcum<sub>n</sub> is given by |
The cumulative [[noise factor]], after ''n'' stages of the overall cascade, Fcum<sub>''n''</sub> is given by |
||
:<math> |
: <math>\mathrm{Fcum}_n = \mathrm{Fcum}_{n - 1} +\frac{F_n -1}{\mathrm{Gcum}_{n-1}}</math> |
||
where Fcum<sub>n |
where Fcum<sub>''n''−1</sub> is the noise factor of the first {{nowrap|''n'' − 1}} stages, ''F''<sub>''n''</sub> is the noise factor of the ''n''th stage, and Gcum<sub>''n''</sub> is the overall gain of ''n'' stages. |
||
The cumulative [[noise figure]] is then |
The cumulative [[noise figure]] is then |
||
:<math> |
: <math>\mathrm{NFcum}_n(dB) = 10 \times \log_{10}(\mathrm{Fcum}_n) = 4.6429 \times \ln(\mathrm{Fcum}_n) </math> |
||
*Note 1: the use of an amplifier with high gain for the first stage will ensure that the noise figure degradations by later stages will be small or negligible. This will be best for system sensitivity, see later. |
* Note 1: the use of an amplifier with high gain for the first stage will ensure that the noise figure degradations by later stages will be small or negligible. This will be best for system sensitivity, see later. |
||
*Note 2: for a passive (lossy) section of the chain, the noise figure of the section equals the loss of that section.<ref name = Brooker>Brooker G., "Sensors for Ranging and Imaging", Chapter 9, Sci Tech Publ. 2009, YesDee Publ. 2012</ref><ref name = Pozar>[[David M. Pozar|Pozar D.M.]], "Microwave Engineering", Wiley, 4th Ed., 2012.</ref>{{rp|55}} So, for example, a 3 dB attenuator has a noise figure of 3 dB. |
* Note 2: for a passive (lossy) section of the chain, the noise figure of the section equals the loss of that section.<ref name = Brooker>Brooker G., "Sensors for Ranging and Imaging", Chapter 9, Sci Tech Publ. 2009, YesDee Publ. 2012</ref><ref name = Pozar>[[David M. Pozar|Pozar D.M.]], "Microwave Engineering", Wiley, 4th Ed., 2012.</ref>{{rp|55}} So, for example, a 3 dB attenuator has a noise figure of 3 dB. |
||
===Cumulative |
=== Cumulative 1 dB compression point === |
||
For spreadsheet purposes, it is convenient to refer the 1 dB compression point<ref name = Frenzel(2) /><ref name = RFCafe>RF Cafe, " |
For spreadsheet purposes, it is convenient to refer the 1 dB compression point<ref name = Frenzel(2) /><ref name = RFCafe>RF Cafe, "Cascaded 1 dB Compression Point (P1dB)". Find at: www.rfcafe.com/references/electrical/p1db.htm</ref> to the input of the RF chain, i.e. P1cum<sub>''n''</sub>(input), |
||
:<math> P1cum_n(input) = \frac{1}{ \frac{1}{P1cum_{n-1}(input)} + \frac{Gcum_n}{P1_n(input)}}</math> |
: <math> P1cum_n(input) = \frac{1}{ \frac{1}{P1cum_{n-1}(input)} + \frac{Gcum_n}{P1_n(input)}}</math> |
||
where P1cum<sub>n-1</sub> is the 1 dB compression point at the input of the first |
where P1cum<sub>n-1</sub> is the 1 dB compression point at the input of the first {{nowrap|''n'' − 1}} stages, P1<sub>''n''</sub> is the 1 dB compression point for the ''n''th stage, referred to its input and Gcum<sub>''n''</sub> is the overall gain including the ''n''th stage. The unit is [mW] or [W]. |
||
*Note: for the best result, i.e. a system tolerant to high level signals, is achieved with a low front end gain. This is in conflict with the need for a low overall noise factor, which requires a high first-stage gain. |
* Note: for the best result, i.e. a system tolerant to high level signals, is achieved with a low front end gain. This is in conflict with the need for a low overall noise factor, which requires a high first-stage gain. |
||
*Note 2: The 1 dB compression point is abbreviated as P1dB, iP1dB, or oP1dB. It is referenced to input or output power level measured in [dBm]. Overall system performance can be practically evaluated by the 1 dB compression method. |
* Note 2: The 1 dB compression point is abbreviated as P1dB, iP1dB, or oP1dB. It is referenced to input or output power level measured in [dBm]. Overall system performance can be practically evaluated by the 1 dB compression method. |
||
Related parameters, such as IP3 or IM3 are helpful fictive numbers used to evaluate the system. The device would burn, applying IP3 input level. Accuracy of the measurement with spectrum analyzer is (HP/Agilent specs: |
Related parameters, such as IP3 or IM3 are helpful fictive numbers used to evaluate the system. The device would burn, applying IP3 input level. Accuracy of the measurement with spectrum analyzer is (HP/Agilent specs: ±1.0 dB, and ±0.5 dB custom device). In linear systems, this all results in AGC. |
||
=== Cumulative noise power === |
=== Cumulative noise power === |
||
The [[thermal noise]] power present at the input of an RF chain,<ref name = Connor>Connor F.R., " |
The [[thermal noise]] power present at the input of an RF chain,<ref name = Connor>Connor F.R., "Noise", Edward Arnold, 2nd Ed. 1982</ref>{{rp|44}}<ref name = Terman>Terman F.E., "Electronic and Radio Engineering", 4th. Ed., 1955</ref>{{rp|435}}<ref name = Vizmuller>Vizmuller P., "RF Design Guide", Artech House, 1955</ref>{{rp|229}} is a maximum in a resistively matched system, and is equal to ''kTB'', where ''k'' is the Boltzmann constant (= {{physconst|k}}), ''T'' is the absolute temperature, and ''B'' is the bandwidth in Hz. |
||
At a temperature of 17 °C (≡ 290 |
At a temperature of 17 °C (≡ 290 K), kTB = 4.003 × 10<sup>−15</sup> W/MHz ≡ −114 dBm for 1 MHz bandwidth. |
||
The thermal noise after n stages of an RF chain, |
The thermal noise after ''n'' stages of an RF chain, with total gain ''G''<sub>T</sub> and noise figure ''F''<sub>T</sub> is given by |
||
:<math>Ncum_n = kTB \times Fcum_n \times Gcum_n</math> |
: <math>Ncum_n = kTB \times Fcum_n \times Gcum_n</math> |
||
where k = Boltzmann |
where ''k'' = the Boltzmann constant, ''T'' is the temperature in kelvins and ''B'' is the bandwidth in hertz, or |
||
:<math>Ncum_n(dBm/Mhz) = -114 +Fcum_n(dB) + Gcum_n(dB)</math> |
: <math>Ncum_n(dBm/Mhz) = -114 +Fcum_n(dB) + Gcum_n(dB)</math> |
||
where Ncum<sub>n</sub>(dBm) is the total noise power in dBm per 1 MHz of bandwidth, |
where Ncum<sub>''n''</sub>(dBm) is the total noise power in dBm per 1 MHz of bandwidth, |
||
In receivers, the cumulative gain is set to ensure that the output noise power of the chain at an appropriate level for the signal processing stages that follow. For example, the noise level at the input to an [[analog-to-digital converter]] ( |
In receivers, the cumulative gain is set to ensure that the output noise power of the chain at an appropriate level for the signal processing stages that follow. For example, the noise level at the input to an [[analog-to-digital converter]] (ADC) must not be at too low a level, otherwise the noise (and any signals within it) is not properly characterized (see the section on ADCs, later). On the other hand, too high a level results in the loss of dynamic range. |
||
==Other related system properties== |
== Other related system properties == |
||
With the basic parameters of the chain determined, other related properties can be derived. |
With the basic parameters of the chain determined, other related properties can be derived. |
||
===Second and third order intercept points === |
=== Second and third order intercept points === |
||
Sometimes performance at high signal levels is defined by means of the "[[second-order intercept point]] (I2)" and the "[[third-order intercept point]] (I3)", rather than by the 1 dB compression point.<ref name = Frenzel(2) /> These are notional signal levels which occur in two-signal testing and correspond to the theoretical points where second and third order inter-modulation products achieve the same power level as the output signal.<ref name = Steer />{{rp|685}}<ref name = Egan />{{rp|91}} The figure illustrates the situation. |
Sometimes performance at high signal levels is defined by means of the "[[second-order intercept point]] (I2)" and the "[[third-order intercept point]] (I3)", rather than by the 1 dB compression point.<ref name = Frenzel(2) /> These are notional signal levels which occur in two-signal testing and correspond to the theoretical points where second and third order inter-modulation products achieve the same power level as the output signal.<ref name = Steer />{{rp|685}}<ref name = Egan />{{rp|91}} The figure illustrates the situation. |
||
| Line 94: | Line 93: | ||
When products, stage to stage, add incoherently, the cumulative results for these products are derived by similar equations to that for the 1 dB compression point. |
When products, stage to stage, add incoherently, the cumulative results for these products are derived by similar equations to that for the 1 dB compression point. |
||
:<math> I2cum_n(input) = \frac{1}{ \frac{1}{I2cum_{n-1}(input)} + \frac{Gcum_n}{I2_n(input)}}</math> |
:<math> I2cum_n(input) = \frac{1}{ \frac{1}{I2cum_{n-1}(input)} + \frac{Gcum_n}{I2_n(input)}}</math> |
||
where I2cum<sub>n |
where I2cum<sub>''n''−1</sub> is the second order intercept point at the input of the first {{nowrap|''n'' − 1}} stages, I2<sub>''n''</sub> is the third order intercept point for the ''n''th stage, referred to its input and Gcum<sub>''n''</sub> is the overall gain including the nth stage. |
||
Similarly, |
Similarly, |
||
:<math> I3cum_n(input) = \frac{1}{ \frac{1}{I3cum_{n-1}(input)} + \frac{Gcum_n}{I3_n(input)}}</math> |
: <math> I3cum_n(input) = \frac{1}{ \frac{1}{I3cum_{n-1}(input)} + \frac{Gcum_n}{I3_n(input)}}</math> |
||
where I3cum<sub>n-1</sub> is the third order intercept point at the input of the first |
where I3cum<sub>n-1</sub> is the third order intercept point at the input of the first {{nowrap|''n'' − 1}} stages, I3<sub>''n''</sub> is the third order intercept point for the ''n''th stage, referred to its input. |
||
The cumulative intercept points are useful when determining the "spurious free dynamic range" |
The cumulative intercept points are useful when determining the "spurious free dynamic range"<ref name = Pozar />{{rp|519}} of a system. |
||
There is an approximate relationship between the third order intercept level and the 1 dB compression level which is<ref name = East1>East P.W., " |
There is an approximate relationship between the third order intercept level and the 1 dB compression level which is<ref name = East1>East P.W., "Microwave System Design Tools and EW Applications", 2nd ed., Artech House 2008</ref>{{rp|59}}<ref name = Vizmuller />{{rp|35}} |
||
:<math>IP3(dB) \approx P1(dB) + 11(dB) </math> |
: <math>IP3(dB) \approx P1(dB) + 11(dB) </math> |
||
Although only an approximation, the relationship is found to apply to a large number of amplifiers.<ref name = RFCafe /> |
Although only an approximation, the relationship is found to apply to a large number of amplifiers.<ref name = RFCafe /> |
||
| Line 109: | Line 108: | ||
=== Signal-to-noise ratio === |
=== Signal-to-noise ratio === |
||
In the spread sheet, the total frequency band of interest B(Hz) is divided into M sub-bands (spreadsheet columns) of B/M (Hz) each, and for each sub-band (m = 1 to M) the thermal noise power is derived, as described above. |
In the spread sheet, the total frequency band of interest ''B''(Hz) is divided into ''M'' sub-bands (spreadsheet columns) of ''B''/''M'' (Hz) each, and for each sub-band (''m'' = 1 to ''M'') the thermal noise power is derived, as described above. In practice, these results will differ slightly, from column to column, if the system has gain ripple. |
||
The signal-to-noise ratio (S:N) is the peak signal power of the pulse ( |
The signal-to-noise ratio (S:N) is the peak signal power of the pulse (''P''<sub>sig</sub>) divided by the total noise power (''P''<sub>noise</sub>) from the ''M'' frequency bins, i.e. |
||
:<math> \frac{S}{N} = \frac{P_{sig}}{ \sum_{m=1}^M P_{noise}(m)} </math> |
: <math> \frac{S}{N} = \frac{P_\text{sig}}{ \sum_{m=1}^M P_\text{noise}(m)} </math> |
||
This is the S:N ratio at RF frequencies. It can be related to the video S:N ratio as shown next. |
This is the S:N ratio at RF frequencies. It can be related to the video S:N ratio as shown next. |
||
| Line 118: | Line 117: | ||
==== Relating RF and video S:N ratios ==== |
==== Relating RF and video S:N ratios ==== |
||
For spreadsheet purposes it can useful to find the RF signal to noise ratio which corresponds to a desired video signal to noise figure after demodulation or detection. |
For spreadsheet purposes it can useful to find the RF signal to noise ratio which corresponds to a desired video signal to noise figure after demodulation or detection. As an RF chain usually has sufficient gain for any noise contribution from the detector diode to be ignored, the video S:N can be shown to be<ref name = East1/>{{rp|115}} |
||
:<math> \Big ( \frac {S}{N} \Big )_{vid} = \frac {G^2.P_S^2}{4.G^2.P_S.kTF'B_V + 2(kTF'G)^2.(B_V.B_R- B_v^2/2)} </math> |
: <math> \Big ( \frac {S}{N} \Big )_\text{vid} = \frac {G^2.P_S^2}{4.G^2.P_S.kTF'B_V + 2(kTF'G)^2.(B_V.B_R- B_v^2/2)} </math> |
||
where |
where |
||
*P<sub>S</sub> =input RF signal power; |
* ''P''<sub>S</sub> = input RF signal power; |
||
*8B<sub>V</sub> and B<sub>R</sub> are the video and RF bandwidths; |
* 8B<sub>V</sub> and B<sub>R</sub> are the video and RF bandwidths; |
||
*F' = F |
* ''F''′ = ''F'' − 1/''G'' where ''G'' is the chain gain and ''F'' is the effective noise figure; |
||
*k = Boltzmann |
* ''k'' = the Boltzmann constant; and |
||
*T = the ambient temperature |
* ''T'' = the ambient temperature |
||
[If there is significant gain variation across the band, then it can be divided into M sub-bands and results summed for these sub-bands, as described earlier.] |
[If there is significant gain variation across the band, then it can be divided into M sub-bands and results summed for these sub-bands, as described earlier.] |
||
From the above equation, as the noise power in the RF band is P<sub>N</sub> = kTB<sub>R</sub>F', a relationship between RF and |
From the above equation, as the noise power in the RF band is ''P''<sub>''N''</sub> = ''kTB''<sub>R</sub>''F''′, a relationship between RF and video S:N ratios can be found. |
||
:<math> \Big ( \frac {S}{N} \Big )_{vid} = \frac {\Big ( \frac {S}{N} \Big )_{rf}^2}{4. \Big ( \frac{S}{N} \Big)_{rf} . \frac{B_V}{B_R} +2. \frac{B_V}{B_R} - \Big ( \frac{B_V}{B_R} \Big ) ^2}</math> |
: <math> \Big ( \frac {S}{N} \Big )_{vid} = \frac {\Big ( \frac {S}{N} \Big )_{rf}^2}{4. \Big ( \frac{S}{N} \Big)_{rf} . \frac{B_V}{B_R} +2. \frac{B_V}{B_R} - \Big ( \frac{B_V}{B_R} \Big ) ^2}</math> |
||
(This result can be found elsewhere<ref name = Lipsky>Lipsky S.E., "Microwave Passive Direction Finding", Wiley, N.Y., 1987</ref>{{rp|188}}). |
(This result can be found elsewhere<ref name = Lipsky>Lipsky S.E., "Microwave Passive Direction Finding", Wiley, N.Y., 1987</ref>{{rp|188}}). |
||
Inverting the relationship gives the RF signal-to-noise ratio required to achieve a given video S:N ratio: |
Inverting the relationship gives the RF signal-to-noise ratio required to achieve a given video S:N ratio: |
||
:<math> \Big ( \frac {S}{N} \Big )_{rf} = \frac{B_V}{B_R}. \Bigg [ 2.\Big( \frac{S}{N} \Big )_{vid} \pm \sqrt { 4. \Big (\frac{S}{N} \Big |
: <math> \Big ( \frac {S}{N} \Big )_{rf} = \frac{B_V}{B_R}. \Bigg [ 2.\Big( \frac{S}{N} \Big )_{vid} \pm \sqrt { 4. \Big (\frac{S}{N} \Big |
||
)_{vid}^2 + \Big( \frac{S}{N} \Big )_{vid} . \Big ( 2. \frac{B_R}{B_V} -1 \Big )} \Bigg ] </math> |
)_{vid}^2 + \Big( \frac{S}{N} \Big )_{vid} . \Big ( 2. \frac{B_R}{B_V} -1 \Big )} \Bigg ] </math> |
||
===Signal sensitivity=== |
=== Signal sensitivity === |
||
Signal sensitivity is important for receiving systems and refers to the minimum signal level at the input that is necessary to give a signal that can be resolved reliably by the detection process at the end of the RF chain. |
Signal sensitivity is important for receiving systems and refers to the minimum signal level at the input that is necessary to give a signal that can be resolved reliably by the detection process at the end of the RF chain. This parameter is less important in the case of repeaters and transmitter drivers where signal levels tend to be higher and other concerns such as stage overload and spurious signal generation tend to be more relevant. |
||
Determining a value for system sensitivity can be difficult and depends on many things, including the method of detection, the signal coding method, the bandwidth of the RF channel, and whether or not digital processing is involved. |
Determining a value for system sensitivity can be difficult and depends on many things, including the method of detection, the signal coding method, the bandwidth of the RF channel, and whether or not digital processing is involved. Two important parameters used in assessing sensitivity performance of a system are<ref>Blake L.V., "Prediction of Radar Range", Ch.2, Radar Handbook, Ed. Skolnik M.L., McGraw-Hill, 1970</ref>{{rp|2.16}}<ref name = Brooker />{{rp|204}} the "probability of detection" and the "false alarm rate". |
||
Statistical methods are often used in the decision process (see Tsui<ref name = Tsui |
Statistical methods are often used in the decision process (see Tsui<ref name = Tsui>Tsui J.B., "Microwave Receivers with Electronic Warfare Applications", Kreiger Pub. Co., USA, 1992</ref>{{rp|20}} and Skolnik<ref name = Skolnik1>Skolnik M.I., "Introduction to Radar Systems", McGraw Hill Kogakusha, 2nd Ed. 1980, 1962</ref>{{rp|16}}). |
||
====Tangential sensitivity==== |
==== Tangential sensitivity ==== |
||
[[File:Tangential_Sensitivity(2).png|thumb|right|Tangential Sensitivity]] |
[[File:Tangential_Sensitivity(2).png|thumb|right|Tangential Sensitivity]] |
||
Tangential sensitivity, (TSS), defines that input power which results in a video signal to noise ratio of approximately 8 dB from the detector.<ref name = Tsui />{{rp|16}} The thumbnail shows an example of a typical detected pulse at the TSS limit, with the pulse + noise sitting at a level just clear of the noise floor. |
Tangential sensitivity, (TSS), defines that input power which results in a video signal to noise ratio of approximately 8 dB from the detector.<ref name = Tsui />{{rp|16}} The thumbnail shows an example of a typical detected pulse at the TSS limit, with the pulse + noise sitting at a level just clear of the noise floor. The TSS level is too low a value for reliable pulse detection in a practical scenario, but it can be determined with sufficient accuracy in bench tests on a receiver to give a quick guide figure for system performance. |
||
In a wideband receiver, with a square-law detector, the TSS value at the chain input terminals is given by |
In a wideband receiver, with a square-law detector, the TSS value at the chain input terminals is given by<ref name = Tsui />{{rp|18}} |
||
:<math>TSS(dBm) = 114 + 10.logF_T +10 |
: <math>TSS(dBm) = 114 + 10.logF_T + 10 \log \Big ( 6.31 B_V = 2.5 \sqrt {2.B_V B_R - B_V^2} \Big ) </math> |
||
From this, the S:N of the RF signal, at the input to the detector can be obtained when the video output is at TSS. |
From this, the S:N of the RF signal, at the input to the detector can be obtained when the video output is at TSS. |
||
:<math>\Big (\frac{S}{N} \Big )_R(dB) =10 |
: <math>\Big (\frac{S}{N} \Big )_R(dB) =10 \log \Bigg [ \frac{B_V}{B_R} \Bigg(6.31 + 2.5 \sqrt{2 \frac{B_R}{B_V} - 1} \Bigg) \Bigg ]</math> |
||
This equation shows that the S:N at RF is typically less than unity, in wideband systems, when the video output is at TSS. |
This equation shows that the S:N at RF is typically less than unity, in wideband systems, when the video output is at TSS. For example, if ''B''<sub>R</sub>/''B''<sub>V</sub> = 500 then the equation gives (S:N)<sub>R</sub> = 0.17 (≈ −7.7 dB). (Note: a similar result is obtained by using the equation relating RF and video S:N ratios, given in the previous section<ref name=Lipsky />{{rp|190}}). |
||
The thumbnail shows the simulated video output (at TSS) corresponding to an RF pulse in wideband noise with S:N = 0.17 and a bandwidth ratio of 500. |
The thumbnail shows the simulated video output (at TSS) corresponding to an RF pulse in wideband noise with S:N = 0.17 and a bandwidth ratio of 500. |
||
{{-}} |
{{-}} |
||
====A S:N guideline figure for pulse detection==== |
==== A S:N guideline figure for pulse detection ==== |
||
The sensitivity of a system may be taken as the "minimum detectable signal". |
The sensitivity of a system may be taken as the "minimum detectable signal". This is that level of signal that exceeds a threshold value by a suitable margin (If the level is set too low, noise spikes will exceed it too frequently and if the signal+noise does not exceed it by a sufficient margin then it may fall below the threshold giving pulse termination prematurely. So, in determining the minimum detectable signal, it is necessary to choose the "false alarm rate" and "probability of detection" values appropriate to the system requirement. To aid the designer, graphs are available, to help determine the necessary S:N ratio at the detector.<ref name = Tsui />{{rp|30}}<ref name = Skolnik1 />{{rp|28}}<ref name = Skolnik2>Skolnik M.I., "Radar Handbook", McGraw Hill 1970</ref>{{rp|2.19}}<ref>{{cite web |last1=Blake |first1=L.V. |date=23 December 1969 |title=A Guide to Basic Pulse-Radar Maximum-Range Calculation: Part 1 - Equations, Definitions, and Aids to Calculation |website=Defence Technical Information Center |citeseerx=10.1.1.881.2809 |url=https://apps.dtic.mil/sti/pdfs/AD0701321.pdf}}</ref>{{rp|21}}<ref name = Brooker />{{rp|357}} |
||
In the case of pulse detection of a signal in noise, following the detector in a wideband receiver, where the RF bandwidth greatly exceeds the video bandwidth, a guideline figure for reliable performance a S:N (at video) is 16 to 18 dB.<ref name = East1/>{{rp|87}} |
In the case of pulse detection of a signal in noise, following the detector in a wideband receiver, where the RF bandwidth greatly exceeds the video bandwidth, a guideline figure for reliable performance a S:N (at video) is 16 to 18 dB.<ref name = East1/>{{rp|87}} This is a useful figure for use in spreadsheets, and it corresponds to a probability of detection of over 99% for a Swerling 1 target<ref>{{cite journal |last1=Swerling |first1=P. |title=Detection of fluctuating pulsed signals in the presence of noise |journal=IEEE Transactions on Information Theory |date=September 1957 |volume=3 |issue=3 |pages=175–178 |doi=10.1109/TIT.1957.1057419 |hdl=2142/74003 |hdl-access=free }}</ref><ref>{{cite web |title=Detection of Signals in Noise §10.1. Receiver Noise |website=University of Sydney |s2cid=5580446 |url=http://www.acfr.usyd.edu.au/pdfs/training/sensorSystems/10%20Detection%20of%20Signals%20in%20Noise.pdf |archive-url=https://web.archive.org/web/20091112005933/http://www.acfr.usyd.edu.au/pdfs/training/sensorSystems/10%20Detection%20of%20Signals%20in%20Noise.pdf |archive-date=2009-11-12}}{{clarify|reason=this source appears to be a chapter in a book; name the book, name the author, name the publisher, etc;|date=July 2023}}</ref> |
||
(Although lower values of S:N can give acceptable " |
(Although lower values of S:N can give acceptable "probability of detection" and "false alarm rate" figures, the measurement of pulse lengths become less reliable because noise spikes on pulses may extend below the chosen threshold level). |
||
[[File:Two_Detected_Pulses.png|thumb|right|Pulses with 18 & 15dB S:N]] |
[[File:Two_Detected_Pulses.png|thumb|right|Pulses with 18 & 15dB S:N]] |
||
| Line 179: | Line 176: | ||
The video S:N ratio can be related to the RF S:N ratio, as shown earlier. |
The video S:N ratio can be related to the RF S:N ratio, as shown earlier. |
||
In scenarios, such as radar pulse detection, integration over several pulses may occur and a lower value of S:N then becomes acceptable.<ref name = Skolnik1 />{{rp|30}} |
In scenarios, such as radar pulse detection, integration over several pulses may occur and a lower value of S:N then becomes acceptable.<ref name = Skolnik1 />{{rp|30}} In general, system sensitivity and pulse detection theory are specialized topics <ref name = Vizmuller />{{rp|12}} and often involve statistical procedures not easily adapted for spreadsheets. |
||
{{-}} |
{{-}} |
||
==Mismatches== |
== Mismatches == |
||
In the past, devices in an RF chain have often been inter-connected |
In the past, devices in an RF chain have often been inter-connected by short [[transmission line]]s, such as [[coaxial cable]],<ref name = Steer />{{rp|165}}<ref>The Microwave Engineer's Handbook, "Coaxial Lines", Horizon House – Microwaves Inc., 1966, but published annually</ref><ref name = Palmer>Palmer R.C., "Introduction to RF Circuit Design for Communication Systems", R.C. Palmer 2016</ref>{{rp|13-3}}<ref name = Matthaei />{{rp|165}} (0.414" and 0.085"semi-rigid cables are popular<ref>Ellis S., "5 Things to Know About Semi-Rigid Cable assemblies", Pasternack Products and Resources, Find at www.paternack.com/t-Semi-Rigid-Cables.aspx</ref><ref name = Frenzel />{{rp|481}}), by [[stripline]]<ref name = Eatman>Eatman J., "Strip Lines" and "Microstrip", Eatman Assoc., Tx., Find at: www.smta.org/chapters/files/Central-Texas_SMTA_Striplines_and_Microstrips-_Jim_Eatman.pdf |
||
</ref><ref name = Matthaei />{{rp|168}}<ref name = Palmer />{{rp|13–4}} or by [[microstrip]].<ref name = Palmer />{{rp|13–6}}<ref name = Eatman /> |
</ref><ref name = Matthaei />{{rp|168}}<ref name = Palmer />{{rp|13–4}} or by [[microstrip]].<ref name = Palmer />{{rp|13–6}}<ref name = Eatman /> Almost invariably, mismatches occur at the various interfaces. |
||
Standard equations for a transmission line, terminated in a mismatch, are<ref>{{cite book |last1=Ragan |first1=George Leslie |title=Microwave transmission circuits |date=1965 |publisher=Dover Publications |oclc=760986760 }}{{page needed|date=November 2021}}</ref><ref name = Vizmuller /> |
Standard equations for a transmission line, terminated in a mismatch, are<ref>{{cite book |last1=Ragan |first1=George Leslie |title=Microwave transmission circuits |date=1965 |publisher=Dover Publications |oclc=760986760 }}{{page needed|date=November 2021}}</ref><ref name = Vizmuller /> |
||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
[[File:Mismatched_Cable.png|thumb|right|Reflections in a Transmission Line]] |
[[File:Mismatched_Cable.png|thumb|right|Reflections in a Transmission Line]] |
||
=== |
=== Response of a mismatched transmission line === |
||
If a transmission line is mismatched at both ends, multiple-reflected signals can be present on the line, resulting in ripple on the frequency response, as seen at the load. |
If a transmission line is mismatched at both ends, multiple-reflected signals can be present on the line, resulting in ripple on the frequency response, as seen at the load. |
||
Where only first time round echoes are considered (i.e. multiple reflections are ignored), the output response is given by |
Where only first time round echoes are considered (i.e. multiple reflections are ignored), the output response is given by |
||
:<math> V_{out} = V_1( 1 + \alpha ^2 |
: <math> V_\text{out} = V_1 ( 1 + \alpha ^2 \ \rho_1 \ \rho_2 \ e^{j \ 2 \pi f \ 2 T_\text{d}} ) </math> |
||
[[File:Response_of_Mismatched_Cable.png|thumb|right|Response of a mismatched cable]] |
[[File:Response_of_Mismatched_Cable.png|thumb|right|Response of a mismatched cable]] |
||
where |
|||
| ⚫ | |||
Where |
|||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
A typical plot is shown in the thumbnail. |
A typical plot is shown in the thumbnail. |
||
This response has a ripple component with a peak-to-peak value ΔA, given by |
This response has a ripple component with a peak-to-peak value Δ''A'', given by |
||
:<math> \Delta A = 2 |
: <math> \Delta A = 2 \frac{1 + \rho_1 \rho_2}{1 - \rho_1 \rho_2} </math> |
||
The frequency difference from peak-to-peak (or trough-to-trough) of the ripple is given by ΔΩ where |
The frequency difference from peak-to-peak (or trough-to-trough) of the ripple is given by ΔΩ where |
||
:<math> \Delta \Omega = \frac{\pi}{T_d} </math> |
: <math> \Delta \Omega = \frac{\pi}{T_d} </math> |
||
{{-}} |
{{-}} |
||
=== |
=== Response of multiple mismatches === |
||
An RF chain may contain many inter-stage links of various lengths. |
An RF chain may contain many inter-stage links of various lengths. The overall result is obtained using |
||
:<math> \text{Overall Result} = \prod_{n=1}^N Vout_n </math> |
: <math> \text{Overall Result} = \prod_{n=1}^N Vout_n </math> |
||
This can give an overall response which is far from flat. |
This can give an overall response which is far from flat. As an example, a random collection of 25 cascaded (but separated) links give the result shown. Here, a random selection of path delays are assumed, with ''α'' taken as unity and ''ρ''<sub>1</sub> and ''ρ''<sub>2</sub> taking the typical value 0.15 (a [[return loss]] ≈ 16 dB), for the frequency range 10 to 20 GHz |
||
[[File:Multiple_Mismatches.png|center|The Response of Multiple Mismatches]] |
[[File:Multiple_Mismatches.png|center|The Response of Multiple Mismatches]] |
||
| Line 231: | Line 225: | ||
For this example, calibration at 50 MHz intervals would be advisable, in order to characterize this response. |
For this example, calibration at 50 MHz intervals would be advisable, in order to characterize this response. |
||
The ripple amplitude would be reduced if the mismatches ρ<sub>1</sub> and ρ<sub>2</sub> were improved but, especially if the lengths of the interconnecting links were made shorter. |
The ripple amplitude would be reduced if the mismatches ''ρ''<sub>1</sub> and ''ρ''<sub>2</sub> were improved but, especially if the lengths of the interconnecting links were made shorter. An RF chain, made up of surface mounted components, interconnected by stripline,<ref name = Matthaei />{{rp|168}} which can be made physically small, may achieve less than 0.5 dB ripple. The use of integrated circuits would give lower ripple still (see, for example ''[[Monolithic microwave integrated circuit]]''). |
||
==Mixers== |
== Mixers == |
||
The presence of a mixer in an RF chain complicates the spreadsheet because the frequency range at the output differs from that at the input. |
The presence of a mixer in an RF chain complicates the spreadsheet because the frequency range at the output differs from that at the input. In addition, because mixers are non-linear devices, they introduce many inter-modulation products, which are undesirable, especially in wide-band systems. |
||
For an input signal at frequency F<sub>sig</sub> and a local oscillator frequency F<sub>lo</sub> |
For an input signal at frequency ''F''<sub>sig</sub> and a local oscillator frequency ''F''<sub>lo</sub>, the output frequencies of a mixer are given by |
||
:<math> \text{Mixer Output} = n\times F_{lo} \pm \ m\times F{sig} </math> |
: <math> \text{Mixer Output} = n\times F_\text{lo} \pm \ m\times F\text{sig} </math> |
||
where m and n are integers. |
where ''m'' and ''n'' are integers. |
||
Usually, for a mixer, the desired output is the frequency with n = m = 1. |
Usually, for a mixer, the desired output is the frequency with ''n'' = ''m'' = 1. The other outputs are often referred to as "spurs" and are usually unwanted. Frequency plans are often drawn up, often as a separate spreadsheet, to minimize the consequences of these unwanted signals<ref>Flores J.L., "The Distances Chart: A New Approach to Spurs Calculation". Find at: www.microwavejournal.com/articles/9084-the-distances-chart-a-new-approach-to-spurs-calculation |
||
</ref><ref name = Egan />{{rp|168}}<ref>Microwaves 101, " |
</ref><ref name = Egan />{{rp|168}}<ref>Microwaves 101, "Mixer Spur Chart" (an Excel spreadsheet). Find at: www.microwaves101.com/encyclopedias/mixer</ref><ref>Kinget P., "RF System Design", Bell Labs N.J. Find at: https://docplayer.net/3629684-Rf-system-design-peter-kinget-bell-laboratories-lucent-technologies-murray-hill-nj-usa.html</ref> |
||
Some general points regarding mixer performance are: |
Some general points regarding mixer performance are: |
||
# Products with m and n small tend to have the largest amplitude so they require the most attention and, if possible, should fall outside the operational pass-band. Products when m and n are high tend to be of smaller amplitude and, often, can be ignored. |
# Products with m and n small tend to have the largest amplitude so they require the most attention and, if possible, should fall outside the operational pass-band. Products when m and n are high tend to be of smaller amplitude and, often, can be ignored. |
||
# Down-converters are best realized with F<sub>LO</sub> set high, i.e. |
# Down-converters are best realized with ''F''<sub>LO</sub> set high, i.e. ''F''<sub>LO</sub> > ''F''<sub>Sig</sub>. |
||
# In receivers, image frequency signals are less troublesome if the IF (intermediate frequency) is set very high.<ref name = Vizmuller />{{rp|10}} |
# In receivers, image frequency signals are less troublesome if the IF (intermediate frequency) is set very high.<ref name = Vizmuller />{{rp|10}} |
||
# Local oscillator leakage can be minimized by using double-balanced mixers<ref name = East1 />{{rp|37}}<ref name = Pozar />{{rp|652}}<ref name = Egan />{{rp|165}} |
# Local oscillator leakage can be minimized by using double-balanced mixers<ref name = East1 />{{rp|37}}<ref name = Pozar />{{rp|652}}<ref name = Egan />{{rp|165}} |
||
# Presenting large amplitude signals to a mixer should be avoided in order to avoid high level spurs. |
# Presenting large amplitude signals to a mixer should be avoided in order to avoid high level spurs. Consequently, it is poor practice to have high gain prior to a mixer (a requirement which may conflict with a need for a low overall noise figure). In any case, the LO power applied to the mixer should greatly exceed the signal power.<ref name = Egan />{{rp|166}} |
||
In a typical mixer, the 1 dB compression point is between 5 and 10 dB below the local oscillator power.<ref name = Browne>Browne J., " |
In a typical mixer, the 1 dB compression point is between 5 and 10 dB below the local oscillator power.<ref name = Browne>Browne J., "Understanding Dynamic Range", Microwaves and RF, Feb. 2011. Find at: www.mwrf.com/test-and-measurement/understanding-dynamic-range</ref> |
||
Note that the approximate relationship between IP3 and P1 differs from that for amplifiers. |
Note that the approximate relationship between IP3 and P1 differs from that for amplifiers. For mixers, a very approximate expression is:<ref name = Vizmuller />{{rp|35}} |
||
:<math>IP3(dB) \approx P1(dB) + 15(dB) </math> |
:<math>IP3(dB) \approx P1(dB) + 15(dB) </math> |
||
| Line 261: | Line 255: | ||
== Dynamic range == |
== Dynamic range == |
||
Dynamic Range (D<sub>R</sub>) is that range of input powers from that of a just detectable signal up to a level at which the chain overloads.<ref name = Browne /> |
Dynamic Range (''D''<sub>R</sub>) is that range of input powers from that of a just detectable signal up to a level at which the chain overloads.<ref name = Browne /> |
||
D<sub>R</sub> is given by |
''D''<sub>R</sub> is given by |
||
:<math> |
: <math>D_\text{R} = P_\text{max} - P_\text{sens} </math> |
||
where P<sub>max</sub> is the |
where ''P''<sub>max</sub> is the maximum signal power, discussed earlier, and ''P''<sub>sens</sub> is the smallest input power for signal detection (see Sensitivity, discussed earlier). |
||
== Field strength, antenna gain and signal power for receiver antennas == |
== Field strength, antenna gain and signal power for receiver antennas == |
||
(Several assumptions are made for the equations that follow. |
(Several assumptions are made for the equations that follow. Firstly, if the incoming signal is polarized, then the antenna is rotated to match that polarization, secondly, it is assumed that the antenna output impedance is matched to that of the chain input port and, thirdly, when gain is quoted, this is the maximum gain of the antenna (sometimes referred to as the boresight gain)) |
||
When the power density of an incoming signal is P<sub>inc</sub> then the power at the antenna terminals is P<sub>R</sub> is given by |
|||
| ⚫ | |||
When the power density of an incoming signal is ''P''<sub>inc</sub> then the power at the antenna terminals is ''P''<sub>R</sub> is given by |
|||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
Where ''A''<sub>eff</sub> is the effective area of the antenna (or the [[Antenna aperture]]). |
|||
The gain of the antenna is related to the effective aperture by.<ref name = Connor2>Connor F.R., " Antennas", Edward Arnold, 1972</ref>{{rp|90}}<ref name = Orfanidis />{{rp|746}} :<math>G = A_{eff}. \frac{4 \pi}{ \lambda ^2} </math> |
|||
| ⚫ | |||
| ⚫ | |||
In practice, the effective aperture of the antenna is smaller than the actual physical area. |
The gain of the antenna is related to the effective aperture by<ref name = Connor2>Connor F.R., "Antennas", Edward Arnold, 1972</ref>{{rp|90}}<ref name = Orfanidis />{{rp|746}} |
||
: <math>G = A_\text{eff} \frac{4 \pi}{ \lambda ^2} </math> |
|||
In practice, the effective aperture of the antenna is smaller than the actual physical area. For a dish, the effective area is about 0.5 to 0.6 times the actual area, and for a rectangular horn antenna it is about 0.7 to 0.8 times the actual area.<ref name = Orfanidis />{{rp|747}} For a dipole there is no actual physical area, but as a half-wave dipole has a power gain<ref name = Connor2 />{{rp|35}} of 1.62 and the effective area can be inferred from that. |
|||
== Front-end losses == |
== Front-end losses == |
||
Front end losses are those losses which occur prior to the first active device of a receiver chain. |
Front end losses are those losses which occur prior to the first active device of a receiver chain. They often arise because of the operational requirements of a particular system, but should be minimized, where possible, to ensure the best possible system sensitivity. These losses add to the effective noise figure of the first amplifier stage, dB for dB.<ref name = Vizmuller />{{rp|15}} |
||
| ⚫ | Some losses are a consequence of the system construction, such as antenna to receiver feeder loss and, may include waveguide-to-coax. transition loss. Other losses arise from the necessity to include devices to protect the chain from high incident powers. For example, a radar system requires a transmit–receive (TR) cell<ref>Keller E.W. & Townsend M.A., "Transmit-Receive Devices", Chapter XI, Principles of Radar, ed. Reintjee J.F., McGraw-Hill, 1946</ref><ref>Kefalas G.P. & Wiltse J.C., "Duplexers", Chapter 8, Radar Handbook, ed. Skolnik M.I., McGraw-Hill 1970</ref><ref>Skolnik, "Introduction to Radar Systems", McGraw-Hill 1962, 1980, pp.361</ref> to protect the chain from the high-power signals of the radar's transmitter. Similarly, a front end limiter<ref>Skolnik M.I., "Solid-state limiters", Chapter 9, Introduction to Radar Systems, McGraw-Hill 1962, 1980, p. 363</ref> is needed, on a ship, to protect the chain from the emissions of high-power transmitters located close by. |
||
| ⚫ | Some losses are a consequence of the system construction, such as antenna to receiver feeder loss and, may include waveguide-to-coax. transition loss. |
||
In addition, the system may include a band-pass filter at its input, to protect it from out-of-band signals, and this device will have some pass-band loss. |
In addition, the system may include a band-pass filter at its input, to protect it from out-of-band signals, and this device will have some pass-band loss. |
||
| Line 292: | Line 288: | ||
=== Detectors (diodes) === |
=== Detectors (diodes) === |
||
Detector [[diode]]s for RF and Microwaves may be point contact diodes, [[Schottky diode]]s, Gallium Arsenide or p-n junction devices.<ref>Bayliss R., " |
Detector [[diode]]s for RF and Microwaves may be point contact diodes, [[Schottky diode]]s, Gallium Arsenide or p-n junction devices.<ref>Bayliss R., "Microwave Diodes...Why Schottky-barrier? Why point-contact?", Microwaves and RF, Sept. 2013</ref> Of these, Schottky diodes and junction diodes require biassing for best results. Also, silicon junction diodes perform less well at high frequencies. |
||
A typical detector diode has a TSS of |
A typical detector diode has a TSS of −45 to −50 dBm <ref name = Tsui />{{rp|136}}<ref>"The Microwave Engineer's Handbook", "Microwave Diode Characteristics", Horizon House, 1966, p.225</ref><ref>Bayliss, "Microwave Diodes, (Fig.24)", Microwaves and RF, Dec 2013. Find at: www.mwrf.com/search/node/Microwave%20Diodes...%20%20Why%20a%20Schottky-barrier |
||
</ref> and peak pulse powers of |
</ref> and peak pulse powers of 20 dBm, although better figures are possible<ref>Massachusetts Bay Technologies: point contact detector diodes with a TSS = −48 dBm, find at: https://massbaytech.com/wp-content/uploads/2016/06/MBT-Catalog-0111.pdf, Macom: Schottky detector diodes with a TSS figure = −52 dBm and a peak power rating of +30 dBm for 1 μs, find at: https://cdn.macom.com/datasheets/Schottky_%20Detector_%20Diodes.pdf; Agilent Technology: Schottky diodes with TSS of −60 dBmm, find at: www.g3ynh.info/circuits/diode_data/AN923.pdf; Micran: gallium arsenide diodes with a TSS −60 dBm and maximum power capability of +20 dBm, find at: http://micran.com/UserFile/File/mmic/QZBD_Process.pdf</ref>). |
||
At low powers, diodes have a square-law characteristic, i.e. the output voltage is proportional to the input power, but at higher powers (above about |
At low powers, diodes have a square-law characteristic, i.e. the output voltage is proportional to the input power, but at higher powers (above about −15 dBm) the device becomes linear, with the output voltage proportional to the input voltage. |
||
Square law detectors can give detectable signals at video, in wideband systems, even when the RF S:N is less than unity. |
Square law detectors can give detectable signals at video, in wideband systems, even when the RF S:N is less than unity. For example, using the RF-to-Video relationships given earlier, for a system which has a bandwidth of 6 GHz, and an RF S:N value of 0.185 (−7 dB), the video S:N (i.e. TSS) will be 6.31 (8 dB). (Tsui's equations give an RF S:N value of 0.171 for this example). |
||
=== Detector-log-video |
=== Detector-log-video amplifiers (DLVAs) === |
||
DLVAs<ref>Kapur R., " |
DLVAs<ref>Kapur R., "Detector Logarithmic Video Amplifier (DLVA)", everything RF, July 2018. Find at www.everythingrf.com/community/what-is-a-detector-log-video-amplifier |
||
</ref><ref name = East1 />{{rp|72}} have been commonly found in direction finding systems, using multiple channels, squinted antennas and amplitude comparison methods.<ref name = East1 />{{rp|155}}<ref>{{cite journal |last1=Ibrahim Ali Al-Sharabi |first1=Khalil |last2=Fiz |first2=Duraid |last3=Mohammad |first3=a |title=Design of Wideband Radio Direction Finder Based On Amplitude Comparison |journal=Al-Rafdain Engineering Journal |date=28 October 2011 |volume=19 |issue=5 |pages=77–86 |doi=10.33899/rengj.2011.26752 |doi-access=free }}</ref> They are also useful for compressing the dynamic range of incoming signals of receivers, prior to digitising. |
</ref><ref name = East1 />{{rp|72}} have been commonly found in direction finding systems, using multiple channels, squinted antennas and amplitude comparison methods.<ref name = East1 />{{rp|155}}<ref>{{cite journal |last1=Ibrahim Ali Al-Sharabi |first1=Khalil |last2=Fiz |first2=Duraid |last3=Mohammad |first3=a |title=Design of Wideband Radio Direction Finder Based On Amplitude Comparison |journal=Al-Rafdain Engineering Journal |date=28 October 2011 |volume=19 |issue=5 |pages=77–86 |doi=10.33899/rengj.2011.26752 |doi-broken-date=7 December 2024 |doi-access=free }}</ref> They are also useful for compressing the dynamic range of incoming signals of receivers, prior to digitising. They cover frequency ranges such as 2–6 GHz and 6–18 GHz. There are also wideband devices available which cover the range 2–18 GHz. |
||
A simple DLVA contains a broadband diode detector followed by an amplifier with a logarithmic characteristic and has an input power range of, typically, |
A simple DLVA contains a broadband diode detector followed by an amplifier with a logarithmic characteristic and has an input power range of, typically, −45 dBm to 0 dBm,<ref>American Microwave Corporation, DLVA Model: LVD-218-50. Find at: www.americanmic.com/catalog/detector-log-video-amplifiers-dlva/ |
||
</ref><ref name = Pasternack>Pasternack, " |
</ref><ref name = Pasternack>Pasternack, "Broadband Log Video Amplifiers". Find at: www.pasternack.com/pages/Featured_Products/broadband-log-video-amplifiers</ref><ref>Gotch D.J., "Detector Log Video Amplifiers", Internal technical note, Filtronic Subsystems, Yorks. U.K.</ref> which may be increased to −45 to +15 dBm in an extended-range DLVA. Two devices, together with an amplifier, can be combined to give an effective range of −65 dBm to +15 dBm. |
||
In a successive-detection DLVA, which includes a low noise amplifier, the power range may to be, typically |
In a successive-detection DLVA, which includes a low noise amplifier, the power range may to be, typically −65 dBm to +10 dBm<ref>American Microwave Corporation, DLVA Model: LVD-218-70. Find at: http://www.americanmic.com/catalog/detector-log-video-amplifiers-dlva/</ref><ref name = Pasternack /> |
||
=== Instantaneous frequency measurement systems (IFMs), digital discriminator units DDUs) === |
=== Instantaneous frequency measurement systems (IFMs), digital discriminator units DDUs) === |
||
IFMs can provide a frequency measurement of a single pulse.<ref name = East1 />{{rp|126}}{{rp|140}} |
IFMs can provide a frequency measurement of a single pulse.<ref name = East1 />{{rp|126}}{{rp|140}} They incorporate a set of delay-line frequency discriminators, with delay lengths increasing in a binary or other sequence.<ref>Sullivan W.B., "Instantaneous Frequency Measurement Receivers for Maritime Patrol", Jour. Electronic Defence, Vol. 25, No. 10</ref><ref name = East2>{{cite journal |last1=East |first1=P.W. |title=Design techniques and performance of digital IFM |journal=IEE Proceedings F - Communications, Radar and Signal Processing |date=1982 |volume=129 |issue=3 |pages=154–163 |doi=10.1049/ip-f-1.1982.0024 }}</ref> They usually incorporate some gain of their own. The discriminator with the longest delay line establishes the frequency measurement accuracy and resolution, the shortest delay line correlator defines the unambiguous bandwidth of the DFD and the remaining correlators serve to resolve ambiguities.<ref>Wide Band Systems Inc., "Digital Frequency Discriminators", find at: www.widebandsystems.com</ref> |
||
Usually, there is an input, limiting amplifier present in the IFM. |
Usually, there is an input, limiting amplifier present in the IFM. This boosts the received signal to a constant level for processing by the correlators, making the frequency-data-decoding task of the frequency processor easier, and to emphasise the "capture effect" when simultaneous signals are present. Normally the RF amplifier will produce a minimum of 10 dB limiting at the lowest specified signal input level. If the RF S:N ratio is too low, the output of the longest delay line correlator (which sets the frequency resolution of the IFM) will become degraded and noisy. At high S:N ratios (+10 dBm), the measured frequency accuracy approaches the correlator-limited rms error, but at approximately −3 dBm SNR, ambiguity errors appear, causing large measurement inaccuracies.<ref name = Sullivan1>{{cite journal |last1=Sullivan |first1=William B. |title=Design optimization improves IFM/DFD receiver accuracy |journal=Microwaves |date=1 September 1992 |volume=31 |issue=9 |pages=96–99 |bibcode=1992MicWa..31...96S }}</ref> |
||
The lowest input power level of a typical DDU is about |
The lowest input power level of a typical DDU is about −75 dBm,<ref name = Sullivan1 /> and with a receiver noise figure of 10 dB, it gives a frequency accuracy of approximately 1 MHz<ref name = East2 /> They have dynamic ranges of 65 to 75 dB and cover frequency bands such as 2–6 GHz, 6–18 GHz and some wideband devices cover 2–18 GHz.<ref>Sullivan W.B., "Ultra-Wideband IFM Receiver Fulfils Design Requirements", MSN & CT, April 1985</ref><ref>Keshavamurthy T. L., "2 to 18 GHz Single-band Digital Frequency Discriminator", Microwave Journal, March 1989</ref><ref name = East2 /> |
||
With the advent of digital techniques, analogous processes to those of an analog system have been realized.<ref>Elisra Electronic Systems, " |
With the advent of digital techniques, analogous processes to those of an analog system have been realized.<ref>Elisra Electronic Systems, "A Digital Instantaneous Frequency Measurement Receiver", May 2007. Find at: www.microwavejournal.com/articles/4772-a-digital-instantaneous-frequency-measurement-receiver</ref><ref>Sullivan W.B., "Advances in Design Improve Wideband Receivers", MSN & Communications Technology, April 1986.</ref> |
||
=== Analog to digital converters ( |
=== Analog to digital converters (ADCs) === |
||
An [[Analog-to-digital converter]],<ref>Kester W., " |
An [[Analog-to-digital converter]],<ref>Kester W., "Analog-Digital Conversion", Analog Devices. Find at: https://www.analog.com/en/education/education-library/data-conversion-handbook.html |
||
</ref><ref>McGlinchy M., " |
</ref><ref>McGlinchy M., "Double the Span and Digitize Signals Using MCU's ADC", Find at: www.electronicdesign.com/print/48825</ref> located at the end of the RF chain, provides digital signals for further signal processing. As the ADC operates with sampled signals, it is necessary for the [[Nyquist–Shannon sampling theorem]] to be satisfied, if data is not to be lost. As shown earlier, a low-amplitude RF pulse immersed in wideband noise, can be detected by a square-law diode detector. Similarly spread spectrum signals can be recovered from below the noise floor by compression. Consequently, to ensure no loss of data, the chain gain should be high enough to ensure that thermal noise will activate the ADC adequately, so that any signals present within the noise, can be recovered correctly by the detection or compression process. Typically, the rms noise voltage present the input to the ADC should be one or two bits of the ADC range, but no lower. On the other hand, having excessive chain gain so that the noise floor is unnecessarily high, will result in the loss of dynamic range. |
||
Consider, as an example, a [[chirp]] signal with time-bandwidth product of 200 and of amplitude of |
Consider, as an example, a [[chirp]] signal with time-bandwidth product of 200 and of amplitude of {{sfrac|1|2}} LSB which is embedded in noise with an rms voltage of 1 LSB, present at the input to an ADC. he digitized, quantised output, relative to the mean value, is similar to the example in the left-hand figure below. After compression in the signal processor, a high amplitude pulse, whose magnitude is well above the noise is obtained, as shown in the right-hand figure. |
||
[[File:Quantised_and_Compressed_Waveforms.png|center]] |
[[File:Quantised_and_Compressed_Waveforms.png|center]] |
||
This example happens to show, unintentionally, the benefits of [[dither]]<ref>Smith S.W., " |
This example happens to show, unintentionally, the benefits of [[dither]]<ref>Smith S.W., "Digital Signal Processing", Newnes, 2003, pp. 38-39</ref><ref>Kester W., "ADC Input Noise", Find at: www.analog.com/media/en/analog-dialogue/volume-40/number-1/articles/adc-input-noise.pdf |
||
</ref><ref>Melconian L., " |
</ref><ref>Melconian L., "Improving ADC Converter Performance Using Dither", National Semiconductor Application Note 804, Texas Instruments Literature No. SNOA232. Find at: www.ti.com.cn/cn/lit/an/snoa232/snoa232.pdf</ref> which is used to improve the linearity and dynamic range of an ADC. In the case of the signal considered here, if there was no noise present, but just the signal alone, its amplitude would be insufficient to operate the ADC. |
||
==References== |
== References == |
||
{{reflist}} |
{{reflist}} |
||
Latest revision as of 16:19, 7 December 2024
An RF chain is a cascade of electronic components and sub-units which may include amplifiers, filters, mixers, attenuators and detectors.[1] It can take many forms, for example, as a wide-band receiver-detector for electronic warfare (EW) applications, as a tunable narrow-band receiver for communications purposes, as a repeater in signal distribution systems, or as an amplifier and up-converters for a transmitter-driver. In this article, the term RF (radio frequency) covers the frequency range "medium Frequencies" up to "microwave Frequencies", i.e. from 100 kHz to 20 GHz.[2]: 15
The key electrical parameters for an RF chain are system gain, noise figure (or noise factor) and overload level.[3]: 2 Other important parameters, related to these properties, are sensitivity (the minimum signal level which can be resolved at the output of the chain); dynamic range (the total range of signals that the chain can handle from a maximum level down to smallest level that can be reliably processed) and spurious signal levels (unwanted signals produced by devices such as mixers and non-linear amplifiers). In addition, there may be concerns regarding the immunity to incoming interference or, conversely, the amount of undesirable radiation emanating from the chain. The tolerance of a system to mechanical vibration may be important too. Furthermore, the physical properties of the chain, such as size, weight and power consumption may also be important considerations.
An addition to considering the performance of the RF chain, the signal and signal-to-noise requirements of the various signal processing components, which may follow it, are discussed because they often determine the target figures for a chain.
Parameter sets
[edit]Each two-port network in an RF chain can be described by a parameter set, which relates the voltages and currents appearing at the terminals of that network.[4]: 29 Examples are: impedance parameters, i.e. z-parameters; admittance parameters, i.e. y-parameters or, for high frequency situations, scattering parameters, i.e. S-parameters.[5][6]: 663 Scattering parameters avoid the need for ports to be open or short-circuited, which are difficult requirements to achieve at microwave frequencies.

In theory, if the parameter set is known for each of the components in an RF chain, then the response of the chain can be calculated precisely, whatever the configuration. Unfortunately, acquiring the detailed information required to carry out this procedure is usually an onerous task, especially when more than two or three components are in cascade. A simpler approach is to assume the chain is a cascade of impedance matched components and then, subsequently, to apply a tolerance spread for mismatch effects (see later).
A system spreadsheet
[edit]A system spreadsheet has been a popular way of displaying the important parameters of a chain, in a stage-by-stage manner, for the frequency range of interest.[3] It has the advantage of highlighting key performance figures and also pin-pointing where possible problem areas may occur within the chain, which are not always apparent from a consideration of overall results. Such a chart can be compiled manually[3]: 139 or, more conveniently, by means of a computer program.[7][8][9][10]
In addition, 'tookits' are available which provide aids to the system designer.[11][12][13]
Some routines, useful for spreadsheet development, are given next.
Key spreadsheet topics
[edit]For the parameters considered below, the chain is assumed to contain a cascade of devices, which are (nominally) impedance matched. The procedures given here allow all calculations to be displayed in the spreadsheet in sequence and no macros are used. Although this makes for a longer spreadsheet, no calculations are hidden from the user. For convenience, the spread sheet columns, show the frequency in sub-bands, with bandwidths sufficiently narrow to ensure that any gain ripple is sufficiently characterized.

Consider the nth stage in a chain of RF devices. The cumulative gain, noise figure, 1 dB compression point[14][3]: 119 and output thermal noise power for the preceding n − 1 devices are given by Gcumn−1, Fcumn−1, Pcumn−1 and Ncumn−1, respectively. We wish to determine the new cumulative figures, when the nth stage is included, i.e. the values of Gcumn, Fcumn, Pcumn and Ncumn, given that the nth stage has values of Gn, Fn, P1n for its gain, noise figure and 1 dB compression point, respectively.
Cumulative gain
[edit]The cumulative gain, Gcumn after n stages, is given by
and Gcumn(dB) is given by
where Gcumn−1 [dB] is the total gain of the first n − 1 stages and Gn [dB] is the gain of the nth stage.
Conversion equations between logarithmic and linear terms are:
and
Cumulative noise factor (noise Figure)
[edit]The cumulative noise factor, after n stages of the overall cascade, Fcumn is given by
where Fcumn−1 is the noise factor of the first n − 1 stages, Fn is the noise factor of the nth stage, and Gcumn is the overall gain of n stages.
The cumulative noise figure is then
- Note 1: the use of an amplifier with high gain for the first stage will ensure that the noise figure degradations by later stages will be small or negligible. This will be best for system sensitivity, see later.
- Note 2: for a passive (lossy) section of the chain, the noise figure of the section equals the loss of that section.[15][16]: 55 So, for example, a 3 dB attenuator has a noise figure of 3 dB.
Cumulative 1 dB compression point
[edit]For spreadsheet purposes, it is convenient to refer the 1 dB compression point[14][17] to the input of the RF chain, i.e. P1cumn(input),
where P1cumn-1 is the 1 dB compression point at the input of the first n − 1 stages, P1n is the 1 dB compression point for the nth stage, referred to its input and Gcumn is the overall gain including the nth stage. The unit is [mW] or [W].
- Note: for the best result, i.e. a system tolerant to high level signals, is achieved with a low front end gain. This is in conflict with the need for a low overall noise factor, which requires a high first-stage gain.
- Note 2: The 1 dB compression point is abbreviated as P1dB, iP1dB, or oP1dB. It is referenced to input or output power level measured in [dBm]. Overall system performance can be practically evaluated by the 1 dB compression method.
Related parameters, such as IP3 or IM3 are helpful fictive numbers used to evaluate the system. The device would burn, applying IP3 input level. Accuracy of the measurement with spectrum analyzer is (HP/Agilent specs: ±1.0 dB, and ±0.5 dB custom device). In linear systems, this all results in AGC.
Cumulative noise power
[edit]The thermal noise power present at the input of an RF chain,[18]: 44 [19]: 435 [20]: 229 is a maximum in a resistively matched system, and is equal to kTB, where k is the Boltzmann constant (= 1.380649×10−23 J⋅K−1[21]), T is the absolute temperature, and B is the bandwidth in Hz.
At a temperature of 17 °C (≡ 290 K), kTB = 4.003 × 10−15 W/MHz ≡ −114 dBm for 1 MHz bandwidth.
The thermal noise after n stages of an RF chain, with total gain GT and noise figure FT is given by
where k = the Boltzmann constant, T is the temperature in kelvins and B is the bandwidth in hertz, or
where Ncumn(dBm) is the total noise power in dBm per 1 MHz of bandwidth,
In receivers, the cumulative gain is set to ensure that the output noise power of the chain at an appropriate level for the signal processing stages that follow. For example, the noise level at the input to an analog-to-digital converter (ADC) must not be at too low a level, otherwise the noise (and any signals within it) is not properly characterized (see the section on ADCs, later). On the other hand, too high a level results in the loss of dynamic range.
Other related system properties
[edit]With the basic parameters of the chain determined, other related properties can be derived.
Second and third order intercept points
[edit]Sometimes performance at high signal levels is defined by means of the "second-order intercept point (I2)" and the "third-order intercept point (I3)", rather than by the 1 dB compression point.[14] These are notional signal levels which occur in two-signal testing and correspond to the theoretical points where second and third order inter-modulation products achieve the same power level as the output signal.[1]: 685 [3]: 91 The figure illustrates the situation.
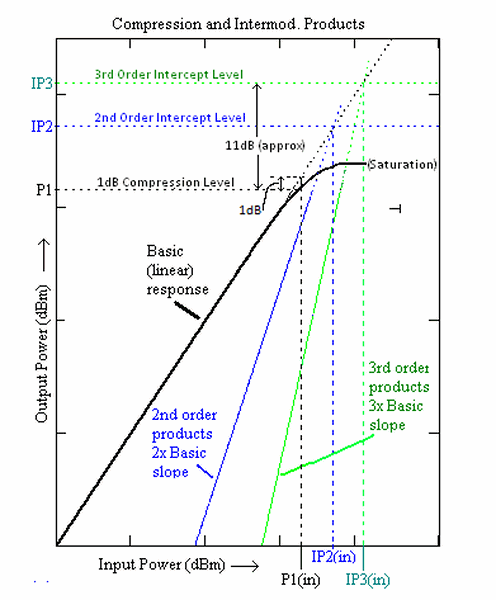
In practice, the intercept levels are never achieved because an amplifier has gone into limiting before they are reached, but they are useful theoretical points from which to predict intercept levels at lower input powers. In dB terms, they decrease at twice the rate (IP2) and three times the rate (IP3) of the fundamental signals.
When products, stage to stage, add incoherently, the cumulative results for these products are derived by similar equations to that for the 1 dB compression point.
where I2cumn−1 is the second order intercept point at the input of the first n − 1 stages, I2n is the third order intercept point for the nth stage, referred to its input and Gcumn is the overall gain including the nth stage.
Similarly,
where I3cumn-1 is the third order intercept point at the input of the first n − 1 stages, I3n is the third order intercept point for the nth stage, referred to its input.
The cumulative intercept points are useful when determining the "spurious free dynamic range"[16]: 519 of a system.
There is an approximate relationship between the third order intercept level and the 1 dB compression level which is[22]: 59 [20]: 35
Although only an approximation, the relationship is found to apply to a large number of amplifiers.[17]
Signal-to-noise ratio
[edit]In the spread sheet, the total frequency band of interest B(Hz) is divided into M sub-bands (spreadsheet columns) of B/M (Hz) each, and for each sub-band (m = 1 to M) the thermal noise power is derived, as described above. In practice, these results will differ slightly, from column to column, if the system has gain ripple.
The signal-to-noise ratio (S:N) is the peak signal power of the pulse (Psig) divided by the total noise power (Pnoise) from the M frequency bins, i.e.
This is the S:N ratio at RF frequencies. It can be related to the video S:N ratio as shown next.
Relating RF and video S:N ratios
[edit]For spreadsheet purposes it can useful to find the RF signal to noise ratio which corresponds to a desired video signal to noise figure after demodulation or detection. As an RF chain usually has sufficient gain for any noise contribution from the detector diode to be ignored, the video S:N can be shown to be[22]: 115
where
- PS = input RF signal power;
- 8BV and BR are the video and RF bandwidths;
- F′ = F − 1/G where G is the chain gain and F is the effective noise figure;
- k = the Boltzmann constant; and
- T = the ambient temperature
[If there is significant gain variation across the band, then it can be divided into M sub-bands and results summed for these sub-bands, as described earlier.]
From the above equation, as the noise power in the RF band is PN = kTBRF′, a relationship between RF and video S:N ratios can be found.
(This result can be found elsewhere[23]: 188 ).
Inverting the relationship gives the RF signal-to-noise ratio required to achieve a given video S:N ratio:
Signal sensitivity
[edit]Signal sensitivity is important for receiving systems and refers to the minimum signal level at the input that is necessary to give a signal that can be resolved reliably by the detection process at the end of the RF chain. This parameter is less important in the case of repeaters and transmitter drivers where signal levels tend to be higher and other concerns such as stage overload and spurious signal generation tend to be more relevant.
Determining a value for system sensitivity can be difficult and depends on many things, including the method of detection, the signal coding method, the bandwidth of the RF channel, and whether or not digital processing is involved. Two important parameters used in assessing sensitivity performance of a system are[24]: 2.16 [15]: 204 the "probability of detection" and the "false alarm rate".
Statistical methods are often used in the decision process (see Tsui[25]: 20 and Skolnik[26]: 16 ).
Tangential sensitivity
[edit]
Tangential sensitivity, (TSS), defines that input power which results in a video signal to noise ratio of approximately 8 dB from the detector.[25]: 16 The thumbnail shows an example of a typical detected pulse at the TSS limit, with the pulse + noise sitting at a level just clear of the noise floor. The TSS level is too low a value for reliable pulse detection in a practical scenario, but it can be determined with sufficient accuracy in bench tests on a receiver to give a quick guide figure for system performance.
In a wideband receiver, with a square-law detector, the TSS value at the chain input terminals is given by[25]: 18
From this, the S:N of the RF signal, at the input to the detector can be obtained when the video output is at TSS.
This equation shows that the S:N at RF is typically less than unity, in wideband systems, when the video output is at TSS. For example, if BR/BV = 500 then the equation gives (S:N)R = 0.17 (≈ −7.7 dB). (Note: a similar result is obtained by using the equation relating RF and video S:N ratios, given in the previous section[23]: 190 ).
The thumbnail shows the simulated video output (at TSS) corresponding to an RF pulse in wideband noise with S:N = 0.17 and a bandwidth ratio of 500.
A S:N guideline figure for pulse detection
[edit]The sensitivity of a system may be taken as the "minimum detectable signal". This is that level of signal that exceeds a threshold value by a suitable margin (If the level is set too low, noise spikes will exceed it too frequently and if the signal+noise does not exceed it by a sufficient margin then it may fall below the threshold giving pulse termination prematurely. So, in determining the minimum detectable signal, it is necessary to choose the "false alarm rate" and "probability of detection" values appropriate to the system requirement. To aid the designer, graphs are available, to help determine the necessary S:N ratio at the detector.[25]: 30 [26]: 28 [27]: 2.19 [28]: 21 [15]: 357
In the case of pulse detection of a signal in noise, following the detector in a wideband receiver, where the RF bandwidth greatly exceeds the video bandwidth, a guideline figure for reliable performance a S:N (at video) is 16 to 18 dB.[22]: 87 This is a useful figure for use in spreadsheets, and it corresponds to a probability of detection of over 99% for a Swerling 1 target[29][30]
(Although lower values of S:N can give acceptable "probability of detection" and "false alarm rate" figures, the measurement of pulse lengths become less reliable because noise spikes on pulses may extend below the chosen threshold level).

As examples, thumbnails show simulated examples of a detected pulse, in noise, where S:N = 18 dB and 15 dB. As can be seen, if the S:N falls to 15 dB or lower, it becomes difficult to set a threshold level for pulse detection, that is clear of the noise floor, and yet does not result in early termination.
The video S:N ratio can be related to the RF S:N ratio, as shown earlier.
In scenarios, such as radar pulse detection, integration over several pulses may occur and a lower value of S:N then becomes acceptable.[26]: 30 In general, system sensitivity and pulse detection theory are specialized topics [20]: 12 and often involve statistical procedures not easily adapted for spreadsheets.
Mismatches
[edit]In the past, devices in an RF chain have often been inter-connected by short transmission lines, such as coaxial cable,[1]: 165 [31][32]: 13–3 [4]: 165 (0.414" and 0.085"semi-rigid cables are popular[33][2]: 481 ), by stripline[34][4]: 168 [32]: 13–4 or by microstrip.[32]: 13–6 [34] Almost invariably, mismatches occur at the various interfaces.
Standard equations for a transmission line, terminated in a mismatch, are[35][20]
- Voltage Reflection coefficient = Γ, where Γ = (ZI − Z0)/(ZI + Z0)
- Return loss(power) = 20 log |Γ| VSWR = (1 + Γ)/(1 − Γ) (see Standing wave ratio)
- Mismatch loss = −10 log(1 − Γ2)

Response of a mismatched transmission line
[edit]If a transmission line is mismatched at both ends, multiple-reflected signals can be present on the line, resulting in ripple on the frequency response, as seen at the load.
Where only first time round echoes are considered (i.e. multiple reflections are ignored), the output response is given by

where
- α is the loss for a single pass through the cable,
- ρ1 and ρ2 are the voltage reflection coefficients of the terminations,
- f is the frequency,
- Td is the (single pass) propagation delay of the cable
A typical plot is shown in the thumbnail.
This response has a ripple component with a peak-to-peak value ΔA, given by
The frequency difference from peak-to-peak (or trough-to-trough) of the ripple is given by ΔΩ where
Response of multiple mismatches
[edit]An RF chain may contain many inter-stage links of various lengths. The overall result is obtained using
This can give an overall response which is far from flat. As an example, a random collection of 25 cascaded (but separated) links give the result shown. Here, a random selection of path delays are assumed, with α taken as unity and ρ1 and ρ2 taking the typical value 0.15 (a return loss ≈ 16 dB), for the frequency range 10 to 20 GHz
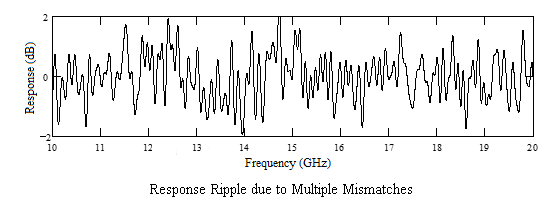
For this example, calibration at 50 MHz intervals would be advisable, in order to characterize this response.
The ripple amplitude would be reduced if the mismatches ρ1 and ρ2 were improved but, especially if the lengths of the interconnecting links were made shorter. An RF chain, made up of surface mounted components, interconnected by stripline,[4]: 168 which can be made physically small, may achieve less than 0.5 dB ripple. The use of integrated circuits would give lower ripple still (see, for example Monolithic microwave integrated circuit).
Mixers
[edit]The presence of a mixer in an RF chain complicates the spreadsheet because the frequency range at the output differs from that at the input. In addition, because mixers are non-linear devices, they introduce many inter-modulation products, which are undesirable, especially in wide-band systems.
For an input signal at frequency Fsig and a local oscillator frequency Flo, the output frequencies of a mixer are given by
where m and n are integers.
Usually, for a mixer, the desired output is the frequency with n = m = 1. The other outputs are often referred to as "spurs" and are usually unwanted. Frequency plans are often drawn up, often as a separate spreadsheet, to minimize the consequences of these unwanted signals[36][3]: 168 [37][38]
Some general points regarding mixer performance are:
- Products with m and n small tend to have the largest amplitude so they require the most attention and, if possible, should fall outside the operational pass-band. Products when m and n are high tend to be of smaller amplitude and, often, can be ignored.
- Down-converters are best realized with FLO set high, i.e. FLO > FSig.
- In receivers, image frequency signals are less troublesome if the IF (intermediate frequency) is set very high.[20]: 10
- Local oscillator leakage can be minimized by using double-balanced mixers[22]: 37 [16]: 652 [3]: 165
- Presenting large amplitude signals to a mixer should be avoided in order to avoid high level spurs. Consequently, it is poor practice to have high gain prior to a mixer (a requirement which may conflict with a need for a low overall noise figure). In any case, the LO power applied to the mixer should greatly exceed the signal power.[3]: 166
In a typical mixer, the 1 dB compression point is between 5 and 10 dB below the local oscillator power.[39]
Note that the approximate relationship between IP3 and P1 differs from that for amplifiers. For mixers, a very approximate expression is:[20]: 35
As this is very approximate, it is advisable to refer to the specification of the mixer in question, for clarification.
Dynamic range
[edit]Dynamic Range (DR) is that range of input powers from that of a just detectable signal up to a level at which the chain overloads.[39]
DR is given by
where Pmax is the maximum signal power, discussed earlier, and Psens is the smallest input power for signal detection (see Sensitivity, discussed earlier).
Field strength, antenna gain and signal power for receiver antennas
[edit](Several assumptions are made for the equations that follow. Firstly, if the incoming signal is polarized, then the antenna is rotated to match that polarization, secondly, it is assumed that the antenna output impedance is matched to that of the chain input port and, thirdly, when gain is quoted, this is the maximum gain of the antenna (sometimes referred to as the boresight gain))
When the power density of an incoming signal is Pinc then the power at the antenna terminals is PR is given by
Where Aeff is the effective area of the antenna (or the Antenna aperture). Power density, which is in watts per metre squared, can be related to electric field strength ER, given in volts per metre, by
The gain of the antenna is related to the effective aperture by[40]: 90 [6]: 746
In practice, the effective aperture of the antenna is smaller than the actual physical area. For a dish, the effective area is about 0.5 to 0.6 times the actual area, and for a rectangular horn antenna it is about 0.7 to 0.8 times the actual area.[6]: 747 For a dipole there is no actual physical area, but as a half-wave dipole has a power gain[40]: 35 of 1.62 and the effective area can be inferred from that.
Front-end losses
[edit]Front end losses are those losses which occur prior to the first active device of a receiver chain. They often arise because of the operational requirements of a particular system, but should be minimized, where possible, to ensure the best possible system sensitivity. These losses add to the effective noise figure of the first amplifier stage, dB for dB.[20]: 15
Some losses are a consequence of the system construction, such as antenna to receiver feeder loss and, may include waveguide-to-coax. transition loss. Other losses arise from the necessity to include devices to protect the chain from high incident powers. For example, a radar system requires a transmit–receive (TR) cell[41][42][43] to protect the chain from the high-power signals of the radar's transmitter. Similarly, a front end limiter[44] is needed, on a ship, to protect the chain from the emissions of high-power transmitters located close by.
In addition, the system may include a band-pass filter at its input, to protect it from out-of-band signals, and this device will have some pass-band loss.
Signal and S:N requirements of signal processing devices
[edit]Detectors (diodes)
[edit]Detector diodes for RF and Microwaves may be point contact diodes, Schottky diodes, Gallium Arsenide or p-n junction devices.[45] Of these, Schottky diodes and junction diodes require biassing for best results. Also, silicon junction diodes perform less well at high frequencies. A typical detector diode has a TSS of −45 to −50 dBm [25]: 136 [46][47] and peak pulse powers of 20 dBm, although better figures are possible[48]).
At low powers, diodes have a square-law characteristic, i.e. the output voltage is proportional to the input power, but at higher powers (above about −15 dBm) the device becomes linear, with the output voltage proportional to the input voltage.
Square law detectors can give detectable signals at video, in wideband systems, even when the RF S:N is less than unity. For example, using the RF-to-Video relationships given earlier, for a system which has a bandwidth of 6 GHz, and an RF S:N value of 0.185 (−7 dB), the video S:N (i.e. TSS) will be 6.31 (8 dB). (Tsui's equations give an RF S:N value of 0.171 for this example).
Detector-log-video amplifiers (DLVAs)
[edit]DLVAs[49][22]: 72 have been commonly found in direction finding systems, using multiple channels, squinted antennas and amplitude comparison methods.[22]: 155 [50] They are also useful for compressing the dynamic range of incoming signals of receivers, prior to digitising. They cover frequency ranges such as 2–6 GHz and 6–18 GHz. There are also wideband devices available which cover the range 2–18 GHz.
A simple DLVA contains a broadband diode detector followed by an amplifier with a logarithmic characteristic and has an input power range of, typically, −45 dBm to 0 dBm,[51][52][53] which may be increased to −45 to +15 dBm in an extended-range DLVA. Two devices, together with an amplifier, can be combined to give an effective range of −65 dBm to +15 dBm.
In a successive-detection DLVA, which includes a low noise amplifier, the power range may to be, typically −65 dBm to +10 dBm[54][52]
Instantaneous frequency measurement systems (IFMs), digital discriminator units DDUs)
[edit]IFMs can provide a frequency measurement of a single pulse.[22]: 126 : 140 They incorporate a set of delay-line frequency discriminators, with delay lengths increasing in a binary or other sequence.[55][56] They usually incorporate some gain of their own. The discriminator with the longest delay line establishes the frequency measurement accuracy and resolution, the shortest delay line correlator defines the unambiguous bandwidth of the DFD and the remaining correlators serve to resolve ambiguities.[57] Usually, there is an input, limiting amplifier present in the IFM. This boosts the received signal to a constant level for processing by the correlators, making the frequency-data-decoding task of the frequency processor easier, and to emphasise the "capture effect" when simultaneous signals are present. Normally the RF amplifier will produce a minimum of 10 dB limiting at the lowest specified signal input level. If the RF S:N ratio is too low, the output of the longest delay line correlator (which sets the frequency resolution of the IFM) will become degraded and noisy. At high S:N ratios (+10 dBm), the measured frequency accuracy approaches the correlator-limited rms error, but at approximately −3 dBm SNR, ambiguity errors appear, causing large measurement inaccuracies.[58]
The lowest input power level of a typical DDU is about −75 dBm,[58] and with a receiver noise figure of 10 dB, it gives a frequency accuracy of approximately 1 MHz[56] They have dynamic ranges of 65 to 75 dB and cover frequency bands such as 2–6 GHz, 6–18 GHz and some wideband devices cover 2–18 GHz.[59][60][56]
With the advent of digital techniques, analogous processes to those of an analog system have been realized.[61][62]
Analog to digital converters (ADCs)
[edit]An Analog-to-digital converter,[63][64] located at the end of the RF chain, provides digital signals for further signal processing. As the ADC operates with sampled signals, it is necessary for the Nyquist–Shannon sampling theorem to be satisfied, if data is not to be lost. As shown earlier, a low-amplitude RF pulse immersed in wideband noise, can be detected by a square-law diode detector. Similarly spread spectrum signals can be recovered from below the noise floor by compression. Consequently, to ensure no loss of data, the chain gain should be high enough to ensure that thermal noise will activate the ADC adequately, so that any signals present within the noise, can be recovered correctly by the detection or compression process. Typically, the rms noise voltage present the input to the ADC should be one or two bits of the ADC range, but no lower. On the other hand, having excessive chain gain so that the noise floor is unnecessarily high, will result in the loss of dynamic range.
Consider, as an example, a chirp signal with time-bandwidth product of 200 and of amplitude of 1/2 LSB which is embedded in noise with an rms voltage of 1 LSB, present at the input to an ADC. he digitized, quantised output, relative to the mean value, is similar to the example in the left-hand figure below. After compression in the signal processor, a high amplitude pulse, whose magnitude is well above the noise is obtained, as shown in the right-hand figure.

This example happens to show, unintentionally, the benefits of dither[65][66][67] which is used to improve the linearity and dynamic range of an ADC. In the case of the signal considered here, if there was no noise present, but just the signal alone, its amplitude would be insufficient to operate the ADC.
References
[edit]- ^ a b c Steer M., "Microwave and RF Design", Scitech Publ., Inc., N.C., 2010, also from Yes Dee Publ., India, 2016
- ^ a b Frenzel L.E. "Principles of Electronic Communication Systems", 3rd Ed., McGraw Hill, 2008
- ^ a b c d e f g h Egan W.F., "Practical RF System Design", Wiley, 2003
- ^ a b c d Matthaei G., Young L., Jones E.M.T., "Microwave Filters, Impedance-Matching Networks, and Coupling Structures", McGraw Hill 1964, Artech House 1980
- ^ Agilent Technologies Inc., "s-Parameter Design", Application note AN154, 2006. Find at: http://sss-mag.com/pdf/AN154.pdf
- ^ a b c Orfanidis S.J., "Electromagnetic Waves and Antennas", Rutgers University, 1999
- ^ Analog Devices, "ADIsimRF Signal Chain Calculator". Find at: www.analog.com/en/design-center/adisimrf.
- ^ RFdude System Tools. Find at: http://tools.rfdude.com/rfsyscalc/cascade.html
- ^ RF Cafe, RF Cafe Calculator Workbook, v.7.7. Find at: www.rfcafe.com/business/software/rf-cafe-calculator-workbook/
- ^ Kelley R., RF Chain Calculator, Atmospheric Radar Research Center. Find at: https://arrc.ou.edu/tools/RF%20Chain%20Calculator%20(8-6-2012%20Release).xlsx
- ^ Teledyne Inc. "Teledyne Toolbox" Find at: www.softpedia.com/get/Science-CAD/Teledyne-Microelectronics-RF-Toolbox.shtml
- ^ Avago Technologies, AppCAD v. 4.0.0 (previously Agilent v. 3.02), Find at: www.hp.woodshot.comwww.hp.woodshot.com
- ^ Mathworks, "Four Steps for Building Smarter RF Systems with MATLAB"
- ^ a b c Frenzel L., "What's the difference between the third order intercept and the 1-dB compression points?" Find at: http://electronicdesign.com/what-s-difference-between-third-order-intercept-and-1-db-compression-point
- ^ a b c Brooker G., "Sensors for Ranging and Imaging", Chapter 9, Sci Tech Publ. 2009, YesDee Publ. 2012
- ^ a b c Pozar D.M., "Microwave Engineering", Wiley, 4th Ed., 2012.
- ^ a b RF Cafe, "Cascaded 1 dB Compression Point (P1dB)". Find at: www.rfcafe.com/references/electrical/p1db.htm
- ^ Connor F.R., "Noise", Edward Arnold, 2nd Ed. 1982
- ^ Terman F.E., "Electronic and Radio Engineering", 4th. Ed., 1955
- ^ a b c d e f g Vizmuller P., "RF Design Guide", Artech House, 1955
- ^ "2022 CODATA Value: Boltzmann constant". The NIST Reference on Constants, Units, and Uncertainty. NIST. May 2024. Retrieved 2024-05-18.
- ^ a b c d e f g East P.W., "Microwave System Design Tools and EW Applications", 2nd ed., Artech House 2008
- ^ a b Lipsky S.E., "Microwave Passive Direction Finding", Wiley, N.Y., 1987
- ^ Blake L.V., "Prediction of Radar Range", Ch.2, Radar Handbook, Ed. Skolnik M.L., McGraw-Hill, 1970
- ^ a b c d e Tsui J.B., "Microwave Receivers with Electronic Warfare Applications", Kreiger Pub. Co., USA, 1992
- ^ a b c Skolnik M.I., "Introduction to Radar Systems", McGraw Hill Kogakusha, 2nd Ed. 1980, 1962
- ^ Skolnik M.I., "Radar Handbook", McGraw Hill 1970
- ^ Blake, L.V. (23 December 1969). "A Guide to Basic Pulse-Radar Maximum-Range Calculation: Part 1 - Equations, Definitions, and Aids to Calculation" (PDF). Defence Technical Information Center. CiteSeerX 10.1.1.881.2809.
- ^ Swerling, P. (September 1957). "Detection of fluctuating pulsed signals in the presence of noise". IEEE Transactions on Information Theory. 3 (3): 175–178. doi:10.1109/TIT.1957.1057419. hdl:2142/74003.
- ^ "Detection of Signals in Noise §10.1. Receiver Noise" (PDF). University of Sydney. S2CID 5580446. Archived from the original (PDF) on 2009-11-12.[clarification needed]
- ^ The Microwave Engineer's Handbook, "Coaxial Lines", Horizon House – Microwaves Inc., 1966, but published annually
- ^ a b c Palmer R.C., "Introduction to RF Circuit Design for Communication Systems", R.C. Palmer 2016
- ^ Ellis S., "5 Things to Know About Semi-Rigid Cable assemblies", Pasternack Products and Resources, Find at www.paternack.com/t-Semi-Rigid-Cables.aspx
- ^ a b Eatman J., "Strip Lines" and "Microstrip", Eatman Assoc., Tx., Find at: www.smta.org/chapters/files/Central-Texas_SMTA_Striplines_and_Microstrips-_Jim_Eatman.pdf
- ^ Ragan, George Leslie (1965). Microwave transmission circuits. Dover Publications. OCLC 760986760.[page needed]
- ^ Flores J.L., "The Distances Chart: A New Approach to Spurs Calculation". Find at: www.microwavejournal.com/articles/9084-the-distances-chart-a-new-approach-to-spurs-calculation
- ^ Microwaves 101, "Mixer Spur Chart" (an Excel spreadsheet). Find at: www.microwaves101.com/encyclopedias/mixer
- ^ Kinget P., "RF System Design", Bell Labs N.J. Find at: https://docplayer.net/3629684-Rf-system-design-peter-kinget-bell-laboratories-lucent-technologies-murray-hill-nj-usa.html
- ^ a b Browne J., "Understanding Dynamic Range", Microwaves and RF, Feb. 2011. Find at: www.mwrf.com/test-and-measurement/understanding-dynamic-range
- ^ a b Connor F.R., "Antennas", Edward Arnold, 1972
- ^ Keller E.W. & Townsend M.A., "Transmit-Receive Devices", Chapter XI, Principles of Radar, ed. Reintjee J.F., McGraw-Hill, 1946
- ^ Kefalas G.P. & Wiltse J.C., "Duplexers", Chapter 8, Radar Handbook, ed. Skolnik M.I., McGraw-Hill 1970
- ^ Skolnik, "Introduction to Radar Systems", McGraw-Hill 1962, 1980, pp.361
- ^ Skolnik M.I., "Solid-state limiters", Chapter 9, Introduction to Radar Systems, McGraw-Hill 1962, 1980, p. 363
- ^ Bayliss R., "Microwave Diodes...Why Schottky-barrier? Why point-contact?", Microwaves and RF, Sept. 2013
- ^ "The Microwave Engineer's Handbook", "Microwave Diode Characteristics", Horizon House, 1966, p.225
- ^ Bayliss, "Microwave Diodes, (Fig.24)", Microwaves and RF, Dec 2013. Find at: www.mwrf.com/search/node/Microwave%20Diodes...%20%20Why%20a%20Schottky-barrier
- ^ Massachusetts Bay Technologies: point contact detector diodes with a TSS = −48 dBm, find at: https://massbaytech.com/wp-content/uploads/2016/06/MBT-Catalog-0111.pdf, Macom: Schottky detector diodes with a TSS figure = −52 dBm and a peak power rating of +30 dBm for 1 μs, find at: https://cdn.macom.com/datasheets/Schottky_%20Detector_%20Diodes.pdf; Agilent Technology: Schottky diodes with TSS of −60 dBmm, find at: www.g3ynh.info/circuits/diode_data/AN923.pdf; Micran: gallium arsenide diodes with a TSS −60 dBm and maximum power capability of +20 dBm, find at: http://micran.com/UserFile/File/mmic/QZBD_Process.pdf
- ^ Kapur R., "Detector Logarithmic Video Amplifier (DLVA)", everything RF, July 2018. Find at www.everythingrf.com/community/what-is-a-detector-log-video-amplifier
- ^ Ibrahim Ali Al-Sharabi, Khalil; Fiz, Duraid; Mohammad, a (28 October 2011). "Design of Wideband Radio Direction Finder Based On Amplitude Comparison". Al-Rafdain Engineering Journal. 19 (5): 77–86. doi:10.33899/rengj.2011.26752 (inactive 7 December 2024).
{{cite journal}}: CS1 maint: DOI inactive as of December 2024 (link) - ^ American Microwave Corporation, DLVA Model: LVD-218-50. Find at: www.americanmic.com/catalog/detector-log-video-amplifiers-dlva/
- ^ a b Pasternack, "Broadband Log Video Amplifiers". Find at: www.pasternack.com/pages/Featured_Products/broadband-log-video-amplifiers
- ^ Gotch D.J., "Detector Log Video Amplifiers", Internal technical note, Filtronic Subsystems, Yorks. U.K.
- ^ American Microwave Corporation, DLVA Model: LVD-218-70. Find at: http://www.americanmic.com/catalog/detector-log-video-amplifiers-dlva/
- ^ Sullivan W.B., "Instantaneous Frequency Measurement Receivers for Maritime Patrol", Jour. Electronic Defence, Vol. 25, No. 10
- ^ a b c East, P.W. (1982). "Design techniques and performance of digital IFM". IEE Proceedings F - Communications, Radar and Signal Processing. 129 (3): 154–163. doi:10.1049/ip-f-1.1982.0024.
- ^ Wide Band Systems Inc., "Digital Frequency Discriminators", find at: www.widebandsystems.com
- ^ a b Sullivan, William B. (1 September 1992). "Design optimization improves IFM/DFD receiver accuracy". Microwaves. 31 (9): 96–99. Bibcode:1992MicWa..31...96S.
- ^ Sullivan W.B., "Ultra-Wideband IFM Receiver Fulfils Design Requirements", MSN & CT, April 1985
- ^ Keshavamurthy T. L., "2 to 18 GHz Single-band Digital Frequency Discriminator", Microwave Journal, March 1989
- ^ Elisra Electronic Systems, "A Digital Instantaneous Frequency Measurement Receiver", May 2007. Find at: www.microwavejournal.com/articles/4772-a-digital-instantaneous-frequency-measurement-receiver
- ^ Sullivan W.B., "Advances in Design Improve Wideband Receivers", MSN & Communications Technology, April 1986.
- ^ Kester W., "Analog-Digital Conversion", Analog Devices. Find at: https://www.analog.com/en/education/education-library/data-conversion-handbook.html
- ^ McGlinchy M., "Double the Span and Digitize Signals Using MCU's ADC", Find at: www.electronicdesign.com/print/48825
- ^ Smith S.W., "Digital Signal Processing", Newnes, 2003, pp. 38-39
- ^ Kester W., "ADC Input Noise", Find at: www.analog.com/media/en/analog-dialogue/volume-40/number-1/articles/adc-input-noise.pdf
- ^ Melconian L., "Improving ADC Converter Performance Using Dither", National Semiconductor Application Note 804, Texas Instruments Literature No. SNOA232. Find at: www.ti.com.cn/cn/lit/an/snoa232/snoa232.pdf
















![{\displaystyle {\Big (}{\frac {S}{N}}{\Big )}_{rf}={\frac {B_{V}}{B_{R}}}.{\Bigg [}2.{\Big (}{\frac {S}{N}}{\Big )}_{vid}\pm {\sqrt {4.{\Big (}{\frac {S}{N}}{\Big )}_{vid}^{2}+{\Big (}{\frac {S}{N}}{\Big )}_{vid}.{\Big (}2.{\frac {B_{R}}{B_{V}}}-1{\Big )}}}{\Bigg ]}}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/e31166da718107228402ad19049c39bf3ec33734)

![{\displaystyle {\Big (}{\frac {S}{N}}{\Big )}_{R}(dB)=10\log {\Bigg [}{\frac {B_{V}}{B_{R}}}{\Bigg (}6.31+2.5{\sqrt {2{\frac {B_{R}}{B_{V}}}-1}}{\Bigg )}{\Bigg ]}}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/3df61cb0b3defd2f44de021a624f41556ee1cbb1)









