Perrin number: Difference between revisions
Ce:streamlining |
→top: Added link. Tags: Mobile edit Mobile app edit Android app edit App section source |
||
| (47 intermediate revisions by 7 users not shown) | |||
| Line 1: | Line 1: | ||
{{short description|Number sequence 3,0,2,3,2,5,5,7,10,...}} |
{{short description|Number sequence 3,0,2,3,2,5,5,7,10,...}} |
||
[[File:Perrin triangles.png|upright=1.33|thumb|Spiral of [[equilateral triangle]]s with side lengths equal to Perrin numbers.]] |
|||
In [[mathematics]], the '''Perrin numbers''' are a doubly infinite [[constant-recursive sequence|constant-recursive]] [[integer sequence]] with [[Characteristic equation (calculus)|characteristic equation]] {{math|''x''{{sup|3}} {{=}} ''x'' + 1}}. The Perrin numbers bear the same relationship to the [[Padovan sequence]] as the [[Lucas numbers]] do to the [[Fibonacci sequence]]. |
|||
==Definition== |
|||
In mathematics, the '''Perrin numbers''' are an [[integer sequence]] defined by the [[recurrence relation]] |
|||
The Perrin numbers are defined by the [[recurrence relation]] |
|||
:{{math|P(n) {{=}} P(n − 2) + P(n − 3)}} for {{math|n > 2}}, |
|||
:<math>\begin{align} |
|||
with initial values |
|||
P(0)&=3, \\ |
|||
:{{math|1= P(0) = 3, P(1) = 0, P(2) = 2}}. |
|||
P(1)&=0, \\ |
|||
P(2)&=2, \\ |
|||
P(n)&=P(n-2) +P(n-3) \mbox{ for }n>2, |
|||
\end{align}</math> |
|||
and the reverse |
|||
:<math>P(n) =P(n+3) -P(n+1) \mbox{ for }n<0.</math> |
|||
The first few terms are |
The first few terms in both directions are |
||
{| class="wikitable" style="text-align: right;" |
|||
:3, 0, 2, 3, 2, 5, 5, 7, 10, 12, 17, 22, 29, 39, 51, 68, 90, ... {{OEIS|A001608}}. |
|||
| n ||0||1||2||3||4||5||6||7||8||9||10||11||12||13||14||15||16||17|| |
|||
The recurrence relation is the same as for the [[Padovan sequence]], but the initial values are different. |
|||
|- |
|||
|P(n)||3||0||2||3||2||5||5||7||10||12||17||22||29||39||51||68||90||119||...<ref name=A001608>{{cite OEIS|A001608|2=Perrin sequence (or Ondrej Such sequence): a(n) = a(n-2) + a(n-3) with a(0) = 3, a(1) = 0, a(2) = 2}}</ref> |
|||
|- |
|||
|{{nowrap|P(−n)}} ||...||−1||1||2||−3||4||−2||−1||5||−7||6||−1||−6||12||−13||7||5||−18||...<ref>{{cite OEIS|A078712|Series expansion of (-3 - 2*x)/(1 + x - x^3) in powers of x}}</ref> |
|||
|} |
|||
Perrin numbers can be expressed as sums of the three initial terms |
|||
The sequence can be extended to negative indices using {{math|P(n) {{=}} P(n + 3) − P(n + 1)}} |
|||
:<math>\begin{array}{c|c|c} |
|||
:3,−1, 1, 2,−3, 4,−2,−1, 5,−7, 6,−1,−6, 12,−13, 7, 5, ... {{OEIS|A078712}}. |
|||
n & P(n) & P(-n) \\ |
|||
\hline |
|||
0 & P(0) & ... \\ |
|||
1 & P(1) & P(2) -P(0) \\ |
|||
2 & P(2) & -P(2) +P(1) +P(0) \\ |
|||
3 & P(1) +P(0) & P(2) -P(1) \\ |
|||
4 & P(2) +P(1) & P(1) -P(0) \\ |
|||
5 & P(2) +P(1) +P(0) & -P(2) +2P(0) \\ |
|||
6 & P(2) +2P(1) +P(0) & 2P(2) -P(1) -2P(0) \\ |
|||
7 & 2P(2) +2P(1) +P(0) & -2P(2) +2P(1) +P(0) \\ |
|||
8 & 2P(2) +3P(1) +2P(0) & P(2) -2P(1) +P(0) |
|||
\end{array}</math> |
|||
The first |
The first fourteen prime Perrin numbers are |
||
{| class="wikitable" style="text-align: right;" |
|||
:2, 3, 2, 5, 5, 7, 17, 29, 277, 367, 853, 14197, 43721, 1442968193, 792606555396977, ... {{OEIS|A074788}}, |
|||
| n ||2||3||4||5||6||7||10||12||20||21||24||34||38||75||...<ref>{{cite OEIS|A112881|Indices of prime Perrin numbers; values of n such that A001608(n) is prime}}</ref> |
|||
corresponding to the indices |
|||
|- |
|||
:2, 3, 4, 5, 6, 7, 10, 12, 20, 21, 24, 34, 38, 75, 122, ... {{OEIS|A112881}}. |
|||
|P(n)||2||3||2||5||5||7||17||29||277||367||853||14197||43721||1442968193||...<ref>{{cite OEIS|A074788|2=Prime numbers in the Perrin sequence b(n+1) = b(n-1) + b(n-2) with initial values b(1)=3, b(2)=0, b(3)=2}}</ref> |
|||
|} |
|||
===History=== |
|||
The sequence was mentioned implicitly by [[Édouard Lucas]] in 1876,<ref>{{harvtxt|Lucas|1876|p=62}}</ref> his ideas were further developed by [[w:fr:Raoul_Perrin|Raoul Perrin]] in 1899.<ref>{{harvtxt|Perrin|1899}}</ref> The most extensive treatment was given by William Adams and [[Daniel Shanks]] in 1982,<ref>{{harvtxt|Adams|Shanks|1982}}</ref> with a sequel appearing four years later.<ref>{{harvtxt|Kurtz|Shanks|Williams|1986}}</ref> |
|||
In 1876 the sequence and its equation were initially mentioned by [[Édouard Lucas]], who noted that the index ''n'' divides term {{math|P(n)}} if ''n'' is prime.<ref>{{harvtxt|Lucas|1878}}</ref> In 1899 {{ill|Raoul Perrin|fr|Raoul_Perrin}} asked if there were any counterexamples to this property.<ref>{{harvtxt|Perrin|1899}}</ref> The first {{math|P(n)}} divisible by composite index ''n'' was found only in 1982 by William Adams and [[Daniel Shanks]].<ref>{{harvtxt|Adams|Shanks|1982}}</ref> They presented a detailed investigation of the sequence, with a sequel appearing four years later.<ref>{{harvtxt|Kurtz|Shanks|Williams|1986}}</ref> |
|||
The number of different [[maximal independent set]]s in an ''n''-vertex [[cycle graph]] is counted by the ''n''th Perrin number for {{math|n > 1}}.<ref>{{harvtxt|Füredi|1987}}</ref> |
|||
==Properties== |
==Properties== |
||
[[File:Perrin function Newton map.png|upright=1.4|thumb|A Perrin microcosm: the [[Plotting_algorithms_for_the_Mandelbrot_set#Escape time algorithm|escape time algorithm]] is applied to the [[Newton fractal|Newton map]] of the [[Entire function|entire]] [[#Pfun|Perrin function]] {{math|F(z)}} around [[Critical_point_(mathematics)|critical point]] z = 1.225432 with viewport width 0.05320. The [[Attractor#Basins_of_attraction|basins of attraction]] emanating from the centre correspond to the infinite number of real (left) and complex roots (right) {{math|F(z) {{=}} 0}}.]] |
|||
[[File:Perrin triangles.png|upright=1.33|thumb|Spiral of [[equilateral triangle]]s with side lengths equal to Perrin numbers.]] |
|||
The Perrin sequence also satisfies the recurrence relation <math> P(n) =P(n-1) +P(n-5).</math> Starting from this and the defining recurrence, one can create an infinite number of further relations, for example <math> P(n) =P(n-3) +P(n-4) +P(n-5).</math> |
|||
The [[generating function]] of the Perrin sequence is |
The [[generating function]] of the Perrin sequence is |
||
:<math> |
:<math> \frac{3 -x^2}{1 -x^2 -x^3} =\sum_{n=0}^{\infty} P(n)\,x^n</math> |
||
The sequence is related to sums of [[binomial coefficient]]s by |
|||
:<math> P(n) =n \times \sum_{k =\lfloor (n +2)/3 \rfloor}^{\lfloor n /2 \rfloor} \binom{k}{n -2k} /k,</math><ref name=A001608/> |
|||
<math> P(-n) =n \times \sum_{k =0}^{\lfloor n /3 \rfloor} (-1)^{n -k} \binom{n -2k}{k} /(n -2k).</math> |
|||
Perrin numbers can be expressed in terms of partial sums |
|||
:<math>\begin{align} |
|||
P(n+5) -2&=\sum_{k=0}^{n} P(k) \\ |
|||
P(2n+3)&=\sum_{k=0}^{n} P(2k) \\ |
|||
5 -P(4-n)&=\sum_{k=0}^{n} P(-k) \\ |
|||
3 -P(1-2n)&=\sum_{k=0}^{n} P(-2k). |
|||
\end{align}</math> |
|||
The Perrin numbers are obtained as integral powers {{math|n ≥ 0}} of the [[Matrix (mathematics)|matrix]] |
|||
:<math>\begin{pmatrix} |
|||
0 & 1 & 0 \\ |
|||
0 & 0 & 1 \\ |
|||
1 & 1 & 0 |
|||
\end{pmatrix}^{n} |
|||
\begin{pmatrix} |
|||
3 \\ 0 \\ 2 |
|||
\end{pmatrix} = |
|||
\begin{pmatrix} |
|||
P(n) \\ P(n+1) \\ P(n+2) |
|||
\end{pmatrix},</math> |
|||
and its [[Invertible matrix|inverse]] |
|||
:<math>\begin{pmatrix} |
|||
-1 & 0 & 1 \\ |
|||
1 & 0 & 0 \\ |
|||
0 & 1 & 0 |
|||
\end{pmatrix}^{n} |
|||
\begin{pmatrix} |
|||
3 \\ 0 \\ 2 |
|||
\end{pmatrix} = |
|||
\begin{pmatrix} |
|||
P(-n) \\ P(1-n) \\ P(2-n) |
|||
\end{pmatrix}.</math> |
|||
The Perrin analogue of the [[Cassini and Catalan identities|Simson identity]] for [[Fibonacci number]]s is given by the determinant |
|||
:<math>\begin{vmatrix} |
|||
P(n+2) & P(n+1) & P(n) \\ |
|||
P(n+1) & P(n) & P(n-1) \\ |
|||
P(n) & P(n-1) & P(n-2) |
|||
\end{vmatrix} =-23.</math> |
|||
The number of different [[maximal independent set]]s in an ''n''-vertex [[cycle graph]] is counted by the ''n''th Perrin number for {{math|n ≥ 2}}.<ref>{{harvtxt|Füredi|1987}}</ref> |
|||
The Perrin numbers are obtained as integral powers {{math|n > 2}} of the [[Matrix (mathematics)|matrix]] |
|||
:<math>\begin{pmatrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 1 & 1 & 0 \end{pmatrix}^{\!n} |
|||
\begin{pmatrix} 3 \\ 0 \\ 2 \end{pmatrix} = |
|||
\begin{pmatrix} P\left(n\right) \\ P\left(n+1\right) \\ P\left(n+2\right) \end{pmatrix}</math> |
|||
===Binet formula=== |
===Binet formula=== |
||
[[File:Perrin function real.svg|upright=1.4|thumb|The Perrin function extends the sequence to real numbers.]] |
|||
The Perrin numbers can be written in terms of powers of the [[root of a polynomial|roots]] of [[cubic equation]] <math>x^3 - x - 1 = 0.</math> This equation has 3 roots; one [[real number|real]] root ''p'' (known as the [[plastic ratio]]) and two [[complex conjugate]] roots ''q'' and ''r''. Given these three roots, the Perrin sequence analogue of the [[Lucas sequence]] Binet formula is <math>P(n) = p^n + q^n + r^n.</math> |
|||
The [[Linear recurrence with constant coefficients#General solution|solution]] of the recurrence <math>P(n) =P(n-2) +P(n-3)</math> can be written in terms of the [[Cubic equation#Cardano's formula|roots]] of [[Characteristic equation (calculus)|characteristic equation]] <math>x^3 -x -1=0</math>. If the three solutions are [[real number|real]] root {{tmath|\alpha}} (with approximate value 1.324718 and known as the [[plastic ratio]]) and [[complex conjugate]] roots {{tmath|\beta}} and {{tmath|\gamma}}, the Perrin numbers can be computed with the [[Lucas sequence#Explicit expressions|Binet formula]] <math id="Pfun">P(n) =\alpha^{n} +\beta^{n} +\gamma^{n},</math> which also holds for negative ''n''. |
|||
The [[Polar coordinate system|polar form]] is <math>P(n) =\alpha^{n} +2\cos(n\,\theta) \sqrt{\alpha^{-n}},</math> with <math>\theta =\arccos(-\sqrt{\alpha^{3}} /2).</math> Since <math> \lim_{n \to \infty} \alpha^{-n} =0,</math> the formula reduces to either the first or the second term successively for large positive or negative ''n'', and numbers with negative subscripts oscillate. Provided ''α'' is computed to sufficient precision, these formulas can be used to calculate Perrin numbers for large ''n''. |
|||
Expanding the identity <math> P^{2}(n) =( \alpha^{n} +\beta^{n} +\gamma^{n} )^{2} </math> gives the important index-doubling rule <math> P(2n) =P^{2}(n) -2P(-n),</math> by which the forward and reverse parts of the sequence are linked. |
|||
The ratio of successive Perrin numbers approaches the [[plastic ratio]] ''p'', which has a value of approximately 1.324718. This constant bears the same relationship to the Perrin numbers as the [[golden ratio]] does to the [[Lucas number]]s. |
|||
===Prime index ''p'' divides ''P(p)''=== |
|||
If the characteristic equation of the sequence is written as <math> f(x) =x^{3} -\sigma_1 x^{2} +\sigma_2 x -\sigma_3 </math> then the coefficients {{tmath|\sigma_k}} can be expressed in terms of roots <math> \alpha,\beta,\gamma </math> with [[Vieta's formulas]]: |
|||
:<math>\begin{alignat}{3} |
|||
\sigma_1 &=\alpha +\beta +\gamma &&= 0\\ |
|||
\sigma_2 &=\alpha\beta +\alpha\gamma +\beta\gamma &&=-1\\ |
|||
\sigma_3 &=\alpha\beta\gamma &&= 1. |
|||
\end{alignat}</math> |
|||
These integer valued functions are the [[elementary symmetric polynomials]] in <math> \alpha,\beta,\gamma.</math> |
|||
* The [[Symmetric polynomial#Relation with the roots of a monic univariate polynomial|fundamental theorem on symmetric polynomials]] states that every symmetric polynomial in the complex roots of monic {{tmath|f}} can be represented as another polynomial function in the integer coefficients of {{tmath|f.}} |
|||
* The analogue of [[Lucas's theorem]] for [[Multinomial theorem|multinomial coefficients]] <math> \frac{p!}{i!j!k!} </math> says that if {{tmath|i,j,k < p}} then <math> \binom{p}{i,j,k} </math> is divisible by prime {{tmath|p.}} |
|||
Given integers {{math|a, b, c}} and {{math|n > 0,}} |
|||
:<math> (a +b +c)^n = \sum_{i +j +k =n} \binom{n}{i,j,k} a^i b^j c^k.</math> |
|||
Rearrange into symmetric [[monomial]] summands, [[permutation|permuting]] exponents {{math|i, j, k:}} |
|||
:<math> (a +b +c)^n - (a^n +b^n +c^n) = </math> <math> \sum_{\begin{align} i \le j \le k &<n \\ i +j +k &=n \end{align}} \binom{n}{i,j,k} \sum_{\pi(i,j,k)} a^i b^j c^k.</math> |
|||
Substitute prime {{tmath|p}} for power {{tmath|n}} and complex roots <math> \alpha,\beta,\gamma </math> for integers {{tmath|a, b, c}} and compute representations in terms of <math> \sigma_1,\sigma_2,\sigma_3 </math> for all symmetric polynomial functions. For example, <math> ( \alpha +\beta +\gamma )^{p}</math> is <math> \sigma_1^{p} =0</math> and the [[Power sum symmetric polynomial|power sum]] <math> \alpha^{p} +\beta^{p} +\gamma^{p} =P(p)</math> can be expressed in the coefficients {{tmath|\sigma_k}} with [[Newton's identities|Newton's recursive scheme]]. It follows that the identity has integer terms and both sides divisible by prime {{tmath|p.}} |
|||
To show that prime {{tmath|p}} divides {{tmath|P(-p) + 1}} in the reverse sequence, the characteristic equation has to be [[Reciprocal polynomial|reflected]]. The roots are then <math> \alpha^{-1},\beta^{-1},\gamma^{-1},</math> the coefficients <math> \sigma_1 =-1, \sigma_2 =0, \sigma_3 =1,</math> and the same reasoning applies. |
|||
==Perrin primality test== |
==Perrin primality test== |
||
<blockquote> |
|||
Query 1484. The curious [[Chinese hypothesis|proposition of Chinese origin]] which is the subject of query 1401<ref>{{harvtxt|Tarry|1898}}</ref> would provide, if it is true, a more practical criterium than [[Wilson's theorem]] for verifying whether a given number m is prime or not; it would suffice to calculate the residues with respect to m of successive terms of the recurrence sequence<br/> |
|||
u<sub>n</sub> = 3u<sub>n−1</sub> − 2u<sub>n−2</sub> with initial values u<sub>0</sub> = −1, u<sub>1</sub> = 0.<ref>{{cite OEIS|A000918|2=a(n) = 2^n - 2}}</ref><br/> |
|||
I have found another recurrence sequence that seems to possess the same property; it is the one whose general term is<br/> |
|||
v<sub>n</sub> = v<sub>n−2</sub> + v<sub>n−3</sub> with initial values v<sub>0</sub> = 3, v<sub>1</sub> = 0, v<sub>2</sub> = 2. It is easy to demonstrate that v<sub>n</sub> is divisible by n, if n is prime; I have verified, up to fairly high values of n, that in the opposite case it is not; but it would be interesting to know if this is really so, especially since the sequence v<sub>n</sub> gives much less rapidly increasing numbers than the sequence u<sub>n</sub> (for n = 17, for example, one finds u<sub>n</sub> = 131070, v<sub>n</sub> = 119), which leads to simpler calculations when n is a large number.<br/> |
|||
The same proof, applicable to one of the sequences, will undoubtedly bear upon the other, if the stated property is true for both: it is only a matter of discovering it.<ref>{{harvtxt|Perrin|1899}} translated from the French</ref> |
|||
</blockquote> |
|||
The Perrin sequence has the [[Fermat's little theorem|Fermat property]]: if {{math|p}} is [[prime number|prime]], {{math|P(p) ≡ P(1) ≡ 0 (mod p)}}. However, the [[converse (logic)|converse]] is not true: some [[composite number|composite]] {{math|n}} may still divide {{math|P(n)}}. A number with this property is called a Perrin [[pseudoprime]]. |
The Perrin sequence has the [[Fermat's little theorem|Fermat property]]: if {{math|p}} is [[prime number|prime]], {{math|P(p) ≡ P(1) ≡ 0 (mod p)}}. However, the [[converse (logic)|converse]] is not true: some [[composite number|composite]] {{math|n}} may still divide {{math|P(n)}}. A number with this property is called a Perrin [[pseudoprime]]. |
||
The question of the existence of Perrin pseudoprimes was considered by Malo and Jarden,<ref>{{harvtxt|Malo|1900}}, {{harvtxt|Jarden|1966}}</ref> but none were known until Adams and Shanks found the smallest one, 271441 = 521<sup>2</sup> (the number {{math|P(271441)}} has 33150 decimal digits).<ref>{{harvtxt|Adams|Shanks|1982|p=255}}</ref> Jon Grantham later proved that there are infinitely many Perrin pseudoprimes.<ref>{{harvtxt|Grantham|2010}}, {{harvtxt|Stephan|2020}}</ref> |
|||
The seventeen Perrin pseudoprimes below {{math|10{{sup|9}}}} are |
|||
:271441, 904631, 16532714, 24658561, 27422714, 27664033, 46672291, 102690901, 130944133, 196075949, 214038533, 517697641, 545670533, 801123451, 855073301, 903136901, 970355431 {{OEIS|A013998}}. |
|||
The seventeen Perrin pseudoprimes below {{math|10{{sup|9}}}} are |
|||
The question of the existence of Perrin pseudoprimes was considered by Perrin himself, but none were known until Adams and Shanks (1982) discovered the smallest one, 271441 = 521<sup>2</sup> (the number {{math|P(271441)}} has 33150 decimal digits).<ref>{{harvtxt|Adams|Shanks|1982|p=255}}</ref> Jon Grantham later proved that there are infinitely many Perrin pseudoprimes.<ref>{{harvtxt|Grantham|2010}}</ref> |
|||
:271441, 904631, 16532714, 24658561, 27422714, 27664033, 46672291, 102690901, 130944133, 196075949, 214038533, 517697641, 545670533, 801123451, 855073301, 903136901, 970355431.<ref>{{cite OEIS|A013998|Unrestricted Perrin pseudoprimes}}</ref> |
|||
Adams and Shanks noted that primes also satisfy the congruence {{math|P(−p) ≡ P(−1) ≡ −1 (mod p)}}. Composites for which both properties hold are called restricted Perrin pseudoprimes. There are only nine such numbers below {{math|10{{sup|9}}}}.<ref>{{OEIS|A018187}}</ref> |
Adams and Shanks noted that primes also satisfy the congruence {{math|P(−p) ≡ P(−1) ≡ −1 (mod p)}}. Composites for which both properties hold are called restricted Perrin pseudoprimes. There are only nine such numbers below {{math|10{{sup|9}}}}.<ref>{{cite OEIS|A018187|Restricted Perrin pseudoprimes}}</ref><ref>{{cite OEIS|A275612|Restricted Perrin pseudoprimes (Adams and Shanks definition)}}</ref><ref>{{cite OEIS|A275613|Restricted Perrin pseudoprimes (Grantham definition).}}</ref> |
||
While Perrin pseudoprimes are rare, they overlap with [[Fermat pseudoprime]]s. Of the above |
While Perrin pseudoprimes are rare, they overlap with [[Fermat pseudoprime]]s. Of the above seventeen numbers, four are base 2 Fermatians as well. In contrast, the [[Lucas pseudoprime]]s are anti-correlated.<ref>None of the 2402549 Lucas-Selfridge pseudoprimes below 10<sup>15</sup> listed by Dana {{harvtxt|Jacobsen|2020}} is also a Perrin pseudoprime.</ref> Presumably, combining the Perrin and Lucas tests should make a [[primality test]] as strong as the reliable [[Baillie–PSW_primality_test|BPSW test]] which has no known pseudoprimes – though at higher computational cost. |
||
===Pseudocode=== |
===Pseudocode=== |
||
The 1982 Adams and Shanks {{math|O(log n)}} |
The 1982 Adams and Shanks {{math|O(log n)}} Perrin primality test.<ref>{{harvtxt|Adams|Shanks|1982|p=265, 269-270}}</ref> |
||
Two integer arrays u(3) and v(3) are initialized to the lowest terms of the Perrin sequence, with positive indices {{math|t {{=}} 0, 1, 2}} in u( ) and negative indices {{math|t {{=}} 0,−1,−2}} in v( ). |
Two integer arrays u(3) and v(3) are initialized to the lowest terms of the Perrin sequence, with positive indices {{math|t {{=}} 0, 1, 2}} in u( ) and negative indices {{math|t {{=}} 0,−1,−2}} in v( ). |
||
The main [[addition chain#Methods for computing addition chains|double-and-add]] loop, originally devised to run on an [[HP-41C]] pocket calculator, |
The main [[addition chain#Methods for computing addition chains|double-and-add]] loop, originally devised to run on an [[HP-41C]] pocket calculator, computes {{math|P(n) mod n}} and the reverse {{math|P(−n) mod n}} at the cost of six modular squarings for each bit of {{math|n}}. |
||
The subscripts of the Perrin numbers are doubled |
The subscripts of the Perrin numbers are doubled using the identity {{math|P(2t) {{=}} P{{sup|2}}(t) − 2P(−t)}}. The resulting gaps between {{math|P(±2t)}} and {{math|P(±2t ± 2)}} are closed by applying the defining relation {{math|P(t) {{=}} P(t − 2) + P(t − 3)}}. |
||
''Initial values'' |
|||
The gaps between {{math|P(±2t)}} and {{math|P(±2t ± 2)}} due to the doubling step are closed by applying the defining relation {{math|P(t) {{=}} P(t − 2) + P(t − 3)}}. |
|||
'''let''' ''int'' u(0):= 3, u(1):= 0, {{nowrap|u(2):{{=}} 2}} |
|||
'''let''' ''int'' v(0):= 3, v(1):=−1, {{nowrap|v(2):{{=}} 1}} |
|||
Initial values |
|||
LET u(0):= 3, u(1):= 0, {{nowrap|u(2):{{=}} 2}} |
|||
LET v(0):= 3, v(1):=−1, {{nowrap|v(2):{{=}} 1}} |
|||
''Test odd positive number n'' |
|||
'''input''' ''int'' n |
|||
'''set''' ''int'' h:= most significant bit of n |
|||
'''for''' k:= h − 1 '''downto''' 0 |
|||
Double the indices of |
''Double the indices of'' |
||
the six Perrin numbers. |
''the six Perrin numbers.'' |
||
'''for''' i = 0, 1, 2 |
|||
temp:= u(i)^2 − 2v(i) {{nowrap|(mod n)}} |
temp:= u(i)^2 − 2v(i) {{nowrap|(mod n)}} |
||
v(i):= v(i)^2 − 2u(i) {{nowrap|(mod n)}} |
v(i):= v(i)^2 − 2u(i) {{nowrap|(mod n)}} |
||
u(i):= temp |
u(i):= temp |
||
'''endfor''' |
|||
ENDFOR |
|||
Copy P(2t + 2) and {{nowrap|P(−2t − 2)}} |
''Copy P(2t + 2) and {{nowrap|P(−2t − 2)}}'' |
||
to the array ends and use |
''to the array ends and use'' |
||
in the |
''in the if-statement below.'' |
||
u(3):= u(2) |
u(3):= u(2) |
||
v(3):= v(2) |
v(3):= v(2) |
||
Overwrite P(2t ± 2) with {{nowrap|P(2t ± 1)}} |
''Overwrite P(2t ± 2) with {{nowrap|P(2t ± 1)}}'' |
||
temp:= u(2) − u(1) |
temp:= u(2) − u(1) |
||
u(2):= u(0) + temp |
u(2):= u(0) + temp |
||
u(0):= temp |
u(0):= temp |
||
Overwrite P(−2t ± 2) with {{nowrap|P(−2t ± 1)}} |
''Overwrite P(−2t ± 2) with {{nowrap|P(−2t ± 1)}}'' |
||
temp:= v(0) − v(1) |
temp:= v(0) − v(1) |
||
v(0):= v(2) + temp |
v(0):= v(2) + temp |
||
v(2):= temp |
v(2):= temp |
||
'''if''' n has bit k set '''then''' |
|||
Increase the indices of |
''Increase the indices of'' |
||
both Perrin triples by 1. |
''both Perrin triples by 1.'' |
||
'''for''' i = 0, 1, 2 |
|||
u(i):= u(i + 1) |
u(i):= u(i + 1) |
||
v(i):= v(i + 1) |
v(i):= v(i + 1) |
||
'''endfor''' |
|||
'''endif''' |
|||
'''endfor''' |
|||
ENDFOR |
|||
''Result'' |
|||
Show the results |
|||
'''print''' v(2), v(1), v(0) |
|||
'''print''' u(0), u(1), u(2) |
|||
Successively {{math|P( |
Successively {{math|P(−n − 1), P(−n), P(−n + 1)}} and {{math|P(n − 1), P(n), P(n + 1) (mod n)}}. |
||
If {{math|P( |
If {{math|P(−n) {{=}} −1}} and {{math|P(n) {{=}} 0}} then ''n'' is a [[probable prime]], that is: actually prime or a restricted Perrin pseudoprime. |
||
Shanks ''et al.'' observed that for all restricted pseudoprimes they found, the final state of the above six registers (the "signature" of ''n'') equals the initial state 1,−1,3, 3,0,2.<ref>{{harvtxt|Adams|Shanks|1982|p=275}}, {{harvtxt|Kurtz|Shanks|Williams|1986|p=694}}. This was later confirmed for {{math|n < 10{{sup|14}}}} by Steven {{harvtxt|Arno|1991}}.</ref> The same occurs with {{math|≈ 1'''/'''6}} of all primes, so the two sets cannot be distinguished on the strength of this test alone.<ref>The signature does give discriminating information on the remaining two types of primes. |
|||
Adams and Shanks enhanced the test by defining "acceptable signatures" comprising all six residues.<ref>{{harvtxt|Adams|Shanks|1982|p=257}}, {{OEIS|A275612}}, {{OEIS|A275613}}.</ref> An even stronger test also uses the [[Supergolden_ratio#Narayana sequence|Narayana-Lucas sister sequence]],<ref>dubbed ''Secundo'' in {{harvtxt|Kurtz|Shanks|Williams|1986|p=697}}</ref> with recurrence relation {{math|A(n) {{=}} A(n − 1) + A(n − 3)}} and initial values |
|||
For example, the smallest Q-type pseudoprime 50,972,694,899,204,437,633 computed by Holger {{harvtxt|Stephan|2019}} is exposed by signature conditions 14a and 14c in {{harvtxt|Adams|Shanks|1982|p=257}}.</ref> For those cases, they recommend to also use the [[Supergolden_ratio#Narayana sequence|Narayana-Lucas sister sequence]] with recurrence relation {{math|A(n) {{=}} A(n − 1) + A(n − 3)}} and initial values |
|||
u(0):= 3, u(1):= 1, u(2):= 1 |
u(0):= 3, u(1):= 1, u(2):= 1 |
||
| Line 131: | Line 229: | ||
v(0):= temp |
v(0):= temp |
||
Here, ''n'' is a |
Here, ''n'' is a probable prime if {{math|A(−n) {{=}} 0}} and {{math|A(n) {{=}} 1}}. |
||
Kurtz ''et al.'' found no overlap between the odd pseudoprimes for the two sequences below {{math|50∙10{{sup|9}}}} and supposed that 2,277,740,968,903 = 1067179 ∙ 2134357 is the smallest composite number to pass both tests.<ref>{{harvtxt|Kurtz|Shanks|Williams|1986|p=697}}</ref> |
|||
If the [[Supersilver ratio#Third-order Pell sequences|third-order Pell-Lucas recurrence]] {{math|A(n) {{=}} 2A(n − 1) + A(n − 3)}} is used as well, this bound will be pushed up to 4,057,052,731,496,380,171 = 1424263447 ∙ 2848526893.<ref>{{harvtxt|Stephan|2019}}</ref> |
|||
Additionally, roots of the doubling rule-congruence <math>x^2 -2x \equiv 3 =P(0) \pmod{n}\,</math> other than {{math|−1}} or {{math|3}} expose composite numbers, like non-trivial square roots of {{math|1}} in the [[Miller–Rabin primality test|Miller-Rabin test]].<ref>{{harvtxt|Adams|Shanks|1982|p=280-283}}</ref> This reduces the number of restricted pseudoprimes for each sequence by roughly one-third and is especially efficient in detecting [[Carmichael number]]s.<ref>A C/C++ implementation of the extended Perrin test can be found in the final subsection of a [[Special:Diff/1219750354|previous version]] of this article.</ref> |
|||
The least strong restricted Perrin pseudoprime is 46672291 and the above two bounds expand to successively 173,536,465,910,671 and 79,720,990,309,209,574,421.<ref>{{harvtxt|Stephan|2019}}</ref> |
|||
==Notes== |
==Notes== |
||
| Line 139: | Line 243: | ||
==References== |
==References== |
||
*{{cite |
*{{cite journal |
||
| last = Lucas | first = E. | author-link = Édouard Lucas |
|||
| url = http://visualiseur.bnf.fr/CadresFenetre?O=NUMM-201152&I=131&M=pagination |
|||
| title = Théorie des fonctions numériques simplement périodiques |
|||
| author = Lucas, E. | author-link = Édouard Lucas |
|||
| language = French |
|||
| title = Sur la recherche des grands nombres premiers |
|||
| journal =[[American Journal of Mathematics]] |
|||
| publisher = Association française pour l'avancement des sciences |
|||
| publisher = Johns Hopkins University Press |
|||
| conference = Congrès de Clermont-Ferrand |
|||
| year = |
| year = 1878 |
||
| |
| volume = 1 |
||
| |
| issue = 3 |
||
| pages = 229–231 |
|||
| doi = 10.2307/2369311 |
|||
| doi-access = free |
|||
| jstor = 2369311 |
|||
}} |
}} |
||
*{{cite journal |
*{{cite journal |
||
| |
| last = Tarry | first = G. | author-link = Gaston Tarry |
||
| title = |
| title = Question 1401 |
||
| journal =[[L'Intermédiaire des Mathématiciens]] |
| journal =[[L'Intermédiaire des Mathématiciens]] |
||
| publisher = Gauthier-Villars et fils |
| publisher = Gauthier-Villars et fils |
||
| year = |
| year = 1898 |
||
| volume = 5 |
|||
| pages = 266–267 |
|||
}} |
|||
*{{cite journal |
|||
| url = https://archive.org/details/lintermdiairede03lemogoog/page/76/mode/2up?view=theater |
|||
| last = Perrin | first = R. | author-link =:fr:Raoul Perrin |
|||
| title = Question 1484 |
|||
| journal =[[L'Intermédiaire des Mathématiciens]] |
|||
| publisher = Gauthier-Villars et fils |
|||
| year = 1899 |
|||
| volume = 6 |
| volume = 6 |
||
| pages = |
| pages = 76–77 |
||
}} |
|||
*{{cite journal |
|||
| last = Malo | first = E. |
|||
| title = Réponse à 1484 |
|||
| journal =[[L'Intermédiaire des Mathématiciens]] |
|||
| publisher = Gauthier-Villars et fils |
|||
| year = 1900 |
|||
| volume = 7 |
|||
| pages = 280-282, 312-314 |
|||
}} |
|||
*{{cite book |
|||
| last = Jarden |
|||
| first = Dov |
|||
| date = 1966 |
|||
| title = Recurring sequences |
|||
| url = https://oeis.org/A001602/a001602.pdf |
|||
| location = Jerusalem |
|||
| publisher = Riveon LeMatematika |
|||
| edition = 2 |
|||
| pages = 86–93 |
|||
}} |
}} |
||
*{{cite journal |
*{{cite journal |
||
| |
| last1 = Adams | first1= William |
||
| |
| last2 = Shanks | first2= Daniel | author-link2=Daniel Shanks |
||
| title = Strong primality tests that are not sufficient |
| title = Strong primality tests that are not sufficient |
||
| journal =[[Mathematics of Computation]] |
| journal =[[Mathematics of Computation]] |
||
| publisher =[[American Mathematical Society]] |
| publisher =[[American Mathematical Society]] |
||
| year = 1982 |
| year = 1982 |
||
| volume = 39 |
| volume = 39 |
||
| issue = 159 |
| issue = 159 |
||
| pages = |
| pages = 255–300 |
||
| doi = 10.1090/S0025-5718-1982-0658231-9 |
| doi = 10.1090/S0025-5718-1982-0658231-9 |
||
| doi-access = free |
| doi-access = free |
||
| Line 173: | Line 311: | ||
}} |
}} |
||
*{{cite journal |
*{{cite journal |
||
| |
| last1 = Kurtz|first1= G. C. |
||
| |
| last2 = Shanks|first2= Daniel | author-link2=Daniel Shanks |
||
| |
| last3 = Williams|first3= H. C. | author-link3=Hugh C. Williams |
||
| title = Fast primality tests for numbers less than 50∙10{{sup|9}} |
| title = Fast primality tests for numbers less than 50∙10{{sup|9}} |
||
| journal =[[Mathematics of Computation]] |
| journal =[[Mathematics of Computation]] |
||
| publisher =[[American Mathematical Society]] |
| publisher =[[American Mathematical Society]] |
||
| year = 1986 |
| year = 1986 |
||
| volume = 46 |
| volume = 46 |
||
| issue = 174 |
| issue = 174 |
||
| pages = |
| pages = 691–701 |
||
| doi = 10.1090/S0025-5718-1986-0829639-7 |
| doi = 10.1090/S0025-5718-1986-0829639-7 |
||
| doi-access = free |
| doi-access = free |
||
| Line 194: | Line 332: | ||
| volume = 11 |
| volume = 11 |
||
| issue = 4 |
| issue = 4 |
||
| pages = |
| pages = 463–470 |
||
| doi = 10.1002/jgt.3190110403 |
| doi = 10.1002/jgt.3190110403 |
||
}} |
|||
*{{cite journal |
|||
| last = Arno | first = Steven |
|||
| title = A note on Perrin pseudoprimes |
|||
| journal =[[Mathematics of Computation]] |
|||
| publisher =[[American Mathematical Society]] |
|||
| year = 1991 |
|||
| volume = 56 |
|||
| issue = 193 |
|||
| pages = 371–376 |
|||
| doi = 10.1090/S0025-5718-1991-1052083-9 |
|||
| doi-access = free |
|||
| jstor = 2008548 |
|||
| bibcode = 1991MaCom..56..371A |
|||
}} |
}} |
||
*{{cite journal |
*{{cite journal |
||
| Line 204: | Line 356: | ||
| volume = 130 |
| volume = 130 |
||
| issue = 5 |
| issue = 5 |
||
| pages = |
| pages = 1117–1128 |
||
| arxiv = 1903.06825 |
| arxiv = 1903.06825 |
||
| doi = 10.1016/j.jnt.2009.11.008 |
| doi = 10.1016/j.jnt.2009.11.008 |
||
}} |
}} |
||
*{{cite web |
|||
| url = https://ntheory.org/pseudoprimes.html |
|||
| title = Pseudoprime statistics and tables |
|||
| last = Jacobsen | first = Dana |
|||
| date = 2020 |
|||
| website = ntheory.org |
|||
| access-date = 7 March 2024 |
|||
| quote = #LPSP Lucas-Selfridge |
|||
}} |
|||
*{{cite arXiv |
|||
| last = Stephan | first = Holger |
|||
| title = Millions of Perrin pseudoprimes including a few giants |
|||
| date = 2020 |
|||
| class = math.NA |
|||
| eprint = 2002.03756v1 |
|||
}} |
|||
*{{cite report |
|||
| last = Stephan | first = Holger |
|||
| title = Perrin pseudoprimes |
|||
| type = WIAS Research Data No. 4 |
|||
| publisher = [[Weierstrass Institute]] |
|||
| location = Berlin |
|||
| date = 2019 |
|||
| doi = 10.20347/WIAS.DATA.4 |
|||
| doi-access = free |
|||
}} |
|||
==External links== |
==External links== |
||
* [https://ntheory.org/primality/perrin.html Jacobsen, Dana (2016). "Perrin Primality Tests".] |
|||
* [https://www.solipsys.co.uk/new/FindingPerrinPseudoPrimes_Part1.html Wright, Colin (2015). "Finding Perrin Pseudo-primes".] |
|||
*{{MathPages|id=home/kmath345/kmath345|title=Perrin's Sequence}} |
*{{MathPages|id=home/kmath345/kmath345|title=Perrin's Sequence}} |
||
*{{MathPages|id=home/kmath127/kmath127|title=Lucas and Perrin Pseudoprimes}} |
*{{MathPages|id=home/kmath127/kmath127|title=Lucas and Perrin Pseudoprimes}} |
||
* [http://ntheory.org/primality/perrin.html Jacobsen, Dana (2016). "Perrin Primality Tests".] |
|||
* [https://web.archive.org/web/20051108035017/http://www.ai.univie.ac.at/perrin.html Holzbaur, Christian (1997). "Perrin Pseudoprimes".] |
* [https://web.archive.org/web/20051108035017/http://www.ai.univie.ac.at/perrin.html Holzbaur, Christian (1997). "Perrin Pseudoprimes".] |
||
* [https://perrin088.org Turk, Richard (2014). "The Perrin Chalkboard".] |
|||
{{Prime number classes}} |
{{Prime number classes}} |
||
Latest revision as of 01:46, 13 December 2024

In mathematics, the Perrin numbers are a doubly infinite constant-recursive integer sequence with characteristic equation x3 = x + 1. The Perrin numbers bear the same relationship to the Padovan sequence as the Lucas numbers do to the Fibonacci sequence.
Definition
[edit]The Perrin numbers are defined by the recurrence relation
and the reverse
The first few terms in both directions are
| n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | |
| P(n) | 3 | 0 | 2 | 3 | 2 | 5 | 5 | 7 | 10 | 12 | 17 | 22 | 29 | 39 | 51 | 68 | 90 | 119 | ...[1] |
| P(−n) | ... | −1 | 1 | 2 | −3 | 4 | −2 | −1 | 5 | −7 | 6 | −1 | −6 | 12 | −13 | 7 | 5 | −18 | ...[2] |
Perrin numbers can be expressed as sums of the three initial terms
The first fourteen prime Perrin numbers are
| n | 2 | 3 | 4 | 5 | 6 | 7 | 10 | 12 | 20 | 21 | 24 | 34 | 38 | 75 | ...[3] |
| P(n) | 2 | 3 | 2 | 5 | 5 | 7 | 17 | 29 | 277 | 367 | 853 | 14197 | 43721 | 1442968193 | ...[4] |
History
[edit]In 1876 the sequence and its equation were initially mentioned by Édouard Lucas, who noted that the index n divides term P(n) if n is prime.[5] In 1899 Raoul Perrin asked if there were any counterexamples to this property.[6] The first P(n) divisible by composite index n was found only in 1982 by William Adams and Daniel Shanks.[7] They presented a detailed investigation of the sequence, with a sequel appearing four years later.[8]
Properties
[edit]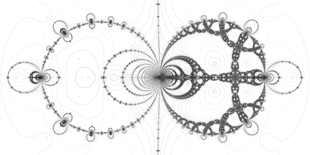
The Perrin sequence also satisfies the recurrence relation Starting from this and the defining recurrence, one can create an infinite number of further relations, for example
The generating function of the Perrin sequence is
The sequence is related to sums of binomial coefficients by
Perrin numbers can be expressed in terms of partial sums
The Perrin numbers are obtained as integral powers n ≥ 0 of the matrix
and its inverse
The Perrin analogue of the Simson identity for Fibonacci numbers is given by the determinant
The number of different maximal independent sets in an n-vertex cycle graph is counted by the nth Perrin number for n ≥ 2.[9]
Binet formula
[edit]
The solution of the recurrence can be written in terms of the roots of characteristic equation . If the three solutions are real root (with approximate value 1.324718 and known as the plastic ratio) and complex conjugate roots and , the Perrin numbers can be computed with the Binet formula which also holds for negative n.
The polar form is with Since the formula reduces to either the first or the second term successively for large positive or negative n, and numbers with negative subscripts oscillate. Provided α is computed to sufficient precision, these formulas can be used to calculate Perrin numbers for large n.
Expanding the identity gives the important index-doubling rule by which the forward and reverse parts of the sequence are linked.
Prime index p divides P(p)
[edit]If the characteristic equation of the sequence is written as then the coefficients can be expressed in terms of roots with Vieta's formulas:
These integer valued functions are the elementary symmetric polynomials in
- The fundamental theorem on symmetric polynomials states that every symmetric polynomial in the complex roots of monic can be represented as another polynomial function in the integer coefficients of
- The analogue of Lucas's theorem for multinomial coefficients says that if then is divisible by prime
Given integers a, b, c and n > 0,
Rearrange into symmetric monomial summands, permuting exponents i, j, k:
Substitute prime for power and complex roots for integers and compute representations in terms of for all symmetric polynomial functions. For example, is and the power sum can be expressed in the coefficients with Newton's recursive scheme. It follows that the identity has integer terms and both sides divisible by prime
To show that prime divides in the reverse sequence, the characteristic equation has to be reflected. The roots are then the coefficients and the same reasoning applies.
Perrin primality test
[edit]Query 1484. The curious proposition of Chinese origin which is the subject of query 1401[10] would provide, if it is true, a more practical criterium than Wilson's theorem for verifying whether a given number m is prime or not; it would suffice to calculate the residues with respect to m of successive terms of the recurrence sequence
un = 3un−1 − 2un−2 with initial values u0 = −1, u1 = 0.[11]
I have found another recurrence sequence that seems to possess the same property; it is the one whose general term is
vn = vn−2 + vn−3 with initial values v0 = 3, v1 = 0, v2 = 2. It is easy to demonstrate that vn is divisible by n, if n is prime; I have verified, up to fairly high values of n, that in the opposite case it is not; but it would be interesting to know if this is really so, especially since the sequence vn gives much less rapidly increasing numbers than the sequence un (for n = 17, for example, one finds un = 131070, vn = 119), which leads to simpler calculations when n is a large number.
The same proof, applicable to one of the sequences, will undoubtedly bear upon the other, if the stated property is true for both: it is only a matter of discovering it.[12]
The Perrin sequence has the Fermat property: if p is prime, P(p) ≡ P(1) ≡ 0 (mod p). However, the converse is not true: some composite n may still divide P(n). A number with this property is called a Perrin pseudoprime.
The question of the existence of Perrin pseudoprimes was considered by Malo and Jarden,[13] but none were known until Adams and Shanks found the smallest one, 271441 = 5212 (the number P(271441) has 33150 decimal digits).[14] Jon Grantham later proved that there are infinitely many Perrin pseudoprimes.[15]
The seventeen Perrin pseudoprimes below 109 are
- 271441, 904631, 16532714, 24658561, 27422714, 27664033, 46672291, 102690901, 130944133, 196075949, 214038533, 517697641, 545670533, 801123451, 855073301, 903136901, 970355431.[16]
Adams and Shanks noted that primes also satisfy the congruence P(−p) ≡ P(−1) ≡ −1 (mod p). Composites for which both properties hold are called restricted Perrin pseudoprimes. There are only nine such numbers below 109.[17][18][19]
While Perrin pseudoprimes are rare, they overlap with Fermat pseudoprimes. Of the above seventeen numbers, four are base 2 Fermatians as well. In contrast, the Lucas pseudoprimes are anti-correlated.[20] Presumably, combining the Perrin and Lucas tests should make a primality test as strong as the reliable BPSW test which has no known pseudoprimes – though at higher computational cost.
Pseudocode
[edit]The 1982 Adams and Shanks O(log n) Perrin primality test.[21]
Two integer arrays u(3) and v(3) are initialized to the lowest terms of the Perrin sequence, with positive indices t = 0, 1, 2 in u( ) and negative indices t = 0,−1,−2 in v( ).
The main double-and-add loop, originally devised to run on an HP-41C pocket calculator, computes P(n) mod n and the reverse P(−n) mod n at the cost of six modular squarings for each bit of n.
The subscripts of the Perrin numbers are doubled using the identity P(2t) = P2(t) − 2P(−t). The resulting gaps between P(±2t) and P(±2t ± 2) are closed by applying the defining relation P(t) = P(t − 2) + P(t − 3).
Initial values let int u(0):= 3, u(1):= 0, u(2):= 2 let int v(0):= 3, v(1):=−1, v(2):= 1 Test odd positive number n input int n set int h:= most significant bit of n for k:= h − 1 downto 0 Double the indices of the six Perrin numbers. for i = 0, 1, 2 temp:= u(i)^2 − 2v(i) (mod n) v(i):= v(i)^2 − 2u(i) (mod n) u(i):= temp endfor Copy P(2t + 2) and P(−2t − 2) to the array ends and use in the if-statement below. u(3):= u(2) v(3):= v(2) Overwrite P(2t ± 2) with P(2t ± 1) temp:= u(2) − u(1) u(2):= u(0) + temp u(0):= temp Overwrite P(−2t ± 2) with P(−2t ± 1) temp:= v(0) − v(1) v(0):= v(2) + temp v(2):= temp if n has bit k set then Increase the indices of both Perrin triples by 1. for i = 0, 1, 2 u(i):= u(i + 1) v(i):= v(i + 1) endfor endif endfor Result print v(2), v(1), v(0) print u(0), u(1), u(2)
Successively P(−n − 1), P(−n), P(−n + 1) and P(n − 1), P(n), P(n + 1) (mod n).
If P(−n) = −1 and P(n) = 0 then n is a probable prime, that is: actually prime or a restricted Perrin pseudoprime.
Shanks et al. observed that for all restricted pseudoprimes they found, the final state of the above six registers (the "signature" of n) equals the initial state 1,−1,3, 3,0,2.[22] The same occurs with ≈ 1/6 of all primes, so the two sets cannot be distinguished on the strength of this test alone.[23] For those cases, they recommend to also use the Narayana-Lucas sister sequence with recurrence relation A(n) = A(n − 1) + A(n − 3) and initial values
u(0):= 3, u(1):= 1, u(2):= 1 v(0):= 3, v(1):= 0, v(2):=−2
The same doubling rule applies and the formulas for filling the gaps are
temp:= u(0) + u(1)
u(0):= u(2) − temp
u(2):= temp
temp:= v(2) + v(1)
v(2):= v(0) − temp
v(0):= temp
Here, n is a probable prime if A(−n) = 0 and A(n) = 1.
Kurtz et al. found no overlap between the odd pseudoprimes for the two sequences below 50∙109 and supposed that 2,277,740,968,903 = 1067179 ∙ 2134357 is the smallest composite number to pass both tests.[24]
If the third-order Pell-Lucas recurrence A(n) = 2A(n − 1) + A(n − 3) is used as well, this bound will be pushed up to 4,057,052,731,496,380,171 = 1424263447 ∙ 2848526893.[25]
Additionally, roots of the doubling rule-congruence other than −1 or 3 expose composite numbers, like non-trivial square roots of 1 in the Miller-Rabin test.[26] This reduces the number of restricted pseudoprimes for each sequence by roughly one-third and is especially efficient in detecting Carmichael numbers.[27]
The least strong restricted Perrin pseudoprime is 46672291 and the above two bounds expand to successively 173,536,465,910,671 and 79,720,990,309,209,574,421.[28]
Notes
[edit]- ^ a b Sloane, N. J. A. (ed.). "Sequence A001608 (Perrin sequence (or Ondrej Such sequence): a(n) = a(n-2) + a(n-3) with a(0) = 3, a(1) = 0, a(2) = 2)". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ^ Sloane, N. J. A. (ed.). "Sequence A078712 (Series expansion of (-3 - 2*x)/(1 + x - x^3) in powers of x)". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ^ Sloane, N. J. A. (ed.). "Sequence A112881 (Indices of prime Perrin numbers; values of n such that A001608(n) is prime)". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ^ Sloane, N. J. A. (ed.). "Sequence A074788 (Prime numbers in the Perrin sequence b(n+1) = b(n-1) + b(n-2) with initial values b(1)=3, b(2)=0, b(3)=2)". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ^ Lucas (1878)
- ^ Perrin (1899)
- ^ Adams & Shanks (1982)
- ^ Kurtz, Shanks & Williams (1986)
- ^ Füredi (1987)
- ^ Tarry (1898)
- ^ Sloane, N. J. A. (ed.). "Sequence A000918 (a(n) = 2^n - 2)". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ^ Perrin (1899) translated from the French
- ^ Malo (1900), Jarden (1966)
- ^ Adams & Shanks (1982, p. 255)
- ^ Grantham (2010), Stephan (2020)
- ^ Sloane, N. J. A. (ed.). "Sequence A013998 (Unrestricted Perrin pseudoprimes)". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ^ Sloane, N. J. A. (ed.). "Sequence A018187 (Restricted Perrin pseudoprimes)". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ^ Sloane, N. J. A. (ed.). "Sequence A275612 (Restricted Perrin pseudoprimes (Adams and Shanks definition))". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ^ Sloane, N. J. A. (ed.). "Sequence A275613 (Restricted Perrin pseudoprimes (Grantham definition).)". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ^ None of the 2402549 Lucas-Selfridge pseudoprimes below 1015 listed by Dana Jacobsen (2020) is also a Perrin pseudoprime.
- ^ Adams & Shanks (1982, p. 265, 269-270)
- ^ Adams & Shanks (1982, p. 275), Kurtz, Shanks & Williams (1986, p. 694). This was later confirmed for n < 1014 by Steven Arno (1991).
- ^ The signature does give discriminating information on the remaining two types of primes. For example, the smallest Q-type pseudoprime 50,972,694,899,204,437,633 computed by Holger Stephan (2019) is exposed by signature conditions 14a and 14c in Adams & Shanks (1982, p. 257).
- ^ Kurtz, Shanks & Williams (1986, p. 697)
- ^ Stephan (2019)
- ^ Adams & Shanks (1982, p. 280-283)
- ^ A C/C++ implementation of the extended Perrin test can be found in the final subsection of a previous version of this article.
- ^ Stephan (2019)
References
[edit]- Lucas, E. (1878). "Théorie des fonctions numériques simplement périodiques". American Journal of Mathematics (in French). 1 (3). Johns Hopkins University Press: 229–231. doi:10.2307/2369311. JSTOR 2369311.
- Tarry, G. (1898). "Question 1401". L'Intermédiaire des Mathématiciens. 5. Gauthier-Villars et fils: 266–267.
- Perrin, R. [in French] (1899). "Question 1484". L'Intermédiaire des Mathématiciens. 6. Gauthier-Villars et fils: 76–77.
- Malo, E. (1900). "Réponse à 1484". L'Intermédiaire des Mathématiciens. 7. Gauthier-Villars et fils: 280–282, 312–314.
- Jarden, Dov (1966). Recurring sequences (PDF) (2 ed.). Jerusalem: Riveon LeMatematika. pp. 86–93.
- Adams, William; Shanks, Daniel (1982). "Strong primality tests that are not sufficient". Mathematics of Computation. 39 (159). American Mathematical Society: 255–300. doi:10.1090/S0025-5718-1982-0658231-9. JSTOR 2007637.
- Kurtz, G. C.; Shanks, Daniel; Williams, H. C. (1986). "Fast primality tests for numbers less than 50∙109". Mathematics of Computation. 46 (174). American Mathematical Society: 691–701. doi:10.1090/S0025-5718-1986-0829639-7. JSTOR 2008007.
- Füredi, Zoltán (1987). "The number of maximal independent sets in connected graphs". Journal of Graph Theory. 11 (4): 463–470. doi:10.1002/jgt.3190110403.
- Arno, Steven (1991). "A note on Perrin pseudoprimes". Mathematics of Computation. 56 (193). American Mathematical Society: 371–376. Bibcode:1991MaCom..56..371A. doi:10.1090/S0025-5718-1991-1052083-9. JSTOR 2008548.
- Grantham, Jon (2010). "There are infinitely many Perrin pseudoprimes". Journal of Number Theory. 130 (5): 1117–1128. arXiv:1903.06825. doi:10.1016/j.jnt.2009.11.008.
- Jacobsen, Dana (2020). "Pseudoprime statistics and tables". ntheory.org. Retrieved 7 March 2024.
#LPSP Lucas-Selfridge
- Stephan, Holger (2020). "Millions of Perrin pseudoprimes including a few giants". arXiv:2002.03756v1 [math.NA].
- Stephan, Holger (2019). Perrin pseudoprimes (WIAS Research Data No. 4). Berlin: Weierstrass Institute. doi:10.20347/WIAS.DATA.4.
















































