Abbe number: Difference between revisions
Lynoreabbott (talk | contribs) m Added external link to multi-vendor Abbe data |
Citation bot (talk | contribs) Add: editors 1-2. | Use this bot. Report bugs. | Suggested by Dominic3203 | Category:Dimensionless numbers | #UCB_Category 10/57 |
||
| (87 intermediate revisions by 45 users not shown) | |||
| Line 1: | Line 1: | ||
{{Short description|Material dispersion property}} |
|||
[[Image:Abbe-diagram 2.svg|right|thumb|380px|An Abbe diagram plots the Abbe number against refractive index for a range of different glasses (red dots). Glasses are classified using the Schott Glass letter-number code to reflect their composition and position on the diagram.]] |
|||
In [[optics]] and [[lens design]], the '''Abbe number''', also known as the '''Vd-number''' or '''constringence''' of a [[Transparency (optics)|transparent]] material, is an approximate measure of the material's [[dispersion (optics)|dispersion]] (change of [[refractive index]] versus wavelength), with high values of ''Vd'' indicating low dispersion. It is named after [[Ernst Abbe]] (1840–1905), the German physicist who defined it. The term Vd-number should not be confused with the [[Normalized frequency (fiber optics)|normalized frequency in fibers]]. |
|||
[[File:Abbe_number_calculation.svg|right|thumb|300px|Refractive index variation for SF11 flint glass, BK7 borosilicate crown glass, and fused quartz, and calculation for two Abbe numbers for SF11.]] |
|||
[[Image:SpiderGraph Abbe Number-en.svg|250px|thumb|Influences of selected [[glass]] component additions on the Abbe number of a specific base glass.<ref>[http://glassproperties.com/abbe_number/ Abbe number calculation of glasses]</ref>]] |
|||
The Abbe number,<ref>{{cite book |title=The Properties of Optical Glass |year=1998 |series=Schott Series on Glass and Glass Ceramics |language=en |publisher=[[Schott Glass]] |doi=10.1007/978-3-642-57769-7 |isbn=978-3-642-63349-2 |url=https://link.springer.com/book/10.1007/978-3-642-57769-7 |editor1=Bach, Hans |editor2=Neuroth, Norbert }}</ref> <math> V_\mathsf d\ ,</math> of a material is defined as |
|||
:<math> V_\mathsf d \equiv \frac{ n_\mathsf d - 1 }{\ n_\mathsf F - n_\mathsf C\ }</math>, |
|||
In [[physics]] and [[optics]], the '''Abbe number''', also known as the '''V-number''' or '''constringence''' of a [[Transparency (optics)|transparent]] material, is a measure of the material's [[dispersion (optics)|dispersion]] (variation of refractive index with wavelength) in relation to the [[refractive index]], with high values of ''V'' indicating low dispersion (low [[chromatic aberration]]). It is named after [[Ernst Abbe]] (1840–1905), the German physicist who defined it. |
|||
where <math>n_\mathsf C,</math> <math>n_\mathsf d,</math> and <math>n_\mathsf F</math> are the [[refractive indices]] of the material at the wavelengths of the [[Fraunhofer lines|Fraunhofer's]] C, d, and F [[spectral line]]s (656.3 [[nanometre|nm]], 587.56 nm, and 486.1 nm respectively). This formulation only applies to the [[visible spectrum|human vision]]. Outside this range requires the use of different spectral lines. For non-visible spectral lines the term "V-number" is more commonly used. The more general formulation defined as, |
|||
The Abbe number,<ref>{{cite book|last=Hovestadt|first=H.|title=Jena Glass and Its Scientific and Industrial Applications|year=1902|publisher=Macmillan and Co.|location=London|pages=1–81}}</ref><ref>{{cite book|last=Bergmann|first=Ludwig|title=Optics of Waves and Particles|year=1999|publisher=Walter de Gruyter|location=Berlin|isbn=3-11-014318-6|pages=198–201|author2=Clemens Schaefer}}</ref> ''V<sub>D</sub>'', of a material is defined as |
|||
:<math> |
:<math> V \equiv \frac{ n_\mathsf{center} - 1 }{ n_\mathsf{short} - n_\mathsf{long} }</math>, |
||
where |
where <math>n_\mathsf{short},</math> <math>n_\mathsf{center},</math> and <math>n_\mathsf{long},</math> are the refractive indices of the material at three different wavelengths. The shortest wavelength's index is <math>n_\mathsf{short}</math>, and the longest's is <math>n_\mathsf{long}</math>. |
||
Abbe numbers are used to classify [[glass]] and other |
Abbe numbers are used to classify [[glass]] and other optical materials in terms of their [[chromaticity]]. For example, the higher dispersion [[flint glass]]es have relatively small Abbe numbers <math>V < 55</math> whereas the lower dispersion [[crown glass (optics)|crown glass]]es have larger Abbe numbers. Values of <math>V_\mathsf d</math> range from below 25 for very dense flint glasses, around 34 for [[polycarbonate]] plastics, up to 65 for common crown glasses, and 75 to 85 for some fluorite and phosphate crown glasses. |
||
[[File:Eyesensitivity.svg|thumb|Most of the human eye's wavelength sensitivity curve, shown here, is bracketed by the Abbe number reference wavelengths of 486.1 nm (blue) and 656.3 nm (red)]] |
|||
Due to the difficulty and inconvenience in producing sodium and hydrogen lines, alternate definitions of the Abbe number are used in some contexts ([[ISO]] 7944).<ref>{{cite web|last=Meister|first=Darryl|title=Understanding Reference Wavelengths|url=http://www.opticampus.com/files/memo_on_reference_wavelengths.pdf|publisher=Carl Zeiss Vision|accessdate=2013-03-13}}</ref> The value ''V''<sub>d</sub> is given by |
|||
Abbe numbers are used in the design of [[achromatic lens]]es, as their [[reciprocal (mathematics)|''reciprocal'']] is proportional to dispersion (slope of refractive index versus wavelength) in the wavelength region where the human eye is most sensitive (see graph). For different wavelength regions, or for higher precision in characterizing a system's chromaticity (such as in the design of [[apochromat]]s), the full dispersion relation (refractive index as a function of wavelength) is used. |
|||
:<math> V_d = \frac{n_d-1}{ n_F - n_C }</math> |
|||
which defines the Abbe number with respect to the yellow Fraunhofer d (or D<sub>3</sub>) [[helium]] line at 587.5618 nm wavelength. It can also be defined using the green [[mercury (element)|mercury]] E-line at 546.073 nm: |
|||
:<math> V_e = \frac{n_e-1}{ n_{F'} - n_{C'}}</math> |
|||
where F' and C' are the blue and red [[cadmium]] lines at 480.0 nm and 643.8 nm, respectively. |
|||
== Abbe diagram == |
|||
An '''Abbe diagram''' is produced by plotting the Abbe number ''V''<sub>d</sub> of a material versus its refractive index ''n''<sub>d</sub>. Glasses can then be categorised by their composition and position on the diagram. This can be a letter-number code, as used in the [[Schott Glass]] catalogue, or a 6-digit [[glass code]]. |
|||
[[Image:Abbe-diagram 2.svg|right|thumb|380px|An Abbe diagram, also known as 'the glass veil', plots the Abbe number against refractive index for a range of different glasses (red dots). Glasses are classified using the Schott Glass letter-number code to reflect their composition and position on the diagram.]] |
|||
[[Image:SpiderGraph Abbe Number-en.svg|250px|thumb|Influences of selected [[glass]] component additions on the Abbe number of a specific base glass.<ref>{{cite web |first = Alexander |last = Fluegel |date = 2007-12-07 |title = Abbe number calculation of glasses |website = Statistical Calculation and Development of Glass Properties (glassproperties.com) |url = http://glassproperties.com/abbe_number/ |access-date = 2022-01-16}}</ref>]] |
|||
An '''Abbe diagram''', also called 'the glass veil', is produced by plotting the Abbe number <math>V_\mathsf d</math> of a material versus its refractive index <math>n_\mathsf d .</math> Glasses can then be categorised and selected according to their positions on the diagram. This can be a letter-number code, as used in the [[Schott Glass]] catalogue, or a 6 digit [[glass code]]. |
|||
Abbe numbers are used |
Glasses' Abbe numbers, along with their mean refractive indices, are used in the calculation of the required [[refractive power]]s of the elements of [[achromatic lens]]es in order to cancel [[chromatic aberration]] to first order. These two parameters which enter into the equations for design of achromatic doublets are exactly what is plotted on an Abbe diagram. |
||
Due to the difficulty and inconvenience in producing sodium and hydrogen lines, alternate definitions of the Abbe number are often substituted ([[ISO]] 7944).<ref>{{cite report |last=Meister |first=Darryl |date=12 April 2010 |title=Understanding reference wavelengths |type=memo |publisher=Carl Zeiss Vision |website=opticampus.opti.vision |url=http://opticampus.opti.vision/files/memo_on_reference_wavelengths.pdf |archive-url=https://ghostarchive.org/archive/20221009/http://opticampus.opti.vision/files/memo_on_reference_wavelengths.pdf |archive-date=2022-10-09 |url-status=live |access-date=2013-03-13}}</ref> For example, rather than the standard definition given above, that uses the refractive index variation between the F and C [[Fraunhofer lines#Naming|hydrogen lines]], one alternative measure using the subscript "e" for [[mercury (element)|mercury]]'s e line compared to [[cadmium]]'s {{prime|F}} and {{prime|C}} lines is |
|||
The following table lists standard wavelengths at which n is usually determined, indicated by subscripts.<ref>L. D. Pye, V. D. Frechette, N. J. Kreidl: "Borate Glasses"; Plenum Press, New York, 1977</ref> For example, n<sub>D</sub> is measured at 589.3 nm: |
|||
:<math> V_\mathsf e = \frac{ n_\mathsf e - 1 }{\ n_\mathsf{F'} - n_\mathsf{C'}\ } ~.</math> |
|||
This alternate takes the difference between cadmium's blue ({{prime|C}}) and red ({{prime|F}}) refractive indices at wavelengths 480.0 nm and 643.8 nm, relative to <math>\ n_\mathsf e\ </math> for mercury's e line at 546.073 nm, all of which are close by, and somewhat easier to produce than the C, F, and e lines. Other definitions can similarly be employed; the following table lists standard wavelengths at which <math>\ n\ </math> is commonly determined, including the [[Fraunhofer lines|standard subscripts]] used.<ref>{{cite book |first1=L.D. |last1=Pye |first2=V.D. |last2=Frechette |first3=N.J. |last3=Kreidl |year=1977 |title=Borate Glasses |publisher=Plenum Press |place=New York, NY}}</ref> |
|||
{| class="wikitable" |
{| class="wikitable" |
||
|- |
|- |
||
! {{mvar|λ}}<br/>(nm) !! [[Fraunhofer lines|Fraunhofer's<br/>symbol]] !! Light<br/>source !! Color |
|||
! λ in nm |
|||
! [[Fraunhofer lines|Fraunhofer's symbol]] |
|||
! Light source |
|||
! Color |
|||
|- |
|- |
||
| 365.01 ||align=center| i || [[Mercury (element)|Hg]] || [[Ultraviolet light|UV-A]] |
|||
| 365.01 |
|||
| i |
|||
| Hg |
|||
| UV |
|||
|- |
|- |
||
| 404.66 ||align=center| h || [[Mercury (element)|Hg]] || violet |
|||
| 404.66 |
|||
| h |
|||
| Hg |
|||
| violet |
|||
|- |
|- |
||
| 435.84 ||align=center| g || [[Mercury (element)|Hg]] || blue |
|||
| 435.84 |
|||
| g |
|||
| Hg |
|||
| blue |
|||
|- |
|- |
||
| 479.99 ||align=center| {{prime|F}} || [[Cadmium|Cd]] || blue |
|||
| 479.99 |
|||
| F' |
|||
| Cd |
|||
| blue |
|||
|- |
|- |
||
| 486.13 ||align=center| F || [[Hydrogen|H]] || blue |
|||
| 486.13 |
|||
| F |
|||
| H |
|||
| blue |
|||
|- |
|- |
||
| 546.07 ||align=center| e || [[Mercury (element)|Hg]] || green |
|||
| 546.07 |
|||
| e |
|||
| Hg |
|||
| green |
|||
|- |
|- |
||
| 587.56 ||align=center| d || [[Helium|He]] || yellow |
|||
| 587.56 |
|||
| d |
|||
| He |
|||
| yellow |
|||
|- |
|- |
||
| 589.3 ||align=center| D || [[Sodium|Na]] || yellow |
|||
| 589.3 |
|||
| D |
|||
| Na |
|||
| yellow |
|||
|- |
|- |
||
| 643.85 ||align=center| {{prime|C}} || [[Cadmium|Cd]] || red |
|||
| 643.85 |
|||
| C' |
|||
| Cd |
|||
| red |
|||
|- |
|- |
||
| 656.27 ||align=center| C || [[Hydrogen|H]] || red |
|||
| 656.27 |
|||
| C |
|||
| H |
|||
| red |
|||
|- |
|- |
||
| 706.52 ||align=center| r || [[Helium|He]] || red |
|||
| 706.52 |
|||
| r |
|||
| He |
|||
| red |
|||
|- |
|- |
||
| 768.2 ||align=center| {{prime|A}} || [[Potassium|K]] || [[Infrared light|IR-A]] |
|||
| 768.2 |
|||
| A' |
|||
| K |
|||
| IR |
|||
|- |
|- |
||
| 852.11 ||align=center| s || [[Cesium|Cs]] || [[Infrared light|IR-A]] |
|||
| 852.11 |
|||
| s |
|||
| Cs |
|||
| IR |
|||
|- |
|- |
||
| 1013.98 ||align=center| t || [[Mercury (element)|Hg]] || [[Infrared light|IR-A]] |
|||
| 1013.98 |
|||
| t |
|||
| Hg |
|||
| IR |
|||
|} |
|} |
||
==Derivation== |
|||
Starting from the [[Lens#Lensmaker's equation|'''Lensmaker's equation''']] we obtain the [[Lens#Thin lens approximation|'''thin lens''' equation]] by dropping a small term that accounts for lens thickness, <math>\ d\ </math>:<ref>{{Cite book |last=Hecht |first=Eugene |title=Optics |date=2017 |publisher=Pearson |isbn=978-1-292-09693-3 |edition=5 ed/fifth edition, global |location=Boston Columbus Indianapolis New York San Francisco Amsterdam Cape Town Dubai London Madrid Milan Munich}}</ref> |
|||
:<math> P = \frac{ 1 }{\ f ~} = (n - 1) \Biggl[ \frac{ 1 }{\ R_1\ } - \frac{ 1 }{\ R_2\ } + \frac{\ (n-1)\ d ~}{\ n\ R_1 R_2\ } \Biggr] \approx (n - 1) \left( \frac{ 1 }{\ R_1\ } - \frac{ 1 }{\ R_2\ } \right)\ ,</math> |
|||
when <math> d \ll \sqrt{\ R_1 R_2\ } ~.</math> |
|||
The change of [[refractive power]] <math>\ P\ </math> between the two wavelengths <math>\ \lambda_\mathsf{short}\ </math> and <math>\ \lambda_\mathsf{long}\ </math> is given by |
|||
:<math> \Delta P = P_\mathsf{short} - P_\mathsf{\ \!long} = (n_\mathsf s - n_\mathsf \ell) \left( \frac{ 1 }{\ R_1\ } - \frac{ 1 }{\ R_2\ } \right)\ ,</math> |
|||
where <math>\ n_\mathsf s\ </math> and <math>\ n_\mathsf \ell\ </math> are the short and long wavelengths' refractive indexes, respectively, and <math>\ n_\mathsf c\ ,</math> below, is for the center. |
|||
The power difference can be expressed relative to the power at the center wavelength (<math>\ \lambda_\mathsf{center}\ </math>) |
|||
: <math>\ P_\mathsf c\ = (n_\mathsf c - 1) \left( \frac{ 1 }{\ R_1\ } - \frac{ 1 }{\ R_2\ } \right)\, ;</math> |
|||
by multiplying and dividing by <math>\ n_\mathsf c - 1\ </math> and regrouping, get |
|||
:<math> \Delta P = \left( n_\mathsf s - n_\mathsf\ell \right) \left( \frac{\ n_\mathsf c - 1\ }{ n_\mathsf c - 1 } \right) \left( \frac{ 1 }{\ R_1\ } - \frac{ 1 }{\ R_2\ } \right)= \left( \frac{\ \ n_\mathsf s - n_\mathsf\ell\ }{ n_\mathsf c - 1 } \right) P_\mathsf c = \frac{\ P_\mathsf c\ }{ V_\mathsf c } ~.</math> |
|||
The relative change is [[inversely proportional]] to <math>\ V_\mathsf c\ :</math> |
|||
:<math> \frac{\ \Delta P\ }{ P_\mathsf c } = \frac{ 1 }{\ V_\mathsf c\ } ~.</math> |
|||
==See also== |
==See also== |
||
| Line 108: | Line 83: | ||
*[[Calculation of glass properties]], including Abbe number |
*[[Calculation of glass properties]], including Abbe number |
||
*[[Glass code]] |
*[[Glass code]] |
||
*[[Sellmeier equation]], more comprehensive and physically based modeling of dispersion |
|||
==References== |
==References== |
||
| Line 113: | Line 89: | ||
==External links== |
==External links== |
||
*[http://www.lacroixoptical.com/sites/default/files/content/LaCroix%20Dynamic%20Material%20Selection%20Data%20Tool%20vJanuary%202015.xlsm Abbe graph and data for 356 glasses from Ohara, Hoya, and Schott] |
*[https://web.archive.org/web/20151011033820/http://www.lacroixoptical.com/sites/default/files/content/LaCroix%20Dynamic%20Material%20Selection%20Data%20Tool%20vJanuary%202015.xlsm Abbe graph and data for 356 glasses from Ohara, Hoya, and Schott] |
||
{{DEFAULTSORT:Abbe Number}} |
{{DEFAULTSORT:Abbe Number}} |
||
[[Category:Dimensionless numbers]] |
[[Category:Dimensionless numbers]] |
||
[[Category: |
[[Category:Optical quantities]] |
||
[[Category:Glass physics]] |
[[Category:Glass physics]] |
||
Revision as of 08:38, 20 December 2024
In optics and lens design, the Abbe number, also known as the Vd-number or constringence of a transparent material, is an approximate measure of the material's dispersion (change of refractive index versus wavelength), with high values of Vd indicating low dispersion. It is named after Ernst Abbe (1840–1905), the German physicist who defined it. The term Vd-number should not be confused with the normalized frequency in fibers.
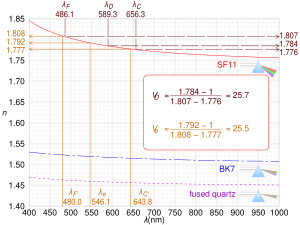
The Abbe number,[1] of a material is defined as
- ,
where and are the refractive indices of the material at the wavelengths of the Fraunhofer's C, d, and F spectral lines (656.3 nm, 587.56 nm, and 486.1 nm respectively). This formulation only applies to the human vision. Outside this range requires the use of different spectral lines. For non-visible spectral lines the term "V-number" is more commonly used. The more general formulation defined as,
- ,
where and are the refractive indices of the material at three different wavelengths. The shortest wavelength's index is , and the longest's is .
Abbe numbers are used to classify glass and other optical materials in terms of their chromaticity. For example, the higher dispersion flint glasses have relatively small Abbe numbers whereas the lower dispersion crown glasses have larger Abbe numbers. Values of range from below 25 for very dense flint glasses, around 34 for polycarbonate plastics, up to 65 for common crown glasses, and 75 to 85 for some fluorite and phosphate crown glasses.
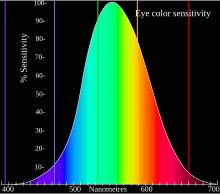
Abbe numbers are used in the design of achromatic lenses, as their reciprocal is proportional to dispersion (slope of refractive index versus wavelength) in the wavelength region where the human eye is most sensitive (see graph). For different wavelength regions, or for higher precision in characterizing a system's chromaticity (such as in the design of apochromats), the full dispersion relation (refractive index as a function of wavelength) is used.
Abbe diagram

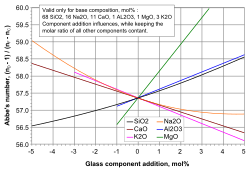
An Abbe diagram, also called 'the glass veil', is produced by plotting the Abbe number of a material versus its refractive index Glasses can then be categorised and selected according to their positions on the diagram. This can be a letter-number code, as used in the Schott Glass catalogue, or a 6 digit glass code.
Glasses' Abbe numbers, along with their mean refractive indices, are used in the calculation of the required refractive powers of the elements of achromatic lenses in order to cancel chromatic aberration to first order. These two parameters which enter into the equations for design of achromatic doublets are exactly what is plotted on an Abbe diagram.
Due to the difficulty and inconvenience in producing sodium and hydrogen lines, alternate definitions of the Abbe number are often substituted (ISO 7944).[3] For example, rather than the standard definition given above, that uses the refractive index variation between the F and C hydrogen lines, one alternative measure using the subscript "e" for mercury's e line compared to cadmium's F′ and C′ lines is
This alternate takes the difference between cadmium's blue (C′) and red (F′) refractive indices at wavelengths 480.0 nm and 643.8 nm, relative to for mercury's e line at 546.073 nm, all of which are close by, and somewhat easier to produce than the C, F, and e lines. Other definitions can similarly be employed; the following table lists standard wavelengths at which is commonly determined, including the standard subscripts used.[4]
| λ (nm) |
Fraunhofer's symbol |
Light source |
Color |
|---|---|---|---|
| 365.01 | i | Hg | UV-A |
| 404.66 | h | Hg | violet |
| 435.84 | g | Hg | blue |
| 479.99 | F′ | Cd | blue |
| 486.13 | F | H | blue |
| 546.07 | e | Hg | green |
| 587.56 | d | He | yellow |
| 589.3 | D | Na | yellow |
| 643.85 | C′ | Cd | red |
| 656.27 | C | H | red |
| 706.52 | r | He | red |
| 768.2 | A′ | K | IR-A |
| 852.11 | s | Cs | IR-A |
| 1013.98 | t | Hg | IR-A |
Derivation
Starting from the Lensmaker's equation we obtain the thin lens equation by dropping a small term that accounts for lens thickness, :[5]
when
The change of refractive power between the two wavelengths and is given by
where and are the short and long wavelengths' refractive indexes, respectively, and below, is for the center.
The power difference can be expressed relative to the power at the center wavelength ()
by multiplying and dividing by and regrouping, get
The relative change is inversely proportional to
See also
- Abbe prism
- Abbe refractometer
- Calculation of glass properties, including Abbe number
- Glass code
- Sellmeier equation, more comprehensive and physically based modeling of dispersion
References
- ^ Bach, Hans; Neuroth, Norbert, eds. (1998). The Properties of Optical Glass. Schott Series on Glass and Glass Ceramics. Schott Glass. doi:10.1007/978-3-642-57769-7. ISBN 978-3-642-63349-2.
- ^ Fluegel, Alexander (2007-12-07). "Abbe number calculation of glasses". Statistical Calculation and Development of Glass Properties (glassproperties.com). Retrieved 2022-01-16.
- ^ Meister, Darryl (12 April 2010). Understanding reference wavelengths (PDF). opticampus.opti.vision (memo). Carl Zeiss Vision. Archived (PDF) from the original on 2022-10-09. Retrieved 2013-03-13.
- ^ Pye, L.D.; Frechette, V.D.; Kreidl, N.J. (1977). Borate Glasses. New York, NY: Plenum Press.
- ^ Hecht, Eugene (2017). Optics (5 ed/fifth edition, global ed.). Boston Columbus Indianapolis New York San Francisco Amsterdam Cape Town Dubai London Madrid Milan Munich: Pearson. ISBN 978-1-292-09693-3.



















![{\displaystyle P={\frac {1}{\ f~}}=(n-1){\Biggl [}{\frac {1}{\ R_{1}\ }}-{\frac {1}{\ R_{2}\ }}+{\frac {\ (n-1)\ d~}{\ n\ R_{1}R_{2}\ }}{\Biggr ]}\approx (n-1)\left({\frac {1}{\ R_{1}\ }}-{\frac {1}{\ R_{2}\ }}\right)\ ,}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/b602cb9282f31d6b69e2264556dcfbdef4d468d7)













