User:Econdeck/sandbox: Difference between revisions
No edit summary |
m Remove template per TFD outcome |
||
| (3 intermediate revisions by 3 users not shown) | |||
| Line 8: | Line 8: | ||
pdf =<math>\frac{|a|x^{ap-1}(1-(1-c)(x/b)^a)^{q-1}} {b^{ap}\mathrm{B}(p,q)(1+c(x/b)^a)^{p+q}}</math>| |
pdf =<math>\frac{|a|x^{ap-1}(1-(1-c)(x/b)^a)^{q-1}} {b^{ap}\mathrm{B}(p,q)(1+c(x/b)^a)^{p+q}}</math>| |
||
cdf =no closed form| |
cdf =no closed form| |
||
mean =<math>\frac{b\mathrm{B}(p+1/a,q)}{\mathrm{B}(p,q)}{}_2F_1 \left[\begin{matrix} p+1/a & 1/a \\ p+q+1/a \end{matrix} ; c \right]</math><br> (see [[basic hypergeometric series|hypergeometric series]])| |
|||
mean =<math>\frac{\alpha}{\alpha+\beta}\!</math>| |
|||
median =no closed form| |
median =no closed form| |
||
mode =<math>\frac{\alpha-1}{\alpha+\beta-2}\!</math> for <math>\alpha>1, \beta>1</math>| |
mode =<math>\frac{\alpha-1}{\alpha+\beta-2}\!</math> for <math>\alpha>1, \beta>1</math>| |
||
variance =<math>\frac{\ |
variance =<math>\frac{b^2\mathrm{B}(p+2/a,q)}{\mathrm{B}(p,q)}{}_2F_1 \left[\begin{matrix} p+2/a & 2/a \\ p+q+2/a \end{matrix} ; c \right]-\mu^2</math><br> where <math>\mu</math> is the mean.| |
||
skewness =<math>\frac{1}{\sigma^3}\left(\frac{b^3\mathrm{B}(p+3/a,q)}{\mathrm{B}(p,q)}{}_2F_1 \left[\begin{matrix} p+3/a & 3/a \\ p+q+3/a \end{matrix} ; c \right]-3\mu\sigma^2-\mu^3\right)</math><br> where <math>\mu</math> is the mean and <math>\sigma^3</math> is the variance.| |
|||
skewness =<math>\frac{2\,(\beta-\alpha)\sqrt{\alpha+\beta+1}}{(\alpha+\beta+2)\sqrt{\alpha\beta}}</math>| |
|||
kurtosis =''see text''| |
kurtosis =''see text''| |
||
entropy =''see text''| |
entropy =''see text''| |
||
| Line 38: | Line 38: | ||
===Cumulative distribution function=== |
===Cumulative distribution function=== |
||
There does not exist a closed-form expression for the [[cumulative distribution function]], so it must be computed numerically. However, the cumulative distribution functions of most of the GB's special cases can be derived analytically. For example, by setting <math>c=0</math> one obtains the GB1 distribution with CDF: |
There does not exist a closed-form expression for the [[cumulative distribution function]], so it must be computed [[numerical analysis|numerically]]. However, the cumulative distribution functions of most of the GB's special cases can be derived analytically. For example, by setting <math>c=0</math> one obtains the GB1 distribution with CDF: |
||
:<math>F(x;a,b,c=0,p,q) = \frac{_2F_1[p,1-q;p+1;z]z^p}{p\mathrm{B}(p,q)} = \mathrm{B}_z(p,q) \!</math> |
:<math>F(x;a,b,c=0,p,q) = \frac{_2F_1[p,1-q;p+1;z]z^p}{p\mathrm{B}(p,q)} = \mathrm{B}_z(p,q) \!</math> |
||
| Line 52: | Line 52: | ||
:<math>\begin{align} |
:<math>\begin{align} |
||
\frac{\alpha - 1}{\alpha + \beta - 2} \\ |
\frac{\alpha - 1}{\alpha + \beta - 2} \\ |
||
\end{align}</math><ref>Johnson, Norman L., Samuel Kotz, and N. Balakrishnan (1995). "Continuous Univariate Distributions, Vol. 2", Wiley, ISBN |
\end{align}</math><ref>Johnson, Norman L., Samuel Kotz, and N. Balakrishnan (1995). "Continuous Univariate Distributions, Vol. 2", Wiley, {{ISBN|978-0471584940}}.</ref> |
||
The |
The <math>k</math>th raw moment of a GB-distributed random variable ''X'' is: |
||
:<math>\operatorname{E}[X^k] = \frac{b^k\mathrm{B}(p+k/a,q)}{\mathrm{B}(p,q)}{}_2F_1 \left[\begin{matrix} p+k/a & k/a \\ p+q+k/a \end{matrix} ; c \right]</math> |
|||
:<math>\begin{align} |
|||
where <math>_2F_1</math> is the [[basic hypergeometric series|hypergeometric series]]. Therefore, the [[expected value]] (mean) (<math>\mu </math>), [[variance]] (second central moment), [[skewness]] (third central moment), and [[kurtosis excess]] (fourth central moment) of a GB-distributed [[random variable]] ''X'' are: |
|||
\mu &= \operatorname{E}(X) &&= \frac{\alpha}{\alpha + \beta} \\ |
|||
:<math>\mu = \operatorname{E}(X) = \frac{b\mathrm{B}(p+1/a,q)}{\mathrm{B}(p,q)}{}_2F_1 \left[\begin{matrix} p+1/a & 1/a \\ p+q+1/a \end{matrix} ; c \right]</math> |
|||
\end{align}</math> |
|||
The [[ |
The [[variance]] is: |
||
:<math>\ |
:<math>\sigma^2 = \operatorname{E}(X - \mu)^2 = \frac{b^2\mathrm{B}(p+2/a,q)}{\mathrm{B}(p,q)}{}_2F_1 \left[\begin{matrix} p+2/a & 2/a \\ p+q+2/a \end{matrix} ; c \right]-\mu^2</math> |
||
{(\alpha + \beta + 2) \sqrt{\alpha \beta}} |
|||
The [[skewness]] is: |
|||
</math> |
|||
:<math>\gamma_1 = \frac{\operatorname{E}(X - \mu)^3}{[\operatorname{E}(X - \mu)^2]^{3/2}} = \frac{1}{\sigma^3}\left(\frac{b^3\mathrm{B}(p+3/a,q)}{\mathrm{B}(p,q)}{}_2F_1 \left[\begin{matrix} p+3/a & 3/a \\ p+q+3/a \end{matrix} ; c \right]-3\mu\sigma^2-\mu^3\right)</math> |
|||
The [[kurtosis excess]] is: |
The [[kurtosis excess]] is: |
||
:<math>\frac{\operatorname{E}(X - \mu)^4}{[\operatorname{E}(X - \mu)^2]^{2}}-3 = \frac{ |
:<math>\gamma_2 = \frac{\operatorname{E}(X - \mu)^4}{[\operatorname{E}(X - \mu)^2]^{2}}-3 = \frac{1}{\sigma^4}\left(\frac{b^4\mathrm{B}(p+4/a,q)}{\mathrm{B}(p,q)}{}_2F_1 \left[\begin{matrix} p+4/a & 4/a \\ p+q+4/a \end{matrix} ; c \right]-4\mu\gamma_1\sigma^3-6\mu^{2}\sigma^2-\mu^4\right)-3</math> |
||
{\alpha \beta (\alpha + \beta + 2) (\alpha + \beta + 3)}</math> |
|||
or: |
|||
:<math>\frac{6[(\alpha - \beta)^2 (\alpha +\beta + 1) - \alpha \beta (\alpha + \beta + 2)]} |
|||
{\alpha \beta (\alpha + \beta + 2) (\alpha + \beta + 3)}</math> |
|||
In general, the <math>k</math>th [[raw moment]] is given by |
|||
:<math>\operatorname{E}(X^k) = \frac{\operatorname{B}(\alpha + k, \beta)}{\operatorname{B}(\alpha,\beta)} = \frac{(\alpha)_{k}}{(\alpha + \beta)_{k}}</math> |
|||
where <math>(x)_{k}</math> is a [[Pochhammer symbol]] representing rising factorial. It can also be written in a recursive form as |
|||
:<math>\operatorname{E}(X^k) = \frac{\alpha + k - 1}{\alpha + \beta + k - 1}\operatorname{E}(X^{k - 1})</math> |
|||
One can also show that |
|||
:<math>\operatorname{E}(\log X) = \psi(\alpha) - \psi(\alpha + \beta)</math> |
|||
===Quantities of information=== |
===Quantities of information=== |
||
| Line 139: | Line 127: | ||
==Generating beta-distributed random variates== |
==Generating beta-distributed random variates== |
||
If <math>X</math> and <math>Y</math> are independent, with <math>X \sim {\rm \Gamma}(\alpha, \theta)\,</math> and <math>Y \sim {\rm \Gamma}(\beta, \theta)\,</math> then <math>\tfrac{X}{X+Y} \sim {\rm Beta}(\alpha, \beta)\,</math>, so one algorithm for generating beta variates is to generate ''X''/(''X+Y''), where ''X'' is a gamma variate with parameters (<math>\alpha, 1</math>) and ''Y'' is an independent gamma variate with parameters (<math>\beta, 1</math>).<ref>van der Waerden, B. L., "Mathematical Statistics", Springer, ISBN |
If <math>X</math> and <math>Y</math> are independent, with <math>X \sim {\rm \Gamma}(\alpha, \theta)\,</math> and <math>Y \sim {\rm \Gamma}(\beta, \theta)\,</math> then <math>\tfrac{X}{X+Y} \sim {\rm Beta}(\alpha, \beta)\,</math>, so one algorithm for generating beta variates is to generate ''X''/(''X+Y''), where ''X'' is a gamma variate with parameters (<math>\alpha, 1</math>) and ''Y'' is an independent gamma variate with parameters (<math>\beta, 1</math>).<ref>van der Waerden, B. L., "Mathematical Statistics", Springer, {{ISBN|978-3540045076}}.</ref> |
||
Also, the ''k''th [[order statistic]] of <math>n</math> [[Uniform distribution (continuous)|uniformly distributed]] variates is <math>{\rm Beta}(k, n+1-k)</math>, so an alternative if <math>\alpha</math> and <math>\beta</math> are small integers is to generate <math>\alpha + \beta - 1</math> uniform variates and choose the <math>\alpha</math>-th largest.<ref name=David1/> |
Also, the ''k''th [[order statistic]] of <math>n</math> [[Uniform distribution (continuous)|uniformly distributed]] variates is <math>{\rm Beta}(k, n+1-k)</math>, so an alternative if <math>\alpha</math> and <math>\beta</math> are small integers is to generate <math>\alpha + \beta - 1</math> uniform variates and choose the <math>\alpha</math>-th largest.<ref name=David1/> |
||
| Line 186: | Line 174: | ||
===Order statistics=== |
===Order statistics=== |
||
{{Main|Order statistic}} |
{{Main|Order statistic}} |
||
The beta distribution has an important application in the theory of [[order statistic]]s. A basic result is that the distribution of the k'th largest of a sample of size ''n'' from a continuous [[Uniform distribution (continuous)|uniform distribution]] has a beta distribution.<ref name=David1>David, H. A., Nagaraja, H. N. (2003) ''Order Statistics'' (3rd Edition). Wiley, New Jersey pp 458. ISBN |
The beta distribution has an important application in the theory of [[order statistic]]s. A basic result is that the distribution of the k'th largest of a sample of size ''n'' from a continuous [[Uniform distribution (continuous)|uniform distribution]] has a beta distribution.<ref name=David1>David, H. A., Nagaraja, H. N. (2003) ''Order Statistics'' (3rd Edition). Wiley, New Jersey pp 458. {{ISBN|0-471-38926-9}}</ref> This result is summarized as: |
||
:<math>U_{(k)} \sim B(k,n+1-k).</math> |
:<math>U_{(k)} \sim B(k,n+1-k).</math> |
||
From this, and application of the theory related to the [[probability integral transform]], the distribution of any individual order statistic from any [[continuous distribution]] can be derived.<ref name=David1/> |
From this, and application of the theory related to the [[probability integral transform]], the distribution of any individual order statistic from any [[continuous distribution]] can be derived.<ref name=David1/> |
||
| Line 270: | Line 258: | ||
{{ProbDistributions|continuous-bounded}} |
{{ProbDistributions|continuous-bounded}} |
||
{{Common univariate probability distributions}} |
|||
{{DEFAULTSORT:Beta Distribution}} |
{{DEFAULTSORT:Beta Distribution}} |
||
[[Category:Continuous distributions]] |
[[:Category:Continuous distributions]] |
||
[[Category:Factorial and binomial topics]] |
[[:Category:Factorial and binomial topics]] |
||
[[Category:Conjugate prior distributions]] |
[[:Category:Conjugate prior distributions]] |
||
Latest revision as of 02:10, 10 October 2018
|
Probability density function 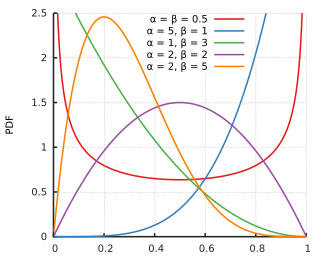 | |||
|
Cumulative distribution function 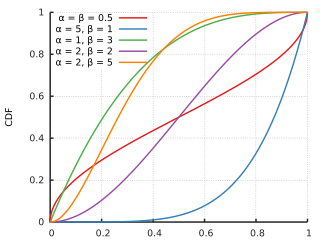 | |||
| Parameters |
(kurtosis) (real) (scale) (real) (domain) (real) (shape) (real) (shape) (real) | ||
|---|---|---|---|
| Support | |||
| CDF | no closed form | ||
| Mean |
(see hypergeometric series) | ||
| Median | no closed form | ||
| Mode | for | ||
| Variance |
where is the mean. | ||
| Skewness |
where is the mean and is the variance. | ||
| Excess kurtosis | see text | ||
| Entropy | see text | ||
| MGF | |||
| CF | (see Confluent hypergeometric function) | ||
In statistics and econometrics, the generalized beta distribution (or GB) is a family of continuous probability distributions of positive random variables with five parameters. The GB distribution includes as special or limiting cases such popular distributions as the beta (both first and second kinds), chi-squared, gamma, F, half-normal, and uniform distributions, among others. The generalized beta distribution allows for considerable flexibility in statistical modeling and testing.
Characterization
[edit]Probability density function
[edit]The probability density function of the generalized beta distribution is:
where is the beta function.
A random variable X that is distributed generalized beta with parameters is denoted
Cumulative distribution function
[edit]There does not exist a closed-form expression for the cumulative distribution function, so it must be computed numerically. However, the cumulative distribution functions of most of the GB's special cases can be derived analytically. For example, by setting one obtains the GB1 distribution with CDF:
where , is a hypergeometric series, and is the incomplete beta function. Conversely, by setting one obtains the GB2 distribution with CDF:
where .
Properties
[edit]The mode of a Beta distributed random variable X with parameters α > 1 and β > 1 is:
The th raw moment of a GB-distributed random variable X is:
where is the hypergeometric series. Therefore, the expected value (mean) (), variance (second central moment), skewness (third central moment), and kurtosis excess (fourth central moment) of a GB-distributed random variable X are:
The variance is:
The skewness is:
The kurtosis excess is:
Quantities of information
[edit]Given two beta distributed random variables, X ~ Beta(α, β) and Y ~ Beta(α', β'), the differential entropy of X is [2]
where is the digamma function.
The cross entropy is
It follows that the Kullback–Leibler divergence between these two beta distributions is
Shapes
[edit]The beta density function can take on different shapes depending on the values of the two parameters:
- is the uniform [0,1] distribution
- is U-shaped (blue plot)
- is the arcsine distribution
- or is strictly decreasing (red plot)
- or is strictly increasing (green plot)
- is strictly convex
- is a straight line
- is strictly concave
- is unimodal (magenta & cyan plots)
Moreover, if then the density function is symmetric about 1/2 (blue & teal plots).
Parameter estimation
[edit]Let
be the sample mean and
be the sample variance. The method-of-moments estimates of the parameters are
When the distribution is required over an interval other than [0, 1], say , then replace with and with in the above equations.[3][4]
There is no closed-form of the maximum likelihood estimates for the parameters.
Generating beta-distributed random variates
[edit]If and are independent, with and then , so one algorithm for generating beta variates is to generate X/(X+Y), where X is a gamma variate with parameters () and Y is an independent gamma variate with parameters ().[5]
Also, the kth order statistic of uniformly distributed variates is , so an alternative if and are small integers is to generate uniform variates and choose the -th largest.[6]
Related distributions
[edit]Transformations
[edit]- If then
- If then . The beta prime distribution, also called "beta distribution of the second kind".
- If then (assuming n>0 and m>0)
- If then where PERT denotes a distribution used in PERT analysis.[citation needed]
- If then Kumaraswamy distribution with parameters
- If then Kumaraswamy distribution with parameters
- If then
Special and limiting cases
[edit]- the standard uniform distribution.
- If and then Wigner semicircle distribution.
- is the Jeffreys prior for a proportion and is equivalent to arcsine distribution.
- the exponential distribution
- the gamma distribution
Derived from other distributions
[edit]- The kth order statistic of a sample of size n from the uniform distribution is a beta random variable, [6]
- If and then
- If and then
- If and then .
- If , then , which is a special case of the Beta distribution called the power-function distribution.[clarification needed]
Combination with other distributions
[edit]- and then for all x > 0.
Compounding with other distributions
[edit]- If and then beta-binomial distribution
- If and then beta negative binomial distribution
Generalisations
[edit]- The Dirichlet distribution is a multivariate generalization of the beta distribution. Univariate marginals of the Dirichlet distribution have a beta distribution.
- The beta distribution is a special case of the Pearson type I distribution
- the noncentral beta distribution
Other
[edit]- Binomial opinions in subjective logic are equivalent to Beta distributions.[citation needed]
Applications
[edit]Order statistics
[edit]The beta distribution has an important application in the theory of order statistics. A basic result is that the distribution of the k'th largest of a sample of size n from a continuous uniform distribution has a beta distribution.[6] This result is summarized as:
From this, and application of the theory related to the probability integral transform, the distribution of any individual order statistic from any continuous distribution can be derived.[6]
Rule of succession
[edit]A classic application of the beta distribution is the rule of succession, introduced in the 18th century by Pierre-Simon Laplace in the course of treating the sunrise problem. It states that, given s successes in n conditionally independent Bernoulli trials with probability p, that p should be estimated as . This estimate may be regarded as the expected value of the posterior distribution over p, namely Beta(s + 1, n − s + 1), which is given by Bayes' rule if one assumes a uniform prior over p (i.e., Beta(1, 1)) and then observes that p generated s successes in n trials.
Bayesian inference
[edit]Beta distributions are used extensively in Bayesian inference, since beta distributions provide a family of conjugate prior distributions for binomial (including Bernoulli) and geometric distributions. The Beta(0,0) distribution is an improper prior and sometimes used to represent ignorance of parameter values.
The domain of the beta distribution can be viewed as a probability, and in fact the beta distribution is often used to describe the distribution of an unknown probability value — typically, as the prior distribution over a probability parameter, such as the probability of success in a binomial distribution or Bernoulli distribution. In fact, the beta distribution is the conjugate prior of the binomial distribution and Bernoulli distribution.
The beta distribution is the special case of the Dirichlet distribution with only two parameters, and the beta is conjugate to the binomial and Bernoulli distributions in exactly the same way as the Dirichlet distribution is conjugate to the multinomial distribution and categorical distribution.
In Bayesian inference, the beta distribution can be derived as the posterior probability of the parameter p of a binomial distribution after observing α − 1 successes (with probability p of success) and β − 1 failures (with probability 1 − p of failure). Another way to express this is that placing a prior distribution of Beta(α,β) on the parameter p of a binomial distribution is equivalent to adding α pseudo-observations of "success" and β pseudo-observations of "failure" to the actual number of successes and failures observed, then estimating the parameter p by the proportion of successes over both real- and pseudo-observations. If α and β are greater than 0, this has the effect of smoothing out the distribution of the parameters by ensuring that some positive probability mass is assigned to all parameters even when no actual observations corresponding to those parameters is observed. Values of α and β less than 1 favor sparsity, i.e. distributions where the parameter p is close to either 0 or 1. In effect, α and β, when operating together, function as a concentration parameter; see that article for more details.
Task duration modeling
[edit]The beta distribution can be used to model events which are constrained to take place within an interval defined by a minimum and maximum value. For this reason, the beta distribution — along with the triangular distribution — is used extensively in PERT, critical path method (CPM) and other project management / control systems to describe the time to completion of a task. In project management, shorthand computations are widely used to estimate the mean and standard deviation of the beta distribution:
where a is the minimum, c is the maximum, and b is the most likely value.
Using this set of approximations is known as three-point estimation and are exact only for particular values of α and β, specifically when[7]:
or vice versa.
These are notably poor approximations for most other beta distributions exhibiting average errors of 40% in the mean and 549% in the variance[8][9][10]
Alternative parameterizations
[edit]Mean and sample size
[edit]The beta distribution may also be reparameterized in terms of its mean μ (0 ≤ μ ≤ 1) and sample size ν = α + β (ν > 0). This is useful in Bayesian parameter estimation if one wants to place an unbiased (uniform) prior over the mean. For example, one may administer a test to a number of individuals. If it is assumed that each person's score (0 ≤ θ ≤ 1) is drawn from a population-level Beta distribution, then an important statistic is the mean of this population-level distribution. The mean and sample size parameters are related to the shape parameters α and β via[11]
Under this parameterization, one can place a uniform prior over the mean, and a vague prior (such as an exponential or gamma distribution) over the positive reals for the sample size.
The Balding–Nichols model is a similar two-parameter reparameterization of the beta distribution.
Four parameters
[edit]A beta distribution with the two shape parameters α and β is supported on the range [0,1]. It is possible to alter the location and scale of the distribution by introducing two further parameters representing the minimum and maximum values of the distribution.[12]
The probability density function of the four parameter beta distribution is given by
The mean, mode and variance of the four parameters Beta distribution are:
The standard form can be obtained by letting
References
[edit]- ^ Johnson, Norman L., Samuel Kotz, and N. Balakrishnan (1995). "Continuous Univariate Distributions, Vol. 2", Wiley, ISBN 978-0471584940.
- ^ A. C. G. Verdugo Lazo and P. N. Rathie. "On the entropy of continuous probability distributions," IEEE Trans. Inf. Theory, IT-24:120–122,1978.
- ^ Engineering Statistics Handbook
- ^ Brighton Webs Ltd. Data & Analysis Services for Industry & Education
- ^ van der Waerden, B. L., "Mathematical Statistics", Springer, ISBN 978-3540045076.
- ^ a b c d David, H. A., Nagaraja, H. N. (2003) Order Statistics (3rd Edition). Wiley, New Jersey pp 458. ISBN 0-471-38926-9
- ^ Grubbs, Frank E. (1962). Attempts to Validate Certain PERT Statistics or ‘Picking on PERT’. Operations Research 10(6), p. 912–915.
- ^ Keefer, Donald L. and Verdini, William A. (1993). Better Estimation of PERT Activity Time Parameters. Management Science 39(9), p. 1086–1091.
- ^ Keefer, Donald L. and Bodily, Samuel E. (1983). Three-point Approximations for Continuous Random variables. Management Science 29(5), p. 595–609.
- ^ DRMI Newsletter, Issue 12, April 8, 2005
- ^ Kruschke, J. (2011). Doing Bayesian data analysis: A tutorial with R and BUGS. Academic Press / Elsevier, p. 83.
- ^ Beta4 distribution
External links
[edit]- Weisstein, Eric W. "Beta Distribution". MathWorld.
- "Beta Distribution" by Fiona Maclachlan, the Wolfram Demonstrations Project, 2007.
- Beta Distribution – Overview and Example, xycoon.com
- Beta Distribution, brighton-webs.co.uk
Category:Continuous distributions
Category:Factorial and binomial topics
Category:Conjugate prior distributions



![{\displaystyle c\in [0,1]}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/02b2796dc5e3cb6527d1ac6e766dc1da2ef1e120)




![{\displaystyle {\frac {b\mathrm {B} (p+1/a,q)}{\mathrm {B} (p,q)}}{}_{2}F_{1}\left[{\begin{matrix}p+1/a&1/a\\p+q+1/a\end{matrix}};c\right]}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/bf0880bbd6917723101a396f55c1729ae947fcbe)


![{\displaystyle {\frac {b^{2}\mathrm {B} (p+2/a,q)}{\mathrm {B} (p,q)}}{}_{2}F_{1}\left[{\begin{matrix}p+2/a&2/a\\p+q+2/a\end{matrix}};c\right]-\mu ^{2}}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/015dbc06e3b63704714939a79efd497ba0b1b755)

![{\displaystyle {\frac {1}{\sigma ^{3}}}\left({\frac {b^{3}\mathrm {B} (p+3/a,q)}{\mathrm {B} (p,q)}}{}_{2}F_{1}\left[{\begin{matrix}p+3/a&3/a\\p+q+3/a\end{matrix}};c\right]-3\mu \sigma ^{2}-\mu ^{3}\right)}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/a8a17a162ddc403feaa7d2ad95d2739c43780e3a)








![{\displaystyle F(x;a,b,c=0,p,q)={\frac {_{2}F_{1}[p,1-q;p+1;z]z^{p}}{p\mathrm {B} (p,q)}}=\mathrm {B} _{z}(p,q)\!}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/78412e48011b6ac5f7727db7d9856bf78d971aad)







![{\displaystyle \operatorname {E} [X^{k}]={\frac {b^{k}\mathrm {B} (p+k/a,q)}{\mathrm {B} (p,q)}}{}_{2}F_{1}\left[{\begin{matrix}p+k/a&k/a\\p+q+k/a\end{matrix}};c\right]}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/65fc13de0a8506b4ad1082b8152070d28e37883e)
![{\displaystyle \mu =\operatorname {E} (X)={\frac {b\mathrm {B} (p+1/a,q)}{\mathrm {B} (p,q)}}{}_{2}F_{1}\left[{\begin{matrix}p+1/a&1/a\\p+q+1/a\end{matrix}};c\right]}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/b641e77bce65be0fca1af55dee5c8c13c1600e77)
![{\displaystyle \sigma ^{2}=\operatorname {E} (X-\mu )^{2}={\frac {b^{2}\mathrm {B} (p+2/a,q)}{\mathrm {B} (p,q)}}{}_{2}F_{1}\left[{\begin{matrix}p+2/a&2/a\\p+q+2/a\end{matrix}};c\right]-\mu ^{2}}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/974f1468e4195f1a4dea21870412f5736d40fe49)
![{\displaystyle \gamma _{1}={\frac {\operatorname {E} (X-\mu )^{3}}{[\operatorname {E} (X-\mu )^{2}]^{3/2}}}={\frac {1}{\sigma ^{3}}}\left({\frac {b^{3}\mathrm {B} (p+3/a,q)}{\mathrm {B} (p,q)}}{}_{2}F_{1}\left[{\begin{matrix}p+3/a&3/a\\p+q+3/a\end{matrix}};c\right]-3\mu \sigma ^{2}-\mu ^{3}\right)}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/68759aaffbd4d468b8c9d174287c78d4b48a2e94)
![{\displaystyle \gamma _{2}={\frac {\operatorname {E} (X-\mu )^{4}}{[\operatorname {E} (X-\mu )^{2}]^{2}}}-3={\frac {1}{\sigma ^{4}}}\left({\frac {b^{4}\mathrm {B} (p+4/a,q)}{\mathrm {B} (p,q)}}{}_{2}F_{1}\left[{\begin{matrix}p+4/a&4/a\\p+q+4/a\end{matrix}};c\right]-4\mu \gamma _{1}\sigma ^{3}-6\mu ^{2}\sigma ^{2}-\mu ^{4}\right)-3}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/5062b8add2ae7c6d29a6ab7fea6ca92feb1355fc)























![{\displaystyle \scriptstyle [\ell ,h]}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/bcc4e5aba23f2120854fa2229d97dba92c7ca2c4)











































![{\displaystyle X\sim {\rm {U}}(0,1]\,}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/de74bb323a07dccdd103dfd537ce9f9b85d0d5ce)

















