Galton board: Difference between revisions
Tom.Reding (talk | contribs) m +{{Authority control}} (2 IDs from Wikidata), WP:GenFixes on |
Removing link(s) to "Index Fund Advisors": Removing links to deleted page Index Fund Advisors. |
||
| (37 intermediate revisions by 29 users not shown) | |||
| Line 1: | Line 1: | ||
{{short description|Device invented by Francis Galton}} |
|||
{{more citations needed|date=March 2018}} |
|||
[[File:Galton box.jpg|thumb|180px| |
[[File:Galton box.jpg|thumb|180px|Galton box]] |
||
[[File:Galton box.webm|thumb|A Galton box demonstrated]] |
[[File:Galton box.webm|thumb|A Galton box demonstrated]] |
||
The ''' |
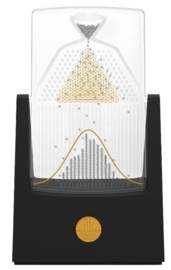
The '''Galton board''', also known as the '''Galton box''' or '''[[quincunx]]''' or '''bean machine''' (or incorrectly '''Dalton board'''), is a device invented by [[Francis Galton]]<ref name="Galton">{{cite book|last=Galton|first=Sir Francis|title=Natural Inheritance|url=https://archive.org/details/naturalinherita01galtgoog|date=1894|publisher=Macmillan}} {{ISBN|978-1297895982}}</ref> to demonstrate the [[central limit theorem]], in particular that with sufficient sample size the [[binomial distribution]] approximates a [[normal distribution]]. |
||
Galton designed it to illustrate his idea of [[Regression toward the mean|regression to the mean]],<ref name=":0">{{Cite journal |last=Kunert |first=Joachim |last2=Montag |first2=Astrid |last3=Pöhlmann |first3=Sigrid |date=2001-04-01 |title=The quincunx: history and mathematics |url=https://link.springer.com/article/10.1007/s003620100048 |journal=Statistical Papers |language=en |volume=42 |issue=2 |pages=143–169 |doi=10.1007/s003620100048 |issn=1613-9798}}</ref> which he called "reversion to mediocrity" and made part of his [[Eugenics|eugenist]] ideology.<ref>{{Cite journal |last=Renwick |first=Chris |date=2011 |title=From political economy to sociology: Francis Galton and the social-scientific origins of eugenics |url=https://www.jstor.org/stable/41241682 |journal=The British Journal for the History of Science |volume=44 |issue=3 |pages=343–369 |issn=0007-0874}}</ref> |
|||
==Description== |
==Description== |
||
The Galton |
The Galton board consists of a vertical board with interleaved rows of pegs. Beads are dropped from the top and, when the device is level, bounce either left or right as they hit the pegs. Eventually they are collected into bins at the bottom, where the height of bead columns accumulated in the bins approximate a [[normal distribution|bell curve]]. Overlaying [[Pascal's triangle]] onto the pins shows the number of different paths that can be taken to get to each bin.<ref name="GBweb">{{cite web|title=The Galton Board|url=http://www.galtonboard.com|website=www.galtonboard.com|publisher=Four Pines Publishing, Inc.|accessdate=2018-03-06|language=en}}</ref> |
||
Large-scale working models of this device created by [[Charles and Ray Eames]] can be seen in the ''[[Mathematica: A World of Numbers... and Beyond]]'' exhibits permanently on view at the [[Boston Museum of Science]], the [[New York Hall of Science]], or the [[Henry Ford Museum]].<ref name="Ford">{{cite web|title=Henry Ford museum acquires Eames' Mathematica exhibit|url=https://www.liveauctioneers.com/news/top-news/museums/henry-ford-museum-acquires-eames-mathematica-exhibit/|website=Auction Central News|publisher=LiveAuctioneers|accessdate=2018-03-06|date=20 March 2015}}</ref> Another large-scale version is displayed in the lobby of |
Large-scale working models of this device created by [[Charles and Ray Eames]] can be seen in the ''[[Mathematica: A World of Numbers... and Beyond]]'' exhibits permanently on view at the [[Boston Museum of Science]], the [[New York Hall of Science]], or the [[Henry Ford Museum]].<ref name="Ford">{{cite web|title=Henry Ford museum acquires Eames' Mathematica exhibit|url=https://www.liveauctioneers.com/news/top-news/museums/henry-ford-museum-acquires-eames-mathematica-exhibit/|website=Auction Central News|publisher=LiveAuctioneers|accessdate=2018-03-06|date=20 March 2015}}</ref> The Ford Museum machine was displayed at the IBM Pavilion during [[1964-65 New York World's Fair]], later appearing at [[Pacific Science Center]] in Seattle.<ref>{{cite web |url=http://nywf64.com/ibm06.shtml |title=Pavilions & Attractions - IBM - Page Six |access-date=22 December 2011 |website=New York World's Fair}}</ref><ref>{{cite web|type=press release|title=Mathematica Exhibition from the Office of Charles and Ray Eames Opens inside Henry Ford Museum of American Innovation, Sept. 23|publisher=Henry Ford Museum of American Innovation|date=September 21, 2017|url=https://www.prweb.com/releases/mathematica_exhibition_from_the_office_of_charles_and_ray_eames_opens_inside_henry_ford_museum_of_american_innovation_sept_23/prweb14717323.htm}}</ref> Another large-scale version is displayed in the lobby of Index Fund Advisors in [[Irvine, California]].<ref name="IFA">Archived at [https://ghostarchive.org/varchive/youtube/20211211/9xUBhhM4vbM Ghostarchive]{{cbignore}} and the [https://web.archive.org/web/20130726023016/http://www.youtube.com/watch?v=9xUBhhM4vbM Wayback Machine]{{cbignore}}: {{cite web|title=IFA.tv - From Chaos to Order on the Galton Board -- A Random Walker| website=[[YouTube]] |url=https://www.youtube.com/watch?v=9xUBhhM4vbM&t=10s|accessdate=2018-03-06|date=23 December 2009}}{{cbignore}}</ref> |
||
Boards can be constructed for other distributions by changing the shape of the pins or biasing them towards one direction, and even bimodal boards are possible.<ref>Brehmer et al 2018, [https://arxiv.org/abs/1805.12244 "Mining gold from implicit models to improve likelihood-free inference"]: [https://github.com/johannbrehmer/simulator-mining-example "Simulator Mining Example"]</ref> A board for the [[log-normal distribution]] (common in [[Log-normal distribution#Occurrence and applications|many natural processes]], particularly biological ones), which uses isosceles triangles of varying widths to 'multiply' the distance the bead travels instead of fixed sizes steps which would 'sum', was constructed by [[Jacobus Kapteyn]] while studying and popularizing the statistics of the log-normal in order to help visualize it and demonstrate its plausibility.<ref>Kapteyn 1903, [https://babel.hathitrust.org/cgi/pt?id=wu.89098679251;view=image ''Skew frequency curves in biology and statistics'' v1]; Kapteyn & van Uven 1916, [https://babel.hathitrust.org/cgi/pt?id=mdp.39015017409502;view=1up;seq=9 ''Skew frequency curves in biology and statistics'' v2]</ref> As of 1963, it was preserved in the [[University of Groningen]].<ref>[[John Aitchison|Aitchison]] & Brown 1963, [https://www.gwern.net/docs/statistics/1963-aitchison-thelognormaldistribution.pdf#page=24 ''The Lognormal Distribution, with Special Reference to its Uses in Economics''] {{Webarchive|url=https://web.archive.org/web/20190802141029/https://www.gwern.net/docs/statistics/1963-aitchison-thelognormaldistribution.pdf#page=24 |date=2019-08-02 }}</ref> There is also an improved log-normal machine that uses skewed triangles whose right sides are longer, and thus avoiding shifting the median of the beads to the left.<ref>Limpert et al 2001, [https://stat.ethz.ch/~stahel/lognormal/bioscience2001.pdf#page=3 "Log-normal Distributions across the Sciences: Keys and Clues"]</ref> |
|||
==Distribution of the beads== |
==Distribution of the beads== |
||
{{Unsourced section|date=May 2024}} |
|||
If a bead bounces to the right ''k'' times on its way down (and to the left on the remaining pegs) it ends up in the ''k''th bin counting from the left. Denoting the number of rows of pegs in a Galton Board by ''n'', the number of paths to the ''k''th bin on the bottom is given by the [[binomial coefficient]] <math>{n\choose k}</math>. Note that the leftmost bin is the ''0''-bin, next to it is the ''1''-bin, etc. and the furthest one to the right is the ''n''-bin - making thus the total number of bins equal to ''n+1'' (each row does not need to have more pegs than the number that identifies the row itself, e.g. the first row has 1 peg, the second 2 pegs, until the ''n''-th row that has ''n'' pegs which correspond to the ''n+1'' bins). If the probability of bouncing right on a peg is ''p'' (which equals 0.5 on an unbiased level machine) the probability that the ball ends up in the ''k''th bin equals <math>{n\choose k} p^k (1-p)^{n-k}</math>. This is the probability mass function of a [[binomial distribution]]. The number of rows correspond to the size of a binomial distribution in number of trials, while the probability ''p'' of each pin is the binomial's ''p''. |
If a bead bounces to the right ''k'' times on its way down (and to the left on the remaining pegs) it ends up in the ''k''th bin counting from the left. Denoting the number of rows of pegs in a Galton Board by ''n'', the number of paths to the ''k''th bin on the bottom is given by the [[binomial coefficient]] <math>{n\choose k}</math>. Note that the leftmost bin is the ''0''-bin, next to it is the ''1''-bin, etc. and the furthest one to the right is the ''n''-bin - making thus the total number of bins equal to ''n+1'' (each row does not need to have more pegs than the number that identifies the row itself, e.g. the first row has 1 peg, the second 2 pegs, until the ''n''-th row that has ''n'' pegs which correspond to the ''n+1'' bins). If the probability of bouncing right on a peg is ''p'' (which equals 0.5 on an unbiased level machine) the probability that the ball ends up in the ''k''th bin equals <math>{n\choose k} p^k (1-p)^{n-k}</math>. This is the probability mass function of a [[binomial distribution]]. The number of rows correspond to the size of a binomial distribution in number of trials, while the probability ''p'' of each pin is the binomial's ''p''. |
||
According to the [[central limit theorem]] (more specifically, the [[de Moivre–Laplace theorem]]), the binomial distribution approximates the normal distribution provided that the number of rows and the number of balls are both large. Varying the rows will result in different [[standard deviations]] or widths of the bell-shaped curve or the [[normal distribution]] in the bins. |
According to the [[central limit theorem]] (more specifically, the [[de Moivre–Laplace theorem]]), the binomial distribution approximates the normal distribution provided that the number of rows and the number of balls are both large. Varying the rows will result in different [[standard deviations]] or widths of the bell-shaped curve or the [[normal distribution]] in the bins. |
||
Another interpretation more accurate from the physical view is given by the [[Entropy]]: since the energy that is carried by every falling bead is finite, so even that on any tip their collisions are chaotic because the derivative is undefined (there is no way to previously figure out for which side is going to fall), the mean and variance of each bean is restricted to be finite (they will never bound out of the box), and the Gaussian shape arises because it is the [[maximum entropy probability distribution]] for a continuous process with defined mean and variance. The rise of the [[normal distribution]] could be interpreted as that all possible information carried by each bean related to which path it has travelled has been already completely lost through their downhill collisions. |
|||
== Examples == |
== Examples == |
||
<gallery mode=packed heights=180> |
<gallery mode="packed" heights="180"> |
||
File:GaltonBoard.png|Galton Board (7.5 in by 4.5 in) |
File:GaltonBoard.png|Galton Board (7.5 in by 4.5 in) |
||
File:Tabuleiros de Galton (antes e depois).jpg|Before and after the spin |
File:Tabuleiros de Galton (antes e depois).jpg|Before and after the spin |
||
File:Planche de Galton.jpg|A working replica of the machine (following a slightly modified design) |
File:Planche de Galton.jpg|A working replica of the machine (following a slightly modified design) |
||
File:Quincunx (Galton Box) - Galton 1889 diagram.png|The bean machine, as drawn by [[Francis Galton|Sir Francis Galton]] |
|||
</gallery> |
</gallery> |
||
==History== |
==History== |
||
[[Francis Galton]] designed his board as part of a presentation for the Royal Institution Discourses on February 27th, 1874. His goal was to promote the use of ranking instead of measurement in statistics, so that qualities such as intelligence could be assigned numbers without requiring experimental data. The piling of the balls into a normal distribution was supposed to illustrate how a mean value would emerge from multiple tests.<ref name=":1">{{Cite journal |last=Pritchard |first=Chris |date=2006 |title=Bagatelle as the inspiration for Galton's Quincunx |url=http://www.tandfonline.com/doi/abs/10.1080/17498430600804118 |journal=BSHM Bulletin: Journal of the British Society for the History of Mathematics |language=en |volume=21 |issue=2 |pages=102–110 |doi=10.1080/17498430600804118 |issn=1749-8430}}</ref>[[File:Quincunx (Galton Box) - Galton 1889 diagram.png|The quincunx, as drawn by [[Francis Galton]]|thumb]]Francis Galton wrote in 1889 his book ''Natural Inheritance'':<blockquote>Order in Apparent Chaos: I know of scarcely anything so apt to impress the imagination as the wonderful form of cosmic order expressed by the Law of Frequency of Error. The law would have been personified by the Greeks and deified, if they had known of it. It reigns with serenity and in complete self-effacement amidst the wildest confusion. The huger the mob, and the greater the apparent anarchy, the more perfect is its sway. It is the supreme law of Unreason. Whenever a large sample of chaotic elements are taken in hand and marshalled in the order of their magnitude, an unsuspected and most beautiful form of regularity proves to have been latent all along.<ref name="Galton" />{{rp|66}}</blockquote>However, Galton also wished to demonstrate that extreme values of intelligence result from heredity, in apparent contradiction with his experiment since it produces extreme values as dispersion from randomness alone. Aware of this issue, he tried to address it in 1875 by arguing that his box did not reflect situations where bias would be introduced by what he called ''a main influence factor''.<ref name=":0" /> |
|||
[[Sir Francis Galton]] was fascinated with the order of the bell curve that emerges from the apparent chaos of beads bouncing off of pegs in the Galton Board. He eloquently described this relationship in his book ''Natural Inheritance'' (1889): |
|||
In a 1877 letter to George Darwin, Galton described a second version of the board, with two stages, where the compartments at the bottom of the highest stage had small trapdoors that would allow the balls of one chosen compartment to fall through the second stage. His goal was to illustrate his concept of "reversion to mediocrity", i.e. that without marriage control the "best" parts of the population would mix with the "mediocre", so that their offspring would gradually revert towards an average value. This version, however, was not built. |
|||
<blockquote>Order in Apparent Chaos: I know of scarcely anything so apt to impress the imagination as the wonderful form of cosmic order expressed by the Law of Frequency of Error. The law would have been personified by the Greeks and deified, if they had known of it. It reigns with serenity and in complete self-effacement amidst the wildest confusion. The huger the mob, and the greater the apparent anarchy, the more perfect is its sway. It is the supreme law of Unreason. Whenever a large sample of chaotic elements are taken in hand and marshalled in the order of their magnitude, an unsuspected and most beautiful form of regularity proves to have been latent all along.<ref name="Galton" />{{rp|66}}</blockquote> |
|||
==Games== |
==Games== |
||
Several games have been developed |
Several games have been developed using the idea of pins changing the route of balls or other objects: |
||
*[[Bagatelle]] |
|||
*[[Pachinko]] |
*[[Pachinko]] |
||
*[[Payazzo]] |
*[[Payazzo]] |
||
| Line 37: | Line 43: | ||
*[[Plinko]] |
*[[Plinko]] |
||
*[[The Wall (game show)|The Wall]] |
*[[The Wall (game show)|The Wall]] |
||
It is suggested that these games provided inspiration for Galton's device.<ref name=":1" /> |
|||
| ⚫ | |||
| ⚫ | |||
== External links == |
== External links == |
||
{{Commons category|Galton box}} |
{{Commons category|Galton box}} |
||
* [http://www.galtonboard.com Galton Board informational website with resource links] |
* [http://www.galtonboard.com Galton Board informational website with resource links] |
||
* [https://www.youtube.com/watch?v=J7AGOptcR1E&feature=youtu.be An {{convert|8|ft|m|adj=mid|-tall}} |
* [https://www.youtube.com/watch?v=J7AGOptcR1E&feature=youtu.be An {{convert|8|ft|m|adj=mid|-tall}} Sir Francis: the Probability Machine - From Chaos to Order - Randomness in Stock Prices] from Index Fund Advisors [http://www.ifa.com IFA.com] |
||
* [https://www.mathsisfun.com/data/quincunx-explained.html Quincunx and its relationship to normal distribution] from |
* [https://www.mathsisfun.com/data/quincunx-explained.html Quincunx and its relationship to normal distribution] from Math Is Fun |
||
* [https://www.gwern.net/docs/statistics/order/beanmachine-multistage/index.html A multi-stage bean machine simulation (JS)] |
* [https://www.gwern.net/docs/statistics/order/beanmachine-multistage/index.html A multi-stage bean machine simulation (JS)] |
||
* [http://www.karlsims.com/marbles/ Pascal's Marble Run: a deterministic Galton board] |
* [http://www.karlsims.com/marbles/ Pascal's Marble Run: a deterministic Galton board] |
||
* [https://github.com/babeheim/multiplicative-galton Log-normal |
* [https://github.com/babeheim/multiplicative-galton Log-normal Galton board] ([https://twitter.com/babeheim/status/1130463937302917120 animation]) |
||
* [https://www.mctague.org/carl/blog/2021/04/23/central-limit-theorem/ A music video featuring a Galton board] by Carl McTague |
* [https://www.mctague.org/carl/blog/2021/04/23/central-limit-theorem/ A music video featuring a Galton board] by Carl McTague |
||
| ⚫ | |||
{{Commons category|Galton box}} |
|||
| ⚫ | |||
{{Authority control}} |
{{Authority control}} |
||
[[Category:Central limit theorem]] |
[[Category:Central limit theorem]] |
||
[[Category:Normal distribution]] |
[[Category:Normal distribution]] |
||
[[Category:Data visualization]] |
|||
Latest revision as of 05:17, 21 December 2024

The Galton board, also known as the Galton box or quincunx or bean machine (or incorrectly Dalton board), is a device invented by Francis Galton[1] to demonstrate the central limit theorem, in particular that with sufficient sample size the binomial distribution approximates a normal distribution.
Galton designed it to illustrate his idea of regression to the mean,[2] which he called "reversion to mediocrity" and made part of his eugenist ideology.[3]
Description
[edit]The Galton board consists of a vertical board with interleaved rows of pegs. Beads are dropped from the top and, when the device is level, bounce either left or right as they hit the pegs. Eventually they are collected into bins at the bottom, where the height of bead columns accumulated in the bins approximate a bell curve. Overlaying Pascal's triangle onto the pins shows the number of different paths that can be taken to get to each bin.[4]
Large-scale working models of this device created by Charles and Ray Eames can be seen in the Mathematica: A World of Numbers... and Beyond exhibits permanently on view at the Boston Museum of Science, the New York Hall of Science, or the Henry Ford Museum.[5] The Ford Museum machine was displayed at the IBM Pavilion during 1964-65 New York World's Fair, later appearing at Pacific Science Center in Seattle.[6][7] Another large-scale version is displayed in the lobby of Index Fund Advisors in Irvine, California.[8]
Boards can be constructed for other distributions by changing the shape of the pins or biasing them towards one direction, and even bimodal boards are possible.[9] A board for the log-normal distribution (common in many natural processes, particularly biological ones), which uses isosceles triangles of varying widths to 'multiply' the distance the bead travels instead of fixed sizes steps which would 'sum', was constructed by Jacobus Kapteyn while studying and popularizing the statistics of the log-normal in order to help visualize it and demonstrate its plausibility.[10] As of 1963, it was preserved in the University of Groningen.[11] There is also an improved log-normal machine that uses skewed triangles whose right sides are longer, and thus avoiding shifting the median of the beads to the left.[12]
Distribution of the beads
[edit]If a bead bounces to the right k times on its way down (and to the left on the remaining pegs) it ends up in the kth bin counting from the left. Denoting the number of rows of pegs in a Galton Board by n, the number of paths to the kth bin on the bottom is given by the binomial coefficient . Note that the leftmost bin is the 0-bin, next to it is the 1-bin, etc. and the furthest one to the right is the n-bin - making thus the total number of bins equal to n+1 (each row does not need to have more pegs than the number that identifies the row itself, e.g. the first row has 1 peg, the second 2 pegs, until the n-th row that has n pegs which correspond to the n+1 bins). If the probability of bouncing right on a peg is p (which equals 0.5 on an unbiased level machine) the probability that the ball ends up in the kth bin equals . This is the probability mass function of a binomial distribution. The number of rows correspond to the size of a binomial distribution in number of trials, while the probability p of each pin is the binomial's p.
According to the central limit theorem (more specifically, the de Moivre–Laplace theorem), the binomial distribution approximates the normal distribution provided that the number of rows and the number of balls are both large. Varying the rows will result in different standard deviations or widths of the bell-shaped curve or the normal distribution in the bins.
Another interpretation more accurate from the physical view is given by the Entropy: since the energy that is carried by every falling bead is finite, so even that on any tip their collisions are chaotic because the derivative is undefined (there is no way to previously figure out for which side is going to fall), the mean and variance of each bean is restricted to be finite (they will never bound out of the box), and the Gaussian shape arises because it is the maximum entropy probability distribution for a continuous process with defined mean and variance. The rise of the normal distribution could be interpreted as that all possible information carried by each bean related to which path it has travelled has been already completely lost through their downhill collisions.
Examples
[edit]-
Galton Board (7.5 in by 4.5 in)
-
Before and after the spin
-
A working replica of the machine (following a slightly modified design)
History
[edit]Francis Galton designed his board as part of a presentation for the Royal Institution Discourses on February 27th, 1874. His goal was to promote the use of ranking instead of measurement in statistics, so that qualities such as intelligence could be assigned numbers without requiring experimental data. The piling of the balls into a normal distribution was supposed to illustrate how a mean value would emerge from multiple tests.[13]

Francis Galton wrote in 1889 his book Natural Inheritance:
Order in Apparent Chaos: I know of scarcely anything so apt to impress the imagination as the wonderful form of cosmic order expressed by the Law of Frequency of Error. The law would have been personified by the Greeks and deified, if they had known of it. It reigns with serenity and in complete self-effacement amidst the wildest confusion. The huger the mob, and the greater the apparent anarchy, the more perfect is its sway. It is the supreme law of Unreason. Whenever a large sample of chaotic elements are taken in hand and marshalled in the order of their magnitude, an unsuspected and most beautiful form of regularity proves to have been latent all along.[1]: 66
However, Galton also wished to demonstrate that extreme values of intelligence result from heredity, in apparent contradiction with his experiment since it produces extreme values as dispersion from randomness alone. Aware of this issue, he tried to address it in 1875 by arguing that his box did not reflect situations where bias would be introduced by what he called a main influence factor.[2]
In a 1877 letter to George Darwin, Galton described a second version of the board, with two stages, where the compartments at the bottom of the highest stage had small trapdoors that would allow the balls of one chosen compartment to fall through the second stage. His goal was to illustrate his concept of "reversion to mediocrity", i.e. that without marriage control the "best" parts of the population would mix with the "mediocre", so that their offspring would gradually revert towards an average value. This version, however, was not built.
Games
[edit]Several games have been developed using the idea of pins changing the route of balls or other objects:
It is suggested that these games provided inspiration for Galton's device.[13]
External links
[edit]- Galton Board informational website with resource links
- An 8-foot-tall (2.4 m) Sir Francis: the Probability Machine - From Chaos to Order - Randomness in Stock Prices from Index Fund Advisors IFA.com
- Quincunx and its relationship to normal distribution from Math Is Fun
- A multi-stage bean machine simulation (JS)
- Pascal's Marble Run: a deterministic Galton board
- Log-normal Galton board (animation)
- A music video featuring a Galton board by Carl McTague
References
[edit]- ^ a b Galton, Sir Francis (1894). Natural Inheritance. Macmillan. ISBN 978-1297895982
- ^ a b Kunert, Joachim; Montag, Astrid; Pöhlmann, Sigrid (2001-04-01). "The quincunx: history and mathematics". Statistical Papers. 42 (2): 143–169. doi:10.1007/s003620100048. ISSN 1613-9798.
- ^ Renwick, Chris (2011). "From political economy to sociology: Francis Galton and the social-scientific origins of eugenics". The British Journal for the History of Science. 44 (3): 343–369. ISSN 0007-0874.
- ^ "The Galton Board". www.galtonboard.com. Four Pines Publishing, Inc. Retrieved 2018-03-06.
- ^ "Henry Ford museum acquires Eames' Mathematica exhibit". Auction Central News. LiveAuctioneers. 20 March 2015. Retrieved 2018-03-06.
- ^ "Pavilions & Attractions - IBM - Page Six". New York World's Fair. Retrieved 22 December 2011.
- ^ "Mathematica Exhibition from the Office of Charles and Ray Eames Opens inside Henry Ford Museum of American Innovation, Sept. 23" (press release). Henry Ford Museum of American Innovation. September 21, 2017.
- ^ Archived at Ghostarchive and the Wayback Machine: "IFA.tv - From Chaos to Order on the Galton Board -- A Random Walker". YouTube. 23 December 2009. Retrieved 2018-03-06.
- ^ Brehmer et al 2018, "Mining gold from implicit models to improve likelihood-free inference": "Simulator Mining Example"
- ^ Kapteyn 1903, Skew frequency curves in biology and statistics v1; Kapteyn & van Uven 1916, Skew frequency curves in biology and statistics v2
- ^ Aitchison & Brown 1963, The Lognormal Distribution, with Special Reference to its Uses in Economics Archived 2019-08-02 at the Wayback Machine
- ^ Limpert et al 2001, "Log-normal Distributions across the Sciences: Keys and Clues"
- ^ a b Pritchard, Chris (2006). "Bagatelle as the inspiration for Galton's Quincunx". BSHM Bulletin: Journal of the British Society for the History of Mathematics. 21 (2): 102–110. doi:10.1080/17498430600804118. ISSN 1749-8430.