Unit sphere: Difference between revisions
→Unit balls in normed vector spaces: At the beginning of a section, nothing can be "more precisely", since nothing has been discussed yet.Removed. in->of as in 2 subsequent sentences and as is standard. Added some more poetic wording. |
Undid revision 1225891555 by Cosmia Nebula (talk) Needs a citation to establish that it is noteworthy |
||
| (48 intermediate revisions by 15 users not shown) | |||
| Line 1: | Line 1: | ||
{{Short description|Sphere with radius one, usually centered on the origin of the space}} |
|||
{{more citations needed|date=March 2010}} |
|||
[[File:Vector norms.svg|frame|right|Some 1-spheres |
[[File:Vector norms.svg|frame|right|Some 1-spheres: {{math|‖'''x'''‖<sub>2</sub>}} is the norm for Euclidean space.]] |
||
In [[mathematics]], a '''unit sphere''' is simply a [[sphere]] of [[radius]] one around a given [[center (geometry)|center]]. More generally, it is the [[Locus (mathematics)|set of points]] of [[distance]] 1 from a fixed central point, where different [[norm (mathematics)|norms]] can be used as general notions of "distance". A '''unit ball''' is the [[closed set]] of points of distance less than or equal to 1 from a fixed central point. Usually the center is at the [[origin (mathematics)|origin]] of the space, so one speaks of "the unit ball" or "the unit sphere". |
|||
Special cases are the [[unit circle]] and the [[unit disk]]. |
|||
In [[mathematics]], a '''unit sphere''' is a [[sphere]] of unit [[radius]]: the [[locus (mathematics)|set of points]] at [[Euclidean distance]] [[1]] from some [[center (geometry)|center point]] in [[three-dimensional space]]. More generally, the ''unit <math>n</math>-sphere'' is an [[n-sphere|<math>n</math>-sphere]] of unit radius in <math>(n+1)</math>-[[dimension]]al [[Euclidean space]]; the [[unit circle]] is a special case, the unit <math>1</math>-sphere in the [[Euclidean plane|plane]]. An ([[Open set|open]]) '''unit ball''' is the region inside of a unit sphere, the set of points of distance less than 1 from the center. |
|||
| ⚫ | |||
| ⚫ | A sphere or ball with unit radius and center at the [[origin (mathematics)|origin]] of the space is called ''the'' unit sphere or ''the'' unit ball. Any arbitrary sphere can be transformed to the unit sphere by a combination of [[translation (geometry)|translation]] and [[scaling (geometry)|scaling]], so the study of spheres in general can often be reduced to the study of the unit sphere. |
||
| ⚫ | |||
The unit sphere is often used as a model for [[spherical geometry]] because it has constant [[sectional curvature]] of 1, which simplifies calculations. In [[trigonometry]], circular [[arc length]] on the unit circle is called [[radian]]s and used for measuring [[angular distance]]; in [[spherical trigonometry]] surface area on the unit sphere is called [[steradian]]s and used for measuring [[solid angle]]. |
|||
| ⚫ | |||
In more general contexts, a ''unit sphere'' is the set of points of [[distance]] 1 from a fixed central point, where different [[norm (mathematics)|norms]] can be used as general notions of "distance", and an (open) ''unit ball'' is the region inside. |
|||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
The open unit <math>n</math>-ball is the set of all points satisfying the [[inequality (mathematics)|inequality]] |
|||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
=== Volume and area === |
|||
| ⚫ | |||
{{see also|Volume of an n-ball}} |
|||
| ⚫ | |||
| ⚫ | |||
===General area and volume formulas=== |
|||
| ⚫ | |||
| ⚫ | |||
| ⚫ | The volume of the unit ball in Euclidean <math>n</math>-space, and the surface area of the unit sphere, appear in many important formulas of [[mathematical analysis|analysis]]. The volume of the unit <math>n</math>-ball, which we denote <math>V_n,</math> can be expressed by making use of the [[gamma function]]. It is |
||
| ⚫ | |||
:<math> |
: <math>V_n = \frac{\pi ^ {n/2}}{\Gamma(1+n/2)} = \begin{cases} |
||
| ⚫ | |||
| ⚫ | |||
| ⚫ | The volume of the unit ball in |
||
| ⚫ | |||
| ⚫ | |||
~\\ |
|||
| ⚫ | |||
\end{cases} </math> |
\end{cases} </math> |
||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
{2 \pi^{n/2}}/{(n/2 - 1)!} & \mathrm{if~}n \ge 1\mathrm{~is~even} \\[6mu] |
|||
| ⚫ | |||
{2(2\pi)^{(n-1)/2}}/{(n-2)!!} & \mathrm{if~}n \ge 1\mathrm{~is~odd.} |
|||
\end{cases}</math> |
|||
:<math>A_{n-1} = n V_n = \frac{n \pi ^ {n/2}}{\Gamma(1+n/2)} = \frac{2 \pi ^ {n/2}}{\Gamma(n/2)}\,,</math> |
|||
For example, <math>A_0 = 2</math> is the "area" of the boundary of the unit ball <math>[-1,1] \subset \mathbb{R}</math>, which simply counts the two points. Then <math>A_1 = 2\pi</math> is the "area" of the boundary of the unit disc, which is the circumference of the unit circle. <math>A_2 = 4\pi</math> is the area of the boundary of the unit ball <math>\{ x \in \R^3 : x_1^2 + x_2^2 + x_3^2 \leq 1 \}</math>, which is the surface area of the unit sphere <math>\{ x \in \R^3 : x_1^2 + x_2^2 + x_3^2 = 1 \}</math>. |
|||
The surface areas and the volumes for some values of <math>n</math> are as follows: |
The surface areas and the volumes for some values of <math>n</math> are as follows: |
||
| Line 81: | Line 81: | ||
| <math>10(1/5!)\pi^5 = (1/12)\pi^5 </math> || 25.50 || <math>(1/5!)\pi^5 = (1/120)\pi^5 </math> || 2.550 |
| <math>10(1/5!)\pi^5 = (1/12)\pi^5 </math> || 25.50 || <math>(1/5!)\pi^5 = (1/120)\pi^5 </math> || 2.550 |
||
|} |
|} |
||
where the decimal expanded values for |
where the decimal expanded values for <math>n \geq 2</math> are rounded to the displayed precision. |
||
====Recursion==== |
==== Recursion ==== |
||
The |
The <math>A_n</math> values satisfy the recursion: |
||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
The <math>V_n</math> values satisfy the recursion: |
|||
:<math> |
: <math>V_0 = 1</math> |
||
:<math> |
: <math>V_1 = 2</math> |
||
: <math>V_n = \frac{2 \pi}{n} V_{n-2}</math> for <math>n > 1</math>. |
|||
| ⚫ | |||
The ''V''<sub>''n''</sub> values satisfy the recursion: |
|||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
{{Main|Hausdorff measure}} |
{{Main|Hausdorff measure}} |
||
The |
The value <math display=inline>2^{-n} V_n = \pi ^ {n/2} \big/\, 2^n \Gamma\bigl(1+\tfrac12n\bigr)</math> at non-negative real values of <math>n</math> is sometimes used for normalization of Hausdorff measure.<ref>[https://www.math.cuhk.edu.hk/course_builder/1415/math5011/MATH5011_Chapter_3.2014.pdf The Chinese University of Hong Kong, Math 5011, Chapter 3, Lebesgue and Hausdorff Measures]</ref><ref>{{cite journal | last = Manin | first = Yuri I. | author-link = | title = The notion of dimension in geometry and algebra | journal = Bulletin of the American Mathematical Society | volume = 43 | issue = 2 | pages = 139–161 | date = 2006| language = | url = https://www.ams.org/bull/2006-43-02/S0273-0979-06-01081-0/S0273-0979-06-01081-0.pdf | jstor = | issn = | doi = 10.1090/S0273-0979-06-01081-0| id = | mr = | zbl = | jfm = | access-date = 17 December 2021}}</ref> |
||
====Other radii==== |
==== Other radii ==== |
||
{{Main| |
{{Main|N-sphere#Volume and area}} |
||
The surface area of an ( |
The surface area of an <math>(n-1)</math>-sphere with radius <math>r</math> is <math>A_{n-1} r^{n-1}</math> and the volume of an <math>n</math>- ball with radius <math>r</math> is <math>V_{n} r^{n}.</math> For instance, the area is <math>A_2 = 4\pi r^2</math> for the two-dimensional surface of the three-dimensional ball of radius <math>r.</math> The volume is <math>V_3 = \tfrac43\pi r^3</math> for the three-dimensional ball of radius <math>r</math>. |
||
==Unit balls in normed vector spaces== |
== Unit balls in normed vector spaces == |
||
The '''open unit ball''' of a [[normed vector space]] <math>V</math> with the [[Norm (mathematics)|norm]] <math>\|\cdot\|</math> is |
The '''open unit ball''' of a [[normed vector space]] <math>V</math> with the [[Norm (mathematics)|norm]] <math>\|\cdot\|</math> is given by |
||
| ⚫ | |||
It is the [[interior (topology)|topological interior]] of the '''closed unit ball''' of <math>(V, \|\cdot\|)\colon</math> |
|||
| ⚫ | |||
| ⚫ | |||
The latter is the disjoint union of the former and their common border, the '''unit sphere''' of <math>(V, \|\cdot\|)\colon</math> |
|||
| ⚫ | |||
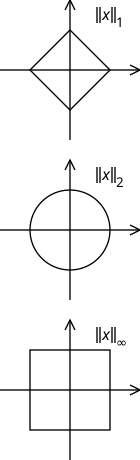
| ⚫ | The "shape" of the ''unit ball'' is entirely dependent on the chosen norm; it may well have "corners", and for example may look like <math>[-1,1]^n</math> in the case of the max-norm in <math>\mathbb{R}^n</math>. One obtains a naturally ''round ball'' as the unit ball pertaining to the usual [[Hilbert space]] norm, based in the finite-dimensional case on the [[Euclidean distance]]; its boundary is what is usually meant by the ''unit sphere''. |
||
| ⚫ | |||
| ⚫ | |||
The latter is the disjoint union of the former and their common border, the '''unit sphere''' of (''V'',||·||): |
|||
| ⚫ | |||
| ⚫ | |||
| ⚫ | The |
||
| ⚫ | |||
| ⚫ | |||
Then <math>\|x\|_2</math> is the usual [[Hilbert space]] norm. |
Then <math>\|x\|_2</math> is the usual [[Hilbert space]] norm. |
||
<math>\|x\|_1</math> is called the Hamming norm, or <math>\ell_1</math>-norm. |
<math>\|x\|_1</math> is called the Hamming norm, or <math>\ell_1</math>-norm. |
||
The condition |
The condition <math>p \geq 1</math> is necessary in the definition of the <math>\ell_p</math> norm, as the unit ball in any normed space must be [[convex set|convex]] as a consequence of the [[triangle inequality]]. |
||
Let <math>\|x\|_\infty</math> denote the max-norm or <math>\ell_\infty</math>-norm of x. |
Let <math>\|x\|_\infty</math> denote the max-norm or <math>\ell_\infty</math>-norm of <math>x</math>. |
||
Note that for the one-dimensional circumferences <math>C_p</math> of the two-dimensional unit balls, we have: |
Note that for the one-dimensional circumferences <math>C_p</math> of the two-dimensional unit balls, we have: |
||
| ⚫ | |||
: <math>C_{2} = 2 \pi</math> |
|||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
===Metric spaces=== |
=== Metric spaces === |
||
All three of the above definitions can be straightforwardly generalized to a [[metric space]], with respect to a chosen origin. However, topological considerations (interior, closure, border) need not apply in the same way (e.g., in [[ultrametric]] spaces, all of the three are simultaneously open and closed sets), and the unit sphere may even be empty in some metric spaces. |
All three of the above definitions can be straightforwardly generalized to a [[metric space]], with respect to a chosen origin. However, topological considerations (interior, closure, border) need not apply in the same way (e.g., in [[ultrametric]] spaces, all of the three are simultaneously open and closed sets), and the unit sphere may even be empty in some metric spaces. |
||
===Quadratic forms=== |
=== Quadratic forms === |
||
If |
If <math>V</math> is a linear space with a real [[quadratic form]] <math>F : V \to \R,</math> then <math>\{ p \in V : F(p) = 1\}</math> may be called the unit sphere<ref>Takashi Ono (1994) ''Variations on a Theme of Euler: quadratic forms, elliptic curves, and Hopf maps'', chapter 5: Quadratic spherical maps, page 165, [[Plenum Press]], {{isbn|0-306-44789-4}}</ref><ref>F. Reese Harvey (1990) ''Spinors and calibrations'', "Generalized Spheres", page 42, [[Academic Press]], {{isbn|0-12-329650-1}}</ref> or [[hyperboloid#Relation to the sphere|unit quasi-sphere]] of <math>V.</math> For example, the quadratic form <math>x^2 - y^2</math>, when set equal to one, produces the [[unit hyperbola]], which plays the role of the "unit circle" in the plane of [[split-complex number]]s. Similarly, the quadratic form <math>x^2</math> yields a pair of lines for the unit sphere in the [[dual number]] plane. |
||
==See also== |
== See also == |
||
*[[Ball (mathematics)|Ball]] |
* [[Ball (mathematics)|Ball]] |
||
* [[n-sphere|<math>n</math>-sphere]] |
|||
*[[Hypersphere]] |
|||
*[[Sphere]] |
* [[Sphere]] |
||
*[[Superellipse]] |
* [[Superellipse]] |
||
*[[Unit circle]] |
* [[Unit circle]] |
||
*[[Unit disk]] |
* [[Unit disk]] |
||
*[[Unit |
* [[Unit tangent bundle]] |
||
*[[Unit square]] |
* [[Unit square]] |
||
==Notes and references== |
== Notes and references == |
||
{{reflist}} |
{{reflist}} |
||
* Mahlon M. Day (1958) ''Normed Linear Spaces'', page 24, [[Springer-Verlag]]. |
* Mahlon M. Day (1958) ''Normed Linear Spaces'', page 24, [[Springer-Verlag]]. |
||
*{{citation|last1=Deza|first1=E.|first2=M.|last2=Deza|title=Dictionary of Distances|year=2006|publisher=Elsevier|isbn=0-444-52087-2}}. Reviewed in [https://www.scribd.com/doc/2668595/Newsletter-of-the-European-Mathematical-Society-20070664-featuring-Let-Platonism-Die ''Newsletter of the European Mathematical Society'' '''64''' (June 2007)], p. 57. This book is organized as a list of distances of many types, each with a brief description. |
* {{citation|last1=Deza|first1=E.|author1-link=Elena Deza|first2=M.|last2=Deza|title=Dictionary of Distances|year=2006|publisher=Elsevier|isbn=0-444-52087-2}}. Reviewed in [https://www.scribd.com/doc/2668595/Newsletter-of-the-European-Mathematical-Society-20070664-featuring-Let-Platonism-Die ''Newsletter of the European Mathematical Society'' '''64''' (June 2007)], p. 57. This book is organized as a list of distances of many types, each with a brief description. |
||
== External links == |
== External links == |
||
Latest revision as of 13:26, 28 May 2024
In mathematics, a unit sphere is a sphere of unit radius: the set of points at Euclidean distance 1 from some center point in three-dimensional space. More generally, the unit -sphere is an -sphere of unit radius in -dimensional Euclidean space; the unit circle is a special case, the unit -sphere in the plane. An (open) unit ball is the region inside of a unit sphere, the set of points of distance less than 1 from the center.
A sphere or ball with unit radius and center at the origin of the space is called the unit sphere or the unit ball. Any arbitrary sphere can be transformed to the unit sphere by a combination of translation and scaling, so the study of spheres in general can often be reduced to the study of the unit sphere.
The unit sphere is often used as a model for spherical geometry because it has constant sectional curvature of 1, which simplifies calculations. In trigonometry, circular arc length on the unit circle is called radians and used for measuring angular distance; in spherical trigonometry surface area on the unit sphere is called steradians and used for measuring solid angle.
In more general contexts, a unit sphere is the set of points of distance 1 from a fixed central point, where different norms can be used as general notions of "distance", and an (open) unit ball is the region inside.
Unit spheres and balls in Euclidean space
[edit]In Euclidean space of dimensions, the -dimensional unit sphere is the set of all points which satisfy the equation
The open unit -ball is the set of all points satisfying the inequality
and closed unit -ball is the set of all points satisfying the inequality
Volume and area
[edit]
The classical equation of a unit sphere is that of the ellipsoid with a radius of 1 and no alterations to the -, -, or - axes:
The volume of the unit ball in Euclidean -space, and the surface area of the unit sphere, appear in many important formulas of analysis. The volume of the unit -ball, which we denote can be expressed by making use of the gamma function. It is
where is the double factorial.
The hypervolume of the -dimensional unit sphere (i.e., the "area" of the boundary of the -dimensional unit ball), which we denote can be expressed as
For example, is the "area" of the boundary of the unit ball , which simply counts the two points. Then is the "area" of the boundary of the unit disc, which is the circumference of the unit circle. is the area of the boundary of the unit ball , which is the surface area of the unit sphere .
The surface areas and the volumes for some values of are as follows:
| (surface area) | (volume) | |||
|---|---|---|---|---|
| 0 | 1 | |||
| 1 | 2 | 2 | ||
| 2 | 6.283 | 3.141 | ||
| 3 | 12.57 | 4.189 | ||
| 4 | 19.74 | 4.935 | ||
| 5 | 26.32 | 5.264 | ||
| 6 | 31.01 | 5.168 | ||
| 7 | 33.07 | 4.725 | ||
| 8 | 32.47 | 4.059 | ||
| 9 | 29.69 | 3.299 | ||
| 10 | 25.50 | 2.550 | ||
where the decimal expanded values for are rounded to the displayed precision.
Recursion
[edit]The values satisfy the recursion:
- for .
The values satisfy the recursion:
- for .
Non-negative real-valued dimensions
[edit]The value at non-negative real values of is sometimes used for normalization of Hausdorff measure.[1][2]
Other radii
[edit]The surface area of an -sphere with radius is and the volume of an - ball with radius is For instance, the area is for the two-dimensional surface of the three-dimensional ball of radius The volume is for the three-dimensional ball of radius .
Unit balls in normed vector spaces
[edit]The open unit ball of a normed vector space with the norm is given by
It is the topological interior of the closed unit ball of
The latter is the disjoint union of the former and their common border, the unit sphere of
The "shape" of the unit ball is entirely dependent on the chosen norm; it may well have "corners", and for example may look like in the case of the max-norm in . One obtains a naturally round ball as the unit ball pertaining to the usual Hilbert space norm, based in the finite-dimensional case on the Euclidean distance; its boundary is what is usually meant by the unit sphere.
Let Define the usual -norm for as:
Then is the usual Hilbert space norm. is called the Hamming norm, or -norm. The condition is necessary in the definition of the norm, as the unit ball in any normed space must be convex as a consequence of the triangle inequality. Let denote the max-norm or -norm of .
Note that for the one-dimensional circumferences of the two-dimensional unit balls, we have:
- is the minimum value.
- is the maximum value.
Generalizations
[edit]Metric spaces
[edit]All three of the above definitions can be straightforwardly generalized to a metric space, with respect to a chosen origin. However, topological considerations (interior, closure, border) need not apply in the same way (e.g., in ultrametric spaces, all of the three are simultaneously open and closed sets), and the unit sphere may even be empty in some metric spaces.
Quadratic forms
[edit]If is a linear space with a real quadratic form then may be called the unit sphere[3][4] or unit quasi-sphere of For example, the quadratic form , when set equal to one, produces the unit hyperbola, which plays the role of the "unit circle" in the plane of split-complex numbers. Similarly, the quadratic form yields a pair of lines for the unit sphere in the dual number plane.
See also
[edit]Notes and references
[edit]- ^ The Chinese University of Hong Kong, Math 5011, Chapter 3, Lebesgue and Hausdorff Measures
- ^ Manin, Yuri I. (2006). "The notion of dimension in geometry and algebra" (PDF). Bulletin of the American Mathematical Society. 43 (2): 139–161. doi:10.1090/S0273-0979-06-01081-0. Retrieved 17 December 2021.
- ^ Takashi Ono (1994) Variations on a Theme of Euler: quadratic forms, elliptic curves, and Hopf maps, chapter 5: Quadratic spherical maps, page 165, Plenum Press, ISBN 0-306-44789-4
- ^ F. Reese Harvey (1990) Spinors and calibrations, "Generalized Spheres", page 42, Academic Press, ISBN 0-12-329650-1
- Mahlon M. Day (1958) Normed Linear Spaces, page 24, Springer-Verlag.
- Deza, E.; Deza, M. (2006), Dictionary of Distances, Elsevier, ISBN 0-444-52087-2. Reviewed in Newsletter of the European Mathematical Society 64 (June 2007), p. 57. This book is organized as a list of distances of many types, each with a brief description.














![{\displaystyle V_{n}={\frac {\pi ^{n/2}}{\Gamma (1+n/2)}}={\begin{cases}{\pi ^{n/2}}/{(n/2)!}&\mathrm {if~} n\geq 0\mathrm {~is~even} \\[6mu]{2(2\pi )^{(n-1)/2}}/{n!!}&\mathrm {if~} n\geq 0\mathrm {~is~odd,} \end{cases}}}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/eaf208735d51b452fb423a2e121ada1e6c269bf9)


![{\displaystyle A_{n-1}=nV_{n}={\frac {n\pi ^{n/2}}{\Gamma (1+n/2)}}={\frac {2\pi ^{n/2}}{\Gamma (n/2)}}={\begin{cases}{2\pi ^{n/2}}/{(n/2-1)!}&\mathrm {if~} n\geq 1\mathrm {~is~even} \\[6mu]{2(2\pi )^{(n-1)/2}}/{(n-2)!!}&\mathrm {if~} n\geq 1\mathrm {~is~odd.} \end{cases}}}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/ef608cca0068ac18865a9203858bacc8780fe7ac)

![{\displaystyle [-1,1]\subset \mathbb {R} }](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/2016a25b4496666df761c56045fc221d3fbd2c08)















































![{\displaystyle [-1,1]^{n}}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/6a008254b1bf6d63ac3b13548c4c31180bcd43de)


















