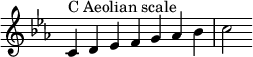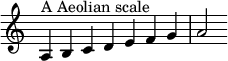Aeolian mode: Difference between revisions
inserted anchor; math font for legible |
rm second person |
||
| (One intermediate revision by one other user not shown) | |||
| Line 2: | Line 2: | ||
{{Use dmy dates|date=January 2023}} |
{{Use dmy dates|date=January 2023}} |
||
The '''Aeolian mode''' is a [[Mode (music)|musical mode]] or, in modern usage, a [[diatonic scale]] also called the [[natural minor scale]]. On the piano, using only the white keys, it is the scale that starts with A and continues to the next A only striking white keys. |
The '''Aeolian mode''' is a [[Mode (music)|musical mode]] or, in modern usage, a [[diatonic scale]] also called the [[natural minor scale]]. On the piano, using only the white keys, it is the scale that starts with A and continues to the next A only striking white keys. |
||
Its ascending [[musical interval|interval form]] consists of a ''key note, whole step, half step, whole step, whole step, half step, whole step, whole step.'' That means that, in A aeolian (or A minor), |
Its ascending [[musical interval|interval form]] consists of a ''key note, whole step, half step, whole step, whole step, half step, whole step, whole step.'' That means that, in A aeolian (or A minor), a scale would be played beginning in A, move up a whole step (two piano keys) to B, move up a half step (one piano key) to C, then up a whole step to D, a whole step to E, a half step to F, a whole step to G, and a final whole step to a high A. |
||
: <score sound="1"> { |
: <score sound="1"> { |
||
\override Score.TimeSignature #'stencil = ##f |
\override Score.TimeSignature #'stencil = ##f |
||
| Line 13: | Line 13: | ||
== History<span class="anchor" id="Ancient_Greek_anchor"></span> == |
== History<span class="anchor" id="Ancient_Greek_anchor"></span> == |
||
The word ''Aeolian'', like the names for the other ancient Greek ''tonoi'' and ''harmoniai'', is an ethnic designation: |
The word ''Aeolian'', like the names for the other ancient Greek ''tonoi'' and ''harmoniai'', is an ethnic designation: in this case, for the inhabitants of [[Aeolis]] ({{math|Αἰολίς}}) — the [[Aeolian Islands]] and adjacent coastal district of [[Anatolia]].<ref>{{OED |Aeolian}}</ref> In the [[music theory]] of [[ancient Greece]], it was an alternative name (used by some later writers, such as [[Cleonides]]) for what [[Aristoxenus]] called the Low Lydian ''tonos'' (in the sense of a particular overall pitching of the musical system—not a scale), nine semitones higher than the lowest "position of the voice", which was called [[Hypodorian mode|Hypodorian]].<ref>Egert Pöhlmann, Olympia Psychopedis-Frangou, and Rudolf Maria Brandl, "Griechenland", ''[[Die Musik in Geschichte und Gegenwart]]'', second, newly compiled edition, edited by [[Ludwig Finscher]], part 1 (Sachteil), vol. 3 (Eng–Hamb) (Kassel & New York: Bärenreiter; Stuttgart: Metzler, 1995), 1652, {{ISBN|978-3-7618-1101-6}} (Bärenreiter); {{ISBN|3-7618-1101-2}} (Bärenreiter); {{ISBN|978-3-476-41000-9}} (Metzler); {{ISBN|3-476-41000-5}} (Metzler); [[Thomas J. Mathiesen]], "Greece, §I: Ancient", ''[[The New Grove Dictionary of Music and Musicians]]'', edited by [[Stanley Sadie]] and [[John Tyrrell (musicologist)|John Tyrrell]] (London: Macmillan; New York: Grove's Dictionaries, 2001), 10:339. {{ISBN|0-333-60800-3}}; {{ISBN|1-56159-239-0}}; {{ISBN |978-0-333-60800-5}}; {{ISBN|978-1-56159-239-5}}; {{ISBN|0-19-517067-9}} (set); {{ISBN|978-0-19-517067-2}} (set).</ref> In the mid-16th century, this name was given by [[Heinrich Glarean]] to his newly defined ninth mode, with the [[Diatonic and chromatic|diatonic]] [[octave species]] of the natural notes extending one octave from A to A—corresponding to the modern natural minor scale.<ref name = aeoliani>Harold S. Powers, "Aeolian (i)", ''The New Grove Dictionary of Music and Musicians'', second edition, edited by Stanley Sadie and John Tyrrell, 29 volumes (London: Macmillan; New York: Grove's Dictionaries, 2001), 1:{{Page needed |date=August 2010}}. {{ISBN|0-333-60800-3}}; {{ISBN|1-56159-239-0}}; {{ISBN|978-0-333-60800-5}}; {{ISBN|978-1-56159-239-5}}; {{ISBN|0-19-517067-9}} (set); {{ISBN|978-0-19-517067-2}} (set).</ref> Up until this time, chant theory recognized eight [[musical mode]]s: the relative natural scales in D, E, F and G, each with their [[authentic mode|authentic]] and [[plagal mode|plagal]] counterparts, and with the option of B{{music|flat}} instead of B{{music|natural}} in several modes.<ref>Harold S. Powers, "Mode, §II. Medieval Modal Theory, 3: 11th-Century Syntheses, (i) Italian Theory of Modal Functions, (b) Ambitus." ''The New Grove Dictionary of Music and Musicians'', edited by Stanley Sadie and John Tyrrell (London: Macmillan; New York: Grove's Dictionaries, 2001){{Page needed|date=August 2010}} (Example 5). {{ISBN|0-333-60800-3}}; {{ISBN|1-56159-239-0}}; {{ISBN|978-0-333-60800-5}}; {{ISBN|978-1-56159-239-5}}; {{ISBN|0-19-517067-9}} (set); {{ISBN|978-0-19-517067-2}} (set).</ref> |
||
In 1547, [[Henricus Petrus|Heinrich Petri]] published [[Heinrich Glarean]]'s ''Dodecachordon'' in Basel.<ref>Clement A. Miller, "Glarean, Heinrich [Glareanus, Henricus; Loriti]", ''The New Grove Dictionary of Music and Musicians'', second edition, edited by [[Stanley Sadie]] and [[John Tyrrell (musicologist)|John Tyrrell]] (London: Macmillan, 2001).</ref> His premise had as its central idea the existence of twelve [[diatonic]] modes rather than eight, including a separate pair of modes each on the finals A and C.<ref>Clement A. Miller, "Glarean, Heinrich [Glareanus, Henricus; Loriti]", ''The New Grove Dictionary of Music and Musicians'', second edition, edited by [[Stanley Sadie]] and [[John Tyrrell (musicologist)|John Tyrrell]] (London: Macmillan, 2001); Harold S. Powers, "Mode, §III. Modal Theories and Polyphonic Music, 4: Systems of 12 Modes, (ii): Glarean's 12 Modes." ''The New Grove Dictionary of Music and Musicians'', edited by Stanley Sadie and John Tyrrell (London: Macmillan; New York: Grove's Dictionaries, 2001).</ref> Finals on these notes, as well as on B{{music|natural}}, had been recognized in chant theory at least since [[Hucbald]] in the early tenth century, but they were regarded as merely transpositions from the regular finals a fifth lower. In the eleventh century, [[Guido d'Arezzo]], in chapter 8 of his ''Micrologus'', designated these transposed finals A, B{{music|natural}}, and C as "affinals", and later still the term "confinal" was used in the same way.<ref>Harold S. Powers, "Mode, §II. Medieval Modal Theory, 2. Carolingian Synthesis, 9th–10th Centuries, (i) The Boethian Double Octave and the Modes, (b) Tetrachordal Degrees and Modal Quality." ''The New Grove Dictionary of Music and Musicians'', edited by Stanley Sadie and John Tyrrell (London: Macmillan; New York: Grove's Dictionaries, 2001). {{ISBN|0-333-60800-3}}; {{ISBN|1-56159-239-0}}; {{ISBN|978-0-333-60800-5}}; {{ISBN|978-1-56159-239-5}}; {{ISBN|0-19-517067-9}} (set); {{ISBN|978-0-19-517067-2}} (set).</ref> In 1525, [[Pietro Aaron]] was the first theorist to explain polyphonic modal usage in terms of the eightfold system, including these transpositions.<ref>Harold S. Powers, "Is Mode Real? Pietro Aron, the Octenary System, and Polyphony", ''Basler Jahrbuch für historische Musikpraxis'' 16 (1992): 9–52.</ref> As late as 1581, Illuminato Aiguino da Brescia published the most elaborate theory defending the eightfold system for polyphonic music against Glarean's innovations, in which he regarded the traditional plainchant modes 1 and 2 ([[Dorian mode|Dorian]] and Hypodorian) at the affinal position (that is, with their finals on A instead of D) as a composite of species from two modes, which he described as "mixed modes".<ref>Harold S. Powers, "Mode, III: Modal Theories and Polyphonic Music, 3: Polyphonic Modal Theory and the Eightfold System, (ii) Composite Modes," ''The New Grove Dictionary of Music and Musicians'', edited by Stanley Sadie and John Tyrrell (London: Macmillan; New York: Grove's Dictionaries, 2001){{Page needed|date=August 2010}}. {{ISBN|0-333-60800-3}}; {{ISBN|1-56159-239-0}}; {{ISBN|978-0-333-60800-5}}; {{ISBN|978-1-56159-239-5}}; {{ISBN|0-19-517067-9}} (set); {{ISBN|978-0-19-517067-2}} (set).</ref> Glarean added ''Aeolian'' as the name of the ''new'' ninth mode: the relative natural mode in A with the [[perfect fifth]] as its dominant, [[reciting tone|reciting tone, reciting note]], or ''tenor''. The tenth mode, the plagal version of the Aeolian mode, Glarean called ''Hypoaeolian'' ("under Aeolian"), based on the same relative scale, but with the [[minor third]] as its tenor, and having a melodic range from a [[perfect fourth]] below the tonic to a [[perfect fifth]] above it. |
In 1547, [[Henricus Petrus|Heinrich Petri]] published [[Heinrich Glarean]]'s ''Dodecachordon'' in Basel.<ref>Clement A. Miller, "Glarean, Heinrich [Glareanus, Henricus; Loriti]", ''The New Grove Dictionary of Music and Musicians'', second edition, edited by [[Stanley Sadie]] and [[John Tyrrell (musicologist)|John Tyrrell]] (London: Macmillan, 2001).</ref> His premise had as its central idea the existence of twelve [[diatonic]] modes rather than eight, including a separate pair of modes each on the finals A and C.<ref>Clement A. Miller, "Glarean, Heinrich [Glareanus, Henricus; Loriti]", ''The New Grove Dictionary of Music and Musicians'', second edition, edited by [[Stanley Sadie]] and [[John Tyrrell (musicologist)|John Tyrrell]] (London: Macmillan, 2001); Harold S. Powers, "Mode, §III. Modal Theories and Polyphonic Music, 4: Systems of 12 Modes, (ii): Glarean's 12 Modes." ''The New Grove Dictionary of Music and Musicians'', edited by Stanley Sadie and John Tyrrell (London: Macmillan; New York: Grove's Dictionaries, 2001).</ref> Finals on these notes, as well as on B{{music|natural}}, had been recognized in chant theory at least since [[Hucbald]] in the early tenth century, but they were regarded as merely transpositions from the regular finals a fifth lower. In the eleventh century, [[Guido d'Arezzo]], in chapter 8 of his ''Micrologus'', designated these transposed finals A, B{{music|natural}}, and C as "affinals", and later still the term "confinal" was used in the same way.<ref>Harold S. Powers, "Mode, §II. Medieval Modal Theory, 2. Carolingian Synthesis, 9th–10th Centuries, (i) The Boethian Double Octave and the Modes, (b) Tetrachordal Degrees and Modal Quality." ''The New Grove Dictionary of Music and Musicians'', edited by Stanley Sadie and John Tyrrell (London: Macmillan; New York: Grove's Dictionaries, 2001). {{ISBN|0-333-60800-3}}; {{ISBN|1-56159-239-0}}; {{ISBN|978-0-333-60800-5}}; {{ISBN|978-1-56159-239-5}}; {{ISBN|0-19-517067-9}} (set); {{ISBN|978-0-19-517067-2}} (set).</ref> In 1525, [[Pietro Aaron]] was the first theorist to explain polyphonic modal usage in terms of the eightfold system, including these transpositions.<ref>Harold S. Powers, "Is Mode Real? Pietro Aron, the Octenary System, and Polyphony", ''Basler Jahrbuch für historische Musikpraxis'' 16 (1992): 9–52.</ref> As late as 1581, Illuminato Aiguino da Brescia published the most elaborate theory defending the eightfold system for polyphonic music against Glarean's innovations, in which he regarded the traditional plainchant modes 1 and 2 ([[Dorian mode|Dorian]] and Hypodorian) at the affinal position (that is, with their finals on A instead of D) as a composite of species from two modes, which he described as "mixed modes".<ref>Harold S. Powers, "Mode, III: Modal Theories and Polyphonic Music, 3: Polyphonic Modal Theory and the Eightfold System, (ii) Composite Modes," ''The New Grove Dictionary of Music and Musicians'', edited by Stanley Sadie and John Tyrrell (London: Macmillan; New York: Grove's Dictionaries, 2001){{Page needed|date=August 2010}}. {{ISBN|0-333-60800-3}}; {{ISBN|1-56159-239-0}}; {{ISBN|978-0-333-60800-5}}; {{ISBN|978-1-56159-239-5}}; {{ISBN|0-19-517067-9}} (set); {{ISBN|978-0-19-517067-2}} (set).</ref> Glarean added ''Aeolian'' as the name of the ''new'' ninth mode: the relative natural mode in A with the [[perfect fifth]] as its dominant, [[reciting tone|reciting tone, reciting note]], or ''tenor''. The tenth mode, the plagal version of the Aeolian mode, Glarean called ''Hypoaeolian'' ("under Aeolian"), based on the same relative scale, but with the [[minor third]] as its tenor, and having a melodic range from a [[perfect fourth]] below the tonic to a [[perfect fifth]] above it. |
||
Latest revision as of 05:07, 26 October 2024
The Aeolian mode is a musical mode or, in modern usage, a diatonic scale also called the natural minor scale. On the piano, using only the white keys, it is the scale that starts with A and continues to the next A only striking white keys. Its ascending interval form consists of a key note, whole step, half step, whole step, whole step, half step, whole step, whole step. That means that, in A aeolian (or A minor), a scale would be played beginning in A, move up a whole step (two piano keys) to B, move up a half step (one piano key) to C, then up a whole step to D, a whole step to E, a half step to F, a whole step to G, and a final whole step to a high A.
History
[edit]The word Aeolian, like the names for the other ancient Greek tonoi and harmoniai, is an ethnic designation: in this case, for the inhabitants of Aeolis (Αἰολίς) — the Aeolian Islands and adjacent coastal district of Anatolia.[1] In the music theory of ancient Greece, it was an alternative name (used by some later writers, such as Cleonides) for what Aristoxenus called the Low Lydian tonos (in the sense of a particular overall pitching of the musical system—not a scale), nine semitones higher than the lowest "position of the voice", which was called Hypodorian.[2] In the mid-16th century, this name was given by Heinrich Glarean to his newly defined ninth mode, with the diatonic octave species of the natural notes extending one octave from A to A—corresponding to the modern natural minor scale.[3] Up until this time, chant theory recognized eight musical modes: the relative natural scales in D, E, F and G, each with their authentic and plagal counterparts, and with the option of B♭ instead of B♮ in several modes.[4]
In 1547, Heinrich Petri published Heinrich Glarean's Dodecachordon in Basel.[5] His premise had as its central idea the existence of twelve diatonic modes rather than eight, including a separate pair of modes each on the finals A and C.[6] Finals on these notes, as well as on B♮, had been recognized in chant theory at least since Hucbald in the early tenth century, but they were regarded as merely transpositions from the regular finals a fifth lower. In the eleventh century, Guido d'Arezzo, in chapter 8 of his Micrologus, designated these transposed finals A, B♮, and C as "affinals", and later still the term "confinal" was used in the same way.[7] In 1525, Pietro Aaron was the first theorist to explain polyphonic modal usage in terms of the eightfold system, including these transpositions.[8] As late as 1581, Illuminato Aiguino da Brescia published the most elaborate theory defending the eightfold system for polyphonic music against Glarean's innovations, in which he regarded the traditional plainchant modes 1 and 2 (Dorian and Hypodorian) at the affinal position (that is, with their finals on A instead of D) as a composite of species from two modes, which he described as "mixed modes".[9] Glarean added Aeolian as the name of the new ninth mode: the relative natural mode in A with the perfect fifth as its dominant, reciting tone, reciting note, or tenor. The tenth mode, the plagal version of the Aeolian mode, Glarean called Hypoaeolian ("under Aeolian"), based on the same relative scale, but with the minor third as its tenor, and having a melodic range from a perfect fourth below the tonic to a perfect fifth above it.
Scholars for the past three centuries have regarded the modes added by Glarean as the basis of the minor/major division of classical European music, as homophonic music replaced Renaissance polyphony. Howard S Powers considers this to be an oversimplification, since the key of A minor is as closely related to the old transposed modes 1 and 2 (Dorian and Hypodorian) with finals on A—as well as to mode 3 (Phrygian)—as it is to Glarean's Aeolian.[3]
In modern usage, the Aeolian mode is the sixth mode of the major scale and has the following formula:
- 1, 2, ♭3, 4, 5, ♭6, ♭7, 8
The Aeolian mode is the sixth mode of the major scale, that is, it is formed by starting on the sixth degree (submediant) of the major scale. For example, if the Aeolian mode is used in its all-white-note pitch based on A, this would be an A-minor triad, which would be the submediant in the relative major key of C major.
Aeolian harmony
[edit]

Aeolian harmony[10] is harmony or chord progression created from chords of the Aeolian mode. Commonly known as the "natural minor" scale, it allows for the construction of the following triads (three note chords built from major or minor thirds), in popular music symbols: i, ♭III, iv, v, ♭VI, and ♭VII. The scale also produces iio, which is avoided since it is diminished. The leading-tone and major V which contains it are also not used, as they are not part of the Aeolian mode (natural minor scale). However, Aeolian harmony may be used with mode mixture.
For example, ♭VII is a major chord built on the seventh scale degree, indicated by capital Roman numerals for seven.
There are common subsets including i–♭VII–♭VI, i–iv–v and blues minor pentatonic derived chord sequences such as I–♭III–IV, I–IV, ♭VII (The verse of "I'm Your Man").[11] All these lack perfect cadences (V–I), and may be thought of as derived from rewrite rules using recursive fourth structures (repeated progression by perfect fourth, see circle progression).[11] Middleton[11] suggests of modal and fourth-oriented structures that, rather than being, "distortions or surface transformations of Schenker's favoured V–I kernel, it is more likely that both are branches of a deeper principle, that of tonic/not-tonic differentiation."
Songs that use Aeolian mode
[edit]The Aeolian mode is identical with the natural minor scale. Thus, it is ubiquitous in minor-key music. The following is a list of some examples that are distinguishable from ordinary minor tonality, which also uses the melodic minor scale and the harmonic minor scale as required.
- Traditional – "God Rest You Merry, Gentlemen"
- Bob Dylan – "All Along the Watchtower"[12]
- R.E.M. – "Losing My Religion"[12]
- Phil Collins – "In the Air Tonight"
- Alter Bridge – "Blackbird"
- Fleetwood Mac – "Isn't It Midnight"
- Pink Floyd – "Shine on you Crazy Diamond"
- Dido – "White Flag"
- Radiohead – "Street Spirit"
- Red Hot Chili Peppers – "Californication"
See also
[edit]- Borrowed chord (or mode mixture)
- Relative minor
- Minor scale
- Asavari, the equivalent scale (thaat) in Hindustani music
- Natabhairavi, the equivalent scale (melakarta) in Carnatic music
References
[edit]- ^ "Aeolian". Oxford English Dictionary (Online ed.). Oxford University Press. (Subscription or participating institution membership required.)
- ^ Egert Pöhlmann, Olympia Psychopedis-Frangou, and Rudolf Maria Brandl, "Griechenland", Die Musik in Geschichte und Gegenwart, second, newly compiled edition, edited by Ludwig Finscher, part 1 (Sachteil), vol. 3 (Eng–Hamb) (Kassel & New York: Bärenreiter; Stuttgart: Metzler, 1995), 1652, ISBN 978-3-7618-1101-6 (Bärenreiter); ISBN 3-7618-1101-2 (Bärenreiter); ISBN 978-3-476-41000-9 (Metzler); ISBN 3-476-41000-5 (Metzler); Thomas J. Mathiesen, "Greece, §I: Ancient", The New Grove Dictionary of Music and Musicians, edited by Stanley Sadie and John Tyrrell (London: Macmillan; New York: Grove's Dictionaries, 2001), 10:339. ISBN 0-333-60800-3; ISBN 1-56159-239-0; ISBN 978-0-333-60800-5; ISBN 978-1-56159-239-5; ISBN 0-19-517067-9 (set); ISBN 978-0-19-517067-2 (set).
- ^ a b Harold S. Powers, "Aeolian (i)", The New Grove Dictionary of Music and Musicians, second edition, edited by Stanley Sadie and John Tyrrell, 29 volumes (London: Macmillan; New York: Grove's Dictionaries, 2001), 1:[page needed]. ISBN 0-333-60800-3; ISBN 1-56159-239-0; ISBN 978-0-333-60800-5; ISBN 978-1-56159-239-5; ISBN 0-19-517067-9 (set); ISBN 978-0-19-517067-2 (set).
- ^ Harold S. Powers, "Mode, §II. Medieval Modal Theory, 3: 11th-Century Syntheses, (i) Italian Theory of Modal Functions, (b) Ambitus." The New Grove Dictionary of Music and Musicians, edited by Stanley Sadie and John Tyrrell (London: Macmillan; New York: Grove's Dictionaries, 2001)[page needed] (Example 5). ISBN 0-333-60800-3; ISBN 1-56159-239-0; ISBN 978-0-333-60800-5; ISBN 978-1-56159-239-5; ISBN 0-19-517067-9 (set); ISBN 978-0-19-517067-2 (set).
- ^ Clement A. Miller, "Glarean, Heinrich [Glareanus, Henricus; Loriti]", The New Grove Dictionary of Music and Musicians, second edition, edited by Stanley Sadie and John Tyrrell (London: Macmillan, 2001).
- ^ Clement A. Miller, "Glarean, Heinrich [Glareanus, Henricus; Loriti]", The New Grove Dictionary of Music and Musicians, second edition, edited by Stanley Sadie and John Tyrrell (London: Macmillan, 2001); Harold S. Powers, "Mode, §III. Modal Theories and Polyphonic Music, 4: Systems of 12 Modes, (ii): Glarean's 12 Modes." The New Grove Dictionary of Music and Musicians, edited by Stanley Sadie and John Tyrrell (London: Macmillan; New York: Grove's Dictionaries, 2001).
- ^ Harold S. Powers, "Mode, §II. Medieval Modal Theory, 2. Carolingian Synthesis, 9th–10th Centuries, (i) The Boethian Double Octave and the Modes, (b) Tetrachordal Degrees and Modal Quality." The New Grove Dictionary of Music and Musicians, edited by Stanley Sadie and John Tyrrell (London: Macmillan; New York: Grove's Dictionaries, 2001). ISBN 0-333-60800-3; ISBN 1-56159-239-0; ISBN 978-0-333-60800-5; ISBN 978-1-56159-239-5; ISBN 0-19-517067-9 (set); ISBN 978-0-19-517067-2 (set).
- ^ Harold S. Powers, "Is Mode Real? Pietro Aron, the Octenary System, and Polyphony", Basler Jahrbuch für historische Musikpraxis 16 (1992): 9–52.
- ^ Harold S. Powers, "Mode, III: Modal Theories and Polyphonic Music, 3: Polyphonic Modal Theory and the Eightfold System, (ii) Composite Modes," The New Grove Dictionary of Music and Musicians, edited by Stanley Sadie and John Tyrrell (London: Macmillan; New York: Grove's Dictionaries, 2001)[page needed]. ISBN 0-333-60800-3; ISBN 1-56159-239-0; ISBN 978-0-333-60800-5; ISBN 978-1-56159-239-5; ISBN 0-19-517067-9 (set); ISBN 978-0-19-517067-2 (set).
- ^ Alf Björnberg ([full citation needed]1985). Cited in Middleton 1990, p. 198.
- ^ a b c Richard Middleton, Studying Popular Music (Milton Keynes and Philadelphia: Open University Press, 1990), p. 198. ISBN 0-335-15275-9.
- ^ a b Gary Ewer, "Dorian Mode, Aeolian Mode, Minor Key... What’s the Difference?", The Essential Secrets of Songwriting Blog (accessed 14 December 2014).