Force field (physics): Difference between revisions

Content deleted Content added

Inline

Latest revision as of 08:19, 14 August 2024

Plot of a two-dimensional slice of the gravitational potential in and around a uniform spherical body. The inflection points of the cross-section are at the surface of the body.

In physics, a force field is a vector field corresponding with a non-contact force acting on a particle at various positions in space. Specifically, a force field is a vector field $\mathbf {F}$ , where $\mathbf {F} (\mathbf {r} )$ is the force that a particle would feel if it were at the position $\mathbf {r}$ .^[1]

Examples

Gravity is the force of attraction between two objects. A gravitational force field models this influence that a massive body (or more generally, any quantity of energy) extends into the space around itself.^[2] In Newtonian gravity, a particle of mass M creates a gravitational field $\mathbf {g} ={\frac {-GM}{r^{2}}}{\hat {\mathbf {r} }}$ , where the radial unit vector ${\hat {\mathbf {r} }}$ points away from the particle. The gravitational force experienced by a particle of light mass m, close to the surface of Earth is given by $\mathbf {F} =m\mathbf {g}$ , where g is Earth's gravity.^[3]^[4]
An electric field $\mathbf {E}$ exerts a force on a point charge q, given by $\mathbf {F} =q\mathbf {E}$ .^[5]
In a magnetic field $\mathbf {B}$ , a point charge moving through it experiences a force perpendicular to its own velocity and to the direction of the field, following the relation: $\mathbf {F} =q\mathbf {v} \times \mathbf {B}$ .

Work

Work is dependent on the displacement as well as the force acting on an object. As a particle moves through a force field along a path C, the work done by the force is a line integral:

W=\int _{C}\mathbf {F} \cdot d\mathbf {r}

This value is independent of the velocity /momentum that the particle travels along the path.

Conservative force field

For a conservative force field, it is also independent of the path itself, depending only on the starting and ending points. Therefore, the work for an object travelling in a closed path is zero, since its starting and ending points are the same:

\oint _{C}\mathbf {F} \cdot d\mathbf {r} =0

If the field is conservative, the work done can be more easily evaluated by realizing that a conservative vector field can be written as the gradient of some scalar potential function:

\mathbf {F} =-\nabla \phi

The work done is then simply the difference in the value of this potential in the starting and end points of the path. If these points are given by x = a and x = b, respectively:

W=\phi (b)-\phi (a)

References

^ Mathematical methods in chemical engineering, by V. G. Jenson and G. V. Jeffreys, p211
^ Geroch, Robert (1981). General relativity from A to B. University of Chicago Press. p. 181. ISBN 0-226-28864-1., Chapter 7, page 181
^ Vector calculus, by Marsden and Tromba, p288
^ Engineering mechanics, by Kumar, p104
^ Calculus: Early Transcendental Functions, by Larson, Hostetler, Edwards, p1055

External links

Conservative and non-conservative force-fields, Classical Mechanics, University of Texas at Austin

[1] Mathematical methods in chemical engineering, by V. G. Jenson and G. V. Jeffreys, p211

[2] Geroch, Robert (1981). General relativity from A to B. University of Chicago Press. p. 181. ISBN 0-226-28864-1., Chapter 7, page 181

[3] Vector calculus, by Marsden and Tromba, p288

[4] Engineering mechanics, by Kumar, p104

[5] Calculus: Early Transcendental Functions, by Larson, Hostetler, Edwards, p1055

[1]

[2]

[3]

[4]

[5]

@@ Line 1: / Line 1: @@
+{{short description|Region of space in which a force acts}}
+{{Other uses|Force field (disambiguation){{!}}Force field}}
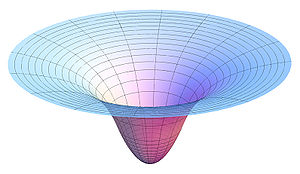
 [[Image:GravityPotential.jpg|thumb|300px|Plot of a two-dimensional slice of the gravitational potential in and around a uniform spherical body. The [[inflection point]]s of the cross-section are at the surface of the body.]]
-{{Otheruses|Force field}}
-In [[[physics]] a '''Force Field''' is a special kind of [[vector field]] that models the intensity of a [[non-contact force]] at various positions in [[space-time]]. The term appears to have been coined by Michael Faraday<ref>J. Chem. Soc., Faraday Trans., 1996, 92, 353 - 362, DOI: 10.1039/FT9969200353</ref>.
+In [[physics]], a '''force field''' is a [[vector field]] corresponding with a [[non-contact force]] acting on a particle at various positions in [[space]]. Specifically, a force field is a vector field <math>\mathbf F</math>, where <math>\mathbf F(\mathbf r)</math> is the force that a particle would feel if it were at the position <math>\mathbf r</math>.<ref>[https://books.google.com/books?id=akbi_iLSMa4C&pg=PA211 Mathematical methods in chemical engineering, by V. G. Jenson and G. V. Jeffreys, p211]</ref>
+==Examples==
+*[[Gravity]] is the force of attraction between two objects. A gravitational force field models this influence that a massive body (or more generally, any quantity of [[Mass–energy equivalence|energy]]) extends into the space around itself.<ref>{{cite book
+|title=General relativity from A to B
+|first1=Robert
+|last1=Geroch
+|publisher=University of Chicago Press
+|year=1981
+|isbn=0-226-28864-1
+|page=181
+|url=https://books.google.com/books?id=UkxPpqHs0RkC&pg=PA181}}, [https://books.google.com/books?id=UkxPpqHs0RkC&pg=PA181 Chapter 7, page 181] </ref> In [[Newtonian gravity]], a particle of mass ''M'' creates a [[gravitational field]] <math>\mathbf g=\frac{-G M}{r^2}\hat\mathbf r</math>, where the radial [[unit vector]] <math>\hat\mathbf r</math> points away from the particle. The gravitational force experienced by a particle of light mass ''m'', close to the surface of [[Earth]] is given by <math>\mathbf F = m \mathbf g</math>, where ''g'' is [[Earth's gravity]].<ref>[https://books.google.com/books?id=LiRLJf2m_dwC&pg=PA288 Vector calculus, by Marsden and Tromba, p288]</ref><ref>[https://books.google.com/books?id=bCP68dm49OkC&pg=PA104 Engineering mechanics, by Kumar, p104]</ref>
+*An [[electric field]] <math>\mathbf E</math> exerts a force on a [[point charge]] ''q'', given by <math>\mathbf F = q\mathbf E</math>.<ref>[https://books.google.com/books?id=9ue4xAjkU2oC&pg=PA1055 Calculus: Early Transcendental Functions, by Larson, Hostetler, Edwards, p1055]</ref>
+*In a [[magnetic field]] <math>\mathbf B</math>, a point charge moving through it experiences a force perpendicular to its own velocity and to the direction of the field, following the relation: <math>\mathbf F = q\mathbf v\times\mathbf B</math>.
+== Work ==
+Work is dependent on the displacement as well as the force acting on an object. As a particle moves through a force field along a path ''C'', the [[Work (physics)|work]] done by the force is a [[line integral]]:
+:<math> W = \int_C \mathbf F \cdot d\mathbf r</math>
+This value is independent of the [[velocity]][[Momentum|/momentum]] that the particle travels along the path.
+=== Conservative force field ===
+For a [[conservative force|conservative force field]], it is also independent of the path itself, depending only on the starting and ending points. Therefore, the work for an object travelling in a closed path is zero, since its starting and ending points are the same:
+:<math> \oint_C \mathbf F \cdot d\mathbf r = 0</math>
+If the field is conservative, the work done can be more easily evaluated by realizing that a conservative vector field can be written as the gradient of some scalar potential function:
+:<math> \mathbf F = -\nabla \phi</math>
+The work done is then simply the difference in the value of this potential in the starting and end points of the path. If these points are given by ''x'' = ''a'' and ''x'' = ''b'', respectively:
-==Advantages and Restrictions=
-An important point to remember when employing force fields is that the [[vector field]] in question does not exist. It is a map of the vectors which ''would'' exist, were a particle in that location in that moment; this kind of mathematical tool is called a [[Kuhnian construct]]. The force field is linked inseparably from the [[Line of force|lines of force]] one object exerts on another object or a collection of other objects. The force field is simple to collection of many of these lines in one location.
+:<math> W = \phi(b) - \phi(a) </math>
-==Examples of force fields==
-*A local [[Newtonian gravitational field]] near Earth ground typically consists of a uniform array of vectors pointing in one direction---downwards, towards the ground; its force field is represented by the Cartesian [[Vector (geometric)|vector]] <math>\vec{F}=m\cdot g (-\hat{z})</math>, where <math>\hat{z}</math> points in a [[Direction (geometry, geography)|direction]] away from the ground, and m refers to the mass, and g refers to the [[acceleration]] due to [[gravity]].
-*A global [[Gravitational field]] consists of a spherical array of vectors pointing towards the center of gravity. Its classical force field, in spherical coordinates, is represented by the vector, <math>\vec{F}=\frac{G m M}{r^2}(-\hat{r})</math>, which is just [[Newton's Law of Gravity]], with the radial unit <math>\hat{r}</math> vector pointing towards the origin of the sphere (center of the Earth).
-*A conservative [[Electric field]] has an [[electric charge]] (or a smeared plum pudding of electric charges) as its source object. In the case of the point charges, the force field is represented by <math>\vec{F}=\frac{kqQ}{r^2}(-\vec{R})</math>, where <math>\vec{R}</math> is the position vector that represents the straightest line between the source charge and the other charge.
-* A static [[Magnetic field]] has a magnetic charge (a [[magnetic monopole]] or a charge distribution).
 ==See also==
-*[[Field line]]
+* [[Classical mechanics]]
+* [[Field line]]
 * [[Force]]
+* [[Work (physics)|Mechanical work]]
+==References==
-{{DEFAULTSORT:Force Field (Physics)}}
+{{Reflist}}
+== External links ==
+{{wikiquote}}
+* [http://farside.ph.utexas.edu/teaching/301/lectures/node59.html Conservative and non-conservative force-fields], [http://farside.ph.utexas.edu/teaching/301/lectures/lectures.html Classical Mechanics], University of Texas at Austin
+{{Authority control}}
-{{Classicalmechanics-stub}}
-{{Electromagnetism-stub}}
-[[cy:Maes grym]]
+[[Category:Force]]
-[[zh-min-nan:La̍t-tiûⁿ]]
-[[de:Kraftfeld (Physik)]]
-[[ru:Силовое поле (физика)]]
-[[zh:分子力场]]