Redshift: Difference between revisions
m Reverted edits by 24.92.38.112 (talk) to last revision by Kurtan (HG) |
Reverted good faith edits by 107.203.166.49 (talk): Not an improvement |
||
| Line 1: | Line 1: | ||
{{short description|Change of wavelength in photons during travel}} |
|||
{{About|the astronomical phenomenon}} |
|||
{{About|the astronomical phenomenon||}} |
|||
[[Image:Redshift.png|thumb|upright|[[spectral line|Absorption lines]] in the [[visible spectrum|optical spectrum]] of a supercluster of distant galaxies (right), as compared to absorption lines in the optical spectrum of the Sun (left). Arrows indicate redshift. Wavelength increases up towards the red and beyond (frequency decreases).]] |
|||
[[File:Redshift.svg|thumb|upright|[[Spectral line|Absorption lines]] in the [[visible spectrum]] of a [[supercluster]] of distant galaxies (right), as compared to absorption lines in the visible spectrum of the [[Sun]] (left). Arrows indicate redshift. Wavelength increases up towards the red and beyond (frequency decreases).]] |
|||
{{General relativity sidebar}} |
|||
{{Physical cosmology}} |
|||
{{Special relativity sidebar}} |
|||
In [[physics]], a '''redshift''' is an increase in the [[wavelength]], and corresponding decrease in the [[frequency]] and [[photon energy]], of [[electromagnetic radiation]] (such as [[light]]). The opposite change, a decrease in wavelength and increase in frequency and energy, is known as a [[#Blueshift|blueshift]], or negative redshift. The terms derive from the colours [[red]] and [[blue]] which form the extremes of the [[Visible spectrum|visible light spectrum]]. The main causes of electromagnetic redshift in [[astronomy]] and [[cosmology]] are the relative motions of radiation sources, which give rise to the [[relativistic Doppler effect]], and gravitational potentials, which [[gravitational redshift|gravitationally redshift]] escaping radiation. All sufficiently distant light sources show [[cosmological redshift]] corresponding to recession speeds proportional to their distances from Earth, a fact known as [[Hubble's law]] that implies the [[expansion of the universe|universe is expanding]]. |
|||
All redshifts can be understood under the umbrella of [[Frame of reference|frame transformation laws]]. [[Gravitational wave]]s, which also travel at [[Speed of light|the speed of light]], are subject to the same redshift phenomena.<ref>{{cite journal | title=Detectability of primordial black hole binaries at high redshift | last=Ding | first=Qianhang | journal=Physical Review D | volume=104 | issue=4 | at=id. 043527 | date=August 2021 | doi=10.1103/PhysRevD.104.043527 | arxiv=2011.13643 | bibcode=2021PhRvD.104d3527D }}</ref> The value of a redshift is often denoted by the letter {{math|''z''}}, corresponding to the fractional change in wavelength (positive for redshifts, negative for blueshifts), and by the wavelength ratio {{math|1 + ''z''}} (which is greater than 1 for redshifts and less than 1 for blueshifts). |
|||
In [[physics]] (especially the physics of [[astronomical objects]]), '''redshift''' happens when [[light]] seen coming from an object is [[Proportionality (mathematics)|proportion]]ally shifted to appear more red. Here, the term "redder" refers to what happens when [[Visible spectrum|visible light]] is shifted toward the red end of the visible spectrum. More generally, where an observer detects [[electromagnetic radiation]] [[electromagnetic spectrum|outside the visible spectrum]], "redder" amounts to a technical shorthand for "increased in electromagnetic [[wavelength]]" — which also implies lower [[frequency]] and [[photon|photon energy]] in accord with, respectively, the [[Light#Wave theory|wave]] and [[Light#Quantum theory|quantum]] theories of light. |
|||
Examples of strong redshifting are a [[gamma ray]] perceived as an [[X-ray]], or initially visible light perceived as [[radio wave]]s. Subtler redshifts are seen in the [[astronomical spectroscopy|spectroscopic]] observations of [[astronomical]] objects, and are used in terrestrial technologies such as [[Doppler radar]] and [[radar gun]]s. |
|||
Redshifts are attributable to three different physical effects. The first discovered was the [[Doppler effect]], familiar in the changes in the apparent [[Pitch (music)|pitch]]es of sirens and [[frequency]] of the [[sound|sound waves]] emitted by speeding vehicles; an observed redshift due to the Doppler effect occurs whenever a light source moves away from an observer. [[Cosmology|Cosmological redshift]] is seen due to the [[Metric expansion of space|expansion of the universe]], and sufficiently distant light sources (generally more than a few million [[light years]] away) show redshift corresponding to the rate of increase of their distance from Earth. Finally, [[gravitational redshift]]s are a [[general relativity|relativistic]] effect observed in electromagnetic radiation moving out of [[gravitational field]]s. Conversely, a ''decrease'' in wavelength is called [[blue shift]] and is generally seen when a light-emitting object moves toward an observer or when electromagnetic radiation moves into a gravitational field. |
|||
Other physical processes exist that can lead to a shift in the frequency of electromagnetic radiation, including [[scattering]] and [[physical optics|optical effects]]; however, the resulting changes are distinguishable from (astronomical) redshift and are not generally referred to as such (see section on [[#Effects from physical optics or radiative transfer|physical optics and radiative transfer]]). |
|||
Although observing redshifts and blue shifts have several terrestrial applications (e.g., [[Doppler radar]] and [[radar gun]]s),<ref>See Feynman, Leighton and Sands (1989) or any introductory undergraduate (and many high school) [[Physics#Further reading|physics textbooks]]. See Taylor (1992) for a relativistic discussion.</ref> redshifts are most famously seen in the [[astronomical spectroscopy|spectroscopic]] observations of astronomical objects.<ref name=basicastronomy>See Binney and Merrifeld (1998), Carroll and Ostlie (1996), Kutner (2003) for applications in astronomy.</ref> |
|||
A [[special relativity|special relativistic]] [[#Redshift formulae|redshift formula]] (and its [[classical physics|classical approximation]]) can be used to calculate the redshift of an object when [[spacetime]] is [[Minkowski space|flat]]. However, many cases such as [[black hole]]s and [[Big Bang cosmology]] require that redshifts be calculated using [[general relativity]].<ref>See Misner, Thorne and Wheeler (1973) and Weinberg (1971) or any of the [[physical cosmology#Textbooks|physical cosmology textbooks]]</ref> Special relativistic, gravitational, and cosmological redshifts can be understood under the umbrella of [[Frame of reference|frame transformation laws]]. There exist other physical processes that can lead to a shift in the frequency of electromagnetic radiation, including [[scattering]] and [[physical optics|optical effects]]; however, the resulting changes are distinguishable from true redshift and not generally referred as such. (See section on [[#Effects due to physical optics or radiative transfer|physical optics and radiative transfer]]). |
|||
[[Image:Redshift blueshift.svg|thumb|Redshift and blue shift]] |
|||
==History== |
==History== |
||
The history of the subject began in the 19th century, with the development of classical [[wave]] mechanics and the exploration of phenomena which are associated with the [[Doppler effect]]. The effect is named after the [[Austria|Austrian]] mathematician, [[Christian Doppler]], who offered the first known physical explanation for the phenomenon in 1842.<ref> |
|||
The history of the subject began with the development in the 19th century of [[wave mechanics]] and the exploration of phenomena associated with the [[Doppler effect]]. The effect is named after [[Christian Andreas Doppler]], who offered the first known physical explanation for the phenomenon in 1842.<ref>Doppler, Christian, (1846), ''Prag, Druck von G. Haase sohne''</ref> The hypothesis was tested and confirmed for [[sound|sound waves]] by the [[Netherlands|Dutch]] scientist [[C.H.D. Buys Ballot|Christoph Hendrik Diederik Buys Ballot]] in 1845.<ref>Dev Maulik, "[http://books.google.com/books?id=HedeGJms0n4C&vid=ISBN3540230882&dq=%22Buys+Ballot%22&pg=PA3&lpg=PA3&sig=1Y0ETpNemutmPYNF8KbWSbLrF7E&q=%22Ballot%22 Doppler Sonography: A Brief History]" in ''[http://www.springer.com/west/home/medicine/gynecology?SGWID=4-10066-22-46625046-0 Doppler Ultrasound in Obstetrics And Gynecology]'' (2005) by Dev (EDT) Maulik, Ivica Zalud</ref> Doppler correctly predicted that the phenomenon should apply to all [[wave]]s, and in particular suggested that the varying [[color]]s of [[star]]s could be attributed to their motion with respect to the Earth.<ref>{{MacTutor Biography|id=Doppler}}</ref> While this attribution turned out to be incorrect (stellar colors are indicators of a star's [[color temperature|temperature]], not motion), Doppler would later be vindicated by verified redshift observations. |
|||
{{cite book |
|||
|last=Doppler | first=Christian |
|||
|date=1846 |
|||
|title=Beiträge zur fixsternenkunde |
|||
|location=Prague |publisher=G. Haase Söhne |
|||
|bibcode=1846befi.book.....D |
|||
|volume=69 |
|||
}}</ref> In 1845, the hypothesis was tested and confirmed for [[sound wave]]s by the [[Netherlands|Dutch]] scientist [[C. H. D. Buys Ballot|Christophorus Buys Ballot]].<ref> |
|||
{{cite book |
|||
|last=Maulik | first=Dev |
|||
|chapter=Doppler Sonography: A Brief History |
|||
|chapter-url=https://books.google.com/books?id=HedeGJms0n4C&q=%22Ballot%22&pg=PA3 |
|||
|editor1-last=Maulik | editor1-first=Dev |
|||
|editor2-last=Zalud | editor2-first=Ivica |
|||
|date=2005 |
|||
|title=Doppler Ultrasound in Obstetrics And Gynecology |
|||
|url= https://www.springer.com/west/home/medicine/gynecology?SGWID=4-10066-22-46625046-0 |
|||
|isbn=978-3-540-23088-5 |
|||
|publisher=Springer |
|||
}}</ref> Doppler correctly predicted that the phenomenon would apply to all waves and, in particular, suggested that the varying [[color]]s of [[star]]s could be attributed to their motion with respect to the Earth.<ref> |
|||
{{cite web |
|||
|last1=O'Connor | first1=John J. |
|||
|last2=Robertson | first2=Edmund F. |
|||
|date=1998 |
|||
|url=http://www-history.mcs.st-andrews.ac.uk/Biographies/Doppler.html |
|||
|title=Christian Andreas Doppler |
|||
|work=[[MacTutor History of Mathematics archive]] |
|||
|publisher=[[University of St Andrews]] |
|||
}}</ref> Before this was verified, it was found that stellar colors were primarily due to a star's [[color temperature|temperature]], not motion. Only later was Doppler vindicated by verified redshift observations.{{cn|date=March 2023}} |
|||
The |
The Doppler redshift was first described by French physicist [[Hippolyte Fizeau]] in 1848, who noted the shift in [[spectral line]]s seen in stars as being due to the Doppler effect. The effect is sometimes called the "Doppler–Fizeau effect". In 1868, British astronomer [[William Huggins]] was the first to determine the velocity of a star moving away from the Earth by the method.<ref name=Huggins> |
||
{{cite journal |
|||
|last=Huggins | first=William |
|||
|date=1868 |
|||
|title=Further Observations on the Spectra of Some of the Stars and Nebulae, with an Attempt to Determine Therefrom Whether These Bodies are Moving towards or from the Earth, Also Observations on the Spectra of the Sun and of Comet II |
|||
|journal=[[Philosophical Transactions of the Royal Society of London]] |
|||
|volume= 158 |pages=529–564 |
|||
|bibcode=1868RSPT..158..529H |
|||
|doi=10.1098/rstl.1868.0022 |
|||
}}</ref> In 1871, optical redshift was confirmed when the phenomenon was observed in [[Fraunhofer lines]], using solar rotation, about 0.1 Å in the red.<ref> |
|||
{{cite journal |
|||
|last=Reber | first=G. |
|||
|date=1995 |
|||
|title=Intergalactic Plasma |
|||
|journal=[[Astrophysics and Space Science]] |
|||
|volume=227 |
|||
|issue=1–2 |pages=93–96 |
|||
|doi=10.1007/BF00678069 |
|||
|bibcode=1995Ap&SS.227...93R |
|||
|s2cid=30000639 |
|||
}}</ref> In 1887, Vogel and Scheiner discovered the "annual Doppler effect", the yearly change in the Doppler shift of stars located near the ecliptic, due to the orbital velocity of the Earth.<ref>{{cite book|last=Pannekoek|first=A.|title=A History of Astronomy |date=1961|publisher=Dover|page=451|isbn=978-0-486-65994-7}}</ref> In 1901, [[Aristarkh Belopolsky]] verified optical redshift in the laboratory using a system of rotating mirrors.<ref> |
|||
{{cite journal |
|||
|last=Bélopolsky | first=A. |
|||
|date=1901 |
|||
|bibcode=1901ApJ....13...15B |
|||
|title=On an Apparatus for the Laboratory Demonstration of the Doppler-Fizeau Principle |
|||
|journal=[[Astrophysical Journal]] |
|||
|volume=13 |page=15 |
|||
|doi=10.1086/140786 |
|||
|doi-access=free |
|||
}}</ref> |
|||
[[Arthur Eddington]] used the term "red-shift" as early as 1923,<ref>{{Cite book |last=Eddington |first=Arthur Stanley |url=https://books.google.com/books?id=errkj2WXGzIC&pg=PA164 |title=The Mathematical Theory of Relativity |date=1923 |publisher=The University Press |page=164 |language=en |author-link=Arthur Eddington}}</ref><ref>{{Cite OED|term=redshift|id=160477|access-date=2023-03-17}}</ref> although the word does not appear unhyphenated until about 1934, when [[Willem de Sitter]] used it.<ref> |
|||
In 1871, optical redshift was confirmed when the phenomenon was observed in [[Fraunhofer lines]] using solar rotation, about 0.1 Å in the red.<ref>Reber, G., "[http://adsabs.harvard.edu/cgi-bin/nph-bib_query?bibcode=1995Ap%26SS.227...93R&db_key=AST&data_type=HTML&format=&high=4521318e0222293 Intergalactic Plasma]"(1995) Astrophysics and Space Science, v. 227, p. 93–96.</ref> In 1901 [[Aristarkh Apollonovich Belopolsky|Aristarkh Belopolsky]] verified optical redshift in the laboratory using a system of rotating mirrors.<ref>Bélopolsky, A., "[http://adsabs.harvard.edu/cgi-bin/nph-bib_query?bibcode=1901ApJ....13...15B&db_key=AST&data_type=HTML&format=&high=4521318e0220955 On an Apparatus for the Laboratory Demonstration of the Doppler-Fizeau Principle]" (1901) Astrophysical Journal, vol. 13, p.15 </ref> |
|||
{{cite journal |
|||
|last=de Sitter | first=W. |
|||
|date=1934 |
|||
|title=On distance, magnitude, and related quantities in an expanding universe |
|||
|journal=[[Bulletin of the Astronomical Institutes of the Netherlands]] |
|||
|volume=7 |page=205 |
|||
|bibcode=1934BAN.....7..205D |
|||
|quote=It thus becomes urgent to investigate the effect of the redshift and of the metric of the universe on the apparent magnitude and observed numbers of nebulae of given magnitude |
|||
}}</ref> |
|||
Beginning with observations in 1912, [[Vesto Slipher]] discovered that most [[spiral galaxy|spiral galaxies]], then mostly thought to be [[Spiral galaxy#Spiral nebula|spiral nebulae]], had considerable redshifts. Slipher first reported on his measurement in the inaugural volume of the ''[[Lowell Observatory]] Bulletin''.<ref> |
|||
The earliest occurrence of the term "red-shift" in print (in this hyphenated form), appears to be by American astronomer [[Walter S. Adams]] in 1908, where he mentions "Two methods of investigating that nature of the nebular red-shift".<ref>Adams, Walter S., "[http://adsabs.harvard.edu/cgi-bin/nph-bib_query?bibcode=1908CMWCI..22....1A No. 22. Preliminary catalogue of lines affected in sun-spots]" (1908) ''Contributions from the Mount Wilson Observatory'' / Carnegie Institution of Washington, vol. 22, pp.1–21</ref> The word doesn't appear unhyphenated, perhaps indicating a more common usage of its German equivalent, ''Rotverschiebung'', until about 1934 by [[Willem de Sitter]].<ref>W. de Sitter, "[http://articles.adsabs.harvard.edu/cgi-bin/nph-iarticle_query?journal=BAN&year=1934&volume=7&page_ind=210&letter=.&type=SCREEN_GIF On distance, magnitude, and related quantities in an expanding universe], (1934) ''Bulletin of the Astronomical Institutes of the Netherlands'', Vol. 7, p.205. He writes: "It thus becomes urgent to investigate the effect of the redshift and of the metric of the universe on the apparent magnitude and observed numbers of nebulae of given magnitude"</ref> |
|||
{{cite journal |
|||
|last=Slipher | first=Vesto |
|||
|date=1912 |
|||
|title=The radial velocity of the Andromeda Nebula |
|||
|journal=[[Lowell Observatory Bulletin]] |
|||
|volume=1 |issue=8 |
|||
|pages=2.56–2.57 |
|||
|bibcode=1913LowOB...2...56S |
|||
|quote=The magnitude of this velocity, which is the greatest hitherto observed, raises the question whether the velocity-like displacement might not be due to some other cause, but I believe we have at present no other interpretation for it |
|||
}}</ref> Three years later, he wrote a review in the journal ''[[Popular Astronomy (US magazine)|Popular Astronomy]]''.<ref> |
|||
{{cite journal |
|||
|last=Slipher | first=Vesto |
|||
|title=Spectrographic Observations of Nebulae |
|||
|journal=[[Popular Astronomy (US magazine)|Popular Astronomy]] |
|||
|volume=23 |pages=21–24 |date=1915 |
|||
|bibcode=1915PA.....23...21S |
|||
}}</ref> In it he stated that "the early discovery that the great Andromeda spiral had the quite exceptional velocity of –300 km(/s) showed the means then available, capable of investigating not only the spectra of the spirals but their velocities as well."<ref> |
|||
{{cite journal |last=Slipher | first=Vesto |date=1915 |title=Spectrographic Observations of Nebulae |journal=[[Popular Astronomy (US magazine)|Popular Astronomy]] |volume=23 |page=22 |bibcode=1915PA.....23...21S}}</ref> |
|||
Slipher reported the velocities for 15 spiral nebulae spread across the entire [[celestial sphere]], all but three having observable "positive" (that is recessional) velocities. Subsequently, [[Edwin Hubble]] discovered an approximate relationship between the redshifts of such "nebulae", and the [[distance]]s to them, with the formulation of his eponymous [[Hubble's law]].<ref> |
|||
Beginning with observations in 1912, [[Vesto Slipher]] discovered that most [[spiral nebula]]e had considerable redshifts.<ref>Slipher first reports on his measurement in the inaugural volume of the Lowell Observatory Bulletin, pp.2.56-2.57 [http://adsabs.harvard.edu/cgi-bin/nph-bib_query?bibcode=1913LowOB...1b..56S&db_key=AST&data_type=HTML&format=&high=448f04e38822894]. His article entitled ''The radial velocity of the Andromeda Nebula'' reports making the first Doppler measurement on September 17, 1912. In his report, Slipher writes: "The magnitude of this velocity, which is the greatest hitherto observed, raises the question whether the velocity-like displacement might not be due to some other cause, but I believe we have at present no other interpretation for it." Three years later, in the journal ''Popular Astronomy'', Vol. 23, p. 21–24 [http://adsabs.harvard.edu/cgi-bin/nph-bib_query?bibcode=1915PA.....23...21S&db_key=AST&data_type=HTML&format=&high=448f04e38822894], Slipher wrote a review entitled ''Spectrographic Observations of Nebulae''. In it he states, "The early discovery that the great Andromeda spiral had the quite exceptional velocity of - 300 km(/s) showed the means then available, capable of investigating not only the spectra of the spirals but their velocities as well." Slipher reported the velocities for 15 spiral nebulae spread across the entire [[celestial sphere]], all but three having observable "positive" (that is recessional) velocities.</ref> Subsequently, [[Edwin Hubble]] discovered an approximate relationship between the redshift of such "nebulae" (now known to be [[galaxy|galaxies]] in their own right) and the [[distance]] to them with the formulation of his eponymous [[Hubble's law]].<ref>Hubble, Edwin, "[http://adsabs.harvard.edu/cgi-bin/nph-bib_query?bibcode=1929PNAS...15..168H&db_key=AST&data_type=HTML&format=&high=42ca922c9c30954 A Relation between Distance and Radial Velocity among Extra-Galactic Nebulae]" (1929) ''Proceedings of the National Academy of Sciences of the United States of America'', Volume 15, Issue 3, pp. 168–173 ([http://www.pnas.org/cgi/reprint/15/3/168 Full article], PDF)</ref> These observations corroborated [[Alexander Friedman]]'s 1922 work, in which he derived the famous [[Friedmann equations]].<ref>Friedman, A: Über die Krümmung des Raumes, Z. Phys. 10 (1922), 377–386. (English translation in: Gen. Rel. Grav. 31 (1999), 1991–2000.)</ref> They are today considered strong evidence for an [[expanding universe]] and the [[Big Bang]] theory.<ref name=Eddington>This was recognized early on by physicists and astronomers working in cosmology in the 1930s. The earliest layman publication describing the details of this correspondence was [[Sir Arthur Eddington]]'s book ''The Expanding Universe: Astronomy's 'Great Debate', 1900–1931'', published by Press Syndicate of the University of Cambridge in 1933.</ref> |
|||
{{cite journal |
|||
|doi=10.1073/pnas.15.3.168 |
|||
|last=Hubble |first=Edwin |
|||
|date=1929 |
|||
|bibcode=1929PNAS...15..168H |
|||
|title=A Relation between Distance and Radial Velocity among Extra-Galactic Nebulae |
|||
|journal=[[Proceedings of the National Academy of Sciences of the United States of America]] |
|||
|volume=15 |issue=3 |pages=168–173 |
|||
|pmid=16577160 |
|||
|pmc=522427 |
|||
|doi-access=free |
|||
}}</ref> [[Milton Humason]] worked on those observations with Hubble.<ref>{{Cite web|url=https://imagine.gsfc.nasa.gov/educators/programs/cosmictimes/online_edition/1929/expanding.html|title=Universe is Expanding|date=2017-12-08|access-date=2023-09-06}}</ref> These observations corroborated [[Alexander Friedmann]]'s 1922 work, in which he derived the [[Friedmann equations|Friedmann–Lemaître equations]].<ref>{{cite journal |
|||
|last=Friedman |first=A. A. |
|||
|date=1922 |
|||
|title=Über die Krümmung des Raumes |
|||
|journal=[[Zeitschrift für Physik]] |
|||
|volume=10 |
|||
|issue=1 |pages=377–386 |
|||
|doi=10.1007/BF01332580 |
|||
|bibcode = 1922ZPhy...10..377F |s2cid=125190902 |
|||
}} English translation in {{cite journal |title=On the Curvature of Space|doi=10.1023/A:1026751225741 |last=Friedman |first=A. |date=1999 |journal=[[General Relativity and Gravitation]] |volume=31 |issue=12 |pages=1991–2000 |bibcode=1999GReGr..31.1991F|s2cid=122950995 }})</ref> They are now considered to be strong evidence for an [[expanding universe]] and the [[Big Bang]] theory.<ref name=Eddington>This was recognized early on by physicists and astronomers working in cosmology in the 1930s. The earliest layman publication describing the details of this correspondence is {{cite book |
|||
|last=Eddington |first=Arthur | author-link=Arthur Eddington |
|||
|date=1933 |
|||
|title=The Expanding Universe: Astronomy's 'Great Debate', 1900–1931 |
|||
|url=https://archive.org/details/in.ernet.dli.2015.220736 |
|||
|publisher=[[Cambridge University Press]] |
|||
}} (Reprint: {{ISBN|978-0-521-34976-5}})</ref> |
|||
==Measurement, characterization, and interpretation== |
==Measurement, characterization, and interpretation== |
||
[[File:High-redshift galaxy candidates in the Hubble Ultra Deep Field 2012.jpg|thumb|High-redshift galaxy candidates in the [[Hubble Ultra Deep Field]], 2012<ref>{{cite news|title=Hubble census finds galaxies at redshifts 9 to 12|url=https://esahubble.org/news/heic1219/|access-date=13 December 2012|newspaper=ESA/Hubble Press Release}}</ref> ]] |
|||
The [[visible spectrum|spectrum]] of light that comes from a single source (see idealized spectrum illustration top-right) can be measured. To determine the redshift, one searches for features in the spectrum such as [[spectral line|absorption lines]], [[spectral line|emission lines]], or other variations in [[light intensity]]. If found, these features can be compared with known features in the spectrum of various chemical compounds found in experiments where that compound is located on earth. A very common [[chemical element|atomic element]] in space is [[hydrogen]]. The spectrum of originally featureless light shone through hydrogen will show a [[hydrogen spectrum|signature spectrum]] specific to hydrogen that has features at regular intervals. If restricted to absorption lines it would look similar to the illustration (top right). If the same pattern of intervals is seen in an observed spectrum from a distant source but occurring at shifted wavelengths, it can be identified as hydrogen too. If the same spectral line is identified in both spectra but at different wavelengths then the redshift can be calculated using the table below. Determining the redshift of an object in this way requires a frequency- or wavelength-range. In order to calculate the redshift one has to know the wavelength of the emitted light in the rest frame of the source, in other words, the wavelength that would be measured by an observer located adjacent to and comoving with the source. Since in astronomical applications this measurement cannot be done directly, because that would require travelling to the distant star of interest, the method using spectral lines described here is used instead. Redshifts cannot be calculated by looking at unidentified features whose rest-frame frequency is unknown, or with a spectrum that is featureless or [[white noise]] (random fluctuations in a spectrum).<ref>See, for example, this 25 May 2004 [http://heasarc.gsfc.nasa.gov/docs/swift/about_swift/redshift.html press release] from [[NASA]]'s [[Swift Gamma-Ray Burst Mission|Swift]] [[space telescope]] that is researching [[gamma-ray burst]]s: "Measurements of the gamma-ray spectra obtained during the main outburst of the GRB have found little value as redshift indicators, due to the lack of well-defined features. However, optical observations of GRB afterglows have produced spectra with identifiable lines, leading to precise redshift measurements."</ref> |
|||
The [[visible spectrum|spectrum]] of light that comes from a source (see idealized spectrum illustration top-right) can be measured. To determine the redshift, one searches for features in the spectrum such as [[spectral line|absorption lines]], [[spectral line|emission lines]], or other variations in light intensity<!--Don't link to disambiguation page-->. If found, these features can be compared with known features in the spectrum of various chemical compounds found in experiments where that compound is located on Earth. A very common [[chemical element|atomic element]] in space is [[hydrogen]]. |
|||
The spectrum of originally featureless light shone through hydrogen will show a [[hydrogen spectrum|signature spectrum]] specific to hydrogen that has features at regular intervals. If restricted to absorption lines it would look similar to the illustration (top right). If the same pattern of intervals is seen in an observed spectrum from a distant source but occurring at shifted wavelengths, it can be identified as hydrogen too. If the same spectral line is identified in both spectra—but at different wavelengths—then the redshift can be calculated using the table below. |
|||
Determining the redshift of an object in this way requires a frequency or wavelength range. In order to calculate the redshift, one has to know the wavelength of the emitted light in the rest frame of the source: in other words, the wavelength that would be measured by an observer located adjacent to and comoving with the source. Since in astronomical applications this measurement cannot be done directly, because that would require traveling to the distant star of interest, the method using spectral lines described here is used instead. Redshifts cannot be calculated by looking at unidentified features whose rest-frame frequency is unknown, or with a spectrum that is featureless or [[white noise]] (random fluctuations in a spectrum).<ref>See, for example, this 25 May 2004 [http://heasarc.gsfc.nasa.gov/docs/swift/about_swift/redshift.html press release] from [[NASA]]'s [[Swift Gamma-Ray Burst Mission|Swift]] [[space telescope]] that is researching [[gamma-ray burst]]s: "Measurements of the gamma-ray spectra obtained during the main outburst of the GRB have found little value as redshift indicators, due to the lack of well-defined features. However, optical observations of GRB afterglows have produced spectra with identifiable lines, leading to precise redshift measurements."</ref> |
|||
Redshift (and |
Redshift (and blueshift) may be characterized by the relative difference between the observed and emitted wavelengths (or frequency) of an object. In astronomy, it is customary to refer to this change using a [[dimensionless quantity]] called {{math|''z''}}. If {{math|''λ''}} represents wavelength and {{math|''f''}} represents frequency (note, {{math|''λf'' {{=}} ''c''}} where {{math|''c''}} is the [[speed of light]]), then {{math|''z''}} is defined by the equations:<ref>For a tutorial on how to define and interpret large redshift measurements, see:<br />{{cite web |
||
| title=Extragalactic Redshifts |
|||
| first=John |
|||
| last=Huchra |
|||
| publisher=Harvard-Smithsonian Center for Astrophysics |
|||
| website=NASA/IPAC Extragalactic Database |
|||
| url=http://ned.ipac.caltech.edu/help/zdef.html |
|||
| access-date=2023-03-16 |
|||
| archive-date=2013-12-22 |
|||
| archive-url=https://web.archive.org/web/20131222052715/http://ned.ipac.caltech.edu/help/zdef.html |
|||
}}</ref> |
|||
{| class="wikitable" |
{| class="wikitable" style="margin:auto;" |
||
|+ '''Calculation of redshift, <math>z</math>''' |
|+ '''Calculation of redshift, <math>z</math>''' |
||
! '''Based on wavelength''' !! '''Based on frequency''' |
! '''Based on wavelength''' !! '''Based on frequency''' |
||
| Line 38: | Line 170: | ||
|} |
|} |
||
After ''z'' is measured, the distinction between redshift and |
After {{math|''z''}} is measured, the distinction between redshift and blueshift is simply a matter of whether {{math|''z''}} is positive or negative. For example, [[Doppler effect]] blueshifts ({{math|''z'' < 0}}) are associated with objects approaching (moving closer to) the observer with the light shifting to greater [[energy|energies]]. Conversely, Doppler effect redshifts ({{math|''z'' > 0}}) are associated with objects receding (moving away) from the observer with the light shifting to lower energies. Likewise, gravitational blueshifts are associated with light emitted from a source residing within a weaker [[gravitational field]] as observed from within a stronger gravitational field, while gravitational redshifting implies the opposite conditions. |
||
==Redshift formulae== |
== Redshift formulae == |
||
In general relativity one can derive several important special-case formulae for redshift in certain special spacetime geometries, as summarized in the following table. In all cases the magnitude of the shift (the value of ''z'') is independent of the wavelength.<ref name=basicastronomy /> |
In general relativity one can derive several important special-case formulae for redshift in certain special spacetime geometries, as summarized in the following table. In all cases the magnitude of the shift (the value of {{math|''z''}}) is independent of the wavelength.<ref name="basicastronomy">See Binney and Merrifeld (1998), Carroll and Ostlie (1996), Kutner (2003) for applications in astronomy.</ref> |
||
[[Image:Suzredshift.gif|thumb|Doppler effect, [[yellow]] (~575 [[nanometer|nm]] wavelength) ball appears [[green]]ish (blueshift to ~565 nm wavelength) approaching observer, turns [[Orange (colour)|orange]] (redshift to ~585 nm wavelength) as it passes, and returns to yellow when motion stops. To observe such a change in color, the object would have to be traveling at approximately 5200 [[kilometer per second|km/s]], or about 75 times faster than the speed record for the [[Helios II|fastest manmade space probe]].]] |
|||
{| class="wikitable" |
{| class="wikitable" style="max-width:1000px;" |
||
|+ '''Redshift |
|+ '''Redshift summary''' |
||
! Redshift type !! Geometry !! Formula<ref>Where z = redshift; v<sub>||</sub> = [[velocity]] parallel to line-of-sight (positive if moving away from receiver); c = [[speed of light]]; ''γ'' = [[Lorentz factor]]; ''a'' = [[scale factor (Universe)|scale factor]]; G = [[gravitational constant]]; M = object [[mass]]; r = [[Schwarzschild coordinates|radial Schwarzschild coordinate]], g<sub>tt</sub> = t,t component of the [[metric tensor]]</ref> |
! Redshift type !! Geometry !! Formula<ref>Where z = redshift; v<sub>||</sub> = [[velocity]] parallel to line-of-sight (positive if moving away from receiver); c = [[speed of light]]; ''γ'' = [[Lorentz factor]]; ''a'' = [[scale factor (Universe)|scale factor]]; G = [[gravitational constant]]; M = object [[mass]]; r = [[Schwarzschild coordinates|radial Schwarzschild coordinate]], g<sub>tt</sub> = t,t component of the [[metric tensor]]</ref> |
||
|- |
|||
|- align=center |
|||
| Relativistic Doppler || [[Minkowski space]] (flat spacetime) || |
| [[Relativistic Doppler effect|Relativistic Doppler]]|| [[Minkowski space]]<br />(flat spacetime) || |
||
For motion completely in the radial or<br />line-of-sight direction: |
|||
|- align=center |
|||
| Cosmological redshift || [[Friedmann-Lemaître-Robertson-Walker|FLRW spacetime]] (expanding Big Bang universe) || <math>1 + z = \frac{a_{\mathrm{now}}}{a_{\mathrm{then}}}</math> |
|||
|- align=center |
|||
| Gravitational redshift || any [[stationary spacetime]] (e.g. the [[Schwarzschild geometry]]) || <math>1 + z = \sqrt{\frac{g_{tt}(\text{receiver})}{g_{tt}(\text{source})}}</math><br>(for the Schwarzschild geometry, <math>1 + z = \sqrt{\frac{1 - \frac{2GM}{r_{\text{receiver}}}}{1 - \frac{2GM}{r_{\text{source}}}}}</math>) |
|||
|} |
|||
:<math>1 + z = \gamma \left(1 + \frac{v_{\parallel}}{c}\right) = \sqrt{\frac{1+\frac{v_{\parallel}}{c}}{1-\frac{v_{\parallel}}{c}}}</math> |
|||
===Doppler effect=== |
|||
:<math>z \approx \frac{v_{\parallel}}{c}</math>  for small <math>v_{\parallel}</math> |
|||
{{main|Doppler effect}} |
|||
If a source of the light is moving away from an observer, then redshift (''z'' > 0) occurs; if the source moves towards the observer, then [[blue shift]] (''z'' < 0) occurs. This is true for all electromagnetic waves and is explained by the [[Doppler effect]]. Consequently, this type of redshift is called the ''Doppler redshift''. If the source moves away from the observer with [[velocity]] ''v'', which is much less than the speed of light (v << c), the redshift is given by |
|||
<br /> |
|||
:<math>z \approx \frac{v}{c}</math> (Since <math>\gamma \approx 1</math>, [[#Relativistic Doppler effect|see below]]) |
|||
For motion completely in the transverse direction: |
|||
:<math>1 + z=\frac{1}{\sqrt{1-\frac{v_\perp^2}{c^2}}}</math> |
|||
where ''c'' is the [[speed of light]]. In the classical Doppler effect, the frequency of the source is not modified, but the recessional motion causes the illusion of a lower frequency. |
|||
:<math>z \approx \frac{1}{2} \left( \frac{v_{\perp}}{c} \right)^2</math>  for small <math>v_{\perp}</math> |
|||
|- |
|||
===Relativistic Doppler effect=== |
|||
| [[Cosmological redshift]]|| [[Friedmann–Lemaître–Robertson–Walker|FLRW spacetime]]<br />(expanding Big Bang universe) || |
|||
{{main|Relativistic Doppler effect}} |
|||
:<math>1 + z = \frac{a_{\mathrm{now}}}{a_{\mathrm{then}}}</math> |
|||
A more complete treatment of the Doppler redshift requires considering relativistic effects associated with motion of sources close to the speed of light. A complete derivation of the effect can be found in the article on the [[relativistic Doppler effect]]. In brief, objects moving close to the speed of light will experience deviations from the above formula due to the [[time dilation]] of [[special relativity]] which can be corrected for by introducing the [[Lorentz factor]] ''γ'' into the classical Doppler formula as follows: |
|||
[[Hubble's law]]: |
|||
:<math>1 + z = \left(1 + \frac{v}{c}\right) \gamma</math> |
|||
:<math>z \approx \frac{H_0 D}{c}</math>  for <math>D \ll \frac{c}{H_0}</math> |
|||
This phenomenon was first observed in a 1938 experiment performed by Herbert E. Ives and G.R. Stilwell, called the [[Ives-Stilwell experiment]].<ref>H. Ives and G. Stilwell, An Experimental study of the rate of a moving atomic clock, J. Opt. Soc. Am. 28, 215–226 (1938) [http://www.opticsinfobase.org/abstract.cfm?URI=josa-28-7-215] </ref> |
|||
|- |
|||
Since the Lorentz factor is dependent only on the [[magnitude (mathematics)|magnitude]] of the velocity, this causes the redshift associated with the relativistic correction to be independent of the orientation of the source movement. In contrast, the classical part of the formula is dependent on the [[scalar resolute|projection]] of the movement of the source into the [[Line-of-sight propagation|line-of-sight]] which yields different results for different orientations. Consequently, for an object moving at an angle ''θ'' to the observer (zero angle is directly away from the observer), the full form for the relativistic Doppler effect becomes: |
|||
| [[Gravitational redshift]]|| any [[stationary spacetime]] || |
|||
:<math>1 + z = \sqrt{\frac{g_{tt}(\text{receiver})}{g_{tt}(\text{source})}}</math> |
|||
For the [[Schwarzschild geometry]]: |
|||
:<math>1+ z = \frac{1 |
:<math>1 + z = \sqrt{\frac{1 - \frac{r_S}{r_{\text{receiver}}}}{1 - \frac{r_S}{r_{\text{source} }}}} = \sqrt{\frac{1 - \frac{2GM}{ c^2 r_{\text{receiver}}}}{1 - \frac{2GM}{ c^2 r_{\text{source} }}}} </math> |
||
:<math>z \approx \frac{1}{2} \left( \frac{r_S}{r_\text{source}} - \frac{r_S}{r_\text{receiver}} \right)</math>  for <math>r \gg r_S</math> |
|||
and for motion solely in the line of sight (θ = 0°), this equation reduces to: |
|||
In terms of [[escape velocity]]: |
|||
:<math>1 + z = \sqrt{\frac{1 + \frac{v}{c}}{1 - \frac{v}{c}}}</math> |
|||
:<math>z \approx \frac{1}{2} \left(\frac{v_\text{e}}{c}\right)_\text{source}^2 - \frac{1}{2} \left(\frac{v_\text{e}}{c}\right)_\text{receiver}^2 </math> |
|||
For the special case that the source is moving at [[right angle]]s (θ = 90°) to the detector, the relativistic redshift is known as the [[Transverse Doppler effect|transverse redshift]], and a redshift: |
|||
for <math>v_\text{e} \ll c</math> |
|||
|} |
|||
:<math>1 + z = \frac{1}{\sqrt{1-v^2/c^2}}</math> |
|||
===Doppler effect=== |
|||
is measured, even though the object is not moving away from the observer. Even if the source is moving towards the observer, if there is a transverse component to the motion then there is some speed at which the dilation just cancels the expected blue shift and at higher speed the approaching source will be redshifted.<ref>See "[http://www.physics.uq.edu.au/people/ross/phys2100/doppler.htm Photons, Relativity, Doppler shift]" at the University of Queensland</ref> |
|||
{{Main|Doppler effect|Relativistic Doppler effect}} |
|||
[[Image:Suzredshift.gif|thumb|[[Doppler effect]], yellow (~575 [[Nanometre|nm]] wavelength) ball appears greenish (blueshift to ~565 nm wavelength) approaching observer, turns [[Orange (colour)|orange]] (redshift to ~585 nm wavelength) as it passes, and returns to yellow when motion stops. To observe such a change in color, the object would have to be traveling at approximately 5,200 [[Metre per second|km/s]], or about 32 times faster than the speed record for the [[Parker Solar Probe|fastest space probe]].]] |
|||
[[File:Redshift blueshift.svg|thumb|Redshift and blueshift]] |
|||
If a source of the light is moving away from an observer, then redshift ({{math|''z'' > 0}}) occurs; if the source moves towards the observer, then [[blueshift]] ({{math|''z'' < 0}}) occurs. This is true for all electromagnetic waves and is explained by the [[Doppler effect]]. Consequently, this type of redshift is called the ''Doppler redshift''. If the source moves away from the observer with [[velocity]] {{math|''v''}}, which is much less than the speed of light ({{math|''v'' ≪ ''c''}}), the redshift is given by |
|||
===Expansion of space=== |
|||
{{main|Metric expansion of space}} |
|||
In the early part of the twentieth century, Slipher, Hubble and others made the first measurements of the redshifts and blue shifts of galaxies beyond the [[Milky Way]]. They initially interpreted these redshifts and blue shifts as due solely to the Doppler effect, but later Hubble discovered a rough correlation between the increasing redshifts and the increasing distance of galaxies. Theorists almost immediately realized that these observations could be explained by a different mechanism for producing redshifts. [[Hubble's law]] of the correlation between redshifts and distances is required by models of cosmology derived from general relativity that have a [[metric expansion of space]].<ref name=Eddington /> As a result, photons propagating through the expanding space are stretched, creating the [[cosmological redshift]]. |
|||
:<math>z \approx \frac{v}{c}</math> (since <math>\gamma \approx 1</math>) |
|||
====Difference from a Doppler effect==== |
|||
where {{math|''c''}} is the [[speed of light]]. In the classical Doppler effect, the frequency of the source is not modified, but the recessional motion causes the illusion of a lower frequency. |
|||
This differs from a Doppler-effect redshift because it is not a consequence of the speed of the source; instead, the photons increase in wavelength and redshift as the space through which they are traveling expands.<ref name=Harrison1>The distinction is made clear in {{cite book |author=Edward Robert Harrison |year= 2000 |title=Cosmology: The Science of the Universe |publisher=Cambridge University Press |edition=2 |url=http://books.google.com/books?id=-8PJbcA2lLoC&pg=PA315#PPA306,M1 |pages=306''ff'' |isbn=052166148X}}</ref> |
|||
A more complete treatment of the Doppler redshift requires considering relativistic effects associated with motion of sources close to the speed of light. A complete derivation of the effect can be found in the article on the [[relativistic Doppler effect]]. In brief, objects moving close to the speed of light will experience deviations from the above formula due to the [[time dilation]] of [[special relativity]] which can be corrected for by introducing the [[Lorentz factor]] {{math|''γ''}} into the classical Doppler formula as follows (for motion solely in the line of sight): |
|||
In a universe in which space expands at an accelerating rate, the distance between remote galaxies will eventually increase at more than 3{{e|8}} m/s, but this does not imply that the galaxies themselves exceed the speed of light. |
|||
:<math>1 + z = \left(1 + \frac{v}{c}\right) \gamma.</math> |
|||
====The red shift in cosmological models==== |
|||
This phenomenon was first observed in a 1938 experiment performed by Herbert E. Ives and G.R. Stilwell, called the [[Ives–Stilwell experiment]].<ref>{{cite journal | last1 = Ives | first1 = H. | last2 = Stilwell | first2 = G. | year = 1938 | title = An Experimental study of the rate of a moving atomic clock | journal = Journal of the Optical Society of America | volume = 28 | issue = 7| pages = 215–226 | doi=10.1364/josa.28.000215 | bibcode = 1938JOSA...28..215I}}</ref> |
|||
The observational consequences of this effect can be derived using [[Friedmann-Robertson-Walker metric|the equations]] from [[general relativity]] that describe a [[cosmological principle|homogeneous and isotropic universe]]. |
|||
Since the Lorentz factor is dependent only on the [[magnitude (mathematics)|magnitude]] of the velocity, this causes the redshift associated with the relativistic correction to be independent of the orientation of the source movement. In contrast, the classical part of the formula is dependent on the [[scalar resolute|projection]] of the movement of the source into the [[Line-of-sight propagation|line-of-sight]] which yields different results for different orientations. If {{math|''θ''}} is the angle between the direction of relative motion and the direction of emission in the observer's frame<ref>{{cite book|last=Freund|first=Jurgen|title=Special Relativity for Beginners|date=2008|publisher=World Scientific|page=120|isbn=978-981-277-160-5}}</ref> (zero angle is directly away from the observer), the full form for the relativistic Doppler effect becomes: |
|||
To derive the redshift effect, use the [[geodesic equation]] for a light wave, which is |
|||
:<math> |
:<math>1+ z = \frac{1 + v \cos (\theta)/c}{\sqrt{1-v^2/c^2}}</math> |
||
and for motion solely in the line of sight ({{math|''θ'' {{=}} 0°}}), this equation reduces to: |
|||
where |
|||
:<math>1 + z = \sqrt{\frac{1+v/c}{1-v/c}}</math> |
|||
*<math>ds</math> is the Lorentzian [[line element]] |
|||
*<math>dt</math> is the time interval |
|||
*<math>dr</math> is the spatial interval |
|||
*<math>c</math> is the speed of light |
|||
*<math>a</math> is the time-dependent cosmic [[scale factor (Universe)|scale factor]] or [[Friedmann-Lemaître-Robertson-Walker metric|Robertson-Walker scale factor]] |
|||
*<math>k</math> is the [[curvature]] per unit area. |
|||
For the special case that the light is moving at [[right angle]] ({{math|''θ'' {{=}} 90°}}) to the direction of relative motion in the observer's frame,<ref>{{cite book|last=Ditchburn|first=R. |title=Light|date=1961|publisher=Dover|page=329|isbn=978-0-12-218101-6}}</ref> the relativistic redshift is known as the [[Relativistic Doppler effect|transverse redshift]], and a redshift: |
|||
For an observer observing the crest of a light wave at a position <math>r=0</math> and time <math>t=t_\mathrm{now}</math>, the crest of the light wave was emitted at a time <math>t=t_\mathrm{then}</math> in the past and a distant position <math>r=R</math>. Integrating over the path in both space and time that the light wave travels yields: |
|||
:<math>1 + z = \frac{1}{\sqrt{1-v^2/c^2}}</math> |
|||
:<math> |
|||
c \int_{t_\mathrm{then}}^{t_\mathrm{now}} \frac{dt}{a}\; = |
|||
\int_{R}^{0} \frac{dr}{\sqrt{1-kr^2}}\,. |
|||
</math> |
|||
In general, the wavelength of light is not the same for the two positions and times considered due to the changing properties of the metric. When the wave was emitted, it had a wavelength <math>\lambda_\mathrm{then}</math>. The next crest of the light wave was emitted at a time |
|||
:<math>t=t_\mathrm{then}+\lambda_\mathrm{then}/c\,.</math> |
|||
The observer sees the next crest of the observed light wave with a wavelength <math>\lambda_\mathrm{now}</math> to arrive at a time |
|||
:<math>t=t_\mathrm{now}+\lambda_\mathrm{now}/c\,.</math> |
|||
Since the subsequent crest is again emitted from <math>r=R</math> and is observed at <math>r=0</math>, the following equation can be written: |
|||
:<math> |
|||
c \int_{t_\mathrm{then}+\lambda_\mathrm{then}/c}^{t_\mathrm{now}+\lambda_\mathrm{now}/c} \frac{dt}{a}\; = |
|||
\int_{R}^{0} \frac{dr}{\sqrt{1-kr^2}}\,. |
|||
</math> |
|||
The right-hand side of the two integral equations above are identical which means |
|||
:<math> |
|||
c \int_{t_\mathrm{then}+\lambda_\mathrm{then}/c}^{t_\mathrm{now}+\lambda_\mathrm{now}/c} \frac{dt}{a}\; = |
|||
c \int_{t_\mathrm{then}}^{t_\mathrm{now}} \frac{dt}{a}\, |
|||
</math> |
|||
or, alternatively, |
|||
:<math> |
|||
\int_{t_\mathrm{now}}^{t_\mathrm{now}+\lambda_\mathrm{now}/c} \frac{dt}{a}\; = |
|||
\int_{t_\mathrm{then}}^{t_\mathrm{then}+\lambda_\mathrm{then}/c} \frac{dt}{a}\,. |
|||
</math> |
|||
For very small variations in time (over the period of one cycle of a light wave) the scale factor is essentially a constant (<math>a=a_\mathrm{now}</math> today and <math>a=a_\mathrm{then}</math> previously). This yields |
|||
is measured, even though the object is not moving away from the observer. Even when the source is moving towards the observer, if there is a transverse component to the motion then there is some speed at which the dilation just cancels the expected blueshift and at higher speed the approaching source will be redshifted.<ref> |
|||
:<math>\frac{t_\mathrm{now}+\lambda_\mathrm{now}/c}{a_\mathrm{now}}-\frac{t_\mathrm{now}}{a_\mathrm{now}}\; = \frac{t_\mathrm{then}+\lambda_\mathrm{then}/c}{a_\mathrm{then}}-\frac{t_\mathrm{then}}{a_\mathrm{then}} |
|||
See "[http://www.physics.uq.edu.au/people/ross/phys2100/doppler.htm Photons, Relativity, Doppler shift] {{Webarchive|url=https://web.archive.org/web/20060827063802/http://www.physics.uq.edu.au/people/ross/phys2100/doppler.htm |date=2006-08-27 }} " at the University of Queensland |
|||
</math> |
|||
</ref> |
|||
===Cosmic expansion=== |
|||
which can be rewritten as |
|||
{{Main|Expansion of the universe}} |
|||
In the earlier part of the twentieth century, Slipher, Wirtz and others made the first measurements of the redshifts and blueshifts of galaxies beyond the [[Milky Way]]. They initially interpreted these redshifts and blueshifts as being due to random motions, but later Lemaître (1927) and Hubble (1929), using previous data, discovered a roughly linear correlation between the increasing redshifts of, and distances to, galaxies. Lemaître realized that these observations could be explained by a mechanism of producing redshifts seen in Friedmann's solutions to [[Einstein's equations]] of [[general relativity]]. The correlation between redshifts and distances arises in all expanding models.<ref name=Eddington/> |
|||
This [[cosmological redshift]] is commonly attributed to stretching of the wavelengths of photons propagating through the expanding space. This interpretation can be misleading, however; expanding space is only a choice of [[coordinate conditions|coordinates]] and thus cannot have physical consequences. The cosmological redshift is more naturally interpreted as a Doppler shift arising due to the recession of distant objects.<ref name="Hogg">{{cite journal |author=Bunn |first1=E. F. |last2=Hogg |first2=D. W. |year=2009 |title=The kinematic origin of the cosmological redshift |journal=American Journal of Physics |volume=77 |issue=8 |pages=688–694 |arxiv=0808.1081 |bibcode=2009AmJPh..77..688B |doi=10.1119/1.3129103 |s2cid=1365918}}</ref> |
|||
:<math>\frac{\lambda_\mathrm{now}}{\lambda_\mathrm{then}}=\frac{a_\mathrm{now}}{a_\mathrm{then}}\,.</math> |
|||
The observational consequences of this effect can be derived using [[Friedmann–Lemaître–Robertson–Walker metric|the equations]] from [[general relativity]] that describe a [[cosmological principle|homogeneous and isotropic universe]]. The cosmological redshift can thus be written as a function of {{math|''a''}}, the time-dependent cosmic [[Scale factor (cosmology)|scale factor]]: |
|||
Using the definition of redshift provided [[#Measurement, characterization, and interpretation|above]], the equation |
|||
:<math>1+z = \frac{a_\mathrm{now}}{a_\mathrm{then}}</math> |
:<math>1+z = \frac{a_\mathrm{now}}{a_\mathrm{then}}</math> |
||
In an expanding universe such as the one we inhabit, the scale factor is [[monotonic function|monotonically increasing]] as time passes, thus, {{math|''z''}} is positive and distant galaxies appear redshifted. |
|||
Using a model of the expansion of the universe, redshift can be related to the age of an observed object, the so-called ''[[cosmic time]]–redshift relation''. Denote a density ratio as {{math|Ω<sub>0</sub>}}: |
|||
---- |
|||
:<math>\Omega_0 = \frac {\rho}{ \rho_\text{crit}} \ , </math> |
|||
Using a model of the expansion of the universe, redshift can be related to the age of an observed object, the so-called ''[[cosmic time]]–redshift relation''. Denote a density ratio as Ω<sub>0</sub>: |
|||
with {{math|''ρ''<sub>crit</sub>}} the critical density demarcating a universe that eventually crunches from one that simply expands. This density is about three hydrogen atoms per cubic meter of space.<ref Name=Weinberg>{{cite book |first=Steven | last=Weinberg |edition=2nd |title=The First Three Minutes: A Modern View of the Origin of the Universe | page=34 |isbn=9780-465-02437-7 |date=1993 |publisher=Basic Books|title-link=The First Three Minutes: A Modern View of the Origin of the Universe }}</ref> At large redshifts, {{math| ''1 + z'' > Ω<sub>0</sub><sup>−1</sup>}}, one finds: |
|||
[[File:Two redshifts.JPG|thumb |350px |Two different sources of redshift: ''Top, Doppler shift'': the star moving to the left emits light that is blue shifted in the direction of the receiving antenna that the star approaches, and red shifted in the direction of the receiving antenna that the star is leaving. ''Center and bottom panels: cosmological expansion'': The distance between the emitting star and both antennas increases while the light is propagating, increasing the wavelength of the light seen by both antennas. Each panel shows the propagation of light over two periods: in the center panel at time of emission the wavelength is short, and in the bottom panel at time of reception the wavelength has stretched with the expansion of space. Patterned after Koupelis & Kuhn.<ref name=Kuhn>{{cite book |title=In Quest of the Universe |author=Theo Koupelis, Karl F. Kuhn |edition=5 |url=http://books.google.com/books?id=6rTttN4ZdyoC&pg=PA556#PPA557,M1 |page=557 |publisher=Jones & Bartlett Publishers |year=2007 |isbn=0763743879}}</ref> The reader is cautioned that too literal an interpretation of this figure can be misleading.<ref name=Lewis>"It is perfectly valid to interpret the equations of relativity in terms of an expanding space. The mistake is to push analogies too far and imbue space with physical properties that are not consistent with the equations of relativity." {{cite journal |title=Cosmological Radar Ranging in an Expanding Universe |url=http://arxiv.org/abs/0805.2197v1 |journal=Monthly Notices of the Royal Astronomical Society |author=Geraint F. Lewis ''et al.'' |year=2008 |pages=960–964 |volume=388 |doi=10.1111/j.1365-2966.2008.13477.x }}</ref> In particular, the Doppler shift panel is seen from a single inertial frame, that of the two antennas. The cosmological expansion panels are a concatenation of local inertial frames spanning the space between the various locally stationary objects.<ref name=Chodorowski>{{cite journal |author=Michal Chodorowski |title=Is space really expanding? A counterexample |year=2007 |url=http://arxiv.org/abs/astro-ph/0601171v2 |journal=Concepts Phys |volume=4 |pages=17–34}}</ref>]] |
|||
:<math> |
:<math> t(z) \approx \frac {2}{3 H_0 {\Omega_0}^{1/2} } z^{-3/2}\ , </math> |
||
where {{math|''H''<sub>0</sub>}} is the present-day [[Hubble constant]], and {{math|''z''}} is the redshift.<ref name="Bergström">{{cite book |title=Cosmology and Particle Astrophysics |url=https://books.google.com/books?id=CQYu_sutWAoC&pg=PA77 |page=77, Eq.4.79 |isbn=978-3-540-32924-4 |publisher=Springer |edition=2nd|date=2006|first1 = Lars |last1=Bergström|first2 = Ariel |last2=Goobar|author-link1=Lars Bergström (physicist) |author-link2=Ariel Goobar }}</ref><ref name = Longair>{{cite book |title=Galaxy Formation |first=M. S. |last=Longair |url=https://books.google.com/books?id=2ARuLT-tk5EC&pg=PA161 |page=161 |isbn=978-3-540-63785-1 |publisher=Springer |date=1998}}</ref> |
|||
with ρ<sub>crit</sub> the critical density demarcating a universe that eventually crunches from one that simply expands. This density is about three hydrogen atoms per thousand liters of space.<ref Name=Weinberg>{{cite book |author=Steven Weinberg |edition=2 |title=The First Three Minutes: A Modern View of the Origin of the Universe |url=http://books.google.com/books?id=oxfoF_gasvsC&pg=PA34 |page=34 |isbn=0465024378 |year=1993 |publisher=Basic Books}}</ref> At large redshifts one finds: |
|||
There are several websites for calculating various times and distances from redshift, as the precise calculations require numerical integrals for most values of the parameters.<ref name="UCLA-2015">{{cite web |author=Staff |title=UCLA Cosmological Calculator |url=http://www.astro.ucla.edu/~wright/ACC.html |date=2015 |work=[[UCLA]] |access-date=6 August 2022 }} Light travel distance was calculated from redshift value using the UCLA Cosmological Calculator, with parameters values as of 2015: H<sub>0</sub>=67.74 and Omega<sub>M</sub>=0.3089 (see Table/Planck2015 at "[[Lambda-CDM model#Parameters]]" )</ref><ref name="UCLA-2018">{{cite web |author=Staff |title=UCLA Cosmological Calculator |url=http://www.astro.ucla.edu/~wright/ACC.html |date=2018 |work=[[UCLA]] |access-date=6 August 2022 }} Light travel distance was calculated from redshift value using the UCLA Cosmological Calculator, with parameters values as of 2018: H<sub>0</sub>=67.4 and Omega<sub>M</sub>=0.315 (see Table/Planck2018 at "[[Lambda-CDM model#Parameters]]" )</ref><ref name="ICRAR-2022">{{cite web |author=Staff |title=ICRAR Cosmology Calculator |url=https://cosmocalc.icrar.org/ |date=2022 |work=[[International Centre for Radio Astronomy Research]] |access-date=6 August 2022 }} ICRAR Cosmology Calculator - Set H<sub>0</sub>=67.4 and Omega<sub>M</sub>=0.315 (see Table/Planck2018 at "[[Lambda-CDM model#Parameters]]")</ref><ref name="KEMP-2022">{{cite web |last=Kempner |first=Joshua |title=KEMPNER Cosmology Calculator |url=https://www.kempner.net/cosmic.php |date=2022 |work=Kempner.net |access-date=6 August 2022 }} KEMP Cosmology Calculator - Set H<sub>0</sub>=67.4, Omega<sub>M</sub>=0.315, and Omega<sub>Λ</sub>=0.6847 (see Table/Planck2018 at "[[Lambda-CDM model#Parameters]]")</ref> |
|||
:<math> t(z) = \frac {2}{3 H_0 {\Omega_0}^{1/2} (1+ z )^{3/2}} \ , </math> |
|||
====Distinguishing between cosmological and local effects==== |
|||
where ''H<sub>0</sub>'' = present-day [[Hubble constant]], and ''z'' = redshift.<ref name="Bergström">{{cite book |author=[[Lars Bergström (physicist)|Lars Bergström]], [[Ariel Goobar]] |title=Cosmology and Particle Astrophysics |url=http://books.google.com/books?id=CQYu_sutWAoC&pg=PA77 |page=77, Eq.4.79 |isbn=3540329242 |publisher=Springer |edition=2|year=2006}}</ref><ref name = Longair>{{cite book |title=Galaxy Formation |author=M.S. Longair |url=http://books.google.com/books?id=2ARuLT-tk5EC&pg=PA161 |page=161 |isbn=3540637850 |publisher=Springer |year=1998}}</ref><ref name=Sanchez>{{cite book |editor=Norma Sanchez |page=223 |title=Current Topics in Astrofundamental Physics |url=http://books.google.com/books?id=GOJoas-Dg7QC&pg=PA223 |isbn=0792368568 |year=2001 |publisher=Springer |
|||
For cosmological redshifts of {{math|''z'' < 0.01}} additional Doppler redshifts and blueshifts due to the [[peculiar velocity|peculiar motions]] of the galaxies relative to one another cause a wide [[variance|scatter]] from the standard [[Hubble Law]].<ref>Measurements of the peculiar velocities out to 5 [[parsec|Mpc]] using the [[Hubble Space Telescope]] were reported in 2003 by {{cite journal |
|||
|chapter=The High Redshift Radio Universe |author=Yu N Parijskij}}</ref> |
|||
| title=Local galaxy flows within 5 Mpc |
|||
| last1=Karachentsev | first1=I. D. | last2=Makarov | first2=D. I. |
|||
| last3=Sharina | first3=M. E. | last4=Dolphin | first4=A. E. |
|||
| last5=Grebel | first5=E. K. | last6=Geisler | first6=D. |
|||
| last7=Guhathakurta | first7=P. | last8=Hodge | first8=P. W. |
|||
| last9=Karachentseva | first9=V. E. | last10=Sarajedini | first10=A. |
|||
| last11=Seitzer | first11=P. | display-authors=1 |
|||
| journal=[[Astronomy and Astrophysics]] |
|||
| volume=398 | issue=2 | pages=479–491 | year=2003 |
|||
| doi=10.1051/0004-6361:20021566 | bibcode=2003A&A...398..479K |
|||
| s2cid=26822121 | arxiv=astro-ph/0211011 |
|||
}}</ref> The resulting situation can be illustrated by the [[Expansion of the universe#Other conceptual models of expansion|Expanding Rubber Sheet Universe]], a common cosmological analogy used to describe the expansion of the universe. If two objects are represented by ball bearings and spacetime by a stretching rubber sheet, the Doppler effect is caused by rolling the balls across the sheet to create peculiar motion. The cosmological redshift occurs when the ball bearings are stuck to the sheet and the sheet is stretched.<ref name=Kuhn>{{cite book |title=In Quest of the Universe | first1=Theo | last1=Koupelis | first2=Karl F. | last2=Kuhn |edition=5th |url=https://archive.org/details/inquestofunivers00koup |url-access=registration |page=[https://archive.org/details/inquestofunivers00koup/page/557 557] |publisher=Jones & Bartlett Publishers |date=2007 |isbn=978-0-7637-4387-1}}</ref><ref name=Lewis>{{cite journal | quote=It is perfectly valid to interpret the equations of relativity in terms of an expanding space. The mistake is to push analogies too far and imbue space with physical properties that are not consistent with the equations of relativity. |title=Cosmological Radar Ranging in an Expanding Universe |arxiv=0805.2197 |journal=[[Monthly Notices of the Royal Astronomical Society]] | first1=Geraint F. | last1=Lewis |date=2008 |pages=960–964 |issue=3 |volume=388 |doi=10.1111/j.1365-2966.2008.13477.x |bibcode=2008MNRAS.388..960L|display-authors=4|last2=Francis |first2=Matthew J. |last3=Barnes |first3=Luke A. |last4=Kwan |first4=Juliana |last5=James |first5=J. Berian |doi-access=free |s2cid=15147382 }}</ref><ref name=Chodorowski>{{Cite journal | first=Michal | last=Chodorowski |title=Is space really expanding? A counterexample |date=2007 |arxiv=astro-ph/0601171 |journal=Concepts Phys |volume=4 |issue=1 |pages=17–34|bibcode = 2007ONCP....4...15C |doi = 10.2478/v10005-007-0002-2 |s2cid=15931627 }}</ref> |
|||
The redshifts of galaxies include both a component related to [[recessional velocity]] from expansion of the universe, and a component related to [[peculiar motion]] (Doppler shift).<ref>{{cite journal |
|||
====Cosmological and Doppler red shifts==== |
|||
| title=A comparison between the Doppler and cosmological redshifts |
|||
| last=Bedran | first=M. L. | year=2002 |
|||
| journal=American Journal of Physics |
|||
| volume=70 | issue=4 | pages=406–408 |
|||
| doi=10.1119/1.1446856 | bibcode=2002AmJPh..70..406B |
|||
| url=http://www.df.uba.ar/users/sgil/physics_paper_doc/papers_phys/cosmo/doppler_redshift.pdf |
|||
| access-date=2023-03-16 |
|||
}}</ref> The redshift due to expansion of the universe depends upon the recessional velocity in a fashion determined by the cosmological model chosen to describe the expansion of the universe, which is very different from how Doppler redshift depends upon local velocity.<ref name="Harrison2">{{cite journal |last=Harrison |first=Edward |date=1992 |title=The redshift-distance and velocity-distance laws |journal=Astrophysical Journal, Part 1 |volume=403 |pages=28–31 |bibcode=1993ApJ...403...28H |doi=10.1086/172179 |doi-access=free}}. A pdf file can be found here [http://articles.adsabs.harvard.edu/cgi-bin/nph-iarticle_query?1993ApJ...403...28H&data_type=PDF_HIGH&whole_paper=YES&type=PRINTER&filetype=.pdf].</ref> Describing the cosmological expansion origin of redshift, cosmologist [[Edward Robert Harrison]] said, "Light leaves a galaxy, which is stationary in its local region of space, and is eventually received by observers who are stationary in their own local region of space. Between the galaxy and the observer, light travels through vast regions of expanding space. As a result, all wavelengths of the light are stretched by the expansion of space. It is as simple as that..."<ref>{{Harvnb|Harrison|2000|p=302}}.</ref> [[Steven Weinberg]] clarified, "The increase of wavelength from emission to absorption of light does not depend on the rate of change of {{math|''a''(''t'')}} [the [[Scale factor (cosmology)|scale factor]]] at the times of emission or absorption, but on the increase of {{math|''a''(''t'')}} in the whole period from emission to absorption."<ref name=Weinberg_Cosmology>{{cite book |url=https://books.google.com/books?id=48C-ym2EmZkC&pg=PA11 |first=Steven | last=Weinberg |title=Cosmology |publisher=Oxford University Press |page=11 |date=2008 |isbn=978-0-19-852682-7}}</ref> |
|||
If the universe were contracting instead of expanding, we would see distant galaxies blueshifted by an amount proportional to their distance instead of redshifted.<ref>This is only true in a universe where there are no [[peculiar velocity|peculiar velocities]]. Otherwise, redshifts combine as |
|||
For cosmological redshifts of z < 0.01 the effects of [[spacetime]] expansion are minimal and cosmological redshifts can be dominated by additional Doppler redshifts and blue shifts caused by the peculiar motions of the galaxies relative to one another.<ref>Measurements of the peculiar velocities out to 5 [[parsec|Mpc]] using the [[Hubble Space Telescope]] were reported in 2003 by Karachentsev et al. ''Local galaxy flows within 5 Mpc''. 02/2003 ''[[Astronomy and Astrophysics]]'', '''398''', 479-491.[http://arxiv.org/abs/astro-ph/0211011]</ref> The difference between physical velocity and space expansion can be illustrated by the [[Metric expansion of space#Other models of expansion|Expanding Rubber Sheet Universe]], a common cosmological analogy used to describe the expansion of space. If two objects are represented by ball bearings and spacetime by a stretching rubber sheet, the Doppler effect is caused by rolling the balls across the sheet to create peculiar motion. The cosmological redshift occurs when the ball bearings are stuck to the sheet and the sheet is stretched. |
|||
The redshifts of galaxies include both a component related to recessional velocity from expansion of the universe, and a component related to [[peculiar motion]] (Doppler shift). The redshift due to expansion of the universe depends upon the recessional velocity in a fashion determined by the cosmological model chosen to describe the expansion of the universe, which is very different from how Doppler redshift depends upon local velocity. Harrison provides a summary of this and related distinctions.<ref name=Harrison2>{{cite journal |title=The redshift-distance and velocity-distance laws |author=Edward Harrison |year=1992 |url=http://adsabs.harvard.edu/abs/1993ApJ...403...28H |journal=Astrophysical Journal, Part 1 |pages=28–31 |volume=403 |doi=10.1086/172179}}. A pdf file can be found [http://articles.adsabs.harvard.edu/cgi-bin/nph-iarticle_query?1993ApJ...403...28H&data_type=PDF_HIGH&whole_paper=YES&type=PRINTER&filetype=.pdf here].</ref> Describing the cosmological expansion origin of redshift, Harrison says: “Light leaves a galaxy, which is stationary in its local region of space, and is eventually received by observers who are stationary in their own local region of space. Between the galaxy and the observer, light travels through vast regions of expanding space. As a result, all wavelengths of the light are stretched by the expansion of space. It is as simple as that.” See Harrison, p. 315.<ref name=Harrison1/> “The increase of wavelength from emission to absorption of light does not depend on the rate of change of ''a(t)'' [here ''a(t)'' is the [[Friedmann-Lemaître-Robertson-Walker metric|Robertson-Walker scale factor]]] at the times of emission or absorption, but on the increase of ''a(t)'' in the whole period from emission to absorption.”<ref name=Weinberg_Cosmology>{{cite book |url=http://books.google.com/books?id=48C-ym2EmZkC&pg=PA11 |author=Steven Weinberg |title=Cosmology |publisher=Oxford University Press |page=11 |year=2008 |isbn=9780198526827}}</ref> |
|||
Nonetheless, popular literature often uses the expression "Doppler redshift" instead of "cosmological redshift" to describe the redshift of galaxies dominated by the expansion of spacetime, despite the fact that the redshift is not found using the relativistic Doppler equation.<ref>Odenwald & Fienberg 1993</ref> In particular, Doppler redshift is bound by [[special relativity]]; thus ''v > c'' is impossible while, in contrast, ''v > c'' is possible for cosmological redshift because the space which separates the objects (for example, a quasar from the Earth) can expand faster than the speed of light.<ref>Speed faster than light is allowed because the [[metric expansion of space|expansion]] of the [[spacetime]] [[Metric (mathematics)|metric]] is described by [[general relativity]] in terms of sequences of only locally valid inertial frames as opposed to a global [[Minkowski metric]]. Expansion faster than light is an integrated effect over many local inertial frames and is allowed because no single inertial frame is involved. The speed-of-light limitation applies only locally. See {{cite journal |author=Michal Chodorowski |title=Is space really expanding? A counterexample |year=2007 |url=http://arxiv.org/abs/astro-ph/0601171v2 |journal=Concepts Phys |volume=4 |pages=17–34}} </ref> More mathematically, the viewpoint that "distant galaxies are receding" and the viewpoint that "the space between galaxies is expanding" are related by changing [[coordinate system]]s. Expressing this precisely requires working with the mathematics of the [[Friedmann-Robertson-Walker metric]].<ref>M. Weiss, What Causes the Hubble Redshift?, entry in the Physics [[FAQ]] (1994), available via [[John Baez]]'s [http://math.ucr.edu/home/baez/physics/Relativity/GR/hubble.html website]</ref> |
|||
====Blue shift in a contracting universe==== |
|||
If the universe were contracting instead of expanding, we would see distant galaxies blue shifted by an amount proportional to their distance instead of redshifted.<ref>This is only true in a universe where there are no [[peculiar velocity|peculiar velocities]]. Otherwise, redshifts combine as |
|||
:<math>1+z=(1+z_{\mathrm{Doppler}})(1+z_{\mathrm{expansion}})</math> |
:<math>1+z=(1+z_{\mathrm{Doppler}})(1+z_{\mathrm{expansion}})</math> |
||
which yields solutions where certain objects that "recede" are |
which yields solutions where certain objects that "recede" are blueshifted and other objects that "approach" are redshifted. For more on this bizarre result see: {{cite journal |
||
| last1=Davis | first1=T. M. | last2=Lineweaver | first2=C. H. | last3=Webb | first3=J. K. |
|||
| title=Solutions to the tethered galaxy problem in an expanding universe and the observation of receding blueshifted objects |
|||
| journal=American Journal of Physics |
|||
| volume=71 | issue=4 | pages=358–364 |
|||
| date=April 2003 | doi=10.1119/1.1528916 |
|||
| arxiv=astro-ph/0104349 | bibcode=2003AmJPh..71..358D | s2cid=3219383 }}</ref> |
|||
===Gravitational redshift=== |
===Gravitational redshift=== |
||
{{ |
{{Main|Gravitational redshift}} |
||
In the theory of [[general relativity]], there is time dilation within a gravitational well. This is known as the [[gravitational redshift]] or ''Einstein Shift''.<ref> |
In the theory of [[general relativity]], there is time dilation within a gravitational well. This is known as the [[gravitational redshift]] or ''Einstein Shift''.<ref>{{cite journal | last=Chant | first=C. A. | bibcode = 1930JRASC..24..390C | title = Notes and Queries (Telescopes and Observatory Equipment – The Einstein Shift of Solar Lines) | date = 1930 | journal = [[Journal of the Royal Astronomical Society of Canada]] | volume = 24 | page = 390 }}</ref> The theoretical derivation of this effect follows from the [[Schwarzschild solution]] of the [[Einstein field equations|Einstein equations]] which yields the following formula for redshift associated with a photon traveling in the [[gravitational field]] of an [[Electric charge|uncharged]], [[rotation|nonrotating]], [[spherical symmetry|spherically symmetric]] mass: |
||
:<math>1+z=\frac{1}{\sqrt{1- |
:<math>1+z=\frac{1}{\sqrt{1-\frac{2GM}{rc^2}}},</math> |
||
where |
where |
||
* |
* {{math|''G''}} is the [[gravitational constant]], |
||
* |
* {{math|''M''}} is the [[mass]] of the object creating the gravitational field, |
||
* |
* {{math|''r''}} is the radial coordinate of the source (which is analogous to the classical distance from the center of the object, but is actually a [[Schwarzschild coordinates|Schwarzschild coordinate]]), and |
||
* |
* {{math|''c''}} is the [[speed of light]]. |
||
This gravitational redshift result can be derived from the assumptions of [[special relativity]] and the [[equivalence principle]]; the full theory of general relativity is not required.<ref>{{cite journal | last = Einstein | first = A | |
This gravitational redshift result can be derived from the assumptions of [[special relativity]] and the [[equivalence principle]]; the full theory of general relativity is not required.<ref>{{cite journal | last = Einstein | first = A. | author-link = Albert Einstein | date = 1907 | title = Über das Relativitätsprinzip und die aus demselben gezogenen Folgerungen | journal = Jahrbuch der Radioaktivität und Elektronik | volume = 4 | pages = 411–462 | bibcode=1908JRE.....4..411E}} See p. 458 ''The influence of a gravitational field on clocks''</ref> |
||
The effect is very small but measurable on Earth using the [[Mössbauer effect]] and was first observed in the [[ |
The effect is very small but measurable on Earth using the [[Mössbauer effect]] and was first observed in the [[Pound–Rebka experiment]].<ref>{{cite journal | doi = 10.1103/PhysRevLett.4.337 | title = Apparent Weight of Photons | date = 1960 | last1 = Pound | first1 = R. | last2 = Rebka | first2 = G. | journal = Physical Review Letters | volume = 4 | issue = 7 | pages = 337–341 | bibcode=1960PhRvL...4..337P| doi-access = free }}. This paper was the first measurement.</ref> However, it is significant near a [[black hole]], and as an object approaches the [[event horizon]] the red shift becomes infinite. It is also the dominant cause of large angular-scale temperature fluctuations in the [[cosmic microwave background]] radiation (see [[Sachs–Wolfe effect]]).<ref>{{cite journal | last1=Sachs | first1=R. K. | author-link=Rainer K. Sachs | last2=Wolfe | first2=A. M. | author-link2=Arthur M. Wolfe | date=1967 | title=Perturbations of a cosmological model and angular variations of the cosmic microwave background | journal=Astrophysical Journal | volume=147 | issue=73 | doi=10.1086/148982 | page=73 | bibcode=1967ApJ...147...73S }}</ref> |
||
==Observations in astronomy== |
==Observations in astronomy== |
||
[[File:Look-back time by redshift.png|thumb|The [[lookback time]] of extragalactic observations by their redshift up to z=20.<ref name="Pilipenko">S.V. Pilipenko (2013-2021) [https://arxiv.org/abs/1303.5961 "Paper-and-pencil cosmological calculator"] arxiv:1303.5961, including [https://code.google.com/archive/p/cosmonom/downloads Fortran-90 code] upon which the citing charts and formulae are based.</ref> There are websites for calculating many such physical measures from redshift.<ref name="UCLA-2015"/><ref name="UCLA-2018"/><ref name="ICRAR-2022"/><ref name="KEMP-2022"/>]] |
|||
The redshift observed in astronomy can be measured because the [[emission spectrum|emission]] and [[absorption spectrum|absorption]] spectra for [[atom]]s are distinctive and well known, calibrated from [[spectroscopy|spectroscopic experiments]] in [[laboratory|laboratories]] on Earth. When the redshift of various absorption and emission lines from a single astronomical object is measured, ''z'' is found to be remarkably constant. Although distant objects may be slightly blurred and lines broadened, it is by no more than can be explained by [[thermal motion|thermal]] or [[motion (physics)|mechanical motion]] of the source. For these reasons and others, the consensus among astronomers is that the redshifts they observe are due to some combination of the three established forms of Doppler-like redshifts. Alternative hypotheses and explanations for redshift such as [[tired light]] are not generally considered plausible.<ref name=reboul> When cosmological redshifts were first discovered, [[Fritz Zwicky]] proposed an effect known as tired light. While usually considered for historical interests, it is sometimes, along with [[intrinsic redshift]] suggestions, utilized by [[nonstandard cosmologies]]. In 1981, H. J. Reboul summarised many [http://adsabs.harvard.edu/cgi-bin/nph-bib_query?bibcode=1981A%26AS...45..129R&db_key=AST&data_type=HTML&format=&high=42ca922c9c23806 alternative redshift mechanisms] that had been discussed in the literature since the 1930s. In 2001, [[Geoffrey Burbidge]] remarked in a [http://adsabs.harvard.edu/cgi-bin/nph-bib_query?bibcode=2001PASP..113..899B&db_key=AST&data_type=HTML review] that the wider astronomical community has marginalized such discussions since the 1960s. Burbidge and [[Halton Arp]], while investigating the mystery of [[Quasar#History of quasar observation|the nature of quasars]], tried to develop alternative redshift mechanisms, and very few of their fellow scientists acknowledged let alone accepted their work. Moreover, Goldhaber ''et al.'' 2001; "Timescale Stretch Parameterization of Type Ia Supernova B-Band Lightcurves", ApJ, 558:359-386, 2001 September 1 pointed out that alternative theories are unable to account for timescale stretch observed in [[type Ia supernovae]]</ref> |
|||
The redshift observed in astronomy can be measured because the [[emission spectrum|emission]] and [[Absorption spectroscopy|absorption]] spectra for [[atom]]s are distinctive and well known, calibrated from [[spectroscopic]] experiments in [[laboratories]] on Earth. When the redshift of various absorption and emission lines from a single astronomical object is measured, {{math|''z''}} is found to be remarkably constant. Although distant objects may be slightly blurred and lines broadened, it is by no more than can be explained by [[Kinetic theory of gases|thermal]] or mechanical [[motion]] of the source. For these reasons and others, the consensus among astronomers is that the redshifts they observe are due to some combination of the three established forms of Doppler-like redshifts. Alternative hypotheses and explanations for redshift such as [[tired light]] are not generally considered plausible.<ref name=reboul>When cosmological redshifts were first discovered, [[Fritz Zwicky]] proposed an effect known as tired light. While usually considered for historical interests, it is sometimes, along with [[intrinsic redshift]] suggestions, utilized by [[nonstandard cosmologies]]. In 1981, H. J. Reboul summarised many [http://adsabs.harvard.edu/cgi-bin/nph-bib_query?bibcode=1981A%26AS...45..129R&db_key=AST&data_type=HTML&format=&high=42ca922c9c23806 alternative redshift mechanisms] that had been discussed in the literature since the 1930s. In 2001, [[Geoffrey Burbidge]] remarked in a [http://adsabs.harvard.edu/cgi-bin/nph-bib_query?bibcode=2001PASP..113..899B&db_key=AST&data_type=HTML review] that the wider astronomical community has marginalized such discussions since the 1960s. Burbidge and [[Halton Arp]], while investigating the mystery of [[Quasar#History of quasar observation|the nature of quasars]], tried to develop alternative redshift mechanisms, and very few of their fellow scientists acknowledged let alone accepted their work. Moreover, {{cite journal | title=Timescale Stretch Parameterization of Type Ia Supernova B-Band Lightcurves | first1=G. | last1=Goldhaber | first2=D. E. | last2=Groom | first3=A. | last3=Kim | first4=G. | last4=Aldering | first5=P. | last5=Astier | first6=A. | last6=Conley | first7=S. E. | last7=Deustua | first8=R. | last8=Ellis | first9=S. | last9=Fabbro | first10=A. S. | last10=Fruchter | first11=A. | last11=Goobar | first12=I. | last12=Hook | first13=M. | last13=Irwin | first14=M. | last14=Kim | first15=R. A. | last15=Knop | first16=C. | last16=Lidman | first17=R. | last17=McMahon | first18=P. E. | last18=Nugent | first19=R. | last19=Pain | first20=N. | last20=Panagia | first21=C. R. | last21=Pennypacker | first22=S. | last22=Perlmutter | first23=P. | last23=Ruiz-Lapuente | first24=B. | last24=Schaefe | first25=N. A. | last25=Walton | first26=T. | last26=York | display-authors=1 | year=2001 | journal=Astrophysical Journal | volume=558 | issue=1 | pages=359–386 | doi=10.1086/322460 | arxiv=astro-ph/0104382 | bibcode=2001ApJ...558..359G | s2cid=17237531| doi-access=free }} pointed out that alternative theories are unable to account for timescale stretch observed in [[type Ia supernovae]]</ref> |
|||
Spectroscopy, as a measurement, is considerably more difficult than simple [[photometry (astronomy)|photometry]], which measures the [[brightness]] of astronomical objects through certain [[Optical filter|filters]].<ref>For a review of the subject of photometry, consider: {{cite book | last=Budding | first=E. | title=Introduction to Astronomical Photometry | publisher=Cambridge University Press | date=September 24, 1993 | isbn=0-521-41867-4 }}</ref> When photometric data is all that is available (for example, the [[Hubble Deep Field]] and the [[Hubble Ultra Deep Field]]), astronomers rely on a technique for measuring [[photometric redshift]]s.<ref>The technique was first described by: {{cite conference | last=Baum | first=W. A. | year=1962 | editor-first=G. C. | editor-last=McVittie | title=Problems of extra-galactic research | page=390 | conference=IAU Symposium No. 15 }}</ref> Due to the broad wavelength ranges in photometric filters and the necessary assumptions about the nature of the spectrum at the light-source, [[observational error|errors]] for these sorts of measurements can range up to {{math|δ''z'' {{=}} 0.5}}, and are much less reliable than spectroscopic determinations.<ref>{{cite journal | last1=Bolzonella | first1=M. | last2=Miralles | first2=J.-M. | last3=Pelló | first3=R. | title=Photometric redshifts based on standard SED fitting procedures | journal=Astronomy and Astrophysics | volume=363 | pages=476–492 | year=2000 | arxiv=astro-ph/0003380 | bibcode=2000A&A...363..476B }}</ref> |
|||
However, photometry does at least allow a qualitative characterization of a redshift. For example, if a Sun-like spectrum had a redshift of {{math|''z'' {{=}} 1}}, it would be brightest in the [[infrared]](1000nm) rather than at the blue-green(500nm) color associated with the peak of its [[Black body|blackbody]] spectrum, and the light intensity will be reduced in the filter by a factor of four, {{math|(1 + ''z''){{sup|2}}}}. Both the photon count rate and the photon energy are redshifted. (See [[K correction]] for more details on the photometric consequences of redshift.)<ref>A pedagogical overview of the K-correction by David Hogg and other members of the [[Sloan Digital Sky Survey|SDSS]] collaboration can be found at: {{cite arXiv | title=The K correction | last1=Hogg | first1=David W. | last2=Baldry | first2=Ivan K. | last3=Blanton | first3=Michael R. | last4=Eisenstein | first4=Daniel J. | display-authors=1 | date=October 2002 | eprint=astro-ph/0210394}}</ref> |
|||
===Local observations=== |
===Local observations=== |
||
In nearby objects (within our [[Milky Way]] galaxy) observed redshifts are almost always related to the [[Line-of-sight propagation|line-of-sight]] velocities associated with the objects being observed. Observations of such redshifts and blueshifts have enabled astronomers to measure [[velocity|velocities]] and parametrize the [[mass]]es of the [[orbit]]ing [[star]]s in [[spectroscopic binaries]], a method first employed in 1868 by British astronomer [[William Huggins]].<ref name=Huggins/> Similarly, small redshifts and blueshifts detected in the spectroscopic measurements of individual stars are one way astronomers have been able to [[Methods of detecting exoplanets#Radial velocity|diagnose and measure]] the presence and characteristics of [[Exoplanet|planetary systems]] around other stars and have even made very [[Rossiter–McLaughlin effect|detailed differential measurements]] of redshifts during [[Methods of detecting exoplanets|planetary transits]] to determine precise orbital parameters.<ref>The [[Exoplanet Tracker]] is the newest observing project to use this technique, able to track the redshift variations in multiple objects at once, as reported in {{cite journal |last1=Ge |first1=Jian |last2=Van Eyken |first2=Julian |last3=Mahadevan |first3=Suvrath |author3-link=Suvrath Mahadevan |last4=Dewitt |first4=Curtis |last5=Kane |first5=Stephen R. |last6=Cohen |first6=Roger |last7=Vanden Heuvel |first7=Andrew |last8=Fleming |first8=Scott W. |last9=Guo |first9=Pengcheng |last10=Henry |first10=Gregory W. |last11=Schneider |first11=Donald P. |last12=Ramsey |first12=Lawrence W. |last13=Wittenmyer |first13=Robert A. |last14=Endl |first14=Michael |last15=Cochran |first15=William D. |display-authors=4 |date=2006 |title=The First Extrasolar Planet Discovered with a New-Generation High-Throughput Doppler Instrument |journal=The Astrophysical Journal |volume=648 |issue=1 |pages=683–695 |arxiv=astro-ph/0605247 |bibcode=2006ApJ...648..683G |doi=10.1086/505699 |s2cid=13879217 |last16=Ford |first16=Eric B. |last17=Martin |first17=Eduardo L. |last18=Israelian |first18=Garik |last19=Valenti |first19=Jeff |last20=Montes |first20=David}}</ref> |
|||
Finely detailed measurements of redshifts are used in [[helioseismology]] to determine the precise movements of the [[photosphere]] of the [[Sun]].<ref>{{cite journal | doi = 10.1007/BF00243557 | title = Solar and stellar seismology | date = 1988 | last1 = Libbrecht | first1 = Keng | journal = Space Science Reviews | volume = 47 | issue = 3–4 |bibcode=1988SSRv...47..275L | pages=275–301| s2cid = 120897051 | url = https://authors.library.caltech.edu/104214/1/1988SSRv___47__275L.pdf }}</ref> Redshifts have also been used to make the first measurements of the [[rotation]] rates of [[planet]]s,<ref>In 1871 [[Hermann Carl Vogel]] measured the rotation rate of [[Venus]]. [[Vesto Slipher]] was working on such measurements when he turned his attention to spiral nebulae.</ref> velocities of [[interstellar cloud]]s,<ref>An early review by [[Jan Hendrik Oort|Oort, J. H.]] on the subject: {{cite journal | title=The formation of galaxies and the origin of the high-velocity hydrogen | journal=[[Astronomy and Astrophysics]] | volume=7 | page=381 | date=1970 | bibcode=1970A&A.....7..381O | last= Oort | first= J. H. }}</ref> the [[Galaxy rotation curve|rotation of galaxies]],<ref name="basicastronomy" /> and the [[dynamics (mechanics)|dynamics]] of [[Accretion disk|accretion]] onto [[neutron star]]s and [[black hole]]s which exhibit both Doppler and gravitational redshifts.<ref>{{cite journal| last=Asaoka | first=Ikuko | bibcode=1989PASJ...41..763A | title=X-ray spectra at infinity from a relativistic accretion disk around a Kerr black hole | journal=Publications of the Astronomical Society of Japan | volume=41 | issue=4 | date=1989 | pages=763–778 }}</ref> The [[temperature]]s of various emitting and absorbing objects can be obtained by measuring [[Doppler broadening]]—effectively redshifts and blueshifts over a single emission or absorption line.<ref>{{cite book | last1=Rybicki | first1=G. B. | first2=A. R. | last2=Lightman | title=Radiative Processes in Astrophysics | publisher=John Wiley & Sons | year=1979 | page=288 | isbn=0-471-82759-2 }}</ref> By measuring the broadening and shifts of the 21-centimeter [[hydrogen line]] in different directions, astronomers have been able to measure the [[Recessional velocity|recessional velocities]] of [[interstellar gas]], which in turn reveals the [[rotation curve]] of our Milky Way.<ref name=basicastronomy/> Similar measurements have been performed on other galaxies, such as [[Andromeda Galaxy|Andromeda]].<ref name=basicastronomy/> As a diagnostic tool, redshift measurements are one of the most important [[astronomical spectroscopy|spectroscopic measurements]] made in astronomy. |
|||
[[Image:LASCO C1a.png|thumb|200px|A picture of the solar corona taken with the [[LASCO]] C1 coronagraph. The picture is a color coded image of the doppler shift of the FeXIV 5308 Å line, caused by the coronal plasma velocity towards or away from the satellite.]] |
|||
In nearby objects (within our [[Milky Way]] galaxy) observed redshifts are almost always related to the [[Line-of-sight propagation|line-of-sight]] velocities associated with the objects being observed. Observations of such redshifts and blue shifts have enabled astronomers to measure [[velocity|velocities]] and parametrize the [[mass]]es of the [[orbit (celestial mechanics)|orbiting]] [[star]]s in [[Binary star#Spectroscopic binaries|spectroscopic binaries]], a method first employed in 1868 by British astronomer [[William Huggins]].<ref name=Huggins /> Similarly, small redshifts and blue shifts detected in the spectroscopic measurements of individual stars are one way astronomers have been able to [[Methods of detecting extrasolar planets#Radial velocity|diagnose and measure]] the presence and characteristics of [[extrasolar planet|planetary systems]] around other stars and have even made very [[Rossiter-McLaughlin effect|detailed differential measurements]] of redshifts during [[Methods_of_detecting_extrasolar_planets#Transit_method|planetary transits]] to determine precise orbital parameters.<ref>The [[Exoplanet Tracker]] is the newest observing project to use this technique, able to track the redshift variations in multiple objects at once, as reported in Ge, Jian et al. [http://adsabs.harvard.edu/cgi-bin/nph-data_query?bibcode=2006ApJ...648..683G&link_type=ARTICLE&db_key=AST The First Extrasolar Planet Discovered with a New-Generation High-Throughput Doppler Instrument], ''[[The Astrophysical Journal]]'', 2006 '''648''', Issue 1, pp. 683-695.[http://adsabs.harvard.edu/cgi-bin/nph-bib_query?bibcode=2006ApJ...648..683G&db_key=AST&data_type=HTML&format=&high=445165d66216614]</ref> Measurements of redshifts to fine detail are used in [[helioseismology]] to determine the precise movements of the [[photosphere]] of the [[Sun]].<ref>Libbrecht, Ken G., [http://articles.adsabs.harvard.edu/cgi-bin/nph-iarticle_query?1988SSRv...47..275L&data_type=PDF_HIGH&type=PRINTER&filetype=.pdf Solar and stellar seismology], ''Space Science Reviews'', 1988 '''37''' n. 3–4, 275–301.</ref> Redshifts have also been used to make the first measurements of the [[Rotation#Astronomy|rotation rates]] of [[planet]]s,<ref>In 1871 [[Hermann Carl Vogel]] measured the rotation rate of [[Venus]]. [[Vesto Slipher]] was working on such measurements when he turned his attention to spiral nebulae.</ref> velocities of [[interstellar cloud]]s,<ref>An early review by [[Jan Hendrik Oort|Oort, J. H.]] on the subject: [http://articles.adsabs.harvard.edu/cgi-bin/nph-iarticle_query?1970A%26A.....7..381O&data_type=PDF_HIGH&type=PRINTER&filetype=.pdf The formation of galaxies and the origin of the high-velocity hydrogen], [[Astronomy and Astrophysics]], '''7''', 381 (1970) [http://adsabs.harvard.edu/cgi-bin/nph-bib_query?bibcode=1970A%26A.....7..381O&db_key=AST&data_type=HTML&format=&high=4504216b9b04182].</ref> the [[galaxy rotation problem|rotation of galaxies]],<ref name=basicastronomy /> and the [[dynamics (mechanics)|dynamics]] of [[accretion theory|accretion]] onto [[neutron star]]s and [[black hole]]s which exhibit both Doppler and gravitational redshifts.<ref>Asaoka, Ikuko, [http://articles.adsabs.harvard.edu/cgi-bin/nph-iarticle_query?1989PASJ...41..763A&data_type=PDF_HIGH&type=PRINTER&filetype=.pdf X-ray spectra at infinity from a relativistic accretion disk around a Kerr black hole], ''Astronomical Society of Japan, Publications'' (ISSN 0004-6264), ''41'' no. 4, 1989, p. 763–778 [http://adsabs.harvard.edu/cgi-bin/bib_query?1989PASJ...41..763A]</ref> Additionally, the [[temperature]]s of various emitting and absorbing objects can be obtained by measuring [[Doppler broadening]] — effectively redshifts and blue shifts over a single emission or absorption line.<ref>Rybicki, G. B. and A. R. Lightman, ''Radiative Processes in Astrophysics'', John Wiley & Sons, 1979, p. 288 ISBN 0-471-82759-2</ref> By measuring the broadening and shifts of the 21-centimeter [[hydrogen line]] in different directions, astronomers have been able to measure the [[recessional velocity|recessional velocities]] of [[interstellar gas]], which in turn reveals the [[rotation curve]] of our Milky Way.<ref name=basicastronomy /> Similar measurements have been performed on other galaxies, such as [[Andromeda (galaxy)|Andromeda]].<ref name=basicastronomy /> As a diagnostic tool, redshift measurements are one of the most important [[astronomical spectroscopy|spectroscopic measurements]] made in astronomy. |
|||
===Extragalactic observations=== |
===Extragalactic observations=== |
||
[[File:Age by redshift.png|thumb|The age of the universe versus redshift from z=5 to 20.<ref name="Pilipenko" />]] |
|||
{{Cosmology}} |
|||
The most distant objects exhibit larger redshifts corresponding to the [[Hubble's law|Hubble flow]] of the universe. The largest observed redshift, corresponding to the greatest distance and furthest back in time, is that of the [[cosmic microwave background radiation]]; the numerical value of its redshift is about {{nowrap|''z'' {{=}} 1089}} ({{nowrap|''z'' {{=}} 0}} corresponds to present time), and it shows the state of the [[Universe]] about 13.7 billion years ago, and 379,000 years after the initial moments of the [[Big Bang]].<ref>An accurate measurement of the cosmic microwave background was achieved by the [[COBE]] experiment. The final published temperature of 2.73 K was reported in this paper: Fixsen, D. J.; Cheng, E. S.; Cottingham, D. A.; Eplee, R. E., Jr.; Isaacman, R. B.; Mather, J. C.; Meyer, S. S.; Noerdlinger, P. D.; Shafer, R. A.; Weiss, R.; Wright, E. L.; Bennett, C. L.; Boggess, N. W.; Kelsall, T.; Moseley, S. H.; Silverberg, R. F.; Smoot, G. F.; Wilkinson, D. T.. (1994). "Cosmic microwave background dipole spectrum measured by the COBE FIRAS instrument", ''Astrophysical Journal'', 420, 445. The most accurate measurement as of 2006 was achieved by the [[Wilkinson Microwave Anisotropy Probe|WMAP]] experiment.</ref> |
|||
The most distant objects exhibit larger redshifts corresponding to the [[Hubble flow]] of the [[universe]]. The largest-observed redshift, corresponding to the greatest distance and furthest back in time, is that of the [[cosmic microwave background]] radiation; the [[Hubble's law#Redshift velocity|numerical value of its redshift]] is about {{math|''z'' {{=}} 1089}} ({{math|''z'' {{=}} 0}} corresponds to present time), and it shows the state of the universe about 13.8 billion years ago,<ref>{{cite web |
|||
The luminous point-like cores of [[quasar]]s were the first "high-redshift" ({{nowrap|''z'' > 0.1}}) objects discovered before the improvement of telescopes allowed for the discovery of other high-redshift galaxies. |
|||
| title=Cosmic Detectives |
|||
| url=http://www.esa.int/Our_Activities/Space_Science/Cosmic_detectives |
|||
| publisher=The European Space Agency (ESA) |
|||
| date=2013-04-02 |
|||
| access-date=2013-04-25 |
|||
}}</ref> and 379,000 years after the initial moments of the [[Big Bang]].<ref>An accurate measurement of the cosmic microwave background was achieved by the [[Cosmic Background Explorer|COBE]] experiment. The final published temperature of 2.73 K was reported in this paper: {{cite journal | last1=Fixsen | first1=D. J. | last2=Cheng | first2=E. S. | last3=Cottingham | first3=D. A. | last4=Eplee | first4=R. E. Jr. | last5=Isaacman | first5=R. B. | last6=Mather | first6=J. C. | last7=Meyer | first7=S. S. | last8=Noerdlinger | first8=P. D. | last9=Shafer | first9=R. A. | last10=Weiss | first10=R. | last11=Wright | first11=E. L. | last12=Bennett | first12=C. L. | last13=Boggess | first13=N. W. | author-link13 = Nancy Boggess|last14=Kelsall | first14=T. | last15=Moseley | first15=S. H. | last16=Silverberg | first16=R. F. | last17=Smoot | first17=G. F. | last18=Wilkinson | first18=D. T. | date=January 1994 | title=Cosmic microwave background dipole spectrum measured by the COBE FIRAS instrument | journal=Astrophysical Journal | volume=420 | page=445 | doi=10.1086/173575 | bibcode=1994ApJ...420..445F }}. The most accurate measurement as of 2006 was achieved by the [[Wilkinson Microwave Anisotropy Probe|WMAP]] experiment.</ref> |
|||
The luminous point-like cores of [[quasar]]s were the first "high-redshift" ({{math|''z'' > 0.1}}) objects discovered before the improvement of telescopes allowed for the discovery of other high-redshift galaxies.{{cn|date=March 2023}} |
|||
For galaxies more distant than the [[Local Group]] and the nearby [[Virgo Cluster]], but within a thousand [[parsec|megaparsecs]] or so, the redshift is approximately proportional to the galaxy's distance. This correlation was first observed by [[Edwin Hubble]] and has come to be known as [[Hubble's law]]. [[Vesto Slipher]] was the first to discover galactic redshifts, in about the year 1912, while Hubble correlated Slipher's measurements with distances he [[cosmic distance ladder|measured by other means]] to formulate his Law. In the widely accepted cosmological model based on [[general relativity]], redshift is mainly a result of the expansion of space: this means that the farther away a galaxy is from us, the more the space has expanded in the time since the light left that galaxy, so the more the light has been stretched, the more redshifted the light is, and so the faster it appears to be moving away from us. [[Hubble's law]] follows in part from the [[Copernican principle]].<ref name="Peebles-1993">Peebles (1993).</ref> Because it is usually not known how [[luminosity|luminous]] objects are, measuring the redshift is easier than more direct distance measurements, so redshift is sometimes in practice converted to a crude distance measurement using Hubble's law. |
|||
For galaxies more distant than the [[Local Group]] and the nearby [[Virgo Cluster]], but within a thousand mega[[parsec]]s or so, the redshift is approximately proportional to the galaxy's distance. This correlation was first observed by [[Edwin Hubble]] and has come to be known as [[Hubble's law]]. [[Vesto Slipher]] was the first to discover galactic redshifts, in about 1912, while Hubble correlated Slipher's measurements with distances he [[cosmic distance ladder|measured by other means]] to formulate his Law.<ref name="Peebles-1993"/> Hubble's law follows in part from the [[Copernican principle]].<ref name="Peebles-1993">Peebles (1993).</ref> Because it is usually not known how [[luminosity|luminous]] objects are, measuring the redshift is easier than more direct distance measurements, so redshift is sometimes in practice converted to a crude distance measurement using Hubble's law.{{cn|date=March 2023}} |
|||
[[Gravitation|Gravitational interactions]] of galaxies with each other and clusters cause a significant [[variance|scatter]] in the normal plot of the Hubble diagram. The [[peculiar velocity|peculiar velocities]] associated with galaxies superimpose a rough trace of the [[mass]] of [[virial theorem|virialized objects]] in the universe. This effect leads to such phenomena as nearby galaxies (such as the [[Andromeda Galaxy]]) exhibiting blue shifts as we fall towards a common [[barycenter]], and redshift maps of clusters showing a [[Fingers of God|Finger of God]] effect due to the scatter of peculiar velocities in a roughly spherical distribution.<ref name="Peebles-1993"/> This added component gives cosmologists a chance to measure the masses of objects independent of the ''[[mass to light ratio]]'' (the ratio of a galaxy's mass in solar masses to its brightness in solar luminosities), an important tool for measuring [[dark matter]].<ref>{{cite book|first=James|last=Binney|coauthors=and Scott Treimane|title=Galactic dynamics|publisher=Princeton University Press|isbn=0-691-08445-9|year=1994}}</ref> |
|||
[[Gravitation]]al interactions of galaxies with each other and clusters cause a significant [[variance|scatter]] in the normal plot of the Hubble diagram. The [[peculiar velocity|peculiar velocities]] associated with galaxies superimpose a rough trace of the [[mass]] of [[virial theorem|virialized objects]] in the universe. This effect leads to such phenomena as nearby galaxies (such as the [[Andromeda Galaxy]]) exhibiting blueshifts as we fall towards a common [[barycenter]], and redshift maps of clusters showing a [[fingers of god]] effect due to the scatter of peculiar velocities in a roughly spherical distribution.<ref name="Peebles-1993"/> This added component gives cosmologists a chance to measure the masses of objects independent of the [[mass-to-light ratio]] (the ratio of a galaxy's mass in solar masses to its brightness in solar luminosities), an important tool for measuring [[dark matter]].<ref>{{cite book | first1=James | last1=Binney | first2=Scott | last2=Treimane | title=Galactic dynamics|publisher=Princeton University Press | isbn=978-0-691-08445-9 | date=1994 }}</ref>{{Page needed|date=March 2023}} |
|||
The Hubble law's linear relationship between distance and redshift assumes that the rate of expansion of the universe is constant. However, when the universe was much younger, the expansion rate, and thus the Hubble "constant", was larger than it is today. For more distant galaxies, then, whose light has been travelling to us for much longer times, the approximation of constant expansion rate fails, and the Hubble law becomes a non-linear integral relationship and dependent on the history of the expansion rate since the emission of the light from the galaxy in question. Observations of the redshift-distance relationship can be used, then, to determine the expansion history of the universe and thus the matter and energy content. |
|||
The Hubble law's linear relationship between distance and redshift assumes that the rate of expansion of the universe is constant. However, when the universe was much younger, the expansion rate, and thus the Hubble "constant", was larger than it is today. For more distant galaxies, then, whose light has been travelling to us for much longer times, the approximation of constant expansion rate fails, and the Hubble law becomes a non-linear integral relationship and dependent on the history of the expansion rate since the emission of the light from the galaxy in question. Observations of the redshift-distance relationship can be used, then, to determine the expansion history of the universe and thus the matter and energy content.{{cn|date=March 2023}} |
|||
While it was long believed that the expansion rate has been continuously decreasing since the Big Bang, recent observations of the redshift-distance relationship using [[Type Ia supernova]]e have suggested that in comparatively recent times the expansion rate of the universe has [[Accelerating universe|begun to accelerate]]. |
|||
While it was long believed that the expansion rate has been continuously decreasing since the Big Bang, observations beginning in 1988 of the redshift-distance relationship using [[Type Ia supernova]]e have suggested that in comparatively recent times the expansion rate of the universe has [[Accelerating expansion of the universe|begun to accelerate]].<ref>{{cite web|url=https://www.nobelprize.org/uploads/2019/05/popular-physicsprize2011.pdf |title=The Nobel Prize in Physics 2011: Information for the Public |website=nobelprize.org |access-date=2023-06-13}}</ref> |
|||
===Highest redshifts=== |
===Highest redshifts=== |
||
{{see also|List of the most distant astronomical objects#List of most distant objects by type{{!}}List of most distant objects by type}} |
|||
Currently, the objects with the highest known redshifts are galaxies and the objects producing gamma ray bursts. The most reliable redshifts are from [[spectroscopic]] data, and the highest confirmed [[spectroscopic]] redshift of a galaxy is that of [[IOK-1]],<ref> {{cite journal |
|||
[[File:Comoving distance and lookback time (Planck 2018).png|thumb|upright=1.8|[[Comoving and proper distances|Comoving distance]] and [[lookback time]] for the Planck 2018 cosmology parameters, from redshift 0 to 15, with distance (blue solid line) on the left axis, and time (orange dashed line) on the right. Note that the time that has passed (in giga years) from a given redshift until now is not the same as the distance (in giga light years) light would have traveled from that redshift, due to the expansion of the universe over the intervening period.]] |
|||
| author=Masanori Iye, ''et al.'' |
|||
| title=A galaxy at a redshift z = 6.96 |
|||
| url=http://www.nature.com/nature/journal/v443/n7108/abs/nature05104.html |
|||
| journal=Nature |
|||
| volume=443 |
|||
| issue=7108 |
|||
| pages=186–188 |
|||
| doi=10.1038/nature05104 |
|||
| year=2006 |
|||
| pmid=16971942 |
|||
}} |
|||
</ref> at a redshift z = 6.96, corresponding to just 750 million years after the Big Bang. Slightly less reliable are [[Lyman-alpha forest|Lyman-break]] redshifts, the highest of which is the lensed galaxy A1689-zD1 at a redshift z = 7.6<ref>Bradley, L.., et al., Discovery of a Very Bright Strongly Lensed Galaxy Candidate at z ~ 7.6, ''[[Astrophysical Journal|The Astrophysical Journal]]'' (2008), Volume 678, Issue 2, pp. 647-654. [http://adsabs.harvard.edu/abs/2008ApJ...678..647B</ref> and the next highest being <math>z=7.0</math><ref>Egami, E., et al., Spitzer and Hubble Space Telescope Constraints on the Physical Properties of the z~7 Galaxy Strongly Lensed by A2218, ''[[Astrophysical Journal|The Astrophysical Journal]]'' (2005), v. 618, Issue 1, pp. L5-L8 [http://adsabs.harvard.edu/cgi-bin/nph-bib_query?bibcode=2005ApJ...618L...5E&db_key=AST&data_type=HTML&format=&high=43a73989ff16910].</ref> while as-yet unconfirmed reports by Ellis R. et al. from a [[gravitational lens]] observed in a distant [[galaxy groups and clusters|galaxy cluster]] may indicate a galaxy with a redshift of <math>z=10.1</math>. |
|||
Currently, the objects with the highest known redshifts are galaxies and the objects producing gamma ray bursts.{{cn|date=August 2024}} The most reliable redshifts are from [[spectroscopic]] data,{{cn|date=August 2024}} and the highest-confirmed spectroscopic redshift of a galaxy is that of [[JADES-GS-z14-0]] with a redshift of {{math|''z'' {{=}} 14.32}}, corresponding to 290 million years after the Big Bang.<ref>{{Cite journal |last1=Carniani |first1=Stefano |last2=Hainline |first2=Kevin |last3=D’Eugenio |first3=Francesco |last4=Eisenstein |first4=Daniel J. |last5=Jakobsen |first5=Peter |last6=Witstok |first6=Joris |last7=Johnson |first7=Benjamin D. |last8=Chevallard |first8=Jacopo |last9=Maiolino |first9=Roberto |last10=Helton |first10=Jakob M. |last11=Willott |first11=Chris |last12=Robertson |first12=Brant |last13=Alberts |first13=Stacey |last14=Arribas |first14=Santiago |last15=Baker |first15=William M. |date=2024-07-29 |title=Spectroscopic confirmation of two luminous galaxies at a redshift of 14 |journal=Nature |volume=633 |issue=8029 |language=en |pages=318–322 |doi=10.1038/s41586-024-07860-9 |issn=1476-4687|doi-access=free |pmid=39074505 |pmc=11390484 }}</ref> The previous record was held by [[GN-z11]],<ref>{{cite journal |
|||
The most distant observed gamma ray burst was [[GRB 090423]], which had a redshift of 8.2.<ref>{{cite journal |
|||
| title=A Remarkably Luminous Galaxy at z=11.1 Measured with Hubble Space Telescope Grism Spectroscopy |
|||
|title=GRB 090423 reveals an exploding star at the epoch of re-ionization |
|||
| last1=Oesch | first1=P. A. | last2=Brammer | first2=G. |
|||
|author= Salvaterra, R. ''et al.'' |
|||
| last3=van Dokkum | first3=P. G. | last4=Illingworth | first4=G. D. |
|||
|journal=Submitted to Nature |
|||
| last5=Bouwens | first5=R. J. | last6=Labbé | first6=I. |
|||
|url=http://adsabs.harvard.edu/abs/2009arXiv0906.1578S |
|||
| last7=Franx | first7=M. | last8=Momcheva | first8=I. |
|||
|year=2009 |
|||
| last9=Ashby | first9=M. L. N. | last10=Fazio | first10=G. G. |
|||
|doi=10.1038/nature08445 |
|||
| last11=Gonzalez | first11=V. | last12=Holden | first12=B. |
|||
|volume=461 |
|||
| last13=Magee | first13=D. | last14=Skelton | first14=R. E. |
|||
|pages=1258 |
|||
| last15=Smit | first15=R. | last16=Spitler | first16=L. R. |
|||
}}</ref> |
|||
| last17=Trenti | first17=M. | last18=Willner | first18=S. P. |
|||
| display-authors=1 | journal=The Astrophysical Journal |
|||
| date=March 1, 2016 | volume=819 | issue=2 | page=129 |
|||
| arxiv=1603.00461 | doi=10.3847/0004-637X/819/2/129 |
|||
| bibcode=2016ApJ...819..129O | s2cid=119262750 |
|||
| doi-access=free }}</ref> with a redshift of {{math|''z'' {{=}} 11.1}}, corresponding to 400 million years after the Big Bang, and by [[UDFy-38135539]]<ref> |
|||
{{cite journal |
|||
| display-authors=4 | first1=M. D. | last1=Lehnert |
|||
| last2=Nesvadba | first2=N. P. | last3=Cuby | first3=J. G. |
|||
| last4=Swinbank | first4=A. M. | last5=Morris | first5=S. |
|||
| last6=Clément | first6=B. | last7=Evans | first7=C. J. |
|||
| last8=Bremer | first8=M. N. | last9=Basa | first9=S. |
|||
| title=Spectroscopic Confirmation of a galaxy at redshift z = 8.6 |
|||
| journal=Nature | year=2010 |
|||
| volume=467 | issue=7318 | pages=940–942 |
|||
| doi=10.1038/nature09462 | pmid=20962840 |
|||
| bibcode=2010Natur.467..940L | arxiv=1010.4312 |
|||
| s2cid=4414781 |
|||
}}</ref> at a redshift of {{math|''z'' {{=}} 8.6}}, corresponding to 600 million years after the Big Bang. |
|||
Slightly less reliable are [[Lyman-break galaxy|Lyman-break]] redshifts, the highest of which is the lensed galaxy A1689-zD1 at a redshift {{math|''z'' {{=}} 7.5}}<ref>{{Cite journal|last1=Watson|first1=Darach|last2=Christensen|first2=Lise|last3=Knudsen|first3=Kirsten Kraiberg|last4=Richard|first4=Johan|last5=Gallazzi|first5=Anna|last6=Michałowski|first6=Michał Jerzy|title=A dusty, normal galaxy in the epoch of reionization|journal=Nature|volume=519|issue=7543|pages=327–330|doi=10.1038/nature14164|arxiv = 1503.00002 |bibcode = 2015Natur.519..327W|pmid=25731171|year=2015|s2cid=2514879}}</ref><ref>{{cite journal |
|||
The most distant known quasar, CFHQS J2329-0301, is at <math>z = 6.43 </math>.<ref>Willott, Chris J. et al., Four Quasars Above Redshift 6 Discovered by the Canada-France High-z Quasar Survey, ''[[Astronomical Journal|The Astronomical Journal]]'' (2007), v. 134, pp. 2435–2450 [http://adsabs.harvard.edu/abs/2007AJ....134.2435W&db_key=AST&data_type=HTML&format=].</ref> The highest known redshift radio galaxy (TN J0924-2201) is at a redshift z = 5.2<ref>Klamer et al., 2005, ApJ 621, L1</ref> and the highest known redshift molecular material is the detection of emission from the CO molecule from the quasar SDSS J1148+5251 at z = 6.42<ref>Walter, Fabian et al., Molecular gas in the host galaxy of a quasar at redshift z = 6.42, ''[[Nature]]'' (2003), v. 424, pp. 406–408 [http://adsabs.harvard.edu/cgi-bin/bib_query?2003Natur.424..406W&db_key=AST&data_type=HTML&format=].</ref> |
|||
| title=Discovery of a Very Bright Strongly Lensed Galaxy Candidate at z ~ 7.6 |
|||
| first1=L. D. | last1=Bradley | first2=R. J. | last2=Bouwens |
|||
| first3=H. C. | last3=Ford | first4=G. D. | last4=Illingworth |
|||
| first5=M. J. | last5=Jee | first6=N. | last6=Benítez |
|||
| first7=T. J. | last7=Broadhurst | first8=M. | last8=Franx |
|||
| first9=B. L. | last9=Frye | first10=L. | last10=Infante |
|||
| display-authors=1 | journal=[[The Astrophysical Journal]] |
|||
| volume=678 | issue=2 | pages=647–654 | year=2008 |
|||
| bibcode=2008ApJ...678..647B | s2cid=15574239 |
|||
| doi=10.1086/533519 | arxiv=0802.2506 |
|||
}}</ref> and the next highest being {{math|''z'' {{=}} 7.0}}.<ref>{{cite journal |
|||
| display-authors=1 | first1=E. | last1=Egami |
|||
| first2=J.-P. | last2=Kneib | first3=G. H. | last3=Rieke |
|||
| first4=R. S. | last4=Ellis | first5=J. | last5=Richard |
|||
| first6=J. | last6=Rigby | first7=C. | last7=Papovich |
|||
| first8=D. | last8=Stark | first9=M. R. | last9=Santos |
|||
| first10=J.-S. | last10=Huang | first11=H. | last11=Dole |
|||
| first12=E. Le | last12=Floc'H | first13=P. G. | last13=Pérez-González |
|||
| title=Spitzer and Hubble Space Telescope Constraints on the Physical Properties of the z~7 Galaxy Strongly Lensed by A2218 |
|||
| journal=[[The Astrophysical Journal]] |
|||
| volume=618 | issue=1 | pages=L5–L8 | year=2005 |
|||
| bibcode=2005ApJ...618L...5E | doi=10.1086/427550 |
|||
| arxiv=astro-ph/0411117 | s2cid=15920310 }}</ref> The most distant-observed [[gamma-ray burst]] with a spectroscopic redshift measurement was [[GRB 090423]], which had a redshift of {{math|''z'' {{=}} 8.2}}.<ref>{{cite journal |
|||
| title=GRB 090423 reveals an exploding star at the epoch of re-ionization |
|||
| last1=Salvaterra | first1=R. | first2=M. Della | last2=Valle |
|||
| last3=Campana | first3=S. |author-link3=Sergio Campana (astrophysicist)| last4=Chincarini | first4=G. |
|||
| last5=Covino | first5=S. | last6=d'Avanzo | first6=P. |
|||
| last7=Fernández-Soto | first7=A. | last8=Guidorzi | first8=C. |
|||
| last9=Mannucci | first9=F. | last10=Margutti | first10=R. |
|||
| last11=Thöne | first11=C. C. | last12=Antonelli | first12=L. A. |
|||
| last13=Barthelmy | first13=S. D. | last14=De Pasquale | first14=M. |
|||
| last15=d'Elia | first15=V. | last16=Fiore | first16=F. |
|||
| last17=Fugazza | first17=D. | last18=Hunt | first18=L. K. |
|||
| last19=Maiorano | first19=E. | last20=Marinoni | first20=S. |
|||
| last21=Marshall | first21=F. E. | last22=Molinari | first22=E. |
|||
| last23=Nousek | first23=J. | last24=Pian | first24=E. |
|||
| last25=Racusin | first25=J. L. | last26=Stella | first26=L. |
|||
| last27=Amati | first27=L. | last28=Andreuzzi | first28=G. |
|||
| last29=Cusumano | first29=G. | last30=Fenimore | first30=E. E. |
|||
| display-authors=4 | journal=[[Nature (journal)|Nature]] |
|||
| volume=461 | issue=7268 | pages=1258–60 |
|||
| doi=10.1038/nature08445 | date=2009 | pmid=19865166 |
|||
| s2cid=205218263 | bibcode=2009Natur.461.1258S |arxiv=0906.1578 |
|||
}}</ref> The most distant-known quasar, [[ULAS J1342+0928]], is at {{math|''z'' {{=}} 7.54}}.<ref>{{cite web|url=https://news.mit.edu/2017/scientists-observe-supermassive-black-hole-infant-universe-1206|title=Scientists observe supermassive black hole in infant universe|website=MIT News |publisher=Massachusetts Institute of Technology |date=2017-12-06 |first=Jennifer |last=Chu}}</ref><ref name="Nature-2018-01">{{cite journal |last1=Bañados |first1=Eduardo |last2=Venemans |first2=Bram P. |last3=Mazzucchelli |first3=Chiara |last4=Farina |first4=Emanuele P. |last5=Walter |first5=Fabian |last6=Wang |first6=Feige |last7=Decarli |first7=Roberto |last8=Stern |first8=Daniel |last9=Fan |first9=Xiaohui |last10=Davies |first10=Frederick B. |last11=Hennawi |first11=Joseph F. |last12=Simcoe |first12=Robert A. |last13=Turner |first13=Monica L. |last14=Rix |first14=Hans-Walter |last15=Yang |first15=Jinyi |last16=Kelson |first16=Daniel D. |last17=Rudie |first17=Gwen C. |last18=Winters |first18=Jan Martin |title=An 800-million-solar-mass black hole in a significantly neutral Universe at a redshift of 7.5 |journal=Nature |date=January 2018 |volume=553 |issue=7689 |pages=473–476 |doi=10.1038/nature25180 |pmid=29211709 |arxiv=1712.01860 |bibcode=2018Natur.553..473B |s2cid=205263326 }}</ref> The highest-known redshift radio galaxy (TGSS1530) is at a redshift {{math|''z'' {{=}} 5.72}}<ref>{{cite journal|last1=Saxena|first1=A.|date=2018|title=Discovery of a radio galaxy at z = 5.72|journal=Monthly Notices of the Royal Astronomical Society|volume=480|issue=2|pages=2733–2742|arxiv=1806.01191|bibcode=2018MNRAS.480.2733S|doi=10.1093/mnras/sty1996|doi-access=free |s2cid=118830412}}</ref> and the highest-known redshift molecular material is the detection of emission from the CO molecule from the quasar SDSS J1148+5251 at {{math|''z'' {{=}} 6.42}}.<ref>{{cite journal | doi = 10.1038/nature01821 | title = Molecular gas in the host galaxy of a quasar at redshift z = 6.42 | date = 2003 | last1 = Walter | first1 = Fabian | last2 = Bertoldi | first2 = Frank | last3 = Carilli | first3 = Chris | last4 = Cox | first4 = Pierre | last5 = Lo | first5 = K. Y. | last6 = Neri | first6 = Roberto | last7 = Fan | first7 = Xiaohui | last8 = Omont | first8 = Alain | last9 = Strauss | first9 = Michael A. | last10 = Menten | first10 = Karl M. | journal = Nature | volume = 424 | issue = 6947 | pages = 406–8 | pmid = 12879063 |bibcode=2003Natur.424..406W|arxiv = astro-ph/0307410 |s2cid = 4419009| display-authors = 4 }}</ref> |
|||
''Extremely red objects'' (EROs) are astronomical sources of radiation that radiate energy in the red and near infrared part of the electromagnetic spectrum. These may be starburst galaxies that have |
''Extremely red objects'' (EROs) are [[Radio astronomy#Astronomical sources|astronomical sources]] of radiation that radiate energy in the red and near infrared part of the electromagnetic spectrum. These may be starburst galaxies that have a high redshift accompanied by reddening from intervening dust, or they could be highly redshifted elliptical galaxies with an older (and therefore redder) stellar population.<ref> |
||
{{cite journal |
|||
| display-authors=4 |
|||
| author=Smail, Ian; Owen, F. N.; Morrison, G. E.; Keel, W. C.; Ivison, R. J.; Ledlow, M. J. |
|||
| author=Smail, Ian |
|||
| total=The Diversity of Extremely Red Objects |
|||
| author2=Owen, F. N. |
|||
| author3=Morrison, G. E. |
|||
| author4=Keel, W. C. |
|||
| author5=Ivison, R. J. |
|||
| author6=Ledlow, M. J. |
|||
| journal=The Astrophysical Journal | volume=581 | issue=2 |
| journal=The Astrophysical Journal | volume=581 | issue=2 |
||
| pages= |
| pages=844–864 | doi=10.1086/344440 | bibcode=2002ApJ...581..844S |
||
| title=The Diversity of Extremely Red Objects |
| title=The Diversity of Extremely Red Objects |
||
| date=2002 |
|||
| year=2002 }}</ref> Objects that are even redder than EROs are termed ''hyper extremely red objects'' (HEROs).<ref>{{cite journal |
|||
|arxiv = astro-ph/0208434 | s2cid=51737034 |
|||
| author=Totani, Tomonori; Yoshii, Yuzuru; Iwamuro, Fumihide; Maihara, Toshinori; Motohara, Kentaro |
|||
}}</ref> Objects that are even redder than EROs are termed ''hyper extremely red objects'' (HEROs).<ref> |
|||
{{cite journal |
|||
| display-authors=4 |
|||
| author=Totani, Tomonori |
|||
| author2=Yoshii, Yuzuru |
|||
| author3=Iwamuro, Fumihide |
|||
| author4=Maihara, Toshinori |
|||
| author5=Motohara, Kentaro |
|||
| title=Hyper Extremely Red Objects in the Subaru Deep Field: Evidence for Primordial Elliptical Galaxies in the Dusty Starburst Phase |
| title=Hyper Extremely Red Objects in the Subaru Deep Field: Evidence for Primordial Elliptical Galaxies in the Dusty Starburst Phase |
||
| journal=The Astrophysical Journal | volume=558 | issue=2 |
| journal=The Astrophysical Journal | volume=558 | issue=2 |
||
| |
| date=2001 | pages=L87–L91 | doi=10.1086/323619 |
||
| bibcode=2001ApJ...558L..87T |
| bibcode=2001ApJ...558L..87T |
||
|arxiv = astro-ph/0108145 | s2cid=119511017 |
|||
}}</ref> |
|||
The [[ |
The [[cosmic microwave background]] has a redshift of {{math|z {{=}} 1089}}, corresponding to an age of approximately 379,000 years after the Big Bang and a [[Comoving and proper distances|proper distance]] of more than 46 billion light-years.<ref name="ly93"> |
||
{{cite journal | last1 = Lineweaver | first1 = Charles | first2=Tamara M. | last2=Davis | date = 2005 | title = Misconceptions about the Big Bang | journal = Scientific American | volume = 292 | issue = 3 | pages = 36–45 | doi = 10.1038/scientificamerican0305-36 | bibcode = 2005SciAm.292c..36L }}</ref> The yet-to-be-observed first light from the oldest [[Population III stars]], not long after atoms first formed and the CMB ceased to be absorbed almost completely, may have redshifts in the range of {{math|20 < ''z'' < 100}}.<ref>{{cite journal|bibcode=2006MNRAS.373L..98N|arxiv = astro-ph/0604050 |doi = 10.1111/j.1745-3933.2006.00251.x|title=The first stars in the Universe|date=2006|last1=Naoz|first1=S.|last2=Noter|first2=S.|last3=Barkana|first3=R.|journal=Monthly Notices of the Royal Astronomical Society: Letters|volume=373|issue = 1 |pages=L98–L102 |doi-access = free |s2cid = 14454275 }}</ref> Other high-redshift events predicted by physics but not presently observable are the [[cosmic neutrino background]] from about two seconds after the Big Bang (and a redshift in excess of {{math|''z'' > 10{{sup|10}}}})<ref>{{cite journal|bibcode=2006PhR...429..307L|arxiv = astro-ph/0603494 |doi = 10.1016/j.physrep.2006.04.001|title=Massive neutrinos and cosmology|date=2006|last1=Lesgourgues|first1=J|last2=Pastor|first2=S|journal=Physics Reports|volume=429|issue=6|pages=307–379 |s2cid = 5955312 }}</ref> and the cosmic [[gravitational wave background]] emitted directly from [[inflation (cosmology)|inflation]] at a redshift in excess of {{math|''z'' > 10{{sup|25}}}}.<ref>{{cite journal|bibcode=2005PhyU...48.1235G|arxiv = gr-qc/0504018 |doi = 10.1070/PU2005v048n12ABEH005795|title=Relic gravitational waves and cosmology|date=2005|last1=Grishchuk|first1=Leonid P|journal=Physics-Uspekhi|volume=48|issue=12|pages=1235–1247 |s2cid = 11957123 }}</ref> |
|||
In June 2015, astronomers reported evidence for [[Stellar population#Population III stars|Population III stars]] in the [[Cosmos Redshift 7]] [[galaxy]] at {{math|''z'' {{=}} 6.60}}. Such stars are likely to have existed in the very early universe (i.e., at high redshift), and may have started the production of [[chemical element]]s heavier than [[hydrogen]] that are needed for the later formation of [[planet]]s and [[life]] as we know it.<ref name="AJ-20150604">{{cite journal |last1=Sobral |first1=David |last2=Matthee |first2=Jorryt |last3=Darvish |first3=Behnam |last4=Schaerer |first4=Daniel |last5=Mobasher |first5=Bahram |last6=Röttgering |first6=Huub J. A. |last7=Santos |first7=Sérgio |last8=Hemmati |first8=Shoubaneh |title=Evidence For POPIII-Like Stellar Populations In The Most Luminous LYMAN-α Emitters At The Epoch Of Re-Ionisation: Spectroscopic Confirmation |date=4 June 2015 |journal=[[The Astrophysical Journal]] |doi=10.1088/0004-637x/808/2/139 |bibcode=2015ApJ...808..139S |volume=808 |issue=2 |page=139|arxiv=1504.01734|s2cid=18471887 }}</ref><ref name="NYT-20150617">{{cite news |last=Overbye |first=Dennis |author-link=Dennis Overbye |title=Astronomers Report Finding Earliest Stars That Enriched Cosmos |url=https://www.nytimes.com/2015/06/18/science/space/astronomers-report-finding-earliest-stars-that-enriched-cosmos.html |date=17 June 2015 |work=[[The New York Times]] |access-date=17 June 2015 }}</ref> |
|||
===Redshift surveys=== |
===Redshift surveys=== |
||
[[File:2dfgrs.png|thumb|Rendering of the 2dFGRS data]] |
|||
{{main|Redshift survey}} |
|||
{{Main|Redshift survey}} |
|||
[[Image:2dfgrs.png|left|thumb|300px|Rendering of the 2dFGRS data]] |
|||
With advent of automated [[telescope]]s and improvements in [[astronomical spectroscopy|spectroscopes]], a number of collaborations have been made to map the universe in redshift space. By combining redshift with angular position data, a redshift survey maps the 3D distribution of matter within a field of the sky. These observations are used to measure properties of the [[Observable universe|large-scale structure]] of the universe. The [[CfA2 Great Wall|Great Wall]], a vast [[supercluster]] of galaxies over 500 million [[light-year]]s wide, provides a dramatic example of a large-scale structure that redshift surveys can detect.<ref>{{cite journal | title=Mapping the Universe | first1=M. J. | last1=Geller | first2=J. P. | last2=Huchra | journal=Science | volume=246 | issue=4932 | pages=897–903 | year=1989 | doi=10.1126/science.246.4932.897 | pmid=17812575 | bibcode=1989Sci...246..897G | s2cid=31328798 }}</ref> |
|||
The first redshift survey was the [[CfA Redshift Survey]], started in 1977 with the initial data collection completed in 1982.<ref>See the CfA website for more details: {{cite web |
|||
| title=The CfA Redshift Survey |
|||
| first=John P. | last=Huchra | author-link=John Huchra |
|||
| publisher=Harvard & Smithsonian Center for Astrophysics |
|||
| url=https://lweb.cfa.harvard.edu/~dfabricant/huchra/zcat/ |
|||
| access-date=2023-03-20 |
|||
}}</ref> More recently, the [[2dF Galaxy Redshift Survey]] determined the large-scale structure of one section of the universe, measuring redshifts for over 220,000 galaxies; data collection was completed in 2002, and the final [[data set]] was released 30 June 2003.<ref>{{cite journal |
|||
|title=The 2dF galaxy redshift survey: Power-spectrum analysis of the final dataset and cosmological implications |
|||
| first1=Shaun | last1=Cole | author-link=Shaun Cole |
|||
| last2=Percival | first2=Will J. | last3=Peacock | first3=John A. |
|||
| last4=Norberg | first4=Peder | last5=Baugh | first5=Carlton M. |
|||
| last6=Frenk | first6=Carlos S. | last7=Baldry | first7=Ivan |
|||
| last8=Bland-Hawthorn | first8=Joss | last9=Bridges | first9=Terry |
|||
| last10=Cannon | first10=Russell | last11=Colless | first11=Matthew |
|||
| last12=Collins | first12=Chris | last13=Couch | first13=Warrick |
|||
| last14=Cross | first14=Nicholas J. G. | last15=Dalton | first15=Gavin |
|||
| last16=Eke | first16=Vincent R. | last17=De Propris | first17=Roberto |
|||
| last18=Driver | first18=Simon P. | last19=Efstathiou | first19=George |
|||
| last20=Ellis | first20=Richard S. | last21=Glazebrook | first21=Karl |
|||
| last22=Jackson | first22=Carole | last23=Jenkins | first23=Adrian |
|||
| last24=Lahav | first24=Ofer | last25=Lewis | first25=Ian |
|||
| last26=Lumsden | first26=Stuart | last27=Maddox | first27=Steve |
|||
| last28=Madgwick | first28=Darren | last29=Peterson | first29=Bruce A. |
|||
| last30=Sutherland | first30=Will | last31=Taylor | first31=Keith |
|||
| journal=Monthly Notices of the Royal Astronomical Society |
|||
| volume=362 | issue=2 | pages=505–34 | date=2005 |
|||
| bibcode=2005MNRAS.362..505C | arxiv=astro-ph/0501174 |
|||
| doi=10.1111/j.1365-2966.2005.09318.x |
|||
| doi-access=free | s2cid=6906627| display-authors=4 |
|||
}} [http://msowww.anu.edu.au/2dFGRS/ 2dF Galaxy Redshift Survey homepage] {{Webarchive|url=https://web.archive.org/web/20070205010241/http://msowww.anu.edu.au/2dFGRS/ |date=2007-02-05 }}</ref> The [[Sloan Digital Sky Survey]] (SDSS), is ongoing as of 2013 and aims to measure the redshifts of around 3 million objects.<ref>{{cite web | url=https://www.sdss3.org/ | access-date=2023-03-20 | title=SDSS-III | website=www.sdss3.org }}</ref> SDSS has recorded redshifts for galaxies as high as 0.8, and has been involved in the detection of [[quasar]]s beyond {{math|''z'' {{=}} 6}}. The [[DEEP2 Redshift Survey]] uses the [[Keck telescopes]] with the new "DEIMOS" [[spectrograph]]; a follow-up to the pilot program DEEP1, DEEP2 is designed to measure faint galaxies with redshifts 0.7 and above, and it is therefore planned to provide a high-redshift complement to SDSS and 2dF.<ref>{{cite conference | title=Science objectives and early results of the DEEP2 redshift survey| first1=Marc | last1=Davis | author2=DEEP2 collaboration |date=2002 | conference=Conference on Astronomical Telescopes and Instrumentation, Waikoloa, Hawaii, 22–28 Aug 2002 | arxiv=astro-ph/0209419 | bibcode=2003SPIE.4834..161D | doi=10.1117/12.457897 }}</ref> |
|||
==Effects from physical optics or radiative transfer== |
|||
The interactions and phenomena summarized in the subjects of [[radiative transfer]] and [[physical optics]] can result in shifts in the wavelength and frequency of electromagnetic radiation. In such cases, the shifts correspond to a physical energy transfer to matter or other photons rather than being by a transformation between reference frames. Such shifts can be from such physical phenomena as [[Wolf effect|coherence effects]] or the [[scattering]] of [[electromagnetic radiation]] whether from [[electric charge|charged]] [[elementary particle]]s, from [[particulates]], or from fluctuations of the [[index of refraction]] in a [[dielectric]] medium as occurs in the radio phenomenon of [[Whistler (radio)|radio whistlers]].<ref name=basicastronomy/> While such phenomena are sometimes referred to as "redshifts" and "blueshifts", in astrophysics light-matter interactions that result in energy shifts in the radiation field are generally referred to as "reddening" rather than "redshifting" which, as a term, is normally reserved for the [[#Redshift formulae|effects discussed above]].<ref name=basicastronomy/> |
|||
In many circumstances scattering causes radiation to redden because [[entropy]] results in the predominance of many low-[[energy]] photons over few high-energy ones (while [[conservation of energy|conserving total energy]]).<ref name=basicastronomy/> Except possibly under carefully controlled conditions, scattering does not produce the same relative change in wavelength across the whole spectrum; that is, any calculated {{math|''z''}} is generally a [[function (mathematics)|function]] of wavelength. Furthermore, scattering from [[randomness|random]] [[matter|media]] generally occurs at many [[angle]]s, and {{math|''z''}} is a function of the scattering angle. If multiple scattering occurs, or the scattering particles have relative motion, then there is generally distortion of [[spectral line]]s as well.<ref name=basicastronomy/> |
|||
In [[interstellar medium|interstellar astronomy]], [[Visible spectrum|visible spectra]] can appear redder due to scattering processes in a phenomenon referred to as [[interstellar reddening]]<ref name=basicastronomy/>—similarly [[Rayleigh scattering]] causes the [[Atmosphere of Earth|atmospheric]] reddening of the Sun seen in the sunrise or sunset and causes the rest of the sky to have a blue color. This phenomenon is distinct from red''shift''ing because the [[spectroscopic]] lines are not shifted to other wavelengths in reddened objects and there is an additional [[extinction (astronomy)|dimming]] and distortion associated with the phenomenon due to photons being scattered in and out of the [[Line-of-sight propagation|line of sight]].{{cn|date=March 2023}} |
|||
==Blueshift== |
|||
{{redirect|Blueshift|the term as used in photochemistry|hypsochromic shift|the political phenomenon|blue shift (politics)|other uses of "blueshift" or "blue shift"}} |
|||
The opposite of a redshift is a '''blueshift'''. A blueshift is any decrease in [[wavelength]] (increase in [[energy]]), with a corresponding increase in frequency, of an [[electromagnetic wave]]. In [[Light|visible light]], this shifts a color towards the blue end of the spectrum. |
|||
=== Doppler blueshift === |
|||
With the advent of automated [[telescope]]s and improvements in [[astronomical spectroscopy|spectroscopes]], a number of collaborations have been made to map the universe in redshift space. By combining redshift with angular position data, a redshift survey maps the 3D distribution of matter within a field of the sky. These observations are used to measure properties of the [[large-scale structure of the cosmos|large-scale structure]] of the universe. The [[Great Wall (astronomy)|Great Wall]], a vast [[supercluster]] of galaxies over 500 million [[light-year]]s wide, provides a dramatic example of a large-scale structure that redshift surveys can detect.<ref>M. J. Geller & J. P. Huchra, ''Science'' '''246''', 897 (1989). [http://www.sciencemag.org/cgi/content/abstract/246/4932/897 online]</ref> |
|||
[[File:Redshift blueshift.svg|thumb|Doppler redshift and blueshift]] |
|||
[[Doppler effect|Doppler]] blueshift is caused by movement of a source towards the observer. The term applies to any decrease in wavelength and increase in frequency caused by relative motion, even outside the [[visible spectrum]]. Only objects moving at near-[[Relativistic speed|relativistic speeds]] toward the observer are noticeably bluer to the [[naked eye]], but the wavelength of any reflected or emitted photon or other particle is shortened in the direction of travel.<ref>{{cite book|title=In Quest of the Universe | first1=Karl F. | last1=Kuhn | first2=Theo | last2=Koupelis |year= 2004|publisher=[[Jones & Bartlett Publishers]]|isbn=978-0-7637-0810-8|pages=122–3}}</ref> |
|||
Doppler blueshift is used in [[astronomy]] to determine relative motion: |
|||
The first redshift survey was the [[CfA Redshift Survey]], started in 1977 with the initial data collection completed in 1982.<ref>See the official CfA [http://cfa-www.harvard.edu/~huchra/zcat/ website] for more details.</ref> More recently, the [[2dF Galaxy Redshift Survey]] determined the large-scale structure of one section of the Universe, measuring ''z''-values for over 220,000 galaxies; data collection was completed in 2002, and the final [[data set]] was released 30 June 2003.<ref>{{cite paper|title=The 2dF galaxy redshift survey: Power-spectrum analysis of the final dataset and cosmological implications|author=Shaun Cole ''et al.'' (The 2dFGRS Collaboration)|journal=Mon. Not. Roy. Astron. Soc.|volume=362|pages=505–34|year=2005|url=http://www.arxiv.org/abs/}} [http://msowww.anu.edu.au/2dFGRS/ 2dF Galaxy Redshift Survey homepage]</ref> (In addition to mapping large-scale patterns of galaxies, 2dF established an upper limit on [[neutrino]] mass.) Another notable investigation, the [[Sloan Digital Sky Survey]] (SDSS), is ongoing as of 2005 and aims to obtain measurements on around 100 million objects.<ref>[http://www.sdss.org/ SDSS Homepage]</ref> SDSS has recorded redshifts for galaxies as high as 0.4, and has been involved in the detection of [[quasar]]s beyond ''z'' = 6. The [[DEEP2 Redshift Survey]] uses the [[Keck telescopes]] with the new "DEIMOS" [[spectrograph]]; a follow-up to the pilot program DEEP1, DEEP2 is designed to measure faint galaxies with redshifts 0.7 and above, and it is therefore planned to provide a complement to SDSS and 2dF.<ref>{{cite conference|title=Science objectives and early results of the DEEP2 redshift survey|author=Marc Davis ''et al.'' (DEEP2 collaboration)|year=2002|booktitle=Conference on Astronomical Telescopes and Instrumentation, Waikoloa, Hawaii, 22–28 Aug 2002| url=http://arxiv.org/abs/astro-ph/0209419 }}</ref> |
|||
* The [[Andromeda Galaxy]] is moving toward our own [[Milky Way]] [[galaxy]] within the [[Local Group]]; thus, when observed from Earth, its light is undergoing a blueshift.<ref>{{cite book |last=Woodhouse |first=Chris |chapter=M31 (Andromeda Galaxy) |date=2017-12-04 |title=The Astrophotography Manual |pages=308–313 |edition=2nd |publisher=Routledge |language=en |doi=10.4324/9781315159225-42 |isbn=978-1-315-15922-5}}</ref> |
|||
* Components of a [[binary star]] system will be blueshifted when moving towards Earth |
|||
* When observing spiral galaxies, the side spinning toward us will have a slight blueshift ''relative to'' the side spinning away from us (see [[Tully–Fisher relation]]). |
|||
* [[Blazar]]s are known to propel [[relativistic jet]]s toward us, emitting [[synchrotron radiation]] and [[bremsstrahlung]] that appears blueshifted.{{cn|date=March 2023}} |
|||
* Nearby stars such as [[Barnard's Star]] are moving toward us, resulting in a very small blueshift. |
|||
* Doppler blueshift of distant objects with a high ''z'' can be subtracted from the much larger [[Hubble's law|cosmological redshift]] to determine relative motion in the [[Metric expansion of space|expanding universe]].<ref name="Aoki2005">{{cite journal | title = The Largest Blueshifts of the [O III] Emission Line in Two Narrow-Line Quasars | journal = Astrophysical Journal | date = January 2005 | first1=Kentaro | last1=Aoki | first2=Toshihiro | last2=Kawaguchi | first3=Kouji | last3=Ohta | volume = 618 | issue = 2 | pages = 601–608 |arxiv = astro-ph/0409546 |bibcode = 2005ApJ...618..601A |doi = 10.1086/426075 | s2cid = 17680991 }}</ref> |
|||
=== Gravitational blueshift === |
|||
==Effects due to physical optics or radiative transfer== |
|||
[[Image:Gravitional well.jpg|thumb|[[Matter waves]] (protons, electrons, photons, etc.) falling into a [[gravity well]] become more energetic and undergo observer-independent blueshifting.]] |
|||
The interactions and phenomena summarized in the subjects of [[radiative transfer]] and [[physical optics]] can result in shifts in the wavelength and frequency of electromagnetic radiation. In such cases the shifts correspond to a physical energy transfer to matter or other photons rather than being due to a transformation between reference frames. These shifts can be due to such physical phenomena as [[Wolf effect|coherence effects]] or the [[scattering]] of [[electromagnetic radiation]] whether from [[electric charge|charged]] [[elementary particle]]s, from particulates, or from fluctuations of the [[index of refraction]] in a [[dielectric medium]] as occurs in the radio phenomenon of [[Whistler (radio)|radio whistlers]].<ref name=basicastronomy /> While such phenomena are sometimes referred to as "redshifts" and "blue shifts", in astrophysics light-matter interactions that result in energy shifts in the radiation field are generally referred to as "reddening" rather than "redshifting" which, as a term, is normally reserved for the [[#Redshift formulae|effects discussed above]].<ref name=basicastronomy /> |
|||
Unlike the ''relative'' Doppler blueshift, caused by movement of a source towards the observer and thus dependent on the received angle of the photon, gravitational blueshift is ''absolute'' and does not depend on the received angle of the photon: |
|||
{{Blockquote|Photons climbing out of a gravitating object become less energetic. This loss of energy is known as a "redshifting", as photons in the visible spectrum would appear more red. Similarly, photons falling into a gravitational field become more energetic and exhibit a blueshifting. ... Note that the magnitude of the redshifting (blueshifting) effect is not a function of the emitted angle or the received angle of the photon—it depends only on how far radially the photon had to climb out of (fall into) the potential well.<ref name=R.N_1>{{cite web| first=R. J. | last=Nemiroff| title=Gravitational Principles and Mathematics| url=http://antwrp.gsfc.nasa.gov/htmltest/gifcity/nslens_math.html| date=1993| publisher=[[NASA]]}}</ref><ref name=R.N_2>{{cite journal| first=R. J. | last=Nemiroff| title=Visual distortions near a neutron star and black hole| date=1993| journal=American Journal of Physics| volume=61| issue=7| pages=619–632| bibcode=1993AmJPh..61..619N| doi=10.1119/1.17224| arxiv=astro-ph/9312003v1| s2cid=16640860}}</ref>}} |
|||
It is a natural consequence of [[conservation of energy]] and [[mass–energy equivalence]], and was confirmed experimentally in 1959 with the [[Pound–Rebka experiment]]. Gravitational blueshift contributes to [[cosmic microwave background]] (CMB) anisotropy via the [[Sachs–Wolfe effect]]: when a gravitational well evolves while a photon is passing, the amount of blueshift on approach will differ from the amount of [[gravitational redshift]] as it leaves the region.<ref name="Bonometto2002">{{cite book | last1 = Bonometto | first1 = Silvio | last2 = Gorini | first2 = Vittorio | last3 = Moschella | first3 = Ugo | title = Modern Cosmology | publisher = [[CRC Press]] | date = 2002 | isbn = 978-0-7503-0810-6 }}</ref> |
|||
In many circumstances scattering causes radiation to redden because [[entropy]] results in the predominance of many low-[[energy]] photons over few high-energy ones (while [[conservation of energy|conserving total energy]]).<ref name=basicastronomy /> Except possibly under carefully controlled conditions, scattering does not produce the same relative change in wavelength across the whole spectrum; that is, any calculated ''z'' is generally a [[function (mathematics)|function]] of wavelength. Furthermore, scattering from [[randomness|random]] [[matter|media]] generally occurs at many [[angle]]s, and ''z'' is a function of the scattering angle. If multiple scattering occurs, or the scattering particles have relative motion, then there is generally distortion of [[spectral line]]s as well.<ref name=basicastronomy /> |
|||
==== Blue outliers ==== |
|||
In [[interstellar medium|interstellar astronomy]], [[visible spectrum|visible spectra]] can appear [[red]]der due to scattering processes in a phenomenon referred to as [[interstellar reddening]]<ref name=basicastronomy /> — similarly [[Rayleigh scattering]] causes the [[Earth's atmosphere|atmospheric]] reddening of the [[Sun]] seen in the [[sunrise]] or [[sunset]] and causes the rest of the [[sky]] to have a [[blue]] color. This phenomenon is distinct from red''shift''ing because the [[atomic spectral line|spectroscopic lines]] are not shifted to other wavelengths in reddened objects and there is an additional [[extinction (astronomy)|dimming]] and distortion associated with the phenomenon due to photons being scattered in and out of the [[Line-of-sight propagation|line-of-sight]]. |
|||
There are faraway [[active galaxies]] that show a blueshift in their [[Doubly ionized oxygen|[O III]]] emission [[Emission spectrum|lines]]. One of the largest blueshifts is found in the narrow-line [[quasar]], [[PG 1543+489]], which has a relative velocity of -1150 km/s.<ref name="Aoki2005" /> These types of galaxies are called "blue outliers".<ref name="Aoki2005" /> |
|||
===Cosmological blueshift=== |
|||
''For a list of scattering processes, see [[Scattering]].'' |
|||
In a hypothetical universe undergoing a runaway [[Big Crunch]] contraction, a cosmological blueshift would be observed, with galaxies further away being increasingly blueshifted—the exact opposite of the actually observed [[cosmological redshift]] in the present [[expanding universe]].{{cn|date=March 2023}} |
|||
==See also== |
|||
* [[Gravitational potential]] |
|||
* [[Relativistic Doppler effect]] |
|||
==References== |
==References== |
||
{{Reflist|30em}} |
|||
===Notes=== |
|||
<div class="references-small" style="column-count:2;-moz-column-count:2;"> |
|||
<references /> |
|||
</div> |
|||
==Sources== |
|||
===Articles=== |
===Articles=== |
||
*Odenwald, S. & Fienberg, RT. 1993; "Galaxy Redshifts Reconsidered" in ''Sky & Telescope'' Feb. 2003; pp31–35 (This article is useful further reading in distinguishing between the 3 types of redshift and their causes.) |
* Odenwald, S. & Fienberg, RT. 1993; "Galaxy Redshifts Reconsidered" in ''Sky & Telescope'' Feb. 2003; pp31–35 (This article is useful further reading in distinguishing between the 3 types of redshift and their causes.) |
||
*Lineweaver, Charles H. and Tamara M. Davis, "[http://www.sciam.com/article.cfm?chanID=sa006&colID=1&articleID=0009F0CA-C523-1213-852383414B7F0147 Misconceptions about the Big Bang]", ''[[Scientific American]]'', March 2005. (This article is useful for explaining the cosmological redshift mechanism as well as clearing up misconceptions regarding the physics of the expansion of space.) |
* Lineweaver, Charles H. and Tamara M. Davis, "[https://web.archive.org/web/20070715030354/http://www.sciam.com/article.cfm?chanID=sa006&colID=1&articleID=0009F0CA-C523-1213-852383414B7F0147 Misconceptions about the Big Bang]", ''[[Scientific American]]'', March 2005. (This article is useful for explaining the cosmological redshift mechanism as well as clearing up misconceptions regarding the physics of the expansion of space.) |
||
=== |
===Books=== |
||
* {{cite book | last= |
* {{cite book | last=Nussbaumer|first=Harry|author2=Lydia Bieri |author2-link=Lydia Bieri|title=Discovering the Expanding Universe|publisher=Cambridge University Press|date=2009|isbn=978-0-521-51484-2}} |
||
* {{cite book | |
* {{cite book | last=Binney|first=James|author2=Michael Merrifeld |title=Galactic Astronomy|publisher=Princeton University Press|date=1998|isbn=978-0-691-02565-0}} |
||
* {{cite book | author= |
* {{cite book | author=Carroll, Bradley W. | author2=Dale A. Ostlie | name-list-style=amp| title=An Introduction to Modern Astrophysics| publisher=Addison-Wesley Publishing Company, Inc.| date=1996| isbn=978-0-201-54730-6}} |
||
* {{cite book | |
* {{cite book | author=Feynman, Richard | author2=Leighton, Robert | author3=Sands, Matthew | title=Feynman Lectures on Physics. Vol. 1 | publisher=Addison-Wesley | date=1989 | isbn=978-0-201-51003-4| title-link=The Feynman Lectures on Physics }} |
||
* {{cite book | author= |
* {{cite book | last = Grøn | first = Øyvind |author-link=Øyvind Grøn|author2=Hervik, Sigbjørn | title = Einstein's General Theory of Relativity | location = New York | publisher = Springer | date = 2007 | isbn = 978-0-387-69199-2}} |
||
* {{cite book | |
* {{cite book |last=Harrison |first=Edward |date=2000 |title=Cosmology: The Science of the Universe |edition=2nd |publisher=Cambridge University Press |isbn=978-0-521-66148-5}} |
||
* {{cite book | |
* {{cite book | author=Kutner, Marc | title=Astronomy: A Physical Perspective | url=https://archive.org/details/astronomyphysica00kutn | url-access=registration | publisher=Cambridge University Press | date=2003 | isbn=978-0-521-52927-3}} |
||
* {{cite book | |
* {{cite book | last = Misner | first = Charles | author2 = Thorne, Kip S. | author3 = Wheeler, John Archibald | title = Gravitation | location = San Francisco | publisher = W. H. Freeman | date = 1973 | isbn = 978-0-7167-0344-0}} |
||
* {{cite book | first = |
* {{cite book | first = P. J. E. | last = Peebles | title = Principles of Physical Cosmology | publisher = Princeton University Press | date = 1993 | isbn = 978-0-691-01933-8 | url = https://archive.org/details/principlesofphys00pjep }} |
||
* {{cite book | title=Spacetime Physics: Introduction to Special Relativity | edition=2nd | publisher=W.H. Freeman | date=1992 | isbn=978-0-7167-2327-1 | last1=Taylor | first1=Edwin F. | last2=Wheeler | first2=John Archibald | author-link2=John Archibald Wheeler | url=https://archive.org/details/spacetimephysics00edwi_0 }} |
|||
* {{cite book | first = Steven | last = Weinberg | title = Gravitation and Cosmology | publisher = John Wiley | date = 1971 | isbn = 978-0-471-92567-5 | url = https://archive.org/details/gravitationcosmo00stev_0 }} |
|||
* See also [[physical cosmology#Textbooks|physical cosmology textbooks]] for applications of the cosmological and gravitational redshifts. |
* See also [[physical cosmology#Textbooks|physical cosmology textbooks]] for applications of the cosmological and gravitational redshifts. |
||
==External links== |
==External links== |
||
{{Commons|Redshift}} |
{{Commons|Redshift}} |
||
*[http://www.astro.ucla.edu/~wright/doppler.htm Ned Wright's Cosmology tutorial] |
|||
{{wiktionary}} |
|||
*[http://www.space.com/scienceastronomy/redshift.html Article on redshift from SPACE.com] |
|||
* [http://www.astro.ucla.edu/~wright/doppler.htm Ned Wright's Cosmology tutorial] |
|||
*[http://coolcosmos.ipac.caltech.edu/cosmic_classroom/cosmic_reference/redshift.html Cosmic reference guide entry on redshift] |
|||
* [https://web.archive.org/web/20051203093117/http://coolcosmos.ipac.caltech.edu/cosmic_classroom/cosmic_reference/redshift.html Cosmic reference guide entry on redshift] |
|||
*[http://www.asterism.org/tutorials/tut29-1.htm Mike Luciuk's Astronomical Redshift tutorial] |
|||
* [https://web.archive.org/web/20051121214031/http://www.asterism.org/tutorials/tut29-1.htm Mike Luciuk's Astronomical Redshift tutorial] |
|||
*[http://www.astronomy.ohio-state.edu/~pogge/Ast162/Unit5/Images/hu_animexp.gif Animated GIF of Cosmological Redshift] by Wayne Hu |
|||
* [http://www.astronomy.ohio-state.edu/~pogge/Ast162/Unit5/Images/hu_animexp.gif Animated GIF of Cosmological Redshift] by Wayne Hu |
|||
* {{cite web|last1=Merrifield|first1=Michael|last2=Hill|first2=Richard|title=Z Redshift|url=http://www.sixtysymbols.com/videos/redshift.htm|work=SIXTψ SYMBΦLS|date=2009|publisher=[[Brady Haran]] for the [[University of Nottingham]]}} |
|||
{{featured article}} |
{{featured article}} |
||
{{Portal bar|Physics|Astronomy|Stars|Spaceflight|Outer space|Solar System}} |
|||
{{Authority control}} |
|||
{{Gravitational waves}} |
|||
{{Cosmology topics}} |
|||
[[Category:Astronomical spectroscopy]] |
[[Category:Astronomical spectroscopy]] |
||
[[Category:Doppler effects]] |
[[Category:Doppler effects]] |
||
[[Category:Effects of gravity]] |
|||
[[Category:Physical cosmology]] |
[[Category:Physical cosmology]] |
||
[[Category:Physical quantities]] |
[[Category:Physical quantities]] |
||
[[Category:Concepts in astronomy]] |
|||
{{Link GA|zh}} |
|||
[[ar:انزياح أحمر]] |
|||
[[az:Qırmızı yerdəyişmə]] |
|||
[[bn:লোহিত সরণ]] |
|||
[[bs:Crveni pomak]] |
|||
[[bg:Червено отместване]] |
|||
[[ca:Desplaçament cap al roig]] |
|||
[[cs:Rudý posuv]] |
|||
[[cy:Rhuddiad]] |
|||
[[da:Rødforskydning]] |
|||
[[de:Rotverschiebung]] |
|||
[[et:Punanihe]] |
|||
[[es:Corrimiento al rojo]] |
|||
[[eo:Ruĝenŝoviĝo]] |
|||
[[fa:انتقال به سرخ]] |
|||
[[fr:Décalage vers le rouge]] |
|||
[[ko:적색 편이]] |
|||
[[hr:Crveni pomak]] |
|||
[[io:Redesko]] |
|||
[[id:Pergeseran merah]] |
|||
[[is:Rauðvik]] |
|||
[[it:Spostamento verso il rosso]] |
|||
[[he:הסחה לאדום]] |
|||
[[ka:წითელი ძვრა]] |
|||
[[lv:Sarkanā nobīde]] |
|||
[[lb:Routverrécklung]] |
|||
[[hu:Vöröseltolódás]] |
|||
[[ms:Anjakan merah]] |
|||
[[nl:Roodverschuiving]] |
|||
[[ja:赤方偏移]] |
|||
[[no:Rødforskyvning]] |
|||
[[nn:Raudforskuving]] |
|||
[[pl:Przesunięcie ku czerwieni]] |
|||
[[pt:Desvio para o vermelho]] |
|||
[[ro:Deplasare spre roșu]] |
|||
[[ru:Красное смещение]] |
|||
[[scn:Spustamentu versu lu russu]] |
|||
[[simple:Red shift]] |
|||
[[sk:Červený posun]] |
|||
[[sl:Rdeči premik]] |
|||
[[sr:Црвени помак]] |
|||
[[fi:Punasiirtymä]] |
|||
[[sv:Rödförskjutning]] |
|||
[[th:การเคลื่อนไปทางแดง]] |
|||
[[tr:Kırmızıya kayma]] |
|||
[[uk:Червоний зсув]] |
|||
[[vi:Dịch chuyển đỏ]] |
|||
[[zh:紅移]] |
|||
Latest revision as of 23:29, 19 December 2024

| General relativity |
|---|
 |
| Part of a series on |
| Physical cosmology |
|---|
 |
| Special relativity |
|---|
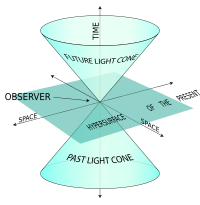 |
In physics, a redshift is an increase in the wavelength, and corresponding decrease in the frequency and photon energy, of electromagnetic radiation (such as light). The opposite change, a decrease in wavelength and increase in frequency and energy, is known as a blueshift, or negative redshift. The terms derive from the colours red and blue which form the extremes of the visible light spectrum. The main causes of electromagnetic redshift in astronomy and cosmology are the relative motions of radiation sources, which give rise to the relativistic Doppler effect, and gravitational potentials, which gravitationally redshift escaping radiation. All sufficiently distant light sources show cosmological redshift corresponding to recession speeds proportional to their distances from Earth, a fact known as Hubble's law that implies the universe is expanding.
All redshifts can be understood under the umbrella of frame transformation laws. Gravitational waves, which also travel at the speed of light, are subject to the same redshift phenomena.[1] The value of a redshift is often denoted by the letter z, corresponding to the fractional change in wavelength (positive for redshifts, negative for blueshifts), and by the wavelength ratio 1 + z (which is greater than 1 for redshifts and less than 1 for blueshifts).
Examples of strong redshifting are a gamma ray perceived as an X-ray, or initially visible light perceived as radio waves. Subtler redshifts are seen in the spectroscopic observations of astronomical objects, and are used in terrestrial technologies such as Doppler radar and radar guns.
Other physical processes exist that can lead to a shift in the frequency of electromagnetic radiation, including scattering and optical effects; however, the resulting changes are distinguishable from (astronomical) redshift and are not generally referred to as such (see section on physical optics and radiative transfer).
History
[edit]The history of the subject began in the 19th century, with the development of classical wave mechanics and the exploration of phenomena which are associated with the Doppler effect. The effect is named after the Austrian mathematician, Christian Doppler, who offered the first known physical explanation for the phenomenon in 1842.[2] In 1845, the hypothesis was tested and confirmed for sound waves by the Dutch scientist Christophorus Buys Ballot.[3] Doppler correctly predicted that the phenomenon would apply to all waves and, in particular, suggested that the varying colors of stars could be attributed to their motion with respect to the Earth.[4] Before this was verified, it was found that stellar colors were primarily due to a star's temperature, not motion. Only later was Doppler vindicated by verified redshift observations.[citation needed]
The Doppler redshift was first described by French physicist Hippolyte Fizeau in 1848, who noted the shift in spectral lines seen in stars as being due to the Doppler effect. The effect is sometimes called the "Doppler–Fizeau effect". In 1868, British astronomer William Huggins was the first to determine the velocity of a star moving away from the Earth by the method.[5] In 1871, optical redshift was confirmed when the phenomenon was observed in Fraunhofer lines, using solar rotation, about 0.1 Å in the red.[6] In 1887, Vogel and Scheiner discovered the "annual Doppler effect", the yearly change in the Doppler shift of stars located near the ecliptic, due to the orbital velocity of the Earth.[7] In 1901, Aristarkh Belopolsky verified optical redshift in the laboratory using a system of rotating mirrors.[8]
Arthur Eddington used the term "red-shift" as early as 1923,[9][10] although the word does not appear unhyphenated until about 1934, when Willem de Sitter used it.[11]
Beginning with observations in 1912, Vesto Slipher discovered that most spiral galaxies, then mostly thought to be spiral nebulae, had considerable redshifts. Slipher first reported on his measurement in the inaugural volume of the Lowell Observatory Bulletin.[12] Three years later, he wrote a review in the journal Popular Astronomy.[13] In it he stated that "the early discovery that the great Andromeda spiral had the quite exceptional velocity of –300 km(/s) showed the means then available, capable of investigating not only the spectra of the spirals but their velocities as well."[14]
Slipher reported the velocities for 15 spiral nebulae spread across the entire celestial sphere, all but three having observable "positive" (that is recessional) velocities. Subsequently, Edwin Hubble discovered an approximate relationship between the redshifts of such "nebulae", and the distances to them, with the formulation of his eponymous Hubble's law.[15] Milton Humason worked on those observations with Hubble.[16] These observations corroborated Alexander Friedmann's 1922 work, in which he derived the Friedmann–Lemaître equations.[17] They are now considered to be strong evidence for an expanding universe and the Big Bang theory.[18]
Measurement, characterization, and interpretation
[edit]
The spectrum of light that comes from a source (see idealized spectrum illustration top-right) can be measured. To determine the redshift, one searches for features in the spectrum such as absorption lines, emission lines, or other variations in light intensity. If found, these features can be compared with known features in the spectrum of various chemical compounds found in experiments where that compound is located on Earth. A very common atomic element in space is hydrogen.
The spectrum of originally featureless light shone through hydrogen will show a signature spectrum specific to hydrogen that has features at regular intervals. If restricted to absorption lines it would look similar to the illustration (top right). If the same pattern of intervals is seen in an observed spectrum from a distant source but occurring at shifted wavelengths, it can be identified as hydrogen too. If the same spectral line is identified in both spectra—but at different wavelengths—then the redshift can be calculated using the table below.
Determining the redshift of an object in this way requires a frequency or wavelength range. In order to calculate the redshift, one has to know the wavelength of the emitted light in the rest frame of the source: in other words, the wavelength that would be measured by an observer located adjacent to and comoving with the source. Since in astronomical applications this measurement cannot be done directly, because that would require traveling to the distant star of interest, the method using spectral lines described here is used instead. Redshifts cannot be calculated by looking at unidentified features whose rest-frame frequency is unknown, or with a spectrum that is featureless or white noise (random fluctuations in a spectrum).[20]
Redshift (and blueshift) may be characterized by the relative difference between the observed and emitted wavelengths (or frequency) of an object. In astronomy, it is customary to refer to this change using a dimensionless quantity called z. If λ represents wavelength and f represents frequency (note, λf = c where c is the speed of light), then z is defined by the equations:[21]
| Based on wavelength | Based on frequency |
|---|---|
After z is measured, the distinction between redshift and blueshift is simply a matter of whether z is positive or negative. For example, Doppler effect blueshifts (z < 0) are associated with objects approaching (moving closer to) the observer with the light shifting to greater energies. Conversely, Doppler effect redshifts (z > 0) are associated with objects receding (moving away) from the observer with the light shifting to lower energies. Likewise, gravitational blueshifts are associated with light emitted from a source residing within a weaker gravitational field as observed from within a stronger gravitational field, while gravitational redshifting implies the opposite conditions.
Redshift formulae
[edit]In general relativity one can derive several important special-case formulae for redshift in certain special spacetime geometries, as summarized in the following table. In all cases the magnitude of the shift (the value of z) is independent of the wavelength.[22]
| Redshift type | Geometry | Formula[23] |
|---|---|---|
| Relativistic Doppler | Minkowski space (flat spacetime) |
For motion completely in the radial or
|
| Cosmological redshift | FLRW spacetime (expanding Big Bang universe) |
|
| Gravitational redshift | any stationary spacetime |
For the Schwarzschild geometry:
In terms of escape velocity: for |
Doppler effect
[edit]

If a source of the light is moving away from an observer, then redshift (z > 0) occurs; if the source moves towards the observer, then blueshift (z < 0) occurs. This is true for all electromagnetic waves and is explained by the Doppler effect. Consequently, this type of redshift is called the Doppler redshift. If the source moves away from the observer with velocity v, which is much less than the speed of light (v ≪ c), the redshift is given by
- (since )
where c is the speed of light. In the classical Doppler effect, the frequency of the source is not modified, but the recessional motion causes the illusion of a lower frequency.
A more complete treatment of the Doppler redshift requires considering relativistic effects associated with motion of sources close to the speed of light. A complete derivation of the effect can be found in the article on the relativistic Doppler effect. In brief, objects moving close to the speed of light will experience deviations from the above formula due to the time dilation of special relativity which can be corrected for by introducing the Lorentz factor γ into the classical Doppler formula as follows (for motion solely in the line of sight):
This phenomenon was first observed in a 1938 experiment performed by Herbert E. Ives and G.R. Stilwell, called the Ives–Stilwell experiment.[24]
Since the Lorentz factor is dependent only on the magnitude of the velocity, this causes the redshift associated with the relativistic correction to be independent of the orientation of the source movement. In contrast, the classical part of the formula is dependent on the projection of the movement of the source into the line-of-sight which yields different results for different orientations. If θ is the angle between the direction of relative motion and the direction of emission in the observer's frame[25] (zero angle is directly away from the observer), the full form for the relativistic Doppler effect becomes:
and for motion solely in the line of sight (θ = 0°), this equation reduces to:
For the special case that the light is moving at right angle (θ = 90°) to the direction of relative motion in the observer's frame,[26] the relativistic redshift is known as the transverse redshift, and a redshift:
is measured, even though the object is not moving away from the observer. Even when the source is moving towards the observer, if there is a transverse component to the motion then there is some speed at which the dilation just cancels the expected blueshift and at higher speed the approaching source will be redshifted.[27]
Cosmic expansion
[edit]In the earlier part of the twentieth century, Slipher, Wirtz and others made the first measurements of the redshifts and blueshifts of galaxies beyond the Milky Way. They initially interpreted these redshifts and blueshifts as being due to random motions, but later Lemaître (1927) and Hubble (1929), using previous data, discovered a roughly linear correlation between the increasing redshifts of, and distances to, galaxies. Lemaître realized that these observations could be explained by a mechanism of producing redshifts seen in Friedmann's solutions to Einstein's equations of general relativity. The correlation between redshifts and distances arises in all expanding models.[18]
This cosmological redshift is commonly attributed to stretching of the wavelengths of photons propagating through the expanding space. This interpretation can be misleading, however; expanding space is only a choice of coordinates and thus cannot have physical consequences. The cosmological redshift is more naturally interpreted as a Doppler shift arising due to the recession of distant objects.[28]
The observational consequences of this effect can be derived using the equations from general relativity that describe a homogeneous and isotropic universe. The cosmological redshift can thus be written as a function of a, the time-dependent cosmic scale factor:
In an expanding universe such as the one we inhabit, the scale factor is monotonically increasing as time passes, thus, z is positive and distant galaxies appear redshifted.
Using a model of the expansion of the universe, redshift can be related to the age of an observed object, the so-called cosmic time–redshift relation. Denote a density ratio as Ω0:
with ρcrit the critical density demarcating a universe that eventually crunches from one that simply expands. This density is about three hydrogen atoms per cubic meter of space.[29] At large redshifts, 1 + z > Ω0−1, one finds:
where H0 is the present-day Hubble constant, and z is the redshift.[30][31]
There are several websites for calculating various times and distances from redshift, as the precise calculations require numerical integrals for most values of the parameters.[32][33][34][35]
Distinguishing between cosmological and local effects
[edit]For cosmological redshifts of z < 0.01 additional Doppler redshifts and blueshifts due to the peculiar motions of the galaxies relative to one another cause a wide scatter from the standard Hubble Law.[36] The resulting situation can be illustrated by the Expanding Rubber Sheet Universe, a common cosmological analogy used to describe the expansion of the universe. If two objects are represented by ball bearings and spacetime by a stretching rubber sheet, the Doppler effect is caused by rolling the balls across the sheet to create peculiar motion. The cosmological redshift occurs when the ball bearings are stuck to the sheet and the sheet is stretched.[37][38][39]
The redshifts of galaxies include both a component related to recessional velocity from expansion of the universe, and a component related to peculiar motion (Doppler shift).[40] The redshift due to expansion of the universe depends upon the recessional velocity in a fashion determined by the cosmological model chosen to describe the expansion of the universe, which is very different from how Doppler redshift depends upon local velocity.[41] Describing the cosmological expansion origin of redshift, cosmologist Edward Robert Harrison said, "Light leaves a galaxy, which is stationary in its local region of space, and is eventually received by observers who are stationary in their own local region of space. Between the galaxy and the observer, light travels through vast regions of expanding space. As a result, all wavelengths of the light are stretched by the expansion of space. It is as simple as that..."[42] Steven Weinberg clarified, "The increase of wavelength from emission to absorption of light does not depend on the rate of change of a(t) [the scale factor] at the times of emission or absorption, but on the increase of a(t) in the whole period from emission to absorption."[43]
If the universe were contracting instead of expanding, we would see distant galaxies blueshifted by an amount proportional to their distance instead of redshifted.[44]
Gravitational redshift
[edit]In the theory of general relativity, there is time dilation within a gravitational well. This is known as the gravitational redshift or Einstein Shift.[45] The theoretical derivation of this effect follows from the Schwarzschild solution of the Einstein equations which yields the following formula for redshift associated with a photon traveling in the gravitational field of an uncharged, nonrotating, spherically symmetric mass:
where
- G is the gravitational constant,
- M is the mass of the object creating the gravitational field,
- r is the radial coordinate of the source (which is analogous to the classical distance from the center of the object, but is actually a Schwarzschild coordinate), and
- c is the speed of light.
This gravitational redshift result can be derived from the assumptions of special relativity and the equivalence principle; the full theory of general relativity is not required.[46]
The effect is very small but measurable on Earth using the Mössbauer effect and was first observed in the Pound–Rebka experiment.[47] However, it is significant near a black hole, and as an object approaches the event horizon the red shift becomes infinite. It is also the dominant cause of large angular-scale temperature fluctuations in the cosmic microwave background radiation (see Sachs–Wolfe effect).[48]
Observations in astronomy
[edit]
The redshift observed in astronomy can be measured because the emission and absorption spectra for atoms are distinctive and well known, calibrated from spectroscopic experiments in laboratories on Earth. When the redshift of various absorption and emission lines from a single astronomical object is measured, z is found to be remarkably constant. Although distant objects may be slightly blurred and lines broadened, it is by no more than can be explained by thermal or mechanical motion of the source. For these reasons and others, the consensus among astronomers is that the redshifts they observe are due to some combination of the three established forms of Doppler-like redshifts. Alternative hypotheses and explanations for redshift such as tired light are not generally considered plausible.[50]
Spectroscopy, as a measurement, is considerably more difficult than simple photometry, which measures the brightness of astronomical objects through certain filters.[51] When photometric data is all that is available (for example, the Hubble Deep Field and the Hubble Ultra Deep Field), astronomers rely on a technique for measuring photometric redshifts.[52] Due to the broad wavelength ranges in photometric filters and the necessary assumptions about the nature of the spectrum at the light-source, errors for these sorts of measurements can range up to δz = 0.5, and are much less reliable than spectroscopic determinations.[53]
However, photometry does at least allow a qualitative characterization of a redshift. For example, if a Sun-like spectrum had a redshift of z = 1, it would be brightest in the infrared(1000nm) rather than at the blue-green(500nm) color associated with the peak of its blackbody spectrum, and the light intensity will be reduced in the filter by a factor of four, (1 + z)2. Both the photon count rate and the photon energy are redshifted. (See K correction for more details on the photometric consequences of redshift.)[54]
Local observations
[edit]In nearby objects (within our Milky Way galaxy) observed redshifts are almost always related to the line-of-sight velocities associated with the objects being observed. Observations of such redshifts and blueshifts have enabled astronomers to measure velocities and parametrize the masses of the orbiting stars in spectroscopic binaries, a method first employed in 1868 by British astronomer William Huggins.[5] Similarly, small redshifts and blueshifts detected in the spectroscopic measurements of individual stars are one way astronomers have been able to diagnose and measure the presence and characteristics of planetary systems around other stars and have even made very detailed differential measurements of redshifts during planetary transits to determine precise orbital parameters.[55]
Finely detailed measurements of redshifts are used in helioseismology to determine the precise movements of the photosphere of the Sun.[56] Redshifts have also been used to make the first measurements of the rotation rates of planets,[57] velocities of interstellar clouds,[58] the rotation of galaxies,[22] and the dynamics of accretion onto neutron stars and black holes which exhibit both Doppler and gravitational redshifts.[59] The temperatures of various emitting and absorbing objects can be obtained by measuring Doppler broadening—effectively redshifts and blueshifts over a single emission or absorption line.[60] By measuring the broadening and shifts of the 21-centimeter hydrogen line in different directions, astronomers have been able to measure the recessional velocities of interstellar gas, which in turn reveals the rotation curve of our Milky Way.[22] Similar measurements have been performed on other galaxies, such as Andromeda.[22] As a diagnostic tool, redshift measurements are one of the most important spectroscopic measurements made in astronomy.
Extragalactic observations
[edit]
The most distant objects exhibit larger redshifts corresponding to the Hubble flow of the universe. The largest-observed redshift, corresponding to the greatest distance and furthest back in time, is that of the cosmic microwave background radiation; the numerical value of its redshift is about z = 1089 (z = 0 corresponds to present time), and it shows the state of the universe about 13.8 billion years ago,[61] and 379,000 years after the initial moments of the Big Bang.[62]
The luminous point-like cores of quasars were the first "high-redshift" (z > 0.1) objects discovered before the improvement of telescopes allowed for the discovery of other high-redshift galaxies.[citation needed]
For galaxies more distant than the Local Group and the nearby Virgo Cluster, but within a thousand megaparsecs or so, the redshift is approximately proportional to the galaxy's distance. This correlation was first observed by Edwin Hubble and has come to be known as Hubble's law. Vesto Slipher was the first to discover galactic redshifts, in about 1912, while Hubble correlated Slipher's measurements with distances he measured by other means to formulate his Law.[63] Hubble's law follows in part from the Copernican principle.[63] Because it is usually not known how luminous objects are, measuring the redshift is easier than more direct distance measurements, so redshift is sometimes in practice converted to a crude distance measurement using Hubble's law.[citation needed]
Gravitational interactions of galaxies with each other and clusters cause a significant scatter in the normal plot of the Hubble diagram. The peculiar velocities associated with galaxies superimpose a rough trace of the mass of virialized objects in the universe. This effect leads to such phenomena as nearby galaxies (such as the Andromeda Galaxy) exhibiting blueshifts as we fall towards a common barycenter, and redshift maps of clusters showing a fingers of god effect due to the scatter of peculiar velocities in a roughly spherical distribution.[63] This added component gives cosmologists a chance to measure the masses of objects independent of the mass-to-light ratio (the ratio of a galaxy's mass in solar masses to its brightness in solar luminosities), an important tool for measuring dark matter.[64][page needed]
The Hubble law's linear relationship between distance and redshift assumes that the rate of expansion of the universe is constant. However, when the universe was much younger, the expansion rate, and thus the Hubble "constant", was larger than it is today. For more distant galaxies, then, whose light has been travelling to us for much longer times, the approximation of constant expansion rate fails, and the Hubble law becomes a non-linear integral relationship and dependent on the history of the expansion rate since the emission of the light from the galaxy in question. Observations of the redshift-distance relationship can be used, then, to determine the expansion history of the universe and thus the matter and energy content.[citation needed]
While it was long believed that the expansion rate has been continuously decreasing since the Big Bang, observations beginning in 1988 of the redshift-distance relationship using Type Ia supernovae have suggested that in comparatively recent times the expansion rate of the universe has begun to accelerate.[65]
Highest redshifts
[edit]
Currently, the objects with the highest known redshifts are galaxies and the objects producing gamma ray bursts.[citation needed] The most reliable redshifts are from spectroscopic data,[citation needed] and the highest-confirmed spectroscopic redshift of a galaxy is that of JADES-GS-z14-0 with a redshift of z = 14.32, corresponding to 290 million years after the Big Bang.[66] The previous record was held by GN-z11,[67] with a redshift of z = 11.1, corresponding to 400 million years after the Big Bang, and by UDFy-38135539[68] at a redshift of z = 8.6, corresponding to 600 million years after the Big Bang.
Slightly less reliable are Lyman-break redshifts, the highest of which is the lensed galaxy A1689-zD1 at a redshift z = 7.5[69][70] and the next highest being z = 7.0.[71] The most distant-observed gamma-ray burst with a spectroscopic redshift measurement was GRB 090423, which had a redshift of z = 8.2.[72] The most distant-known quasar, ULAS J1342+0928, is at z = 7.54.[73][74] The highest-known redshift radio galaxy (TGSS1530) is at a redshift z = 5.72[75] and the highest-known redshift molecular material is the detection of emission from the CO molecule from the quasar SDSS J1148+5251 at z = 6.42.[76]
Extremely red objects (EROs) are astronomical sources of radiation that radiate energy in the red and near infrared part of the electromagnetic spectrum. These may be starburst galaxies that have a high redshift accompanied by reddening from intervening dust, or they could be highly redshifted elliptical galaxies with an older (and therefore redder) stellar population.[77] Objects that are even redder than EROs are termed hyper extremely red objects (HEROs).[78]
The cosmic microwave background has a redshift of z = 1089, corresponding to an age of approximately 379,000 years after the Big Bang and a proper distance of more than 46 billion light-years.[79] The yet-to-be-observed first light from the oldest Population III stars, not long after atoms first formed and the CMB ceased to be absorbed almost completely, may have redshifts in the range of 20 < z < 100.[80] Other high-redshift events predicted by physics but not presently observable are the cosmic neutrino background from about two seconds after the Big Bang (and a redshift in excess of z > 1010)[81] and the cosmic gravitational wave background emitted directly from inflation at a redshift in excess of z > 1025.[82]
In June 2015, astronomers reported evidence for Population III stars in the Cosmos Redshift 7 galaxy at z = 6.60. Such stars are likely to have existed in the very early universe (i.e., at high redshift), and may have started the production of chemical elements heavier than hydrogen that are needed for the later formation of planets and life as we know it.[83][84]
Redshift surveys
[edit]
With advent of automated telescopes and improvements in spectroscopes, a number of collaborations have been made to map the universe in redshift space. By combining redshift with angular position data, a redshift survey maps the 3D distribution of matter within a field of the sky. These observations are used to measure properties of the large-scale structure of the universe. The Great Wall, a vast supercluster of galaxies over 500 million light-years wide, provides a dramatic example of a large-scale structure that redshift surveys can detect.[85]
The first redshift survey was the CfA Redshift Survey, started in 1977 with the initial data collection completed in 1982.[86] More recently, the 2dF Galaxy Redshift Survey determined the large-scale structure of one section of the universe, measuring redshifts for over 220,000 galaxies; data collection was completed in 2002, and the final data set was released 30 June 2003.[87] The Sloan Digital Sky Survey (SDSS), is ongoing as of 2013 and aims to measure the redshifts of around 3 million objects.[88] SDSS has recorded redshifts for galaxies as high as 0.8, and has been involved in the detection of quasars beyond z = 6. The DEEP2 Redshift Survey uses the Keck telescopes with the new "DEIMOS" spectrograph; a follow-up to the pilot program DEEP1, DEEP2 is designed to measure faint galaxies with redshifts 0.7 and above, and it is therefore planned to provide a high-redshift complement to SDSS and 2dF.[89]
Effects from physical optics or radiative transfer
[edit]The interactions and phenomena summarized in the subjects of radiative transfer and physical optics can result in shifts in the wavelength and frequency of electromagnetic radiation. In such cases, the shifts correspond to a physical energy transfer to matter or other photons rather than being by a transformation between reference frames. Such shifts can be from such physical phenomena as coherence effects or the scattering of electromagnetic radiation whether from charged elementary particles, from particulates, or from fluctuations of the index of refraction in a dielectric medium as occurs in the radio phenomenon of radio whistlers.[22] While such phenomena are sometimes referred to as "redshifts" and "blueshifts", in astrophysics light-matter interactions that result in energy shifts in the radiation field are generally referred to as "reddening" rather than "redshifting" which, as a term, is normally reserved for the effects discussed above.[22]
In many circumstances scattering causes radiation to redden because entropy results in the predominance of many low-energy photons over few high-energy ones (while conserving total energy).[22] Except possibly under carefully controlled conditions, scattering does not produce the same relative change in wavelength across the whole spectrum; that is, any calculated z is generally a function of wavelength. Furthermore, scattering from random media generally occurs at many angles, and z is a function of the scattering angle. If multiple scattering occurs, or the scattering particles have relative motion, then there is generally distortion of spectral lines as well.[22]
In interstellar astronomy, visible spectra can appear redder due to scattering processes in a phenomenon referred to as interstellar reddening[22]—similarly Rayleigh scattering causes the atmospheric reddening of the Sun seen in the sunrise or sunset and causes the rest of the sky to have a blue color. This phenomenon is distinct from redshifting because the spectroscopic lines are not shifted to other wavelengths in reddened objects and there is an additional dimming and distortion associated with the phenomenon due to photons being scattered in and out of the line of sight.[citation needed]
Blueshift
[edit]The opposite of a redshift is a blueshift. A blueshift is any decrease in wavelength (increase in energy), with a corresponding increase in frequency, of an electromagnetic wave. In visible light, this shifts a color towards the blue end of the spectrum.
Doppler blueshift
[edit]
Doppler blueshift is caused by movement of a source towards the observer. The term applies to any decrease in wavelength and increase in frequency caused by relative motion, even outside the visible spectrum. Only objects moving at near-relativistic speeds toward the observer are noticeably bluer to the naked eye, but the wavelength of any reflected or emitted photon or other particle is shortened in the direction of travel.[90]
Doppler blueshift is used in astronomy to determine relative motion:
- The Andromeda Galaxy is moving toward our own Milky Way galaxy within the Local Group; thus, when observed from Earth, its light is undergoing a blueshift.[91]
- Components of a binary star system will be blueshifted when moving towards Earth
- When observing spiral galaxies, the side spinning toward us will have a slight blueshift relative to the side spinning away from us (see Tully–Fisher relation).
- Blazars are known to propel relativistic jets toward us, emitting synchrotron radiation and bremsstrahlung that appears blueshifted.[citation needed]
- Nearby stars such as Barnard's Star are moving toward us, resulting in a very small blueshift.
- Doppler blueshift of distant objects with a high z can be subtracted from the much larger cosmological redshift to determine relative motion in the expanding universe.[92]
Gravitational blueshift
[edit]
Unlike the relative Doppler blueshift, caused by movement of a source towards the observer and thus dependent on the received angle of the photon, gravitational blueshift is absolute and does not depend on the received angle of the photon:
Photons climbing out of a gravitating object become less energetic. This loss of energy is known as a "redshifting", as photons in the visible spectrum would appear more red. Similarly, photons falling into a gravitational field become more energetic and exhibit a blueshifting. ... Note that the magnitude of the redshifting (blueshifting) effect is not a function of the emitted angle or the received angle of the photon—it depends only on how far radially the photon had to climb out of (fall into) the potential well.[93][94]
It is a natural consequence of conservation of energy and mass–energy equivalence, and was confirmed experimentally in 1959 with the Pound–Rebka experiment. Gravitational blueshift contributes to cosmic microwave background (CMB) anisotropy via the Sachs–Wolfe effect: when a gravitational well evolves while a photon is passing, the amount of blueshift on approach will differ from the amount of gravitational redshift as it leaves the region.[95]
Blue outliers
[edit]There are faraway active galaxies that show a blueshift in their [O III] emission lines. One of the largest blueshifts is found in the narrow-line quasar, PG 1543+489, which has a relative velocity of -1150 km/s.[92] These types of galaxies are called "blue outliers".[92]
Cosmological blueshift
[edit]In a hypothetical universe undergoing a runaway Big Crunch contraction, a cosmological blueshift would be observed, with galaxies further away being increasingly blueshifted—the exact opposite of the actually observed cosmological redshift in the present expanding universe.[citation needed]
See also
[edit]References
[edit]- ^ Ding, Qianhang (August 2021). "Detectability of primordial black hole binaries at high redshift". Physical Review D. 104 (4). id. 043527. arXiv:2011.13643. Bibcode:2021PhRvD.104d3527D. doi:10.1103/PhysRevD.104.043527.
- ^ Doppler, Christian (1846). Beiträge zur fixsternenkunde. Vol. 69. Prague: G. Haase Söhne. Bibcode:1846befi.book.....D.
- ^ Maulik, Dev (2005). "Doppler Sonography: A Brief History". In Maulik, Dev; Zalud, Ivica (eds.). Doppler Ultrasound in Obstetrics And Gynecology. Springer. ISBN 978-3-540-23088-5.
- ^ O'Connor, John J.; Robertson, Edmund F. (1998). "Christian Andreas Doppler". MacTutor History of Mathematics archive. University of St Andrews.
- ^ a b Huggins, William (1868). "Further Observations on the Spectra of Some of the Stars and Nebulae, with an Attempt to Determine Therefrom Whether These Bodies are Moving towards or from the Earth, Also Observations on the Spectra of the Sun and of Comet II". Philosophical Transactions of the Royal Society of London. 158: 529–564. Bibcode:1868RSPT..158..529H. doi:10.1098/rstl.1868.0022.
- ^ Reber, G. (1995). "Intergalactic Plasma". Astrophysics and Space Science. 227 (1–2): 93–96. Bibcode:1995Ap&SS.227...93R. doi:10.1007/BF00678069. S2CID 30000639.
- ^ Pannekoek, A. (1961). A History of Astronomy. Dover. p. 451. ISBN 978-0-486-65994-7.
- ^ Bélopolsky, A. (1901). "On an Apparatus for the Laboratory Demonstration of the Doppler-Fizeau Principle". Astrophysical Journal. 13: 15. Bibcode:1901ApJ....13...15B. doi:10.1086/140786.
- ^ Eddington, Arthur Stanley (1923). The Mathematical Theory of Relativity. The University Press. p. 164.
- ^ "redshift". Oxford English Dictionary (Online ed.). Oxford University Press. Retrieved 2023-03-17. (Subscription or participating institution membership required.)
- ^
de Sitter, W. (1934). "On distance, magnitude, and related quantities in an expanding universe". Bulletin of the Astronomical Institutes of the Netherlands. 7: 205. Bibcode:1934BAN.....7..205D.
It thus becomes urgent to investigate the effect of the redshift and of the metric of the universe on the apparent magnitude and observed numbers of nebulae of given magnitude
- ^
Slipher, Vesto (1912). "The radial velocity of the Andromeda Nebula". Lowell Observatory Bulletin. 1 (8): 2.56 – 2.57. Bibcode:1913LowOB...2...56S.
The magnitude of this velocity, which is the greatest hitherto observed, raises the question whether the velocity-like displacement might not be due to some other cause, but I believe we have at present no other interpretation for it
- ^ Slipher, Vesto (1915). "Spectrographic Observations of Nebulae". Popular Astronomy. 23: 21–24. Bibcode:1915PA.....23...21S.
- ^ Slipher, Vesto (1915). "Spectrographic Observations of Nebulae". Popular Astronomy. 23: 22. Bibcode:1915PA.....23...21S.
- ^ Hubble, Edwin (1929). "A Relation between Distance and Radial Velocity among Extra-Galactic Nebulae". Proceedings of the National Academy of Sciences of the United States of America. 15 (3): 168–173. Bibcode:1929PNAS...15..168H. doi:10.1073/pnas.15.3.168. PMC 522427. PMID 16577160.
- ^ "Universe is Expanding". 2017-12-08. Retrieved 2023-09-06.
- ^ Friedman, A. A. (1922). "Über die Krümmung des Raumes". Zeitschrift für Physik. 10 (1): 377–386. Bibcode:1922ZPhy...10..377F. doi:10.1007/BF01332580. S2CID 125190902. English translation in Friedman, A. (1999). "On the Curvature of Space". General Relativity and Gravitation. 31 (12): 1991–2000. Bibcode:1999GReGr..31.1991F. doi:10.1023/A:1026751225741. S2CID 122950995.)
- ^ a b This was recognized early on by physicists and astronomers working in cosmology in the 1930s. The earliest layman publication describing the details of this correspondence is Eddington, Arthur (1933). The Expanding Universe: Astronomy's 'Great Debate', 1900–1931. Cambridge University Press. (Reprint: ISBN 978-0-521-34976-5)
- ^ "Hubble census finds galaxies at redshifts 9 to 12". ESA/Hubble Press Release. Retrieved 13 December 2012.
- ^ See, for example, this 25 May 2004 press release from NASA's Swift space telescope that is researching gamma-ray bursts: "Measurements of the gamma-ray spectra obtained during the main outburst of the GRB have found little value as redshift indicators, due to the lack of well-defined features. However, optical observations of GRB afterglows have produced spectra with identifiable lines, leading to precise redshift measurements."
- ^ For a tutorial on how to define and interpret large redshift measurements, see:
Huchra, John. "Extragalactic Redshifts". NASA/IPAC Extragalactic Database. Harvard-Smithsonian Center for Astrophysics. Archived from the original on 2013-12-22. Retrieved 2023-03-16. - ^ a b c d e f g h i See Binney and Merrifeld (1998), Carroll and Ostlie (1996), Kutner (2003) for applications in astronomy.
- ^ Where z = redshift; v|| = velocity parallel to line-of-sight (positive if moving away from receiver); c = speed of light; γ = Lorentz factor; a = scale factor; G = gravitational constant; M = object mass; r = radial Schwarzschild coordinate, gtt = t,t component of the metric tensor
- ^ Ives, H.; Stilwell, G. (1938). "An Experimental study of the rate of a moving atomic clock". Journal of the Optical Society of America. 28 (7): 215–226. Bibcode:1938JOSA...28..215I. doi:10.1364/josa.28.000215.
- ^ Freund, Jurgen (2008). Special Relativity for Beginners. World Scientific. p. 120. ISBN 978-981-277-160-5.
- ^ Ditchburn, R. (1961). Light. Dover. p. 329. ISBN 978-0-12-218101-6.
- ^ See "Photons, Relativity, Doppler shift Archived 2006-08-27 at the Wayback Machine " at the University of Queensland
- ^ Bunn, E. F.; Hogg, D. W. (2009). "The kinematic origin of the cosmological redshift". American Journal of Physics. 77 (8): 688–694. arXiv:0808.1081. Bibcode:2009AmJPh..77..688B. doi:10.1119/1.3129103. S2CID 1365918.
- ^ Weinberg, Steven (1993). The First Three Minutes: A Modern View of the Origin of the Universe (2nd ed.). Basic Books. p. 34. ISBN 9780-465-02437-7.
- ^ Bergström, Lars; Goobar, Ariel (2006). Cosmology and Particle Astrophysics (2nd ed.). Springer. p. 77, Eq.4.79. ISBN 978-3-540-32924-4.
- ^ Longair, M. S. (1998). Galaxy Formation. Springer. p. 161. ISBN 978-3-540-63785-1.
- ^ a b Staff (2015). "UCLA Cosmological Calculator". UCLA. Retrieved 6 August 2022. Light travel distance was calculated from redshift value using the UCLA Cosmological Calculator, with parameters values as of 2015: H0=67.74 and OmegaM=0.3089 (see Table/Planck2015 at "Lambda-CDM model#Parameters" )
- ^ a b Staff (2018). "UCLA Cosmological Calculator". UCLA. Retrieved 6 August 2022. Light travel distance was calculated from redshift value using the UCLA Cosmological Calculator, with parameters values as of 2018: H0=67.4 and OmegaM=0.315 (see Table/Planck2018 at "Lambda-CDM model#Parameters" )
- ^ a b Staff (2022). "ICRAR Cosmology Calculator". International Centre for Radio Astronomy Research. Retrieved 6 August 2022. ICRAR Cosmology Calculator - Set H0=67.4 and OmegaM=0.315 (see Table/Planck2018 at "Lambda-CDM model#Parameters")
- ^ a b Kempner, Joshua (2022). "KEMPNER Cosmology Calculator". Kempner.net. Retrieved 6 August 2022. KEMP Cosmology Calculator - Set H0=67.4, OmegaM=0.315, and OmegaΛ=0.6847 (see Table/Planck2018 at "Lambda-CDM model#Parameters")
- ^ Measurements of the peculiar velocities out to 5 Mpc using the Hubble Space Telescope were reported in 2003 by Karachentsev, I. D.; et al. (2003). "Local galaxy flows within 5 Mpc". Astronomy and Astrophysics. 398 (2): 479–491. arXiv:astro-ph/0211011. Bibcode:2003A&A...398..479K. doi:10.1051/0004-6361:20021566. S2CID 26822121.
- ^ Koupelis, Theo; Kuhn, Karl F. (2007). In Quest of the Universe (5th ed.). Jones & Bartlett Publishers. p. 557. ISBN 978-0-7637-4387-1.
- ^ Lewis, Geraint F.; Francis, Matthew J.; Barnes, Luke A.; Kwan, Juliana; et al. (2008). "Cosmological Radar Ranging in an Expanding Universe". Monthly Notices of the Royal Astronomical Society. 388 (3): 960–964. arXiv:0805.2197. Bibcode:2008MNRAS.388..960L. doi:10.1111/j.1365-2966.2008.13477.x. S2CID 15147382.
It is perfectly valid to interpret the equations of relativity in terms of an expanding space. The mistake is to push analogies too far and imbue space with physical properties that are not consistent with the equations of relativity.
- ^ Chodorowski, Michal (2007). "Is space really expanding? A counterexample". Concepts Phys. 4 (1): 17–34. arXiv:astro-ph/0601171. Bibcode:2007ONCP....4...15C. doi:10.2478/v10005-007-0002-2. S2CID 15931627.
- ^ Bedran, M. L. (2002). "A comparison between the Doppler and cosmological redshifts" (PDF). American Journal of Physics. 70 (4): 406–408. Bibcode:2002AmJPh..70..406B. doi:10.1119/1.1446856. Retrieved 2023-03-16.
- ^ Harrison, Edward (1992). "The redshift-distance and velocity-distance laws". Astrophysical Journal, Part 1. 403: 28–31. Bibcode:1993ApJ...403...28H. doi:10.1086/172179.. A pdf file can be found here [1].
- ^ Harrison 2000, p. 302.
- ^ Weinberg, Steven (2008). Cosmology. Oxford University Press. p. 11. ISBN 978-0-19-852682-7.
- ^ This is only true in a universe where there are no peculiar velocities. Otherwise, redshifts combine as
- ^ Chant, C. A. (1930). "Notes and Queries (Telescopes and Observatory Equipment – The Einstein Shift of Solar Lines)". Journal of the Royal Astronomical Society of Canada. 24: 390. Bibcode:1930JRASC..24..390C.
- ^ Einstein, A. (1907). "Über das Relativitätsprinzip und die aus demselben gezogenen Folgerungen". Jahrbuch der Radioaktivität und Elektronik. 4: 411–462. Bibcode:1908JRE.....4..411E. See p. 458 The influence of a gravitational field on clocks
- ^ Pound, R.; Rebka, G. (1960). "Apparent Weight of Photons". Physical Review Letters. 4 (7): 337–341. Bibcode:1960PhRvL...4..337P. doi:10.1103/PhysRevLett.4.337.. This paper was the first measurement.
- ^ Sachs, R. K.; Wolfe, A. M. (1967). "Perturbations of a cosmological model and angular variations of the cosmic microwave background". Astrophysical Journal. 147 (73): 73. Bibcode:1967ApJ...147...73S. doi:10.1086/148982.
- ^ a b S.V. Pilipenko (2013-2021) "Paper-and-pencil cosmological calculator" arxiv:1303.5961, including Fortran-90 code upon which the citing charts and formulae are based.
- ^ When cosmological redshifts were first discovered, Fritz Zwicky proposed an effect known as tired light. While usually considered for historical interests, it is sometimes, along with intrinsic redshift suggestions, utilized by nonstandard cosmologies. In 1981, H. J. Reboul summarised many alternative redshift mechanisms that had been discussed in the literature since the 1930s. In 2001, Geoffrey Burbidge remarked in a review that the wider astronomical community has marginalized such discussions since the 1960s. Burbidge and Halton Arp, while investigating the mystery of the nature of quasars, tried to develop alternative redshift mechanisms, and very few of their fellow scientists acknowledged let alone accepted their work. Moreover, Goldhaber, G.; et al. (2001). "Timescale Stretch Parameterization of Type Ia Supernova B-Band Lightcurves". Astrophysical Journal. 558 (1): 359–386. arXiv:astro-ph/0104382. Bibcode:2001ApJ...558..359G. doi:10.1086/322460. S2CID 17237531. pointed out that alternative theories are unable to account for timescale stretch observed in type Ia supernovae
- ^ For a review of the subject of photometry, consider: Budding, E. (September 24, 1993). Introduction to Astronomical Photometry. Cambridge University Press. ISBN 0-521-41867-4.
- ^ The technique was first described by: Baum, W. A. (1962). McVittie, G. C. (ed.). Problems of extra-galactic research. IAU Symposium No. 15. p. 390.
- ^ Bolzonella, M.; Miralles, J.-M.; Pelló, R. (2000). "Photometric redshifts based on standard SED fitting procedures". Astronomy and Astrophysics. 363: 476–492. arXiv:astro-ph/0003380. Bibcode:2000A&A...363..476B.
- ^ A pedagogical overview of the K-correction by David Hogg and other members of the SDSS collaboration can be found at: Hogg, David W.; et al. (October 2002). "The K correction". arXiv:astro-ph/0210394.
- ^ The Exoplanet Tracker is the newest observing project to use this technique, able to track the redshift variations in multiple objects at once, as reported in Ge, Jian; Van Eyken, Julian; Mahadevan, Suvrath; Dewitt, Curtis; et al. (2006). "The First Extrasolar Planet Discovered with a New-Generation High-Throughput Doppler Instrument". The Astrophysical Journal. 648 (1): 683–695. arXiv:astro-ph/0605247. Bibcode:2006ApJ...648..683G. doi:10.1086/505699. S2CID 13879217.
- ^ Libbrecht, Keng (1988). "Solar and stellar seismology" (PDF). Space Science Reviews. 47 (3–4): 275–301. Bibcode:1988SSRv...47..275L. doi:10.1007/BF00243557. S2CID 120897051.
- ^ In 1871 Hermann Carl Vogel measured the rotation rate of Venus. Vesto Slipher was working on such measurements when he turned his attention to spiral nebulae.
- ^ An early review by Oort, J. H. on the subject: Oort, J. H. (1970). "The formation of galaxies and the origin of the high-velocity hydrogen". Astronomy and Astrophysics. 7: 381. Bibcode:1970A&A.....7..381O.
- ^ Asaoka, Ikuko (1989). "X-ray spectra at infinity from a relativistic accretion disk around a Kerr black hole". Publications of the Astronomical Society of Japan. 41 (4): 763–778. Bibcode:1989PASJ...41..763A.
- ^ Rybicki, G. B.; Lightman, A. R. (1979). Radiative Processes in Astrophysics. John Wiley & Sons. p. 288. ISBN 0-471-82759-2.
- ^ "Cosmic Detectives". The European Space Agency (ESA). 2013-04-02. Retrieved 2013-04-25.
- ^ An accurate measurement of the cosmic microwave background was achieved by the COBE experiment. The final published temperature of 2.73 K was reported in this paper: Fixsen, D. J.; Cheng, E. S.; Cottingham, D. A.; Eplee, R. E. Jr.; Isaacman, R. B.; Mather, J. C.; Meyer, S. S.; Noerdlinger, P. D.; Shafer, R. A.; Weiss, R.; Wright, E. L.; Bennett, C. L.; Boggess, N. W.; Kelsall, T.; Moseley, S. H.; Silverberg, R. F.; Smoot, G. F.; Wilkinson, D. T. (January 1994). "Cosmic microwave background dipole spectrum measured by the COBE FIRAS instrument". Astrophysical Journal. 420: 445. Bibcode:1994ApJ...420..445F. doi:10.1086/173575.. The most accurate measurement as of 2006 was achieved by the WMAP experiment.
- ^ a b c Peebles (1993).
- ^ Binney, James; Treimane, Scott (1994). Galactic dynamics. Princeton University Press. ISBN 978-0-691-08445-9.
- ^ "The Nobel Prize in Physics 2011: Information for the Public" (PDF). nobelprize.org. Retrieved 2023-06-13.
- ^ Carniani, Stefano; Hainline, Kevin; D’Eugenio, Francesco; Eisenstein, Daniel J.; Jakobsen, Peter; Witstok, Joris; Johnson, Benjamin D.; Chevallard, Jacopo; Maiolino, Roberto; Helton, Jakob M.; Willott, Chris; Robertson, Brant; Alberts, Stacey; Arribas, Santiago; Baker, William M. (2024-07-29). "Spectroscopic confirmation of two luminous galaxies at a redshift of 14". Nature. 633 (8029): 318–322. doi:10.1038/s41586-024-07860-9. ISSN 1476-4687. PMC 11390484. PMID 39074505.
- ^ Oesch, P. A.; et al. (March 1, 2016). "A Remarkably Luminous Galaxy at z=11.1 Measured with Hubble Space Telescope Grism Spectroscopy". The Astrophysical Journal. 819 (2): 129. arXiv:1603.00461. Bibcode:2016ApJ...819..129O. doi:10.3847/0004-637X/819/2/129. S2CID 119262750.
- ^ Lehnert, M. D.; Nesvadba, N. P.; Cuby, J. G.; Swinbank, A. M.; et al. (2010). "Spectroscopic Confirmation of a galaxy at redshift z = 8.6". Nature. 467 (7318): 940–942. arXiv:1010.4312. Bibcode:2010Natur.467..940L. doi:10.1038/nature09462. PMID 20962840. S2CID 4414781.
- ^ Watson, Darach; Christensen, Lise; Knudsen, Kirsten Kraiberg; Richard, Johan; Gallazzi, Anna; Michałowski, Michał Jerzy (2015). "A dusty, normal galaxy in the epoch of reionization". Nature. 519 (7543): 327–330. arXiv:1503.00002. Bibcode:2015Natur.519..327W. doi:10.1038/nature14164. PMID 25731171. S2CID 2514879.
- ^ Bradley, L. D.; et al. (2008). "Discovery of a Very Bright Strongly Lensed Galaxy Candidate at z ~ 7.6". The Astrophysical Journal. 678 (2): 647–654. arXiv:0802.2506. Bibcode:2008ApJ...678..647B. doi:10.1086/533519. S2CID 15574239.
- ^ Egami, E.; et al. (2005). "Spitzer and Hubble Space Telescope Constraints on the Physical Properties of the z~7 Galaxy Strongly Lensed by A2218". The Astrophysical Journal. 618 (1): L5 – L8. arXiv:astro-ph/0411117. Bibcode:2005ApJ...618L...5E. doi:10.1086/427550. S2CID 15920310.
- ^ Salvaterra, R.; Valle, M. Della; Campana, S.; Chincarini, G.; et al. (2009). "GRB 090423 reveals an exploding star at the epoch of re-ionization". Nature. 461 (7268): 1258–60. arXiv:0906.1578. Bibcode:2009Natur.461.1258S. doi:10.1038/nature08445. PMID 19865166. S2CID 205218263.
- ^ Chu, Jennifer (2017-12-06). "Scientists observe supermassive black hole in infant universe". MIT News. Massachusetts Institute of Technology.
- ^ Bañados, Eduardo; Venemans, Bram P.; Mazzucchelli, Chiara; Farina, Emanuele P.; Walter, Fabian; Wang, Feige; Decarli, Roberto; Stern, Daniel; Fan, Xiaohui; Davies, Frederick B.; Hennawi, Joseph F.; Simcoe, Robert A.; Turner, Monica L.; Rix, Hans-Walter; Yang, Jinyi; Kelson, Daniel D.; Rudie, Gwen C.; Winters, Jan Martin (January 2018). "An 800-million-solar-mass black hole in a significantly neutral Universe at a redshift of 7.5". Nature. 553 (7689): 473–476. arXiv:1712.01860. Bibcode:2018Natur.553..473B. doi:10.1038/nature25180. PMID 29211709. S2CID 205263326.
- ^ Saxena, A. (2018). "Discovery of a radio galaxy at z = 5.72". Monthly Notices of the Royal Astronomical Society. 480 (2): 2733–2742. arXiv:1806.01191. Bibcode:2018MNRAS.480.2733S. doi:10.1093/mnras/sty1996. S2CID 118830412.
- ^ Walter, Fabian; Bertoldi, Frank; Carilli, Chris; Cox, Pierre; et al. (2003). "Molecular gas in the host galaxy of a quasar at redshift z = 6.42". Nature. 424 (6947): 406–8. arXiv:astro-ph/0307410. Bibcode:2003Natur.424..406W. doi:10.1038/nature01821. PMID 12879063. S2CID 4419009.
- ^ Smail, Ian; Owen, F. N.; Morrison, G. E.; Keel, W. C.; et al. (2002). "The Diversity of Extremely Red Objects". The Astrophysical Journal. 581 (2): 844–864. arXiv:astro-ph/0208434. Bibcode:2002ApJ...581..844S. doi:10.1086/344440. S2CID 51737034.
- ^ Totani, Tomonori; Yoshii, Yuzuru; Iwamuro, Fumihide; Maihara, Toshinori; et al. (2001). "Hyper Extremely Red Objects in the Subaru Deep Field: Evidence for Primordial Elliptical Galaxies in the Dusty Starburst Phase". The Astrophysical Journal. 558 (2): L87 – L91. arXiv:astro-ph/0108145. Bibcode:2001ApJ...558L..87T. doi:10.1086/323619. S2CID 119511017.
- ^ Lineweaver, Charles; Davis, Tamara M. (2005). "Misconceptions about the Big Bang". Scientific American. 292 (3): 36–45. Bibcode:2005SciAm.292c..36L. doi:10.1038/scientificamerican0305-36.
- ^ Naoz, S.; Noter, S.; Barkana, R. (2006). "The first stars in the Universe". Monthly Notices of the Royal Astronomical Society: Letters. 373 (1): L98 – L102. arXiv:astro-ph/0604050. Bibcode:2006MNRAS.373L..98N. doi:10.1111/j.1745-3933.2006.00251.x. S2CID 14454275.
- ^ Lesgourgues, J; Pastor, S (2006). "Massive neutrinos and cosmology". Physics Reports. 429 (6): 307–379. arXiv:astro-ph/0603494. Bibcode:2006PhR...429..307L. doi:10.1016/j.physrep.2006.04.001. S2CID 5955312.
- ^ Grishchuk, Leonid P (2005). "Relic gravitational waves and cosmology". Physics-Uspekhi. 48 (12): 1235–1247. arXiv:gr-qc/0504018. Bibcode:2005PhyU...48.1235G. doi:10.1070/PU2005v048n12ABEH005795. S2CID 11957123.
- ^ Sobral, David; Matthee, Jorryt; Darvish, Behnam; Schaerer, Daniel; Mobasher, Bahram; Röttgering, Huub J. A.; Santos, Sérgio; Hemmati, Shoubaneh (4 June 2015). "Evidence For POPIII-Like Stellar Populations In The Most Luminous LYMAN-α Emitters At The Epoch Of Re-Ionisation: Spectroscopic Confirmation". The Astrophysical Journal. 808 (2): 139. arXiv:1504.01734. Bibcode:2015ApJ...808..139S. doi:10.1088/0004-637x/808/2/139. S2CID 18471887.
- ^ Overbye, Dennis (17 June 2015). "Astronomers Report Finding Earliest Stars That Enriched Cosmos". The New York Times. Retrieved 17 June 2015.
- ^ Geller, M. J.; Huchra, J. P. (1989). "Mapping the Universe". Science. 246 (4932): 897–903. Bibcode:1989Sci...246..897G. doi:10.1126/science.246.4932.897. PMID 17812575. S2CID 31328798.
- ^ See the CfA website for more details: Huchra, John P. "The CfA Redshift Survey". Harvard & Smithsonian Center for Astrophysics. Retrieved 2023-03-20.
- ^ Cole, Shaun; Percival, Will J.; Peacock, John A.; Norberg, Peder; et al. (2005). "The 2dF galaxy redshift survey: Power-spectrum analysis of the final dataset and cosmological implications". Monthly Notices of the Royal Astronomical Society. 362 (2): 505–34. arXiv:astro-ph/0501174. Bibcode:2005MNRAS.362..505C. doi:10.1111/j.1365-2966.2005.09318.x. S2CID 6906627. 2dF Galaxy Redshift Survey homepage Archived 2007-02-05 at the Wayback Machine
- ^ "SDSS-III". www.sdss3.org. Retrieved 2023-03-20.
- ^ Davis, Marc; DEEP2 collaboration (2002). Science objectives and early results of the DEEP2 redshift survey. Conference on Astronomical Telescopes and Instrumentation, Waikoloa, Hawaii, 22–28 Aug 2002. arXiv:astro-ph/0209419. Bibcode:2003SPIE.4834..161D. doi:10.1117/12.457897.
{{cite conference}}: CS1 maint: numeric names: authors list (link) - ^ Kuhn, Karl F.; Koupelis, Theo (2004). In Quest of the Universe. Jones & Bartlett Publishers. pp. 122–3. ISBN 978-0-7637-0810-8.
- ^ Woodhouse, Chris (2017-12-04). "M31 (Andromeda Galaxy)". The Astrophotography Manual (2nd ed.). Routledge. pp. 308–313. doi:10.4324/9781315159225-42. ISBN 978-1-315-15922-5.
- ^ a b c Aoki, Kentaro; Kawaguchi, Toshihiro; Ohta, Kouji (January 2005). "The Largest Blueshifts of the [O III] Emission Line in Two Narrow-Line Quasars". Astrophysical Journal. 618 (2): 601–608. arXiv:astro-ph/0409546. Bibcode:2005ApJ...618..601A. doi:10.1086/426075. S2CID 17680991.
- ^ Nemiroff, R. J. (1993). "Gravitational Principles and Mathematics". NASA.
- ^ Nemiroff, R. J. (1993). "Visual distortions near a neutron star and black hole". American Journal of Physics. 61 (7): 619–632. arXiv:astro-ph/9312003v1. Bibcode:1993AmJPh..61..619N. doi:10.1119/1.17224. S2CID 16640860.
- ^ Bonometto, Silvio; Gorini, Vittorio; Moschella, Ugo (2002). Modern Cosmology. CRC Press. ISBN 978-0-7503-0810-6.
Sources
[edit]Articles
[edit]- Odenwald, S. & Fienberg, RT. 1993; "Galaxy Redshifts Reconsidered" in Sky & Telescope Feb. 2003; pp31–35 (This article is useful further reading in distinguishing between the 3 types of redshift and their causes.)
- Lineweaver, Charles H. and Tamara M. Davis, "Misconceptions about the Big Bang", Scientific American, March 2005. (This article is useful for explaining the cosmological redshift mechanism as well as clearing up misconceptions regarding the physics of the expansion of space.)
Books
[edit]- Nussbaumer, Harry; Lydia Bieri (2009). Discovering the Expanding Universe. Cambridge University Press. ISBN 978-0-521-51484-2.
- Binney, James; Michael Merrifeld (1998). Galactic Astronomy. Princeton University Press. ISBN 978-0-691-02565-0.
- Carroll, Bradley W. & Dale A. Ostlie (1996). An Introduction to Modern Astrophysics. Addison-Wesley Publishing Company, Inc. ISBN 978-0-201-54730-6.
- Feynman, Richard; Leighton, Robert; Sands, Matthew (1989). Feynman Lectures on Physics. Vol. 1. Addison-Wesley. ISBN 978-0-201-51003-4.
- Grøn, Øyvind; Hervik, Sigbjørn (2007). Einstein's General Theory of Relativity. New York: Springer. ISBN 978-0-387-69199-2.
- Harrison, Edward (2000). Cosmology: The Science of the Universe (2nd ed.). Cambridge University Press. ISBN 978-0-521-66148-5.
- Kutner, Marc (2003). Astronomy: A Physical Perspective. Cambridge University Press. ISBN 978-0-521-52927-3.
- Misner, Charles; Thorne, Kip S.; Wheeler, John Archibald (1973). Gravitation. San Francisco: W. H. Freeman. ISBN 978-0-7167-0344-0.
- Peebles, P. J. E. (1993). Principles of Physical Cosmology. Princeton University Press. ISBN 978-0-691-01933-8.
- Taylor, Edwin F.; Wheeler, John Archibald (1992). Spacetime Physics: Introduction to Special Relativity (2nd ed.). W.H. Freeman. ISBN 978-0-7167-2327-1.
- Weinberg, Steven (1971). Gravitation and Cosmology. John Wiley. ISBN 978-0-471-92567-5.
- See also physical cosmology textbooks for applications of the cosmological and gravitational redshifts.
External links
[edit]- Ned Wright's Cosmology tutorial
- Cosmic reference guide entry on redshift
- Mike Luciuk's Astronomical Redshift tutorial
- Animated GIF of Cosmological Redshift by Wayne Hu
- Merrifield, Michael; Hill, Richard (2009). "Z Redshift". SIXTψ SYMBΦLS. Brady Haran for the University of Nottingham.































