Quantum mechanics: Difference between revisions
Hickorybark (talk | contribs) |
Citation bot (talk | contribs) Altered author-link. Removed parameters. | Use this bot. Report bugs. | Suggested by Dominic3203 | Linked from User:Mathbot/Most_linked_math_articles | #UCB_webform_linked 398/1913 |
||
| Line 1: | Line 1: | ||
{{Short description|Description of physical properties at the atomic and subatomic scale}} |
|||
{{seeintro}} |
|||
{{Pp|small=yes}} |
|||
{{Good article}} |
|||
{{For introduction}} |
|||
[[File:Hydrogen Density Plots.png|thumb|upright=1.6|[[Wave function]]s of the [[electron]] in a hydrogen atom at different energy levels. Quantum mechanics cannot predict the exact location of a particle in space, only the probability of finding it at different locations.<ref name=Born1926>{{cite journal|author-link1= Max Born |last=Born|first=M.|title=Zur Quantenmechanik der Stoßvorgänge|trans-title=On the Quantum Mechanics of Collision Processes|journal=Zeitschrift für Physik|volume=37|pages=863–867|year=1926|doi=10.1007/BF01397477|bibcode = 1926ZPhy...37..863B|issue=12|s2cid=119896026 |issn=1434-6001 }}</ref> The brighter areas represent a higher probability of finding the electron.]] |
|||
{{Quantum mechanics}} |
{{Quantum mechanics}} |
||
[[Image:HAtomOrbitals.png|thumb|275px|Fig. 1: [[probability amplitude|Probability densities]] corresponding to the [[wavefunction]]s of an [[electron]] in a [[hydrogen atom]] possessing definite [[energy level]]s (increasing from the top of the image to the bottom: ''n'' = 1, 2, 3, ...) and [[angular momentum]] (increasing across from left to right: ''s'', ''p'', ''d'',...). Brighter areas correspond to higher probability density in a position measurement. Wavefunctions like these are directly comparable to [[Chladni's figures]] of [[acoustics|acoustic]] modes of vibration [[classical physics]] and are indeed modes of oscillation as well: they possess a sharp [[energy]] and thus a keen [[frequency]]. The [[angular momentum]] and energy are [[quantization (physics)|quantized]], and only take on discrete values like those shown (as is the case for [[Resonant frequency|resonant frequencies]] in acoustics).]] |
|||
'''Quantum mechanics''' is a fundamental [[Scientific theory|theory]] that describes the behavior of [[nature]] at and below the scale of [[atom]]s.<ref name="Feynman">{{cite book| last1 = Feynman| first1 = Richard| last2 = Leighton| first2 = Robert| last3 = Sands| first3 = Matthew| title = The Feynman Lectures on Physics| volume = 3| publisher = California Institute of Technology| date = 1964| url = https://feynmanlectures.caltech.edu/III_01.html|isbn=978-0-201-50064-6| access-date = 19 December 2020}}</ref>{{rp|1.1}} It is the foundation of all '''quantum physics''', which includes [[quantum chemistry]], [[quantum field theory]], [[quantum technology]], and [[quantum information science]]. |
|||
'''Quantum mechanics (QM)''', also known as '''quantum physics''' or '''quantum theory''', is a branch of [[physics]] providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of [[energy]] and [[matter]]. It departs from [[classical mechanics]] primarily at the atomic and subatomic scales. In advanced topics of QM, some of these behaviors are macroscopic and only emerge at very low or very high energies or [[temperature]]s. The name, coined by [[Max Planck]], derives from the observation that some physical quantities can be changed only by discrete amounts, or [[quanta]], as multiples of the [[Planck constant]], rather than being capable of varying continuously or by any arbitrary amount. For example, the [[angular momentum]], or more generally the [[action (physics)|action]], of an electron bound into an atom or molecule is quantized. An electron bound in an [[atomic orbital]] has quantized values of angular momentum while an unbound electron does not exhibit quantized energy levels. In the context of QM, the [[wave–particle duality]] of energy and matter and the [[uncertainty principle]] provide a unified view of the behavior of [[photon]]s, [[electron]]s and other atomic-scale objects. |
|||
Quantum mechanics can describe many systems that [[classical physics]] cannot. Classical physics can describe many aspects of nature at an ordinary ([[Macroscopic scale|macroscopic]] and [[Microscopic scale|(optical) microscopic]]) scale, but is not sufficient for describing them at very small [[submicroscopic]] (atomic and [[Subatomic particle|subatomic]]) scales. Most theories in classical physics can be derived from quantum mechanics as an approximation, valid at large (macroscopic/microscopic) scale.<ref>{{cite journal|last1=Jaeger|first1=Gregg|title=What in the (quantum) world is macroscopic?|journal=American Journal of Physics| date=September 2014|volume=82|issue=9|pages=896–905| doi=10.1119/1.4878358| bibcode = 2014AmJPh..82..896J }}</ref> |
|||
The [[mathematical formulations of quantum mechanics]] are abstract and the implications are often non-intuitive in terms of classic physics. The centerpiece of the mathematical system is the [[wavefunction]]. The wavefunction is a mathematical function that can provide information about the [[probability amplitude]] of position and momentum of a particle. Mathematical manipulations of the wavefunction usually involve the [[bra-ket notation]], which requires an understanding of [[complex number]]s and [[linear functional]]s. The wavefunction emphasizes the object as a [[quantum harmonic oscillator]] and the mathematics is akin to that of [[acoustics]], [[resonance]]. Many of the results of QM do not have models that are easily visualized in terms of [[classical mechanics]]; for instance, the [[ground state]] in the quantum mechanical model is a non-zero energy state that is the lowest permitted energy state of a system, rather than a more traditional system that is thought of as simply being at rest with zero kinetic energy. |
|||
Quantum systems have [[Bound state|bound]] states that are [[Quantization (physics)|quantized]] to [[Discrete mathematics|discrete values]] of [[energy]], [[momentum]], [[angular momentum]], and other quantities, in contrast to classical systems where these quantities can be measured continuously. Measurements of quantum systems show characteristics of both [[particle]]s and [[wave]]s ([[wave–particle duality]]), and there are limits to how accurately the value of a physical quantity can be predicted prior to its measurement, given a complete set of initial conditions (the [[uncertainty principle]]). |
|||
Historically, the earliest versions of QM were formulated in the first decade of the 20th century at around the same time as the [[atomic theory]] and the [[corpuscular theory of light]] as updated by Einstein first came to be widely accepted as scientific fact; these latter theories can be viewed as "quantum theories" of matter and electromagnetic radiation. QM underwent a significant re-formulation in the mid-1920's away from [[old quantum theory]] with the acceptance of the [[Copenhagen interpretation]] of [[Niels Bohr]], [[Werner Heisenberg]], [[Wolfgang Pauli]] and their associates. By 1930, QM had been further unified and formalized by the work of [[Paul Dirac]] and [[John von Neumann]], with a greater emphasis placed on [[measurement in quantum mechanics]], the statistical nature of our knowledge of reality and philosophical speculation about the [[Quantum mind–body problem|role of the observer]]. QM has since branched out into almost every aspect of 20th century physics and other disciplines such as [[quantum chemistry]], [[quantum electronics]], [[quantum optics]] and [[quantum information science]]. Much of what might be considered 19th century physics has been re-evaluated as the classical limit of QM, and its more advanced developments in terms of [[quantum field theory]] and speculative [[quantum gravity]] theories. |
|||
Quantum mechanics [[History of quantum mechanics|arose gradually]] from theories to explain observations that could not be reconciled with classical physics, such as [[Max Planck]]'s solution in 1900 to the [[black-body radiation]] problem, and the correspondence between energy and frequency in [[Albert Einstein]]'s [[Annus Mirabilis papers#Photoelectric effect|1905 paper]], which explained the [[photoelectric effect]]. These early attempts to understand microscopic phenomena, now known as the "[[old quantum theory]]", led to the full development of quantum mechanics in the mid-1920s by [[Niels Bohr]], [[Erwin Schrödinger]], [[Werner Heisenberg]], [[Max Born]], [[Paul Dirac]] and others. The modern theory is formulated in various [[mathematical formulations of quantum mechanics|specially developed mathematical formalisms]]. In one of them, a mathematical entity called the [[wave function]] provides information, in the form of [[probability amplitude]]s, about what measurements of a particle's energy, momentum, and other physical properties may yield. |
|||
==History== |
|||
{{Main|History of quantum mechanics}} |
|||
The early history of quantum mechanics can be traced to the 1838 discovery of [[cathode rays]] by [[Michael Faraday]]. This was followed by the 1859 statement of the [[black body radiation]] problem by [[Gustav Kirchhoff]], the 1877 suggestion by [[Ludwig Boltzmann]] that the energy states of a physical system can be discrete, and the 1900 quantum hypothesis of [[Max Planck]].<ref>J. Mehra and H. Rechenberg, ''The historical development of quantum theory'', Springer-Verlag, 1982.</ref> Planck's hypothesis that energy is radiated and absorbed in discrete "quanta," or "energy elements," enabled the correct derivation of the observed patterns of black body radiation. According to Planck, each energy element ''E'' is proportional to its [[frequency]] ''ν'': |
|||
:<math> E = h \nu\ </math> |
|||
== Overview and fundamental concepts == |
|||
where ''h'' is [[Planck constant|Planck's action constant]]. Planck insisted that this was simply an aspect of the processes of absorption and emission of radiation and had nothing to do with the physical reality of the radiation itself.<ref>[[Thomas Samuel Kuhn|T.S. Kuhn]], ''Black-body theory and the quantum discontinuity 1894-1912'', Clarendon Press, Oxford, 1978.</ref> However, in 1905 [[Albert Einstein]] interpreted Planck's quantum hypothesis realistically and used it to explain the [[photoelectric effect]], in which shining light on certain materials can eject electrons from the material. Einstein postulated that [[light]] itself consists of individual quanta of energy, later called [[photons]].<ref>A. Einstein, ''Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt (On a heuristic point of view concerning the production and transformation of light)'', [[Annalen der Physik]] '''17''' (1905) 132-148 (reprinted in ''The collected papers of Albert Einstein,'' John Stachel, editor, Princeton University Press, 1989, Vol. 2, pp. 149-166, in German; see also ''Einstein's early work on the quantum hypothesis,'' ibid. pp. 134-148).</ref> |
|||
Quantum mechanics allows the calculation of properties and behaviour of physical systems. It is typically applied to microscopic systems: molecules, atoms and sub-atomic particles. It has been demonstrated to hold for complex molecules with thousands of atoms,<ref>{{cite journal |author=Fein |first1=Yaakov Y. |last2=Geyer |first2=Philipp |last3=Zwick |first3=Patrick |last4=Kiałka |first4=Filip |last5=Pedalino |first5=Sebastian |last6=Mayor |first6=Marcel |last7=Gerlich |first7=Stefan |last8=Arndt |first8=Markus |date=September 2019 |title=Quantum superposition of molecules beyond 25 kDa |journal=Nature Physics |volume=15 |issue=12 |pages=1242–1245 |bibcode=2019NatPh..15.1242F |doi=10.1038/s41567-019-0663-9 |s2cid=203638258}}</ref> but its application to human beings raises philosophical problems, such as [[Wigner's friend]], and its application to the universe as a whole remains speculative.<ref>{{cite journal |last1=Bojowald |first1=Martin |title=Quantum cosmology: a review |journal=Reports on Progress in Physics |date=2015 |volume=78 |issue=2 |page=023901 |doi=10.1088/0034-4885/78/2/023901|pmid=25582917 |arxiv=1501.04899 |
|||
The foundations of quantum mechanics were established during the first half of the twentieth century by [[Niels Bohr]], [[Werner Heisenberg]], [[Max Planck]], [[Louis de Broglie]], [[Albert Einstein]], [[Erwin Schrödinger]], [[Max Born]], [[von Neumann|John von Neumann]], [[Paul Dirac]], [[Wolfgang Pauli]], [[David Hilbert]], and [[:Category:Quantum physicists|others]]. In the mid-1920s, developments in quantum mechanics quickly led to its becoming the standard formulation for atomic physics. In the summer of 1925, Bohr and Heisenberg published results that closed the [[Old quantum theory|"Old Quantum Theory"]]. Light quanta came to be called [[photons]] (1926). From Einstein's simple postulation was born a flurry of debating, theorizing and testing, and thus the entire field of quantum physics emerged, leading to its wider acceptance at the Fifth [[Solvay Conference]] in 1927. |
|||
|bibcode=2015RPPh...78b3901B |s2cid=18463042 }}</ref> Predictions of quantum mechanics have been verified experimentally to an extremely high degree of [[accuracy]]. For example, the refinement of quantum mechanics for the interaction of light and matter, known as [[quantum electrodynamics]] (QED), has been [[Precision tests of QED|shown to agree with experiment]] to within 1 part in 10<sup>12</sup> when predicting the magnetic properties of an electron.<ref>{{cite journal|first1=X. |last1=Fan |first2=T. G. |last2=Myers |first3=B. A. D. |last3=Sukra |first4=G. |last4=Gabrielse |title=Measurement of the Electron Magnetic Moment |journal=Physical Review Letters |volume=130 |pages=071801 |date=2023-02-13 |issue=7 |doi=10.1103/PhysRevLett.130.071801 |pmid=36867820 |arxiv=2209.13084 |bibcode=2023PhRvL.130g1801F}}</ref> |
|||
A fundamental feature of the theory is that it usually cannot predict with certainty what will happen, but only give probabilities. Mathematically, a probability is found by taking the square of the absolute value of a [[complex number]], known as a probability amplitude. This is known as the [[Born rule]], named after physicist [[Max Born]]. For example, a quantum particle like an [[electron]] can be described by a wave function, which associates to each point in space a probability amplitude. Applying the Born rule to these amplitudes gives a [[probability density function]] for the position that the electron will be found to have when an experiment is performed to measure it. This is the best the theory can do; it cannot say for certain where the electron will be found. The [[Schrödinger equation]] relates the collection of probability amplitudes that pertain to one moment of time to the collection of probability amplitudes that pertain to another.<ref name="Zwiebach2022"/>{{rp|67–87}} |
|||
The other [[exemplar]] that led to quantum mechanics was the study of [[electromagnetic wave]]s such as light. When it was found in 1900 by Max Planck that the energy of waves could be described as consisting of small packets or quanta, [[Albert Einstein]] further developed this idea to show that an electromagnetic wave such as light could be described by a particle called the [[photon]] with a discrete energy dependent on its frequency. This led to a [[Photon polarization|theory of unity]] between subatomic particles and electromagnetic waves called [[wave–particle duality]] in which particles and waves were neither one nor the other, but had certain properties of both. While quantum mechanics describes the world of the very small, it also is needed to explain certain [[macroscopic]] quantum systems such as [[superconductivity|superconductors]] and [[superfluid]]s. |
|||
One consequence of the mathematical rules of quantum mechanics is a tradeoff in predictability between measurable quantities. The most famous form of this [[uncertainty principle]] says that no matter how a quantum particle is prepared or how carefully experiments upon it are arranged, it is impossible to have a precise prediction for a measurement of its position and also at the same time for a measurement of its [[momentum]].<ref name="Zwiebach2022"/>{{rp|427–435}} |
|||
The word ''quantum'' derives from [[Latin language|Latin]] meaning "how great" or "how much".<ref>[http://www.merriam-webster.com/dictionary/quantum Merriam-Webster.com]</ref> In quantum mechanics, it refers to a discrete unit that quantum theory assigns to certain [[Physical quantity|physical quantities]], such as the [[energy]] of an [[atom]] at rest (see Figure 1). The discovery that particles are discrete packets of energy with wave-like properties led to the branch of physics that deals with atomic and subatomic systems which is today called quantum mechanics. It is the underlying [[mathematical]] framework of many fields of [[physics]] and [[chemistry]], including [[condensed matter physics]], [[solid-state physics]], [[atomic physics]], [[molecular physics]], [[computational physics]], [[computational chemistry]], [[quantum chemistry]], [[particle physics]], [[nuclear chemistry]], and [[nuclear physics]].<ref>[http://mooni.fccj.org/~ethall/quantum/quant.htm FCCJ.org]</ref> Some fundamental aspects of the theory are still actively studied.<ref>Compare the list of conferences presented [http://ysfine.com here].</ref> Quantum mechanics is essential to understand the behavior of systems at [[atom]]ic length scales and smaller. For example, if [[classical mechanics]] governed the workings of an atom, [[electron]]s would rapidly travel towards and collide with the [[atomic nucleus|nucleus]], making stable atoms impossible. However, in the natural world the electrons normally remain in an uncertain, non-deterministic "smeared" (wave–particle wave function) orbital path around or through the nucleus, defying [[classical electromagnetism]].<ref>[http://www.oocities.com/mik_malm/quantmech.html Oocities.com]</ref> Quantum mechanics was initially developed to provide a better explanation of the atom, especially the [[spectrum|spectra]] of [[light]] emitted by different [[isotope|atomic species]]. The quantum theory of the atom was developed as an explanation for the electron's staying in its [[atomic orbital|orbital]], which could not be explained by [[Newton's laws of motion]] and by [[Maxwell's equations|Maxwell's laws]] of classical electromagnetism. Broadly speaking, quantum mechanics incorporates four classes of phenomena for which classical physics cannot account: |
|||
[[File:Double-slit.svg|thumb|left|upright=1.2|An illustration of the double-slit experiment in physics.]] |
|||
* The [[quantization (physics)|quantization]] (discretization) of [[Canonical conjugate variables|certain physical quantities]] |
|||
Another consequence of the mathematical rules of quantum mechanics is the phenomenon of [[quantum interference]], which is often illustrated with the [[double-slit experiment]]. In the basic version of this experiment, a [[Coherence (physics)|coherent light source]], such as a [[laser]] beam, illuminates a plate pierced by two parallel slits, and the light passing through the slits is observed on a screen behind the plate.<ref name="Lederman">{{cite book|last1=Lederman|first1=Leon M.|url=https://books.google.com/books?id=qY_yOwHg_WYC&pg=PA102|title=Quantum Physics for Poets|first2=Christopher T. |last2=Hill|publisher=Prometheus Books|year=2011|isbn=978-1-61614-281-0|location=US}}</ref>{{rp|102–111}}<ref name="Feynman"/>{{rp|1.1–1.8}} The wave nature of light causes the light waves passing through the two slits to [[Interference (wave propagation)|interfere]], producing bright and dark bands on the screen – a result that would not be expected if light consisted of classical particles.<ref name="Lederman" /> However, the light is always found to be absorbed at the screen at discrete points, as individual particles rather than waves; the interference pattern appears via the varying density of these particle hits on the screen. Furthermore, versions of the experiment that include detectors at the slits find that each detected [[photon]] passes through one slit (as would a classical particle), and not through both slits (as would a wave).<ref name="Lederman"/>{{rp|109}}<ref name="Müller-Kirsten">{{cite book|last=Müller-Kirsten|first=H. J. W.|url=https://books.google.com/books?id=p1_Z81Le58MC&pg=PA14|title=Introduction to Quantum Mechanics: Schrödinger Equation and Path Integral|publisher=World Scientific|year=2006|isbn=978-981-256-691-1|location=US|page=14}}</ref><ref name="Plotnitsky">{{cite book|last=Plotnitsky|first=Arkady|url=https://books.google.com/books?id=dmdUp97S4AYC&pg=PA75|title=Niels Bohr and Complementarity: An Introduction|publisher=Springer|year=2012|isbn=978-1-4614-4517-3|location=US|pages=75–76}}</ref> However, [[Double-slit experiment#Which way|such experiments]] demonstrate that particles do not form the interference pattern if one detects which slit they pass through. This behavior is known as [[wave–particle duality]]. In addition to light, [[electrons]], [[atoms]], and [[molecules]] are all found to exhibit the same dual behavior when fired towards a double slit.<ref name="Feynman" /> |
|||
* [[wave–particle duality]] |
|||
[[File:QuantumTunnel.jpg|left|thumb|upright=1.2|A (simplified) diagram of Quantum Tunneling, a phenomenon by which a particle may move through a barrier which would be impossible under classical mechanics.]] |
|||
* [[uncertainty principle]] |
|||
Another non-classical phenomenon predicted by quantum mechanics is [[quantum tunnelling]]: a particle that goes up against a [[potential barrier]] can cross it, even if its kinetic energy is smaller than the maximum of the potential.<ref>{{cite book |first=David J. |last=Griffiths |author-link=David J. Griffiths |title=Introduction to Quantum Mechanics |title-link=Introduction to Quantum Mechanics (book) |date=1995 |publisher=Prentice Hall |isbn=0-13-124405-1}}</ref> In classical mechanics this particle would be trapped. Quantum tunnelling has several important consequences, enabling [[radioactive decay]], [[nuclear fusion]] in stars, and applications such as [[scanning tunnelling microscopy]], [[tunnel diode]] and [[tunnel field-effect transistor]].<ref name="Trixler2013">{{cite journal|last=Trixler|first=F.| title=Quantum tunnelling to the origin and evolution of life|journal=Current Organic Chemistry|date=2013| volume=17|number=16| pages=1758–1770|doi=10.2174/13852728113179990083|pmid=24039543|pmc=3768233}}</ref><ref>{{Cite web |last=Phifer |first=Arnold |date=2012-03-27 |title=Developing more energy-efficient transistors through quantum tunneling |url=https://news.nd.edu/news/developing-more-energy-efficient-transistors-through-quantum-tunneling/ |access-date=2024-06-07 |website=Notre Dame News |language=en}}</ref> |
|||
* [[quantum entanglement]] |
|||
When quantum systems interact, the result can be the creation of [[quantum entanglement]]: their properties become so intertwined that a description of the whole solely in terms of the individual parts is no longer possible. Erwin Schrödinger called entanglement "...''the'' characteristic trait of quantum mechanics, the one that enforces its entire departure from classical lines of thought".<ref>{{cite book|chapter-url=https://plato.stanford.edu/entries/qt-entangle/ |first=Jeffrey |last=Bub |author-link=Jeffrey Bub |chapter=Quantum entanglement |title=Stanford Encyclopedia of Philosophy |title-link=Stanford Encyclopedia of Philosophy |publisher=Metaphysics Research Lab, Stanford University |editor-first=Edward N. |editor-last=Zalta |year=2019}}</ref> Quantum entanglement enables [[quantum computing]] and is part of quantum communication protocols, such as [[quantum key distribution]] and [[superdense coding]].<ref name="Caves">{{cite book|first=Carlton M. |last=Caves |author-link=Carlton M. Caves |chapter=Quantum Information Science: Emerging No More |title=OSA Century of Optics |publisher=[[The Optical Society]] |arxiv=1302.1864 |bibcode=2013arXiv1302.1864C |year=2015 |isbn=978-1-943580-04-0 |pages=320–323 |editor-first1=Paul |editor-last1=Kelley |editor-first2=Govind |editor-last2=Agrawal |editor-first3=Mike |editor-last3=Bass |editor-first4=Jeff |editor-last4=Hecht |editor-first5=Carlos |editor-last5=Stroud}}</ref> Contrary to popular misconception, entanglement does not allow sending signals [[Faster-than-light|faster than light]], as demonstrated by the [[no-communication theorem]].<ref name="Caves"/> |
|||
==Mathematical formulations== |
|||
{{Main|Mathematical formulations of quantum mechanics}} |
|||
{{See also|Quantum logic}} |
|||
Another possibility opened by entanglement is testing for "[[hidden variable theory|hidden variables]]", hypothetical properties more fundamental than the quantities addressed in quantum theory itself, knowledge of which would allow more exact predictions than quantum theory provides. A collection of results, most significantly [[Bell's theorem]], have demonstrated that broad classes of such hidden-variable theories are in fact incompatible with quantum physics. According to Bell's theorem, if nature actually operates in accord with any theory of ''local'' hidden variables, then the results of a [[Bell test experiments|Bell test]] will be constrained in a particular, quantifiable way. Many Bell tests have been performed and they have shown results incompatible with the constraints imposed by local hidden variables.<ref name="wiseman15">{{Cite journal|last=Wiseman|first=Howard|author-link=Howard M. Wiseman|date=October 2015|title=Death by experiment for local realism|journal=[[Nature (journal)|Nature]]|language=en|volume=526|issue=7575|pages=649–650|doi=10.1038/nature15631|pmid=26503054|issn=0028-0836|doi-access=free}}</ref><ref name="wolchover17">{{Cite web|url=https://www.quantamagazine.org/20170207-bell-test-quantum-loophole/|title=Experiment Reaffirms Quantum Weirdness|last=Wolchover|first=Natalie|author-link=Natalie Wolchover|date=7 February 2017|work=[[Quanta Magazine]]|language=en-US|access-date=8 February 2020}}</ref> |
|||
IN the mathematically rigorous formulation of quantum mechanics, developed by [[Paul Dirac]]<ref>P.A.M. Dirac, ''The Principles of Quantum Mechanics,'' Clarendon Press, Oxford, 1930.</ref> and [[John von Neumann]],<ref>J. von Neumann, ''Mathematische Grundlagen der Quantenmechanik,'' Springer, Berlin, 1932 (English translation: ''Mathematical Foundations of Quantum Mechanics,'' Princeton University Press, 1955).</ref> the possible states of a quantum mechanical system are represented by [[unit vector]]s (called "state vectors") residing in a [[complex number|complex]] [[Separable space|separable]] [[Hilbert space]] (variously called the "[[State space (physics)|state space]]" or the "associated Hilbert space" of the system) well defined up to a complex number of norm 1 (the phase factor). In other words, the possible states are points in the [[projective space|projectivization]] of a Hilbert space, usually called the [[complex projective space]]. The exact nature of this Hilbert space is dependent on the system; for example, the state space for position and momentum states is the space of [[square-integrable]] functions, while the state space for the spin of a single proton is just the product of two complex planes. Each observable is represented by a maximally [[Hermitian adjoint|Hermitian]] (precisely: by a [[self-adjoint operator|self-adjoint]]) linear [[operator]] acting on the state space. Each eigenstate of an observable corresponds to an [[eigenvector]] of the operator, and the associated [[eigenvalue]] corresponds to the value of the observable in that eigenstate. If the operator's spectrum is discrete, the observable can only attain those discrete eigenvalues. |
|||
It is not possible to present these concepts in more than a superficial way without introducing the mathematics involved; understanding quantum mechanics requires not only manipulating complex numbers, but also [[linear algebra]], [[differential equation]]s, [[group theory]], and other more advanced subjects.<ref>{{cite web|url=https://math.ucr.edu/home/baez/books.html |title=How to Learn Math and Physics |date=20 March 2020 |website=University of California, Riverside |access-date=19 December 2020 |first=John C. |last=Baez |author-link=John C. Baez |quote=there's no way to understand the interpretation of quantum mechanics without also being able to ''solve quantum mechanics problems'' – to understand the theory, you need to be able to use it (and vice versa)}}</ref><ref>{{cite book|first=Carl |last=Sagan |author-link=Carl Sagan |title=The Demon-Haunted World: Science as a Candle in the Dark |page=249 |publisher=Ballantine Books |year=1996 |isbn=0-345-40946-9 |title-link=The Demon-Haunted World |quote="For most physics students, (the "mathematical underpinning" of quantum mechanics) might occupy them from, say, third grade to early graduate school{{snd}}roughly 15 years. [...] The job of the popularizer of science, trying to get across some idea of quantum mechanics to a general audience that has not gone through these initiation rites, is daunting. Indeed, there are no successful popularizations of quantum mechanics in my opinion{{snd}}partly for this reason.}}</ref> Accordingly, this article will present a mathematical formulation of quantum mechanics and survey its application to some useful and oft-studied examples. |
|||
In the formalism of quantum mechanics, the state of a system at a given time is described by a [[complex number|complex]] [[wave function]], also referred to as state vector in a complex [[vector space]].<ref>{{Cite book |
|||
|title=Quantum Mechanics Symmetries, Second edition |
|||
|first1=Walter |
|||
|last1=Greiner |
|||
|first2=Berndt |
|||
|last2=Müller |
|||
|publisher=Springer-Verlag |
|||
|year=1994 |
|||
|isbn=3-540-58080-8 |
|||
|page=52 |
|||
|url=http://books.google.com/books?id=gCfvWx6vuzUC&pg=PA52}}, [http://books.google.com/books?id=gCfvWx6vuzUC&pg=PA52 Chapter 1, p. 52] |
|||
</ref> This abstract mathematical object allows for the calculation of [[probability|probabilities]] of outcomes of concrete experiments. For example, it allows one to compute the probability of finding an electron in a particular region around the nucleus at a particular time. Contrary to classical mechanics, one can never make simultaneous predictions of [[conjugate variables]], such as position and momentum, with accuracy. For instance, electrons may be considered to be located somewhere within a region of space, but with their exact positions being unknown. Contours of constant probability, often referred to as "clouds", may be drawn around the nucleus of an atom to conceptualize where the electron might be located with the most probability. Heisenberg's [[uncertainty principle]] quantifies the inability to precisely locate the particle given its conjugate momentum.<ref>[http://www.aip.org/history/heisenberg/p08a.htm AIP.org]</ref> |
|||
== Mathematical formulation == |
|||
As the result of a measurement, the wave function containing the probability information for a system collapses from a given initial state to a particular eigenstate of the observable. The possible results of a measurement are the eigenvalues of the operator representing the observable — which explains the choice of ''Hermitian'' operators, for which all the eigenvalues are real. We can find the probability distribution of an observable in a given state by computing the [[spectral theorem|spectral decomposition]] of the corresponding operator. Heisenberg's [[uncertainty principle]] is represented by the statement that the operators corresponding to certain observables do not [[Commutator|commute]]. |
|||
{{Main|Mathematical formulation of quantum mechanics}} |
|||
In the mathematically rigorous formulation of quantum mechanics, the state of a quantum mechanical system is a vector <math>\psi</math> belonging to a ([[Separable space|separable]]) complex [[Hilbert space]] <math>\mathcal H</math>. This vector is postulated to be normalized under the Hilbert space inner product, that is, it obeys <math>\langle \psi,\psi \rangle = 1</math>, and it is well-defined up to a complex number of modulus 1 (the global phase), that is, <math>\psi</math> and <math>e^{i\alpha}\psi</math> represent the same physical system. In other words, the possible states are points in the [[projective space]] of a Hilbert space, usually called the [[complex projective space]]. The exact nature of this Hilbert space is dependent on the system – for example, for describing position and momentum the Hilbert space is the space of complex [[square-integrable]] functions <math>L^2(\mathbb C)</math>, while the Hilbert space for the [[Spin (physics)|spin]] of a single proton is simply the space of two-dimensional complex vectors <math>\mathbb C^2</math> with the usual inner product. |
|||
The [[probability|probabilistic]] nature of quantum mechanics thus stems from the act of measurement. This is one of the most difficult aspects of quantum systems to understand. It was the central topic in the famous [[Bohr-Einstein debates]], in which the two scientists attempted to clarify these fundamental principles by way of [[thought experiment]]s. In the decades after the formulation of quantum mechanics, the question of what constitutes a "measurement" has been extensively studied. [[Interpretation of quantum mechanics|Interpretations of quantum mechanics]] have been formulated to do away with the concept of "wavefunction collapse"; see, for example, the [[relative state interpretation]]. The basic idea is that when a quantum system interacts with a measuring apparatus, their respective wavefunctions become [[Quantum Entanglement|entangled]], so that the original quantum system ceases to exist as an independent entity. For details, see the article on [[measurement in quantum mechanics]].<ref>{{Cite book |
|||
|title=The Quantum Challenge: Modern Research on the Foundations of Quantum Mechanics, Second edition |
|||
|first1=George |
|||
|last1=Greenstein |
|||
|first2=Arthur |
|||
|last2=Zajonc |
|||
|publisher=Jones and Bartlett Publishers, Inc |
|||
|year=2006 |
|||
|isbn=0-7637-2470-X |
|||
|page=215 |
|||
|url=http://books.google.com/books?id=5t0tm0FB1CsC&pg=PA215}}, [http://books.google.com/books?id=5t0tm0FB1CsC&pg=PA215 Chapter 8, p. 215] |
|||
</ref> |
|||
Generally, quantum mechanics does not assign definite values to observables. Instead, it makes predictions using [[probability distribution]]s; that is, the probability of obtaining possible outcomes from measuring an observable. Often these results are skewed by many causes, such as dense probability clouds<ref>probability clouds are approximate, but better than [[Bohr model|the Bohr model]], whereby electron location is given by a [[probability function]], the [[wave function]] [[eigenvalue]], such that the probability is the squared modulus of the complex amplitude</ref> or quantum state nuclear attraction.<ref>[http://www.actapress.com/PaperInfo.aspx?PaperID=25988&reason=500 Actapress.com]</ref><ref>{{Cite book |
|||
|title=The Dark Side of the Force: Economic Foundations of Conflict Theory |
|||
|first1=Jack |
|||
|last1=Hirshleifer |
|||
|publisher=Campbridge University Press |
|||
|year=2001 |
|||
|isbn=0-521-80412-4 |
|||
|page=265 |
|||
|url=http://books.google.com/books?id=W2J2IXgiZVgC&pg=PA265}}, [http://books.google.com/books?id=W2J2IXgiZVgC&pg=PA265 Chapter , p. ] |
|||
</ref> Naturally, these probabilities will depend on the quantum state at the "instant" of the measurement. Hence, uncertainty is involved in the value. There are, however, certain states that are associated with a definite value of a particular observable. These are known as [[eigenstate]]s of the observable ("eigen" can be translated from [[German language|German]] as inherent or as a characteristic).<ref>[http://www.dict.cc/german-english/eigen.html Dict.cc]<br />[http://de.pons.eu/deutsch-englisch/eigen De.pons.eu]</ref> |
|||
Physical quantities of interest{{snd}}position, momentum, energy, spin{{snd}}are represented by observables, which are [[Hermitian adjoint#Hermitian operators|Hermitian]] (more precisely, [[self-adjoint operator|self-adjoint]]) linear [[Operator (physics)|operator]]s acting on the Hilbert space. A quantum state can be an [[eigenvector]] of an observable, in which case it is called an [[eigenstate]], and the associated [[eigenvalue]] corresponds to the value of the observable in that eigenstate. More generally, a quantum state will be a linear combination of the eigenstates, known as a [[quantum superposition]]. When an observable is measured, the result will be one of its eigenvalues with probability given by the [[Born rule]]: in the simplest case the eigenvalue <math>\lambda</math> is non-degenerate and the probability is given by <math>|\langle \vec\lambda,\psi\rangle|^2</math>, where <math> \vec\lambda</math> is its associated eigenvector. More generally, the eigenvalue is degenerate and the probability is given by <math>\langle \psi,P_\lambda\psi\rangle</math>, where <math>P_\lambda</math> is the projector onto its associated eigenspace. In the continuous case, these formulas give instead the [[probability density]]. |
|||
In the everyday world, it is natural and intuitive to think of everything (every observable) as being in an eigenstate. Everything appears to have a definite position, a definite momentum, a definite energy, and a definite time of occurrence. However, quantum mechanics does not pinpoint the exact values of a particle for its position and momentum (since they are [[Conjugate variables|conjugate pairs]]) or its energy and time (since they too are conjugate pairs); rather, it only provides a range of probabilities of where that particle might be given its momentum and momentum probability. Therefore, it is helpful to use different words to describe states having ''[[Uncertainty principle|uncertain]]'' values and states having ''definite'' values (eigenstate). Usually, a system will not be in an [[eigenstate]] of the observable we are interested in. However, if one measures the observable, the wavefunction will instantaneously be an eigenstate (or generalized eigenstate) of that observable. This process is known as [[wavefunction collapse]], a debatable process.<ref>[http://www.phy.olemiss.edu/~luca/Topics/qm/collapse.html PHY.olemiss.edu]</ref> It involves expanding the system under study to include the measurement device. If one knows the corresponding wave function at the instant before the measurement, one will be able to compute the probability of collapsing into each of the possible eigenstates. For example, the free particle in the previous example will usually have a wavefunction that is a [[wave packet]] centered around some mean position ''x''<sub>0</sub>, neither an eigenstate of position nor of momentum. When one measures the position of the particle, it is impossible to predict with certainty the result.<ref>{{Cite book |
|||
|title=The Quantum Challenge: Modern Research on the Foundations of Quantum Mechanics, Second edition |
|||
|first1=George |
|||
|last1=Greenstein |
|||
|first2=Arthur |
|||
|last2=Zajonc |
|||
|publisher=Jones and Bartlett Publishers, Inc |
|||
|year=2006 |
|||
|isbn=0-7637-2470-X |
|||
|page=215 |
|||
|url=http://books.google.com/books?id=5t0tm0FB1CsC&pg=PA215}}, [http://books.google.com/books?id=5t0tm0FB1CsC&pg=PA215 Chapter 8, p. 215] |
|||
</ref> It is probable, but not certain, that it will be near ''x''<sub>0</sub>, where the amplitude of the wave function is large. After the measurement is performed, having obtained some result ''x'', the wave function collapses into a position eigenstate centered at ''x''.<ref>[http://farside.ph.utexas.edu/teaching/qmech/lectures/node28.html Farside.ph.utexas.edu]</ref> |
|||
After the measurement, if result <math>\lambda</math> was obtained, the quantum state is postulated to [[Collapse of the wavefunction|collapse]] to <math> \vec\lambda</math>, in the non-degenerate case, or to <math display=inline>P_\lambda\psi\big/\! \sqrt{\langle \psi,P_\lambda\psi\rangle}</math>, in the general case. The [[probability|probabilistic]] nature of quantum mechanics thus stems from the act of measurement. This is one of the most difficult aspects of quantum systems to understand. It was the central topic in the famous [[Bohr–Einstein debates]], in which the two scientists attempted to clarify these fundamental principles by way of [[thought experiment]]s. In the decades after the formulation of quantum mechanics, the question of what constitutes a "measurement" has been extensively studied. Newer [[Interpretation of quantum mechanics|interpretations of quantum mechanics]] have been formulated that do away with the concept of "[[Collapse of the wavefunction|wave function collapse]]" (see, for example, the [[many-worlds interpretation]]). The basic idea is that when a quantum system interacts with a measuring apparatus, their respective wave functions become [[Quantum Entanglement|entangled]] so that the original quantum system ceases to exist as an independent entity (see ''[[Measurement in quantum mechanics]]''<ref name="google215">{{cite book|title=The Quantum Challenge: Modern Research on the Foundations of Quantum Mechanics |edition=2nd |first1=George |last1=Greenstein |first2=Arthur |last2=Zajonc |publisher=Jones and Bartlett |date=2006 |isbn=978-0-7637-2470-2 |page=215 |chapter-url=https://books.google.com/books?id=5t0tm0FB1CsC&pg=PA215 |chapter=8 Measurement |archive-url=https://web.archive.org/web/20230102102134/https://books.google.com/books?id=5t0tm0FB1CsC&pg=PA215 |archive-date=2023-01-02}}</ref>). |
|||
The time evolution of a quantum state is described by the [[Schrödinger equation]], in which the [[Hamiltonian (quantum mechanics)|Hamiltonian]], the [[Operator (physics)|operator]] corresponding to the [[total energy]] of the system, generates time evolution. The [[time evolution]] of wave functions is [[determinism|deterministic]] in the sense that, given a wavefunction at an initial time, it makes a definite prediction of what the wavefunction will be at any later time.<ref>[http://www.reddit.com/r/philosophy/comments/8p2qv/determinism_and_naive_realism/ Reddit.com]</ref> |
|||
=== Time evolution of a quantum state === |
|||
During a [[quantum measurement|measurement]], on the other hand, the change of the wavefunction into another one is not deterministic, but rather unpredictable, i.e., [[random]]. A time-evolution simulation can be seen here.<ref>[http://demonstrations.wolfram.com/TimeEvolutionOfAWavepacketInASquareWell/ Time Evolution of a Wavepacket In a Square Well]</ref> Wave functions can change as time progresses. An equation known as the [[Schrödinger equation]] describes how wave functions change in time, a role similar to [[Newton's second law]] in classical mechanics. The Schrödinger equation, applied to the aforementioned example of the free particle, predicts that the center of a wave packet will move through space at a constant velocity, like a classical particle with no forces acting on it. However, the wave packet will also spread out as time progresses, which means that the position becomes more uncertain. This also has the effect of turning position eigenstates (which can be thought of as infinitely sharp wave packets) into broadened wave packets that are no longer position eigenstates.<ref>{{Cite book |
|||
|title=A Textbook of Quantum Mechanics |
|||
|first1=Piravonu Mathews |
|||
|last1=Mathews |
|||
|first2=K. |
|||
|last2=Venkatesan |
|||
|publisher=Tata McGraw-Hill |
|||
|year=1976 |
|||
|isbn=0-07-096510-2 |
|||
|page=36 |
|||
|url=http://books.google.com/books?id=_qzs1DD3TcsC&pg=PA36}}, [http://books.google.com/books?id=_qzs1DD3TcsC&pg=PA36 Chapter 2, p. 36] |
|||
</ref> |
|||
The time evolution of a quantum state is described by the Schrödinger equation: |
|||
Some wave functions produce probability distributions that are constant, or independent of time, such as when in a [[Eigenstate#Schr.C3.B6dinger_equation|stationary state]] of constant energy, time drops out of the absolute square of the wave function. Many systems that are treated dynamically in classical mechanics are described by such "static" wave functions. For example, a single [[electron]] in an unexcited [[atom]] is pictured classically as a particle moving in a circular trajectory around the [[atomic nucleus]], whereas in quantum mechanics it is described by a static, [[spherical coordinate system|spherically symmetric]] wavefunction surrounding the nucleus ([[:Image:HAtomOrbitals.png|Fig. 1]]). (Note that only the lowest angular momentum states, labeled ''s'', are spherically symmetric).<ref>[http://physics.ukzn.ac.za/~petruccione/Phys120/Wave%20Functions%20and%20the%20Schr%F6dinger%20Equation.pdf Physics.ukzn.ac.za]</ref> |
|||
: <math>i\hbar {\frac {\partial}{\partial t}} \psi (t) =H \psi (t). </math> |
|||
Here <math>H</math> denotes the [[Hamiltonian (quantum mechanics)|Hamiltonian]], the observable corresponding to the [[total energy]] of the system, and <math>\hbar</math> is the reduced [[Planck constant]]. The constant <math>i\hbar</math> is introduced so that the Hamiltonian is reduced to the [[Hamiltonian mechanics|classical Hamiltonian]] in cases where the quantum system can be approximated by a classical system; the ability to make such an approximation in certain limits is called the [[correspondence principle]]. |
|||
The solution of this differential equation is given by |
|||
The Schrödinger equation acts on the entire probability amplitude, not merely its absolute value. Whereas the absolute value of the probability amplitude encodes information about probabilities, its [[phase (waves)|phase]] encodes information about the [[Interference (wave propagation)|interference]] between quantum states. This gives rise to the wave-like behavior of quantum states. It turns out that analytic solutions of Schrödinger's equation are only available for [[List of quantum-mechanical systems with analytical solutions|a small number of model Hamiltonians]], of which the [[quantum harmonic oscillator]], the [[particle in a box]], the [[hydrogen molecular ion]] and the [[hydrogen atom]] are the most important representatives. Even the [[helium]] atom, which contains just one more electron than hydrogen, defies all attempts at a fully analytic treatment. There exist several techniques for generating approximate solutions. For instance, in the method known as [[perturbation theory (quantum mechanics)|perturbation theory]] one uses the analytic results for a simple quantum mechanical model to generate results for a more complicated model related to the simple model by, for example, the addition of a weak [[potential energy]]. Another method is the "semi-classical equation of motion" approach, which applies to systems for which quantum mechanics produces weak deviations from classical behavior. The deviations can be calculated based on the classical motion. This approach is important for the field of [[quantum chaos]]. |
|||
: <math> \psi(t) = e^{-iHt/\hbar }\psi(0). </math> |
|||
The operator <math>U(t) = e^{-iHt/\hbar } </math> is known as the time-evolution operator, and has the crucial property that it is [[Unitarity (physics)|unitary]]. This time evolution is [[determinism|deterministic]] in the sense that – given an initial quantum state <math>\psi(0)</math> – it makes a definite prediction of what the quantum state <math>\psi(t)</math> will be at any later time.<ref>{{cite book |title=Dreams Of A Final Theory: The Search for The Fundamental Laws of Nature |first1=Steven |last1=Weinberg |publisher=Random House |year=2010 |isbn=978-1-4070-6396-6 |page=[https://books.google.com/books?id=OLrZkgPsZR0C&pg=PT82 82] |url=https://books.google.com/books?id=OLrZkgPsZR0C}}</ref> |
|||
[[File:Atomic-orbital-clouds spd m0.png|thumb|upright=1.25|Fig. 1: [[Probability density function|Probability densities]] corresponding to the wave functions of an electron in a hydrogen atom possessing definite energy levels (increasing from the top of the image to the bottom: ''n'' = 1, 2, 3, ...) and angular momenta (increasing across from left to right: ''s'', ''p'', ''d'', ...). Denser areas correspond to higher probability density in a position measurement. Such wave functions are directly comparable to [[Chladni's figures]] of [[acoustics|acoustic]] modes of vibration in classical physics and are modes of oscillation as well, possessing a sharp [[energy]] and thus, a definite [[frequency]]. The [[angular momentum]] and energy are [[quantization (physics)|quantized]] and take '''only''' discrete values like those shown. (As is the case for [[Resonant frequency|resonant frequencies]] in acoustics.)]] |
|||
There are numerous mathematically equivalent formulations of quantum mechanics. One of the oldest and most commonly used formulations is the [[transformation theory (quantum mechanics)|transformation theory]] proposed by Cambridge [[Theoretical physics|theoretical physicist]] [[Paul Dirac]], which unifies and generalizes the two earliest formulations of quantum mechanics, [[matrix mechanics]] (invented by [[Werner Heisenberg]])<ref>[http://www.spaceandmotion.com/physics-quantum-mechanics-werner-heisenberg.htm Spaceandmotion.com]</ref><ref>Especially since [[Werner Heisenberg]] was awarded the [[Nobel Prize in Physics]] in 1932 for the creation of quantum mechanics, the role of [[Max Born]] has been obfuscated. A 2005 biography of Born details his role as the creator of the matrix formulation of quantum mechanics. This was recognized in a paper by Heisenberg, in 1940, honoring [[Max Planck]]. See: Nancy Thorndike Greenspan, "The End of the Certain World: The Life and Science of Max Born" (Basic Books, 2005), pp. 124 - 128, and 285 - 286.</ref> and [[wave mechanics]] (invented by [[Erwin Schrödinger]]).<ref>[http://th-www.if.uj.edu.pl/acta/vol19/pdf/v19p0683.pdf IF.uj.edu.pl]</ref> In this formulation, the [[quantum state|instantaneous state of a quantum system]] encodes the probabilities of its measurable properties, or "[[observable]]s". Examples of observables include [[energy]], [[position operator|position]], [[momentum operator|momentum]], and [[angular momentum]]. Observables can be either [[Continuous function|continuous]] (e.g., the position of a particle) or [[Discrete mathematics|discrete]] (e.g., the energy of an electron bound to a hydrogen atom).<ref>[http://ocw.usu.edu/physics/classical-mechanics/pdf_lectures/06.pdf OCW.ssu.edu]</ref> An alternative formulation of quantum mechanics is [[Feynman]]'s [[path integral formulation]], in which a quantum-mechanical amplitude is considered as a sum over histories between initial and final states; this is the quantum-mechanical counterpart of [[action principle]]s in classical mechanics. |
|||
Some wave functions produce probability distributions that are independent of time, such as [[Eigenstate|eigenstates of the Hamiltonian]].<ref name="Zwiebach2022">{{cite book|first=Barton |last=Zwiebach |title=Mastering Quantum Mechanics: Essentials, Theory, and Applications |author-link=Barton Zwiebach |publisher=MIT Press |year=2022 |isbn=978-0-262-04613-8}}</ref>{{rp|133–137}} Many systems that are treated dynamically in classical mechanics are described by such "static" wave functions. For example, a single electron in an unexcited [[atom]] is pictured classically as a particle moving in a circular trajectory around the [[atomic nucleus]], whereas in quantum mechanics, it is described by a static wave function surrounding the nucleus. For example, the electron wave function for an unexcited hydrogen atom is a spherically symmetric function known as an [[atomic orbital|''s'' orbital]] ([[:File:Atomic-orbital-clouds spd m0.png|Fig. 1]]). |
|||
==Interactions with other scientific theories== |
|||
The fundamental rules of quantum mechanics are very deep. They assert that the state space of a system is a [[Hilbert space]] and the observables are [[Hermitian operators]] acting on that space, but do not tell us which Hilbert space or which operators, or if it even exists. These must be chosen appropriately in order to obtain a quantitative description of a quantum system. An important guide for making these choices is the [[correspondence principle]], which states that the predictions of quantum mechanics reduce to those of classical physics when a system moves to higher energies or equivalently, larger quantum numbers. In other words, classical mechanics is simply a quantum mechanics of large systems. This "high energy" limit is known as the ''classical'' or ''correspondence limit''. One can therefore start from an established classical model of a particular system, and attempt to guess the underlying quantum model that gives rise to the classical model in the correspondence limit. |
|||
Analytic solutions of the Schrödinger equation are known for [[List of quantum-mechanical systems with analytical solutions|very few relatively simple model Hamiltonians]] including the [[quantum harmonic oscillator]], the [[particle in a box]], the [[dihydrogen cation]], and the [[hydrogen atom]]. Even the [[helium]] atom – which contains just two electrons – has defied all attempts at a fully analytic treatment, admitting no solution in [[Closed-form expression|closed form]].<ref>{{Cite journal |last1=Zhang |first1=Ruiqin |last2=Deng |first2=Conghao |date=1993-01-01 |title=Exact solutions of the Schrödinger equation for some quantum-mechanical many-body systems |url=https://link.aps.org/doi/10.1103/PhysRevA.47.71 |journal=Physical Review A |language=en |volume=47 |issue=1 |pages=71–77 |doi=10.1103/PhysRevA.47.71 |pmid=9908895 |bibcode=1993PhRvA..47...71Z |issn=1050-2947}}</ref><ref>{{Cite journal |last1=Li |first1=Jing |last2=Drummond |first2=N. D. |last3=Schuck |first3=Peter |last4=Olevano |first4=Valerio |date=2019-04-01 |title=Comparing many-body approaches against the helium atom exact solution |journal=SciPost Physics |volume=6 |issue=4 |page=040 |doi=10.21468/SciPostPhys.6.4.040 |doi-access=free |arxiv=1801.09977 |bibcode=2019ScPP....6...40L |issn=2542-4653}}</ref><ref>{{cite book |last=Drake |first=Gordon W. F. |chapter=High Precision Calculations for Helium |date=2023 |title=Springer Handbook of Atomic, Molecular, and Optical Physics |series=Springer Handbooks |pages=199–216 |editor-last=Drake |editor-first=Gordon W. F. |place=Cham |publisher=Springer International Publishing |language=en |doi=10.1007/978-3-030-73893-8_12 |isbn=978-3-030-73892-1}}</ref> |
|||
{{unsolved|physics|In the [[correspondence limit]] of '''quantum mechanics''': Is there a preferred interpretation of quantum mechanics? How does the quantum description of [[reality]], which includes elements such as the "[[superposition principle|superposition]] of states" and "[[wavefunction collapse]]", give rise to the reality we [[perception|perceive]]?}} |
|||
When quantum mechanics was originally formulated, it was applied to models whose |
|||
correspondence limit was [[theory of relativity|non-relativistic]] [[classical mechanics]]. For instance, the well-known model of the [[quantum harmonic oscillator]] uses an explicitly non-relativistic expression for the [[kinetic energy]] of the oscillator, and is thus a quantum version of the [[harmonic oscillator|classical harmonic oscillator]]. |
|||
However, there are techniques for finding approximate solutions. One method, called [[perturbation theory (quantum mechanics)|perturbation theory]], uses the analytic result for a simple quantum mechanical model to create a result for a related but more complicated model by (for example) the addition of a weak [[potential energy]].<ref name="Zwiebach2022"/>{{rp|793}} Another approximation method applies to systems for which quantum mechanics produces only small deviations from classical behavior. These deviations can then be computed based on the classical motion.<ref name="Zwiebach2022"/>{{rp|849}} |
|||
Early attempts to merge quantum mechanics with [[special relativity]] involved the replacement of the Schrödinger equation with a covariant equation such as the [[Klein-Gordon equation]] or the [[Dirac equation]]. While these theories were successful in explaining many experimental results, they had certain unsatisfactory qualities stemming from their neglect of the relativistic creation and annihilation of particles. A fully relativistic quantum theory required the development of [[quantum field theory]], which applies quantization to a field rather than a fixed set of particles. The first complete quantum field theory, [[quantum electrodynamics]], provides a fully quantum description of the [[electromagnetism|electromagnetic interaction]]. The full apparatus of quantum field theory is often unnecessary for describing electrodynamic systems. A simpler approach, one employed since the inception of quantum mechanics, is to treat [[electric charge|charged]] particles as quantum mechanical objects being acted on by a classical [[electromagnetic field]]. For example, the elementary quantum model of the [[hydrogen atom]] describes the [[electric field]] of the hydrogen atom using a classical <math>\scriptstyle -\frac{e^2}{4 \pi\ \epsilon_0\ } \frac{1}{r}</math> [[Electric potential|Coulomb potential]]. This "semi-classical" approach fails if quantum fluctuations in the electromagnetic field play an important role, such as in the emission of [[photon]]s by [[charged particle]]s. [[Field (physics)|Quantum field]] theories for the [[strong nuclear force]] and the [[weak nuclear force]] have been developed. The quantum field theory of the strong nuclear force is called [[quantum chromodynamics]], and describes the interactions of the subnuclear particles: [[quark]]s and [[gluon]]s. The [[weak nuclear force]] and the [[electromagnetic force]] were unified, in their quantized forms, into a single quantum field theory known as [[electroweak theory]], by the physicists [[Abdus Salam]], [[Sheldon Glashow]] and [[Steven Weinberg]]. These three men shared the Nobel Prize in Physics in 1979 for this work.<ref>{{cite web |
|||
|url=http://nobelprize.org/nobel_prizes/physics/laureates/1979/index.html |
|||
|title=The Nobel Prize in Physics 1979 |
|||
|publisher=Nobel Foundation |
|||
|accessdate=2010-02-16}}</ref> |
|||
=== Uncertainty principle === |
|||
It has proven difficult to construct quantum models of [[gravity]], the remaining [[fundamental force]]. Semi-classical approximations are workable, and have led to predictions such as [[Hawking radiation]]. However, the formulation of a complete theory of [[quantum gravity]] is hindered by apparent incompatibilities between [[general relativity]], the most accurate theory of gravity currently known, and some of the fundamental assumptions of quantum theory. The resolution of these incompatibilities is an area of active research, and theories such as [[string theory]] are among the possible candidates for a future theory of quantum gravity. Classical mechanics has been extended into the [[complex domain]] and complex classical mechanics exhibits behaviours similar to quantum mechanics.<ref>[http://arxiv.org/abs/1001.0131 Complex Elliptic Pendulum], Carl M. Bender, Daniel W. Hook, Karta Kooner</ref> |
|||
One consequence of the basic quantum formalism is the uncertainty principle. In its most familiar form, this states that no preparation of a quantum particle can imply simultaneously precise predictions both for a measurement of its position and for a measurement of its momentum.<ref name = "Cohen-Tannoudji">{{cite book|last1=Cohen-Tannoudji |first1=Claude |last2=Diu |first2=Bernard |last3=Laloë |first3=Franck |title=Quantum Mechanics |author-link1=Claude Cohen-Tannoudji |publisher=John Wiley & Sons |year=2005 |isbn=0-471-16433-X |translator-first1=Susan Reid |translator-last1=Hemley |translator-first2=Nicole |translator-last2=Ostrowsky |translator-first3=Dan |translator-last3=Ostrowsky}}</ref><ref name="L&L">{{cite book |last1=Landau |first1=Lev D. |author-link1=Lev Landau |url=https://archive.org/details/QuantumMechanics_104 |title=Quantum Mechanics: Non-Relativistic Theory |last2=Lifschitz |first2=Evgeny M. |author-link2=Evgeny Lifshitz |publisher=[[Pergamon Press]] |year=1977 |isbn=978-0-08-020940-1 |edition=3rd |volume=3 |oclc=2284121}}</ref> Both position and momentum are observables, meaning that they are represented by [[Self-adjoint operator|Hermitian operators]]. The position operator <math>\hat{X}</math> and momentum operator <math>\hat{P}</math> do not commute, but rather satisfy the [[canonical commutation relation]]: |
|||
===Quantum mechanics and classical physics=== |
|||
: <math>[\hat{X}, \hat{P}] = i\hbar.</math> |
|||
Predictions of quantum mechanics have been verified experimentally to a very high degree of accuracy. According to the [[correspondence principle]] between classical and quantum mechanics, all objects obey the laws of quantum mechanics, and classical mechanics is just an approximation for large systems (or a statistical quantum mechanics of a large collection of particles). The laws of classical mechanics thus follow from the laws of quantum mechanics as a statistical average at the limit of large systems or large [[quantum number]]s.<ref>[http://www.scribd.com/doc/5998949/Quantum-mechanics-course-iwhatisquantummechanics Scribd.com]</ref> However, [[Chaos theory|chaotic systems]] do not have good quantum numbers, and [[quantum chaos]] studies the relationship between classical and quantum descriptions in these systems. |
|||
Given a quantum state, the Born rule lets us compute expectation values for both <math>X</math> and <math>P</math>, and moreover for powers of them. Defining the uncertainty for an observable by a [[standard deviation]], we have |
|||
: <math>\sigma_X={\textstyle \sqrt{\left\langle X^2 \right\rangle - \left\langle X \right\rangle^2}},</math> |
|||
and likewise for the momentum: |
|||
: <math>\sigma_P=\sqrt{\left\langle P^2 \right\rangle - \left\langle P \right\rangle^2}.</math> |
|||
The uncertainty principle states that |
|||
: <math>\sigma_X \sigma_P \geq \frac{\hbar}{2}.</math> |
|||
Either standard deviation can in principle be made arbitrarily small, but not both simultaneously.<ref name="ballentine1970">Section 3.2 of {{Citation |last=Ballentine |first=Leslie E. |title=The Statistical Interpretation of Quantum Mechanics |journal=Reviews of Modern Physics |volume=42 |issue=4 |pages=358–381 |year=1970 |bibcode=1970RvMP...42..358B |doi=10.1103/RevModPhys.42.358 |s2cid=120024263}}. This fact is experimentally well-known for example in quantum optics; see e.g. chap. 2 and Fig. 2.1 {{Citation |last=Leonhardt |first=Ulf |title=Measuring the Quantum State of Light |year=1997 |url=https://archive.org/details/measuringquantum0000leon |location=Cambridge |publisher=Cambridge University Press |isbn=0-521-49730-2}}.</ref> This inequality generalizes to arbitrary pairs of self-adjoint operators <math>A</math> and <math>B</math>. The [[commutator]] of these two operators is |
|||
: <math>[A,B]=AB-BA,</math> |
|||
and this provides the lower bound on the product of standard deviations: |
|||
: <math>\sigma_A \sigma_B \geq \tfrac12 \left|\bigl\langle[A,B]\bigr\rangle \right|.</math> |
|||
Another consequence of the canonical commutation relation is that the position and momentum operators are [[Fourier transform#Uncertainty principle|Fourier transforms]] of each other, so that a description of an object according to its momentum is the Fourier transform of its description according to its position. The fact that dependence in momentum is the Fourier transform of the dependence in position means that the momentum operator is equivalent (up to an <math>i/\hbar</math> factor) to taking the derivative according to the position, since in Fourier analysis [[Fourier transform#Differentiation|differentiation corresponds to multiplication in the dual space]]. This is why in quantum equations in position space, the momentum <math> p_i</math> is replaced by <math>-i \hbar \frac {\partial}{\partial x}</math>, and in particular in the [[Schrödinger equation#Equation|non-relativistic Schrödinger equation in position space]] the momentum-squared term is replaced with a Laplacian times <math>-\hbar^2</math>.<ref name = "Cohen-Tannoudji"/> |
|||
[[Quantum coherence]] is an essential difference between classical and quantum theories, and is illustrated by the [[EPR paradox|Einstein-Podolsky-Rosen paradox]]. Quantum interference involves the addition of ''[[probability amplitude]]s'', whereas when classical waves interfere there is an addition of ''intensities''. For microscopic bodies, the extension of the system is much smaller than the [[coherence length]], which gives rise to long-range entanglement and other nonlocal phenomena characteristic of quantum systems.<ref>[http://philsci-archive.pitt.edu/archive/00002328/01/handbook.pdf Philsci-archive.pitt.edu]</ref> Quantum coherence is not typically evident at macroscopic scales, although an exception to this rule can occur at extremely low temperatures, when quantum behavior can manifest itself on more macroscopic scales (see [[Bose-Einstein condensate]]). This is in accordance with the following observations: |
|||
* Many macroscopic properties of a classical system are a direct consequences of the quantum behavior of its parts. For example, the stability of bulk matter (which consists of atoms and [[molecule]]s which would quickly collapse under electric forces alone), the rigidity of solids, and the mechanical, thermal, chemical, optical and magnetic properties of matter are all results of the interaction of [[electric charge]]s under the rules of quantum mechanics.<ref>[http://academic.brooklyn.cuny.edu/physics/sobel/Nucphys/atomprop.html Academic.brooklyn.cuny.edu]</ref> |
|||
* While the seemingly exotic behavior of matter posited by quantum mechanics and relativity theory become more apparent when dealing with extremely fast-moving or extremely tiny particles, the laws of classical Newtonian physics remain accurate in predicting the behavior of large objects—of the order of the size of large molecules and bigger—at velocities much smaller than the [[Speed of light|velocity of light]].<ref>[http://assets.cambridge.org/97805218/29526/excerpt/9780521829526_excerpt.pdf Cambridge.org]</ref> |
|||
=== |
=== Composite systems and entanglement === |
||
When two different quantum systems are considered together, the Hilbert space of the combined system is the [[tensor product]] of the Hilbert spaces of the two components. For example, let {{mvar|A}} and {{mvar|B}} be two quantum systems, with Hilbert spaces <math> \mathcal H_A </math> and <math> \mathcal H_B </math>, respectively. The Hilbert space of the composite system is then |
|||
:''Main articles: [[Quantum gravity]] and [[Theory of everything]]'' |
|||
: <math> \mathcal H_{AB} = \mathcal H_A \otimes \mathcal H_B.</math> |
|||
If the state for the first system is the vector <math>\psi_A</math> and the state for the second system is <math>\psi_B</math>, then the state of the composite system is |
|||
: <math>\psi_A \otimes \psi_B.</math> |
|||
Not all states in the joint Hilbert space <math>\mathcal H_{AB}</math> can be written in this form, however, because the superposition principle implies that linear combinations of these "separable" or "product states" are also valid. For example, if <math>\psi_A</math> and <math>\phi_A</math> are both possible states for system <math>A</math>, and likewise <math>\psi_B</math> and <math>\phi_B</math> are both possible states for system <math>B</math>, then |
|||
: <math>\tfrac{1}{\sqrt{2}} \left ( \psi_A \otimes \psi_B + \phi_A \otimes \phi_B \right )</math> |
|||
is a valid joint state that is not separable. States that are not separable are called [[quantum entanglement|entangled]].<ref name=":0">{{Cite book|last1=Nielsen|first1=Michael A.|last2=Chuang|first2=Isaac L.|title=[[Quantum Computation and Quantum Information]]|publisher=Cambridge University Press|location=Cambridge|year=2010|edition=2nd|oclc=844974180|isbn=978-1-107-00217-3|author-link1=Michael Nielsen |author-link2=Isaac Chuang}}</ref><ref name=":1">{{Cite book|title-link= Quantum Computing: A Gentle Introduction |title=Quantum Computing: A Gentle Introduction|last1=Rieffel|first1=Eleanor G.|last2=Polak|first2=Wolfgang H.|year=2011|publisher=MIT Press|isbn=978-0-262-01506-6|language=en|author-link=Eleanor Rieffel}}</ref> |
|||
If the state for a composite system is entangled, it is impossible to describe either component system {{mvar|A}} or system {{mvar|B}} by a state vector. One can instead define [[reduced density matrix|reduced density matrices]] that describe the statistics that can be obtained by making measurements on either component system alone. This necessarily causes a loss of information, though: knowing the reduced density matrices of the individual systems is not enough to reconstruct the state of the composite system.<ref name=":0" /><ref name=":1" /> Just as density matrices specify the state of a subsystem of a larger system, analogously, [[POVM|positive operator-valued measures]] (POVMs) describe the effect on a subsystem of a measurement performed on a larger system. POVMs are extensively used in quantum information theory.<ref name=":0" /><ref name="wilde">{{Cite book|last=Wilde|first=Mark M.|title=Quantum Information Theory|publisher=Cambridge University Press|year=2017|isbn=978-1-107-17616-4|edition=2nd|doi=10.1017/9781316809976.001|arxiv=1106.1445|s2cid=2515538|oclc=973404322}}</ref> |
|||
Even with the defining postulates of both Einstein's theory of general relativity and quantum theory being indisputably supported by rigorous and repeated [[Empirical research|empirical evidence]] and while they do not directly contradict each other theoretically (at least with regard to primary claims), they are resistant to being incorporated within one cohesive model.<ref> |
|||
"There is as yet no logically consistent and complete relativistic quantum field theory.", p. 4. — V. B. Berestetskii, [[Evgeny Lifshitz|E. M. Lifshitz]], L P Pitaevskii (1971). J. B. Sykes, J. S. Bell (translators). ''Relativistic Quantum Theory'' '''4, part I'''. ''Course of Theoretical Physics (Landau and Lifshitz)'' ISBN 0 08 016025 5</ref> |
|||
As described above, entanglement is a key feature of models of measurement processes in which an apparatus becomes entangled with the system being measured. Systems interacting with the environment in which they reside generally become entangled with that environment, a phenomenon known as [[quantum decoherence]]. This can explain why, in practice, quantum effects are difficult to observe in systems larger than microscopic.<ref>{{Cite journal|last=Schlosshauer|first=Maximilian|date=October 2019|title=Quantum decoherence|journal=Physics Reports|language=en|volume=831|pages=1–57|arxiv=1911.06282|bibcode=2019PhR...831....1S|doi=10.1016/j.physrep.2019.10.001|s2cid=208006050}}</ref> |
|||
Einstein himself is well known for rejecting some of the claims of quantum mechanics. While clearly contributing to the field, he did not accept the more philosophical consequences and interpretations of quantum mechanics, such as the lack of deterministic [[causality]] and the assertion that a single subatomic particle can occupy numerous areas of space at one time. He also was the first to notice some of the apparently exotic consequences of [[Quantum entanglement|entanglement]] and used them to formulate the [[Einstein-Podolsky-Rosen paradox]], in the hope of showing that quantum mechanics had unacceptable implications. This was 1935, but in 1964 it was shown by John Bell (see [[Bell inequality]]) that, although Einstein was correct in identifying seemingly paradoxical implications of quantum mechanical nonlocality, these implications could be experimentally tested. Alain Aspect's initial experiments in 1982, and many subsequent experiements since, have verified quantum entanglement. |
|||
=== Equivalence between formulations === |
|||
According to the paper of J. Bell and the [[Copenhagen interpretation]] (the common interpretation of quantum mechanics by physicists since 1927), and contrary to Einstein's ideas, quantum mechanics was not at the same time |
|||
There are many mathematically equivalent formulations of quantum mechanics. One of the oldest and most common is the "[[transformation theory (quantum mechanics)|transformation theory]]" proposed by [[Paul Dirac]], which unifies and generalizes the two earliest formulations of quantum mechanics – [[matrix mechanics]] (invented by [[Werner Heisenberg]]) and wave mechanics (invented by [[Erwin Schrödinger]]).<ref>{{cite journal|last=Rechenberg|first=Helmut|author-link=Helmut Rechenberg|year=1987|title=Erwin Schrödinger and the creation of wave mechanics|url=http://www.actaphys.uj.edu.pl/fulltext?series=Reg&vol=19&page=683|format=PDF|journal=[[Acta Physica Polonica B]]|volume=19|issue=8|pages=683–695|access-date=13 June 2016}}</ref> An alternative formulation of quantum mechanics is [[Feynman]]'s [[path integral formulation]], in which a quantum-mechanical amplitude is considered as a sum over all possible classical and non-classical paths between the initial and final states. This is the quantum-mechanical counterpart of the [[action principle]] in classical mechanics.<ref>{{cite book|first1=Richard P. |last1=Feynman |first2=Albert R. |last2=Hibbs |title=Quantum Mechanics and Path Integrals |edition=Emended |editor-first=Daniel F. |editor-last=Steyer |year=2005 |publisher=McGraw-Hill |isbn=978-0-486-47722-0 |pages=v–vii}}</ref> |
|||
=== Symmetries and conservation laws === |
|||
*a "realistic" theory |
|||
{{Main|Noether's theorem}} |
|||
The Hamiltonian <math>H</math> is known as the ''generator'' of time evolution, since it defines a unitary time-evolution operator <math>U(t) = e^{-iHt/\hbar}</math> for each value of <math>t</math>. From this relation between <math>U(t)</math> and <math>H</math>, it follows that any observable <math>A</math> that commutes with <math>H</math> will be ''conserved'': its expectation value will not change over time.<ref name="Zwiebach2022"/>{{rp|471}} This statement generalizes, as mathematically, any Hermitian operator <math>A</math> can generate a family of unitary operators parameterized by a variable <math>t</math>. Under the evolution generated by <math>A</math>, any observable <math>B</math> that commutes with <math>A</math> will be conserved. Moreover, if <math>B</math> is conserved by evolution under <math>A</math>, then <math>A</math> is conserved under the evolution generated by <math>B</math>. This implies a quantum version of the result proven by [[Emmy Noether]] in classical ([[Lagrangian mechanics|Lagrangian]]) mechanics: for every [[Differentiable function|differentiable]] [[Symmetry (physics)|symmetry]] of a Hamiltonian, there exists a corresponding [[conservation law]]. |
|||
*and a ''[[Principle of locality|local]]'' theory |
|||
== Examples == |
|||
The Einstein-Podolsky-Rosen paradox shows in any case that there exist experiments by which one can measure the state of one particle and instantaneously change the state of its entangled partner, although the two particles can be an arbitrary distance apart; however, this effect does not violate [[causality]], since no transfer of information happens. Quantum entanglement is at the basis of [[quantum cryptography]], with high-security commercial applications in banking and government. |
|||
=== Free particle === |
|||
Gravity is negligible in many areas of particle physics, so that unification between general relativity and quantum mechanics is not an urgent issue in those applications. However, the lack of a correct theory of [[quantum gravity]] is an important issue in [[cosmology]] and physicists' search for an elegant "[[theory of everything]]". Thus, resolving the inconsistencies between both theories has been a major goal of twentieth- and twenty-first-century physics. Many prominent physicists, including [[Stephen Hawking]], have labored in the attempt to discover a theory underlying ''everything'', combining not only different models of subatomic physics, but also deriving the universe's four forces —the [[strong interaction|strong force]], [[electromagnetism]], [[weak interaction|weak force]], and [[gravity]]— from a single force or phenomenon. One of the leaders in this field is [[Edward Witten]], a theoretical physicist who formulated the groundbreaking [[M-theory]], which is an attempt at describing the supersymmetrical based [[string theory]]. |
|||
{{Main|Free particle}} |
|||
[[File:Guassian Dispersion.gif|360 px|thumb|right|Position space probability density of a Gaussian [[wave packet]] moving in one dimension in free space]] |
|||
The simplest example of a quantum system with a position degree of freedom is a free particle in a single spatial dimension. A free particle is one which is not subject to external influences, so that its Hamiltonian consists only of its kinetic energy: |
|||
: <math>H = \frac{1}{2m}P^2 = - \frac {\hbar ^2}{2m} \frac {d ^2}{dx^2}. </math> |
|||
The general solution of the Schrödinger equation is given by |
|||
: <math>\psi (x,t)=\frac {1}{\sqrt {2\pi }}\int _{-\infty}^\infty{\hat {\psi }}(k,0)e^{i(kx -\frac{\hbar k^2}{2m} t)}\mathrm{d}k,</math> |
|||
which is a superposition of all possible [[plane wave]]s <math>e^{i(kx -\frac{\hbar k^2}{2m} t)}</math>, which are eigenstates of the momentum operator with momentum <math>p = \hbar k </math>. The coefficients of the superposition are <math> \hat {\psi }(k,0) </math>, which is the Fourier transform of the initial quantum state <math>\psi(x,0)</math>. |
|||
It is not possible for the solution to be a single momentum eigenstate, or a single position eigenstate, as these are not normalizable quantum states.{{refn|group=note|A momentum eigenstate would be a perfectly monochromatic wave of infinite extent, which is not square-integrable. Likewise, a position eigenstate would be a [[Dirac delta function|Dirac delta distribution]], not square-integrable and technically not a function at all. Consequently, neither can belong to the particle's Hilbert space. Physicists sometimes introduce fictitious "bases" for a Hilbert space comprising elements outside that space. These are invented for calculational convenience and do not represent physical states.<ref name = "Cohen-Tannoudji"/>{{rp|100–105}}}} Instead, we can consider a Gaussian [[wave packet]]: |
|||
===Attempts at a unified field theory=== |
|||
: <math>\psi(x,0) = \frac{1}{\sqrt[4]{\pi a}}e^{-\frac{x^2}{2a}} </math> |
|||
{{Main|Grand unified theory}} |
|||
which has Fourier transform, and therefore momentum distribution |
|||
As of 2010 the quest for unifying the [[fundamental force]]s through quantum mechanics is still ongoing. [[Quantum electrodynamics]] (or "quantum electromagnetism"), which is currently (in the perturbative regime at least) the most accurately tested physical theory,<ref>[http://latticeqcd.blogspot.com/2005/06/most-accurate-theory-we-have.html Life on the lattice: The most accurate theory we have.<!-- Bot generated title -->]</ref> has been successfully merged with the weak nuclear force into the [[electroweak force]] and work is currently being done to merge the electroweak and strong force into the [[electrostrong force]]. Current predictions state that at around 10<sup>14</sup> GeV the three aforementioned forces are fused into a single unified field,<ref>{{cite book|last=Parker |first=B. |year=1993 |title=Overcoming some of the problems |pages=259–279 |publisher= |isbn=}}</ref> Beyond this "grand unification," it is speculated that it may be possible to merge gravity with the other three gauge symmetries, expected to occur at roughly 10<sup>19</sup> GeV. However — and while special relativity is parsimoniously incorporated into quantum electrodynamics — the expanded [[general relativity]], currently the best theory describing the gravitation force, has not been fully incorporated into quantum theory. |
|||
: <math>\hat \psi(k,0) = \sqrt[4]{\frac{a}{\pi}}e^{-\frac{a k^2}{2}}. </math> |
|||
We see that as we make <math>a</math> smaller the spread in position gets smaller, but the spread in momentum gets larger. Conversely, by making <math>a</math> larger we make the spread in momentum smaller, but the spread in position gets larger. This illustrates the uncertainty principle. |
|||
As we let the Gaussian wave packet evolve in time, we see that its center moves through space at a constant velocity (like a classical particle with no forces acting on it). However, the wave packet will also spread out as time progresses, which means that the position becomes more and more uncertain. The uncertainty in momentum, however, stays constant.<ref>{{cite book|title=A Textbook of Quantum Mechanics|first1=Piravonu Mathews|last1=Mathews|first2=K.|last2=Venkatesan|publisher=Tata McGraw-Hill|year=1976|isbn=978-0-07-096510-2|page=[https://books.google.com/books?id=_qzs1DD3TcsC&pg=PA36 36]|chapter=The Schrödinger Equation and Stationary States|chapter-url=https://books.google.com/books?id=_qzs1DD3TcsC&pg=PA36}}</ref> |
|||
==Philosophical implications== |
|||
{{Main|Interpretations of quantum mechanics}} |
|||
=== Particle in a box === |
|||
Since its inception, the many [[counter-intuitive]] results of quantum mechanics have provoked strong [[philosophy|philosophical]] debate and many [[interpretations of quantum mechanics|interpretations]]. Even fundamental issues such as [[Max Born]]'s basic [[Born rule|rules]] concerning [[probability amplitude]]s and [[probability distribution]]s took decades to be appreciated. |
|||
[[File:Infinite potential well.svg|thumb|1-dimensional potential energy box (or infinite potential well)]] |
|||
{{Main|Particle in a box}} |
|||
The particle in a one-dimensional potential energy box is the most mathematically simple example where restraints lead to the quantization of energy levels. The box is defined as having zero potential energy everywhere ''inside'' a certain region, and therefore infinite potential energy everywhere ''outside'' that region.<ref name="Cohen-Tannoudji" />{{Rp|77–78}} For the one-dimensional case in the <math>x</math> direction, the time-independent Schrödinger equation may be written |
|||
The [[Copenhagen interpretation]], due largely to the Danish theoretical physicist [[Niels Bohr]], is the interpretation of quantum mechanical formalism most widely accepted amongst physicists. According to it, the probabilistic nature of quantum mechanics is not a temporary feature which will eventually be replaced by a deterministic theory, but instead must be considered to be a final renunciation of the classical ideal of causality. In this interpretation, it is believed that any well-defined application of the quantum mechanical formalism must always make reference to the experimental arrangement, due to the [[complementarity (physics)|complementarity]] nature of evidence obtained under different experimental situations. |
|||
: <math> - \frac {\hbar ^2}{2m} \frac {d ^2 \psi}{dx^2} = E \psi.</math> |
|||
With the differential operator defined by |
|||
[[Albert Einstein]], himself one of the founders of quantum theory, [[Bohr-Einstein debates|disliked this loss of determinism in measurement]] (this dislike is the source of his famous quote, "God does not play dice with the universe."). Einstein held that there should be a [[local hidden variable theory]] underlying quantum mechanics and that, consequently, the present theory was incomplete. He produced a series of objections to the theory, the most famous of which has become known as the [[Einstein-Podolsky-Rosen paradox]]. [[John Stewart Bell|John Bell]] showed that the EPR paradox led to [[Bell's theorem|experimentally testable differences]] between quantum mechanics and local realistic theories. [[Bell test experiments|Experiments]] have been performed confirming the accuracy of quantum mechanics, thus demonstrating that the physical world cannot be described by local realistic theories.<ref>[http://plato.stanford.edu/entries/qm-action-distance/ Plato.stanford.edu]</ref> The ''[[Bohr-Einstein debates]]'' provide a vibrant critique of the Copenhagen Interpretation from an [[epistemological]] point of view. |
|||
: <math> \hat{p}_x = -i\hbar\frac{d}{dx} </math>the previous equation is evocative of the [[Kinetic energy#Kinetic energy of rigid bodies|classic kinetic energy analogue]], |
|||
: <math> \frac{1}{2m} \hat{p}_x^2 = E,</math> |
|||
with state <math>\psi</math> in this case having energy <math>E</math> coincident with the kinetic energy of the particle. |
|||
The general solutions of the Schrödinger equation for the particle in a box are |
|||
The [[Everett many-worlds interpretation]], formulated in 1956, holds that all the possibilities described by quantum theory simultaneously occur in a [[multiverse]] composed of mostly independent parallel universes.<ref>[http://plato.stanford.edu/entries/qm-everett/ Plato.stanford.edu]</ref> This is not accomplished by introducing some new axiom to quantum mechanics, but on the contrary by ''removing'' the axiom of the collapse of the wave packet: All the possible consistent states of the measured system and the measuring apparatus (including the observer) are present in a ''real'' physical (not just formally mathematical, as in other interpretations) [[quantum superposition]]. Such a superposition of consistent state combinations of different systems is called an [[entangled state]]. While the multiverse is deterministic, we perceive non-deterministic behavior governed by probabilities, because we can observe only the universe, i.e. the consistent state contribution to the mentioned superposition, we inhabit. Everett's interpretation is perfectly consistent with [[John Stewart Bell|John Bell]]'s experiments and makes them intuitively understandable. However, according to the theory of [[quantum decoherence]], the parallel universes will never be accessible to us. This inaccessibility can be understood as follows: Once a measurement is done, the measured system becomes [[Quantum entanglement|entangled]] with both the physicist who measured it and a huge number of other particles, some of which are [[photon]]s flying away towards the other end of the universe; in order to prove that the wave function did not collapse one would have to bring all these particles back and measure them again, together with the system that was measured originally. This is completely impractical, but even if one could theoretically do this, it would destroy any evidence that the original measurement took place (including the physicist's memory). |
|||
: <math> \psi(x) = A e^{ikx} + B e ^{-ikx} \qquad\qquad E = \frac{\hbar^2 k^2}{2m}</math> |
|||
or, from [[Euler's formula]], |
|||
: <math> \psi(x) = C \sin(kx) + D \cos(kx).\!</math> |
|||
The infinite potential walls of the box determine the values of <math>C, D, </math> and <math>k</math> at <math>x=0</math> and <math>x=L</math> where <math>\psi</math> must be zero. Thus, at <math>x=0</math>, |
|||
==Applications== |
|||
: <math>\psi(0) = 0 = C\sin(0) + D\cos(0) = D</math> |
|||
Quantum mechanics has had enormous success in explaining many of the features of our world. The individual behaviour of the subatomic particles that make up all forms of [[matter]]—[[electron]]s, [[proton]]s, [[neutron]]s, [[photon]]s and others—can often only be satisfactorily described using quantum mechanics. Quantum mechanics has strongly influenced [[string theory]], a candidate for a [[theory of everything]] (see [[reductionism]]) and the [[multiverse]] hypothesis. It is also related to [[statistical mechanics]]. |
|||
and <math>D=0</math>. At <math>x=L</math>, |
|||
: <math> \psi(L) = 0 = C\sin(kL),</math> |
|||
in which <math>C</math> cannot be zero as this would conflict with the postulate that <math>\psi</math> has norm 1. Therefore, since <math>\sin(kL)=0</math>, <math>kL</math> must be an integer multiple of <math>\pi</math>, |
|||
: <math>k = \frac{n\pi}{L}\qquad\qquad n=1,2,3,\ldots.</math> |
|||
This constraint on <math>k</math> implies a constraint on the energy levels, yielding |
|||
Quantum mechanics is important for understanding how individual atoms combine covalently to form chemicals or molecules. The application of quantum mechanics to [[chemistry]] is known as [[quantum chemistry]]. (Relativistic) quantum mechanics can in principle mathematically describe most of chemistry. Quantum mechanics can provide quantitative insight into [[Ionic bond|ionic]] and [[covalent bonding]] processes by explicitly showing which molecules are energetically favorable to which others, and by approximately how much.<ref>[http://books.google.com/books?id=vdXU6SD4_UYC Books.google.com]</ref> Most of the calculations performed in [[computational chemistry]] rely on quantum mechanics.<ref>[http://en.wikibooks.org/wiki/Computational_chemistry/Applications_of_molecular_quantum_mechanics en.wikiboos.org]</ref> |
|||
: <math>E_n = \frac{\hbar^2 \pi^2 n^2}{2mL^2} = \frac{n^2h^2}{8mL^2}.</math> |
|||
A [[finite potential well]] is the generalization of the infinite potential well problem to potential wells having finite depth. The finite potential well problem is mathematically more complicated than the infinite particle-in-a-box problem as the wave function is not pinned to zero at the walls of the well. Instead, the wave function must satisfy more complicated mathematical boundary conditions as it is nonzero in regions outside the well. Another related problem is that of the [[rectangular potential barrier]], which furnishes a model for the [[quantum tunneling]] effect that plays an important role in the performance of modern technologies such as [[flash memory]] and [[scanning tunneling microscope|scanning tunneling microscopy]]. |
|||
[[File:Rtd seq v3.gif|thumb|350px|right|A working mechanism of a [[resonant tunneling diode]] device, based on the phenomenon of quantum tunneling through the potential barriers.]] |
|||
=== Harmonic oscillator === |
|||
Much of modern [[technology]] operates at a scale where quantum effects are significant. Examples include the [[laser]], the [[transistor]] (and thus the [[Integrated circuit|microchip]]), the [[electron microscope]], and [[Magnetic Resonance Imaging|magnetic resonance imaging]]. The study of semiconductors led to the invention of the [[diode]] and the [[transistor]], which are indispensable for modern [[electronics]]. |
|||
{{Main|Quantum harmonic oscillator}} |
|||
[[File:QuantumHarmonicOscillatorAnimation.gif|thumb|upright=1.35|right|Some trajectories of a [[harmonic oscillator]] (i.e. a ball attached to a [[Hooke's law|spring]]) in [[classical mechanics]] (A-B) and quantum mechanics (C-H). In quantum mechanics, the position of the ball is represented by a [[wave]] (called the wave function), with the [[real part]] shown in blue and the [[imaginary part]] shown in red. Some of the trajectories (such as C, D, E, and F) are [[standing wave]]s (or "[[stationary state]]s"). Each standing-wave frequency is proportional to a possible [[energy level]] of the oscillator. This "energy quantization" does not occur in classical physics, where the oscillator can have ''any'' energy.]] |
|||
Researchers are currently seeking robust methods of directly manipulating quantum states. Efforts are being made to develop [[quantum cryptography]], which will allow guaranteed secure transmission of [[information]]. A more distant goal is the development of [[quantum computer]]s, which are expected to perform certain computational tasks exponentially faster than classical [[computer]]s. Another active research topic is [[quantum teleportation]], which deals with techniques to transmit quantum states over arbitrary distances. |
|||
As in the classical case, the potential for the quantum harmonic oscillator is given by<ref name="Zwiebach2022"/>{{rp|234}} |
|||
[[Quantum tunneling]] is vital in many devices, even in the simple [[light switch]], as otherwise the electrons in the [[electric current]] could not penetrate the potential barrier made up of a layer of oxide. [[Flash memory]] chips found in [[USB drive]]s use quantum tunneling to erase their memory cells. |
|||
: <math>V(x)=\frac{1}{2}m\omega^2x^2.</math> |
|||
This problem can either be treated by directly solving the Schrödinger equation, which is not trivial, or by using the more elegant "ladder method" first proposed by Paul Dirac. The [[eigenstate]]s are given by |
|||
QM primarily applies to the atomic regimes of matter and energy, but some systems exhibit [[Mechanics#Classical_versus_quantum|quantum mechanical effects]] on a large scale; [[superfluidity]] (the frictionless flow of a liquid at temperatures near absolute zero) is one well-known example. Quantum theory also provides accurate descriptions for many previously unexplained phenomena such as [[black body radiation]] and the stability of [[Atomic orbital|electron orbitals]]. It has also given insight into the workings of many different [[biological systems]], including [[smell receptors]] and [[protein structure]]s.<ref>[http://discovermagazine.com/2009/feb/13-is-quantum-mechanics-controlling-your-thoughts/article_view?b_start:int=1&-C Discovermagazine.com]</ref> Even so, [[classical physics]] often can be a good approximation to results otherwise obtained by '''quantum physics''', typically in circumstances with large numbers of particles or large quantum numbers. (However, some open questions remain in the field of [[quantum chaos]].) |
|||
: <math> \psi_n(x) = \sqrt{\frac{1}{2^n\, n!}} \cdot \left(\frac{m\omega}{\pi \hbar}\right)^{1/4} \cdot e^{ |
|||
- \frac{m\omega x^2}{2 \hbar}} \cdot H_n\left(\sqrt{\frac{m\omega}{\hbar}} x \right), \qquad </math> |
|||
: <math>n = 0,1,2,\ldots. </math> |
|||
where ''H<sub>n</sub>'' are the [[Hermite polynomials]] |
|||
: <math>H_n(x)=(-1)^n e^{x^2}\frac{d^n}{dx^n}\left(e^{-x^2}\right),</math> |
|||
and the corresponding energy levels are |
|||
: <math> E_n = \hbar \omega \left(n + {1\over 2}\right).</math> |
|||
This is another example illustrating the discretization of energy for [[bound state]]s. |
|||
==Examples== |
|||
===Particle in a box=== |
|||
[[File:Infinite potential well.svg|thumb|1-dimensional potential energy box (or infinite potential well)]] |
|||
{{Main|Particle in a box}} |
|||
The particle in a 1-dimensional potential energy box is the most simple example where restraints lead to the quantization of energy levels. |
|||
The box is defined as zero potential energy inside a certain interval and infinite everywhere outside that interval. For the 1-dimensional case in the <math>x</math> direction, the time-independent Schrödinger equation can be written as:<ref>Derivation of particle in a box, [http://chemistry.tidalswan.com/index.php?title=Quantum_Mechanics chemistry.tidalswan.com]</ref> |
|||
: <math> - \frac {\hbar ^2}{2m} \frac {d ^2 \psi}{dx^2} = E \psi.</math> |
|||
Writing the differential operator |
|||
: <math> \hat{p}_x = -i\hbar\frac{d}{dx} </math> |
|||
the previous equation can be seen to be evocative of the [[Kinetic energy#Kinetic energy of rigid bodies|classic analogue]] |
|||
: <math> \frac{1}{2m} \hat{p}_x^2 = E </math> |
|||
with <math>E</math> as the energy for the state <math>\psi</math>, in this case coinciding with the kinetic energy of the particle. |
|||
=== Mach–Zehnder interferometer === |
|||
The general solutions of the Schrödinger equation for the particle in a box are: |
|||
[[File:Mach-Zehnder interferometer.svg|upright=1.3|thumb|right|Schematic of a Mach–Zehnder interferometer]] |
|||
: <math> \psi(x) = A e^{ikx} + B e ^{-ikx} \qquad\qquad E = \frac{\hbar^2 k^2}{2m}</math> |
|||
or, from [[Euler's formula]], |
|||
: <math> \psi(x) = C \sin kx + D \cos kx.\!</math> |
|||
The [[Mach–Zehnder interferometer]] (MZI) illustrates the concepts of superposition and interference with linear algebra in dimension 2, rather than differential equations. It can be seen as a simplified version of the double-slit experiment, but it is of interest in its own right, for example in the [[delayed choice quantum eraser]], the [[Elitzur–Vaidman bomb tester]], and in studies of quantum entanglement.<ref name=Paris1999>{{cite journal |last=Paris |first=M. G. A. |title=Entanglement and visibility at the output of a Mach–Zehnder interferometer |journal=[[Physical Review A]] |date=1999 |volume=59 |issue=2 |pages=1615–1621 |arxiv=quant-ph/9811078 |bibcode=1999PhRvA..59.1615P |doi=10.1103/PhysRevA.59.1615 |s2cid=13963928 }}</ref><ref name=Haack2010>{{Cite journal | last1 = Haack | first1 = G. R. | last2 = Förster | first2 = H. | last3 = Büttiker | first3 = M. | title = Parity detection and entanglement with a Mach-Zehnder interferometer | doi = 10.1103/PhysRevB.82.155303 | journal = [[Physical Review B]] | volume = 82 | issue = 15 | pages = 155303 | year = 2010 |arxiv = 1005.3976 |bibcode = 2010PhRvB..82o5303H | s2cid = 119261326 }}</ref> |
|||
The presence of the walls of the box determines the values of ''C'', ''D'', and ''k''. At each wall ({{nowrap|''x'' {{=}} 0}} and {{nowrap|''x'' {{=}} ''L''}}), {{nowrap|''ψ'' {{=}} 0}}. Thus when {{nowrap|''x'' {{=}} 0}}, |
|||
:<math>\psi(0) = 0 = C\sin 0 + D\cos 0 = D\!</math> |
|||
and so {{nowrap|''D'' {{=}} 0}}. When {{nowrap|''x'' {{=}} ''L''}}, |
|||
:<math> \psi(L) = 0 = C\sin kL.\!</math> |
|||
''C'' cannot be zero, since this would conflict with the Born interpretation. Therefore {{nowrap|sin ''kL'' {{=}} 0}}, and so it must be that ''kL'' is an integer multiple of π. Therefore, |
|||
:<math>k = \frac{n\pi}{L}\qquad\qquad n=1,2,3,\ldots.</math> |
|||
The quantization of energy levels follows from this constraint on ''k'', since |
|||
:<math>E = \frac{\hbar^2 \pi^2 n^2}{2mL^2} = \frac{n^2h^2}{8mL^2}.</math> |
|||
We can model a photon going through the interferometer by considering that at each point it can be in a superposition of only two paths: the "lower" path which starts from the left, goes straight through both beam splitters, and ends at the top, and the "upper" path which starts from the bottom, goes straight through both beam splitters, and ends at the right. The quantum state of the photon is therefore a vector <math>\psi \in \mathbb{C}^2</math> that is a superposition of the "lower" path <math>\psi_l = \begin{pmatrix} 1 \\ 0 \end{pmatrix}</math> and the "upper" path <math>\psi_u = \begin{pmatrix} 0 \\ 1 \end{pmatrix}</math>, that is, <math>\psi = \alpha \psi_l + \beta \psi_u</math> for complex <math>\alpha,\beta</math>. In order to respect the postulate that <math>\langle \psi,\psi\rangle = 1</math> we require that <math>|\alpha|^2+|\beta|^2 = 1</math>. |
|||
===Free particle=== |
|||
[[File:QuantumDot wf.gif|thumb|600px|right|3D confined electron wave functions for each eigenstate in a Quantum Dot. Here, rectangular and triangular-shaped quantum dots are shown. Energy states in rectangular dots are more ‘s-type’ and ‘p-type’. However, in a triangular dot the wave functions are mixed due to confinement symmetry.]] |
|||
For example, consider a [[free particle]]. In quantum mechanics, there is [[wave-particle duality]] so the properties of the particle can be described as the properties of a wave. Therefore, its [[quantum state]] can be represented as a [[wave]] of arbitrary shape and extending over space as a [[wave function]]. The position and momentum of the particle are [[observables]]. The [[Uncertainty Principle]] states that both the position and the momentum cannot simultaneously be measured with full precision at the same time. However, one can measure the position alone of a moving free particle creating an eigenstate of position with a wavefunction that is very large (a [[Dirac delta]]) at a particular position ''x'' and zero everywhere else. If one performs a position measurement on such a wavefunction, the result ''x'' will be obtained with 100% probability (full certainty). This is called an eigenstate of position (mathematically more precise: a ''generalized position eigenstate ([[Distribution (mathematics)|eigendistribution]])''). If the particle is in an eigenstate of position then its momentum is completely unknown. On the other hand, if the particle is in an eigenstate of momentum then its position is completely unknown.<ref>{{Cite book |
|||
|title=Quantum Mechanics, Second edition |
|||
|first1=P. C. W. |
|||
|last1=Davies |
|||
|first2=David S. |
|||
|last2=Betts |
|||
|publisher=Chapman and Hall |
|||
|year=1984 |
|||
|isbn=0-7487-4446-0 |
|||
|page=79 |
|||
|url=http://books.google.com/books?id=XRyHCrGNstoC&pg=PA79}}, [http://books.google.com/books?id=XRyHCrGNstoC&pg=PA79 Chapter 6, p. 79] |
|||
</ref> |
|||
In an eigenstate of momentum having a [[plane wave]] form, it can be shown that the [[wavelength]] is equal to ''h/p'', where ''h'' is [[Planck's constant]] and ''p'' is the momentum of the [[eigenstate]].<ref>[http://books.google.com/books?id=tKm-Ekwke_UC Books.Google.com]</ref> |
|||
Both [[beam splitter]]s are modelled as the unitary matrix <math>B = \frac1{\sqrt2}\begin{pmatrix} 1 & i \\ i & 1 \end{pmatrix}</math>, which means that when a photon meets the beam splitter it will either stay on the same path with a probability amplitude of <math>1/\sqrt{2}</math>, or be reflected to the other path with a probability amplitude of <math>i/\sqrt{2}</math>. The phase shifter on the upper arm is modelled as the unitary matrix <math>P = \begin{pmatrix} 1 & 0 \\ 0 & e^{i\Delta\Phi} \end{pmatrix}</math>, which means that if the photon is on the "upper" path it will gain a relative phase of <math>\Delta\Phi</math>, and it will stay unchanged if it is in the lower path. |
|||
==See also== |
|||
{{Colbegin|colwidth=30em}} |
|||
*[[Copenhagen interpretation]] |
|||
*[[Correspondence rules]] |
|||
*[[De Broglie–Bohm theory]] |
|||
*[[EPR paradox]] |
|||
*[[Fine-structure constant]] |
|||
*[[Introduction to quantum mechanics]] |
|||
*[[Many-worlds interpretation]] |
|||
*[[Measurement in quantum mechanics]] |
|||
*[[Measurement problem]] |
|||
*[[Photon dynamics in the double-slit experiment]] |
|||
*[[Photon polarization]] |
|||
*[[Physical ontology]] |
|||
*[[Quantum chaos]] |
|||
*[[Quantum chemistry]] |
|||
*[[Quantum chemistry computer programs]] |
|||
*[[Quantum chromodynamics]] |
|||
*[[Quantum computer]]s |
|||
*[[Quantum decoherence]] |
|||
*[[Quantum electrochemistry]] |
|||
*[[Quantum electrodynamics]] |
|||
*[[Quantum electronics]] |
|||
*[[Quantum field theory]] |
|||
*[[Quantum information]] |
|||
*[[Quantum mind]]<ref>[http://www-physics.lbl.gov/~stapp/PTRS.pdf www-physics.lbl.gov]</ref> |
|||
*[[Quantum optics]] |
|||
*[[Quantum pseudo-telepathy]] |
|||
*[[Quantum thermodynamics]] |
|||
*[[Quantum triviality]] |
|||
*[[Quantum Zeno effect]] |
|||
*[[Quasi-set theory]] |
|||
*[[Relation between Schrödinger's equation and the path integral formulation of quantum mechanics]] |
|||
*[[Schrödinger's cat]] |
|||
*[[Theoretical and experimental justification for the Schrödinger equation]] |
|||
*[[Theoretical chemistry]] |
|||
*[[Transactional interpretation]] |
|||
*[[Trojan wave packet]] |
|||
{{Colend}} |
|||
A photon that enters the interferometer from the left will then be acted upon with a beam splitter <math>B</math>, a phase shifter <math>P</math>, and another beam splitter <math>B</math>, and so end up in the state |
|||
==Notes== |
|||
: <math>BPB\psi_l = ie^{i\Delta\Phi/2} \begin{pmatrix} -\sin(\Delta\Phi/2) \\ \cos(\Delta\Phi/2) \end{pmatrix},</math> |
|||
{{Reflist|colwidth=40em}} |
|||
and the probabilities that it will be detected at the right or at the top are given respectively by |
|||
: <math> p(u) = |\langle \psi_u, BPB\psi_l \rangle|^2 = \cos^2 \frac{\Delta \Phi}{2},</math> |
|||
: <math> p(l) = |\langle \psi_l, BPB\psi_l \rangle|^2 = \sin^2 \frac{\Delta \Phi}{2}.</math> |
|||
One can therefore use the Mach–Zehnder interferometer to estimate the [[Phase (waves)|phase shift]] by estimating these probabilities. |
|||
It is interesting to consider what would happen if the photon were definitely in either the "lower" or "upper" paths between the beam splitters. This can be accomplished by blocking one of the paths, or equivalently by removing the first beam splitter (and feeding the photon from the left or the bottom, as desired). In both cases, there will be no interference between the paths anymore, and the probabilities are given by <math>p(u)=p(l) = 1/2</math>, independently of the phase <math>\Delta\Phi</math>. From this we can conclude that the photon does not take one path or another after the first beam splitter, but rather that it is in a genuine quantum superposition of the two paths.<ref name="vedral">{{cite book |first=Vlatko |last=Vedral |title=Introduction to Quantum Information Science |date=2006 |publisher=Oxford University Press |isbn=978-0-19-921570-6 |oclc=442351498 |author-link=Vlatko Vedral}}</ref> |
|||
==References== |
|||
{{Refbegin}} |
|||
The following titles, all by working physicists, attempt to communicate quantum theory to lay people, using a minimum of technical apparatus. |
|||
*Chester, Marvin (1987) ''Primer of Quantum Mechanics''. John Wiley. ISBN 0-486-42878-8 |
|||
* [[Richard Feynman]], 1985. ''[[QED: The Strange Theory of Light and Matter]]'', [[Princeton University Press]]. ISBN 0-691-08388-6. Four elementary lectures on [[quantum electrodynamics]] and [[quantum field theory]], yet containing many insights for the expert. |
|||
* Ghirardi, GianCarlo, 2004. ''Sneaking a Look at God's Cards'', Gerald Malsbary, trans. Princeton Univ. Press. The most technical of the works cited here. Passages using [[algebra]], [[trigonometry]], and [[bra-ket notation]] can be passed over on a first reading. |
|||
*[[N. David Mermin]], 1990, "Spooky actions at a distance: mysteries of the QT" in his ''Boojums all the way through''. [[Cambridge University Press]]: 110-76. |
|||
*[[Victor Stenger]], 2000. ''Timeless Reality: Symmetry, Simplicity, and Multiple Universes''. Buffalo NY: Prometheus Books. Chpts. 5-8. Includes [[cosmological]] and [[philosophical]] considerations. |
|||
More technical: |
|||
*[[Bryce DeWitt]], [[R. Neill Graham]], eds., 1973. ''The Many-Worlds Interpretation of Quantum Mechanics'', Princeton Series in Physics, [[Princeton University Press]]. ISBN 0-691-08131-X |
|||
*{{cite book |last=Dirac |first=P. A. M. |authorlink=P. A. M. Dirac |year=1930 |title=The Principles of Quantum Mechanics |isbn=0198520115}} The beginning chapters make up a very clear and comprehensible introduction. |
|||
*[[Hugh Everett]], 1957, "Relative State Formulation of Quantum Mechanics," ''Reviews of Modern Physics'' 29: 454-62. |
|||
*{{cite book |last1=Feynman |first1=Richard P. |authorlink1=Richard Feynman |last2=Leighton |first2=Robert B. |authorlink2=Robert B. Leighton (physicist) |last3=Sands |first3=Matthew |year=1965 |title=[[The Feynman Lectures on Physics]] |volume=1-3 |publisher=[[Addison-Wesley]] |isbn=0738200085}} |
|||
*{{cite book | author=Griffiths, David J.| title=Introduction to Quantum Mechanics (2nd ed.) | publisher=Prentice Hall |year=2004 |isbn=0-13-111892-7 | oclc=40251748}} A standard undergraduate text. |
|||
*[[Max Jammer]], 1966. ''The Conceptual Development of Quantum Mechanics''. McGraw Hill. |
|||
*[[Hagen Kleinert]], 2004. ''Path Integrals in Quantum Mechanics, Statistics, Polymer Physics, and Financial Markets'', 3rd ed. Singapore: World Scientific. [http://www.physik.fu-berlin.de/~kleinert/b5 Draft of 4th edition.] |
|||
*Gunther Ludwig, 1968. ''Wave Mechanics''. London: Pergamon Press. ISBN 0-08-203204-1 |
|||
*[[George Mackey]] (2004). ''The mathematical foundations of quantum mechanics''. Dover Publications. ISBN 0-486-43517-2. |
|||
*[[Albert Messiah]], 1966. ''Quantum Mechanics'' (Vol. I), English translation from French by G. M. Temmer. North Holland, John Wiley & Sons. Cf. chpt. IV, section III. |
|||
*{{cite book | author=[[Roland Omnès|Omnès, Roland]] | title=Understanding Quantum Mechanics | publisher=Princeton University Press |year=1999 |isbn=0-691-00435-8 | oclc=39849482}} |
|||
*Scerri, Eric R., 2006. ''The [[Periodic Table]]: Its Story and Its Significance''. Oxford University Press. Considers the extent to which chemistry and the periodic system have been reduced to quantum mechanics. ISBN 0-19-530573-6 |
|||
*{{cite book | author=[[Transnational College of Lex]]| title=What is Quantum Mechanics? A Physics Adventure | publisher=Language Research Foundation, Boston |year=1996 |isbn=0-9643504-1-6 | oclc=34661512}} |
|||
*{{cite book |last=von Neumann |first=John |authorlink=John von Neumann |year=1955 |title=Mathematical Foundations of Quantum Mechanics |publisher=Princeton University Press |isbn=0691028931}} |
|||
*[[Hermann Weyl]], 1950. ''The Theory of Groups and Quantum Mechanics'', Dover Publications. |
|||
*D. Greenberger, K. Hentschel, F. Weinert, eds., 2009. ''Compendium of quantum physics, Concepts, experiments, history and philosophy,'' Springer-Verlag, Berlin, Heidelberg. |
|||
{{Refend}} |
|||
== Applications == |
|||
==Further reading== |
|||
{{Main|Applications of quantum mechanics}} |
|||
* {{cite book | author=Bernstein, Jeremy|title=Quantum Leaps| publisher=Belknap Press of Harvard University Press | location=Cambridge, Massachusetts|year=2009|isbn=9780674035416|url=http://books.google.com/books?id=j0Me3brYOL0C&printsec=frontcover}} |
|||
Quantum mechanics has had enormous success in explaining many of the features of our universe, with regard to small-scale and discrete quantities and interactions which cannot be explained by [[Classical physics|classical methods]].{{refn|name= feynmanIII |group=note|See, for example, [[the Feynman Lectures on Physics]] for some of the technological applications which use quantum mechanics, e.g., [[transistor]]s (vol '''III''', pp. 14–11 ff), [[integrated circuit]]s, which are follow-on technology in solid-state physics (vol '''II''', pp. 8–6), and [[laser]]s (vol '''III''', pp. 9–13).}} Quantum mechanics is often the only theory that can reveal the individual behaviors of the subatomic particles that make up all forms of matter (electrons, [[proton]]s, [[neutron]]s, [[photon]]s, and others). [[Solid-state physics]] and [[materials science]] are dependent upon quantum mechanics.<ref name=marvincohen2008>{{cite journal|last=Cohen|first=Marvin L.|title=Essay: Fifty Years of Condensed Matter Physics|journal=Physical Review Letters|year=2008|volume=101|issue=25|doi=10.1103/PhysRevLett.101.250001|url=http://prl.aps.org/edannounce/PhysRevLett.101.250001|access-date=31 March 2012|bibcode= 2008PhRvL.101y0001C|pmid=19113681|page=250001}}</ref> |
|||
* {{cite book | author=[[David Bohm|Bohm, David]] | title=Quantum Theory | publisher=[[Dover Publications]] | year=1989 | isbn=0-486-65969-0}} |
|||
* {{cite book | author=Eisberg, Robert; [[Robert Resnick|Resnick, Robert]] | title=Quantum Physics of Atoms, Molecules, Solids, Nuclei, and Particles (2nd ed.) | publisher=Wiley | year=1985 | isbn=0-471-87373-X}} |
|||
* {{cite book | author=[[Liboff, Richard L.]] | title=Introductory Quantum Mechanics | publisher=Addison-Wesley | year=2002 | isbn=0-8053-8714-5}} |
|||
* {{cite book | author=Merzbacher, Eugen | title=Quantum Mechanics | publisher=Wiley, John & Sons, Inc | year=1998 | isbn=0-471-88702-1}} |
|||
* {{cite book | author=[[J. J. Sakurai|Sakurai, J. J.]] | title=Modern Quantum Mechanics| publisher=Addison Wesley | year=1994 | isbn=0-201-53929-2}} |
|||
* {{cite book | author=[[Shankar, R.]] | title=Principles of Quantum Mechanics | publisher=Springer | year=1994| isbn=0-306-44790-8}} |
|||
In many aspects, modern technology operates at a scale where quantum effects are significant. Important applications of quantum theory include [[quantum chemistry]], [[quantum optics]], [[quantum computing]], [[superconducting magnet]]s, [[light-emitting diode]]s, the [[optical amplifier]] and the laser, the [[transistor]] and [[semiconductor]]s such as the [[microprocessor]], [[medical imaging|medical and research imaging]] such as [[magnetic resonance imaging]] and [[electron microscope|electron microscopy]].<ref>{{cite magazine|last1=Matson|first1=John|title=What Is Quantum Mechanics Good for?|url=http://www.scientificamerican.com/article/everyday-quantum-physics/|magazine=Scientific American|access-date=18 May 2016}}</ref> Explanations for many biological and physical phenomena are rooted in the nature of the chemical bond, most notably the macro-molecule [[DNA]]. |
|||
==External links== |
|||
{{sisterlinks|s=Quantum mechanics}} |
|||
== Relation to other scientific theories == |
|||
;General |
|||
{{Modern physics}} |
|||
*[http://www.lightandmatter.com/html_books/6mr/ch01/ch01.html The Modern Revolution in Physics] - an online textbook. |
|||
* J. O'Connor and E. F. Robertson: [http://www-history.mcs.st-andrews.ac.uk/history/HistTopics/The_Quantum_age_begins.html A history of quantum mechanics.] |
|||
*[http://www.quantiki.org/wiki/index.php/Introduction_to_Quantum_Theory Introduction to Quantum Theory at Quantiki.] |
|||
*[http://bethe.cornell.edu/ Quantum Physics Made Relatively Simple]: three video lectures by [[Hans Bethe]] |
|||
*[http://www.nonlocal.com/hbar/ H is for h-bar.] |
|||
*[http://www.freebookcentre.net/Physics/Quantum-Mechanics-Books.html Quantum Mechanics Books Collection]: Collection of free books |
|||
;Course material |
|||
*[http://arxiv.org/abs/quant-ph/0605180 Doron Cohen: Lecture notes in Quantum Mechanics (comprehensive, with advanced topics).] |
|||
*[[MIT OpenCourseWare]]: [http://ocw.mit.edu/OcwWeb/Chemistry/index.htm Chemistry]. See [http://ocw.mit.edu/OcwWeb/Chemistry/5-61Fall-2004/CourseHome/index.htm 5.61], [http://ocw.mit.edu/OcwWeb/Chemistry/5-73Fall-2005/CourseHome/index.htm 5.73], and [http://ocw.mit.edu/OcwWeb/Chemistry/5-74Spring-2005/CourseHome/index.htm 5.74] |
|||
*MIT OpenCourseWare: [http://ocw.mit.edu/OcwWeb/Physics/index.htm Physics]. See [http://ocw.mit.edu/OcwWeb/Physics/8-04Spring-2006/CourseHome/index.htm 8.04], [http://ocw.mit.edu/OcwWeb/Physics/8-05Fall-2004/CourseHome/index.htm 8.05], and [http://ocw.mit.edu/OcwWeb/Physics/8-06Spring-2005/CourseHome/index.htm 8.06] |
|||
*[http://www.youtube.com/stanford#g/c/84C10A9CB1D13841 Stanford Continuing Education PHY 25: Quantum Mechanics] by [[Leonard Susskind]], see [http://continuingstudies.stanford.edu/courses/course.php?cid=20072_PHY%2025 course description] Fall 2007 |
|||
*[http://www.physics.csbsju.edu/QM/ 5½ Examples in Quantum Mechanics] |
|||
*[http://www.imperial.ac.uk/quantuminformation/qi/tutorials Imperial College Quantum Mechanics Course.] |
|||
*[http://www.sparknotes.com/testprep/books/sat2/physics/chapter19section3.rhtml Spark Notes - Quantum Physics.] |
|||
*[http://www.quantum-physics.polytechnique.fr Quantum Physics Online : interactive introduction to quantum mechanics (RS applets).] |
|||
*[http://www.didaktik.physik.uni-erlangen.de/quantumlab/english/index.html Experiments to the foundations of quantum physics with single photons.] |
|||
*[http://www.motionmountain.net/download.html Motion Mountain, Volume IV] - A modern introduction to quantum theory, with several animations. |
|||
*[http://www.nanohub.org/topics/AQME AQME] : Advancing Quantum Mechanics for Engineers — by T.Barzso, D.Vasileska and G.Klimeck online learning resource with simulation tools on [[nanohub]] |
|||
* [http://www.lsr.ph.ic.ac.uk/~plenio/lecture.pdf Quantum Mechanics] by Martin Plenio |
|||
* [http://farside.ph.utexas.edu/teaching/qm/389.pdf Quantum Mechanics] by Richard Fitzpatrick |
|||
* [http://nanohub.org/resources/2039 Online course on ''Quantum Transport''] |
|||
=== Classical mechanics === |
|||
;FAQs |
|||
*[http://www.hedweb.com/manworld.htm Many-worlds or relative-state interpretation.] |
|||
*[http://www.mtnmath.com/faq/meas-qm.html Measurement in Quantum mechanics.] |
|||
The rules of quantum mechanics assert that the state space of a system is a Hilbert space and that observables of the system are Hermitian operators acting on vectors in that space – although they do not tell us which Hilbert space or which operators. These can be chosen appropriately in order to obtain a quantitative description of a quantum system, a necessary step in making physical predictions. An important guide for making these choices is the [[correspondence principle]], a heuristic which states that the predictions of quantum mechanics reduce to those of [[classical mechanics]] in the regime of large [[quantum number]]s.<ref name="Tipler">{{cite book|last1=Tipler|first1=Paul|last2=Llewellyn|first2=Ralph|title=Modern Physics|edition=5th|year=2008|publisher=W.H. Freeman and Company|isbn=978-0-7167-7550-8|pages=160–161}}</ref> One can also start from an established classical model of a particular system, and then try to guess the underlying quantum model that would give rise to the classical model in the correspondence limit. This approach is known as [[Canonical quantization|quantization]].<ref name="Peres1993">{{cite book |last=Peres |first=Asher |author-link=Asher Peres |title=Quantum Theory: Concepts and Methods |title-link=Quantum Theory: Concepts and Methods |publisher=Kluwer |year=1993 |isbn=0-7923-2549-4}}</ref>{{rp|299}}<ref>{{cite web|first=John C. |last=Baez |author-link=John C. Baez |url=https://nautil.us/the-math-that-takes-newton-into-the-quantum-world-237339/ |title=The Math That Takes Newton Into the Quantum World |website=[[Nautilus Quarterly]] |date=2019-02-26 |access-date=2024-03-23}}</ref> |
|||
;Media |
|||
*[http://www.newscientist.com/channel/fundamentals/quantum-world Everything you wanted to know about the quantum world] — archive of articles from ''[[New Scientist]]''. |
|||
*[http://www.sciencedaily.com/news/matter_energy/quantum_physics/ Quantum Physics Research] from [[Science Daily]] |
|||
*{{cite news|url=http://www.nytimes.com/2005/12/27/science/27eins.html?ex=1293339600&en=caf5d835203c3500&ei=5090|title=Quantum Trickery: Testing Einstein's Strangest Theory|date=December 27, 2005|publisher=''[[The New York Times]]'' | first=Dennis | last=Overbye | accessdate=April 12, 2010}} |
|||
*[http://www.astronomycast.com/physics/ep-138-quantum-mechanics/ Audio: Astronomy Cast] Quantum Mechanics - June 2009. [[Fraser Cain]] interviews [[Pamela L. Gay]]. |
|||
When quantum mechanics was originally formulated, it was applied to models whose correspondence limit was [[theory of relativity|non-relativistic]] classical mechanics. For instance, the well-known model of the [[quantum harmonic oscillator]] uses an explicitly non-relativistic expression for the [[kinetic energy]] of the oscillator, and is thus a quantum version of the [[harmonic oscillator|classical harmonic oscillator]].<ref name="Zwiebach2022"/>{{rp|234}} |
|||
;Philosophy |
|||
*{{sep|qm|"Quantum Mechanics"|Jenann Ismael.}} |
|||
*{{sep|qm|"Measurement in Quantum Theory"|[[Henry Krips]].}} |
|||
Complications arise with [[Chaos theory|chaotic systems]], which do not have good quantum numbers, and [[quantum chaos]] studies the relationship between classical and quantum descriptions in these systems.<ref name="Peres1993"/>{{rp|353}} |
|||
{{Physics-footer}} |
|||
[[Quantum decoherence]] is a mechanism through which quantum systems lose [[quantum coherence|coherence]], and thus become incapable of displaying many typically quantum effects: [[quantum superposition]]s become simply probabilistic mixtures, and quantum entanglement becomes simply classical correlations.<ref name="Zwiebach2022"/>{{rp|687-730}} Quantum coherence is not typically evident at macroscopic scales, though at temperatures approaching [[absolute zero]] quantum behavior may manifest macroscopically.{{refn|group=note|See ''[[Macroscopic quantum phenomena]]'', ''[[Bose–Einstein condensate]]'', and ''[[Quantum machine]]''}} |
|||
{{DEFAULTSORT:Quantum Mechanics}} |
|||
[[Category:Quantum mechanics| ]] |
|||
[[Category:Fundamental physics concepts]] |
|||
Many macroscopic properties of a classical system are a direct consequence of the quantum behavior of its parts. For example, the stability of bulk matter (consisting of atoms and [[molecule]]s which would quickly collapse under electric forces alone), the rigidity of solids, and the mechanical, thermal, chemical, optical and magnetic properties of matter are all results of the interaction of [[electric charge]]s under the rules of quantum mechanics.<ref>{{cite web|url=http://academic.brooklyn.cuny.edu/physics/sobel/Nucphys/atomprop.html |title=Atomic Properties |publisher=Academic.brooklyn.cuny.edu |access-date=18 August 2012}}</ref> |
|||
{{Link GA|zh}} |
|||
=== Special relativity and electrodynamics === |
|||
{{Link FA|uk}} |
|||
Early attempts to merge quantum mechanics with [[special relativity]] involved the replacement of the Schrödinger equation with a covariant equation such as the [[Klein–Gordon equation]] or the [[Dirac equation]]. While these theories were successful in explaining many experimental results, they had certain unsatisfactory qualities stemming from their neglect of the relativistic creation and annihilation of particles. A fully relativistic quantum theory required the development of quantum field theory, which applies quantization to a field (rather than a fixed set of particles). The first complete quantum field theory, [[quantum electrodynamics]], provides a fully quantum description of the [[electromagnetism|electromagnetic interaction]]. Quantum electrodynamics is, along with [[general relativity]], one of the most accurate physical theories ever devised.<ref>{{cite book|url=https://books.google.com/books?id=6a-agBFWuyQC&pg=PA61|title=The Nature of Space and Time|date=2010|isbn=978-1-4008-3474-7|last1=Hawking|first1=Stephen|last2=Penrose|first2=Roger|publisher=Princeton University Press }}</ref><ref> |
|||
[[als:Quantenmechanik]] |
|||
{{cite journal |last1=Aoyama |first1=Tatsumi |last2=Hayakawa |first2=Masashi |last3=Kinoshita |first3=Toichiro |last4=Nio |first4=Makiko |year=2012 |title=Tenth-Order QED Contribution to the Electron g-2 and an Improved Value of the Fine Structure Constant |journal=[[Physical Review Letters]] |volume=109 |issue=11 |page=111807 |arxiv=1205.5368 |bibcode=2012PhRvL.109k1807A |doi=10.1103/PhysRevLett.109.111807 |pmid=23005618 |s2cid=14712017}}</ref> |
|||
[[ar:ميكانيكا الكم]] |
|||
[[an:Mecanica quantica]] |
|||
The full apparatus of quantum field theory is often unnecessary for describing electrodynamic systems. A simpler approach, one that has been used since the inception of quantum mechanics, is to treat [[electric charge|charged]] particles as quantum mechanical objects being acted on by a classical [[electromagnetic field]]. For example, the elementary quantum model of the [[hydrogen atom]] describes the [[electric field]] of the hydrogen atom using a classical <math>\textstyle -e^2/(4 \pi\epsilon_{_0}r)</math> [[Electric potential|Coulomb potential]].<ref name="Zwiebach2022"/>{{rp|285}} Likewise, in a [[Stern–Gerlach experiment]], a charged particle is modeled as a quantum system, while the background magnetic field is described classically.<ref name="Peres1993"/>{{rp|26}} This "semi-classical" approach fails if quantum fluctuations in the electromagnetic field play an important role, such as in the emission of photons by [[charged particle]]s. |
|||
[[az:VKB metodu]] |
|||
[[bn:কোয়ান্টাম বলবিজ্ঞান]] |
|||
[[Field (physics)|Quantum field]] theories for the [[strong nuclear force]] and the [[weak nuclear force]] have also been developed. The quantum field theory of the strong nuclear force is called [[quantum chromodynamics]], and describes the interactions of subnuclear particles such as [[quark]]s and [[gluon]]s. The weak nuclear force and the electromagnetic force were unified, in their quantized forms, into a single quantum field theory (known as [[electroweak theory]]), by the physicists [[Abdus Salam]], [[Sheldon Glashow]] and [[Steven Weinberg]].<ref> |
|||
[[zh-min-nan:Liōng-chú la̍t-ha̍k]] |
|||
{{cite web |
|||
[[be:Квантавая механіка]] |
|||
|url=http://nobelprize.org/nobel_prizes/physics/laureates/1979/index.html |
|||
[[be-x-old:Квантавая мэханіка]] |
|||
|title=The Nobel Prize in Physics 1979 |
|||
[[bs:Kvantna mehanika]] |
|||
|publisher=Nobel Foundation |
|||
[[bg:Квантова механика]] |
|||
|access-date=16 December 2020 |
|||
[[ca:Mecànica quàntica]] |
|||
}}</ref> |
|||
[[cv:Квантăллă механика]] |
|||
[[cs:Kvantová mechanika]] |
|||
=== Relation to general relativity === |
|||
[[cy:Mecaneg cwantwm]] |
|||
Even though the predictions of both quantum theory and general relativity have been supported by rigorous and repeated [[empirical evidence]], their abstract formalisms contradict each other and they have proven extremely difficult to incorporate into one consistent, cohesive model. Gravity is negligible in many areas of particle physics, so that unification between general relativity and quantum mechanics is not an urgent issue in those particular applications. However, the lack of a correct theory of [[quantum gravity]] is an important issue in [[physical cosmology]] and the search by physicists for an elegant "[[theory of everything|Theory of Everything]]" (TOE). Consequently, resolving the inconsistencies between both theories has been a major goal of 20th- and 21st-century physics. This TOE would combine not only the models of subatomic physics but also derive the four fundamental forces of nature from a single force or phenomenon.<ref name="NYT-20221010">{{cite news |last=Overbye |first=Dennis |author-link=Dennis Overbye |title=Black Holes May Hide a Mind-Bending Secret About Our Universe – Take gravity, add quantum mechanics, stir. What do you get? Just maybe, a holographic cosmos. |url=https://www.nytimes.com/2022/10/10/science/black-holes-cosmology-hologram.html |date=10 October 2022 |work=[[The New York Times]] |accessdate=10 October 2022 }}</ref> |
|||
[[da:Kvantemekanik]] |
|||
[[File:String Vibrations.gif|thumb|upright=0.8|String vibrations of particles in the quantum world of particles.]] |
|||
[[de:Quantenmechanik]] |
|||
One proposal for doing so is [[string theory]], which posits that the [[Point particle|point-like particles]] of [[particle physics]] are replaced by [[Dimension (mathematics and physics)|one-dimensional]] objects called [[String (physics)|strings]]. String theory describes how these strings propagate through space and interact with each other. On distance scales larger than the string scale, a string looks just like an ordinary particle, with its [[mass]], [[charge (physics)|charge]], and other properties determined by the [[vibration]]al state of the string. In string theory, one of the many vibrational states of the string corresponds to the [[graviton]], a quantum mechanical particle that carries gravitational force.<ref>{{cite book|last1=Becker |first1=Katrin |last2=Becker |first2=Melanie |author-link2=Melanie Becker|last3=Schwarz |first3=John |title=String theory and M-theory: A modern introduction |date=2007 |publisher=Cambridge University Press |isbn=978-0-521-86069-7}}</ref><ref>{{cite book |last1=Zwiebach |first1=Barton |title=A First Course in String Theory |date=2009 |publisher=Cambridge University Press |isbn=978-0-521-88032-9 |author-link=Barton Zwiebach}}</ref> |
|||
[[et:Kvantmehaanika]] |
|||
[[el:Κβαντική μηχανική]] |
|||
Another popular theory is [[loop quantum gravity]] (LQG), which describes quantum properties of gravity and is thus a theory of [[quantum spacetime]]. LQG is an attempt to merge and adapt standard quantum mechanics and standard general relativity. This theory describes space as an extremely fine fabric "woven" of finite loops called [[spin network]]s. The evolution of a spin network over time is called a [[spin foam]]. The characteristic length scale of a spin foam is the [[Planck length]], approximately 1.616×10<sup>−35</sup> m, and so lengths shorter than the Planck length are not physically meaningful in LQG.<ref>{{Cite book|last1=Rovelli|first1=Carlo|url=https://books.google.com/books?id=w6z0BQAAQBAJ|title=Covariant Loop Quantum Gravity: An Elementary Introduction to Quantum Gravity and Spinfoam Theory|last2=Vidotto|first2=Francesca|year=2014|publisher=Cambridge University Press|isbn=978-1-316-14811-2|language=en}}</ref> |
|||
[[es:Mecánica cuántica]] |
|||
[[eo:Kvantuma mekaniko]] |
|||
== Philosophical implications == |
|||
[[eu:Mekanika kuantiko]] |
|||
{{Main|Interpretations of quantum mechanics}} |
|||
[[fa:مکانیک کوانتومی]] |
|||
[[fr:Mécanique quantique]] |
|||
{{unsolved|physics|Is there a preferred interpretation of quantum mechanics? How does the quantum description of reality, which includes elements such as the "[[superposition principle|superposition]] of states" and "[[wave function collapse]]", give rise to the reality we perceive?}} |
|||
[[gl:Mecánica cuántica]] |
|||
Since its inception, the many counter-intuitive aspects and results of quantum mechanics have provoked strong [[philosophy|philosophical]] debates and many [[interpretations of quantum mechanics|interpretations]]. The arguments centre on the probabilistic nature of quantum mechanics, the difficulties with [[wavefunction collapse]] and the related [[measurement problem]], and [[quantum nonlocality]]. Perhaps the only consensus that exists about these issues is that there is no consensus. [[Richard Feynman]] once said, "I think I can safely say that nobody understands quantum mechanics."<ref>{{Cite book|last=Feynman|first=Richard|title=The Character of Physical Law|title-link=The Character of Physical Law|publisher=MIT Press|year=1967|isbn=0-262-56003-8|pages=129|language=en|author-link=Richard Feynman}}</ref> According to [[Steven Weinberg]], "There is now in my opinion no entirely satisfactory interpretation of quantum mechanics."<ref>{{Cite journal |arxiv = 1109.6462|doi = 10.1103/PhysRevA.85.062116|title = Collapse of the state vector|journal = Physical Review A|volume = 85|issue = 6|pages = 062116|year = 2012|last1 = Weinberg|first1 = Steven|bibcode = 2012PhRvA..85f2116W|s2cid = 119273840}}</ref> |
|||
[[ko:양자역학]] |
|||
[[hi:क्वाण्टम यांत्रिकी]] |
|||
The views of [[Niels Bohr]], Werner Heisenberg and other physicists are often grouped together as the "[[Copenhagen interpretation]]".<ref>{{Cite journal|last=Howard|first=Don|date=December 2004|title=Who Invented the 'Copenhagen Interpretation'? A Study in Mythology|url=https://www.journals.uchicago.edu/doi/10.1086/425941|journal=Philosophy of Science|language=en|volume=71|issue=5|pages=669–682|doi=10.1086/425941|s2cid=9454552|issn=0031-8248}}</ref><ref>{{Cite journal|last=Camilleri|first=Kristian|date=May 2009|title=Constructing the Myth of the Copenhagen Interpretation|url=http://www.mitpressjournals.org/doi/10.1162/posc.2009.17.1.26|journal=Perspectives on Science|language=en|volume=17|issue=1|pages=26–57|doi=10.1162/posc.2009.17.1.26|s2cid=57559199|issn=1063-6145}}</ref> According to these views, the probabilistic nature of quantum mechanics is not a ''temporary'' feature which will eventually be replaced by a deterministic theory, but is instead a ''final'' renunciation of the classical idea of "causality". Bohr in particular emphasized that any well-defined application of the quantum mechanical formalism must always make reference to the experimental arrangement, due to the [[complementarity (physics)|complementary]] nature of evidence obtained under different experimental situations. Copenhagen-type interpretations were adopted by Nobel laureates in quantum physics, including Bohr,<ref name="BohrComo">{{Cite journal |last1=Bohr |first1=Neils |author-link=Niels Bohr |year=1928 |title=The Quantum Postulate and the Recent Development of Atomic Theory |journal=Nature |volume=121 |issue=3050 |pages=580–590 |bibcode=1928Natur.121..580B |doi=10.1038/121580a0 |doi-access=free}}</ref> Heisenberg,<ref>{{Cite book |last=Heisenberg |first=Werner |author-link=Werner Heisenberg |title=Physics and philosophy: the revolution in modern science |date=1971 |publisher=Allen & Unwin |isbn=978-0-04-530016-7 |edition=3 |series=World perspectives |location=London |oclc=743037461}}</ref> Schrödinger,<ref>{{Cite journal |last=Schrödinger |first=Erwin |year=1980 |orig-date=1935 |editor-last=Trimmer |editor-first=John |title="Die gegenwärtige Situation in der Quantenmechanik." |trans-title=The Present Situation in Quantum Mechanics |journal=Naturwissenschaften |volume=23 |issue=50 |pages=844–849 |doi=10.1007/BF01491987 |jstor=986572|s2cid=22433857 }}</ref> Feynman,<ref name="Feynman" /> and Zeilinger<ref name=MaKoflerZeilinger>{{Cite journal |last1=Ma |first1=Xiao-song |last2=Kofler |first2=Johannes |last3=Zeilinger |first3=Anton |date=2016-03-03 |title=Delayed-choice gedanken experiments and their realizations |url=https://link.aps.org/doi/10.1103/RevModPhys.88.015005 |journal=Reviews of Modern Physics |language=en |volume=88 |issue=1 |page=015005 |doi=10.1103/RevModPhys.88.015005 |issn=0034-6861|arxiv=1407.2930 |bibcode=2016RvMP...88a5005M |s2cid=34901303 }}</ref> as well as 21st-century researchers in quantum foundations.<ref name=":25">{{Cite journal|last1=Schlosshauer|first1=Maximilian|last2=Kofler|first2=Johannes|last3=Zeilinger|first3=Anton|date=1 August 2013|title=A snapshot of foundational attitudes toward quantum mechanics|journal=Studies in History and Philosophy of Science Part B|volume=44|issue=3|pages=222–230|arxiv=1301.1069|bibcode=2013SHPMP..44..222S|doi=10.1016/j.shpsb.2013.04.004|s2cid=55537196}}</ref> |
|||
[[hr:Kvantna mehanika]] |
|||
[[id:Mekanika kuantum]] |
|||
[[Albert Einstein]], himself one of the founders of [[Old quantum theory|quantum theory]], was troubled by its apparent failure to respect some cherished metaphysical principles, such as [[determinism]] and [[principle of locality|locality]]. Einstein's long-running exchanges with Bohr about the meaning and status of quantum mechanics are now known as the [[Bohr–Einstein debates]]. Einstein believed that underlying quantum mechanics must be a theory that explicitly forbids [[action at a distance]]. He argued that quantum mechanics was incomplete, a theory that was valid but not fundamental, analogous to how [[thermodynamics]] is valid, but the fundamental theory behind it is [[statistical mechanics]]. In 1935, Einstein and his collaborators [[Boris Podolsky]] and [[Nathan Rosen]] published an argument that the principle of locality implies the incompleteness of quantum mechanics, a [[thought experiment]] later termed the [[Einstein–Podolsky–Rosen paradox]].{{refn|group=note|The published form of the EPR argument was due to Podolsky, and Einstein himself was not satisfied with it. In his own publications and correspondence, Einstein used a different argument to insist that quantum mechanics is an incomplete theory.<ref name="spekkens">{{cite journal|author2-link=Robert Spekkens|first1=Nicholas |last1=Harrigan |first2=Robert W. |last2=Spekkens |title=Einstein, incompleteness, and the epistemic view of quantum states |journal=[[Foundations of Physics]] |volume=40 |issue=2 |pages=125 |year=2010 |doi=10.1007/s10701-009-9347-0 |arxiv=0706.2661|bibcode=2010FoPh...40..125H |s2cid=32755624 }}</ref><ref name="howard">{{cite journal |last1=Howard |first1=D. |title=Einstein on locality and separability |journal=Studies in History and Philosophy of Science Part A |date=1985 |volume=16 |issue=3 |pages=171–201 |doi=10.1016/0039-3681(85)90001-9|bibcode=1985SHPSA..16..171H }}</ref><ref>{{Cite journal|last=Sauer|first=Tilman|date=1 December 2007|title=An Einstein manuscript on the EPR paradox for spin observables|url=http://philsci-archive.pitt.edu/3222/|journal=Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics |language=en |volume=38 |issue=4 |pages=879–887 |doi=10.1016/j.shpsb.2007.03.002 |issn=1355-2198|bibcode=2007SHPMP..38..879S|citeseerx=10.1.1.571.6089}}</ref><ref>{{cite encyclopedia |last=Einstein |first=Albert |title=Autobiographical Notes |encyclopedia=Albert Einstein: Philosopher-Scientist |year=1949 |publisher=Open Court Publishing Company |editor-last=Schilpp |editor-first=Paul Arthur}}</ref>}} In 1964, [[John Stewart Bell|John Bell]] showed that EPR's principle of locality, together with determinism, was actually incompatible with quantum mechanics: they implied constraints on the correlations produced by distance systems, now known as [[Bell inequalities]], that can be violated by entangled particles.<ref>{{Cite journal |last=Bell |first=John Stewart |author-link=John Stewart Bell |date=1 November 1964 |title=On the Einstein Podolsky Rosen paradox |journal=[[Physics Physique Fizika]] |language=en |volume=1 |issue=3 |pages=195–200 |doi=10.1103/PhysicsPhysiqueFizika.1.195 |doi-access=free}}</ref> Since then [[Bell test|several experiments]] have been performed to obtain these correlations, with the result that they do in fact violate Bell inequalities, and thus falsify the conjunction of locality with determinism.<ref name="wiseman15"/><ref name="wolchover17"/> |
|||
[[ia:Mechanica quantic]] |
|||
[[is:Skammtafræði]] |
|||
[[Bohmian mechanics]] shows that it is possible to reformulate quantum mechanics to make it deterministic, at the price of making it explicitly nonlocal. It attributes not only a wave function to a physical system, but in addition a real position, that evolves deterministically under a nonlocal guiding equation. The evolution of a physical system is given at all times by the Schrödinger equation together with the guiding equation; there is never a collapse of the wave function. This solves the measurement problem.<ref>{{cite book|chapter-url=https://plato.stanford.edu/entries/qm-bohm/ |last=Goldstein |first=Sheldon |chapter=Bohmian Mechanics |title=Stanford Encyclopedia of Philosophy |year=2017|publisher=Metaphysics Research Lab, Stanford University }}</ref> |
|||
[[it:Meccanica quantistica]] |
|||
[[File:Schroedingers cat film.svg|thumb|upright=1|[[Schrödinger's cat]] in the many-worlds interpretation of quantum mechanics, where a branching of the universe occurs through a superposition of two quantum mechanical states.]] |
|||
[[he:מכניקת הקוונטים]] |
|||
Everett's [[many-worlds interpretation]], formulated in 1956, holds that ''all'' the possibilities described by quantum theory ''simultaneously'' occur in a multiverse composed of mostly independent parallel universes.<ref>{{Cite book|first=Jeffrey |last=Barrett|title=[[Stanford Encyclopedia of Philosophy]]|publisher=Metaphysics Research Lab, Stanford University|year=2018|editor-last=Zalta|editor-first=Edward N.|chapter=Everett's Relative-State Formulation of Quantum Mechanics|chapter-url=https://plato.stanford.edu/entries/qm-everett/}}</ref> This is a consequence of removing the axiom of the collapse of the wave packet. All possible states of the measured system and the measuring apparatus, together with the observer, are present in a real physical quantum superposition. While the multiverse is deterministic, we perceive non-deterministic behavior governed by probabilities, because we do not observe the multiverse as a whole, but only one parallel universe at a time. Exactly how this is supposed to work has been the subject of much debate. Several attempts have been made to make sense of this and derive the Born rule,<ref name=dewitt73>{{cite book |editor-last1=DeWitt |editor-first1=Bryce |editor-link1=Bryce DeWitt |editor-last2=Graham |editor-first2=R. Neill |last1=Everett |first1=Hugh |author-link1=Hugh Everett III |last2=Wheeler |first2=J. A. |author-link2=John Archibald Wheeler |last3=DeWitt |first3=B. S. |author-link3=Bryce DeWitt |last4=Cooper |first4=L. N. |author-link4=Leon Cooper |last5=Van Vechten |first5=D. |last6=Graham |first6=N. |title=The Many-Worlds Interpretation of Quantum Mechanics |series=Princeton Series in Physics |publisher=[[Princeton University Press]] |location=Princeton, NJ |year=1973 |isbn=0-691-08131-X |page=v }}</ref><ref name="wallace2003">{{cite journal|last1=Wallace|first1=David|year=2003|title=Everettian Rationality: defending Deutsch's approach to probability in the Everett interpretation|journal=Stud. Hist. Phil. Mod. Phys.|volume=34|issue=3|pages=415–438|arxiv=quant-ph/0303050|bibcode=2003SHPMP..34..415W|doi=10.1016/S1355-2198(03)00036-4|s2cid=1921913}}</ref> with no consensus on whether they have been successful.<ref name="ballentine1973">{{cite journal|first1=L. E. |last1=Ballentine|date=1973|title=Can the statistical postulate of quantum theory be derived? – A critique of the many-universes interpretation|journal=Foundations of Physics|volume=3|issue=2|pages=229–240|doi=10.1007/BF00708440|bibcode=1973FoPh....3..229B|s2cid=121747282}}</ref><ref>{{cite book|first=N. P. |last=Landsman |chapter=The Born rule and its interpretation |chapter-url=http://www.math.ru.nl/~landsman/Born.pdf |quote=The conclusion seems to be that no generally accepted derivation of the Born rule has been given to date, but this does not imply that such a derivation is impossible in principle. |title=Compendium of Quantum Physics |editor-first1=F. |editor-last1=Weinert |editor-first2=K. |editor-last2=Hentschel |editor-first3=D. |editor-last3=Greenberger |editor-first4=B. |editor-last4=Falkenburg |publisher=Springer |year=2008 |isbn=978-3-540-70622-9}}</ref><ref name="kent2009">{{Cite book|last1=Kent|first1=Adrian|author-link=Adrian Kent|title=Many Worlds? Everett, Quantum Theory and Reality|publisher=Oxford University Press|year=2010|editor=S. Saunders|chapter=One world versus many: The inadequacy of Everettian accounts of evolution, probability, and scientific confirmation|arxiv=0905.0624|bibcode=2009arXiv0905.0624K|editor2=J. Barrett|editor3=A. Kent|editor4=D. Wallace}}</ref> |
|||
[[kn:ಕ್ವಾಂಟಮ್ ಭೌತಶಾಸ್ತ್ರ]] |
|||
[[ka:კვანტური მექანიკა]] |
|||
[[Relational quantum mechanics]] appeared in the late 1990s as a modern derivative of Copenhagen-type ideas,<ref>{{Cite journal|last=Van Fraassen|first=Bas C.|author-link=Bas van Fraassen|date=April 2010|title=Rovelli's World|url=http://link.springer.com/10.1007/s10701-009-9326-5|journal=[[Foundations of Physics]]|language=en|volume=40|issue=4|pages=390–417|doi=10.1007/s10701-009-9326-5|bibcode=2010FoPh...40..390V|s2cid=17217776|issn=0015-9018}}</ref> and [[QBism]] was developed some years later.<ref name=":23">{{Cite book|last=Healey|first=Richard|title=[[Stanford Encyclopedia of Philosophy]]|publisher=Metaphysics Research Lab, Stanford University|year=2016|editor-last=Zalta|editor-first=Edward N.|chapter=Quantum-Bayesian and Pragmatist Views of Quantum Theory|chapter-url=https://plato.stanford.edu/entries/quantum-bayesian/}}</ref> |
|||
[[la:Mechanica quantica]] |
|||
[[lv:Kvantu mehānika]] |
|||
== History == |
|||
[[lt:Kvantinė mechanika]] |
|||
{{Main|History of quantum mechanics|Atomic theory}} |
|||
[[li:Kwantummechanica]] |
|||
[[lmo:Mecàniga di quanta]] |
|||
Quantum mechanics was developed in the early decades of the 20th century, driven by the need to explain phenomena that, in some cases, had been observed in earlier times. Scientific inquiry into the wave nature of light began in the 17th and 18th centuries, when scientists such as [[Robert Hooke]], [[Christiaan Huygens]] and [[Leonhard Euler]] proposed a wave theory of light based on experimental observations.<ref name="Born & Wolf">{{cite book|first1=Max |last1=Born |author-link1=Max Born |first2=Emil |last2=Wolf |author-link2=Emil Wolf |title=Principles of Optics |title-link=Principles of Optics |year=1999 |publisher=Cambridge University Press |isbn=0-521-64222-1 |oclc=1151058062}}</ref> In 1803 English [[polymath]] [[Thomas Young (scientist)|Thomas Young]] described the famous [[Young's interference experiment|double-slit experiment]].<ref>{{Cite journal|last=Scheider|first=Walter|date=April 1986|title=Bringing one of the great moments of science to the classroom|url=http://www.cavendishscience.org/phys/tyoung/tyoung.htm|journal=[[The Physics Teacher]]|language=en|volume=24|issue=4|pages=217–219|doi=10.1119/1.2341987|bibcode=1986PhTea..24..217S|issn=0031-921X}}</ref> This experiment played a major role in the general acceptance of the [[wave theory of light]]. |
|||
[[hu:Kvantummechanika]] |
|||
[[mk:Квантна механика]] |
|||
During the early 19th century, [[chemistry|chemical]] research by [[John Dalton]] and [[Amedeo Avogadro]] lent weight to the [[atomic theory]] of matter, an idea that [[James Clerk Maxwell]], [[Ludwig Boltzmann]] and others built upon to establish the [[kinetic theory of gases]]. The successes of kinetic theory gave further credence to the idea that matter is composed of atoms, yet the theory also had shortcomings that would only be resolved by the development of quantum mechanics.<ref name="Feynman-kinetic-theory"> |
|||
[[ml:ക്വാണ്ടം ബലതന്ത്രം]] |
|||
{{cite book |
|||
[[mt:Mekkanika kwantistika]] |
|||
| last1 = Feynman |
|||
[[mr:पुंज यामिक]] |
|||
| first1 = Richard |
|||
[[ms:Mekanik kuantum]] |
|||
| last2 = Leighton |
|||
[[nl:Kwantummechanica]] |
|||
| first2 = Robert |
|||
[[ja:量子力学]] |
|||
| last3 = Sands |
|||
[[no:Kvantemekanikk]] |
|||
| first3 = Matthew |
|||
[[nn:Kvantemekanikk]] |
|||
| title = The Feynman Lectures on Physics |
|||
[[pl:Mechanika kwantowa]] |
|||
| volume = 1 |
|||
[[pt:Mecânica quântica]] |
|||
| publisher = California Institute of Technology |
|||
[[ro:Mecanică cuantică]] |
|||
| date = 1964 |
|||
[[ru:Квантовая механика]] |
|||
| url = https://feynmanlectures.caltech.edu/I_40.html |
|||
[[sq:Mekanika kuantike]] |
|||
| isbn=978-0-201-50064-6 |
|||
[[scn:Miccànica quantìstica]] |
|||
| access-date = 30 September 2021 |
|||
[[simple:Quantum mechanics]] |
|||
}}</ref> While the early conception of atoms from [[Ancient Greek philosophy|Greek philosophy]] had been that they were indivisible units{{snd}}the word "atom" deriving from the [[Greek language|Greek]] for "uncuttable"{{snd}} the 19th century saw the formulation of hypotheses about subatomic structure. One important discovery in that regard was [[Michael Faraday]]'s 1838 observation of a glow caused by an electrical discharge inside a glass tube containing gas at low pressure. [[Julius Plücker]], [[Johann Wilhelm Hittorf]] and [[Eugen Goldstein]] carried on and improved upon Faraday's work, leading to the identification of [[cathode rays]], which [[J. J. Thomson]] found to consist of subatomic particles that would be called electrons.<ref> |
|||
[[sk:Kvantová mechanika]] |
|||
{{citation |
|||
[[sl:Kvantna mehanika]] |
|||
| first =Andre |
|||
[[sr:Квантна механика]] |
|||
| last =Martin |
|||
[[sh:Kvantna mehanika]] |
|||
| contribution =Cathode Ray Tubes for Industrial and Military Applications |
|||
[[su:Mékanika kuantum]] |
|||
| editor-last =Hawkes |
|||
[[fi:Kvanttimekaniikka]] |
|||
| editor-first =Peter |
|||
[[sv:Kvantmekanik]] |
|||
| title =Advances in Electronics and Electron Physics, Volume 67 |
|||
[[tl:Mekaniks na kuwantum]] |
|||
| publisher =Academic Press |
|||
[[ta:குவாண்டம் பொறிமுறை]] |
|||
| year =1986 |
|||
[[tt:Квант механикасы]] |
|||
| isbn=978-0-08-057733-3 |
|||
[[th:กลศาสตร์ควอนตัม]] |
|||
| page =183 |
|||
[[tr:Kuantum mekaniği]] |
|||
| quote ="Evidence for the existence of "cathode-rays" was first found by Plücker and Hittorf ..." |
|||
[[uk:Квантова механіка]] |
|||
}}</ref><ref>{{Cite book|last=Dahl|first=Per F.|url=https://books.google.com/books?id=xUzaWGocMdMC|title=Flash of the Cathode Rays: A History of J J Thomson's Electron|year=1997|publisher=CRC Press|isbn=978-0-7503-0453-5|pages=47–57|language=en}}</ref> |
|||
[[ur:مقداریہ آلاتیات]] |
|||
[[File:Max Planck (1858-1947).jpg|thumb|upright|[[Max Planck]] is considered the father of the quantum theory.]] |
|||
[[vi:Cơ học lượng tử]] |
|||
[[fiu-vro:Kvantmekaaniga]] |
|||
The [[black-body radiation]] problem was discovered by [[Gustav Kirchhoff]] in 1859. In 1900, Max Planck proposed the hypothesis that energy is radiated and absorbed in discrete "quanta" (or energy packets), yielding a calculation that precisely matched the observed patterns of black-body radiation.<ref>{{cite book |first1=J. |last1=Mehra |author-link1=Jagdish Mehra |first2=H. |last2=Rechenberg |title=The Historical Development of Quantum Theory, Vol. 1: The Quantum Theory of Planck, Einstein, Bohr and Sommerfeld. Its Foundation and the Rise of Its Difficulties (1900–1925)|location=New York |publisher=Springer-Verlag |year=1982 |isbn=978-0-387-90642-3 }}</ref> The word ''quantum'' derives from the [[Latin language|Latin]], meaning "how great" or "how much".<ref>{{cite web|title=Quantum – Definition and More |url=http://www.merriam-webster.com/dictionary/quantum|access-date=18 August 2012|publisher=Merriam-Webster Dictionary |url-status=live |archive-url=https://web.archive.org/web/20121026104456/http://www.merriam-webster.com/dictionary/quantum |archive-date= Oct 26, 2012 }}</ref> According to Planck, quantities of energy could be thought of as divided into "elements" whose size (''E'') would be proportional to their [[frequency]] (''ν''): |
|||
[[war:Mekanika kwantum]] |
|||
: <math> E = h \nu\ </math>, |
|||
[[wuu:量子力学]] |
|||
where ''h'' is the [[Planck constant]]. Planck cautiously insisted that this was only an aspect of the processes of absorption and emission of radiation and was not the ''physical reality'' of the radiation.<ref>{{cite book|last=Kuhn|first=T. S.|title=Black-body theory and the quantum discontinuity 1894–1912|publisher=Clarendon Press|year=1978|isbn=978-0-19-502383-1|location=Oxford|author-link=Thomas Samuel Kuhn}}</ref> In fact, he considered his quantum hypothesis a mathematical trick to get the right answer rather than a sizable discovery.<ref name="Kragh">{{cite web|last=Kragh|first=Helge|author-link=Helge Kragh |title=Max Planck: the reluctant revolutionary|date=1 December 2000|url=https://physicsworld.com/a/max-planck-the-reluctant-revolutionary/|website=[[Physics World]] |access-date=12 December 2020}}</ref> However, in 1905 Albert Einstein interpreted Planck's quantum hypothesis [[local realism|realistically]] and used it to explain the [[photoelectric effect]], in which shining light on certain materials can eject electrons from the material. Niels Bohr then developed Planck's ideas about radiation into a [[Bohr model|model of the hydrogen atom]] that successfully predicted the [[spectral line]]s of hydrogen.<ref>{{cite book|last=Stachel |first=John |title=Quantum Reality, Relativistic Causality, and Closing the Epistemic Circle |author-link=John Stachel |year=2009 |chapter=Bohr and the Photon |series=The Western Ontario Series in Philosophy of Science |volume=73 |location=Dordrecht |publisher=Springer |pages=69–83 |doi=10.1007/978-1-4020-9107-0_5|isbn=978-1-4020-9106-3 }}</ref> Einstein further developed this idea to show that an [[electromagnetic wave]] such as light could also be described as a particle (later called the photon), with a discrete amount of energy that depends on its frequency.<ref>{{cite journal |last=Einstein |first=Albert |year=1905 |title=Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt |trans-title=On a heuristic point of view concerning the production and transformation of light |journal=[[Annalen der Physik]] |volume=17 |issue=6 |pages=132–148 |bibcode=1905AnP...322..132E |doi=10.1002/andp.19053220607 |doi-access=free}} Reprinted in {{cite book |title=The Collected Papers of Albert Einstein |publisher=Princeton University Press |year=1989 |editor-last=Stachel |editor-first=John |editor-link=John Stachel |volume=2 |pages=149–166 |language=de}} See also "Einstein's early work on the quantum hypothesis", ibid. pp. 134–148.</ref> In his paper "On the Quantum Theory of Radiation", Einstein expanded on the interaction between energy and matter to explain the absorption and emission of energy by atoms. Although overshadowed at the time by his general theory of relativity, this paper articulated the mechanism underlying the stimulated emission of radiation,<ref>{{cite journal|first=Albert |last=Einstein |author-link=Albert Einstein |year=1917 |title=Zur Quantentheorie der Strahlung|trans-title=On the Quantum Theory of Radiation|language=de |journal=[[Physikalische Zeitschrift]] |volume=18 |pages=121–128|bibcode=1917PhyZ...18..121E }} Translated in {{cite book|title=The Old Quantum Theory|date=1967|pages=167–183|chapter=On the Quantum Theory of Radiation|publisher=Elsevier|doi=10.1016/b978-0-08-012102-4.50018-8|isbn=978-0-08-012102-4|last1=Einstein|first1=A.}}</ref> which became the basis of the laser.<ref>{{cite web|first=Philip |last=Ball |url=https://physicsworld.com/a/a-century-ago-einstein-sparked-the-notion-of-the-laser/ |title=A century ago Einstein sparked the notion of the laser |author-link=Philip Ball |website=[[Physics World]] |date=2017-08-31 |access-date=2024-03-23}}</ref> |
|||
[[bat-smg:Kvantėnė mekanėka]] |
|||
[[zh:量子力学]] |
|||
[[File:Solvay conference 1927.jpg|left|thumb|upright=1.4|The 1927 [[Solvay Conference]] in [[Brussels]] was the fifth world physics conference.]] |
|||
This phase is known as the [[old quantum theory]]. Never complete or self-consistent, the old quantum theory was rather a set of [[heuristic]] corrections to classical mechanics.<ref name="terHaar">{{cite book|last=ter Haar|first=D.|url=https://archive.org/details/oldquantumtheory0000haar|title=The Old Quantum Theory|publisher=Pergamon Press|year=1967|isbn=978-0-08-012101-7 |lccn=66-29628 |pages=3–75 |url-access=registration}}</ref><ref>{{cite SEP|title=Bohr's Correspondence Principle |date=2020-08-13 |author-first1=Alisa |author-last1=Bokulich |author-first2=Peter |author-last2=Bokulich |url-id=bohr-correspondence}}</ref> The theory is now understood as a [[WKB approximation#Application to the Schr.C3.B6dinger equation|semi-classical approximation]] to modern quantum mechanics.<ref>{{cite web|title=Semi-classical approximation|url=https://www.encyclopediaofmath.org/index.php?title=Semi-classical_approximation|access-date=1 February 2020|website=Encyclopedia of Mathematics}}</ref><ref>{{cite book|last1=Sakurai|first1=J. J.|title=Modern Quantum Mechanics|title-link=Modern Quantum Mechanics|last2=Napolitano|first2=J.|publisher=Pearson|year=2014|isbn=978-1-292-02410-3|chapter=Quantum Dynamics|oclc=929609283|author-link1=J. J. Sakurai}}</ref> Notable results from this period include, in addition to the work of Planck, Einstein and Bohr mentioned above, Einstein and [[Peter Debye]]'s work on the [[specific heat]] of solids, Bohr and [[Hendrika Johanna van Leeuwen]]'s [[Bohr–Van Leeuwen theorem|proof]] that classical physics cannot account for [[diamagnetism]], and [[Arnold Sommerfeld]]'s extension of the Bohr model to include special-relativistic effects.<ref name="terHaar"/><ref name=Aharoni>{{cite book |last=Aharoni |first=Amikam |author-link=Amikam Aharoni |title=Introduction to the Theory of Ferromagnetism |publisher=[[Clarendon Press]] |year=1996 |isbn=0-19-851791-2 |pages=[https://archive.org/details/introductiontoth00ahar/page/6 6–7] |url=https://archive.org/details/introductiontoth00ahar/page/6 }}</ref> |
|||
In the mid-1920s quantum mechanics was developed to become the standard formulation for atomic physics. In 1923, the French physicist [[Louis-Victor de Broglie|Louis de Broglie]] put forward his theory of matter waves by stating that particles can exhibit wave characteristics and vice versa. Building on de Broglie's approach, modern quantum mechanics was born in 1925, when the German physicists Werner Heisenberg, Max Born, and [[Pascual Jordan]]<ref name=Edwards79>David Edwards, "The Mathematical Foundations of Quantum Mechanics", ''Synthese'', Volume 42, Number 1/September, 1979, pp. 1–70.</ref><ref name="Edwards81">David Edwards, "The Mathematical Foundations of Quantum Field Theory: Fermions, Gauge Fields, and Super-symmetry, Part I: Lattice Field Theories", ''International Journal of Theoretical Physics'', Vol. 20, No. 7 (1981).</ref> developed [[matrix mechanics]] and the Austrian physicist Erwin Schrödinger invented [[Schrödinger equation|wave mechanics]]. Born introduced the probabilistic interpretation of Schrödinger's wave function in July 1926.<ref>{{Cite journal|last=Bernstein|first=Jeremy|author-link=Jeremy Bernstein|date=November 2005|title=Max Born and the quantum theory|journal=[[American Journal of Physics]]|language=en|volume=73|issue=11|pages=999–1008|doi=10.1119/1.2060717|bibcode=2005AmJPh..73..999B|issn=0002-9505|doi-access=free}}</ref> Thus, the entire field of quantum physics emerged, leading to its wider acceptance at the Fifth [[Solvay Conference]] in 1927.<ref name="pais1997">{{cite book |last=Pais |first=Abraham |author-link=Abraham Pais |title = A Tale of Two Continents: A Physicist's Life in a Turbulent World |year=1997 |publisher = Princeton University Press |location = Princeton, New Jersey |isbn=0-691-01243-1 |url-access = registration |url = https://archive.org/details/taleoftwocontine00pais }}</ref> |
|||
By 1930, quantum mechanics had been further unified and formalized by [[David Hilbert]], Paul Dirac and [[John von Neumann]]<ref>{{cite journal|last=Van Hove|first=Leon|title=Von Neumann's contributions to quantum mechanics|journal=[[Bulletin of the American Mathematical Society]]|year=1958|volume=64|issue=3|pages =Part 2:95–99 |url=https://www.ams.org/journals/bull/1958-64-03/S0002-9904-1958-10206-2/S0002-9904-1958-10206-2.pdf |doi=10.1090/s0002-9904-1958-10206-2|doi-access=free |url-status=live |archive-url=https://web.archive.org/web/20240120073106/https://www.ams.org/journals/bull/1958-64-03/S0002-9904-1958-10206-2/S0002-9904-1958-10206-2.pdf |archive-date= Jan 20, 2024 }}</ref> with greater emphasis on [[measurement in quantum mechanics|measurement]], the statistical nature of our knowledge of reality, and [[Interpretations of quantum mechanics|philosophical speculation about the 'observer']]. It has since permeated many disciplines, including quantum chemistry, [[quantum electronics]], [[quantum optics]], and [[quantum information science]]. It also provides a useful framework for many features of the modern [[periodic table|periodic table of elements]], and describes the behaviors of [[atoms]] during [[chemical bond]]ing and the flow of electrons in computer [[semiconductor]]s, and therefore plays a crucial role in many modern technologies. While quantum mechanics was constructed to describe the world of the very small, it is also needed to explain some [[macroscopic]] phenomena such as [[superconductivity|superconductors]]<ref name="feynman2015">{{cite web |url=https://feynmanlectures.caltech.edu/III_21.html#Ch21-S5 |title= The Feynman Lectures on Physics Vol. III Ch. 21: The Schrödinger Equation in a Classical Context: A Seminar on Superconductivity, 21-4 |quote=...it was long believed that the wave function of the Schrödinger equation would never have a macroscopic representation analogous to the macroscopic representation of the amplitude for photons. On the other hand, it is now realized that the phenomena of superconductivity presents us with just this situation. |last=Feynman |first= Richard|author-link= Richard Feynman |publisher= [[California Institute of Technology]] |access-date=24 November 2015 |url-status=live |archive-url=https://archive.today/20161215225248/http://www.feynmanlectures.caltech.edu/III_21.html%23Ch21-S5 |archive-date= 15 Dec 2016 }}</ref> and [[superfluid]]s.<ref>{{cite web|url=http://physics.berkeley.edu/sites/default/files/_/lt24_berk_expts_on_macro_sup_effects.pdf |first=Richard |last=Packard |year=2006 |title=Berkeley Experiments on Superfluid Macroscopic Quantum Effects |publisher=Physics Department, University of California, Berkeley |archive-url=https://web.archive.org/web/20151125112132/http://research.physics.berkeley.edu/packard/publications/Articles/LT24_Berk_expts_on_macro_sup_effects.pdf |archive-date=25 November 2015 |access-date=24 November 2015}}</ref> |
|||
== See also == |
|||
{{cols|colwidth=35em}} |
|||
* [[Bra–ket notation]] |
|||
* [[Einstein's thought experiments]] |
|||
* [[List of textbooks on classical and quantum mechanics]] |
|||
* [[Macroscopic quantum phenomena]] |
|||
* [[Phase-space formulation]] |
|||
* [[Regularization (physics)]] |
|||
* [[Two-state quantum system]] |
|||
{{colend}} |
|||
== Explanatory notes == |
|||
{{reflist|group=note}} |
|||
== References == |
|||
{{reflist}} |
|||
== Further reading == |
|||
{{Refbegin|30em}} |
|||
The following titles, all by working physicists, attempt to communicate quantum theory to lay people, using a minimum of technical apparatus. |
|||
* [[Marvin Chester|Chester, Marvin]] (1987). ''Primer of Quantum Mechanics''. John Wiley. {{isbn|0-486-42878-8}} |
|||
* {{cite book | first1= Brian | last1= Cox |author-link1=Brian Cox (physicist)| first2= Jeff | last2= Forshaw |author-link2=Jeff Forshaw| title= The Quantum Universe: Everything That Can Happen Does Happen | publisher = Allen Lane | year = 2011 |isbn=978-1-84614-432-5 | title-link= The Quantum Universe }} |
|||
* [[Richard Feynman]], 1985. ''[[QED: The Strange Theory of Light and Matter]]'', Princeton University Press. {{isbn|0-691-08388-6}}. Four elementary lectures on quantum electrodynamics and [[quantum field theory]], yet containing many insights for the expert. |
|||
* [[Giancarlo Ghirardi|Ghirardi, GianCarlo]], 2004. ''Sneaking a Look at God's Cards'', Gerald Malsbary, trans. Princeton Univ. Press. The most technical of the works cited here. Passages using [[algebra]], [[trigonometry]], and [[bra–ket notation]] can be passed over on a first reading. |
|||
* [[N. David Mermin]], 1990, "Spooky actions at a distance: mysteries of the QT" in his ''Boojums All the Way Through''. Cambridge University Press: 110–76. |
|||
* [[Victor Stenger]], 2000. ''Timeless Reality: Symmetry, Simplicity, and Multiple Universes''. Buffalo, NY: Prometheus Books. Chpts. 5–8. Includes [[cosmological]] and [[philosophical]] considerations. |
|||
More technical: |
|||
* {{cite book | author=Bernstein, Jeremy|author-link=Jeremy Bernstein|title=Quantum Leaps| publisher=Belknap Press of Harvard University Press | location=Cambridge, Massachusetts|year=2009|isbn=978-0-674-03541-6|url=https://books.google.com/books?id=j0Me3brYOL0C}} |
|||
* {{cite book | author=Bohm, David | title=Quantum Theory | url=https://archive.org/details/quantumtheory0000bohm | url-access=registration | publisher=Dover Publications| year=1989 |isbn=978-0-486-65969-5| author-link=David Bohm }} |
|||
* {{cite book |author1=Binney, James |author1-link=James Binney |author2=Skinner, David |title=The Physics of Quantum Mechanics |year=2008 |publisher=Oxford University Press |isbn=978-0-19-968857-9}} |
|||
* {{cite book |author1=Eisberg, Robert |author2-link=Robert Resnick |author2=Resnick, Robert |title=Quantum Physics of Atoms, Molecules, Solids, Nuclei, and Particles|edition = 2nd|publisher=Wiley |year=1985 |isbn=978-0-471-87373-0 |url=https://archive.org/details/quantumphysicsof00eisb }} |
|||
* [[Bryce DeWitt]], R. Neill Graham, eds., 1973. ''The Many-Worlds Interpretation of Quantum Mechanics'', Princeton Series in Physics, Princeton University Press. {{isbn|0-691-08131-X}} |
|||
* {{cite journal | last1 = Everett | first1 = Hugh | author-link = Hugh Everett | year = 1957 | title = Relative State Formulation of Quantum Mechanics | journal = Reviews of Modern Physics | volume = 29 | issue = 3 | pages = 454–462 | doi = 10.1103/RevModPhys.29.454 | bibcode = 1957RvMP...29..454E | s2cid = 17178479 }} |
|||
* {{cite book |last1=Feynman |first1=Richard P. |author-link1=Richard Feynman |last2=Leighton |first2=Robert B. |author-link2=Robert B. Leighton |last3=Sands |first3=Matthew |year=1965 |title=The Feynman Lectures on Physics |volume=1–3 |publisher=Addison-Wesley |isbn=978-0-7382-0008-8|title-link=The Feynman Lectures on Physics }} |
|||
* [[Daniel Greenberger|D. Greenberger]], [[Klaus Hentschel|K. Hentschel]], F. Weinert, eds., 2009. ''Compendium of quantum physics, Concepts, experiments, history and philosophy'', Springer-Verlag, Berlin, Heidelberg. Short articles on many QM topics. |
|||
* {{cite book | author=Griffiths, David J.|author-link=David J. Griffiths| title=[[Introduction to Quantum Mechanics (book)|Introduction to Quantum Mechanics]]|edition=2nd | publisher=Prentice Hall |year=2004 |isbn=978-0-13-111892-8 | oclc=40251748}} A standard undergraduate text. |
|||
* [[Max Jammer]], 1966. ''The Conceptual Development of Quantum Mechanics''. McGraw Hill. |
|||
* [[Hagen Kleinert]], 2004. ''Path Integrals in Quantum Mechanics, Statistics, Polymer Physics, and Financial Markets'', 3rd ed. Singapore: World Scientific. [http://www.physik.fu-berlin.de/~kleinert/b5 Draft of 4th edition.] {{Webarchive|url=https://web.archive.org/web/20080615134934/http://www.physik.fu-berlin.de/~kleinert/b5 |date=2008-06-15 }} |
|||
* {{cite book |
|||
|author=[[Lev Landau|L.D. Landau]], [[Evgeny Lifshitz|E.M. Lifshitz]] |
|||
|year=1977 |
|||
|title=Quantum Mechanics: Non-Relativistic Theory |
|||
|edition=3rd |volume=3 |
|||
|publisher=[[Pergamon Press]] |
|||
|isbn=978-0-08-020940-1 |
|||
}} [https://archive.org/details/QuantumMechanics_104 Online copy] |
|||
* {{cite book | author=Liboff, Richard L. | title=Introductory Quantum Mechanics | publisher=Addison-Wesley | year=2002 |isbn=978-0-8053-8714-8| author-link=Liboff, Richard }} |
|||
* Gunther Ludwig, 1968. ''Wave Mechanics''. London: Pergamon Press. {{isbn|0-08-203204-1}} |
|||
* [[George Mackey]] (2004). ''The mathematical foundations of quantum mechanics''. Dover Publications. {{isbn|0-486-43517-2}}. |
|||
* {{cite book | author=Merzbacher, Eugen|author-link=Eugen Merzbacher | title=Quantum Mechanics | publisher=Wiley, John & Sons, Inc | year=1998 |isbn=978-0-471-88702-7}} |
|||
* [[Albert Messiah]], 1966. ''Quantum Mechanics'' (Vol. I), English translation from French by G.M. Temmer. North Holland, John Wiley & Sons. Cf. chpt. IV, section III. [https://archive.org/details/QuantumMechanicsVolumeI online] |
|||
* {{cite book | author=Omnès, Roland | title=Understanding Quantum Mechanics | publisher=Princeton University Press | year=1999 |isbn=978-0-691-00435-8 | oclc=39849482 | author-link=Roland Omnès | url=https://archive.org/details/understandingqua00omne }} |
|||
* {{cite book |last=Scerri |first=Eric. R. |author-link=Eric R. Scerri |year=2006 |title=The Periodic Table: Its Story and Its Significance |publisher=Oxford University Press|isbn=0-19-530573-6}} Considers the extent to which chemistry and the periodic system have been reduced to quantum mechanics. |
|||
* {{Cite book |last=Schiff |first=Leonard I. |author-link=Leonard I. Schiff |title=Quantum Mechanics |date=1955 |publisher=Mc-Graw Hill, Inc. }} |
|||
* {{cite book | author=Shankar, R. |author-link=Ramamurti Shankar| title=Principles of Quantum Mechanics | publisher=Springer | year=1994|isbn=978-0-306-44790-7}} |
|||
* {{cite book | author=Stone, A. Douglas |author-link=A. Douglas Stone| title=Einstein and the Quantum | publisher=Princeton University Press | year=2013 |isbn=978-0-691-13968-5 | url-access=registration | url=https://archive.org/details/einsteinquantumq0000ston }} |
|||
* {{cite book | author=Transnational College of Lex| title=What is Quantum Mechanics? A Physics Adventure | publisher=Language Research Foundation, Boston |year=1996 |isbn=978-0-9643504-1-0 | oclc=34661512| author-link=Transnational College of Lex }} |
|||
* [[Martinus J. G. Veltman|Veltman, Martinus J.G.]] (2003), ''Facts and Mysteries in Elementary Particle Physics''. |
|||
{{refend}} |
|||
== External links == |
|||
{{Sister project links|s=Quantum mechanics}} |
|||
* J. O'Connor and E. F. Robertson: [http://www-history.mcs.st-andrews.ac.uk/history/HistTopics/The_Quantum_age_begins.html A history of quantum mechanics.] |
|||
* [https://web.archive.org/web/20080913201312/http://www.quantiki.org/wiki/index.php/Introduction_to_Quantum_Theory Introduction to Quantum Theory at Quantiki.] |
|||
* [http://bethe.cornell.edu/ Quantum Physics Made Relatively Simple]: three video lectures by [[Hans Bethe]]. |
|||
; Course material : |
|||
* [http://oyc.yale.edu/sites/default/files/notes_quantum_cookbook.pdf Quantum Cook Book] and [http://oyc.yale.edu/physics/phys-201#sessions PHYS 201: Fundamentals of Physics II] by [[Ramamurti Shankar]], Yale OpenCourseware. |
|||
* ''[http://www.lightandmatter.com/mod/ Modern Physics: With waves, thermodynamics, and optics]'' – an online textbook. |
|||
* [[MIT OpenCourseWare]]: [https://ocw.mit.edu/courses/chemistry/ Chemistry] and [https://ocw.mit.edu/courses/physics/ Physics]. See [https://ocw.mit.edu/courses/physics/8-04-quantum-physics-i-spring-2016/ 8.04], [https://ocw.mit.edu/courses/physics/8-05-quantum-physics-ii-fall-2013/index.htm 8.05] and [https://ocw.mit.edu/courses/physics/8-06-quantum-physics-iii-spring-2018/index.htm 8.06]. |
|||
* [http://www.physics.csbsju.edu/QM/ {{sfrac|5|1|2}} Examples in Quantum Mechanics]. |
|||
* [http://www.imperial.ac.uk/quantuminformation/qi/tutorials Imperial College Quantum Mechanics Course.] |
|||
; Philosophy : |
|||
* {{cite SEP |url-id=qm |title=Quantum Mechanics |last=Ismael |first=Jenann}} |
|||
* {{cite SEP |url-id=qt-measurement |title=Measurement in Quantum Theory |last=Krips |first=Henry}} |
|||
{{Quantum mechanics topics}} |
|||
{{Physics-footer}} |
|||
{{Portal bar|Astronomy|Chemistry|Electronics|Energy|History of science|Mathematics|Physics|Science|Stars}} |
|||
{{Authority control}} |
|||
{{DEFAULTSORT:Quantum Mechanics}} |
|||
[[Category:Quantum mechanics| ]] |
|||
Latest revision as of 23:57, 15 December 2024

| Part of a series of articles about |
| Quantum mechanics |
|---|
Quantum mechanics is a fundamental theory that describes the behavior of nature at and below the scale of atoms.[2]: 1.1 It is the foundation of all quantum physics, which includes quantum chemistry, quantum field theory, quantum technology, and quantum information science.
Quantum mechanics can describe many systems that classical physics cannot. Classical physics can describe many aspects of nature at an ordinary (macroscopic and (optical) microscopic) scale, but is not sufficient for describing them at very small submicroscopic (atomic and subatomic) scales. Most theories in classical physics can be derived from quantum mechanics as an approximation, valid at large (macroscopic/microscopic) scale.[3]
Quantum systems have bound states that are quantized to discrete values of energy, momentum, angular momentum, and other quantities, in contrast to classical systems where these quantities can be measured continuously. Measurements of quantum systems show characteristics of both particles and waves (wave–particle duality), and there are limits to how accurately the value of a physical quantity can be predicted prior to its measurement, given a complete set of initial conditions (the uncertainty principle).
Quantum mechanics arose gradually from theories to explain observations that could not be reconciled with classical physics, such as Max Planck's solution in 1900 to the black-body radiation problem, and the correspondence between energy and frequency in Albert Einstein's 1905 paper, which explained the photoelectric effect. These early attempts to understand microscopic phenomena, now known as the "old quantum theory", led to the full development of quantum mechanics in the mid-1920s by Niels Bohr, Erwin Schrödinger, Werner Heisenberg, Max Born, Paul Dirac and others. The modern theory is formulated in various specially developed mathematical formalisms. In one of them, a mathematical entity called the wave function provides information, in the form of probability amplitudes, about what measurements of a particle's energy, momentum, and other physical properties may yield.
Overview and fundamental concepts
Quantum mechanics allows the calculation of properties and behaviour of physical systems. It is typically applied to microscopic systems: molecules, atoms and sub-atomic particles. It has been demonstrated to hold for complex molecules with thousands of atoms,[4] but its application to human beings raises philosophical problems, such as Wigner's friend, and its application to the universe as a whole remains speculative.[5] Predictions of quantum mechanics have been verified experimentally to an extremely high degree of accuracy. For example, the refinement of quantum mechanics for the interaction of light and matter, known as quantum electrodynamics (QED), has been shown to agree with experiment to within 1 part in 1012 when predicting the magnetic properties of an electron.[6]
A fundamental feature of the theory is that it usually cannot predict with certainty what will happen, but only give probabilities. Mathematically, a probability is found by taking the square of the absolute value of a complex number, known as a probability amplitude. This is known as the Born rule, named after physicist Max Born. For example, a quantum particle like an electron can be described by a wave function, which associates to each point in space a probability amplitude. Applying the Born rule to these amplitudes gives a probability density function for the position that the electron will be found to have when an experiment is performed to measure it. This is the best the theory can do; it cannot say for certain where the electron will be found. The Schrödinger equation relates the collection of probability amplitudes that pertain to one moment of time to the collection of probability amplitudes that pertain to another.[7]: 67–87
One consequence of the mathematical rules of quantum mechanics is a tradeoff in predictability between measurable quantities. The most famous form of this uncertainty principle says that no matter how a quantum particle is prepared or how carefully experiments upon it are arranged, it is impossible to have a precise prediction for a measurement of its position and also at the same time for a measurement of its momentum.[7]: 427–435
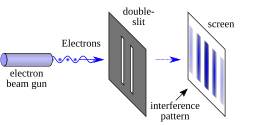
Another consequence of the mathematical rules of quantum mechanics is the phenomenon of quantum interference, which is often illustrated with the double-slit experiment. In the basic version of this experiment, a coherent light source, such as a laser beam, illuminates a plate pierced by two parallel slits, and the light passing through the slits is observed on a screen behind the plate.[8]: 102–111 [2]: 1.1–1.8 The wave nature of light causes the light waves passing through the two slits to interfere, producing bright and dark bands on the screen – a result that would not be expected if light consisted of classical particles.[8] However, the light is always found to be absorbed at the screen at discrete points, as individual particles rather than waves; the interference pattern appears via the varying density of these particle hits on the screen. Furthermore, versions of the experiment that include detectors at the slits find that each detected photon passes through one slit (as would a classical particle), and not through both slits (as would a wave).[8]: 109 [9][10] However, such experiments demonstrate that particles do not form the interference pattern if one detects which slit they pass through. This behavior is known as wave–particle duality. In addition to light, electrons, atoms, and molecules are all found to exhibit the same dual behavior when fired towards a double slit.[2]

Another non-classical phenomenon predicted by quantum mechanics is quantum tunnelling: a particle that goes up against a potential barrier can cross it, even if its kinetic energy is smaller than the maximum of the potential.[11] In classical mechanics this particle would be trapped. Quantum tunnelling has several important consequences, enabling radioactive decay, nuclear fusion in stars, and applications such as scanning tunnelling microscopy, tunnel diode and tunnel field-effect transistor.[12][13]
When quantum systems interact, the result can be the creation of quantum entanglement: their properties become so intertwined that a description of the whole solely in terms of the individual parts is no longer possible. Erwin Schrödinger called entanglement "...the characteristic trait of quantum mechanics, the one that enforces its entire departure from classical lines of thought".[14] Quantum entanglement enables quantum computing and is part of quantum communication protocols, such as quantum key distribution and superdense coding.[15] Contrary to popular misconception, entanglement does not allow sending signals faster than light, as demonstrated by the no-communication theorem.[15]
Another possibility opened by entanglement is testing for "hidden variables", hypothetical properties more fundamental than the quantities addressed in quantum theory itself, knowledge of which would allow more exact predictions than quantum theory provides. A collection of results, most significantly Bell's theorem, have demonstrated that broad classes of such hidden-variable theories are in fact incompatible with quantum physics. According to Bell's theorem, if nature actually operates in accord with any theory of local hidden variables, then the results of a Bell test will be constrained in a particular, quantifiable way. Many Bell tests have been performed and they have shown results incompatible with the constraints imposed by local hidden variables.[16][17]
It is not possible to present these concepts in more than a superficial way without introducing the mathematics involved; understanding quantum mechanics requires not only manipulating complex numbers, but also linear algebra, differential equations, group theory, and other more advanced subjects.[18][19] Accordingly, this article will present a mathematical formulation of quantum mechanics and survey its application to some useful and oft-studied examples.
Mathematical formulation
In the mathematically rigorous formulation of quantum mechanics, the state of a quantum mechanical system is a vector belonging to a (separable) complex Hilbert space . This vector is postulated to be normalized under the Hilbert space inner product, that is, it obeys , and it is well-defined up to a complex number of modulus 1 (the global phase), that is, and represent the same physical system. In other words, the possible states are points in the projective space of a Hilbert space, usually called the complex projective space. The exact nature of this Hilbert space is dependent on the system – for example, for describing position and momentum the Hilbert space is the space of complex square-integrable functions , while the Hilbert space for the spin of a single proton is simply the space of two-dimensional complex vectors with the usual inner product.
Physical quantities of interest – position, momentum, energy, spin – are represented by observables, which are Hermitian (more precisely, self-adjoint) linear operators acting on the Hilbert space. A quantum state can be an eigenvector of an observable, in which case it is called an eigenstate, and the associated eigenvalue corresponds to the value of the observable in that eigenstate. More generally, a quantum state will be a linear combination of the eigenstates, known as a quantum superposition. When an observable is measured, the result will be one of its eigenvalues with probability given by the Born rule: in the simplest case the eigenvalue is non-degenerate and the probability is given by , where is its associated eigenvector. More generally, the eigenvalue is degenerate and the probability is given by , where is the projector onto its associated eigenspace. In the continuous case, these formulas give instead the probability density.
After the measurement, if result was obtained, the quantum state is postulated to collapse to , in the non-degenerate case, or to , in the general case. The probabilistic nature of quantum mechanics thus stems from the act of measurement. This is one of the most difficult aspects of quantum systems to understand. It was the central topic in the famous Bohr–Einstein debates, in which the two scientists attempted to clarify these fundamental principles by way of thought experiments. In the decades after the formulation of quantum mechanics, the question of what constitutes a "measurement" has been extensively studied. Newer interpretations of quantum mechanics have been formulated that do away with the concept of "wave function collapse" (see, for example, the many-worlds interpretation). The basic idea is that when a quantum system interacts with a measuring apparatus, their respective wave functions become entangled so that the original quantum system ceases to exist as an independent entity (see Measurement in quantum mechanics[20]).
Time evolution of a quantum state
The time evolution of a quantum state is described by the Schrödinger equation:
Here denotes the Hamiltonian, the observable corresponding to the total energy of the system, and is the reduced Planck constant. The constant is introduced so that the Hamiltonian is reduced to the classical Hamiltonian in cases where the quantum system can be approximated by a classical system; the ability to make such an approximation in certain limits is called the correspondence principle.
The solution of this differential equation is given by
The operator is known as the time-evolution operator, and has the crucial property that it is unitary. This time evolution is deterministic in the sense that – given an initial quantum state – it makes a definite prediction of what the quantum state will be at any later time.[21]

Some wave functions produce probability distributions that are independent of time, such as eigenstates of the Hamiltonian.[7]: 133–137 Many systems that are treated dynamically in classical mechanics are described by such "static" wave functions. For example, a single electron in an unexcited atom is pictured classically as a particle moving in a circular trajectory around the atomic nucleus, whereas in quantum mechanics, it is described by a static wave function surrounding the nucleus. For example, the electron wave function for an unexcited hydrogen atom is a spherically symmetric function known as an s orbital (Fig. 1).
Analytic solutions of the Schrödinger equation are known for very few relatively simple model Hamiltonians including the quantum harmonic oscillator, the particle in a box, the dihydrogen cation, and the hydrogen atom. Even the helium atom – which contains just two electrons – has defied all attempts at a fully analytic treatment, admitting no solution in closed form.[22][23][24]
However, there are techniques for finding approximate solutions. One method, called perturbation theory, uses the analytic result for a simple quantum mechanical model to create a result for a related but more complicated model by (for example) the addition of a weak potential energy.[7]: 793 Another approximation method applies to systems for which quantum mechanics produces only small deviations from classical behavior. These deviations can then be computed based on the classical motion.[7]: 849
Uncertainty principle
One consequence of the basic quantum formalism is the uncertainty principle. In its most familiar form, this states that no preparation of a quantum particle can imply simultaneously precise predictions both for a measurement of its position and for a measurement of its momentum.[25][26] Both position and momentum are observables, meaning that they are represented by Hermitian operators. The position operator and momentum operator do not commute, but rather satisfy the canonical commutation relation:
Given a quantum state, the Born rule lets us compute expectation values for both and , and moreover for powers of them. Defining the uncertainty for an observable by a standard deviation, we have
and likewise for the momentum:
The uncertainty principle states that
Either standard deviation can in principle be made arbitrarily small, but not both simultaneously.[27] This inequality generalizes to arbitrary pairs of self-adjoint operators and . The commutator of these two operators is
and this provides the lower bound on the product of standard deviations:
Another consequence of the canonical commutation relation is that the position and momentum operators are Fourier transforms of each other, so that a description of an object according to its momentum is the Fourier transform of its description according to its position. The fact that dependence in momentum is the Fourier transform of the dependence in position means that the momentum operator is equivalent (up to an factor) to taking the derivative according to the position, since in Fourier analysis differentiation corresponds to multiplication in the dual space. This is why in quantum equations in position space, the momentum is replaced by , and in particular in the non-relativistic Schrödinger equation in position space the momentum-squared term is replaced with a Laplacian times .[25]
Composite systems and entanglement
When two different quantum systems are considered together, the Hilbert space of the combined system is the tensor product of the Hilbert spaces of the two components. For example, let A and B be two quantum systems, with Hilbert spaces and , respectively. The Hilbert space of the composite system is then
If the state for the first system is the vector and the state for the second system is , then the state of the composite system is
Not all states in the joint Hilbert space can be written in this form, however, because the superposition principle implies that linear combinations of these "separable" or "product states" are also valid. For example, if and are both possible states for system , and likewise and are both possible states for system , then
is a valid joint state that is not separable. States that are not separable are called entangled.[28][29]
If the state for a composite system is entangled, it is impossible to describe either component system A or system B by a state vector. One can instead define reduced density matrices that describe the statistics that can be obtained by making measurements on either component system alone. This necessarily causes a loss of information, though: knowing the reduced density matrices of the individual systems is not enough to reconstruct the state of the composite system.[28][29] Just as density matrices specify the state of a subsystem of a larger system, analogously, positive operator-valued measures (POVMs) describe the effect on a subsystem of a measurement performed on a larger system. POVMs are extensively used in quantum information theory.[28][30]
As described above, entanglement is a key feature of models of measurement processes in which an apparatus becomes entangled with the system being measured. Systems interacting with the environment in which they reside generally become entangled with that environment, a phenomenon known as quantum decoherence. This can explain why, in practice, quantum effects are difficult to observe in systems larger than microscopic.[31]
Equivalence between formulations
There are many mathematically equivalent formulations of quantum mechanics. One of the oldest and most common is the "transformation theory" proposed by Paul Dirac, which unifies and generalizes the two earliest formulations of quantum mechanics – matrix mechanics (invented by Werner Heisenberg) and wave mechanics (invented by Erwin Schrödinger).[32] An alternative formulation of quantum mechanics is Feynman's path integral formulation, in which a quantum-mechanical amplitude is considered as a sum over all possible classical and non-classical paths between the initial and final states. This is the quantum-mechanical counterpart of the action principle in classical mechanics.[33]
Symmetries and conservation laws
The Hamiltonian is known as the generator of time evolution, since it defines a unitary time-evolution operator for each value of . From this relation between and , it follows that any observable that commutes with will be conserved: its expectation value will not change over time.[7]: 471 This statement generalizes, as mathematically, any Hermitian operator can generate a family of unitary operators parameterized by a variable . Under the evolution generated by , any observable that commutes with will be conserved. Moreover, if is conserved by evolution under , then is conserved under the evolution generated by . This implies a quantum version of the result proven by Emmy Noether in classical (Lagrangian) mechanics: for every differentiable symmetry of a Hamiltonian, there exists a corresponding conservation law.
Examples
Free particle

The simplest example of a quantum system with a position degree of freedom is a free particle in a single spatial dimension. A free particle is one which is not subject to external influences, so that its Hamiltonian consists only of its kinetic energy:
The general solution of the Schrödinger equation is given by
which is a superposition of all possible plane waves , which are eigenstates of the momentum operator with momentum . The coefficients of the superposition are , which is the Fourier transform of the initial quantum state .
It is not possible for the solution to be a single momentum eigenstate, or a single position eigenstate, as these are not normalizable quantum states.[note 1] Instead, we can consider a Gaussian wave packet:
which has Fourier transform, and therefore momentum distribution
We see that as we make smaller the spread in position gets smaller, but the spread in momentum gets larger. Conversely, by making larger we make the spread in momentum smaller, but the spread in position gets larger. This illustrates the uncertainty principle.
As we let the Gaussian wave packet evolve in time, we see that its center moves through space at a constant velocity (like a classical particle with no forces acting on it). However, the wave packet will also spread out as time progresses, which means that the position becomes more and more uncertain. The uncertainty in momentum, however, stays constant.[34]
Particle in a box

The particle in a one-dimensional potential energy box is the most mathematically simple example where restraints lead to the quantization of energy levels. The box is defined as having zero potential energy everywhere inside a certain region, and therefore infinite potential energy everywhere outside that region.[25]: 77–78 For the one-dimensional case in the direction, the time-independent Schrödinger equation may be written
With the differential operator defined by
- the previous equation is evocative of the classic kinetic energy analogue,
with state in this case having energy coincident with the kinetic energy of the particle.
The general solutions of the Schrödinger equation for the particle in a box are
or, from Euler's formula,
The infinite potential walls of the box determine the values of and at and where must be zero. Thus, at ,
and . At ,
in which cannot be zero as this would conflict with the postulate that has norm 1. Therefore, since , must be an integer multiple of ,
This constraint on implies a constraint on the energy levels, yielding
A finite potential well is the generalization of the infinite potential well problem to potential wells having finite depth. The finite potential well problem is mathematically more complicated than the infinite particle-in-a-box problem as the wave function is not pinned to zero at the walls of the well. Instead, the wave function must satisfy more complicated mathematical boundary conditions as it is nonzero in regions outside the well. Another related problem is that of the rectangular potential barrier, which furnishes a model for the quantum tunneling effect that plays an important role in the performance of modern technologies such as flash memory and scanning tunneling microscopy.
Harmonic oscillator

As in the classical case, the potential for the quantum harmonic oscillator is given by[7]: 234
This problem can either be treated by directly solving the Schrödinger equation, which is not trivial, or by using the more elegant "ladder method" first proposed by Paul Dirac. The eigenstates are given by
where Hn are the Hermite polynomials
and the corresponding energy levels are
This is another example illustrating the discretization of energy for bound states.
Mach–Zehnder interferometer

The Mach–Zehnder interferometer (MZI) illustrates the concepts of superposition and interference with linear algebra in dimension 2, rather than differential equations. It can be seen as a simplified version of the double-slit experiment, but it is of interest in its own right, for example in the delayed choice quantum eraser, the Elitzur–Vaidman bomb tester, and in studies of quantum entanglement.[35][36]
We can model a photon going through the interferometer by considering that at each point it can be in a superposition of only two paths: the "lower" path which starts from the left, goes straight through both beam splitters, and ends at the top, and the "upper" path which starts from the bottom, goes straight through both beam splitters, and ends at the right. The quantum state of the photon is therefore a vector that is a superposition of the "lower" path and the "upper" path , that is, for complex . In order to respect the postulate that we require that .
Both beam splitters are modelled as the unitary matrix , which means that when a photon meets the beam splitter it will either stay on the same path with a probability amplitude of , or be reflected to the other path with a probability amplitude of . The phase shifter on the upper arm is modelled as the unitary matrix , which means that if the photon is on the "upper" path it will gain a relative phase of , and it will stay unchanged if it is in the lower path.
A photon that enters the interferometer from the left will then be acted upon with a beam splitter , a phase shifter , and another beam splitter , and so end up in the state
and the probabilities that it will be detected at the right or at the top are given respectively by
One can therefore use the Mach–Zehnder interferometer to estimate the phase shift by estimating these probabilities.
It is interesting to consider what would happen if the photon were definitely in either the "lower" or "upper" paths between the beam splitters. This can be accomplished by blocking one of the paths, or equivalently by removing the first beam splitter (and feeding the photon from the left or the bottom, as desired). In both cases, there will be no interference between the paths anymore, and the probabilities are given by , independently of the phase . From this we can conclude that the photon does not take one path or another after the first beam splitter, but rather that it is in a genuine quantum superposition of the two paths.[37]
Applications
Quantum mechanics has had enormous success in explaining many of the features of our universe, with regard to small-scale and discrete quantities and interactions which cannot be explained by classical methods.[note 2] Quantum mechanics is often the only theory that can reveal the individual behaviors of the subatomic particles that make up all forms of matter (electrons, protons, neutrons, photons, and others). Solid-state physics and materials science are dependent upon quantum mechanics.[38]
In many aspects, modern technology operates at a scale where quantum effects are significant. Important applications of quantum theory include quantum chemistry, quantum optics, quantum computing, superconducting magnets, light-emitting diodes, the optical amplifier and the laser, the transistor and semiconductors such as the microprocessor, medical and research imaging such as magnetic resonance imaging and electron microscopy.[39] Explanations for many biological and physical phenomena are rooted in the nature of the chemical bond, most notably the macro-molecule DNA.
Relation to other scientific theories
| Modern physics |
|---|
| |
Classical mechanics
The rules of quantum mechanics assert that the state space of a system is a Hilbert space and that observables of the system are Hermitian operators acting on vectors in that space – although they do not tell us which Hilbert space or which operators. These can be chosen appropriately in order to obtain a quantitative description of a quantum system, a necessary step in making physical predictions. An important guide for making these choices is the correspondence principle, a heuristic which states that the predictions of quantum mechanics reduce to those of classical mechanics in the regime of large quantum numbers.[40] One can also start from an established classical model of a particular system, and then try to guess the underlying quantum model that would give rise to the classical model in the correspondence limit. This approach is known as quantization.[41]: 299 [42]
When quantum mechanics was originally formulated, it was applied to models whose correspondence limit was non-relativistic classical mechanics. For instance, the well-known model of the quantum harmonic oscillator uses an explicitly non-relativistic expression for the kinetic energy of the oscillator, and is thus a quantum version of the classical harmonic oscillator.[7]: 234
Complications arise with chaotic systems, which do not have good quantum numbers, and quantum chaos studies the relationship between classical and quantum descriptions in these systems.[41]: 353
Quantum decoherence is a mechanism through which quantum systems lose coherence, and thus become incapable of displaying many typically quantum effects: quantum superpositions become simply probabilistic mixtures, and quantum entanglement becomes simply classical correlations.[7]: 687–730 Quantum coherence is not typically evident at macroscopic scales, though at temperatures approaching absolute zero quantum behavior may manifest macroscopically.[note 3]
Many macroscopic properties of a classical system are a direct consequence of the quantum behavior of its parts. For example, the stability of bulk matter (consisting of atoms and molecules which would quickly collapse under electric forces alone), the rigidity of solids, and the mechanical, thermal, chemical, optical and magnetic properties of matter are all results of the interaction of electric charges under the rules of quantum mechanics.[43]
Special relativity and electrodynamics
Early attempts to merge quantum mechanics with special relativity involved the replacement of the Schrödinger equation with a covariant equation such as the Klein–Gordon equation or the Dirac equation. While these theories were successful in explaining many experimental results, they had certain unsatisfactory qualities stemming from their neglect of the relativistic creation and annihilation of particles. A fully relativistic quantum theory required the development of quantum field theory, which applies quantization to a field (rather than a fixed set of particles). The first complete quantum field theory, quantum electrodynamics, provides a fully quantum description of the electromagnetic interaction. Quantum electrodynamics is, along with general relativity, one of the most accurate physical theories ever devised.[44][45]
The full apparatus of quantum field theory is often unnecessary for describing electrodynamic systems. A simpler approach, one that has been used since the inception of quantum mechanics, is to treat charged particles as quantum mechanical objects being acted on by a classical electromagnetic field. For example, the elementary quantum model of the hydrogen atom describes the electric field of the hydrogen atom using a classical Coulomb potential.[7]: 285 Likewise, in a Stern–Gerlach experiment, a charged particle is modeled as a quantum system, while the background magnetic field is described classically.[41]: 26 This "semi-classical" approach fails if quantum fluctuations in the electromagnetic field play an important role, such as in the emission of photons by charged particles.
Quantum field theories for the strong nuclear force and the weak nuclear force have also been developed. The quantum field theory of the strong nuclear force is called quantum chromodynamics, and describes the interactions of subnuclear particles such as quarks and gluons. The weak nuclear force and the electromagnetic force were unified, in their quantized forms, into a single quantum field theory (known as electroweak theory), by the physicists Abdus Salam, Sheldon Glashow and Steven Weinberg.[46]
Relation to general relativity
Even though the predictions of both quantum theory and general relativity have been supported by rigorous and repeated empirical evidence, their abstract formalisms contradict each other and they have proven extremely difficult to incorporate into one consistent, cohesive model. Gravity is negligible in many areas of particle physics, so that unification between general relativity and quantum mechanics is not an urgent issue in those particular applications. However, the lack of a correct theory of quantum gravity is an important issue in physical cosmology and the search by physicists for an elegant "Theory of Everything" (TOE). Consequently, resolving the inconsistencies between both theories has been a major goal of 20th- and 21st-century physics. This TOE would combine not only the models of subatomic physics but also derive the four fundamental forces of nature from a single force or phenomenon.[47]

One proposal for doing so is string theory, which posits that the point-like particles of particle physics are replaced by one-dimensional objects called strings. String theory describes how these strings propagate through space and interact with each other. On distance scales larger than the string scale, a string looks just like an ordinary particle, with its mass, charge, and other properties determined by the vibrational state of the string. In string theory, one of the many vibrational states of the string corresponds to the graviton, a quantum mechanical particle that carries gravitational force.[48][49]
Another popular theory is loop quantum gravity (LQG), which describes quantum properties of gravity and is thus a theory of quantum spacetime. LQG is an attempt to merge and adapt standard quantum mechanics and standard general relativity. This theory describes space as an extremely fine fabric "woven" of finite loops called spin networks. The evolution of a spin network over time is called a spin foam. The characteristic length scale of a spin foam is the Planck length, approximately 1.616×10−35 m, and so lengths shorter than the Planck length are not physically meaningful in LQG.[50]
Philosophical implications
Since its inception, the many counter-intuitive aspects and results of quantum mechanics have provoked strong philosophical debates and many interpretations. The arguments centre on the probabilistic nature of quantum mechanics, the difficulties with wavefunction collapse and the related measurement problem, and quantum nonlocality. Perhaps the only consensus that exists about these issues is that there is no consensus. Richard Feynman once said, "I think I can safely say that nobody understands quantum mechanics."[51] According to Steven Weinberg, "There is now in my opinion no entirely satisfactory interpretation of quantum mechanics."[52]
The views of Niels Bohr, Werner Heisenberg and other physicists are often grouped together as the "Copenhagen interpretation".[53][54] According to these views, the probabilistic nature of quantum mechanics is not a temporary feature which will eventually be replaced by a deterministic theory, but is instead a final renunciation of the classical idea of "causality". Bohr in particular emphasized that any well-defined application of the quantum mechanical formalism must always make reference to the experimental arrangement, due to the complementary nature of evidence obtained under different experimental situations. Copenhagen-type interpretations were adopted by Nobel laureates in quantum physics, including Bohr,[55] Heisenberg,[56] Schrödinger,[57] Feynman,[2] and Zeilinger[58] as well as 21st-century researchers in quantum foundations.[59]
Albert Einstein, himself one of the founders of quantum theory, was troubled by its apparent failure to respect some cherished metaphysical principles, such as determinism and locality. Einstein's long-running exchanges with Bohr about the meaning and status of quantum mechanics are now known as the Bohr–Einstein debates. Einstein believed that underlying quantum mechanics must be a theory that explicitly forbids action at a distance. He argued that quantum mechanics was incomplete, a theory that was valid but not fundamental, analogous to how thermodynamics is valid, but the fundamental theory behind it is statistical mechanics. In 1935, Einstein and his collaborators Boris Podolsky and Nathan Rosen published an argument that the principle of locality implies the incompleteness of quantum mechanics, a thought experiment later termed the Einstein–Podolsky–Rosen paradox.[note 4] In 1964, John Bell showed that EPR's principle of locality, together with determinism, was actually incompatible with quantum mechanics: they implied constraints on the correlations produced by distance systems, now known as Bell inequalities, that can be violated by entangled particles.[64] Since then several experiments have been performed to obtain these correlations, with the result that they do in fact violate Bell inequalities, and thus falsify the conjunction of locality with determinism.[16][17]
Bohmian mechanics shows that it is possible to reformulate quantum mechanics to make it deterministic, at the price of making it explicitly nonlocal. It attributes not only a wave function to a physical system, but in addition a real position, that evolves deterministically under a nonlocal guiding equation. The evolution of a physical system is given at all times by the Schrödinger equation together with the guiding equation; there is never a collapse of the wave function. This solves the measurement problem.[65]

Everett's many-worlds interpretation, formulated in 1956, holds that all the possibilities described by quantum theory simultaneously occur in a multiverse composed of mostly independent parallel universes.[66] This is a consequence of removing the axiom of the collapse of the wave packet. All possible states of the measured system and the measuring apparatus, together with the observer, are present in a real physical quantum superposition. While the multiverse is deterministic, we perceive non-deterministic behavior governed by probabilities, because we do not observe the multiverse as a whole, but only one parallel universe at a time. Exactly how this is supposed to work has been the subject of much debate. Several attempts have been made to make sense of this and derive the Born rule,[67][68] with no consensus on whether they have been successful.[69][70][71]
Relational quantum mechanics appeared in the late 1990s as a modern derivative of Copenhagen-type ideas,[72] and QBism was developed some years later.[73]
History
Quantum mechanics was developed in the early decades of the 20th century, driven by the need to explain phenomena that, in some cases, had been observed in earlier times. Scientific inquiry into the wave nature of light began in the 17th and 18th centuries, when scientists such as Robert Hooke, Christiaan Huygens and Leonhard Euler proposed a wave theory of light based on experimental observations.[74] In 1803 English polymath Thomas Young described the famous double-slit experiment.[75] This experiment played a major role in the general acceptance of the wave theory of light.
During the early 19th century, chemical research by John Dalton and Amedeo Avogadro lent weight to the atomic theory of matter, an idea that James Clerk Maxwell, Ludwig Boltzmann and others built upon to establish the kinetic theory of gases. The successes of kinetic theory gave further credence to the idea that matter is composed of atoms, yet the theory also had shortcomings that would only be resolved by the development of quantum mechanics.[76] While the early conception of atoms from Greek philosophy had been that they were indivisible units – the word "atom" deriving from the Greek for "uncuttable" – the 19th century saw the formulation of hypotheses about subatomic structure. One important discovery in that regard was Michael Faraday's 1838 observation of a glow caused by an electrical discharge inside a glass tube containing gas at low pressure. Julius Plücker, Johann Wilhelm Hittorf and Eugen Goldstein carried on and improved upon Faraday's work, leading to the identification of cathode rays, which J. J. Thomson found to consist of subatomic particles that would be called electrons.[77][78]

The black-body radiation problem was discovered by Gustav Kirchhoff in 1859. In 1900, Max Planck proposed the hypothesis that energy is radiated and absorbed in discrete "quanta" (or energy packets), yielding a calculation that precisely matched the observed patterns of black-body radiation.[79] The word quantum derives from the Latin, meaning "how great" or "how much".[80] According to Planck, quantities of energy could be thought of as divided into "elements" whose size (E) would be proportional to their frequency (ν):
- ,
where h is the Planck constant. Planck cautiously insisted that this was only an aspect of the processes of absorption and emission of radiation and was not the physical reality of the radiation.[81] In fact, he considered his quantum hypothesis a mathematical trick to get the right answer rather than a sizable discovery.[82] However, in 1905 Albert Einstein interpreted Planck's quantum hypothesis realistically and used it to explain the photoelectric effect, in which shining light on certain materials can eject electrons from the material. Niels Bohr then developed Planck's ideas about radiation into a model of the hydrogen atom that successfully predicted the spectral lines of hydrogen.[83] Einstein further developed this idea to show that an electromagnetic wave such as light could also be described as a particle (later called the photon), with a discrete amount of energy that depends on its frequency.[84] In his paper "On the Quantum Theory of Radiation", Einstein expanded on the interaction between energy and matter to explain the absorption and emission of energy by atoms. Although overshadowed at the time by his general theory of relativity, this paper articulated the mechanism underlying the stimulated emission of radiation,[85] which became the basis of the laser.[86]

This phase is known as the old quantum theory. Never complete or self-consistent, the old quantum theory was rather a set of heuristic corrections to classical mechanics.[87][88] The theory is now understood as a semi-classical approximation to modern quantum mechanics.[89][90] Notable results from this period include, in addition to the work of Planck, Einstein and Bohr mentioned above, Einstein and Peter Debye's work on the specific heat of solids, Bohr and Hendrika Johanna van Leeuwen's proof that classical physics cannot account for diamagnetism, and Arnold Sommerfeld's extension of the Bohr model to include special-relativistic effects.[87][91]
In the mid-1920s quantum mechanics was developed to become the standard formulation for atomic physics. In 1923, the French physicist Louis de Broglie put forward his theory of matter waves by stating that particles can exhibit wave characteristics and vice versa. Building on de Broglie's approach, modern quantum mechanics was born in 1925, when the German physicists Werner Heisenberg, Max Born, and Pascual Jordan[92][93] developed matrix mechanics and the Austrian physicist Erwin Schrödinger invented wave mechanics. Born introduced the probabilistic interpretation of Schrödinger's wave function in July 1926.[94] Thus, the entire field of quantum physics emerged, leading to its wider acceptance at the Fifth Solvay Conference in 1927.[95]
By 1930, quantum mechanics had been further unified and formalized by David Hilbert, Paul Dirac and John von Neumann[96] with greater emphasis on measurement, the statistical nature of our knowledge of reality, and philosophical speculation about the 'observer'. It has since permeated many disciplines, including quantum chemistry, quantum electronics, quantum optics, and quantum information science. It also provides a useful framework for many features of the modern periodic table of elements, and describes the behaviors of atoms during chemical bonding and the flow of electrons in computer semiconductors, and therefore plays a crucial role in many modern technologies. While quantum mechanics was constructed to describe the world of the very small, it is also needed to explain some macroscopic phenomena such as superconductors[97] and superfluids.[98]
See also
Explanatory notes
- ^ A momentum eigenstate would be a perfectly monochromatic wave of infinite extent, which is not square-integrable. Likewise, a position eigenstate would be a Dirac delta distribution, not square-integrable and technically not a function at all. Consequently, neither can belong to the particle's Hilbert space. Physicists sometimes introduce fictitious "bases" for a Hilbert space comprising elements outside that space. These are invented for calculational convenience and do not represent physical states.[25]: 100–105
- ^ See, for example, the Feynman Lectures on Physics for some of the technological applications which use quantum mechanics, e.g., transistors (vol III, pp. 14–11 ff), integrated circuits, which are follow-on technology in solid-state physics (vol II, pp. 8–6), and lasers (vol III, pp. 9–13).
- ^ See Macroscopic quantum phenomena, Bose–Einstein condensate, and Quantum machine
- ^ The published form of the EPR argument was due to Podolsky, and Einstein himself was not satisfied with it. In his own publications and correspondence, Einstein used a different argument to insist that quantum mechanics is an incomplete theory.[60][61][62][63]
References
- ^ Born, M. (1926). "Zur Quantenmechanik der Stoßvorgänge" [On the Quantum Mechanics of Collision Processes]. Zeitschrift für Physik. 37 (12): 863–867. Bibcode:1926ZPhy...37..863B. doi:10.1007/BF01397477. ISSN 1434-6001. S2CID 119896026.
- ^ a b c d Feynman, Richard; Leighton, Robert; Sands, Matthew (1964). The Feynman Lectures on Physics. Vol. 3. California Institute of Technology. ISBN 978-0-201-50064-6. Retrieved 19 December 2020.
- ^ Jaeger, Gregg (September 2014). "What in the (quantum) world is macroscopic?". American Journal of Physics. 82 (9): 896–905. Bibcode:2014AmJPh..82..896J. doi:10.1119/1.4878358.
- ^ Fein, Yaakov Y.; Geyer, Philipp; Zwick, Patrick; Kiałka, Filip; Pedalino, Sebastian; Mayor, Marcel; Gerlich, Stefan; Arndt, Markus (September 2019). "Quantum superposition of molecules beyond 25 kDa". Nature Physics. 15 (12): 1242–1245. Bibcode:2019NatPh..15.1242F. doi:10.1038/s41567-019-0663-9. S2CID 203638258.
- ^ Bojowald, Martin (2015). "Quantum cosmology: a review". Reports on Progress in Physics. 78 (2): 023901. arXiv:1501.04899. Bibcode:2015RPPh...78b3901B. doi:10.1088/0034-4885/78/2/023901. PMID 25582917. S2CID 18463042.
- ^ Fan, X.; Myers, T. G.; Sukra, B. A. D.; Gabrielse, G. (2023-02-13). "Measurement of the Electron Magnetic Moment". Physical Review Letters. 130 (7): 071801. arXiv:2209.13084. Bibcode:2023PhRvL.130g1801F. doi:10.1103/PhysRevLett.130.071801. PMID 36867820.
- ^ a b c d e f g h i j Zwiebach, Barton (2022). Mastering Quantum Mechanics: Essentials, Theory, and Applications. MIT Press. ISBN 978-0-262-04613-8.
- ^ a b c Lederman, Leon M.; Hill, Christopher T. (2011). Quantum Physics for Poets. US: Prometheus Books. ISBN 978-1-61614-281-0.
- ^ Müller-Kirsten, H. J. W. (2006). Introduction to Quantum Mechanics: Schrödinger Equation and Path Integral. US: World Scientific. p. 14. ISBN 978-981-256-691-1.
- ^ Plotnitsky, Arkady (2012). Niels Bohr and Complementarity: An Introduction. US: Springer. pp. 75–76. ISBN 978-1-4614-4517-3.
- ^ Griffiths, David J. (1995). Introduction to Quantum Mechanics. Prentice Hall. ISBN 0-13-124405-1.
- ^ Trixler, F. (2013). "Quantum tunnelling to the origin and evolution of life". Current Organic Chemistry. 17 (16): 1758–1770. doi:10.2174/13852728113179990083. PMC 3768233. PMID 24039543.
- ^ Phifer, Arnold (2012-03-27). "Developing more energy-efficient transistors through quantum tunneling". Notre Dame News. Retrieved 2024-06-07.
- ^ Bub, Jeffrey (2019). "Quantum entanglement". In Zalta, Edward N. (ed.). Stanford Encyclopedia of Philosophy. Metaphysics Research Lab, Stanford University.
- ^ a b Caves, Carlton M. (2015). "Quantum Information Science: Emerging No More". In Kelley, Paul; Agrawal, Govind; Bass, Mike; Hecht, Jeff; Stroud, Carlos (eds.). OSA Century of Optics. The Optical Society. pp. 320–323. arXiv:1302.1864. Bibcode:2013arXiv1302.1864C. ISBN 978-1-943580-04-0.
- ^ a b Wiseman, Howard (October 2015). "Death by experiment for local realism". Nature. 526 (7575): 649–650. doi:10.1038/nature15631. ISSN 0028-0836. PMID 26503054.
- ^ a b Wolchover, Natalie (7 February 2017). "Experiment Reaffirms Quantum Weirdness". Quanta Magazine. Retrieved 8 February 2020.
- ^ Baez, John C. (20 March 2020). "How to Learn Math and Physics". University of California, Riverside. Retrieved 19 December 2020.
there's no way to understand the interpretation of quantum mechanics without also being able to solve quantum mechanics problems – to understand the theory, you need to be able to use it (and vice versa)
- ^ Sagan, Carl (1996). The Demon-Haunted World: Science as a Candle in the Dark. Ballantine Books. p. 249. ISBN 0-345-40946-9.
"For most physics students, (the "mathematical underpinning" of quantum mechanics) might occupy them from, say, third grade to early graduate school – roughly 15 years. [...] The job of the popularizer of science, trying to get across some idea of quantum mechanics to a general audience that has not gone through these initiation rites, is daunting. Indeed, there are no successful popularizations of quantum mechanics in my opinion – partly for this reason.
- ^ Greenstein, George; Zajonc, Arthur (2006). "8 Measurement". The Quantum Challenge: Modern Research on the Foundations of Quantum Mechanics (2nd ed.). Jones and Bartlett. p. 215. ISBN 978-0-7637-2470-2. Archived from the original on 2023-01-02.
- ^ Weinberg, Steven (2010). Dreams Of A Final Theory: The Search for The Fundamental Laws of Nature. Random House. p. 82. ISBN 978-1-4070-6396-6.
- ^ Zhang, Ruiqin; Deng, Conghao (1993-01-01). "Exact solutions of the Schrödinger equation for some quantum-mechanical many-body systems". Physical Review A. 47 (1): 71–77. Bibcode:1993PhRvA..47...71Z. doi:10.1103/PhysRevA.47.71. ISSN 1050-2947. PMID 9908895.
- ^ Li, Jing; Drummond, N. D.; Schuck, Peter; Olevano, Valerio (2019-04-01). "Comparing many-body approaches against the helium atom exact solution". SciPost Physics. 6 (4): 040. arXiv:1801.09977. Bibcode:2019ScPP....6...40L. doi:10.21468/SciPostPhys.6.4.040. ISSN 2542-4653.
- ^ Drake, Gordon W. F. (2023). "High Precision Calculations for Helium". In Drake, Gordon W. F. (ed.). Springer Handbook of Atomic, Molecular, and Optical Physics. Springer Handbooks. Cham: Springer International Publishing. pp. 199–216. doi:10.1007/978-3-030-73893-8_12. ISBN 978-3-030-73892-1.
- ^ a b c d Cohen-Tannoudji, Claude; Diu, Bernard; Laloë, Franck (2005). Quantum Mechanics. Translated by Hemley, Susan Reid; Ostrowsky, Nicole; Ostrowsky, Dan. John Wiley & Sons. ISBN 0-471-16433-X.
- ^ Landau, Lev D.; Lifschitz, Evgeny M. (1977). Quantum Mechanics: Non-Relativistic Theory. Vol. 3 (3rd ed.). Pergamon Press. ISBN 978-0-08-020940-1. OCLC 2284121.
- ^ Section 3.2 of Ballentine, Leslie E. (1970), "The Statistical Interpretation of Quantum Mechanics", Reviews of Modern Physics, 42 (4): 358–381, Bibcode:1970RvMP...42..358B, doi:10.1103/RevModPhys.42.358, S2CID 120024263. This fact is experimentally well-known for example in quantum optics; see e.g. chap. 2 and Fig. 2.1 Leonhardt, Ulf (1997), Measuring the Quantum State of Light, Cambridge: Cambridge University Press, ISBN 0-521-49730-2.
- ^ a b c Nielsen, Michael A.; Chuang, Isaac L. (2010). Quantum Computation and Quantum Information (2nd ed.). Cambridge: Cambridge University Press. ISBN 978-1-107-00217-3. OCLC 844974180.
- ^ a b Rieffel, Eleanor G.; Polak, Wolfgang H. (2011). Quantum Computing: A Gentle Introduction. MIT Press. ISBN 978-0-262-01506-6.
- ^ Wilde, Mark M. (2017). Quantum Information Theory (2nd ed.). Cambridge University Press. arXiv:1106.1445. doi:10.1017/9781316809976.001. ISBN 978-1-107-17616-4. OCLC 973404322. S2CID 2515538.
- ^ Schlosshauer, Maximilian (October 2019). "Quantum decoherence". Physics Reports. 831: 1–57. arXiv:1911.06282. Bibcode:2019PhR...831....1S. doi:10.1016/j.physrep.2019.10.001. S2CID 208006050.
- ^ Rechenberg, Helmut (1987). "Erwin Schrödinger and the creation of wave mechanics" (PDF). Acta Physica Polonica B. 19 (8): 683–695. Retrieved 13 June 2016.
- ^ Feynman, Richard P.; Hibbs, Albert R. (2005). Steyer, Daniel F. (ed.). Quantum Mechanics and Path Integrals (Emended ed.). McGraw-Hill. pp. v–vii. ISBN 978-0-486-47722-0.
- ^ Mathews, Piravonu Mathews; Venkatesan, K. (1976). "The Schrödinger Equation and Stationary States". A Textbook of Quantum Mechanics. Tata McGraw-Hill. p. 36. ISBN 978-0-07-096510-2.
- ^ Paris, M. G. A. (1999). "Entanglement and visibility at the output of a Mach–Zehnder interferometer". Physical Review A. 59 (2): 1615–1621. arXiv:quant-ph/9811078. Bibcode:1999PhRvA..59.1615P. doi:10.1103/PhysRevA.59.1615. S2CID 13963928.
- ^ Haack, G. R.; Förster, H.; Büttiker, M. (2010). "Parity detection and entanglement with a Mach-Zehnder interferometer". Physical Review B. 82 (15): 155303. arXiv:1005.3976. Bibcode:2010PhRvB..82o5303H. doi:10.1103/PhysRevB.82.155303. S2CID 119261326.
- ^ Vedral, Vlatko (2006). Introduction to Quantum Information Science. Oxford University Press. ISBN 978-0-19-921570-6. OCLC 442351498.
- ^ Cohen, Marvin L. (2008). "Essay: Fifty Years of Condensed Matter Physics". Physical Review Letters. 101 (25): 250001. Bibcode:2008PhRvL.101y0001C. doi:10.1103/PhysRevLett.101.250001. PMID 19113681. Retrieved 31 March 2012.
- ^ Matson, John. "What Is Quantum Mechanics Good for?". Scientific American. Retrieved 18 May 2016.
- ^ Tipler, Paul; Llewellyn, Ralph (2008). Modern Physics (5th ed.). W.H. Freeman and Company. pp. 160–161. ISBN 978-0-7167-7550-8.
- ^ a b c Peres, Asher (1993). Quantum Theory: Concepts and Methods. Kluwer. ISBN 0-7923-2549-4.
- ^ Baez, John C. (2019-02-26). "The Math That Takes Newton Into the Quantum World". Nautilus Quarterly. Retrieved 2024-03-23.
- ^ "Atomic Properties". Academic.brooklyn.cuny.edu. Retrieved 18 August 2012.
- ^ Hawking, Stephen; Penrose, Roger (2010). The Nature of Space and Time. Princeton University Press. ISBN 978-1-4008-3474-7.
- ^ Aoyama, Tatsumi; Hayakawa, Masashi; Kinoshita, Toichiro; Nio, Makiko (2012). "Tenth-Order QED Contribution to the Electron g-2 and an Improved Value of the Fine Structure Constant". Physical Review Letters. 109 (11): 111807. arXiv:1205.5368. Bibcode:2012PhRvL.109k1807A. doi:10.1103/PhysRevLett.109.111807. PMID 23005618. S2CID 14712017.
- ^ "The Nobel Prize in Physics 1979". Nobel Foundation. Retrieved 16 December 2020.
- ^ Overbye, Dennis (10 October 2022). "Black Holes May Hide a Mind-Bending Secret About Our Universe – Take gravity, add quantum mechanics, stir. What do you get? Just maybe, a holographic cosmos". The New York Times. Retrieved 10 October 2022.
- ^ Becker, Katrin; Becker, Melanie; Schwarz, John (2007). String theory and M-theory: A modern introduction. Cambridge University Press. ISBN 978-0-521-86069-7.
- ^ Zwiebach, Barton (2009). A First Course in String Theory. Cambridge University Press. ISBN 978-0-521-88032-9.
- ^ Rovelli, Carlo; Vidotto, Francesca (2014). Covariant Loop Quantum Gravity: An Elementary Introduction to Quantum Gravity and Spinfoam Theory. Cambridge University Press. ISBN 978-1-316-14811-2.
- ^ Feynman, Richard (1967). The Character of Physical Law. MIT Press. p. 129. ISBN 0-262-56003-8.
- ^ Weinberg, Steven (2012). "Collapse of the state vector". Physical Review A. 85 (6): 062116. arXiv:1109.6462. Bibcode:2012PhRvA..85f2116W. doi:10.1103/PhysRevA.85.062116. S2CID 119273840.
- ^ Howard, Don (December 2004). "Who Invented the 'Copenhagen Interpretation'? A Study in Mythology". Philosophy of Science. 71 (5): 669–682. doi:10.1086/425941. ISSN 0031-8248. S2CID 9454552.
- ^ Camilleri, Kristian (May 2009). "Constructing the Myth of the Copenhagen Interpretation". Perspectives on Science. 17 (1): 26–57. doi:10.1162/posc.2009.17.1.26. ISSN 1063-6145. S2CID 57559199.
- ^ Bohr, Neils (1928). "The Quantum Postulate and the Recent Development of Atomic Theory". Nature. 121 (3050): 580–590. Bibcode:1928Natur.121..580B. doi:10.1038/121580a0.
- ^ Heisenberg, Werner (1971). Physics and philosophy: the revolution in modern science. World perspectives (3 ed.). London: Allen & Unwin. ISBN 978-0-04-530016-7. OCLC 743037461.
- ^ Schrödinger, Erwin (1980) [1935]. Trimmer, John (ed.). ""Die gegenwärtige Situation in der Quantenmechanik."" [The Present Situation in Quantum Mechanics]. Naturwissenschaften. 23 (50): 844–849. doi:10.1007/BF01491987. JSTOR 986572. S2CID 22433857.
- ^ Ma, Xiao-song; Kofler, Johannes; Zeilinger, Anton (2016-03-03). "Delayed-choice gedanken experiments and their realizations". Reviews of Modern Physics. 88 (1): 015005. arXiv:1407.2930. Bibcode:2016RvMP...88a5005M. doi:10.1103/RevModPhys.88.015005. ISSN 0034-6861. S2CID 34901303.
- ^ Schlosshauer, Maximilian; Kofler, Johannes; Zeilinger, Anton (1 August 2013). "A snapshot of foundational attitudes toward quantum mechanics". Studies in History and Philosophy of Science Part B. 44 (3): 222–230. arXiv:1301.1069. Bibcode:2013SHPMP..44..222S. doi:10.1016/j.shpsb.2013.04.004. S2CID 55537196.
- ^ Harrigan, Nicholas; Spekkens, Robert W. (2010). "Einstein, incompleteness, and the epistemic view of quantum states". Foundations of Physics. 40 (2): 125. arXiv:0706.2661. Bibcode:2010FoPh...40..125H. doi:10.1007/s10701-009-9347-0. S2CID 32755624.
- ^ Howard, D. (1985). "Einstein on locality and separability". Studies in History and Philosophy of Science Part A. 16 (3): 171–201. Bibcode:1985SHPSA..16..171H. doi:10.1016/0039-3681(85)90001-9.
- ^ Sauer, Tilman (1 December 2007). "An Einstein manuscript on the EPR paradox for spin observables". Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics. 38 (4): 879–887. Bibcode:2007SHPMP..38..879S. CiteSeerX 10.1.1.571.6089. doi:10.1016/j.shpsb.2007.03.002. ISSN 1355-2198.
- ^ Einstein, Albert (1949). "Autobiographical Notes". In Schilpp, Paul Arthur (ed.). Albert Einstein: Philosopher-Scientist. Open Court Publishing Company.
- ^ Bell, John Stewart (1 November 1964). "On the Einstein Podolsky Rosen paradox". Physics Physique Fizika. 1 (3): 195–200. doi:10.1103/PhysicsPhysiqueFizika.1.195.
- ^ Goldstein, Sheldon (2017). "Bohmian Mechanics". Stanford Encyclopedia of Philosophy. Metaphysics Research Lab, Stanford University.
- ^ Barrett, Jeffrey (2018). "Everett's Relative-State Formulation of Quantum Mechanics". In Zalta, Edward N. (ed.). Stanford Encyclopedia of Philosophy. Metaphysics Research Lab, Stanford University.
- ^ Everett, Hugh; Wheeler, J. A.; DeWitt, B. S.; Cooper, L. N.; Van Vechten, D.; Graham, N. (1973). DeWitt, Bryce; Graham, R. Neill (eds.). The Many-Worlds Interpretation of Quantum Mechanics. Princeton Series in Physics. Princeton, NJ: Princeton University Press. p. v. ISBN 0-691-08131-X.
- ^ Wallace, David (2003). "Everettian Rationality: defending Deutsch's approach to probability in the Everett interpretation". Stud. Hist. Phil. Mod. Phys. 34 (3): 415–438. arXiv:quant-ph/0303050. Bibcode:2003SHPMP..34..415W. doi:10.1016/S1355-2198(03)00036-4. S2CID 1921913.
- ^ Ballentine, L. E. (1973). "Can the statistical postulate of quantum theory be derived? – A critique of the many-universes interpretation". Foundations of Physics. 3 (2): 229–240. Bibcode:1973FoPh....3..229B. doi:10.1007/BF00708440. S2CID 121747282.
- ^ Landsman, N. P. (2008). "The Born rule and its interpretation" (PDF). In Weinert, F.; Hentschel, K.; Greenberger, D.; Falkenburg, B. (eds.). Compendium of Quantum Physics. Springer. ISBN 978-3-540-70622-9.
The conclusion seems to be that no generally accepted derivation of the Born rule has been given to date, but this does not imply that such a derivation is impossible in principle.
- ^ Kent, Adrian (2010). "One world versus many: The inadequacy of Everettian accounts of evolution, probability, and scientific confirmation". In S. Saunders; J. Barrett; A. Kent; D. Wallace (eds.). Many Worlds? Everett, Quantum Theory and Reality. Oxford University Press. arXiv:0905.0624. Bibcode:2009arXiv0905.0624K.
- ^ Van Fraassen, Bas C. (April 2010). "Rovelli's World". Foundations of Physics. 40 (4): 390–417. Bibcode:2010FoPh...40..390V. doi:10.1007/s10701-009-9326-5. ISSN 0015-9018. S2CID 17217776.
- ^ Healey, Richard (2016). "Quantum-Bayesian and Pragmatist Views of Quantum Theory". In Zalta, Edward N. (ed.). Stanford Encyclopedia of Philosophy. Metaphysics Research Lab, Stanford University.
- ^ Born, Max; Wolf, Emil (1999). Principles of Optics. Cambridge University Press. ISBN 0-521-64222-1. OCLC 1151058062.
- ^ Scheider, Walter (April 1986). "Bringing one of the great moments of science to the classroom". The Physics Teacher. 24 (4): 217–219. Bibcode:1986PhTea..24..217S. doi:10.1119/1.2341987. ISSN 0031-921X.
- ^ Feynman, Richard; Leighton, Robert; Sands, Matthew (1964). The Feynman Lectures on Physics. Vol. 1. California Institute of Technology. ISBN 978-0-201-50064-6. Retrieved 30 September 2021.
- ^
Martin, Andre (1986), "Cathode Ray Tubes for Industrial and Military Applications", in Hawkes, Peter (ed.), Advances in Electronics and Electron Physics, Volume 67, Academic Press, p. 183, ISBN 978-0-08-057733-3,
Evidence for the existence of "cathode-rays" was first found by Plücker and Hittorf ...
- ^ Dahl, Per F. (1997). Flash of the Cathode Rays: A History of J J Thomson's Electron. CRC Press. pp. 47–57. ISBN 978-0-7503-0453-5.
- ^ Mehra, J.; Rechenberg, H. (1982). The Historical Development of Quantum Theory, Vol. 1: The Quantum Theory of Planck, Einstein, Bohr and Sommerfeld. Its Foundation and the Rise of Its Difficulties (1900–1925). New York: Springer-Verlag. ISBN 978-0-387-90642-3.
- ^ "Quantum – Definition and More". Merriam-Webster Dictionary. Archived from the original on Oct 26, 2012. Retrieved 18 August 2012.
- ^ Kuhn, T. S. (1978). Black-body theory and the quantum discontinuity 1894–1912. Oxford: Clarendon Press. ISBN 978-0-19-502383-1.
- ^ Kragh, Helge (1 December 2000). "Max Planck: the reluctant revolutionary". Physics World. Retrieved 12 December 2020.
- ^ Stachel, John (2009). "Bohr and the Photon". Quantum Reality, Relativistic Causality, and Closing the Epistemic Circle. The Western Ontario Series in Philosophy of Science. Vol. 73. Dordrecht: Springer. pp. 69–83. doi:10.1007/978-1-4020-9107-0_5. ISBN 978-1-4020-9106-3.
- ^ Einstein, Albert (1905). "Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt" [On a heuristic point of view concerning the production and transformation of light]. Annalen der Physik. 17 (6): 132–148. Bibcode:1905AnP...322..132E. doi:10.1002/andp.19053220607. Reprinted in Stachel, John, ed. (1989). The Collected Papers of Albert Einstein (in German). Vol. 2. Princeton University Press. pp. 149–166. See also "Einstein's early work on the quantum hypothesis", ibid. pp. 134–148.
- ^ Einstein, Albert (1917). "Zur Quantentheorie der Strahlung" [On the Quantum Theory of Radiation]. Physikalische Zeitschrift (in German). 18: 121–128. Bibcode:1917PhyZ...18..121E. Translated in Einstein, A. (1967). "On the Quantum Theory of Radiation". The Old Quantum Theory. Elsevier. pp. 167–183. doi:10.1016/b978-0-08-012102-4.50018-8. ISBN 978-0-08-012102-4.
- ^ Ball, Philip (2017-08-31). "A century ago Einstein sparked the notion of the laser". Physics World. Retrieved 2024-03-23.
- ^ a b ter Haar, D. (1967). The Old Quantum Theory. Pergamon Press. pp. 3–75. ISBN 978-0-08-012101-7. LCCN 66-29628.
- ^ Bokulich, Alisa; Bokulich, Peter (2020-08-13). "Bohr's Correspondence Principle". In Zalta, Edward N. (ed.). Stanford Encyclopedia of Philosophy.
- ^ "Semi-classical approximation". Encyclopedia of Mathematics. Retrieved 1 February 2020.
- ^ Sakurai, J. J.; Napolitano, J. (2014). "Quantum Dynamics". Modern Quantum Mechanics. Pearson. ISBN 978-1-292-02410-3. OCLC 929609283.
- ^ Aharoni, Amikam (1996). Introduction to the Theory of Ferromagnetism. Clarendon Press. pp. 6–7. ISBN 0-19-851791-2.
- ^ David Edwards, "The Mathematical Foundations of Quantum Mechanics", Synthese, Volume 42, Number 1/September, 1979, pp. 1–70.
- ^ David Edwards, "The Mathematical Foundations of Quantum Field Theory: Fermions, Gauge Fields, and Super-symmetry, Part I: Lattice Field Theories", International Journal of Theoretical Physics, Vol. 20, No. 7 (1981).
- ^ Bernstein, Jeremy (November 2005). "Max Born and the quantum theory". American Journal of Physics. 73 (11): 999–1008. Bibcode:2005AmJPh..73..999B. doi:10.1119/1.2060717. ISSN 0002-9505.
- ^ Pais, Abraham (1997). A Tale of Two Continents: A Physicist's Life in a Turbulent World. Princeton, New Jersey: Princeton University Press. ISBN 0-691-01243-1.
- ^ Van Hove, Leon (1958). "Von Neumann's contributions to quantum mechanics" (PDF). Bulletin of the American Mathematical Society. 64 (3): Part 2:95–99. doi:10.1090/s0002-9904-1958-10206-2. Archived (PDF) from the original on Jan 20, 2024.
- ^ Feynman, Richard. "The Feynman Lectures on Physics Vol. III Ch. 21: The Schrödinger Equation in a Classical Context: A Seminar on Superconductivity, 21-4". California Institute of Technology. Archived from the original on 15 Dec 2016. Retrieved 24 November 2015.
...it was long believed that the wave function of the Schrödinger equation would never have a macroscopic representation analogous to the macroscopic representation of the amplitude for photons. On the other hand, it is now realized that the phenomena of superconductivity presents us with just this situation.
- ^ Packard, Richard (2006). "Berkeley Experiments on Superfluid Macroscopic Quantum Effects" (PDF). Physics Department, University of California, Berkeley. Archived from the original (PDF) on 25 November 2015. Retrieved 24 November 2015.
Further reading
The following titles, all by working physicists, attempt to communicate quantum theory to lay people, using a minimum of technical apparatus.
- Chester, Marvin (1987). Primer of Quantum Mechanics. John Wiley. ISBN 0-486-42878-8
- Cox, Brian; Forshaw, Jeff (2011). The Quantum Universe: Everything That Can Happen Does Happen. Allen Lane. ISBN 978-1-84614-432-5.
- Richard Feynman, 1985. QED: The Strange Theory of Light and Matter, Princeton University Press. ISBN 0-691-08388-6. Four elementary lectures on quantum electrodynamics and quantum field theory, yet containing many insights for the expert.
- Ghirardi, GianCarlo, 2004. Sneaking a Look at God's Cards, Gerald Malsbary, trans. Princeton Univ. Press. The most technical of the works cited here. Passages using algebra, trigonometry, and bra–ket notation can be passed over on a first reading.
- N. David Mermin, 1990, "Spooky actions at a distance: mysteries of the QT" in his Boojums All the Way Through. Cambridge University Press: 110–76.
- Victor Stenger, 2000. Timeless Reality: Symmetry, Simplicity, and Multiple Universes. Buffalo, NY: Prometheus Books. Chpts. 5–8. Includes cosmological and philosophical considerations.
More technical:
- Bernstein, Jeremy (2009). Quantum Leaps. Cambridge, Massachusetts: Belknap Press of Harvard University Press. ISBN 978-0-674-03541-6.
- Bohm, David (1989). Quantum Theory. Dover Publications. ISBN 978-0-486-65969-5.
- Binney, James; Skinner, David (2008). The Physics of Quantum Mechanics. Oxford University Press. ISBN 978-0-19-968857-9.
- Eisberg, Robert; Resnick, Robert (1985). Quantum Physics of Atoms, Molecules, Solids, Nuclei, and Particles (2nd ed.). Wiley. ISBN 978-0-471-87373-0.
- Bryce DeWitt, R. Neill Graham, eds., 1973. The Many-Worlds Interpretation of Quantum Mechanics, Princeton Series in Physics, Princeton University Press. ISBN 0-691-08131-X
- Everett, Hugh (1957). "Relative State Formulation of Quantum Mechanics". Reviews of Modern Physics. 29 (3): 454–462. Bibcode:1957RvMP...29..454E. doi:10.1103/RevModPhys.29.454. S2CID 17178479.
- Feynman, Richard P.; Leighton, Robert B.; Sands, Matthew (1965). The Feynman Lectures on Physics. Vol. 1–3. Addison-Wesley. ISBN 978-0-7382-0008-8.
- D. Greenberger, K. Hentschel, F. Weinert, eds., 2009. Compendium of quantum physics, Concepts, experiments, history and philosophy, Springer-Verlag, Berlin, Heidelberg. Short articles on many QM topics.
- Griffiths, David J. (2004). Introduction to Quantum Mechanics (2nd ed.). Prentice Hall. ISBN 978-0-13-111892-8. OCLC 40251748. A standard undergraduate text.
- Max Jammer, 1966. The Conceptual Development of Quantum Mechanics. McGraw Hill.
- Hagen Kleinert, 2004. Path Integrals in Quantum Mechanics, Statistics, Polymer Physics, and Financial Markets, 3rd ed. Singapore: World Scientific. Draft of 4th edition. Archived 2008-06-15 at the Wayback Machine
- L.D. Landau, E.M. Lifshitz (1977). Quantum Mechanics: Non-Relativistic Theory. Vol. 3 (3rd ed.). Pergamon Press. ISBN 978-0-08-020940-1. Online copy
- Liboff, Richard L. (2002). Introductory Quantum Mechanics. Addison-Wesley. ISBN 978-0-8053-8714-8.
- Gunther Ludwig, 1968. Wave Mechanics. London: Pergamon Press. ISBN 0-08-203204-1
- George Mackey (2004). The mathematical foundations of quantum mechanics. Dover Publications. ISBN 0-486-43517-2.
- Merzbacher, Eugen (1998). Quantum Mechanics. Wiley, John & Sons, Inc. ISBN 978-0-471-88702-7.
- Albert Messiah, 1966. Quantum Mechanics (Vol. I), English translation from French by G.M. Temmer. North Holland, John Wiley & Sons. Cf. chpt. IV, section III. online
- Omnès, Roland (1999). Understanding Quantum Mechanics. Princeton University Press. ISBN 978-0-691-00435-8. OCLC 39849482.
- Scerri, Eric. R. (2006). The Periodic Table: Its Story and Its Significance. Oxford University Press. ISBN 0-19-530573-6. Considers the extent to which chemistry and the periodic system have been reduced to quantum mechanics.
- Schiff, Leonard I. (1955). Quantum Mechanics. Mc-Graw Hill, Inc.
- Shankar, R. (1994). Principles of Quantum Mechanics. Springer. ISBN 978-0-306-44790-7.
- Stone, A. Douglas (2013). Einstein and the Quantum. Princeton University Press. ISBN 978-0-691-13968-5.
- Transnational College of Lex (1996). What is Quantum Mechanics? A Physics Adventure. Language Research Foundation, Boston. ISBN 978-0-9643504-1-0. OCLC 34661512.
- Veltman, Martinus J.G. (2003), Facts and Mysteries in Elementary Particle Physics.
External links
- J. O'Connor and E. F. Robertson: A history of quantum mechanics.
- Introduction to Quantum Theory at Quantiki.
- Quantum Physics Made Relatively Simple: three video lectures by Hans Bethe.
- Course material
- Quantum Cook Book and PHYS 201: Fundamentals of Physics II by Ramamurti Shankar, Yale OpenCourseware.
- Modern Physics: With waves, thermodynamics, and optics – an online textbook.
- MIT OpenCourseWare: Chemistry and Physics. See 8.04, 8.05 and 8.06.
- 5+1/2 Examples in Quantum Mechanics.
- Imperial College Quantum Mechanics Course.
- Philosophy
- Ismael, Jenann. "Quantum Mechanics". In Zalta, Edward N. (ed.). Stanford Encyclopedia of Philosophy.
- Krips, Henry. "Measurement in Quantum Theory". In Zalta, Edward N. (ed.). Stanford Encyclopedia of Philosophy.
























![{\displaystyle [{\hat {X}},{\hat {P}}]=i\hbar .}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/803fe39b0eeaff8d1570df480e738cf5a968cc71)







![{\displaystyle [A,B]=AB-BA,}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/b2a47259b42e63c048c65f67d304404867841951)
![{\displaystyle \sigma _{A}\sigma _{B}\geq {\tfrac {1}{2}}\left|{\bigl \langle }[A,B]{\bigr \rangle }\right|.}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/d0fd768b447334e150b8b98181f74b475e41ee52)






















![{\displaystyle \psi (x,0)={\frac {1}{\sqrt[{4}]{\pi a}}}e^{-{\frac {x^{2}}{2a}}}}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/a4c2dae82312897d5fd4c58986c426a6009e6840)
![{\displaystyle {\hat {\psi }}(k,0)={\sqrt[{4}]{\frac {a}{\pi }}}e^{-{\frac {ak^{2}}{2}}}.}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/c4991535bba434314af8c27c16fff74f49ce367e)












































