Henri Poincaré: Difference between revisions
Rober1236jua (talk | contribs) |
Reaper1945 (talk | contribs) URL. Tags: Visual edit Mobile edit Mobile web edit |
||
| Line 1: | Line 1: | ||
{{Short description|French mathematician, physicist and engineer (1854–1912)}} |
|||
{{Infobox Scientist |
|||
{{For|ships with this name|French ship Henri Poincaré}} |
|||
|box_width = 300px |
|||
{{More citations needed|date=April 2016}} |
|||
|name = Henri Poincaré |
|||
{{Use dmy dates|date=November 2020}} |
|||
|image = JH Poincare.jpg |
|||
{{Infobox scientist |
|||
|image_size = 230px |
|||
| name = Henri Poincaré |
|||
|caption = <small>Jules Henri Poincaré (1854–1912). Photograph from the frontispiece of the 1913 edition of ''Last Thoughts.''</small> |
|||
| other_names = Jules Henri Poincaré |
|||
|birth_date = {{birth date|df=yes|1854|4|29}} |
|||
| image = PSM V82 D416 Henri Poincare.png |
|||
|birth_place = [[Nancy]], [[Meurthe-et-Moselle]] |
|||
| caption = |
|||
|death_date = {{death date and age|df=yes|1912|7|17|1854|4|29}} |
|||
| |
| birth_date = {{birth date|df=yes|1854|4|29}} |
||
| |
| birth_place = [[Nancy, France|Nancy]], [[Meurthe-et-Moselle]], France |
||
| death_date = {{death date and age|df=yes|1912|7|17|1854|4|29}} |
|||
|citizenship = |
|||
| |
| death_place = [[Paris]], France |
||
| |
| nationality = French |
||
|fields = |
| fields = {{flatlist| |
||
*Mathematics |
|||
|workplaces = [[Corps des Mines]]<br>[[Caen University]]<br>[[Sorbonne|La Sorbonne]]<br> [[Bureau des Longitudes]] |
|||
*[[physics]] |
|||
|alma_mater = [[Lycée Nancy]]<br>[[École Polytechnique]]<br>[[École des Mines]] |
|||
|doctoral_advisor = [[Charles Hermite]] |
|||
|academic_advisors = |
|||
|doctoral_students = [[Louis Bachelier]]<br>[[Dimitrie Pompeiu]]<br>[[Mihailo Petrović]] |
|||
|notable_students = [[Tobias Dantzig]] |
|||
|known_for = [[Poincaré conjecture]]<br>[[Three-body problem]]<br>[[Topology]]<br>[[Special relativity]]<br>[[Poincaré–Hopf theorem]]<br>[[Poincaré duality]]<br>{{nowrap|[[Poincaré–Birkhoff–Witt theorem]]}}<br>[[Poincaré inequality]]<br> [[Hilbert–Poincaré series]]<br> [[Poincaré metric]]<br> [[Rotation number]]<br> [[Betti number|Coining term 'Betti number']] <br>[[Chaos theory]]<br>[[Sphere-world]]<br>[[Poincaré–Bendixson theorem]]<br>[[Poincaré–Lindstedt method]]<br>[[Poincaré recurrence theorem]] |
|||
|author_abbrev_bot = |
|||
|author_abbrev_zoo = |
|||
|influences = [[Lazarus Fuchs]] |
|||
|influenced = [[Louis Rougier]]<br>[[George David Birkhoff]] |
|||
|awards = {{nowrap|[[Gold Medal of the Royal Astronomical Society|RAS Gold Medal]] (1900)}} <br>[[Sylvester Medal]] (1901)<br>[[Matteucci Medal]] (1905)<br>[[Bolyai Prize]] (1905)<br>[[Bruce Medal]] (1911) |
|||
|religion = [[Roman Catholic]] (until 1872) |
|||
|signature = Henri Poincaré Signature.svg |
|||
|footnotes = He was a cousin of [[Pierre Boutroux]]. |
|||
}} |
}} |
||
| spouse = Jeanne-Louise Poulain d'Andecy |
|||
| workplaces = {{plainlist| |
|||
*[[Corps des Mines]] |
|||
*[[Caen University]] |
|||
*[[University of Paris|La Sorbonne]] |
|||
*[[Bureau des Longitudes]]}} |
|||
| education = {{plainlist| |
|||
*Lycée Nancy (now {{ill|Lycée Henri-Poincaré|fr}}) |
|||
*[[École Polytechnique]] |
|||
*[[École des Mines]] |
|||
*[[University of Paris]] ([[Doctorat|Dr]], 1879)}} |
|||
| thesis_title = Sur les propriétés des fonctions définies par les équations différences |
|||
| thesis_url = https://web.archive.org/web/20160506152142/https://iris.univ-lille1.fr/handle/1908/458 |
|||
| thesis_year = 1879 |
|||
| doctoral_advisor = [[Charles Hermite]] |
|||
| academic_advisors = |
|||
| doctoral_students = {{plainlist| |
|||
*[[Louis Bachelier]] |
|||
*[[Jean Bosler]] |
|||
*[[Dimitrie Pompeiu]] |
|||
*[[Mihailo Petrović Alas]]}} |
|||
| notable_students = {{plainlist| |
|||
*[[Tobias Dantzig]] |
|||
*[[Théophile de Donder]]}} |
|||
| known_for = {{plainlist| |
|||
*[[Poincaré conjecture]] |
|||
*[[Poincaré–Bendixson theorem]] |
|||
*[[Poincaré–Lindstedt method]] |
|||
*[[Poincaré recurrence theorem]] |
|||
*[[Kelvin's circulation theorem#Poincaré–Bjerknes circulation theorem|Poincaré–Bjerknes circulation theorem]] |
|||
*[[Poincaré group]] |
|||
*[[Poincaré gauge]] |
|||
*[[Poincaré–Hopf theorem]] |
|||
*[[Poincaré duality]] |
|||
*{{nowrap|[[Poincaré–Birkhoff–Witt theorem]]}} |
|||
*[[Poincaré inequality]] |
|||
*[[Hilbert–Poincaré series]] |
|||
*[[Poincaré series (modular form)|Poincaré series]] |
|||
*[[Poincaré metric]] |
|||
*[[Automorphic form]] |
|||
*[[Betti number|Coining the term "Betti number"]] |
|||
*[[Brouwer fixed-point theorem]] |
|||
*[[Bifurcation theory]] |
|||
*[[Chaos theory]] |
|||
*[[Dynamical system|Dynamical system theory]] |
|||
*[[Dark matter]] |
|||
*[[French historical epistemology]] |
|||
*[[Fundamental group]] |
|||
*[[Gravitational wave]] |
|||
*[[Hairy ball theorem]] |
|||
*[[Homological algebra]] |
|||
*[[Limit cycle]] |
|||
*[[Phase space]] |
|||
*[[Preintuitionism]]/[[conventionalism]] |
|||
*[[Predicativism]] |
|||
*[[Qualitative theory of differential equations]] |
|||
*[[Special relativity]] |
|||
*[[Quantum mechanics]] |
|||
*[[Sphere-world]] |
|||
*[[Rotation number]] |
|||
*[[Uniformization theorem]] |
|||
*[[Three-body problem]] |
|||
*[[Topology]] |
|||
}} |
|||
| awards = {{plainlist| |
|||
*{{nowrap|[[Gold Medal of the Royal Astronomical Society|RAS Gold Medal]] (1900)}} |
|||
*[[Sylvester Medal]] (1901) |
|||
*[[Matteucci Medal]] (1905) |
|||
*[[Bolyai Prize]] (1905) |
|||
*[[Bruce Medal]] (1911)}} |
|||
| signature = Henri Poincaré Signature.svg |
|||
| footnotes = He was an uncle of [[Pierre Boutroux]]. |
|||
}} |
|||
{{special relativity sidebar}} |
|||
'''Jules Henri Poincaré''' ({{IPAc-en|UK|ˈ|p|w|æ̃|k|ɑr|eɪ}}, {{IPAc-en|US|ˌ|p|w|æ̃|k|ɑː|ˈ|r|eɪ}}; {{IPA|fr|ɑ̃ʁi pwɛ̃kaʁe|lang|Fr-Henri Poincaré.ogg}};<ref>{{Citation |title=Poincaré, n. |date=2023-03-02 |work=Oxford English Dictionary |url=https://oed.com/dictionary/poincare_n |access-date=2024-12-02 |edition=3 |publisher=Oxford University Press |language=en |doi=10.1093/oed/3697720964}}</ref> 29 April 1854{{snd}}17 July 1912) was a French [[mathematician]], [[Theoretical physics|theoretical physicist]], engineer, and [[philosophy of science|philosopher of science]]. He is often described as a [[polymath]], and in mathematics as "The Last Universalist",<ref>{{cite book |last1=Ginoux |first1=J. M. |title=Henri Poincaré: A Biography Through the Daily Papers |last2=Gerini |first2=C. |publisher=[[World Scientific]] |year=2013 |isbn=978-981-4556-61-3 |pages=vii–viii, xiii |doi=10.1142/8956}}</ref> since he excelled in all fields of the discipline as it existed during his lifetime. He has further been called the "[[Carl Friedrich Gauss|Gauss]] of modern mathematics".<ref>{{Cite book |last=Folina |first=Janet |url=https://books.google.com/books?id=EPW-DAAAQBAJ&pg=PAxii |title=Poincaré and the Philosophy of Mathematics |date=1992 |publisher=Palgrave Macmillan UK |isbn=978-1-349-22121-9 |location=London |pages=xii |language=en |doi=10.1007/978-1-349-22119-6}}</ref> Due to his success in science, influence and philosophy, he has been called "the philosopher par excellence of modern science."<ref>{{Cite book |last1=Moulton |first1=Forest Ray |url=https://archive.org/details/autobiographyofs0000unse_n5k3/mode/1up |title=The Autobiography of Science |last2=Jeffries |first2=Justus J. |publisher=Doubleday & Company |year=1945 |pages=509 |language=en |author-link=Forest Ray Moulton}}</ref> |
|||
'''Jules Henri Poincaré''' (29 April 1854 – 17 July 1912) ({{IPA-fr|ˈʒyl ɑ̃ˈʁi pwɛ̃kaˈʁe}})<ref>[http://www.forvo.com/word/poincar%C3%A9/ Poincaré pronunciation examples at Forvo]</ref> was a [[French people|French]] [[mathematician]], [[theoretical physicist]], [[engineer]], and a [[philosophy of science|philosopher of science]]. He is often described as a [[polymath]], and in mathematics as ''The Last Universalist'', since he excelled in all fields of the discipline as it existed during his lifetime. |
|||
As a mathematician and [[physicist]], he made many original fundamental contributions to [[Pure mathematics|pure]] and [[applied mathematics]], [[mathematical physics]], and [[celestial mechanics]].<ref>{{cite journal|author=Hadamard, Jacques|author-link=Jacques Hadamard|title=The early scientific work of Henri Poincaré|journal=The Rice Institute Pamphlet|date=July 1922|volume=9|issue=3|pages=111–183|url=http://catalog.hathitrust.org/Record/100592035}}</ref> In his research on the [[three-body problem]], Poincaré became the first person to discover a chaotic [[deterministic system]] which laid the foundations of modern [[chaos theory]]. Poincaré is regarded as the creator of the field of [[algebraic topology]], and is further credited with introducing [[Automorphic form|automorphic forms]]. He also made important contributions to [[algebraic geometry]], [[number theory]], [[complex analysis]] and [[Lie theory]].<ref>{{Cite book |last=Gray |first=Jeremy |title=Henri Poincaré: A Scientific Biography |date=2013 |publisher=[[Princeton University Press]] |isbn=978-0-691-15271-4 |location= |pages=3, 16, 492 |language=en}}</ref> He famously introduced the concept of the [[Poincaré recurrence theorem]], which states that a state will eventually return arbitrarily close to its initial state after a sufficiently long time, which has far-reaching consequences.<ref>{{Citation |last=Oxtoby |first=John C. |title=The Poincaré Recurrence Theorem |date=1980 |work=Measure and Category |series=Graduate Texts in Mathematics |volume=2 |pages=65–69 |url=http://link.springer.com/10.1007/978-1-4684-9339-9_17 |access-date=2024-12-01 |place=New York, NY |publisher=Springer New York |doi=10.1007/978-1-4684-9339-9_17 |isbn=978-1-4684-9341-2}}</ref> Early in the 20th century he formulated the [[Poincaré conjecture]], which became, over time, one of the famous [[List of unsolved problems in mathematics|unsolved problems in mathematics]]. It was eventually solved in 2002–2003 by [[Grigori Perelman]]. Poincaré popularized the use of [[non-Euclidean geometry]] in mathematics as well.<ref name=":32">{{Citation |last1=Heinzmann |first1=Gerhard |title=Henri Poincaré |date=22 November 2021 |journal=[[Stanford Encyclopedia of Philosophy]] |pages= |url=https://plato.stanford.edu/entries/poincare/ |access-date=3 December 2024 |publisher=Stanford University |last2=Stump |first2=David}}</ref> |
|||
As a mathematician and physicist, he made many original fundamental contributions to [[Pure mathematics|pure]] and [[applied mathematics]], [[mathematical physics]], and [[celestial mechanics]]. He was responsible for formulating the [[Poincaré conjecture]], one of the most famous problems in mathematics. In his research on the [[three-body problem]], Poincaré became the first person to discover a chaotic deterministic system which laid the foundations of modern [[chaos theory]]. He is considered to be one of the founders of the field of [[topology]]. |
|||
Poincaré made clear the importance of paying attention to the [[Invariant (mathematics)|invariance]] of laws of physics under different transformations, and was the first to present the [[Lorentz transformation]]s in their modern symmetrical form. Poincaré discovered the remaining relativistic velocity transformations and recorded them in a letter to [[Hendrik Lorentz]] in 1905. Thus he obtained perfect invariance of all of [[Maxwell's equations]], an important step in the formulation of the theory of [[special relativity]], for which he is also credited with laying down the foundations for,<ref name=":1" /> further writing foundational papers in 1905.<ref name=":3" /> He first proposed [[gravitational wave]]s (''ondes gravifiques'') emanating from a body and propagating at the speed of light as being required by the Lorentz transformations, doing so in 1905.<ref>{{Cite journal |last1=Cervantes-Cota |first1=Jorge L. |last2=Galindo-Uribarri |first2=Salvador |last3=Smoot |first3=George F. |date=2016-09-13 |title=A Brief History of Gravitational Waves |journal=Universe |volume=2 |issue=3 |pages=22 |doi=10.3390/universe2030022 |issn=2218-1997|doi-access=free |arxiv=1609.09400 }}</ref> In 1912, he wrote an influential paper which provided a mathematical argument for [[quantum mechanics]].<ref name="McCormmach" /><ref>{{Cite journal |last=Prentis |first=Jeffrey J. |date=1995-04-01 |title=Poincaré's proof of the quantum discontinuity of nature |url=https://pubs.aip.org/ajp/article/63/4/339/1043285/Poincare-s-proof-of-the-quantum-discontinuity-of |journal=American Journal of Physics |language=en |volume=63 |issue=4 |pages=339–350 |doi=10.1119/1.17919 |issn=0002-9505}}</ref> Poincaré also laid the seeds of the discovery of [[Radioactive decay|radioactivity]] through his interest and study of [[X-ray|X-rays]], which influenced physicist [[Henri Becquerel]], who then discovered the phenomena.<ref>{{Cite journal |last1=Radvanyi |first1=Pierre |last2=Villain |first2=Jacques |date=2017-11-01 |title=The discovery of radioactivity |url=https://www.sciencedirect.com/science/article/pii/S1631070517300786 |journal=Comptes Rendus. Physique |language=en |volume=18 |issue=9–10 |pages=544–550 |doi=10.1016/j.crhy.2017.10.008 |issn=1878-1535}}</ref> The [[Poincaré group]] used in physics and mathematics was named after him, after he introduced the notion of the group.<ref>{{Cite journal |last=Bacry |first=Henri |date=2004 |title=The foundations of the poincaré group and the validity of general relativity |url=https://linkinghub.elsevier.com/retrieve/pii/S0034487704900298 |journal=Reports on Mathematical Physics |language=en |volume=53 |issue=3 |pages=443–473 |doi=10.1016/S0034-4877(04)90029-8}}</ref> |
|||
Poincaré introduced the modern [[principle of relativity]] and was the first to present the [[Lorentz transformations]] in their modern symmetrical form. Poincaré discovered the remaining relativistic velocity transformations and recorded them in a letter to Dutch physicist [[Hendrik Lorentz]] (1853–1928) in 1905. Thus he obtained perfect invariance of all of [[Maxwell's equations]], an important step in the formulation of the theory of [[special relativity]]. |
|||
Poincaré was considered the dominant figure in mathematics and theoretical physics during his time, and was the most respected mathematician of his time, being described as "the living brain of the rational sciences" by mathematician [[Paul Painlevé]].<ref name=":03">{{Cite book |last=Bell |first=E.T. |author-link=Eric Temple Bell |url=https://archive.org/details/in.ernet.dli.2015.59359/page/n295 |title=Men of Mathematics |publisher=[[Penguin Books]] |year=1937 |volume=II |pages=611 |language=en}}</ref> Philosopher [[Karl Popper]] regarded Poincaré as the greatest philosopher of science of all time,<ref name=":22">{{Cite book |url=https://books.google.com/books?id=9F7bY_ltzxIC&pg=PA373 |title=The Scientific Legacy of Poincaré |date=2010 |publisher=The London Mathematical Society |isbn=978-0-8218-4718-3 |editor-last=Charpentier |editor-first=Éric |series=History of Mathematics |location= |pages=373 |language=en |translator-last=Bowman |translator-first=Joshua |editor-last2=Ghys |editor-first2=E. |editor-last3=Lesne |editor-first3=Annick}}</ref> with Poincaré also originating the [[Conventionalism|conventionalist]] view in science.<ref>{{Cite journal |last=Merritt |first=David |date=2017 |title=Cosmology and convention |url=https://linkinghub.elsevier.com/retrieve/pii/S1355219816301563 |journal=Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics |language=en |volume=57 |pages=41–52 |doi=10.1016/j.shpsb.2016.12.002|arxiv=1703.02389 }}</ref> Poincaré was a [[Intellectual#Public intellectual|public intellectual]] in his time, and personally, he believed in [[Political egalitarianism|political equality]] for all, while wary of the influence of anti-intellectual positions that the [[Catholic Church]] held at the time.<ref>{{Cite book |last=Gray |first=Jeremy |title=Henri Poincaré: A Scientific Biography |date=2013 |publisher=[[Princeton University Press]] |isbn=978-0-691-15271-4 |location= |pages=24, 201 |language=en}}</ref> He served as the president of the [[French Academy of Sciences#Presidents|French Academy of Sciences]] (1906), the president of [[Société astronomique de France#Presidents|Société astronomique de France]] (1901–1903), and twice the president of [[Société mathématique de France]] (1886, 1900). |
|||
The [[Poincaré group]] used in physics and mathematics was named after him. |
|||
==Life== |
==Life== |
||
Poincaré was born on 29 April 1854 in Cité Ducale neighborhood, [[Nancy |
Poincaré was born on 29 April 1854 in Cité Ducale neighborhood, [[Nancy, Meurthe-et-Moselle]], into an influential French family.<ref>Belliver, 1956</ref> His father Léon Poincaré (1828–1892) was a professor of medicine at the [[University of Nancy]].<ref>Sagaret, 1911</ref> His younger sister Aline married the spiritual philosopher [[Émile Boutroux]]. Another notable member of Henri's family was his cousin, [[Raymond Poincaré]], a fellow member of the [[Académie française]], who was [[President of France]] from 1913 to 1920, and three-time [[Prime Minister of France]] between 1913 and 1929.<ref name="IEP">[http://www.utm.edu/research/iep/p/poincare.htm The Internet Encyclopedia of Philosophy] {{Webarchive|url=https://web.archive.org/web/20040202060803/http://www.utm.edu/research/iep/p/poincare.htm |date=2 February 2004 }} Jules Henri Poincaré article by Mauro Murzi – Retrieved November 2006.</ref> |
||
===Education=== |
===Education=== |
||
[[File:Henri Poincaré maison natale Nancy plaque.jpg|thumb|right|200px| Plaque on the birthplace of Henri Poincaré at house number 117 on the Grande Rue in the city of Nancy]] |
|||
During his childhood he was seriously ill for a time with [[diphtheria]] and received special instruction from his mother, Eugénie Launois (1830–1897). |
During his childhood he was seriously ill for a time with [[diphtheria]] and received special instruction from his mother, Eugénie Launois (1830–1897). |
||
In 1862, Henri entered the Lycée in [[Nancy]] (now renamed the Lycée Henri |
In 1862, Henri entered the Lycée in [[Nancy, Meurthe-et-Moselle|Nancy]] (now renamed the {{ill|Lycée Henri-Poincaré|fr}} in his honour, along with [[Henri Poincaré University]], also in Nancy). He spent eleven years at the Lycée and during this time he proved to be one of the top students in every topic he studied. He excelled in written composition. His mathematics teacher described him as a "monster of mathematics" and he won first prizes in the [[concours général]], a competition between the top pupils from all the Lycées across France. His poorest subjects were music and physical education, where he was described as "average at best".<ref>O'Connor et al., 2002</ref> Poor eyesight and a tendency towards absentmindedness may explain these difficulties.<ref>Carl, 1968</ref> He graduated from the Lycée in 1871 with a [[baccalauréat]] in both letters and sciences. |
||
During the [[Franco-Prussian War]] of 1870 he served alongside his father in the Ambulance Corps. |
During the [[Franco-Prussian War]] of 1870, he served alongside his father in the [[Ambulance Corps]]. |
||
Poincaré entered the [[École Polytechnique]] in 1873. There he studied mathematics as a student of [[Charles Hermite]], continuing to excel and publishing his first paper (''Démonstration nouvelle des propriétés de l'indicatrice d'une surface'') in 1874. |
Poincaré entered the [[École Polytechnique]] as the top qualifier in 1873 and graduated in 1875. There he studied mathematics as a student of [[Charles Hermite]], continuing to excel and publishing his first paper (''Démonstration nouvelle des propriétés de l'indicatrice d'une surface'') in 1874. From November 1875 to June 1878 he studied at the [[École des Mines]], while continuing the study of mathematics in addition to the [[mining engineering]] syllabus, and received the degree of ordinary mining engineer in March 1879.<ref>F. Verhulst</ref> |
||
As a graduate of the École des Mines he joined the [[Corps des Mines]] as an inspector for the [[Vesoul]] region in northeast France. He was on the scene of a mining disaster at [[Magny-lès-Jussey|Magny]] in August 1879 in which 18 miners died. He carried out the official investigation into the accident |
As a graduate of the École des Mines, he joined the [[Corps des Mines]] as an inspector for the [[Vesoul]] region in northeast France. He was on the scene of a mining disaster at [[Magny-lès-Jussey|Magny]] in August 1879 in which 18 miners died. He carried out the official investigation into the accident. |
||
At the same time, Poincaré was preparing for his |
At the same time, Poincaré was preparing for his [[Doctorate in Science]] in mathematics under the supervision of Charles Hermite. His doctoral thesis was in the field of [[differential equations]]. It was named ''Sur les propriétés des fonctions définies par les équations aux différences partielles''. Poincaré devised a new way of studying the properties of these equations. He not only faced the question of determining the integral of such equations, but also was the first person to study their general geometric properties. He realised that they could be used to model the behaviour of multiple bodies in free motion within the [[Solar System]]. He graduated from the [[University of Paris]] in 1879. |
||
[[Image:Young Poincare.jpg|left| |
[[Image:Young Poincare.jpg|left|upright|thumb|The young Henri Poincaré in 1887 at the age of 33]] |
||
===First scientific achievements=== |
|||
After receiving his degree, Poincaré began teaching as junior [[lecturer]] in mathematics at the [[Caen University|University of Caen]] in Normandy (in December 1879). At the same time he published his first major article concerning the treatment of a class of [[automorphic function]]s. |
|||
There, in [[Caen]], he met his future wife, Louise Poulain d'Andecy (1857–1934), granddaughter of [[Isidore Geoffroy Saint-Hilaire]] and great-granddaughter of [[Étienne Geoffroy Saint-Hilaire]] and on 20 April 1881, they married.<ref>{{Cite journal |last=Rollet |first=Laurent |date=2012-11-15 |title=Jeanne Louise Poulain d'Andecy, épouse Poincaré (1857–1934) |url=https://journals.openedition.org/sabix/1131 |journal=Bulletin de la Sabix. Société des amis de la Bibliothèque et de l'Histoire de l'École polytechnique |language=Fr |issue=51 |pages=18–27 |doi=10.4000/sabix.1131 |s2cid=190028919 |issn=0989-3059}}</ref> Together they had four children: Jeanne (born 1887), Yvonne (born 1889), Henriette (born 1891), and Léon (born 1893). |
|||
Poincaré immediately established himself among the greatest mathematicians of Europe, attracting the attention of many prominent mathematicians. In 1881 Poincaré was invited to take a teaching position at the Faculty of Sciences of the [[University of Paris]]; he accepted the invitation. During the years 1883 to 1897, he taught [[mathematical analysis]] in the [[École Polytechnique]]. |
|||
In 1881–1882, Poincaré created a new branch of mathematics: [[qualitative theory of differential equations]]. He showed how it is possible to derive the most important information about the behavior of a family of solutions without having to solve the equation (since this may not always be possible). He successfully used this approach to problems in [[celestial mechanics]] and [[mathematical physics]]. |
|||
===Career=== |
===Career=== |
||
He never fully abandoned his career in the mining administration to mathematics. He worked at the [[Ministry of Public Services]] as an engineer in charge of northern railway development from 1881 to 1885. He eventually became chief engineer of the [[Corps des Mines]] in 1893 and inspector general in 1910. |
|||
Beginning in 1881 and for the rest of his career, he taught at the University of Paris (the [[Sorbonne]]). He was initially appointed as the ''maître de conférences d'analyse'' (associate professor of analysis) |
Beginning in 1881 and for the rest of his career, he taught at the [[University of Paris]] (the [[University of Paris|Sorbonne]]). He was initially appointed as the ''maître de conférences d'analyse'' (associate professor of analysis).<ref>Sageret, 1911</ref> Eventually, he held the chairs of Physical and Experimental Mechanics, Mathematical Physics and Theory of Probability,<ref>{{cite book|first =Laurent|last= Mazliak|chapter= Poincaré’s Odds |title = Poincaré 1912–2012 : Poincaré Seminar 2012|editor1-first= B.|editor1-last= Duplantier |editor2-first= V.|editor2-last= Rivasseau|volume = 67 |series = Progress in Mathematical Physics|publisher = Springer|isbn = 9783034808347|location = Basel|page = 150|url = https://books.google.com/books?id=njNpBQAAQBAJ|date= 14 November 2014}}</ref> and Celestial Mechanics and Astronomy. |
||
In 1887, at the young age of 32, Poincaré was elected to the [[French Academy of Sciences]]. He became its president in 1906, and was elected to the [[Académie française]] on 5 March 1908. |
|||
Also in that same year, Poincaré married Miss Poulain d'Andecy. Together they had four children: Jeanne (born 1887), Yvonne (born 1889), Henriette (born 1891), and Léon (born 1893). |
|||
In 1887, he won [[Oscar II of Sweden|Oscar II, King of Sweden]]'s mathematical competition for a resolution of the [[three-body problem]] concerning the free motion of multiple orbiting bodies. (See [[#Three-body problem|three-body problem]] section below.) |
|||
In 1887, at the young age of 32, Poincaré was elected to the [[French Academy of Sciences]]. He became its president in 1906, and was elected to the [[Académie française]] in 1909. |
|||
In 1893, Poincaré joined the French [[Bureau des Longitudes]], which engaged him in the [[Clock synchronization|synchronisation of time]] around the world. In 1897 Poincaré backed an unsuccessful proposal for the [[Decimal degrees|decimalisation of circular measure]], and hence time and [[longitude]].<ref>see Galison 2003</ref> It was this post which led him to consider the question of establishing international time zones and the synchronisation of time between bodies in relative motion. (See [[#Work on relativity|work on relativity]] section below.) |
|||
In 1887 he won [[Oscar II of Sweden|Oscar II, King of Sweden]]'s mathematical competition for a resolution of the [[three-body problem]] concerning the free motion of multiple orbiting bodies. (See [[#The three-body problem]] section below) |
|||
In 1904, he intervened in the [[Dreyfus affair|trials]] of [[Alfred Dreyfus]], attacking the spurious scientific claims regarding evidence brought against Dreyfus. |
|||
[[File:Poincaré gravestone.jpg|right|160px|right|thumb|The Poincaré family grave at the [[Cimetière du Montparnasse]]]] |
|||
Poincaré was the President of the [[Société astronomique de France|Société Astronomique de France (SAF)]], the French astronomical society, from 1901 to 1903.<ref name=BSAF1911>{{cite web| url = http://gallica.bnf.fr/ark:/12148/bpt6k9626551q/f616.item| title = ''Bulletin de la Société astronomique de France'', 1911, vol. 25, pp. 581–586| year = 1911}}</ref> |
|||
In 1893, Poincaré joined the French [[Bureau des Longitudes]], which engaged him in the synchronisation of time around the world. In 1897 Poincaré backed an unsuccessful proposal for the decimalisation of circular measure, and hence time and [[longitude]] (see Galison 2003). It was this post which led him to consider the question of establishing international time zones and the synchronisation of time between bodies in relative motion. (See [[#Work on relativity]] section below) |
|||
====Students==== |
|||
In 1899, and again more successfully in 1904, he intervened in the trials of [[Alfred Dreyfus]]. He attacked the spurious scientific claims of some of the evidence brought against Dreyfus, who was a Jewish officer in the French army charged with treason by anti-Semitic colleagues. |
|||
Poincaré had two notable doctoral students at the University of Paris, [[Louis Bachelier]] (1900) and [[Dimitrie Pompeiu]] (1905).<ref>[http://www.genealogy.ams.org/id.php?id=34227 Mathematics Genealogy Project] {{Webarchive|url=https://web.archive.org/web/20071005011853/http://www.genealogy.ams.org/id.php?id=34227 |date=5 October 2007 }} North Dakota State University. Retrieved April 2008.</ref> |
|||
=== Death === |
|||
In 1912, Poincaré underwent surgery for a [[prostate]] problem and subsequently died from an [[embolism]] on 17 July 1912, in Paris. He was 58 years of age. He is buried in the Poincaré family vault in the [[Cimetière du Montparnasse|Cemetery of Montparnasse]], Paris. |
|||
In 1912, Poincaré underwent surgery for a [[prostate]] problem and subsequently died from an [[embolism]] on 17 July 1912, in Paris. He was 58 years of age. He is buried in the Poincaré family vault in the [[Cimetière du Montparnasse|Cemetery of Montparnasse]], Paris, in section 16 close to the gate Rue Émile-Richard. |
|||
A former French Minister of Education, [[Claude Allègre]], has recently (2004) proposed that Poincaré be reburied in the [[Panthéon, Paris|Panthéon]] in Paris, which is reserved for French citizens only of the highest honour.<ref>[http://www.lexpress.fr/idees/tribunes/dossier/allegre/dossier.asp?ida=430274 Lorentz, Poincaré et Einstein]</ref> |
|||
A former French Minister of Education, [[Claude Allègre]], proposed in 2004 that Poincaré be reburied in the [[Panthéon, Paris|Panthéon]] in Paris, which is reserved for French citizens of the highest honour.<ref>{{cite web |url = http://www.lexpress.fr/idees/tribunes/dossier/allegre/dossier.asp?ida=430274 |title = Lorentz, Poincaré et Einstein |archive-url=https://web.archive.org/web/20041127160356/http://www.lexpress.fr/idees/tribunes/dossier/allegre/dossier.asp?ida=430274 |archive-date=27 November 2004 |url-status=dead}}</ref>[[File:Poincaré gravestone.jpg|upright|thumb|The Poincaré family grave at the [[Cimetière du Montparnasse]]]] |
|||
=====Students===== |
|||
Poincaré had two notable doctoral students at the University of Paris, [[Louis Bachelier]] (1900) and [[Dimitrie Pompeiu]] (1905).<ref>[http://www.genealogy.ams.org/id.php?id=34227 Mathematics Genealogy Project] North Dakota State University. Retrieved April 2008.</ref> |
|||
==Work== |
==Work== |
||
===Summary=== |
|||
Poincaré made many contributions to different fields of pure and applied mathematics such as: [[celestial mechanics]], [[fluid mechanics]], [[optics]], [[electricity]], [[telegraphy]], [[capillarity]], [[Elasticity (physics)|elasticity]], [[thermodynamics]], [[potential theory]], [[Quantum mechanics|quantum theory]], [[theory of relativity]] and [[physical cosmology]]. |
|||
===Summary=== |
|||
He was also a populariser of mathematics and physics and wrote several books for the lay public. |
|||
Poincaré made many contributions to different fields of pure and applied mathematics such as: [[celestial mechanics]], [[fluid mechanics]], [[optics]], [[electricity]], [[telegraphy]], [[capillarity]], [[Elasticity (physics)|elasticity]], [[thermodynamics]], [[potential theory]], [[Quantum mechanics]], [[theory of relativity]] and [[physical cosmology]]. |
|||
Among the specific topics he contributed to are the following: |
Among the specific topics he contributed to are the following: |
||
*[[algebraic topology]] |
*[[algebraic topology]] (a field that Poincaré virtually invented) |
||
* |
*the theory of analytic functions of [[several complex variables]] |
||
*[[abelian variety|the theory of abelian functions]] |
*[[abelian variety|the theory of abelian functions]] |
||
*[[algebraic geometry]] |
*[[algebraic geometry]] |
||
* |
*the [[Poincaré conjecture]], proven in 2003 by [[Grigori Perelman]]. |
||
*[[Poincaré recurrence theorem]] |
*[[Poincaré recurrence theorem]] |
||
*[[hyperbolic geometry]] |
*[[hyperbolic geometry]] |
||
*[[number theory]] |
*[[number theory]] |
||
*[[ |
*the [[three-body problem]] |
||
* |
*the theory of [[diophantine equation]]s |
||
*[[ |
*[[electromagnetism]] |
||
*[[ |
*[[special relativity]] |
||
* |
*the [[fundamental group]] |
||
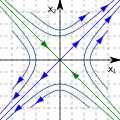
*In the field of [[differential equations]] Poincaré has given many results that are critical for the qualitative theory of differential equations, for example the [[Poincaré homology sphere|Poincaré sphere]] and the [[Poincaré map]]. |
*In the field of [[differential equations]] Poincaré has given many results that are critical for the qualitative theory of differential equations, for example the [[Poincaré homology sphere|Poincaré sphere]] and the [[Poincaré map]]. |
||
*Poincaré on "everybody's belief" in the [[q:Henri Poincaré|''Normal Law of Errors'']] (see [[normal distribution]] for an account of that "law") |
*Poincaré on "everybody's belief" in the [[q:Henri Poincaré|''Normal Law of Errors'']] (see [[normal distribution]] for an account of that "law") |
||
*Published an influential paper providing a novel mathematical argument in support of [[quantum mechanics]].<ref name=McCormmach>{{Citation | last = McCormmach | first = Russell | title = Henri Poincaré and the Quantum Theory | journal = Isis | volume = 58 | issue = 1 | pages = 37–55 | date =Spring 1967 | doi =10.1086/350182| s2cid = 120934561 }}</ref><ref name=Irons>{{Citation | last = Irons | first = F. E. | title = Poincaré's 1911–12 proof of quantum discontinuity interpreted as applying to atoms | journal = American Journal of Physics | volume = 69 | issue = 8 | pages = 879–884 | date = August 2001 | doi =10.1119/1.1356056 |bibcode = 2001AmJPh..69..879I }}</ref> |
|||
*Published an influential paper providing a novel mathematical argument in support of [[quantum mechanics]].<ref name=McCormmach> |
|||
{{Citation |
|||
| last =McCormmach |
|||
| first =Russell |
|||
| title = Henri Poincaré and the Quantum Theory |
|||
| journal = Isis |
|||
| volume = 58 |
|||
| issue = 1 |
|||
| pages = 37–55 |
|||
| date = Spring, 1967 |
|||
| doi =10.1086/350182 |
|||
}}</ref><ref name=Irons> |
|||
{{Citation |
|||
| last =Irons |
|||
| first =F. E. |
|||
| title = Poincaré's 1911–12 proof of quantum discontinuity interpreted as applying to atoms |
|||
| journal = American Journal of Physics |
|||
| volume = 69 |
|||
| issue = 8 |
|||
| pages = 879–884 |
|||
| date = August, 2001 |
|||
| doi =10.1119/1.1356056 |
|||
}}</ref> |
|||
=== |
===Three-body problem=== |
||
The problem of finding the general solution to the motion of more than two orbiting bodies in the |
The problem of finding the general solution to the motion of more than two orbiting bodies in the [[Solar System]] had eluded mathematicians since [[Isaac Newton|Newton's]] time. This was known originally as the three-body problem and later the [[n-body problem|''n''-body problem]], where ''n'' is any number of more than two orbiting bodies. The ''n''-body solution was considered very important and challenging at the close of the 19th century. Indeed, in 1887, in honour of his 60th birthday, [[Oscar II of Sweden|Oscar II, King of Sweden]], advised by [[Gösta Mittag-Leffler]], established a prize for anyone who could find the solution to the problem. The announcement was quite specific: |
||
<blockquote>Given a system of arbitrarily many mass points that attract each according to [[Newton's law of universal gravitation|Newton's law]], under the assumption that no two points ever collide, try to find a representation of the coordinates of each point as a series in a variable that is some known function of time and for all of whose values the series [[uniform convergence|converges uniformly]].</blockquote> |
|||
In case the problem could not be solved, any other important contribution to classical mechanics would then be considered to be prizeworthy. The prize was finally awarded to Poincaré, even though he did not solve the original problem. |
In case the problem could not be solved, any other important contribution to classical mechanics would then be considered to be prizeworthy. The prize was finally awarded to Poincaré, even though he did not solve the original problem. One of the judges, the distinguished [[Karl Weierstrass]], said, ''"This work cannot indeed be considered as furnishing the complete solution of the question proposed, but that it is nevertheless of such importance that its publication will inaugurate a new era in the history of celestial mechanics."'' (The first version of his contribution even contained a serious error; for details see the article by Diacu<ref name=diacu>{{Citation |
||
| last=Diacu|first= Florin | year=1996 | title=The solution of the ''n''-body Problem | journal=The Mathematical Intelligencer | volume =18 | pages =66–70 | doi=10.1007/BF03024313 |
|||
One of the judges, the distinguished [[Karl Weierstrass]], said, ''"This work cannot indeed be considered as furnishing the complete solution of the question proposed, but that it is nevertheless of such importance that its publication will inaugurate a new era in the history of celestial mechanics."'' |
|||
| issue=3|s2cid= 119728316 }}</ref> and the book by [[June Barrow-Green|Barrow-Green]]<ref>{{Cite book|title=Poincaré and the three body problem|title-link= Poincaré and the Three-Body Problem |last=Barrow-Green|first=June|publisher=[[American Mathematical Society]]|year=1997|isbn=978-0821803677|location=Providence, RI|series=History of Mathematics|volume=11|oclc=34357985}}</ref>). The version finally printed<ref>{{Cite book|title=The three-body problem and the equations of dynamics: Poincaré's foundational work on dynamical systems theory|last=Poincaré|first=J. Henri|publisher=Springer International Publishing|others=Popp, Bruce D. (Translator)|year=2017|isbn=9783319528984|location=Cham, Switzerland|oclc=987302273}}</ref> contained many important ideas which led to the [[chaos theory|theory of chaos]]. The problem as stated originally was finally solved by [[Karl F. Sundman]] for ''n'' = 3 in 1912 and was generalised to the case of ''n'' > 3 bodies by [[Qiudong Wang]] in the 1990s. The series solutions have very slow convergence. It would take millions of terms to determine the motion of the particles for even very short intervals of time, so they are unusable in numerical work.<ref name="diacu" /> |
|||
(The first version of his contribution even contained a serious error; for details see the article by Diacu<ref name=diacu>{{Citation |
|||
| author=Diacu, F. | year=1996 | title=The solution of the ''n''-body Problem | journal=The Mathematical Intelligencer | volume =18 | pages =66–70 |
|||
| doi=10.1007/BF03024313}}</ref>). The version finally printed contained many important ideas which lead to the [[chaos theory|theory of chaos]]. The problem as stated originally was finally solved by [[Karl F. Sundman]] for ''n'' = 3 in 1912 and was generalised to the case of ''n'' > 3 bodies by [[Qiudong Wang]] in the 1990s. |
|||
===Work on relativity=== |
===Work on relativity=== |
||
{{Main|Lorentz ether theory|History of special relativity}} |
|||
[[Image:Curie and Poincare 1911 Solvay.jpg|thumb|200px|right|[[Marie Curie]] and Poincaré talk at the 1911 [[Solvay Conference]].]] |
|||
[[Image:Curie and Poincare 1911 Solvay.jpg|thumb|right|[[Marie Curie]] and Poincaré talk at the 1911 [[Solvay Conference]].]] |
|||
{{main|Lorentz ether theory|History of special relativity}} |
|||
====Local time==== |
====Local time==== |
||
Poincaré's work at the Bureau des Longitudes on establishing international time zones led him to consider how clocks at rest on the Earth, which would be moving at different speeds relative to absolute space (or the "[[luminiferous aether]]"), could be synchronised. At the same time |
Poincaré's work at the Bureau des Longitudes on establishing international time zones led him to consider how clocks at rest on the Earth, which would be moving at different speeds relative to absolute space (or the "[[luminiferous aether]]"), could be synchronised. At the same time Dutch theorist [[Hendrik Lorentz]] was developing Maxwell's theory into a theory of the motion of charged particles ("electrons" or "ions"), and their interaction with radiation. In 1895 Lorentz had introduced an auxiliary quantity (without physical interpretation) called "local time" <math>t^\prime = t-v x/c^2 \,</math><ref>{{Citation|title=A broader view of relativity: general implications of Lorentz and Poincaré invariance|volume=10|first1=Jong-Ping|last1=Hsu|first2=Leonardo|last2=Hsu|publisher=World Scientific|year=2006|isbn=978-981-256-651-5|page=37 |
||
|url= |
|url=https://books.google.com/books?id=amLqckyrvUwC}}, [https://books.google.com/books?id=amLqckyrvUwC&pg=PA37 Section A5a, p 37]</ref> |
||
and introduced the hypothesis of [[length contraction]] to explain the failure of optical and electrical experiments to detect motion relative to the aether (see [[Michelson–Morley experiment]]).<ref>{{Citation |
and introduced the hypothesis of [[length contraction]] to explain the failure of optical and electrical experiments to detect motion relative to the aether (see [[Michelson–Morley experiment]]).<ref>{{Citation |
||
| last=Lorentz|first= Hendrik A. | author-link=Hendrik Lorentz| year=1895 | title=Versuch einer theorie der electrischen und optischen erscheinungen in bewegten Kõrpern | place =Leiden| publisher=E.J. Brill| title-link=s:de:Versuch einer Theorie der electrischen und optischen Erscheinungen in bewegten Körpern }}</ref> Poincaré was a constant interpreter (and sometimes friendly critic) of Lorentz's theory. Poincaré as a philosopher was interested in the "deeper meaning". Thus he interpreted Lorentz's theory and in so doing he came up with many insights that are now associated with special relativity. In [[s:The Measure of Time|The Measure of Time]] (1898), Poincaré said, "A little reflection is sufficient to understand that all these affirmations have by themselves no meaning. They can have one only as the result of a convention." He also argued that scientists have to set the constancy of the speed of light as a [[postulate]] to give physical theories the simplest form.<ref>{{Citation |
|||
| author=Lorentz, H.A. | year=1895 | title=[[s:de:Versuch einer Theorie der electrischen und optischen Erscheinungen in bewegten Körpern|Versuch einer theorie der electrischen und optischen erscheinungen in bewegten Kõrpern]] | place =Leiden| publisher=E.J. Brill}}</ref> |
|||
| last=Poincaré|first= Henri | year=1898 | title=The Measure of Time | journal=Revue de Métaphysique et de Morale | volume =6 | pages =1–13| title-link=s:The Measure of Time }}</ref> |
|||
Poincaré was a constant interpreter (and sometimes friendly critic) of Lorentz's theory. Poincaré as a philosopher was interested in the "deeper meaning". Thus he interpreted Lorentz's theory and in so doing he came up with many insights that are now associated with special relativity. In [[s:The Measure of Time|The Measure of Time]] (1898), Poincaré said, " |
|||
A little reflection is sufficient to understand that all these affirmations have by themselves no meaning. They can have one only as the result of a convention." He also argued that scientists have to set the constancy of the speed of light as a [[postulate]] to give physical theories the simplest form.<ref>{{Citation |
|||
| author=Poincaré, H. | year=1898 | title=[[s:The Measure of Time|The Measure of Time]] | journal=Revue de métaphysique et de morale | volume =6 | pages =1–13}}</ref> |
|||
Based on these assumptions he discussed in 1900 Lorentz's "wonderful invention" of local time and remarked that it arose when moving clocks are synchronised by exchanging light signals assumed to travel with the same speed in both directions in a moving frame.<ref name=action>{{Citation |
Based on these assumptions he discussed in 1900 Lorentz's "wonderful invention" of local time and remarked that it arose when moving clocks are synchronised by exchanging light signals assumed to travel with the same speed in both directions in a moving frame.<ref name=action>{{Citation |
||
| |
| last=Poincaré|first= Henri | year=1900 | title=La théorie de Lorentz et le principe de réaction | journal=Archives Néerlandaises des Sciences Exactes et Naturelles | volume =5 | pages =252–278| title-link=s:fr:La théorie de Lorentz et le principe de réaction }}. See also the [http://www.physicsinsights.org/poincare-1900.pdf English translation]</ref> |
||
{{Wikisource author|Henri Poincaré}} |
|||
====Principle of relativity and Lorentz transformations==== |
====Principle of relativity and Lorentz transformations==== |
||
{{Further|History of Lorentz transformations}} |
|||
In 1881 Poincaré described [[hyperbolic geometry]] in terms of the [[hyperboloid model]], formulating transformations leaving invariant the [[Lorentz interval]] <math>x^2+y^2-z^2=-1</math>, which makes them mathematically equivalent to the Lorentz transformations in 2+1 dimensions.<ref>{{Cite journal|author=Poincaré, H.|year=1881|title=Sur les applications de la géométrie non-euclidienne à la théorie des formes quadratiques|journal=Association Française Pour l'Avancement des Sciences|volume=10|pages=132–138|url=http://henripoincarepapers.univ-nantes.fr/chp/hp-pdf/hp1881af.pdf|archive-url=https://web.archive.org/web/20200801124731/http://henripoincarepapers.univ-nantes.fr/chp/hp-pdf/hp1881af.pdf|url-status=dead|archive-date=1 August 2020}}</ref><ref>{{Cite journal|author=Reynolds, W. F.|year=1993|title=Hyperbolic geometry on a hyperboloid|journal=The American Mathematical Monthly|volume=100|issue=5|pages=442–455|jstor=2324297|doi=10.1080/00029890.1993.11990430|s2cid=124088818 }}</ref> In addition, Poincaré's other models of hyperbolic geometry ([[Poincaré disk model]], [[Poincaré half-plane model]]) as well as the [[Beltrami–Klein model]] can be related to the relativistic velocity space (see [[Gyrovector space]]). |
|||
In 1892 Poincaré developed a [[mathematical theory]] of [[light]] including [[polarization (waves)|polarization]]. His vision of the action of polarizers and retarders, acting on a sphere representing polarized states, is called the [[Poincaré sphere (optics)|Poincaré sphere]].<ref>{{Cite book|author=Poincaré, H. |year=1892|title=Théorie mathématique de la lumière II|location=Paris|publisher=Georges Carré|chapter-url=https://archive.org/details/thoriemathma00poin|chapter=Chapitre XII: Polarisation rotatoire}}</ref> It was shown that the Poincaré sphere possesses an underlying Lorentzian symmetry, by which it can be used as a geometrical representation of Lorentz transformations and velocity additions.<ref>{{Cite journal|author=Tudor, T.|year=2018|title=Lorentz Transformation, Poincaré Vectors and Poincaré Sphere in Various Branches of Physics|journal=Symmetry|volume=10|issue=3|pages=52|doi=10.3390/sym10030052|bibcode=2018Symm...10...52T|doi-access=free}}</ref> |
|||
He discussed the "principle of relative motion" in two papers in 1900<ref name=action /><ref>{{Citation |
He discussed the "principle of relative motion" in two papers in 1900<ref name=action /><ref>{{Citation |
||
| author=Poincaré, H. | year=1900 | title= |
| author=Poincaré, H. | year=1900 | title= Les relations entre la physique expérimentale et la physique mathématique | journal=Revue Générale des Sciences Pures et Appliquées | volume =11 | pages =1163–1175 | url=http://gallica.bnf.fr/ark:/12148/bpt6k17075r/f1167.table}}. Reprinted in "Science and Hypothesis", Ch. 9–10.</ref> |
||
and named it the [[principle of relativity]] in 1904, according to which no physical experiment can discriminate between a state of uniform motion and a state of rest.<ref name=louis>{{Citation|author=Poincaré, Henri|year= |
and named it the [[principle of relativity]] in 1904, according to which no physical experiment can discriminate between a state of uniform motion and a state of rest.<ref name=louis>{{Citation|author=Poincaré, Henri|year=1913|chapter=[[s:The Principles of Mathematical Physics|The Principles of Mathematical Physics]]|title=The Foundations of Science (The Value of Science)|pages=297–320|publisher=Science Press|place=New York|postscript=; article translated from 1904 original}} available in [https://books.google.com/books/about/The_Foundations_of_Science.html?id=mBvNabP35zoC&pg=PA297 online chapter from 1913 book]</ref> |
||
In 1905 Poincaré wrote to Lorentz about Lorentz's paper of 1904, which Poincaré described as a "paper of supreme importance |
In 1905 Poincaré wrote to Lorentz about Lorentz's paper of 1904, which Poincaré described as a "paper of supreme importance". In this letter he pointed out an error Lorentz had made when he had applied his transformation to one of Maxwell's equations, that for charge-occupied space, and also questioned the time dilation factor given by Lorentz.<ref name="univ-nantes"> |
||
{{Citation | author=Poincaré, H. | year=2007 | editor=Walter, S. A. | contribution= 38.3, Poincaré to H. A. Lorentz, May 1905 | title=La correspondance entre Henri Poincaré et les physiciens, chimistes, et ingénieurs |pages=255–257 |place=Basel | publisher=Birkhäuser|contribution-url=http://henripoincarepapers.univ-nantes.fr/chp/text/lorentz3.html}}</ref> |
|||
In a second letter to Lorentz, Poincaré gave his own reason why Lorentz's time dilation factor was indeed correct after all: it was necessary to make the Lorentz transformation form a group and gave what is now known as the relativistic velocity-addition law.<ref>[http://www.univ-nancy2.fr/poincare/chp/text/lorentz4.xml Letter from Poincaré to Lorentz, Mai 1905]</ref> |
|||
In a second letter to Lorentz, Poincaré gave his own reason why Lorentz's time dilation factor was indeed correct after all—it was necessary to make the Lorentz transformation form a group—and he gave what is now known as the relativistic velocity-addition law.<ref name="univ-nantes2">{{Citation | author=Poincaré, H. | year=2007 | editor=Walter, S. A. | contribution= 38.4, Poincaré to H. A. Lorentz, May 1905 | title=La correspondance entre Henri Poincaré et les physiciens, chimistes, et ingénieurs |pages=257–258 |place=Basel | publisher=Birkhäuser|contribution-url=http://henripoincarepapers.univ-nantes.fr/chp/text/lorentz4.html}}</ref> |
|||
Poincaré later delivered a paper at the meeting of the Academy of Sciences in Paris on 5 June 1905 in which these issues were addressed. In the published version of that he wrote:<ref name=short>{{Citation | author=Poincaré, H. | year=1905 | title=[[s:On the Dynamics of the Electron (June)|On the Dynamics of the Electron]] | journal=Comptes Rendus | volume =140 | pages =1504–1508}} (Wikisource translation)</ref> |
|||
Poincaré later delivered a paper at the meeting of the Academy of Sciences in Paris on 5 June 1905 in which these issues were addressed. In the published version of that he wrote:<ref name="1905 paper">[http://www.academie-sciences.fr/pdf/dossiers/Poincare/Poincare_pdf/Poincare_CR1905.pdf] (PDF) Membres de l'Académie des sciences depuis sa création : Henri Poincare. Sur la dynamique de l' electron. Note de H. Poincaré. C.R. T.140 (1905) 1504–1508.</ref> |
|||
<blockquote>The essential point, established by Lorentz, is that the equations of the electromagnetic field are not altered by a certain transformation (which I will call by the name of Lorentz) of the form: |
|||
::<math>x^\prime = k\ell\left(x + \varepsilon t\right)\!,\;t^\prime = k\ell\left(t + \varepsilon x\right)\!,\;y^\prime = \ell y,\;z^\prime = \ell z,\;k = 1/\sqrt{1-\varepsilon^2}.</math> |
::<math>x^\prime = k\ell\left(x + \varepsilon t\right)\!,\;t^\prime = k\ell\left(t + \varepsilon x\right)\!,\;y^\prime = \ell y,\;z^\prime = \ell z,\;k = 1/\sqrt{1-\varepsilon^2}.</math></blockquote> |
||
and showed that the arbitrary function <math>\ell\left(\varepsilon\right)</math> must be unity for all <math>\varepsilon</math> (Lorentz had set <math>\ell = 1</math> by a different argument) to make the transformations form a group. In an enlarged version of the paper that appeared in 1906 Poincaré pointed out that the combination <math>x^2+ y^2+ z^2- c^2t^2</math> is [[Invariant (mathematics)|invariant]]. He noted that a Lorentz transformation is merely a rotation in four-dimensional space about the origin by introducing <math>ct\sqrt{-1}</math> as a fourth imaginary coordinate, and he used an early form of [[four-vector]]s.<ref name=long>{{Citation |
and showed that the arbitrary function <math>\ell\left(\varepsilon\right)</math> must be unity for all <math>\varepsilon</math> (Lorentz had set <math>\ell = 1</math> by a different argument) to make the transformations form a group. In an enlarged version of the paper that appeared in 1906 Poincaré pointed out that the combination <math>x^2+ y^2+ z^2- c^2t^2</math> is [[Invariant (mathematics)|invariant]]. He noted that a Lorentz transformation is merely a rotation in four-dimensional space about the origin by introducing <math>ct\sqrt{-1}</math> as a fourth imaginary coordinate, and he used an early form of [[four-vector]]s.<ref name=long>{{Citation |
||
| author=Poincaré, H. | year=1906 | title= |
| author=Poincaré, H. | year=1906 | title=Sur la dynamique de l'électron (On the Dynamics of the Electron) | journal=Rendiconti del Circolo Matematico Rendiconti del Circolo di Palermo | volume =21 | pages =129–176 |
||
| doi=10.1007/BF03013466}} (Wikisource translation)</ref> |
| doi=10.1007/BF03013466| bibcode=1906RCMP...21..129P| hdl=2027/uiug.30112063899089 | s2cid=120211823 | url=https://zenodo.org/record/1428444| hdl-access=free }} (Wikisource translation)</ref> Poincaré expressed a lack of interest in a four-dimensional reformulation of his new mechanics in 1907, because in his opinion the translation of physics into the language of four-dimensional geometry would entail too much effort for limited profit.<ref name="Genesis 4-Vectors">{{cite book | last=Walter | first=Scott | title=The Genesis of General Relativity | chapter=Breaking in the 4-Vectors: The Four-Dimensional Movement in Gravitation, 1905–1910 |volume=3| publisher=Springer Netherlands |publication-place=Dordrecht | date=2007 | isbn=978-1-4020-3999-7 | doi=10.1007/978-1-4020-4000-9_18 | pages=1118–1178}}</ref> So it was [[Hermann Minkowski]] who worked out the consequences of this notion in 1907.<ref name="Genesis 4-Vectors"/><ref name="Raum und Zeit">{{cite journal | last = Minkowski | first = Hermann | date = September 1908 | title = Raum und Zeit | url = https://math.nyu.edu/~tschinke/papers/yuri/14minkowski/raum-und-zeit.pdf | journal = Jahresbericht der Deutschen Mathematiker-Vereinigung | volume = 18 | pages = 75–88 | access-date=11 May 2024 }}</ref> |
||
====Mass–energy relation==== |
====Mass–energy relation==== |
||
Like [[Mass–energy equivalence#Electromagnetic |
Like [[Mass–energy equivalence#Electromagnetic mass|others]] before, Poincaré (1900) discovered a relation between [[mass]] and [[electromagnetic energy]]. While studying the conflict between the [[Newton's laws of motion|action/reaction principle]] and [[Lorentz ether theory]], he tried to determine whether the [[center of gravity]] still moves with a uniform velocity when electromagnetic fields are included.<ref name=action /> He noticed that the action/reaction principle does not hold for matter alone, but that the electromagnetic field has its own momentum. Poincaré concluded that the electromagnetic field energy of an electromagnetic wave behaves like a fictitious [[fluid]] (''fluide fictif'') with a mass density of ''E''/''c''<sup>2</sup>. If the [[center of mass frame]] is defined by both the mass of matter ''and'' the mass of the fictitious fluid, and if the fictitious fluid is indestructible—[[First law of thermodynamics|it's neither created or destroyed]]—then the motion of the center of mass frame remains uniform. But electromagnetic energy can be converted into other forms of energy. So Poincaré assumed that there exists a non-electric energy fluid at each point of space, into which electromagnetic energy can be transformed and which also carries a mass proportional to the energy. In this way, the motion of the center of mass remains uniform. Poincaré said that one should not be too surprised by these assumptions, since they are only mathematical fictions. |
||
However, Poincaré's resolution led to a paradox when changing frames: if a Hertzian oscillator radiates in a certain direction, it will suffer a [[recoil]] from the inertia of the fictitious fluid. Poincaré performed a [[Lorentz boost]] (to order ''v''/''c'') to the frame of the moving source. He noted that energy conservation holds in both frames, but that the law of conservation of momentum is violated. This would allow [[perpetual motion]], a notion which he abhorred. The laws of nature would have to be different in the frames of reference, and the relativity principle would not hold. Therefore he argued that also in this case there has to be another compensating mechanism in the ether. |
However, Poincaré's resolution led to a [[paradox]] when changing frames: if a Hertzian oscillator radiates in a certain direction, it will suffer a [[recoil]] from the inertia of the fictitious fluid. Poincaré performed a [[Lorentz boost]] (to order ''v''/''c'') to the frame of the moving source. He noted that energy conservation holds in both frames, but that the [[Momentum#Conservation|law of conservation of momentum]] is violated. This would allow [[perpetual motion]], a notion which he abhorred. The laws of nature would have to be different in the [[frames of reference]], and the relativity principle would not hold. Therefore, he argued that also in this case there has to be another compensating mechanism in the [[ether]]. |
||
Poincaré himself came back to this topic in his St. Louis lecture (1904).<ref name=louis /> |
Poincaré himself came back to this topic in his St. Louis lecture (1904).<ref name=louis /> He rejected<ref>Miller 1981, Secondary sources on relativity</ref> the possibility that energy carries mass and criticized his own solution to compensate the above-mentioned problems: |
||
{{ |
{{blockquote|The apparatus will recoil as if it were a cannon and the projected energy a ball, and that contradicts the principle of Newton, since our present projectile has no mass; it is not matter, it is energy. [..] Shall we say that the space which separates the oscillator from the receiver and which the disturbance must traverse in passing from one to the other, is not empty, but is filled not only with ether, but with air, or even in inter-planetary space with some subtile, yet ponderable fluid; that this matter receives the shock, as does the receiver, at the moment the energy reaches it, and recoils, when the disturbance leaves it? That would save Newton's principle, but it is not true. If the energy during its propagation remained always attached to some material substratum, this matter would carry the light along with it and Fizeau has shown, at least for the air, that there is nothing of the kind. Michelson and Morley have since confirmed this. We might also suppose that the motions of matter proper were exactly compensated by those of the ether; but that would lead us to the same considerations as those made a moment ago. The principle, if thus interpreted, could explain anything, since whatever the visible motions we could imagine hypothetical motions to compensate them. But if it can explain anything, it will allow us to foretell nothing; it will not allow us to choose between the various possible hypotheses, since it explains everything in advance. It therefore becomes useless. }} |
||
In the above quote he refers to the Hertz assumption of total aether entrainment that was falsified by the [[Fizeau experiment]] but that experiment does indeed show that that light is partially "carried along" with a substance. Finally in 1908<ref name=poinc08>{{cite book |
|||
He also discussed two other unexplained effects: (1) non-conservation of mass implied by Lorentz's variable mass <math>\gamma m</math>, Abraham's theory of variable mass and [[Walter Kaufmann (physicist)|Kaufmann]]'s experiments on the mass of fast moving electrons and (2) the non-conservation of energy in the radium experiments of [[Madame Curie]]. |
|||
|author=Poincaré, Henri |
|||
|year=1908–1913 |
|||
|title=The foundations of science (Science and Method) |
|||
|chapter=[[s:The New Mechanics|The New Mechanics]] |
|||
|location=New York |publisher=Science Press |
|||
|pages=486–522}}</ref> he revisits the problem and ends with abandoning the principle of reaction altogether in favor of supporting a solution based in the inertia of aether itself. |
|||
{{blockquote|But we have seen above that Fizeau's experiment does not permit of our retaining the theory of Hertz; it is necessary therefore to adopt the theory of Lorentz, and consequently to renounce the principle of reaction. }} |
|||
It was [[Albert Einstein]]'s concept of [[mass–energy equivalence]] (1905) that a body losing energy as radiation or heat was losing mass of amount ''m'' = ''E''/''c''<sup>2</sup> that resolved<ref name=darrigol>Darrigol 2005, Secondary sources on relativity</ref> Poincare's paradox, without using any compensating mechanism within the ether.<ref>{{Citation | author=Einstein, A. | year=1905b | title=[http://www.physik.uni-augsburg.de/annalen/history/papers/1905_18_639-641.pdf Ist die Trägheit eines Körpers von dessen Energieinhalt abhängig?] | journal=Annalen der Physik | volume =18 | pages =639–643}}. See also [http://www.fourmilab.ch/etexts/einstein/specrel/www English translation].</ref> The Hertzian oscillator loses mass in the emission process, and momentum is conserved in any frame. However, concerning Poincaré's solution of the Center of Gravity problem, Einstein noted that Poincaré's formulation and his own from 1906 were mathematically equivalent.<ref>{{Citation | author=Einstein, A. | year=1906 | title=[http://www.physik.uni-augsburg.de/annalen/history/papers/1906_20_627-633.pdf Das Prinzip von der Erhaltung der Schwerpunktsbewegung und die Trägheit der Energie] | journal=Annalen der Physik | volume =20 | pages =627–633 | doi=10.1002/andp.19063250814}}</ref> |
|||
He also discussed two other unexplained effects: (1) non-conservation of mass implied by Lorentz's variable mass <math>\gamma m</math>, Abraham's theory of variable mass and [[Walter Kaufmann (physicist)|Kaufmann]]'s experiments on the mass of fast moving electrons and (2) the non-conservation of energy in the radium experiments of [[Marie Curie]]. |
|||
It was [[Albert Einstein]]'s concept of [[mass–energy equivalence]] (1905) that a body losing energy as radiation or heat was losing mass of amount ''m'' = ''E''/''c''<sup>2</sup> that resolved<ref name=darrigol>Darrigol 2005, Secondary sources on relativity</ref> Poincaré's paradox, without using any compensating mechanism within the ether.<ref>{{Citation|author=Einstein, A. |year=1905b |title=Ist die Trägheit eines Körpers von dessen Energieinhalt abhängig? |journal=Annalen der Physik |volume=18 |issue=13 |pages=639–643 |bibcode=1905AnP...323..639E |doi= 10.1002/andp.19053231314 |doi-access=free }}. See also [http://www.fourmilab.ch/etexts/einstein/specrel/www English translation].</ref> The Hertzian oscillator loses mass in the emission process, and momentum is conserved in any frame. However, concerning Poincaré's solution of the Center of Gravity problem, Einstein noted that Poincaré's formulation and his own from 1906 were mathematically equivalent.<ref>{{Citation|author=Einstein, A. |year=1906 |title=Das Prinzip von der Erhaltung der Schwerpunktsbewegung und die Trägheit der Energie |journal=Annalen der Physik |volume=20 |pages=627–633 |doi=10.1002/andp.19063250814 |issue=8 |bibcode=1906AnP...325..627E |s2cid=120361282 |url= http://www.physik.uni-augsburg.de/annalen/history/papers/1906_20_627-633.pdf |archive-url=https://web.archive.org/web/20060318060830/http://www.physik.uni-augsburg.de/annalen/history/papers/1906_20_627-633.pdf |url-status=dead |archive-date=18 March 2006}}</ref> |
|||
====Gravitational waves==== |
|||
In 1905 Poincaré first proposed [[gravitational waves]] (''ondes gravifiques'') emanating from a body and propagating at the speed of light. He wrote: |
|||
{{blockquote|It has become important to examine this hypothesis more closely and in particular to ask in what ways it would require us to modify the laws of gravitation. That is what I have tried to determine; at first I was led to assume that the propagation of gravitation is not instantaneous, but happens with the speed of light.<ref>"''Il importait d'examiner cette hypothèse de plus près et en particulier de rechercher quelles modifications elle nous obligerait à apporter aux lois de la gravitation. C'est ce que j'ai cherché à déterminer; j'ai été d'abord conduit à supposer que la propagation de la gravitation n'est pas instantanée, mais se fait avec la vitesse de la lumière.''"</ref><ref name="1905 paper" />}} |
|||
====Poincaré and Einstein==== |
====Poincaré and Einstein==== |
||
Einstein's first paper on relativity was published three months after Poincaré's short paper,<ref name= |
Einstein's first paper on relativity was published three months after Poincaré's short paper,<ref name="1905 paper" /> but before Poincaré's longer version.<ref name=long /> Einstein relied on the principle of relativity to derive the Lorentz transformations and used a similar clock synchronisation procedure ([[Einstein synchronisation]]) to the one that Poincaré (1900) had described, but Einstein's paper was remarkable in that it contained no references at all. Poincaré never acknowledged Einstein's work on [[special relativity]]. However, Einstein expressed sympathy with Poincaré's outlook obliquely in a letter to [[Hans Vaihinger]] on 3 May 1919, when Einstein considered Vaihinger's general outlook to be close to his own and Poincaré's to be close to Vaihinger's.<ref>{{cite book|series=The Collected Papers of Albert Einstein |url=http://einsteinpapers.press.princeton.edu/vol9-trans/52 |publisher=Princeton U.P. |volume = 9|title = The Berlin Years: Correspondence, January 1919 – April 1920 (English translation supplement)|page = 30}} See also this letter, with commentary, in {{cite journal |last=Sass |first=Hans-Martin | author-link = Hans-Martin Sass|date=1979 |title=Einstein über "wahre Kultur" und die Stellung der Geometrie im Wissenschaftssystem: Ein Brief Albert Einsteins an Hans Vaihinger vom Jahre 1919 |journal=[[Zeitschrift für allgemeine Wissenschaftstheorie]] |volume=10 |issue=2 |pages=316–319 |jstor=25170513 |language=de |doi=10.1007/bf01802352|s2cid=170178963 }}</ref> In public, Einstein acknowledged Poincaré posthumously in the text of a lecture in 1921 titled "''Geometrie und Erfahrung'' (Geometry and Experience)" in connection with [[non-Euclidean geometry]], but not in connection with special relativity. A few years before his death, Einstein commented on Poincaré as being one of the pioneers of relativity, saying "Lorentz had already recognized that the transformation named after him is essential for the analysis of Maxwell's equations, and Poincaré deepened this insight still further ....".<ref>Darrigol 2004, Secondary sources on relativity</ref> |
||
====Assessments==== |
====Assessments on Poincaré and relativity==== |
||
{{ |
{{Further|History of special relativity|Relativity priority dispute}} |
||
Poincaré's work in the development of special relativity is well recognised,<ref name=darrigol /> though most historians stress that despite many similarities with Einstein's work, the two had very different research agendas and interpretations of the work.<ref>Galison 2003 and Kragh 1999, Secondary sources on relativity</ref> Poincaré developed a similar physical interpretation of local time and noticed the connection to signal velocity, but contrary to Einstein he continued to use the ether-concept in his papers and argued that clocks in the ether show the "true" time, and moving clocks show the local time. So Poincaré tried to keep the relativity principle in accordance with classical concepts, while Einstein developed a mathematically equivalent kinematics based on the new physical concepts of the relativity of space and time.<ref>Holton (1988), 196–206</ref><ref>Hentschel |
Poincaré's work in the development of special relativity is well recognised,<ref name=darrigol /> though most historians stress that despite many similarities with Einstein's work, the two had very different research agendas and interpretations of the work.<ref>Galison 2003 and Kragh 1999, Secondary sources on relativity</ref> Poincaré developed a similar physical interpretation of local time and noticed the connection to signal velocity, but contrary to Einstein he continued to use the ether-concept in his papers and argued that clocks at rest in the ether show the "true" time, and moving clocks show the local time. So Poincaré tried to keep the relativity principle in accordance with classical concepts, while Einstein developed a mathematically equivalent kinematics based on the new physical concepts of the relativity of space and time.<ref>Holton (1988), 196–206</ref><ref name="Hentschel PhD">{{cite thesis |last=Hentschel|first=Klaus |date=1990 |title=Interpretationen und Fehlinterpretationen der speziellen und der allgemeinen Relativitätstheorie durch Zeitgenossen Albert Einsteins |degree=PhD |publisher=University of Hamburg|pages=3–13}}</ref><ref>Miller (1981), 216–217</ref><ref>Darrigol (2005), 15–18</ref><ref>Katzir (2005), 286–288</ref> |
||
While this is the view of most historians, a minority go much further, such as [[E. T. Whittaker]], who held that Poincaré and Lorentz were the true discoverers of relativity.<ref>Whittaker 1953, Secondary sources on relativity</ref> |
|||
==Character== |
|||
[[File:Henri Poincaré by H Manuel.jpg|thumb|right|Photographic portrait of H. Poincaré by Henri Manuel]] |
|||
Poincaré's work habits have been compared to a bee flying from flower to flower. Poincaré was interested in the way his mind worked; he studied his habits and gave a talk about his observations in 1908 at the Institute of General Psychology in Paris. He linked his way of thinking to how he made several discoveries. |
|||
===Algebra and number theory=== |
|||
The mathematician Darboux claimed he was ''un intuitif'' (intuitive), arguing that this is demonstrated by the fact that he worked so often by visual representation. He did not care about being rigorous and disliked logic. He believed that logic was not a way to invent but a way to structure ideas and that logic limits ideas. |
|||
Poincaré introduced [[group theory]] to physics, and was the first to study the group of [[Lorentz transformations]].<ref>Poincaré, Selected works in three volumes. page = 682{{full citation needed|date=September 2019}}</ref><ref name="Poincaré Lorentz l’´electron"> {{cite journal | last = Poincaré | first = Henri | date = 1905 | title = Sur la dynamique de l'électron | journal = Comptes rendus des séances de l'Académie des Sciences | volume = 140 | pages = 1504–1508 }}</ref> He also made major contributions to the theory of discrete groups and their representations. |
|||
[[Image:Mug and Torus morph.gif|{{center|Topological transformation of a mug into a torus }}|thumb|190x190px]] |
|||
[[File:Poincaré-7.jpg|alt=Title page to volume I of Les Méthodes Nouvelles de la Mécanique Céleste (1892)|thumb|192x192px|Title page to volume I of ''Les Méthodes Nouvelles de la Mécanique Céleste'' (1892)]] |
|||
===Topology=== |
|||
===Toulouse' characterisation === |
|||
The subject is clearly defined by [[Felix Klein]] in his "Erlangen Program" (1872): the geometry invariants of arbitrary continuous transformation, a kind of geometry. The term "topology" was introduced, as suggested by [[Johann Benedict Listing]], instead of previously used "Analysis situs". Some important concepts were introduced by [[Enrico Betti]] and [[Bernhard Riemann]]. But the foundation of this science, for a space of any dimension, was created by Poincaré. His first article on this topic appeared in 1894.{{sfn|Stillwell|2010|pp=419–435}} |
|||
Poincaré's mental organisation was not only interesting to Poincaré himself but also to Toulouse, a psychologist of the Psychology Laboratory of the School of Higher Studies in Paris. Toulouse wrote a book entitled ''Henri Poincaré'' (1910).<ref>Toulouse, E.,1910. Henri Poincaré</ref> In it, he discussed Poincaré's regular schedule: |
|||
His research in [[geometry]] led to the abstract topological definition of [[homotopy]] and [[Homology (mathematics)|homology]]. He also first introduced the basic concepts and invariants of combinatorial topology, such as [[Betti number]]s and the [[fundamental group]]. Poincaré proved a formula relating the number of edges, [[Triangulated irregular network|vertices]] and faces of ''n''-dimensional [[polyhedron]] (the [[Euler characteristic|Euler–Poincaré theorem]]) and gave the first precise formulation of the intuitive notion of dimension.<ref name="Aleksandrov Poincaré ">{{cite journal | last=Aleksandrov | first=P S | title=Poincaré and topology | journal=Russian Mathematical Surveys | volume=27 | issue=1 | date=28 February 1972 | issn=0036-0279 | doi=10.1070/RM1972v027n01ABEH001365 | pages=157–168}}</ref> |
|||
* He worked during the same times each day in short periods of time. He undertook mathematical research for four hours a day, between 10 a.m. and noon then again from 5 p.m. to 7 p.m.. He would read articles in journals later in the evening. |
|||
===Astronomy and celestial mechanics=== |
|||
* His normal work habit was to solve a problem completely in his head, then commit the completed problem to paper. |
|||
[[File:N-body problem (3).gif|frame|left|{{center| Chaotic motion in three-body problem (computer simulation)}}]] |
|||
Poincaré published two now classical monographs, "New Methods of Celestial Mechanics" (1892–1899) and "Lectures on Celestial Mechanics" (1905–1910). In them, he successfully applied the results of their research to the problem of the motion of three bodies and studied in detail the behavior of solutions (frequency, stability, asymptotic, and so on). They introduced the small parameter method, fixed points, integral invariants, variational equations, the convergence of the asymptotic expansions. Generalizing a theory of Bruns (1887), Poincaré showed that the three-body problem is not integrable. In other words, the general solution of the three-body problem can not be expressed in terms of [[algebra]]ic and [[transcendental functions]] through unambiguous coordinates and velocities of the bodies. His work in this area was the first major achievement in celestial mechanics since [[Isaac Newton]].<ref>J. Stillwell, Mathematics and its history, [https://books.google.com/books?id=V7mxZqjs5yUC&pg=PA254 p. 254]</ref> |
|||
These monographs include an idea of Poincaré, which later became the basis for mathematical "[[chaos theory]]" (see, in particular, the [[Poincaré recurrence theorem]]) and the general theory of [[dynamical system]]s. |
|||
Poincaré authored important works on [[astronomy]] for the [[Hydrostatic equilibrium|equilibrium figures of a gravitating rotating fluid]]. He introduced the important concept of [[Bifurcation theory|bifurcation points]] and proved the existence of equilibrium figures such as the non-ellipsoids, including ring-shaped and pear-shaped figures, and their stability. For this discovery, Poincaré received the Gold Medal of the Royal Astronomical Society (1900).<ref name="Gold Medal to Poincaré ">{{cite journal |author-last=Darwin | author-first=G.H.| title=Address Delivered by the President, Professor G. H. Darwin, on presenting the Gold Medal of the Society to M. H. Poincaré | journal=Monthly Notices of the Royal Astronomical Society | volume=60 | issue=5 | date=1900 | issn=0035-8711 | doi=10.1093/mnras/60.5.406 | pages=406–416| doi-access=free}}</ref> |
|||
===Differential equations and mathematical physics=== |
|||
After defending his doctoral thesis on the study of singular points of the system of [[differential equations]], Poincaré wrote a series of memoirs under the title "On curves defined by differential equations" (1881–1882).<ref>French: "Mémoire sur les courbes définies par une équation différentielle"</ref> In these articles, he built a new branch of mathematics, called "[[qualitative theory of differential equations]]". Poincaré showed that even if the differential equation can not be solved in terms of known functions, yet from the very form of the equation, a wealth of information about the properties and behavior of the solutions can be found. In particular, Poincaré investigated the nature of the trajectories of the integral curves in the plane, gave a classification of singular points ([[Saddle point|saddle]], [[Focus (geometry)|focus]], [[Center (algebra)|center]], [[Vertex (graph theory)|node]]), introduced the concept of a [[limit cycle]] and the [[Control flow#Loop system cross-reference table|loop index]], and showed that the number of limit cycles is always finite, except for some special cases. Poincaré also developed a general theory of integral invariants and solutions of the variational equations. For the [[Finite difference|finite-difference equations]], he created a new direction – the [[asymptotic]] analysis of the solutions. He applied all these achievements to study practical problems of [[mathematical physics]] and [[celestial mechanics]], and the methods used were the basis of its topological works.<ref>{{cite book|editor1-last=Kolmogorov|editor1-first = A.N.|editor2-first = A.P.|editor2-last= Yushkevich|title = Mathematics of the 19th century |volume= 3| pages = 162–174, 283|isbn= 978-3764358457|date = 24 March 1998| publisher=Springer }}</ref> |
|||
<gallery caption="The singular points of the integral curves"> |
|||
File: Phase Portrait Sadle.svg | Saddle |
|||
File: Phase Portrait Stable Focus.svg | Focus |
|||
File: Phase portrait center.svg | Center |
|||
File: Phase Portrait Stable Node.svg | Node |
|||
</gallery> |
|||
==Character== |
|||
[[File:Henri Poincaré by H Manuel.jpg|thumb|right|Photographic portrait of H. Poincaré by Henri Manuel]] |
|||
Poincaré's work habits have been compared to a [[bee]] flying from flower to flower. Poincaré was interested in the way his [[mind]] worked; he studied his habits and gave a talk about his observations in 1908 at the Institute of General Psychology in [[Paris]]. He linked his way of [[Thought|thinking]] to how he made several discoveries. |
|||
The mathematician [[Jean Gaston Darboux|Darboux]] claimed he was ''un intuitif'' (an [[intuitive]]), arguing that this is demonstrated by the fact that he worked so often by visual representation. [[Jacques Hadamard]] wrote that Poincaré's research demonstrated marvelous clarity<ref>J. Hadamard. L'oeuvre de H. Poincaré. Acta Mathematica, 38 (1921), p. 208</ref> and Poincaré himself wrote that he <!-- TODO: Add Poincaré's opinion on rigorousness, see http://www.forgottenbooks.org/readbook/American_Journal_of_Mathematics_1890_v12_1000084889#233 — Each time I can I'm absolute rigour --> believed that logic was not a way to invent but a way to structure ideas and that logic limits ideas. |
|||
* He was ambidextrous and nearsighted. |
|||
===Toulouse's characterisation=== |
|||
Poincaré's mental organisation was interesting not only to Poincaré himself but also to [[Édouard Toulouse]], a [[psychologist]] of the Psychology Laboratory of the School of Higher Studies in Paris. Toulouse wrote a book entitled ''Henri Poincaré'' (1910).<ref>{{cite book| url = http://name.umdl.umich.edu/AAS9989.0001.001| title = Toulouse, Édouard, 1910. ''Henri Poincaré'', E. Flammarion, Paris| year = 2005}}</ref><ref name="google">{{cite book|title=Henri Poincare|author=Toulouse, E.|date=2013|publisher=MPublishing|isbn=9781418165062|url=https://books.google.com/books?id=mpjWPQAACAAJ|access-date=10 October 2014}}</ref> In it, he discussed Poincaré's regular schedule: |
|||
* He worked during the same times each day in short periods of time. He undertook mathematical research for four hours a day, between 10 a.m. and noon then again from 5 p.m. to 7 p.m.. He would read articles in journals later in the evening. |
|||
* His normal work habit was to solve a problem completely in his head, then commit the completed problem to paper. |
|||
* He was [[ambidextrous]] and [[nearsighted]]. |
|||
* His ability to visualise what he heard proved particularly useful when he attended lectures, since his eyesight was so poor that he could not see properly what the lecturer wrote on the blackboard. |
* His ability to visualise what he heard proved particularly useful when he attended lectures, since his eyesight was so poor that he could not see properly what the lecturer wrote on the blackboard. |
||
These abilities were offset to some extent by his shortcomings: |
These abilities were offset to some extent by his shortcomings: |
||
* He was physically clumsy and [[art]]istically inept. |
|||
* He was physically clumsy and artistically inept. |
|||
* He was always in a rush and disliked going back for changes or corrections. |
* He was always in a rush and disliked going back for changes or corrections. |
||
* He never spent a long time on a problem since he believed that the [[subconscious]] would continue working on the problem [[Human multitasking|while he consciously worked on another problem]]. |
|||
* He never spent a long time on a problem since he believed that the subconscious would continue working on the problem while he consciously worked on another problem. |
|||
In addition, Toulouse stated that most mathematicians worked from principles already established while Poincaré started from basic principles each time (O'Connor et al., 2002). |
In addition, Toulouse stated that most mathematicians worked from principles already established while Poincaré started from basic principles each time (O'Connor et al., 2002). |
||
| Line 218: | Line 305: | ||
His method of thinking is well summarised as: |
His method of thinking is well summarised as: |
||
{{blockquote|text=''Habitué à négliger les détails et à ne regarder que les cimes, il passait de l'une à l'autre avec une promptitude surprenante et les faits qu'il découvrait se groupant d'eux-mêmes autour de leur centre étaient instantanément et automatiquement classés dans sa mémoire'' (accustomed to neglecting details and to looking only at mountain tops, he went from one peak to another with surprising rapidity, and the facts he discovered, clustering around their center, were instantly and automatically pigeonholed in his memory).|sign=Belliver (1956)}} |
|||
== Publications == |
|||
* {{Cite book|title=Leçons sur la théorie mathématique de la lumière|volume=|publisher=Carrè|location=Paris|year=1889|language=fr|url=https://gutenberg.beic.it/webclient/DeliveryManager?pid=6569792}} |
|||
* {{Cite book|title=Solutions periodiques, non-existence des integrales uniformes, solutions asymptotiques|volume=1|publisher=Gauthier-Villars|location=Paris|year=1892|language=fr|url=https://gutenberg.beic.it/webclient/DeliveryManager?pid=10996590}} |
|||
* {{Cite book|title=Methodes de mm. Newcomb, Gylden, Lindstedt et Bohlin|volume=2|publisher=Gauthier-Villars|location=Paris|year=1893|language=fr|url=https://gutenberg.beic.it/webclient/DeliveryManager?pid=10997817}} |
|||
* {{Cite book|title=Oscillations électriques|volume=|publisher=Carrè|location=Paris|year=1894|language=fr|url=https://gutenberg.beic.it/webclient/DeliveryManager?pid=6571067}} |
|||
* {{Cite book|title=Invariants integraux, solutions periodiques du deuxieme genre, solutions doublement asymptotiques|volume=3|publisher=Gauthier-Villars|location=Paris|year=1899|language=fr|url=https://gutenberg.beic.it/webclient/DeliveryManager?pid=10999338}} |
|||
* {{Cite book|title=Valeur de la science|volume=|publisher=Flammarion|location=Paris|year=1900|language=fr|url=https://gutenberg.beic.it/webclient/DeliveryManager?pid=3901099}} |
|||
* {{Cite book|title=Electricité et optique|volume=|publisher=Carrè & Naud|location=Paris|year=1901|language=fr|url=https://gutenberg.beic.it/webclient/DeliveryManager?pid=7156481}} |
|||
* {{Cite book|title=Science et l'hypothèse|volume=|publisher=Flammarion|location=Paris|year=1902|language=fr|url=https://gutenberg.beic.it/webclient/DeliveryManager?pid=3901686}} |
|||
* {{Cite book|title=Thermodynamique|volume=|publisher=Gauthier-Villars|location=Paris|year=1908|language=fr|url=https://gutenberg.beic.it/webclient/DeliveryManager?pid=6568325}} |
|||
* {{Cite book|title=Dernières pensées|volume=|publisher=Flammarion|location=Paris|year=1913|language=fr|url=https://gutenberg.beic.it/webclient/DeliveryManager?pid=3902281}} |
|||
* {{Cite book|title=Science et méthode|volume=|publisher=Nelson and Sons|location=London|year=1914|language=en|url=https://gutenberg.beic.it/webclient/DeliveryManager?pid=10947130}} |
|||
==Legacy== |
|||
Poincaré is credited with laying the foundations of [[special relativity]],<ref name=":3">{{Citation |last=Marchal |first=C. |title=Henri Poincaré: A Decisive Contribution to Special Relativity |date=1997 |work=The Dynamical Behaviour of our Planetary System |pages=403–413 |editor-last=Dvorak |editor-first=R. |url=http://link.springer.com/10.1007/978-94-011-5510-6_30 |access-date=2024-12-02 |place=Dordrecht |publisher=Springer Netherlands |language=en |doi=10.1007/978-94-011-5510-6_30 |isbn=978-94-010-6320-3 |editor2-last=Henrard |editor2-first=J.}}</ref><ref name=":1">{{Cite book |last=Ginoux |first=Jean-Marc |url=https://books.google.com/books?id=MI4CEQAAQBAJ&pg=PA47 |title=Poincaré, Einstein and the Discovery of Special Relativity: An End to the Controversy |date=2024 |publisher=Springer |isbn=978-3-031-51386-2 |series=History of Physics |location= |pages=47 |language=en}}</ref> with some [[Relativity priority dispute|arguing]] that he should be credited with its creation.<ref>{{Citation |last=Logunov |first=A. A. |title=Henri Poincare and Relativity Theory |date=2004 |pages=3, 63, 187 |arxiv=physics/0408077 |author-link=Anatoly Logunov}}</ref> He is said to have "dominated the mathematics and the theoretical physics of his time", and that "he was without a doubt the most admired [[mathematician]] while he was alive, and he remains today one of the world's most emblematic scientific figures."<ref name=":2">{{Cite book |url=https://books.google.com/books?id=9F7bY_ltzxIC&pg=PA1 |title=The Scientific Legacy of Poincaré |date=2010 |publisher=The London Mathematical Society |isbn=978-0-8218-4718-3 |editor-last=Charpentier |editor-first=Éric |series=History of Mathematics |location= |pages=1–2 |language=en |translator-last=Bowman |translator-first=Joshua |editor-last2=Ghys |editor-first2=E. |editor-last3=Lesne |editor-first3=Annick}}</ref> Poincaré is regarded as a "universal specialist", as he refined [[celestial mechanics]], he progressed nearly all parts of mathematics of his time, including creating new subjects, is a father of special relativity, participated in all the great debates of his time in physics, was a major actor in the great [[Epistemology|epistemological]] debates of his day in relation to [[philosophy of science]], and Poincaré was the one who investigated the 1879 [[Magny shaft]] firedamp explosion as an engineer.<ref name=":2" /> Due to the breadth of his research, Poincaré was the only member to be elected to every section of the [[French Academy of Sciences]] of the time, those being geometry, mechanics, physics, astronomy and navigation.<ref>{{Cite book |last=Krantz |first=Steven G. |url=https://books.google.com/books?id=ulmAH-6IzNoC&pg=PA291 |title=An Episodic History of Mathematics: Mathematical Culture Through Problem Solving |date=2010 |publisher=Mathematical Association of America |isbn=978-0-88385-766-3 |series= |location=Washington, DC |pages=291 |language=en |oclc=501976977}}</ref> |
|||
Physicist [[Henri Becquerel]] nominated Poincaré for a [[Nobel Prize]] in 1904, as Becquerel took note that "Poincaré's mathematical and philosophical genius surveyed all of physics and was among those that contributed most to human progress by giving researchers a solid basis for their journeys into the unknown."<ref>{{Cite book |last=Gray |first=Jeremy |title=Henri Poincaré: A Scientific Biography |date=2013 |publisher=[[Princeton University Press]] |isbn=978-0-691-15271-4 |location= |pages=195 |language=en}}</ref> After his death, he was praised by many intellectual figures of his time, as the author [[Marie Bonaparte]] wrote to his widowed wife Louise that "He was – as you know better than anyone – not only the greatest thinker, the most powerful genius of our time – but also a deep and incomparable heart; and having been close to him remains the precious memory of a whole life."<ref>{{Cite journal |last=Rollet |first=Laurent |date=2023-06-19 |title="My sincere condolences" |url=https://euromathsoc.org/magazine/articles/141 |journal=European Mathematical Society Magazine |issue=128 |pages=41–50 |doi=10.4171/mag/141 |issn=2747-7894|doi-access=free }}</ref> |
|||
Mathematician [[Eric Temple Bell|E.T. Bell]] titled Poincaré as "The Last Universalist", and noted his prowess in many fields, stating that:<ref name=":0">{{Cite book |last=Bell |first=E.T. |author-link=Eric Temple Bell |title=Men of Mathematics |publisher=[[Penguin Books]] |year=1937 |volume=II |pages=581, 584 |language=en}}</ref> |
|||
{{blockquote|Poincaré was the last man to take practically all mathematics, both pure and applied, as his province . . . few mathematicians have had the breadth of philosophical vision that Poincaré had and none is his superior in the gift of clear exposition.}} |
|||
When philosopher and mathematician [[Bertrand Russell]] was asked who was the greatest man that [[France]] had produced in modern times, he instantly replied "Poincaré".<ref name=":0" /> Bell noted that if Poincaré had been as strong in practical science as he was in theoretical, he might have "made a fourth with the incomparable three, [[Archimedes]], [[Isaac Newton|Newton]], and [[Carl Friedrich Gauss|Gauss]]."<ref name=":02" /> |
|||
Bell further noted his powerful memory, one that was even superior to [[Leonhard Euler]]'s, stating that:<ref name=":02">{{Cite book |last=Bell |first=E.T. |author-link=Eric Temple Bell |title=Men of Mathematics |publisher=[[Penguin Books]] |year=1937 |volume=II |pages=587 |language=en}}</ref> |
|||
{{blockquote|His principal diversion was reading, where his unusual talents first showed up. A book once read - at incredible speed - became a permanent possession, and he could always state the page and line where a particular thing occurred. He retained this powerful memory all his life. This rare faculty, which Poincaré shared with Euler who had it in a lesser degree, might be called visual or spatial memory. In temporal memory - the ability to recall with uncanny precision a sequence of events long passed — he was also unusually strong.}} |
|||
===Attitude towards transfinite numbers=== |
|||
Poincaré was dismayed by [[Georg Cantor]]'s theory of [[transfinite number]]s, and referred to it as a "disease" from which mathematics would eventually be cured.<ref name="daub266">Dauben 1979, p. 266.</ref> |
|||
Poincare said, "There is no actual infinite; the Cantorians have forgotten this, and that is why they have fallen into contradiction."<ref>{{citation |
|||
|title=From Frege to Gödel: a source book in mathematical logic, 1879–1931 |
|||
|first1=Jean |
|||
|last1=Van Heijenoort |
|||
|publisher=Harvard University Press |
|||
|year=1967 |
|||
|isbn=0674324498 |
|||
|page=190 |
|||
|url=http://books.google.com/?id=v4tBTBlU05sC&pg=PA190}}, [http://books.google.com/books?id=v4tBTBlU05sC&pg=PA190 p 190] |
|||
</ref> |
|||
Bell notes the terrible eyesight of Poincaré, he almost completely remembered formulas and theorems by ear, and "unable to see the board distinctly when he became a student of advanced mathematics, he sat back and listened, following and remembering perfectly without taking notes - an easy feat for him, but one incomprehensible to most mathematicians."<ref name=":02" /> |
|||
===View on economics=== |
|||
Poincaré saw mathematical work in [[economics]] and finance as peripheral. In 1900 Poincaré commented on [[Louis Bachelier]]'s thesis "The Theory of Speculation", saying: "M. Bachelier has evidenced an original and precise mind [but] the subject is somewhat remote from those our other candidates are in the habit of treating." (Bernstein, 1996, pp. 199–200) Bachelier's work explained what was then the French government's pricing options on French Bonds and anticipated many of the pricing theories in financial markets used today.<ref>{{Citation |title= Inventing money |last= Dunbar|first= Nicholas|authorlink= Nicholas Dunbar|publisher= JOHN WILEY & SONS, LTD|isbn= 0-471-49811-4 |year= 2000}}</ref> |
|||
==Honours== |
==Honours== |
||
'''Awards''' |
'''Awards''' |
||
*Oscar II, King of Sweden's mathematical competition (1887) |
*Oscar II, King of Sweden's mathematical competition (1887) |
||
*Foreign member of the [[Royal Netherlands Academy of Arts and Sciences]] (1897)<ref>{{cite web |url=http://www.dwc.knaw.nl/biografie/pmknaw/?pagetype=authorDetail&aId=PE00002358 |title=Jules Henri Poincaré (1854–1912) |publisher=Royal Netherlands Academy of Arts and Sciences |access-date=4 August 2015 |archive-url=https://web.archive.org/web/20150905152142/http://www.dwc.knaw.nl/biografie/pmknaw/?pagetype=authorDetail&aId=PE00002358 |archive-date=5 September 2015 |url-status=dead }}</ref> |
|||
*[[American Philosophical Society]] 1899 |
|||
*[[American Philosophical Society]] (1899) |
|||
*[[Gold Medal of the Royal Astronomical Society]] of London (1900) |
*[[Gold Medal of the Royal Astronomical Society]] of London (1900) |
||
*Commander of the [[Legion of Honour]] (1903)<ref>{{cite book |last1=Ginoux |first1=J. M. |url=https://books.google.com/books?id=Xka7CgAAQBAJ&pg=PA59 |title=Henri Poincaré: A Biography Through the Daily Papers |last2=Gerini |first2=C. |publisher=[[World Scientific]] |year=2013 |isbn=978-981-4556-61-3 |pages=59 |doi=10.1142/8956}}</ref> |
|||
*[[Bolyai Prize]] in 1905 |
|||
*[[ |
*[[Bolyai Prize]] (1905) |
||
*[[Matteucci Medal]] (1905) |
|||
*[[French Academy of Sciences]] 1906 |
|||
*[[French Academy of Sciences]] (1906) |
|||
*[[Académie Française]] 1909 |
|||
*[[Académie française]] (1909) |
|||
*[[Bruce Medal]] (1911) |
*[[Bruce Medal]] (1911) |
||
'''Named after him''' |
'''Named after him''' |
||
*[[Institut Henri Poincaré]] (mathematics and theoretical physics centre) |
|||
*[[Poincaré Prize]] (Mathematical Physics International Prize) |
*[[Poincaré Prize]] (Mathematical Physics International Prize) |
||
*[[Annales Henri Poincaré]] (Scientific Journal) |
*[[Annales Henri Poincaré]] (Scientific Journal) |
||
| Line 253: | Line 357: | ||
*The crater [[Poincaré (crater)|Poincaré]] on the Moon |
*The crater [[Poincaré (crater)|Poincaré]] on the Moon |
||
*[[Asteroid]] [[2021 Poincaré]] |
*[[Asteroid]] [[2021 Poincaré]] |
||
*[[List of things named after Henri Poincaré]] |
|||
Henri Poincaré did not receive the [[Nobel Prize in Physics]], but he had influential advocates like [[Henri Becquerel]] or committee member [[Gösta Mittag-Leffler]].<ref name="gray-biography">{{cite book|last1=Gray|first1=Jeremy|title=Henri Poincaré: A Scientific Biography|date=2013|publisher=Princeton University Press|pages=194–196|chapter=The Campaign for Poincaré}}</ref><ref>{{cite book|last1=Crawford|first1=Elizabeth|title=The Beginnings of the Nobel Institution: The Science Prizes, 1901–1915|year= 1987|publisher=Cambridge University Press|pages=141–142}}</ref> The nomination archive reveals that Poincaré received a total of 51 nominations between 1904 and 1912, the year of his death.<ref name="nomination database">{{cite web|title=Nomination database|url=https://www.nobelprize.org/nomination/archive/list.php|website=Nobelprize.org|publisher=Nobel Media AB|access-date=24 September 2015}}</ref> Of the 58 nominations for the 1910 Nobel Prize, 34 named Poincaré.<ref name="nomination database"/> Nominators included Nobel laureates [[Hendrik Lorentz]] and [[Pieter Zeeman]] (both of 1902), [[Marie Curie]] (of 1903), [[Albert Michelson]] (of 1907), [[Gabriel Lippmann]] (of 1908) and [[Guglielmo Marconi]] (of 1909).<ref name="nomination database"/> |
|||
The fact that renowned [[Theoretical physics|theoretical physicists]] like Poincaré, [[Ludwig Boltzmann|Boltzmann]] or [[Josiah Willard Gibbs|Gibbs]] were not awarded the [[Nobel Prize in Physics|Nobel Prize]] is seen as evidence that the Nobel committee had more regard for experimentation than theory.<ref>{{cite journal|last1=Crawford |first1= Elizabeth |title=Nobel: Always the Winners, Never the Losers|journal=[[Science (journal)|Science]]|date=13 November 1998|volume=282|issue=5392|pages=1256–1257|doi=10.1126/science.282.5392.1256|bibcode = 1998Sci...282.1256C |s2cid= 153619456 }}{{dead link|date=July 2016}}</ref><ref>{{cite journal|last1=Nastasi|first1=Pietro|title=A Nobel Prize for Poincaré? |journal=Lettera Matematica|date=16 May 2013|volume=1|issue=1–2|pages=79–82|doi=10.1007/s40329-013-0005-1 |doi-access=free}}</ref> In Poincaré's case, several of those who nominated him pointed out that the greatest problem was to name a specific discovery, invention, or technique.<ref name="gray-biography"/> |
|||
==Philosophy== |
==Philosophy== |
||
Poincaré had philosophical views opposite to those of [[Bertrand Russell]] and [[Gottlob Frege]], who believed that mathematics was a branch of [[logic]]. Poincaré strongly disagreed, claiming that [[intuition (knowledge)|intuition]] was the life of mathematics. Poincaré gives an interesting point of view in his book ''Science and Hypothesis'': |
[[File:Poincaré-16.jpg|alt=First page of Science and hypothesis (1905)|thumb|201x201px|First page of ''Science and hypothesis'' (1905)]] |
||
Poincaré had [[philosophical]] views opposite to those of [[Bertrand Russell]] and [[Gottlob Frege]], who believed that mathematics was a branch of [[logic]]. Poincaré strongly disagreed, claiming that [[intuition (knowledge)|intuition]] was the life of mathematics. Poincaré gives an interesting point of view in his 1902 book ''[[Science and Hypothesis]]'': |
|||
{{blockquote|text=For a superficial observer, scientific truth is beyond the possibility of doubt; the logic of science is infallible, and if the scientists are sometimes mistaken, this is only from their mistaking its rule.}} |
|||
Poincaré believed that [[arithmetic]] is |
Poincaré believed that [[arithmetic]] is [[Analytic/synthetic distinction|synthetic]]. He argued that [[Peano's axioms]] cannot be proven non-circularly with the [[Inductive reasoning|principle of induction]] (Murzi, 1998), therefore concluding that arithmetic is ''[[A priori and a posteriori|a priori]]'' [[Analytic–synthetic distinction|synthetic and not analytic]]. Poincaré then went on to say that mathematics cannot be deduced from logic since it is not analytic. His views were similar to those of [[Immanuel Kant]] (Kolak, 2001, Folina 1992). He strongly opposed [[Cantorian]] [[set theory]], objecting to its use of [[Impredicativity|impredicative]] definitions.<ref>{{Cite book |last=Folina |first=Janet |url=https://books.google.com/books?id=EPW-DAAAQBAJ&pg=PA145 |title=Poincaré and the Philosophy of Mathematics |date=1992 |publisher=Palgrave Macmillan UK |isbn=978-1-349-22121-9 |location=London |pages=145 |language=en |doi=10.1007/978-1-349-22119-6}}</ref> |
||
However, Poincaré did not share Kantian views in all branches of philosophy and mathematics. For example, in geometry, Poincaré believed that the structure of [[Non-Euclidean geometry|non-Euclidean space]] can be known analytically. Poincaré held that convention plays an important role in physics. His view (and some later, more extreme versions of it) came to be known as "[[conventionalism]]". Poincaré believed that [[Newton's first law]] was not empirical but is a conventional framework assumption for mechanics. He also believed that the geometry of physical space is conventional. He considered examples in which either the geometry of the physical fields or gradients of temperature can be changed, either describing a space as non-Euclidean measured by rigid rulers, or as a Euclidean space where the rulers are expanded or shrunk by a variable heat distribution. However, Poincaré thought that we were so accustomed to [[Euclidean geometry]] that we would prefer to change the physical laws to save Euclidean geometry rather than shift to |
However, Poincaré did not share [[Kantianism|Kantian views]] in all branches of philosophy and mathematics. For example, in geometry, Poincaré believed that the structure of [[Non-Euclidean geometry|non-Euclidean space]] can be known analytically. Poincaré held that convention plays an important role in physics. His view (and some later, more extreme versions of it) came to be known as "[[conventionalism]]".<ref>Yemima Ben-Menahem, ''Conventionalism: From Poincare to Quine'', Cambridge University Press, 2006, p. 39.</ref> Poincaré believed that [[Newton's first law]] was not empirical but is a conventional framework assumption for [[mechanics]] (Gargani, 2012).<ref>{{Citation|author=Gargani Julien|title=Poincaré, le hasard et l'étude des systèmes complexes|publisher=L'Harmattan|year=2012|page=124|url=http://www.editions-harmattan.fr/index.asp?navig=catalogue&obj=livre&no=38754|access-date=5 June 2015|archive-url=https://web.archive.org/web/20160304140554/http://www.editions-harmattan.fr/index.asp?navig=catalogue&obj=livre&no=38754|archive-date=4 March 2016|url-status=dead}}</ref> He also believed that the geometry of [[physical space]] is conventional. He considered examples in which either the geometry of the physical fields or [[gradients]] of temperature can be changed, either describing a space as non-Euclidean measured by rigid rulers, or as a [[Euclidean space]] where the rulers are expanded or shrunk by a [[Variable (mathematics)|variable]] heat distribution. However, Poincaré thought that we were so accustomed to [[Euclidean geometry]] that we would prefer to change the physical laws to save Euclidean geometry rather than shift to non-Euclidean physical geometry.<ref>{{Citation|title=Science and Hypothesis|first1=Henri |last1=Poincaré |publisher=Cosimo, Inc. Press|year=2007|isbn=978-1-60206-505-5 |page=50 |
||
|url=https://books.google.com/books?id=2QXqHaVbkgoC&pg=PA50}}</ref> |
|||
===Free will=== |
===Free will=== |
||
Poincaré's famous lectures before the Société de Psychologie in Paris (published as ''[[Science and Hypothesis]]'', ''[[The Value of Science]]'', and ''Science and Method'') were cited by [[Jacques Hadamard]] as the source for the idea that [[creativity]] and [[Innovation|invention]] consist of two mental stages, first random combinations of possible solutions to a problem, followed by a [[critical thinking|critical]] [[evaluation]].<ref>Hadamard, Jacques. ''An Essay on the Psychology of Invention in the Mathematical Field''. Princeton Univ Press (1945)</ref> |
|||
Although he most often spoke of a [[deterministic]] [[universe]], Poincaré said that the [[subconscious]] generation of new possibilities involves [[Randomness|chance]]. |
|||
Poincaré's famous lectures before the Société de Psychologie in Paris (published as ''Science and Hypothesis'', ''The Value of Science'', and ''Science and Method'') were cited by [[Jacques Hadamard]] as the source for the idea that [[creativity]] and [[invention]] consist of two mental stages, first random combinations of possible solutions to a problem, followed by a critical evaluation.<ref>Hadamard, Jacques. ''An Essay On The Psychology Of Invention In The Mathematical Field''. Princeton Univ Press (1949)</ref> |
|||
Although he most often spoke of a deterministic universe, Poincaré said that the subconscious generation of new possibilities involves [[Randomness|chance]]. |
|||
<blockquote> |
<blockquote> |
||
It is certain that the combinations which present themselves to the mind in a kind of sudden illumination after a somewhat prolonged period of unconscious work are generally useful and fruitful combinations... all the combinations are formed as a result of the automatic action of the subliminal ego, but those only which are interesting find their way into the field of consciousness... A few only are harmonious, and consequently at once useful and beautiful, and they will be capable of affecting the geometrician's special sensibility I have been speaking of; which, once aroused, will direct our attention upon them, and will thus give them the opportunity of becoming conscious... In the subliminal ego, on the contrary, there reigns what I would call liberty, if one could give this name to the mere absence of discipline and to disorder born of chance.<ref>{{cite book|title= Science and Method|chapter= 3: Mathematical Creation|date= 1914|chapter-url= http://ebooks.adelaide.edu.au/p/poincare/henri/science-and-method/book1.3.html|first= Henri|last= Poincaré|access-date= 4 September 2019|archive-date= 4 September 2019|archive-url= https://web.archive.org/web/20190904163001/https://ebooks.adelaide.edu.au/p/poincare/henri/science-and-method/book1.3.html|url-status= dead}}</ref> |
|||
</blockquote> |
</blockquote> |
||
Poincaré's two |
Poincaré's two stages—random combinations followed by selection—became the basis for [[Daniel Dennett]]'s two-stage model of [[free will]].<ref>Dennett, Daniel C. 1978. ''Brainstorms: Philosophical Essays on Mind and Psychology''. The MIT Press, p. 293</ref> |
||
===Poincaré Model of the Subconscious Mind in Mathematics=== |
|||
Poincaré proposes a model of the Subconscious Mind stresses the Subconscious or Unconscious mind is capable of evaluating and processing even complex mathematical or scientific ideas, and evaluate and elevate them on the basis of their elegance and beauty<ref>{{Citation|title=Musings of the masters: an anthology of mathematical reflections|first1=Raymond George|last1=Ayoub|publisher=MAA|year=2004|isbn=9780883855492|page=88 |
|||
|url=http://books.google.co.uk/books?id=WfvDhPK65agC&lpg}}]</ref> |
|||
. Poincaré thus shares with Freud a belief that mental functions are at work in creating thinking which are not present to our conscious mind. That the discontinuity in time between thinking of a problem and suddenly relieving a solution proves that some mental function outside the space of conscious awareness must be at work<ref>{{Citation|title=Psychoanalysis at the limit: epistemology, mind, and the question of science|first1=Jon |last1=Mills|publisher=SUNY Press|year=2004|isbn=9780791460658|page=82-85 |
|||
|url=http://books.google.co.uk/books?id=IHwCB44i2JoC}}]</ref> |
|||
==See also== |
|||
{{wikisource author}} |
|||
{{commons|Henri Poincaré}} |
|||
{{Columns-list|colwidth=30em| |
|||
*[[History of special relativity]] |
|||
*[[Institut Henri Poincaré]], Paris |
|||
*[[Poincaré–Bendixson theorem]] |
|||
*[[Poincaré–Birkhoff–Witt theorem]] |
|||
*[[Poincaré conjecture]] |
|||
*[[Poincaré duality]] |
|||
*[[Poincaré group]] |
|||
*[[Poincaré half-plane model]] |
|||
*[[Poincaré–Hopf theorem]] |
|||
*[[Poincaré–Lindstedt method]] |
|||
*[[Poincaré map]] |
|||
*[[Poincaré metric]] |
|||
*[[Poincaré plot]] |
|||
*[[Poincaré–Steklov operator]] |
|||
*[[Poincaré symmetry]] |
|||
*[[Relativity priority dispute]] |
|||
}} |
|||
==References== |
|||
{{planetmath|id=3793|title=Jules Henri Poincaré}} |
|||
===Footnotes and primary sources=== |
|||
{{Reflist|colwidth=30em}} |
|||
==Bibliography== |
|||
=== Poincaré's writings in English translation=== |
|||
===Poincaré's writings in English translation=== |
|||
{{Wikisource|Science and Hypothesis}} |
|||
Popular writings on the [[philosophy of science]]: |
Popular writings on the [[philosophy of science]]: |
||
| Line 320: | Line 394: | ||
|place=New York |
|place=New York |
||
|publisher=Science Press |
|publisher=Science Press |
||
|url= |
|url=https://archive.org/details/foundationsscie01poingoog}}; reprinted in 1921; this book includes the English translations of Science and Hypothesis (1902), The Value of Science (1905), Science and Method (1908). |
||
* 1905. "{{Citation |title=Science and Hypothesis | url=https://en.wikisource.org/wiki/Science_and_Hypothesis}}", The Walter Scott Publishing Co. |
|||
* 1906. "{{Citation |title=The End of Matter | url=https://en.wikisource.org/wiki/Translation:The_End_of_Matter}}", Athenæum |
|||
*1913. {{Citation | title=[http://www.archive.org/details/mathematicsandsc001861mbp Last Essays.] |place=New York |publisher=Dover reprint, 1963}} |
|||
* 1913. "The New Mechanics", ''The Monist'', Vol. XXIII. |
|||
* 1913. "The Relativity of Space", ''The Monist'', Vol. XXIII. |
|||
* 1913. {{Citation | title=Last Essays. |place=New York |publisher=Dover reprint, 1963 | url=https://archive.org/details/mathematicsandsc001861mbp}} |
|||
* 1956. ''Chance.'' In James R. Newman, ed., ''The World of Mathematics'' (4 Vols). |
|||
* 1958. ''The Value of Science,'' New York: Dover. |
|||
On [[algebraic topology]]: |
On [[algebraic topology]]: |
||
* 1895. {{Citation |title=Analysis Situs |
|||
* 1895. ''[[Analysis situs (book)|Analysis situs]]''. The first systematic study of [[topology]]. |
|||
| url=http://www.maths.ed.ac.uk/~aar/papers/poincare2009.pdf |archive-url=https://web.archive.org/web/20120327043041/http://www.maths.ed.ac.uk/~aar/papers/poincare2009.pdf |archive-date=2012-03-27 |url-status=live}}. The first systematic study of [[topology]]. |
|||
On [[celestial mechanics]]: |
On [[celestial mechanics]]: |
||
* 1890. {{cite book |last1=Poincaré |first1=Henri |translator1-last=Popp |translator1-first=Bruce D. |title=The three-body problem and the equations of dynamics: Poincaré's foundational work on dynamical systems theory |date=2017 |publisher=Springer International Publishing |location=Cham, Switzerland |isbn=978-3-319-52898-4}} |
|||
* 1892–99. ''New Methods of Celestial Mechanics'', 3 vols. English trans., 1967. ISBN 1-56396-117-2. |
|||
* 1892–99. ''New Methods of Celestial Mechanics'', 3 vols. English trans., 1967. {{isbn|1-56396-117-2}}. |
|||
* 1905. "The Capture Hypothesis of J. J. See", The Monist, Vol. XV. |
|||
* 1905–10. ''Lessons of Celestial Mechanics''. |
* 1905–10. ''Lessons of Celestial Mechanics''. |
||
On the [[philosophy of mathematics]]: |
On the [[philosophy of mathematics]]: |
||
* Ewald, William B., ed., 1996. ''From Kant to Hilbert: A Source Book in the Foundations of Mathematics'', 2 vols. Oxford Univ. Press. Contains the following works by Poincaré: |
|||
**1894, "On the |
** 1894, "On the Nature of Mathematical Reasoning", 972–981. |
||
**1898, "On the |
** 1898, "On the Foundations of Geometry", 982–1011. |
||
**1900, "Intuition and Logic in |
** 1900, "Intuition and Logic in Mathematics", 1012–1020. |
||
**1905–06, "Mathematics and Logic, I–III |
** 1905–06, "Mathematics and Logic, I–III", 1021–1070. |
||
**1910, "On |
** 1910, "On Transfinite Numbers", 1071–1074. |
||
* 1905. "The Principles of Mathematical Physics", ''The Monist'', Vol. XV. |
|||
* 1910. "The Future of Mathematics", ''The Monist'', Vol. XX. |
|||
* 1910. "Mathematical Creation", ''The Monist'', Vol. XX. |
|||
Other: |
|||
===General references=== |
|||
* 1904. ''Maxwell's Theory and Wireless Telegraphy,'' New York, McGraw Publishing Company. |
|||
* [[Eric Temple Bell|Bell, Eric Temple]], 1986. ''Men of Mathematics'' (reissue edition). Touchstone Books. ISBN 0-671-62818-6. |
|||
* 1905. "The New Logics", ''The Monist'', Vol. XV. |
|||
* Belliver, André, 1956. ''Henri Poincaré ou la vocation souveraine''. Paris: Gallimard. |
|||
* 1905. "The Latest Efforts of the Logisticians", ''The Monist'', Vol. XV. |
|||
*Bernstein, Peter L, 1996. "Against the Gods: A Remarkable Story of Risk". (p. 199–200). John Wiley & Sons. |
|||
* Boyer, B. Carl, 1968. ''A History of Mathematics: Henri Poincaré'', John Wiley & Sons. |
|||
* [[Ivor Grattan-Guinness|Grattan-Guinness, Ivor]], 2000. ''The Search for Mathematical Roots 1870–1940.'' Princeton Uni. Press. |
|||
* {{Citation|surname=Dauben|given= Joseph|year=1993, 2004|chapter=[http://www.acmsonline.org/journal/2004/Dauben-Cantor.pdf Georg Cantor and the Battle for Transfinite Set Theory]|title=Proceedings of the 9th ACMS Conference (Westmont College, Santa Barbara, CA)|pages=1–22}}. Internet version published in Journal of the ACMS 2004. |
|||
* Folina, Janet, 1992. ''Poincare and the Philosophy of Mathematics.'' Macmillan, New York. |
|||
* Gray, Jeremy, 1986. ''Linear differential equations and group theory from Riemann to Poincaré'', Birkhauser |
|||
*{{Citation |url=http://www.ams.org/notices/200509/comm-mawhin.pdf |
|||
|format=PDF|title=Henri Poincaré. A Life in the Service of Science |
|||
|author=Jean Mawhin |journal=Notices of the AMS |
|||
|year=2005 |month=October |volume=52 |issue=9 |pages=1036–1044 }} |
|||
* Kolak, Daniel, 2001. ''Lovers of Wisdom'', 2nd ed. Wadsworth. |
|||
* Murzi, 1998. [http://www.iep.utm.edu/p/poincare.htm "Henri Poincaré"]. |
|||
* O'Connor, J. John, and Robertson, F. Edmund, 2002, [http://www-history.mcs.st-andrews.ac.uk/Mathematicians/Poincare.html "Jules Henri Poincaré"]. University of St. Andrews, Scotland. |
|||
* [[Ivars Peterson|Peterson, Ivars]], 1995. ''Newton's Clock: Chaos in the Solar System'' (reissue edition). W H Freeman & Co. ISBN 0-7167-2724-2. |
|||
* Sageret, Jules, 1911. ''Henri Poincaré''. Paris: Mercure de France. |
|||
* Toulouse, E.,1910. ''[http://quod.lib.umich.edu/cgi/t/text/text-idx?c=umhistmath;idno=AAS9989.0001.001 Henri Poincaré]''.—(Source biography in French) at University of Michigan Historic Math Collection. |
|||
Exhaustive bibliography of English translations: |
|||
===Secondary sources to work on relativity=== |
|||
* 1892–2017. {{Citation |title=Henri Poincaré Papers |url=http://henripoincarepapers.univ-nantes.fr/bibliohp/index.php?a=on&lang=en&action=Chercher |archive-url=https://web.archive.org/web/20200801151000/http://henripoincarepapers.univ-nantes.fr/bibliohp/index.php?a=on&lang=en&action=Chercher |url-status=dead |archive-date=1 August 2020 }}. |
|||
* {{Citation | author=Cuvaj, Camillo | year=1969 | title= Henri Poincaré's Mathematical Contributions to Relativity and the Poincaré Stresses | journal=American Journal of Physics |pages=1102–1113 |volume=36 | issue=12|doi=10.1119/1.1974373}} |
|||
==See also== |
|||
* {{Citation|author=Darrigol, O. |title=Henri Poincaré's criticism of Fin De Siècle electrodynamics |year=1995 |journal=Studies in History and Philosophy of Science |volume=26|issue=1|pages=1–44|doi=10.1016/1355-2198(95)00003-C}} |
|||
===Concepts=== |
|||
{{cols|colwidth=21em}} |
|||
* [[Hopf bifurcation|Poincaré–Andronov–Hopf bifurcation]] |
|||
* [[Poincaré complex]] – an abstraction of the singular chain complex of a closed, orientable manifold |
|||
* [[Poincaré duality]] |
|||
* [[Poincaré disk model]] |
|||
* [[Asymptotic expansion|Poincaré expansion]] |
|||
* [[Gauge fixing#Multipolar gauge|Poincaré gauge]] |
|||
* [[Poincaré group]] |
|||
* [[Poincaré half-plane model]] |
|||
* [[Homology sphere#Poincaré homology sphere|Poincaré homology sphere]] |
|||
* [[Poincaré inequality]] |
|||
* [[Closed and exact differential forms#Poincaré lemma|Poincaré lemma]] |
|||
* [[Poincaré map]] |
|||
* [[Poincaré residue]] |
|||
* [[Poincaré series (modular form)]] |
|||
* [[Poincaré space]] |
|||
* [[Poincaré metric]] |
|||
* [[Poincaré plot]] |
|||
* [[Betti number#Poincaré polynomial|Poincaré polynomial]] |
|||
* [[Hilbert–Poincaré series|Poincaré series]] |
|||
* [[Poincaré sphere (optics)|Poincaré sphere]] |
|||
* [[Einstein synchronisation|Poincaré–Einstein synchronisation]] |
|||
* [[Poincaré–Lelong equation]] |
|||
* [[Poincaré–Lindstedt method]] |
|||
* [[Poincaré–Lindstedt perturbation theory]] |
|||
* [[Poincaré–Steklov operator]] |
|||
* [[Euler characteristic|Euler–Poincaré characteristic]] |
|||
* [[Neumann–Poincaré operator]] |
|||
* [[Reflecting Function]] |
|||
{{colend}} |
|||
===Theorems=== |
|||
* {{Citation | author=Darrigol, O. | year=2000 | title= Electrodynamics from Ampére to Einstein | place=Oxford |publisher=Clarendon Press |isbn=0198505949}} |
|||
Here is a list of theorems proved by Poincaré: |
|||
{{cols|colwidth=26em}} |
|||
* [[Poincaré's recurrence theorem]]: certain systems will, after a sufficiently long but finite time, return to a state very close to the initial state. |
|||
* [[Poincaré–Bendixson theorem]]: a statement about the long-term behaviour of orbits of continuous dynamical systems on the plane, cylinder, or two-sphere. |
|||
* [[Poincaré–Hopf theorem]]: a generalization of the hairy-ball theorem, which states that there is no smooth vector field on a sphere having no sources or sinks. |
|||
* [[Poincaré–Lefschetz duality theorem]]: a version of Poincaré duality in geometric topology, applying to a manifold with boundary |
|||
* [[Poincaré separation theorem]]: gives the upper and lower bounds of eigenvalues of a real symmetric matrix B'AB that can be considered as the orthogonal projection of a larger real symmetric matrix A onto a linear subspace spanned by the columns of B. |
|||
* [[Poincaré–Birkhoff theorem]]: every area-preserving, orientation-preserving homeomorphism of an annulus that rotates the two boundaries in opposite directions has at least two fixed points. |
|||
* [[Poincaré–Birkhoff–Witt theorem]]: an explicit description of the universal enveloping algebra of a Lie algebra. |
|||
* [[Kelvin's circulation theorem#Poincaré–Bjerknes circulation theorem|Poincaré–Bjerknes circulation theorem]]: theorem about a conservation of quantity for the rotating frame. |
|||
* [[Poincaré conjecture]] (now a theorem): Every simply connected, closed 3-manifold is homeomorphic to the 3-sphere. |
|||
* [[Poincaré–Miranda theorem]]: a generalization of the [[intermediate value theorem]] to ''n'' dimensions. |
|||
{{colend}} |
|||
=== Other === |
|||
* {{Citation|author=Darrigol, O. |title=The Mystery of the Einstein–Poincaré Connection| pages=614–626|url=http://www.journals.uchicago.edu/doi/full/10.1086/430652|doi=10.1086/430652|pmid=16011297 |year=2004 |journal=Isis|volume=95| issue=4}} |
|||
{{cols}} |
|||
*[[French epistemology]] |
|||
*[[History of special relativity]] |
|||
*[[List of things named after Henri Poincaré]] |
|||
*[[Institut Henri Poincaré]], Paris |
|||
*[[Brouwer fixed-point theorem]] |
|||
*[[Relativity priority dispute]] |
|||
*[[Epistemic structural realism]]<ref>[http://plato.stanford.edu/entries/structural-realism/#Rel "Structural Realism"]: entry by James Ladyman in the ''[[Stanford Encyclopedia of Philosophy]]''</ref> |
|||
{{colend}} |
|||
==References== |
|||
* {{Citation|author=Darrigol, O. |title=The Genesis of the theory of relativity |year=2005 |journal=Séminaire Poincaré|volume=1|pages=1–22|url=http://www.bourbaphy.fr/darrigol2.pdf|format=PDF}} |
|||
===Footnotes=== |
|||
* {{Citation | author=Galison, P. | year=2003 | title= Einstein's Clocks, Poincaré's Maps: Empires of Time | place=New York |publisher=W.W. Norton|isbn=0393326047}} |
|||
{{Reflist}} |
|||
===Sources=== |
|||
* {{Citation|author=Giannetto, E. |title=The Rise of Special Relativity: Henri Poincaré's Works Before Einstein |year=1998 |journal=Atti del XVIII congresso di storia della fisica e dell'astronomia |pages=171–207}} |
|||
* [[Eric Temple Bell|Bell, Eric Temple]], 1986. ''Men of Mathematics'' (reissue edition). Touchstone Books. {{isbn|0-671-62818-6}}. |
|||
* Belliver, André, 1956. ''Henri Poincaré ou la vocation souveraine''. Paris: Gallimard. |
|||
*[[Peter L. Bernstein|Bernstein, Peter L]], 1996. "Against the Gods: A Remarkable Story of Risk". (pp. 199–200). John Wiley & Sons. |
|||
* [[Carl Benjamin Boyer|Boyer, B. Carl]], 1968. ''A History of Mathematics: Henri Poincaré'', John Wiley & Sons. |
|||
* [[Ivor Grattan-Guinness|Grattan-Guinness, Ivor]], 2000. ''The Search for Mathematical Roots 1870–1940.'' Princeton Uni. Press. |
|||
* {{Citation|last=Dauben|given=Joseph|author-link=Joseph Dauben|orig-year=1993|year=2004|chapter=Georg Cantor and the Battle for Transfinite Set Theory|chapter-url=http://www.acmsonline.org/journal/2004/Dauben-Cantor.pdf|title=Proceedings of the 9th ACMS Conference (Westmont College, Santa Barbara, CA)|pages=1–22|url-status=dead|archive-url=https://web.archive.org/web/20100713115605/http://www.acmsonline.org/journal/2004/Dauben-Cantor.pdf|archive-date=13 July 2010}}. Internet version published in Journal of the ACMS 2004. |
|||
* Folina, Janet, 1992. ''Poincaré and the Philosophy of Mathematics.'' Macmillan, New York. |
|||
* [[Jeremy Gray|Gray, Jeremy]], 1986. ''Linear differential equations and group theory from Riemann to Poincaré'', Birkhauser {{isbn|0-8176-3318-9}} |
|||
* Gray, Jeremy, 2013. ''Henri Poincaré: A scientific biography''. Princeton University Press {{isbn|978-0-691-15271-4}} |
|||
*{{Citation |url=https://www.ams.org/notices/200509/comm-mawhin.pdf |archive-url=https://web.archive.org/web/20070303185921/http://www.ams.org/notices/200509/comm-mawhin.pdf |archive-date=2007-03-03 |url-status=live |
|||
|title=Henri Poincaré. A Life in the Service of Science |
|||
|author=Jean Mawhin | author-link=Jean Mawhin |journal=Notices of the AMS |
|||
|date=October 2005 |volume=52 |issue=9 |pages=1036–1044 }} |
|||
* [[Daniel Kolak|Kolak, Daniel]], 2001. ''Lovers of Wisdom'', 2nd ed. Wadsworth. |
|||
* Gargani, Julien, 2012. ''Poincaré, le hasard et l'étude des systèmes complexes'', L'Harmattan. |
|||
* Murzi, 1998. "Henri Poincaré". |
|||
* O'Connor, J. John, and Robertson, F. Edmund, 2002, "Jules Henri Poincaré". University of St. Andrews, Scotland. |
|||
* [[Ivars Peterson|Peterson, Ivars]], 1995. ''Newton's Clock: Chaos in the Solar System'' (reissue edition). W H Freeman & Co. {{isbn|0-7167-2724-2}}. |
|||
* Sageret, Jules, 1911. [https://books.google.com/books?id=6Mu4AAAAIAAJ ''Henri Poincaré'']. Paris: Mercure de France. |
|||
* Toulouse, E., 1910. ''Henri Poincaré'' – (Source biography in French) at University of Michigan Historic Math Collection. |
|||
* {{cite book |title=Mathematics and Its History |edition=3rd, illustrated |first1=John |last1=Stillwell |author-link=John Stillwell |publisher= Springer Science & Business Media |year=2010 |isbn=978-1-4419-6052-8 |url=https://books.google.com/books?id=V7mxZqjs5yUC }} |
|||
** {{cite book|title=''Papers on Topology: Analysis Situs and Its Five Supplements'' by Henri Poincaré, translated, with an introduction, by John Stillwell |year=2010|publisher=American Mathematical Society|isbn=978-0-8218-5234-7 |url=https://books.google.com/books?id=_WjVAwAAQBAJ}} – {{cite web|author=Satzer, William J.|date=April 26, 2011|title=Review of ''Papers on Topology: Analysis Situs and Its Five Supplements'' by Henri Poincaré, translated and edited by John Stillwell|website=MAA Reviews, Mathematical Association of America|url=https://old.maa.org/press/maa-reviews/papers-on-topology-ianalysis-situsi-and-its-five-supplements|access-date=26 January 2024|archive-date=26 January 2024|archive-url=https://web.archive.org/web/20240126002055/https://maa.org/press/maa-reviews/papers-on-topology-ianalysis-situsi-and-its-five-supplements|url-status=dead}} |
|||
* [[F. Verhulst|Verhulst, Ferdinand]], 2012 ''Henri Poincaré. Impatient Genius''. N.Y.: Springer. |
|||
* ''Henri Poincaré, l'œuvre scientifique, l'œuvre philosophique'', by Vito Volterra, Jacques Hadamard, Paul Langevin and Pierre Boutroux, Felix Alcan, 1914. |
|||
** ''Henri Poincaré, l'œuvre mathématique'', by [[Vito Volterra]]. |
|||
** ''Henri Poincaré, le problème des trois corps'', by [[Jacques Hadamard]]. |
|||
** ''Henri Poincaré, le physicien'', by [[Paul Langevin]]. |
|||
** ''Henri Poincaré, l'œuvre philosophique'', by [[Pierre Boutroux]]. |
|||
* {{PlanetMath attribution|id=3793|title=Jules Henri Poincaré}} |
|||
==Further reading== |
|||
* {{Citation | author=[[Jerzy Giedymin|Giedymin, J.]] | year=1982 | title= Science and Convention: Essays on Henri Poincaré’s Philosophy of Science and the Conventionalist Tradition | place=Oxford |publisher=Pergamon Press|isbn=0080257909}} |
|||
===Secondary sources to work on relativity=== |
|||
* {{Citation | author=Cuvaj, Camillo | year=1969 | title= Henri Poincaré's Mathematical Contributions to Relativity and the Poincaré Stresses | journal=American Journal of Physics |pages=1102–1113 |volume=36 | issue=12|doi=10.1119/1.1974373|bibcode = 1968AmJPh..36.1102C }} |
|||
* {{Citation|author=Darrigol, O. |title=Henri Poincaré's criticism of Fin De Siècle electrodynamics |year=1995 |journal=Studies in History and Philosophy of Science |volume=26|issue=1|pages=1–44|doi=10.1016/1355-2198(95)00003-C|bibcode=1995SHPMP..26....1D}} |
|||
* {{Citation | author=Darrigol, O. | year=2000 | title=Electrodynamics from Ampére to Einstein | place=Oxford | publisher=Clarendon Press | isbn=978-0-19-850594-5 | url-access=registration | url=https://archive.org/details/electrodynamicsf0000darr }} |
|||
* {{Citation|author=Darrigol, O. |title=The Mystery of the Einstein–Poincaré Connection| pages=614–626|doi=10.1086/430652|pmid=16011297 |year=2004 |journal=Isis|volume=95| issue=4|bibcode=2004Isis...95..614D|s2cid=26997100}} |
|||
* {{Citation|author=Darrigol, O. |title=The Genesis of the theory of relativity |year=2005 |journal=Séminaire Poincaré|volume=1|pages=1–22|url=http://www.bourbaphy.fr/darrigol2.pdf |archive-url=https://web.archive.org/web/20080228124558/http://www.bourbaphy.fr/darrigol2.pdf |archive-date=2008-02-28 |url-status=live|doi=10.1007/3-7643-7436-5_1|isbn=978-3-7643-7435-8 |bibcode=2006eins.book....1D }} |
|||
* {{Citation | author=Galison, P. | year=2003 | title= Einstein's Clocks, Poincaré's Maps: Empires of Time | place=New York |publisher=W.W. Norton|isbn=978-0-393-32604-8}} |
|||
* {{Citation|author=Giannetto, E. |title=The Rise of Special Relativity: Henri Poincaré's Works Before Einstein |year=1998 |journal=Atti del XVIII Congresso di Storia della Fisica e dell'astronomia |pages=171–207}} |
|||
* {{Citation | author=Giedymin, J. | year=1982 | title= Science and Convention: Essays on Henri Poincaré's Philosophy of Science and the Conventionalist Tradition | place=Oxford |publisher=Pergamon Press|isbn=978-0-08-025790-7| author-link=Jerzy Giedymin }} |
|||
* {{Citation | author=Goldberg, S. | year=1967 | title= Henri Poincaré and Einstein's Theory of Relativity | journal=American Journal of Physics |pages=934–944 |volume=35 | issue=10|doi=10.1119/1.1973643|bibcode = 1967AmJPh..35..934G }} |
|||
* {{Citation | author=Goldberg, S. | year=1970 | title= Poincaré's silence and Einstein's relativity | journal=British Journal for the History of Science |pages=73–84 |volume=5 | doi=10.1017/S0007087400010633| s2cid=123766991 }} |
|||
*{{Citation | author=Holton, G. | orig-year=1973| year=1988 | chapter=Poincaré and Relativity| title= [[Thematic Origins of Scientific Thought: Kepler to Einstein]] | publisher=Harvard University Press|isbn=978-0-674-87747-4}} |
|||
* {{Citation | author=Katzir, S. | year=2005 | journal=Phys. Perspect. | title= Poincaré's Relativistic Physics: Its Origins and Nature |pages= 268–292 |volume=7 | doi=10.1007/s00016-004-0234-y | issue=3 |bibcode = 2005PhP.....7..268K | s2cid=14751280 }} |
|||
* {{Citation|author=Keswani, G.H., Kilmister, C.W. |year=1983 |journal=Br. J. Philos. Sci. |title=Intimations of Relativity: Relativity Before Einstein |pages=343–354 |volume=34 |doi=10.1093/bjps/34.4.343 |issue=4 |s2cid=65257414 |url=http://osiris.sunderland.ac.uk/webedit/allweb/news/Philosophy_of_Science/PIRT2002/Intimations%20of%20Relativity.doc |url-status=dead |archive-url=https://web.archive.org/web/20090326084436/http://osiris.sunderland.ac.uk/webedit/allweb/news/Philosophy_of_Science/PIRT2002/Intimations%20of%20Relativity.doc |archive-date=26 March 2009}} |
|||
* {{Citation | author=Keswani, G.H. | year=1965| journal=Br. J. Philos. Sci. | title= Origin and Concept of Relativity, Part I |volume=15| issue=60|pages=286–306 |doi=10.1093/bjps/XV.60.286| s2cid=229320737}} |
|||
* {{Citation | author=Keswani, G.H. | year=1965 | journal=Br. J. Philos. Sci. | title= Origin and Concept of Relativity, Part II|volume=16| pages=19–32| issue=61| doi=10.1093/bjps/XVI.61.19| s2cid=229320603 }} |
|||
* {{Citation | author=Keswani, G.H. | year=1966 | journal=Br. J. Philos. Sci. | title= Origin and Concept of Relativity, Part III |volume=16|issue=64| pages=273–294| doi=10.1093/bjps/XVI.64.273 | s2cid=122596290 }} |
|||
* {{Citation | author=Kragh, H. | year=1999 | title= Quantum Generations: A History of Physics in the Twentieth Century |publisher= Princeton University Press|isbn=978-0-691-09552-3}} |
|||
* {{Citation | author=Langevin, P. | year=1913 | journal=Revue de Métaphysique et de Morale | title= L'œuvre d'Henri Poincaré: le physicien |page= 703 |volume=21|url=http://gallica.bnf.fr/ark:/12148/bpt6k111418/f93.chemindefer}} |
|||
* {{Citation | author=Macrossan, M. N. | year=1986 | journal=Br. J. Philos. Sci. | title=A Note on Relativity Before Einstein | pages=232–234 | volume=37 | issue=2 | url=http://espace.library.uq.edu.au/view.php?pid=UQ:9560 | doi=10.1093/bjps/37.2.232 | citeseerx=10.1.1.679.5898 | s2cid=121973100 | access-date=27 March 2007 | archive-url=https://web.archive.org/web/20131029203003/http://espace.library.uq.edu.au/view.php?pid=UQ:9560 | archive-date=29 October 2013 | url-status=dead }} |
|||
*{{Citation|author=Miller, A.I. |title=A study of Henri Poincaré's "Sur la Dynamique de l'Electron |year=1973 |journal=Arch. Hist. Exact Sci.|volume=10|pages=207–328|doi=10.1007/BF00412332|issue=3–5|s2cid=189790975 }} |
|||
* {{Citation | author=Miller, A.I. | year=1981 | title=Albert Einstein's special theory of relativity. Emergence (1905) and early interpretation (1905–1911) | place=Reading | publisher=Addison–Wesley | isbn=978-0-201-04679-3 | url-access=registration | url=https://archive.org/details/alberteinsteinss0000mill }} |
|||
*{{Citation| author=Miller, A.I. |contribution= Why did Poincaré not formulate special relativity in 1905? |year=1996 |editor1=Jean-Louis Greffe |editor2=Gerhard Heinzmann |editor3=Kuno Lorenz | title=Henri Poincaré : science et philosophie| pages=69–100|place=Berlin}} |
|||
* {{Citation | author=Popp, B.D. | year=2020 | title= Henri Poincaré: Electrons to Special Relativity | place=Cham |publisher=Springer Nature |isbn=978-3-030-48038-7}} |
|||
* {{Citation | author=Schwartz, H. M. | year=1971 | title= Poincaré's Rendiconti Paper on Relativity. Part I | journal=American Journal of Physics |pages=1287–1294 |volume=39 | issue=7|doi=10.1119/1.1976641|bibcode = 1971AmJPh..39.1287S }} |
|||
* {{Citation | author=Schwartz, H. M. | year=1972 | title= Poincaré's Rendiconti Paper on Relativity. Part II | journal=American Journal of Physics |pages=862–872 |volume=40 | issue=6| doi=10.1119/1.1986684|bibcode = 1972AmJPh..40..862S | doi-access=free }} |
|||
* {{Citation | author=Schwartz, H. M. | year=1972 | title= Poincaré's Rendiconti Paper on Relativity. Part III | journal=American Journal of Physics |pages=1282–1287 |volume=40 | issue=9| doi=10.1119/1.1986815|bibcode = 1972AmJPh..40.1282S }} |
|||
* {{Citation | author=Scribner, C. | year=1964 | title= Henri Poincaré and the principle of relativity | journal=American Journal of Physics |pages=672–678 |volume=32 | issue=9| doi=10.1119/1.1970936|bibcode =1964AmJPh..32..672S }} |
|||
* {{Citation | author=Walter, S. | year=2005 | editor=Renn, J. | contribution= Henri Poincaré and the theory of relativity | title=Albert Einstein, Chief Engineer of the Universe: 100 Authors for Einstein |pages=162–165 | place=Berlin | publisher=Wiley-VCH|contribution-url=http://scottwalter.free.fr/papers/2005-100authors-poincare-einstein-walter.html}} |
|||
* {{Citation | author=Walter, S. | year=2007 | editor=Renn, J. | contribution= Breaking in the 4-vectors: the four-dimensional movement in gravitation, 1905–1910 | title=The Genesis of General Relativity |pages=193–252 |volume=3 |place=Berlin | publisher=Springer|contribution-url=http://scottwalter.free.fr/papers/2007-genesis-walter.html}} |
|||
* {{Citation | author=Whittaker, E.T.|author-link=E. T. Whittaker | year=1953 | title= [[A History of the Theories of Aether and Electricity|A History of the Theories of Aether and Electricity: The Modern Theories 1900–1926]]| chapter= The Relativity Theory of Poincaré and Lorentz | place=London |publisher=Nelson}} |
|||
* {{Citation| author=Zahar, E. |year=2001 |title=Poincaré's Philosophy: From Conventionalism to Phenomenology |publisher=Open Court Pub Co|place=Chicago|isbn=978-0-8126-9435-2}} |
|||
===Non-mainstream sources=== |
|||
* {{Citation | author=Goldberg, S. | year=1967 | title= Henri Poincaré and Einstein’s Theory of Relativity | journal=American Journal of Physics |pages=934–944 |volume=35 | issue=10|doi=10.1119/1.1973643}} |
|||
* {{Citation | author=Leveugle, J. | year=2004 |title= La Relativité et Einstein, Planck, Hilbert – Histoire véridique de la Théorie de la Relativitén | publisher=L'Harmattan| place=Pars}} |
|||
* {{Citation | author= |
* {{Citation | author=Logunov, A.A. | year=2004 | title= Henri Poincaré and relativity theory | arxiv=physics/0408077 |bibcode = 2004physics...8077L |isbn=978-5-02-033964-4}} |
||
*{{Citation | author=Holton, G. | year=1973/1988 | chapter=Poincaré and Relativity| title= Thematic Origins of Scientific Thought: Kepler to Einstein | publisher=Harvard University Press|isbn=0674877470}} |
|||
* {{Citation | author=Katzir, S. | year=2005 | journal=Phys. Perspect. | title= Poincaré’s Relativistic Physics: Its Origins and Nature |pages= 268–292 |volume=7 | doi=10.1007/s00016-004-0234-y }} |
|||
* {{Citation | author=Keswani, G.H., Kilmister, C.W.| year=1983 | journal=Brit. J. Phil. Sci. | title= [http://osiris.sunderland.ac.uk/webedit/allweb/news/Philosophy_of_Science/PIRT2002/Intimations%20of%20Relativity.doc Intimations Of Relativity: Relativity Before Einstein] |pages= 343–354 |volume=34 | doi=10.1093/bjps/34.4.343 }} |
|||
* {{Citation | author=Kragh, H. | year=1999 | title= Quantum Generations: A History of Physics in the Twentieth Century |publisher= Princeton University Press|isbn=0691095523}} |
|||
* {{Citation | author=Langevin, P. | year=1913 | journal=Revue de métaphysique et de morale | title= L'œuvre d'Henri Poincaré: le physicien |page= 703 |volume=21|url=http://gallica.bnf.fr/ark:/12148/bpt6k111418/f93.chemindefer}} |
|||
* {{Citation | author=Macrossan, M. N. | year=1986 | journal=Brit. J. Phil. Sci. | title= A Note on Relativity Before Einstein |pages= 232–234 |volume=37|url=http://espace.library.uq.edu.au/view.php?pid=UQ:9560}} |
|||
*{{Citation|author=Miller, A.I. |title=A study of Henri Poincaré's "Sur la Dynamique de l'Electron |year=1973 |journal=Arch. Hist. Exact. Scis.|volume=10|pages=207–328|doi=10.1007/BF00412332}} |
|||
* {{Citation | author=Miller, A.I. | year=1981 | title= Albert Einstein’s special theory of relativity. Emergence (1905) and early interpretation (1905–1911) | place= Reading |publisher=Addison–Wesley |isbn=0-201-04679-2}} |
|||
*{{Citation| author=Miller, A.I. |contribution= Why did Poincaré not formulate special relativity in 1905? |year=1996 |editor=Jean-Louis Greffe, Gerhard Heinzmann, Kuno Lorenz| title=Henri Poincaré : science et philosophie| pages=69–100|place=Berlin}} |
|||
* {{Citation | author=Schwartz, H. M. | year=1971 | title= Poincaré's Rendiconti Paper on Relativity. Part I | journal=American Journal of Physics |pages=1287–1294 |volume=39 | issue=7|doi=10.1119/1.1976641}} |
|||
* {{Citation | author=Schwartz, H. M. | year=1972 | title= Poincaré's Rendiconti Paper on Relativity. Part II | journal=American Journal of Physics |pages=862–872 |volume=40 | issue=6| doi=10.1119/1.1986684}} |
|||
* {{Citation | author=Schwartz, H. M. | year=1972 | title= Poincaré's Rendiconti Paper on Relativity. Part III | journal=American Journal of Physics |pages=1282–1287 |volume=40 | issue=9| doi=10.1119/1.1976641}} |
|||
* {{Citation | author=Scribner, C. | year=1964 | title= Henri Poincaré and the principle of relativity | journal=American Journal of Physics |pages=672–678 |volume=32 | issue=9| doi=10.1119/1.1986815}} |
|||
* {{Citation | author=Walter, S. | year=2005 | editor=Renn, J. | contribution= Henri Poincaré and the theory of relativity | journal=Albert Einstein, Chief Engineer of the Universe: 100 Authors for Einstein |pages=162–165 | place=Berlin | publisher=Wiley-VCH|contribution-url=http://www.univ-nancy2.fr/DepPhilo/walter/papers/hpeinstein2005.htm}} |
|||
* {{Citation | author=Walter, S. | year=2007 | editor=Renn, J. | contribution= Breaking in the 4-vectors: the four-dimensional movement in gravitation, 1905–1910 | journal=The Genesis of General Relativity |pages=193–252 |volume=3 |place=Berlin | publisher=Springer|contribution-url=http://www.univ-nancy2.fr/DepPhilo/walter/}} |
|||
*{{Citation| author=Zahar, E. |year=2001 |title=Poincare's Philosophy: From Conventionalism to Phenomenology |publisher=Open Court Pub Co|place=Chicago|isbn=081269435X}} |
|||
;Non-mainstream |
|||
* {{Citation | author=Keswani, G.H., | year=1965| journal=Brit. J. Phil. Sci. | title= Origin and Concept of Relativity, Part I |volume=15| issue=60|pages=286–306 |doi=10.1093/bjps/XV.60.286}} |
|||
* {{Citation | author=Keswani, G.H., | year=1965 | journal=Brit. J. Phil. Sci. | title= Origin and Concept of Relativity, Part II|volume=16| pages=19–32| issue=61| doi=10.1093/bjps/XVI.61.19}} |
|||
* {{Citation | author=Keswani, G.H., | year=11966 | journal=Brit. J. Phil. Sci. | title= Origin and Concept of Relativity, Part III |volume=16|issue=64| pages=273–294| doi=10.1093/bjps/XVI.64.273 }} |
|||
* {{Citation | author=Leveugle, J. | year=2004 |title= La Relativité et Einstein, Planck, Hilbert—Histoire véridique de la Théorie de la Relativitén | publisher=L'Harmattan| place=Pars}} |
|||
* {{Citation | author=Logunov, A.A. | year=2004 | title= [http://arxiv.org/abs/physics/0408077 Henri Poincaré and relativity theory] |publisher=Nauka |place=Moscow |isbn=5-02-033964-4}} |
|||
* {{Citation | author=Whittaker, E.T. | year=1953 | title= A History of the Theories of Aether and Electricity: The Modern Theories 1900–1926| chapter= The Relativity Theory of Poincaré and Lorentz | place=London |publisher=Nelson}} |
|||
==External links== |
==External links== |
||
{{commons category|Henri Poincaré}} |
|||
{{wikiquote}} |
{{wikiquote}} |
||
{{wikisource |
{{wikisource author}} |
||
*{{ |
* {{Gutenberg author |id=5958| name=Henri Poincaré}} |
||
* {{Internet Archive author |sname=Henri Poincaré |sopt=w}} |
|||
*[http://librivox.org/science-and-hypothesis-by-henri-poincare/ Free audio download of Poincaré's ''Science and Hypothesis''], from [[LibriVox]]. |
|||
* {{Librivox author |id=4281}} |
|||
*[[Internet Encyclopedia of Philosophy]]: "[http://www.utm.edu/research/iep/p/poincare.htm Henri Poincare]"—by Mauro Murzi. |
|||
* [http://henripoincarepapers.univ-nantes.fr/en/bibliohp/ Henri Poincaré's Bibliography] |
|||
*[[Internet Encyclopedia of Philosophy]]: "[http://www.utm.edu/research/iep/p/poincare.htm Henri Poincaré] {{Webarchive|url=https://web.archive.org/web/20040202060803/http://www.utm.edu/research/iep/p/poincare.htm |date=2 February 2004 }}" – by Mauro Murzi. |
|||
*[[Internet Encyclopedia of Philosophy]]: "[http://www.iep.utm.edu/poi-math/ Poincaré’s Philosophy of Mathematics]" – by Janet Folina. |
|||
* {{MathGenealogy |id=34227}} |
* {{MathGenealogy |id=34227}} |
||
*[ |
*[https://web.archive.org/web/20090930005045/https://www.informationphilosopher.com/solutions/scientists/poincare/ Henri Poincaré on Information Philosopher] |
||
* {{MacTutor Biography|id=Poincare}} |
* {{MacTutor Biography|id=Poincare}} |
||
*[http:// |
*[http://henripoincarepapers.univ-nantes.fr/chronos.php A timeline of Poincaré's life] University of Nantes (in French). |
||
*[http://henripoincarepapers.univ-nantes.fr Henri Poincaré Papers] University of Nantes (in French). |
|||
*[http://phys-astro.sonoma.edu/brucemedalists/Poincare/index.html Bruce Medal page] |
|||
*[https://web.archive.org/web/20060627062431/https://www.phys-astro.sonoma.edu/BruceMedalists/Poincare/index.html Bruce Medal page] |
|||
*Collins, Graham P., "[http://www.sciam.com/print_version.cfm?articleID=0003848D-1C61-10C7-9C6183414B7F0000 Henri Poincaré, His Conjecture, Copacabana and Higher Dimensions,]" ''[[Scientific American]]'', 9 June 2004. |
|||
*Collins, Graham P., "[https://web.archive.org/web/20071017055831/http://www.sciam.com/print_version.cfm?articleID=0003848D-1C61-10C7-9C6183414B7F0000 Henri Poincaré, His Conjecture, Copacabana and Higher Dimensions]," ''[[Scientific American]]'', 9 June 2004. |
|||
*BBC In Our Time, "[http://www.bbc.co.uk/radio4/history/inourtime/inourtime.shtml Discussion of the Poincaré conjecture,]" 2 November 2006, hosted by Melvynn Bragg. [http://web.archive.org/web/*/http://www.bbc.co.uk/radio4/history/inourtime/inourtime.shtml See Internet Archive] |
|||
*BBC in Our Time, "[https://web.archive.org/web/20090424054425/http://www.bbc.co.uk/radio4/history/inourtime/inourtime.shtml Discussion of the Poincaré conjecture]," 2 November 2006, hosted by [[Melvyn Bragg]]. |
|||
*[http://www.mathpages.com/home/kmath305/kmath305.htm Poincare Contemplates Copernicus] at MathPages |
|||
*[https://web.archive.org/web/20070927190224/http://www.mathpages.com/home/kmath305/kmath305.htm Poincare Contemplates Copernicus] at MathPages |
|||
*H[http://www.youtube.com/user/thedebtgeneration?feature=mhum#p/u/8/5pKrKdNclYs igh Anxieties - The Mathematics of Chaos] (2008) BBC documentary directed by [[David Malone (independent filmmaker)|David Malone]] looking at the influence of Poincare's discoveries on 20th Century mathematics. |
|||
*[https://www.youtube.com/user/thedebtgeneration?feature=mhum#p/u/8/5pKrKdNclYs0 High Anxieties – The Mathematics of Chaos] (2008) BBC documentary directed by [[David Malone (independent filmmaker)|David Malone]] looking at the influence of Poincaré's discoveries on 20th Century mathematics. |
|||
{{s-start}} |
|||
{{Normdaten|LCCN=n/50/020168}} |
|||
{{start box}} |
|||
{{s-culture}} |
{{s-culture}} |
||
{{ |
{{s-bef|before=[[Sully Prudhomme]]}} |
||
{{s-ttl|title=[[List of members of the Académie française#Seat 24|Seat 24]]<br />[[Académie française]]<br />1908–1912|years=}} |
|||
{{s-aft|after=[[Alfred Capus]]}} |
|||
{{s-end}} |
|||
| years=}} |
|||
{{end box}} |
|||
{{philosophy of science}} |
{{philosophy of science}} |
||
{{chaos theory}} |
|||
{{relativity}} |
|||
{{Authority control}} |
|||
<!-- Metadata: see [[Wikipedia:Persondata]] --> |
|||
{{Persondata |
|||
|NAME= Poincaré, Henri |
|||
|ALTERNATIVE NAMES= Poincaré, Jules |
|||
|SHORT DESCRIPTION= [[Mathematician]] and [[physicist]] |
|||
|DATE OF BIRTH= 29 April 1854 |
|||
|PLACE OF BIRTH= [[Nancy]], [[Lorraine (province)|Lorraine]], France |
|||
|DATE OF DEATH= 17 July 1912 |
|||
|PLACE OF DEATH= Paris, France |
|||
}} |
|||
{{DEFAULTSORT:Poincare, Henri}} |
{{DEFAULTSORT:Poincare, Henri}} |
||
[[Category:1854 births]] |
[[Category:1854 births]] |
||
[[Category:1912 deaths]] |
[[Category:1912 deaths]] |
||
[[Category: |
[[Category:Henri Poincaré| ]] |
||
[[Category:French |
[[Category:19th-century French essayists]] |
||
[[Category:French |
[[Category:19th-century French male writers]] |
||
[[Category:19th-century mathematicians]] |
[[Category:19th-century French mathematicians]] |
||
[[Category: |
[[Category:19th-century French non-fiction writers]] |
||
[[Category:19th-century French philosophers]] |
|||
[[Category:20th-century French essayists]] |
|||
[[Category:20th-century French male writers]] |
|||
[[Category:20th-century French mathematicians]] |
|||
[[Category:20th-century French philosophers]] |
|||
[[Category:Algebraic geometers]] |
[[Category:Algebraic geometers]] |
||
[[Category:Burials at Montparnasse Cemetery]] |
|||
[[Category:Chaos theorists]] |
[[Category:Chaos theorists]] |
||
[[Category: |
[[Category:Continental philosophers]] |
||
[[Category: |
[[Category:Corps des mines]] |
||
[[Category:Corresponding members of the Saint Petersburg Academy of Sciences]] |
|||
[[Category:Relativists]] |
|||
[[Category: |
[[Category:Deaths from embolism]] |
||
[[Category: |
[[Category:Determinists]] |
||
[[Category: |
[[Category:Dynamical systems theorists]] |
||
[[Category: |
[[Category:École Polytechnique alumni]] |
||
[[Category: |
[[Category:French fluid dynamicists]] |
||
[[Category: |
[[Category:Foreign associates of the National Academy of Sciences]] |
||
[[Category: |
[[Category:Foreign members of the Royal Society]] |
||
[[Category: |
[[Category:French male essayists]] |
||
[[Category:French male non-fiction writers]] |
|||
[[Category:French male writers]] |
|||
[[Category:French military personnel of the Franco-Prussian War]] |
[[Category:French military personnel of the Franco-Prussian War]] |
||
[[Category:French mining engineers]] |
|||
[[Category:French geometers]] |
|||
[[Category:Hyperbolic geometers]] |
|||
[[Category:Lecturers]] |
|||
[[Category:French mathematical analysts]] |
|||
[[Category:Members of the Académie Française]] |
|||
[[Category:Members of the Royal Netherlands Academy of Arts and Sciences]] |
|||
[[Category:Mines Paris - PSL alumni]] |
|||
[[Category:Officers of the French Academy of Sciences]] |
|||
[[Category:Scientists from Nancy, France]] |
|||
[[Category:Philosophers of logic]] |
|||
[[Category:Philosophers of mathematics]] |
|||
[[Category:Philosophers of psychology]] |
|||
[[Category:French philosophers of science]] |
|||
[[Category:French philosophy academics]] |
|||
[[Category:Philosophy writers]] |
|||
[[Category:Recipients of the Bruce Medal]] |
|||
[[Category:Recipients of the Gold Medal of the Royal Astronomical Society]] |
[[Category:Recipients of the Gold Medal of the Royal Astronomical Society]] |
||
[[Category: |
[[Category:French relativity theorists]] |
||
[[Category:Thermodynamicists]] |
|||
[[Category:Topologists]] |
|||
{{Link GA|es}} |
|||
[[Category:Academic staff of the University of Paris]] |
|||
{{Link GA|ru}} |
|||
[[Category:Recipients of the Matteucci Medal]] |
|||
[[ar:هنري بوانكاريه]] |
|||
[[az:Anri Puankare]] |
|||
[[bn:অঁরি পোয়াঁকারে]] |
|||
[[zh-min-nan:Henri Poincaré]] |
|||
[[bs:Henri Poincaré]] |
|||
[[bg:Анри Поанкаре]] |
|||
[[ca:Henri Poincaré]] |
|||
[[cs:Henri Poincaré]] |
|||
[[da:Henri Poincaré]] |
|||
[[de:Henri Poincaré]] |
|||
[[et:Henri Poincaré]] |
|||
[[el:Ανρί Πουανκαρέ]] |
|||
[[es:Henri Poincaré]] |
|||
[[eo:Henri Poincaré]] |
|||
[[fa:آنری پوانکاره]] |
|||
[[fr:Henri Poincaré]] |
|||
[[fy:Henri Poincaré]] |
|||
[[gl:Henri Poincaré]] |
|||
[[gan:般加黑]] |
|||
[[ko:앙리 푸앵카레]] |
|||
[[hi:आन्री पांकरे]] |
|||
[[hr:Henri Poincaré]] |
|||
[[io:Henri Poincaré]] |
|||
[[it:Henri Poincaré]] |
|||
[[he:אנרי פואנקרה]] |
|||
[[ht:Henri Poincare]] |
|||
[[la:Henricus Poincaré]] |
|||
[[lt:Henri Poincaré]] |
|||
[[hu:Henri Poincaré]] |
|||
[[nl:Henri Poincaré]] |
|||
[[ja:アンリ・ポアンカレ]] |
|||
[[no:Henri Poincaré]] |
|||
[[oc:Henri Poincaré]] |
|||
[[pms:Henri Poincaré]] |
|||
[[pl:Henri Poincaré]] |
|||
[[pt:Henri Poincaré]] |
|||
[[ro:Henri Poincaré]] |
|||
[[ru:Пуанкаре, Анри]] |
|||
[[sq:Henri Poincare]] |
|||
[[simple:Henri Poincaré]] |
|||
[[sk:Henri Poincaré]] |
|||
[[sl:Henri Poincaré]] |
|||
[[sr:Анри Поенкаре]] |
|||
[[fi:Henri Poincaré]] |
|||
[[sv:Henri Poincaré]] |
|||
[[th:อ็องรี ปวงกาเร]] |
|||
[[tr:Henri Poincaré]] |
|||
[[uk:Анрі Пуанкаре]] |
|||
[[vi:Henri Poincaré]] |
|||
[[zh-classical:龐加萊]] |
|||
[[yo:Henri Poincaré]] |
|||
[[zh:儒勒·昂利·庞加莱]] |
|||
Latest revision as of 23:23, 9 December 2024
This article needs additional citations for verification. (April 2016) |
| Special relativity |
|---|
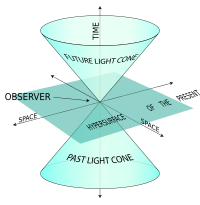 |
Jules Henri Poincaré (UK: /ˈpwæ̃kɑːreɪ/, US: /ˌpwæ̃kɑːˈreɪ/; French: [ɑ̃ʁi pwɛ̃kaʁe] ;[1] 29 April 1854 – 17 July 1912) was a French mathematician, theoretical physicist, engineer, and philosopher of science. He is often described as a polymath, and in mathematics as "The Last Universalist",[2] since he excelled in all fields of the discipline as it existed during his lifetime. He has further been called the "Gauss of modern mathematics".[3] Due to his success in science, influence and philosophy, he has been called "the philosopher par excellence of modern science."[4]
As a mathematician and physicist, he made many original fundamental contributions to pure and applied mathematics, mathematical physics, and celestial mechanics.[5] In his research on the three-body problem, Poincaré became the first person to discover a chaotic deterministic system which laid the foundations of modern chaos theory. Poincaré is regarded as the creator of the field of algebraic topology, and is further credited with introducing automorphic forms. He also made important contributions to algebraic geometry, number theory, complex analysis and Lie theory.[6] He famously introduced the concept of the Poincaré recurrence theorem, which states that a state will eventually return arbitrarily close to its initial state after a sufficiently long time, which has far-reaching consequences.[7] Early in the 20th century he formulated the Poincaré conjecture, which became, over time, one of the famous unsolved problems in mathematics. It was eventually solved in 2002–2003 by Grigori Perelman. Poincaré popularized the use of non-Euclidean geometry in mathematics as well.[8]
Poincaré made clear the importance of paying attention to the invariance of laws of physics under different transformations, and was the first to present the Lorentz transformations in their modern symmetrical form. Poincaré discovered the remaining relativistic velocity transformations and recorded them in a letter to Hendrik Lorentz in 1905. Thus he obtained perfect invariance of all of Maxwell's equations, an important step in the formulation of the theory of special relativity, for which he is also credited with laying down the foundations for,[9] further writing foundational papers in 1905.[10] He first proposed gravitational waves (ondes gravifiques) emanating from a body and propagating at the speed of light as being required by the Lorentz transformations, doing so in 1905.[11] In 1912, he wrote an influential paper which provided a mathematical argument for quantum mechanics.[12][13] Poincaré also laid the seeds of the discovery of radioactivity through his interest and study of X-rays, which influenced physicist Henri Becquerel, who then discovered the phenomena.[14] The Poincaré group used in physics and mathematics was named after him, after he introduced the notion of the group.[15]
Poincaré was considered the dominant figure in mathematics and theoretical physics during his time, and was the most respected mathematician of his time, being described as "the living brain of the rational sciences" by mathematician Paul Painlevé.[16] Philosopher Karl Popper regarded Poincaré as the greatest philosopher of science of all time,[17] with Poincaré also originating the conventionalist view in science.[18] Poincaré was a public intellectual in his time, and personally, he believed in political equality for all, while wary of the influence of anti-intellectual positions that the Catholic Church held at the time.[19] He served as the president of the French Academy of Sciences (1906), the president of Société astronomique de France (1901–1903), and twice the president of Société mathématique de France (1886, 1900).
Life
[edit]Poincaré was born on 29 April 1854 in Cité Ducale neighborhood, Nancy, Meurthe-et-Moselle, into an influential French family.[20] His father Léon Poincaré (1828–1892) was a professor of medicine at the University of Nancy.[21] His younger sister Aline married the spiritual philosopher Émile Boutroux. Another notable member of Henri's family was his cousin, Raymond Poincaré, a fellow member of the Académie française, who was President of France from 1913 to 1920, and three-time Prime Minister of France between 1913 and 1929.[22]
Education
[edit]
During his childhood he was seriously ill for a time with diphtheria and received special instruction from his mother, Eugénie Launois (1830–1897).
In 1862, Henri entered the Lycée in Nancy (now renamed the Lycée Henri-Poincaré in his honour, along with Henri Poincaré University, also in Nancy). He spent eleven years at the Lycée and during this time he proved to be one of the top students in every topic he studied. He excelled in written composition. His mathematics teacher described him as a "monster of mathematics" and he won first prizes in the concours général, a competition between the top pupils from all the Lycées across France. His poorest subjects were music and physical education, where he was described as "average at best".[23] Poor eyesight and a tendency towards absentmindedness may explain these difficulties.[24] He graduated from the Lycée in 1871 with a baccalauréat in both letters and sciences.
During the Franco-Prussian War of 1870, he served alongside his father in the Ambulance Corps.
Poincaré entered the École Polytechnique as the top qualifier in 1873 and graduated in 1875. There he studied mathematics as a student of Charles Hermite, continuing to excel and publishing his first paper (Démonstration nouvelle des propriétés de l'indicatrice d'une surface) in 1874. From November 1875 to June 1878 he studied at the École des Mines, while continuing the study of mathematics in addition to the mining engineering syllabus, and received the degree of ordinary mining engineer in March 1879.[25]
As a graduate of the École des Mines, he joined the Corps des Mines as an inspector for the Vesoul region in northeast France. He was on the scene of a mining disaster at Magny in August 1879 in which 18 miners died. He carried out the official investigation into the accident.
At the same time, Poincaré was preparing for his Doctorate in Science in mathematics under the supervision of Charles Hermite. His doctoral thesis was in the field of differential equations. It was named Sur les propriétés des fonctions définies par les équations aux différences partielles. Poincaré devised a new way of studying the properties of these equations. He not only faced the question of determining the integral of such equations, but also was the first person to study their general geometric properties. He realised that they could be used to model the behaviour of multiple bodies in free motion within the Solar System. He graduated from the University of Paris in 1879.

First scientific achievements
[edit]After receiving his degree, Poincaré began teaching as junior lecturer in mathematics at the University of Caen in Normandy (in December 1879). At the same time he published his first major article concerning the treatment of a class of automorphic functions.
There, in Caen, he met his future wife, Louise Poulain d'Andecy (1857–1934), granddaughter of Isidore Geoffroy Saint-Hilaire and great-granddaughter of Étienne Geoffroy Saint-Hilaire and on 20 April 1881, they married.[26] Together they had four children: Jeanne (born 1887), Yvonne (born 1889), Henriette (born 1891), and Léon (born 1893).
Poincaré immediately established himself among the greatest mathematicians of Europe, attracting the attention of many prominent mathematicians. In 1881 Poincaré was invited to take a teaching position at the Faculty of Sciences of the University of Paris; he accepted the invitation. During the years 1883 to 1897, he taught mathematical analysis in the École Polytechnique.
In 1881–1882, Poincaré created a new branch of mathematics: qualitative theory of differential equations. He showed how it is possible to derive the most important information about the behavior of a family of solutions without having to solve the equation (since this may not always be possible). He successfully used this approach to problems in celestial mechanics and mathematical physics.
Career
[edit]He never fully abandoned his career in the mining administration to mathematics. He worked at the Ministry of Public Services as an engineer in charge of northern railway development from 1881 to 1885. He eventually became chief engineer of the Corps des Mines in 1893 and inspector general in 1910.
Beginning in 1881 and for the rest of his career, he taught at the University of Paris (the Sorbonne). He was initially appointed as the maître de conférences d'analyse (associate professor of analysis).[27] Eventually, he held the chairs of Physical and Experimental Mechanics, Mathematical Physics and Theory of Probability,[28] and Celestial Mechanics and Astronomy.
In 1887, at the young age of 32, Poincaré was elected to the French Academy of Sciences. He became its president in 1906, and was elected to the Académie française on 5 March 1908.
In 1887, he won Oscar II, King of Sweden's mathematical competition for a resolution of the three-body problem concerning the free motion of multiple orbiting bodies. (See three-body problem section below.)
In 1893, Poincaré joined the French Bureau des Longitudes, which engaged him in the synchronisation of time around the world. In 1897 Poincaré backed an unsuccessful proposal for the decimalisation of circular measure, and hence time and longitude.[29] It was this post which led him to consider the question of establishing international time zones and the synchronisation of time between bodies in relative motion. (See work on relativity section below.)
In 1904, he intervened in the trials of Alfred Dreyfus, attacking the spurious scientific claims regarding evidence brought against Dreyfus.
Poincaré was the President of the Société Astronomique de France (SAF), the French astronomical society, from 1901 to 1903.[30]
Students
[edit]Poincaré had two notable doctoral students at the University of Paris, Louis Bachelier (1900) and Dimitrie Pompeiu (1905).[31]
Death
[edit]In 1912, Poincaré underwent surgery for a prostate problem and subsequently died from an embolism on 17 July 1912, in Paris. He was 58 years of age. He is buried in the Poincaré family vault in the Cemetery of Montparnasse, Paris, in section 16 close to the gate Rue Émile-Richard.
A former French Minister of Education, Claude Allègre, proposed in 2004 that Poincaré be reburied in the Panthéon in Paris, which is reserved for French citizens of the highest honour.[32]

Work
[edit]Summary
[edit]Poincaré made many contributions to different fields of pure and applied mathematics such as: celestial mechanics, fluid mechanics, optics, electricity, telegraphy, capillarity, elasticity, thermodynamics, potential theory, Quantum mechanics, theory of relativity and physical cosmology.
Among the specific topics he contributed to are the following:
- algebraic topology (a field that Poincaré virtually invented)
- the theory of analytic functions of several complex variables
- the theory of abelian functions
- algebraic geometry
- the Poincaré conjecture, proven in 2003 by Grigori Perelman.
- Poincaré recurrence theorem
- hyperbolic geometry
- number theory
- the three-body problem
- the theory of diophantine equations
- electromagnetism
- special relativity
- the fundamental group
- In the field of differential equations Poincaré has given many results that are critical for the qualitative theory of differential equations, for example the Poincaré sphere and the Poincaré map.
- Poincaré on "everybody's belief" in the Normal Law of Errors (see normal distribution for an account of that "law")
- Published an influential paper providing a novel mathematical argument in support of quantum mechanics.[12][33]
Three-body problem
[edit]The problem of finding the general solution to the motion of more than two orbiting bodies in the Solar System had eluded mathematicians since Newton's time. This was known originally as the three-body problem and later the n-body problem, where n is any number of more than two orbiting bodies. The n-body solution was considered very important and challenging at the close of the 19th century. Indeed, in 1887, in honour of his 60th birthday, Oscar II, King of Sweden, advised by Gösta Mittag-Leffler, established a prize for anyone who could find the solution to the problem. The announcement was quite specific:
Given a system of arbitrarily many mass points that attract each according to Newton's law, under the assumption that no two points ever collide, try to find a representation of the coordinates of each point as a series in a variable that is some known function of time and for all of whose values the series converges uniformly.
In case the problem could not be solved, any other important contribution to classical mechanics would then be considered to be prizeworthy. The prize was finally awarded to Poincaré, even though he did not solve the original problem. One of the judges, the distinguished Karl Weierstrass, said, "This work cannot indeed be considered as furnishing the complete solution of the question proposed, but that it is nevertheless of such importance that its publication will inaugurate a new era in the history of celestial mechanics." (The first version of his contribution even contained a serious error; for details see the article by Diacu[34] and the book by Barrow-Green[35]). The version finally printed[36] contained many important ideas which led to the theory of chaos. The problem as stated originally was finally solved by Karl F. Sundman for n = 3 in 1912 and was generalised to the case of n > 3 bodies by Qiudong Wang in the 1990s. The series solutions have very slow convergence. It would take millions of terms to determine the motion of the particles for even very short intervals of time, so they are unusable in numerical work.[34]
Work on relativity
[edit]
Local time
[edit]Poincaré's work at the Bureau des Longitudes on establishing international time zones led him to consider how clocks at rest on the Earth, which would be moving at different speeds relative to absolute space (or the "luminiferous aether"), could be synchronised. At the same time Dutch theorist Hendrik Lorentz was developing Maxwell's theory into a theory of the motion of charged particles ("electrons" or "ions"), and their interaction with radiation. In 1895 Lorentz had introduced an auxiliary quantity (without physical interpretation) called "local time" [37] and introduced the hypothesis of length contraction to explain the failure of optical and electrical experiments to detect motion relative to the aether (see Michelson–Morley experiment).[38] Poincaré was a constant interpreter (and sometimes friendly critic) of Lorentz's theory. Poincaré as a philosopher was interested in the "deeper meaning". Thus he interpreted Lorentz's theory and in so doing he came up with many insights that are now associated with special relativity. In The Measure of Time (1898), Poincaré said, "A little reflection is sufficient to understand that all these affirmations have by themselves no meaning. They can have one only as the result of a convention." He also argued that scientists have to set the constancy of the speed of light as a postulate to give physical theories the simplest form.[39] Based on these assumptions he discussed in 1900 Lorentz's "wonderful invention" of local time and remarked that it arose when moving clocks are synchronised by exchanging light signals assumed to travel with the same speed in both directions in a moving frame.[40]
Principle of relativity and Lorentz transformations
[edit]In 1881 Poincaré described hyperbolic geometry in terms of the hyperboloid model, formulating transformations leaving invariant the Lorentz interval , which makes them mathematically equivalent to the Lorentz transformations in 2+1 dimensions.[41][42] In addition, Poincaré's other models of hyperbolic geometry (Poincaré disk model, Poincaré half-plane model) as well as the Beltrami–Klein model can be related to the relativistic velocity space (see Gyrovector space).
In 1892 Poincaré developed a mathematical theory of light including polarization. His vision of the action of polarizers and retarders, acting on a sphere representing polarized states, is called the Poincaré sphere.[43] It was shown that the Poincaré sphere possesses an underlying Lorentzian symmetry, by which it can be used as a geometrical representation of Lorentz transformations and velocity additions.[44]
He discussed the "principle of relative motion" in two papers in 1900[40][45] and named it the principle of relativity in 1904, according to which no physical experiment can discriminate between a state of uniform motion and a state of rest.[46] In 1905 Poincaré wrote to Lorentz about Lorentz's paper of 1904, which Poincaré described as a "paper of supreme importance". In this letter he pointed out an error Lorentz had made when he had applied his transformation to one of Maxwell's equations, that for charge-occupied space, and also questioned the time dilation factor given by Lorentz.[47] In a second letter to Lorentz, Poincaré gave his own reason why Lorentz's time dilation factor was indeed correct after all—it was necessary to make the Lorentz transformation form a group—and he gave what is now known as the relativistic velocity-addition law.[48] Poincaré later delivered a paper at the meeting of the Academy of Sciences in Paris on 5 June 1905 in which these issues were addressed. In the published version of that he wrote:[49]
The essential point, established by Lorentz, is that the equations of the electromagnetic field are not altered by a certain transformation (which I will call by the name of Lorentz) of the form:
and showed that the arbitrary function must be unity for all (Lorentz had set by a different argument) to make the transformations form a group. In an enlarged version of the paper that appeared in 1906 Poincaré pointed out that the combination is invariant. He noted that a Lorentz transformation is merely a rotation in four-dimensional space about the origin by introducing as a fourth imaginary coordinate, and he used an early form of four-vectors.[50] Poincaré expressed a lack of interest in a four-dimensional reformulation of his new mechanics in 1907, because in his opinion the translation of physics into the language of four-dimensional geometry would entail too much effort for limited profit.[51] So it was Hermann Minkowski who worked out the consequences of this notion in 1907.[51][52]
Mass–energy relation
[edit]Like others before, Poincaré (1900) discovered a relation between mass and electromagnetic energy. While studying the conflict between the action/reaction principle and Lorentz ether theory, he tried to determine whether the center of gravity still moves with a uniform velocity when electromagnetic fields are included.[40] He noticed that the action/reaction principle does not hold for matter alone, but that the electromagnetic field has its own momentum. Poincaré concluded that the electromagnetic field energy of an electromagnetic wave behaves like a fictitious fluid (fluide fictif) with a mass density of E/c2. If the center of mass frame is defined by both the mass of matter and the mass of the fictitious fluid, and if the fictitious fluid is indestructible—it's neither created or destroyed—then the motion of the center of mass frame remains uniform. But electromagnetic energy can be converted into other forms of energy. So Poincaré assumed that there exists a non-electric energy fluid at each point of space, into which electromagnetic energy can be transformed and which also carries a mass proportional to the energy. In this way, the motion of the center of mass remains uniform. Poincaré said that one should not be too surprised by these assumptions, since they are only mathematical fictions.
However, Poincaré's resolution led to a paradox when changing frames: if a Hertzian oscillator radiates in a certain direction, it will suffer a recoil from the inertia of the fictitious fluid. Poincaré performed a Lorentz boost (to order v/c) to the frame of the moving source. He noted that energy conservation holds in both frames, but that the law of conservation of momentum is violated. This would allow perpetual motion, a notion which he abhorred. The laws of nature would have to be different in the frames of reference, and the relativity principle would not hold. Therefore, he argued that also in this case there has to be another compensating mechanism in the ether.
Poincaré himself came back to this topic in his St. Louis lecture (1904).[46] He rejected[53] the possibility that energy carries mass and criticized his own solution to compensate the above-mentioned problems:
The apparatus will recoil as if it were a cannon and the projected energy a ball, and that contradicts the principle of Newton, since our present projectile has no mass; it is not matter, it is energy. [..] Shall we say that the space which separates the oscillator from the receiver and which the disturbance must traverse in passing from one to the other, is not empty, but is filled not only with ether, but with air, or even in inter-planetary space with some subtile, yet ponderable fluid; that this matter receives the shock, as does the receiver, at the moment the energy reaches it, and recoils, when the disturbance leaves it? That would save Newton's principle, but it is not true. If the energy during its propagation remained always attached to some material substratum, this matter would carry the light along with it and Fizeau has shown, at least for the air, that there is nothing of the kind. Michelson and Morley have since confirmed this. We might also suppose that the motions of matter proper were exactly compensated by those of the ether; but that would lead us to the same considerations as those made a moment ago. The principle, if thus interpreted, could explain anything, since whatever the visible motions we could imagine hypothetical motions to compensate them. But if it can explain anything, it will allow us to foretell nothing; it will not allow us to choose between the various possible hypotheses, since it explains everything in advance. It therefore becomes useless.
In the above quote he refers to the Hertz assumption of total aether entrainment that was falsified by the Fizeau experiment but that experiment does indeed show that that light is partially "carried along" with a substance. Finally in 1908[54] he revisits the problem and ends with abandoning the principle of reaction altogether in favor of supporting a solution based in the inertia of aether itself.
But we have seen above that Fizeau's experiment does not permit of our retaining the theory of Hertz; it is necessary therefore to adopt the theory of Lorentz, and consequently to renounce the principle of reaction.
He also discussed two other unexplained effects: (1) non-conservation of mass implied by Lorentz's variable mass , Abraham's theory of variable mass and Kaufmann's experiments on the mass of fast moving electrons and (2) the non-conservation of energy in the radium experiments of Marie Curie.
It was Albert Einstein's concept of mass–energy equivalence (1905) that a body losing energy as radiation or heat was losing mass of amount m = E/c2 that resolved[55] Poincaré's paradox, without using any compensating mechanism within the ether.[56] The Hertzian oscillator loses mass in the emission process, and momentum is conserved in any frame. However, concerning Poincaré's solution of the Center of Gravity problem, Einstein noted that Poincaré's formulation and his own from 1906 were mathematically equivalent.[57]
Gravitational waves
[edit]In 1905 Poincaré first proposed gravitational waves (ondes gravifiques) emanating from a body and propagating at the speed of light. He wrote:
It has become important to examine this hypothesis more closely and in particular to ask in what ways it would require us to modify the laws of gravitation. That is what I have tried to determine; at first I was led to assume that the propagation of gravitation is not instantaneous, but happens with the speed of light.[58][49]
Poincaré and Einstein
[edit]Einstein's first paper on relativity was published three months after Poincaré's short paper,[49] but before Poincaré's longer version.[50] Einstein relied on the principle of relativity to derive the Lorentz transformations and used a similar clock synchronisation procedure (Einstein synchronisation) to the one that Poincaré (1900) had described, but Einstein's paper was remarkable in that it contained no references at all. Poincaré never acknowledged Einstein's work on special relativity. However, Einstein expressed sympathy with Poincaré's outlook obliquely in a letter to Hans Vaihinger on 3 May 1919, when Einstein considered Vaihinger's general outlook to be close to his own and Poincaré's to be close to Vaihinger's.[59] In public, Einstein acknowledged Poincaré posthumously in the text of a lecture in 1921 titled "Geometrie und Erfahrung (Geometry and Experience)" in connection with non-Euclidean geometry, but not in connection with special relativity. A few years before his death, Einstein commented on Poincaré as being one of the pioneers of relativity, saying "Lorentz had already recognized that the transformation named after him is essential for the analysis of Maxwell's equations, and Poincaré deepened this insight still further ....".[60]
Assessments on Poincaré and relativity
[edit]Poincaré's work in the development of special relativity is well recognised,[55] though most historians stress that despite many similarities with Einstein's work, the two had very different research agendas and interpretations of the work.[61] Poincaré developed a similar physical interpretation of local time and noticed the connection to signal velocity, but contrary to Einstein he continued to use the ether-concept in his papers and argued that clocks at rest in the ether show the "true" time, and moving clocks show the local time. So Poincaré tried to keep the relativity principle in accordance with classical concepts, while Einstein developed a mathematically equivalent kinematics based on the new physical concepts of the relativity of space and time.[62][63][64][65][66]
While this is the view of most historians, a minority go much further, such as E. T. Whittaker, who held that Poincaré and Lorentz were the true discoverers of relativity.[67]
Algebra and number theory
[edit]Poincaré introduced group theory to physics, and was the first to study the group of Lorentz transformations.[68][69] He also made major contributions to the theory of discrete groups and their representations.


Topology
[edit]The subject is clearly defined by Felix Klein in his "Erlangen Program" (1872): the geometry invariants of arbitrary continuous transformation, a kind of geometry. The term "topology" was introduced, as suggested by Johann Benedict Listing, instead of previously used "Analysis situs". Some important concepts were introduced by Enrico Betti and Bernhard Riemann. But the foundation of this science, for a space of any dimension, was created by Poincaré. His first article on this topic appeared in 1894.[70]
His research in geometry led to the abstract topological definition of homotopy and homology. He also first introduced the basic concepts and invariants of combinatorial topology, such as Betti numbers and the fundamental group. Poincaré proved a formula relating the number of edges, vertices and faces of n-dimensional polyhedron (the Euler–Poincaré theorem) and gave the first precise formulation of the intuitive notion of dimension.[71]
Astronomy and celestial mechanics
[edit]
Poincaré published two now classical monographs, "New Methods of Celestial Mechanics" (1892–1899) and "Lectures on Celestial Mechanics" (1905–1910). In them, he successfully applied the results of their research to the problem of the motion of three bodies and studied in detail the behavior of solutions (frequency, stability, asymptotic, and so on). They introduced the small parameter method, fixed points, integral invariants, variational equations, the convergence of the asymptotic expansions. Generalizing a theory of Bruns (1887), Poincaré showed that the three-body problem is not integrable. In other words, the general solution of the three-body problem can not be expressed in terms of algebraic and transcendental functions through unambiguous coordinates and velocities of the bodies. His work in this area was the first major achievement in celestial mechanics since Isaac Newton.[72]
These monographs include an idea of Poincaré, which later became the basis for mathematical "chaos theory" (see, in particular, the Poincaré recurrence theorem) and the general theory of dynamical systems. Poincaré authored important works on astronomy for the equilibrium figures of a gravitating rotating fluid. He introduced the important concept of bifurcation points and proved the existence of equilibrium figures such as the non-ellipsoids, including ring-shaped and pear-shaped figures, and their stability. For this discovery, Poincaré received the Gold Medal of the Royal Astronomical Society (1900).[73]
Differential equations and mathematical physics
[edit]After defending his doctoral thesis on the study of singular points of the system of differential equations, Poincaré wrote a series of memoirs under the title "On curves defined by differential equations" (1881–1882).[74] In these articles, he built a new branch of mathematics, called "qualitative theory of differential equations". Poincaré showed that even if the differential equation can not be solved in terms of known functions, yet from the very form of the equation, a wealth of information about the properties and behavior of the solutions can be found. In particular, Poincaré investigated the nature of the trajectories of the integral curves in the plane, gave a classification of singular points (saddle, focus, center, node), introduced the concept of a limit cycle and the loop index, and showed that the number of limit cycles is always finite, except for some special cases. Poincaré also developed a general theory of integral invariants and solutions of the variational equations. For the finite-difference equations, he created a new direction – the asymptotic analysis of the solutions. He applied all these achievements to study practical problems of mathematical physics and celestial mechanics, and the methods used were the basis of its topological works.[75]
- The singular points of the integral curves
-
Saddle
-
Focus
-
Center
-
Node
Character
[edit]
Poincaré's work habits have been compared to a bee flying from flower to flower. Poincaré was interested in the way his mind worked; he studied his habits and gave a talk about his observations in 1908 at the Institute of General Psychology in Paris. He linked his way of thinking to how he made several discoveries.
The mathematician Darboux claimed he was un intuitif (an intuitive), arguing that this is demonstrated by the fact that he worked so often by visual representation. Jacques Hadamard wrote that Poincaré's research demonstrated marvelous clarity[76] and Poincaré himself wrote that he believed that logic was not a way to invent but a way to structure ideas and that logic limits ideas.
Toulouse's characterisation
[edit]Poincaré's mental organisation was interesting not only to Poincaré himself but also to Édouard Toulouse, a psychologist of the Psychology Laboratory of the School of Higher Studies in Paris. Toulouse wrote a book entitled Henri Poincaré (1910).[77][78] In it, he discussed Poincaré's regular schedule:
- He worked during the same times each day in short periods of time. He undertook mathematical research for four hours a day, between 10 a.m. and noon then again from 5 p.m. to 7 p.m.. He would read articles in journals later in the evening.
- His normal work habit was to solve a problem completely in his head, then commit the completed problem to paper.
- He was ambidextrous and nearsighted.
- His ability to visualise what he heard proved particularly useful when he attended lectures, since his eyesight was so poor that he could not see properly what the lecturer wrote on the blackboard.
These abilities were offset to some extent by his shortcomings:
- He was physically clumsy and artistically inept.
- He was always in a rush and disliked going back for changes or corrections.
- He never spent a long time on a problem since he believed that the subconscious would continue working on the problem while he consciously worked on another problem.
In addition, Toulouse stated that most mathematicians worked from principles already established while Poincaré started from basic principles each time (O'Connor et al., 2002).
His method of thinking is well summarised as:
Habitué à négliger les détails et à ne regarder que les cimes, il passait de l'une à l'autre avec une promptitude surprenante et les faits qu'il découvrait se groupant d'eux-mêmes autour de leur centre étaient instantanément et automatiquement classés dans sa mémoire (accustomed to neglecting details and to looking only at mountain tops, he went from one peak to another with surprising rapidity, and the facts he discovered, clustering around their center, were instantly and automatically pigeonholed in his memory).
— Belliver (1956)
Publications
[edit]- Leçons sur la théorie mathématique de la lumière (in French). Paris: Carrè. 1889.
- Solutions periodiques, non-existence des integrales uniformes, solutions asymptotiques (in French). Vol. 1. Paris: Gauthier-Villars. 1892.
- Methodes de mm. Newcomb, Gylden, Lindstedt et Bohlin (in French). Vol. 2. Paris: Gauthier-Villars. 1893.
- Oscillations électriques (in French). Paris: Carrè. 1894.
- Invariants integraux, solutions periodiques du deuxieme genre, solutions doublement asymptotiques (in French). Vol. 3. Paris: Gauthier-Villars. 1899.
- Valeur de la science (in French). Paris: Flammarion. 1900.
- Electricité et optique (in French). Paris: Carrè & Naud. 1901.
- Science et l'hypothèse (in French). Paris: Flammarion. 1902.
- Thermodynamique (in French). Paris: Gauthier-Villars. 1908.
- Dernières pensées (in French). Paris: Flammarion. 1913.
- Science et méthode. London: Nelson and Sons. 1914.
Legacy
[edit]Poincaré is credited with laying the foundations of special relativity,[10][9] with some arguing that he should be credited with its creation.[79] He is said to have "dominated the mathematics and the theoretical physics of his time", and that "he was without a doubt the most admired mathematician while he was alive, and he remains today one of the world's most emblematic scientific figures."[80] Poincaré is regarded as a "universal specialist", as he refined celestial mechanics, he progressed nearly all parts of mathematics of his time, including creating new subjects, is a father of special relativity, participated in all the great debates of his time in physics, was a major actor in the great epistemological debates of his day in relation to philosophy of science, and Poincaré was the one who investigated the 1879 Magny shaft firedamp explosion as an engineer.[80] Due to the breadth of his research, Poincaré was the only member to be elected to every section of the French Academy of Sciences of the time, those being geometry, mechanics, physics, astronomy and navigation.[81]
Physicist Henri Becquerel nominated Poincaré for a Nobel Prize in 1904, as Becquerel took note that "Poincaré's mathematical and philosophical genius surveyed all of physics and was among those that contributed most to human progress by giving researchers a solid basis for their journeys into the unknown."[82] After his death, he was praised by many intellectual figures of his time, as the author Marie Bonaparte wrote to his widowed wife Louise that "He was – as you know better than anyone – not only the greatest thinker, the most powerful genius of our time – but also a deep and incomparable heart; and having been close to him remains the precious memory of a whole life."[83]
Mathematician E.T. Bell titled Poincaré as "The Last Universalist", and noted his prowess in many fields, stating that:[84]
Poincaré was the last man to take practically all mathematics, both pure and applied, as his province . . . few mathematicians have had the breadth of philosophical vision that Poincaré had and none is his superior in the gift of clear exposition.
When philosopher and mathematician Bertrand Russell was asked who was the greatest man that France had produced in modern times, he instantly replied "Poincaré".[84] Bell noted that if Poincaré had been as strong in practical science as he was in theoretical, he might have "made a fourth with the incomparable three, Archimedes, Newton, and Gauss."[85]
Bell further noted his powerful memory, one that was even superior to Leonhard Euler's, stating that:[85]
His principal diversion was reading, where his unusual talents first showed up. A book once read - at incredible speed - became a permanent possession, and he could always state the page and line where a particular thing occurred. He retained this powerful memory all his life. This rare faculty, which Poincaré shared with Euler who had it in a lesser degree, might be called visual or spatial memory. In temporal memory - the ability to recall with uncanny precision a sequence of events long passed — he was also unusually strong.
Bell notes the terrible eyesight of Poincaré, he almost completely remembered formulas and theorems by ear, and "unable to see the board distinctly when he became a student of advanced mathematics, he sat back and listened, following and remembering perfectly without taking notes - an easy feat for him, but one incomprehensible to most mathematicians."[85]
Honours
[edit]Awards
- Oscar II, King of Sweden's mathematical competition (1887)
- Foreign member of the Royal Netherlands Academy of Arts and Sciences (1897)[86]
- American Philosophical Society (1899)
- Gold Medal of the Royal Astronomical Society of London (1900)
- Commander of the Legion of Honour (1903)[87]
- Bolyai Prize (1905)
- Matteucci Medal (1905)
- French Academy of Sciences (1906)
- Académie française (1909)
- Bruce Medal (1911)
Named after him
- Institut Henri Poincaré (mathematics and theoretical physics centre)
- Poincaré Prize (Mathematical Physics International Prize)
- Annales Henri Poincaré (Scientific Journal)
- Poincaré Seminar (nicknamed "Bourbaphy")
- The crater Poincaré on the Moon
- Asteroid 2021 Poincaré
- List of things named after Henri Poincaré
Henri Poincaré did not receive the Nobel Prize in Physics, but he had influential advocates like Henri Becquerel or committee member Gösta Mittag-Leffler.[88][89] The nomination archive reveals that Poincaré received a total of 51 nominations between 1904 and 1912, the year of his death.[90] Of the 58 nominations for the 1910 Nobel Prize, 34 named Poincaré.[90] Nominators included Nobel laureates Hendrik Lorentz and Pieter Zeeman (both of 1902), Marie Curie (of 1903), Albert Michelson (of 1907), Gabriel Lippmann (of 1908) and Guglielmo Marconi (of 1909).[90]
The fact that renowned theoretical physicists like Poincaré, Boltzmann or Gibbs were not awarded the Nobel Prize is seen as evidence that the Nobel committee had more regard for experimentation than theory.[91][92] In Poincaré's case, several of those who nominated him pointed out that the greatest problem was to name a specific discovery, invention, or technique.[88]
Philosophy
[edit]
Poincaré had philosophical views opposite to those of Bertrand Russell and Gottlob Frege, who believed that mathematics was a branch of logic. Poincaré strongly disagreed, claiming that intuition was the life of mathematics. Poincaré gives an interesting point of view in his 1902 book Science and Hypothesis:
For a superficial observer, scientific truth is beyond the possibility of doubt; the logic of science is infallible, and if the scientists are sometimes mistaken, this is only from their mistaking its rule.
Poincaré believed that arithmetic is synthetic. He argued that Peano's axioms cannot be proven non-circularly with the principle of induction (Murzi, 1998), therefore concluding that arithmetic is a priori synthetic and not analytic. Poincaré then went on to say that mathematics cannot be deduced from logic since it is not analytic. His views were similar to those of Immanuel Kant (Kolak, 2001, Folina 1992). He strongly opposed Cantorian set theory, objecting to its use of impredicative definitions.[93]
However, Poincaré did not share Kantian views in all branches of philosophy and mathematics. For example, in geometry, Poincaré believed that the structure of non-Euclidean space can be known analytically. Poincaré held that convention plays an important role in physics. His view (and some later, more extreme versions of it) came to be known as "conventionalism".[94] Poincaré believed that Newton's first law was not empirical but is a conventional framework assumption for mechanics (Gargani, 2012).[95] He also believed that the geometry of physical space is conventional. He considered examples in which either the geometry of the physical fields or gradients of temperature can be changed, either describing a space as non-Euclidean measured by rigid rulers, or as a Euclidean space where the rulers are expanded or shrunk by a variable heat distribution. However, Poincaré thought that we were so accustomed to Euclidean geometry that we would prefer to change the physical laws to save Euclidean geometry rather than shift to non-Euclidean physical geometry.[96]
Free will
[edit]Poincaré's famous lectures before the Société de Psychologie in Paris (published as Science and Hypothesis, The Value of Science, and Science and Method) were cited by Jacques Hadamard as the source for the idea that creativity and invention consist of two mental stages, first random combinations of possible solutions to a problem, followed by a critical evaluation.[97]
Although he most often spoke of a deterministic universe, Poincaré said that the subconscious generation of new possibilities involves chance.
It is certain that the combinations which present themselves to the mind in a kind of sudden illumination after a somewhat prolonged period of unconscious work are generally useful and fruitful combinations... all the combinations are formed as a result of the automatic action of the subliminal ego, but those only which are interesting find their way into the field of consciousness... A few only are harmonious, and consequently at once useful and beautiful, and they will be capable of affecting the geometrician's special sensibility I have been speaking of; which, once aroused, will direct our attention upon them, and will thus give them the opportunity of becoming conscious... In the subliminal ego, on the contrary, there reigns what I would call liberty, if one could give this name to the mere absence of discipline and to disorder born of chance.[98]
Poincaré's two stages—random combinations followed by selection—became the basis for Daniel Dennett's two-stage model of free will.[99]
Bibliography
[edit]Poincaré's writings in English translation
[edit]Popular writings on the philosophy of science:
- Poincaré, Henri (1902–1908), The Foundations of Science, New York: Science Press; reprinted in 1921; this book includes the English translations of Science and Hypothesis (1902), The Value of Science (1905), Science and Method (1908).
- 1905. "Science and Hypothesis", The Walter Scott Publishing Co.
- 1906. "The End of Matter", Athenæum
- 1913. "The New Mechanics", The Monist, Vol. XXIII.
- 1913. "The Relativity of Space", The Monist, Vol. XXIII.
- 1913. Last Essays., New York: Dover reprint, 1963
- 1956. Chance. In James R. Newman, ed., The World of Mathematics (4 Vols).
- 1958. The Value of Science, New York: Dover.
- 1895. Analysis Situs (PDF), archived (PDF) from the original on 27 March 2012. The first systematic study of topology.
- 1890. Poincaré, Henri (2017). The three-body problem and the equations of dynamics: Poincaré's foundational work on dynamical systems theory. Translated by Popp, Bruce D. Cham, Switzerland: Springer International Publishing. ISBN 978-3-319-52898-4.
- 1892–99. New Methods of Celestial Mechanics, 3 vols. English trans., 1967. ISBN 1-56396-117-2.
- 1905. "The Capture Hypothesis of J. J. See", The Monist, Vol. XV.
- 1905–10. Lessons of Celestial Mechanics.
On the philosophy of mathematics:
- Ewald, William B., ed., 1996. From Kant to Hilbert: A Source Book in the Foundations of Mathematics, 2 vols. Oxford Univ. Press. Contains the following works by Poincaré:
- 1894, "On the Nature of Mathematical Reasoning", 972–981.
- 1898, "On the Foundations of Geometry", 982–1011.
- 1900, "Intuition and Logic in Mathematics", 1012–1020.
- 1905–06, "Mathematics and Logic, I–III", 1021–1070.
- 1910, "On Transfinite Numbers", 1071–1074.
- 1905. "The Principles of Mathematical Physics", The Monist, Vol. XV.
- 1910. "The Future of Mathematics", The Monist, Vol. XX.
- 1910. "Mathematical Creation", The Monist, Vol. XX.
Other:
- 1904. Maxwell's Theory and Wireless Telegraphy, New York, McGraw Publishing Company.
- 1905. "The New Logics", The Monist, Vol. XV.
- 1905. "The Latest Efforts of the Logisticians", The Monist, Vol. XV.
Exhaustive bibliography of English translations:
- 1892–2017. Henri Poincaré Papers, archived from the original on 1 August 2020.
See also
[edit]Concepts
[edit]- Poincaré–Andronov–Hopf bifurcation
- Poincaré complex – an abstraction of the singular chain complex of a closed, orientable manifold
- Poincaré duality
- Poincaré disk model
- Poincaré expansion
- Poincaré gauge
- Poincaré group
- Poincaré half-plane model
- Poincaré homology sphere
- Poincaré inequality
- Poincaré lemma
- Poincaré map
- Poincaré residue
- Poincaré series (modular form)
- Poincaré space
- Poincaré metric
- Poincaré plot
- Poincaré polynomial
- Poincaré series
- Poincaré sphere
- Poincaré–Einstein synchronisation
- Poincaré–Lelong equation
- Poincaré–Lindstedt method
- Poincaré–Lindstedt perturbation theory
- Poincaré–Steklov operator
- Euler–Poincaré characteristic
- Neumann–Poincaré operator
- Reflecting Function
Theorems
[edit]Here is a list of theorems proved by Poincaré:
- Poincaré's recurrence theorem: certain systems will, after a sufficiently long but finite time, return to a state very close to the initial state.
- Poincaré–Bendixson theorem: a statement about the long-term behaviour of orbits of continuous dynamical systems on the plane, cylinder, or two-sphere.
- Poincaré–Hopf theorem: a generalization of the hairy-ball theorem, which states that there is no smooth vector field on a sphere having no sources or sinks.
- Poincaré–Lefschetz duality theorem: a version of Poincaré duality in geometric topology, applying to a manifold with boundary
- Poincaré separation theorem: gives the upper and lower bounds of eigenvalues of a real symmetric matrix B'AB that can be considered as the orthogonal projection of a larger real symmetric matrix A onto a linear subspace spanned by the columns of B.
- Poincaré–Birkhoff theorem: every area-preserving, orientation-preserving homeomorphism of an annulus that rotates the two boundaries in opposite directions has at least two fixed points.
- Poincaré–Birkhoff–Witt theorem: an explicit description of the universal enveloping algebra of a Lie algebra.
- Poincaré–Bjerknes circulation theorem: theorem about a conservation of quantity for the rotating frame.
- Poincaré conjecture (now a theorem): Every simply connected, closed 3-manifold is homeomorphic to the 3-sphere.
- Poincaré–Miranda theorem: a generalization of the intermediate value theorem to n dimensions.
Other
[edit]References
[edit]Footnotes
[edit]- ^ "Poincaré, n.", Oxford English Dictionary (3 ed.), Oxford University Press, 2 March 2023, doi:10.1093/oed/3697720964, retrieved 2 December 2024
- ^ Ginoux, J. M.; Gerini, C. (2013). Henri Poincaré: A Biography Through the Daily Papers. World Scientific. pp. vii–viii, xiii. doi:10.1142/8956. ISBN 978-981-4556-61-3.
- ^ Folina, Janet (1992). Poincaré and the Philosophy of Mathematics. London: Palgrave Macmillan UK. pp. xii. doi:10.1007/978-1-349-22119-6. ISBN 978-1-349-22121-9.
- ^ Moulton, Forest Ray; Jeffries, Justus J. (1945). The Autobiography of Science. Doubleday & Company. p. 509.
- ^ Hadamard, Jacques (July 1922). "The early scientific work of Henri Poincaré". The Rice Institute Pamphlet. 9 (3): 111–183.
- ^ Gray, Jeremy (2013). Henri Poincaré: A Scientific Biography. Princeton University Press. pp. 3, 16, 492. ISBN 978-0-691-15271-4.
- ^ Oxtoby, John C. (1980), "The Poincaré Recurrence Theorem", Measure and Category, Graduate Texts in Mathematics, vol. 2, New York, NY: Springer New York, pp. 65–69, doi:10.1007/978-1-4684-9339-9_17, ISBN 978-1-4684-9341-2, retrieved 1 December 2024
- ^ Heinzmann, Gerhard; Stump, David (22 November 2021), "Henri Poincaré", Stanford Encyclopedia of Philosophy, Stanford University, retrieved 3 December 2024
- ^ a b Ginoux, Jean-Marc (2024). Poincaré, Einstein and the Discovery of Special Relativity: An End to the Controversy. History of Physics. Springer. p. 47. ISBN 978-3-031-51386-2.
- ^ a b Marchal, C. (1997), Dvorak, R.; Henrard, J. (eds.), "Henri Poincaré: A Decisive Contribution to Special Relativity", The Dynamical Behaviour of our Planetary System, Dordrecht: Springer Netherlands, pp. 403–413, doi:10.1007/978-94-011-5510-6_30, ISBN 978-94-010-6320-3, retrieved 2 December 2024
- ^ Cervantes-Cota, Jorge L.; Galindo-Uribarri, Salvador; Smoot, George F. (13 September 2016). "A Brief History of Gravitational Waves". Universe. 2 (3): 22. arXiv:1609.09400. doi:10.3390/universe2030022. ISSN 2218-1997.
- ^ a b McCormmach, Russell (Spring 1967), "Henri Poincaré and the Quantum Theory", Isis, 58 (1): 37–55, doi:10.1086/350182, S2CID 120934561
- ^ Prentis, Jeffrey J. (1 April 1995). "Poincaré's proof of the quantum discontinuity of nature". American Journal of Physics. 63 (4): 339–350. doi:10.1119/1.17919. ISSN 0002-9505.
- ^ Radvanyi, Pierre; Villain, Jacques (1 November 2017). "The discovery of radioactivity". Comptes Rendus. Physique. 18 (9–10): 544–550. doi:10.1016/j.crhy.2017.10.008. ISSN 1878-1535.
- ^ Bacry, Henri (2004). "The foundations of the poincaré group and the validity of general relativity". Reports on Mathematical Physics. 53 (3): 443–473. doi:10.1016/S0034-4877(04)90029-8.
- ^ Bell, E.T. (1937). Men of Mathematics. Vol. II. Penguin Books. p. 611.
- ^ Charpentier, Éric; Ghys, E.; Lesne, Annick, eds. (2010). The Scientific Legacy of Poincaré. History of Mathematics. Translated by Bowman, Joshua. The London Mathematical Society. p. 373. ISBN 978-0-8218-4718-3.
- ^ Merritt, David (2017). "Cosmology and convention". Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics. 57: 41–52. arXiv:1703.02389. doi:10.1016/j.shpsb.2016.12.002.
- ^ Gray, Jeremy (2013). Henri Poincaré: A Scientific Biography. Princeton University Press. pp. 24, 201. ISBN 978-0-691-15271-4.
- ^ Belliver, 1956
- ^ Sagaret, 1911
- ^ The Internet Encyclopedia of Philosophy Archived 2 February 2004 at the Wayback Machine Jules Henri Poincaré article by Mauro Murzi – Retrieved November 2006.
- ^ O'Connor et al., 2002
- ^ Carl, 1968
- ^ F. Verhulst
- ^ Rollet, Laurent (15 November 2012). "Jeanne Louise Poulain d'Andecy, épouse Poincaré (1857–1934)". Bulletin de la Sabix. Société des amis de la Bibliothèque et de l'Histoire de l'École polytechnique (in French) (51): 18–27. doi:10.4000/sabix.1131. ISSN 0989-3059. S2CID 190028919.
- ^ Sageret, 1911
- ^ Mazliak, Laurent (14 November 2014). "Poincaré's Odds". In Duplantier, B.; Rivasseau, V. (eds.). Poincaré 1912–2012 : Poincaré Seminar 2012. Progress in Mathematical Physics. Vol. 67. Basel: Springer. p. 150. ISBN 9783034808347.
- ^ see Galison 2003
- ^ "Bulletin de la Société astronomique de France, 1911, vol. 25, pp. 581–586". 1911.
- ^ Mathematics Genealogy Project Archived 5 October 2007 at the Wayback Machine North Dakota State University. Retrieved April 2008.
- ^ "Lorentz, Poincaré et Einstein". Archived from the original on 27 November 2004.
- ^ Irons, F. E. (August 2001), "Poincaré's 1911–12 proof of quantum discontinuity interpreted as applying to atoms", American Journal of Physics, 69 (8): 879–884, Bibcode:2001AmJPh..69..879I, doi:10.1119/1.1356056
- ^ a b Diacu, Florin (1996), "The solution of the n-body Problem", The Mathematical Intelligencer, 18 (3): 66–70, doi:10.1007/BF03024313, S2CID 119728316
- ^ Barrow-Green, June (1997). Poincaré and the three body problem. History of Mathematics. Vol. 11. Providence, RI: American Mathematical Society. ISBN 978-0821803677. OCLC 34357985.
- ^ Poincaré, J. Henri (2017). The three-body problem and the equations of dynamics: Poincaré's foundational work on dynamical systems theory. Popp, Bruce D. (Translator). Cham, Switzerland: Springer International Publishing. ISBN 9783319528984. OCLC 987302273.
- ^ Hsu, Jong-Ping; Hsu, Leonardo (2006), A broader view of relativity: general implications of Lorentz and Poincaré invariance, vol. 10, World Scientific, p. 37, ISBN 978-981-256-651-5, Section A5a, p 37
- ^ Lorentz, Hendrik A. (1895), , Leiden: E.J. Brill
- ^ Poincaré, Henri (1898), , Revue de Métaphysique et de Morale, 6: 1–13
- ^ a b c Poincaré, Henri (1900), , Archives Néerlandaises des Sciences Exactes et Naturelles, 5: 252–278. See also the English translation
- ^ Poincaré, H. (1881). "Sur les applications de la géométrie non-euclidienne à la théorie des formes quadratiques" (PDF). Association Française Pour l'Avancement des Sciences. 10: 132–138. Archived from the original (PDF) on 1 August 2020.
- ^ Reynolds, W. F. (1993). "Hyperbolic geometry on a hyperboloid". The American Mathematical Monthly. 100 (5): 442–455. doi:10.1080/00029890.1993.11990430. JSTOR 2324297. S2CID 124088818.
- ^ Poincaré, H. (1892). "Chapitre XII: Polarisation rotatoire". Théorie mathématique de la lumière II. Paris: Georges Carré.
- ^ Tudor, T. (2018). "Lorentz Transformation, Poincaré Vectors and Poincaré Sphere in Various Branches of Physics". Symmetry. 10 (3): 52. Bibcode:2018Symm...10...52T. doi:10.3390/sym10030052.
- ^ Poincaré, H. (1900), "Les relations entre la physique expérimentale et la physique mathématique", Revue Générale des Sciences Pures et Appliquées, 11: 1163–1175. Reprinted in "Science and Hypothesis", Ch. 9–10.
- ^ a b Poincaré, Henri (1913), , The Foundations of Science (The Value of Science), New York: Science Press, pp. 297–320; article translated from 1904 original
{{citation}}: CS1 maint: postscript (link) available in online chapter from 1913 book - ^ Poincaré, H. (2007), "38.3, Poincaré to H. A. Lorentz, May 1905", in Walter, S. A. (ed.), La correspondance entre Henri Poincaré et les physiciens, chimistes, et ingénieurs, Basel: Birkhäuser, pp. 255–257
- ^ Poincaré, H. (2007), "38.4, Poincaré to H. A. Lorentz, May 1905", in Walter, S. A. (ed.), La correspondance entre Henri Poincaré et les physiciens, chimistes, et ingénieurs, Basel: Birkhäuser, pp. 257–258
- ^ a b c [1] (PDF) Membres de l'Académie des sciences depuis sa création : Henri Poincare. Sur la dynamique de l' electron. Note de H. Poincaré. C.R. T.140 (1905) 1504–1508.
- ^ a b Poincaré, H. (1906), "Sur la dynamique de l'électron (On the Dynamics of the Electron)", Rendiconti del Circolo Matematico Rendiconti del Circolo di Palermo, 21: 129–176, Bibcode:1906RCMP...21..129P, doi:10.1007/BF03013466, hdl:2027/uiug.30112063899089, S2CID 120211823 (Wikisource translation)
- ^ a b Walter, Scott (2007). "Breaking in the 4-Vectors: The Four-Dimensional Movement in Gravitation, 1905–1910". The Genesis of General Relativity. Vol. 3. Dordrecht: Springer Netherlands. pp. 1118–1178. doi:10.1007/978-1-4020-4000-9_18. ISBN 978-1-4020-3999-7.
- ^ Minkowski, Hermann (September 1908). "Raum und Zeit" (PDF). Jahresbericht der Deutschen Mathematiker-Vereinigung. 18: 75–88. Retrieved 11 May 2024.
- ^ Miller 1981, Secondary sources on relativity
- ^ Poincaré, Henri (1908–1913). . The foundations of science (Science and Method). New York: Science Press. pp. 486–522.
- ^ a b Darrigol 2005, Secondary sources on relativity
- ^ Einstein, A. (1905b), "Ist die Trägheit eines Körpers von dessen Energieinhalt abhängig?", Annalen der Physik, 18 (13): 639–643, Bibcode:1905AnP...323..639E, doi:10.1002/andp.19053231314. See also English translation.
- ^ Einstein, A. (1906), "Das Prinzip von der Erhaltung der Schwerpunktsbewegung und die Trägheit der Energie" (PDF), Annalen der Physik, 20 (8): 627–633, Bibcode:1906AnP...325..627E, doi:10.1002/andp.19063250814, S2CID 120361282, archived from the original (PDF) on 18 March 2006
- ^ "Il importait d'examiner cette hypothèse de plus près et en particulier de rechercher quelles modifications elle nous obligerait à apporter aux lois de la gravitation. C'est ce que j'ai cherché à déterminer; j'ai été d'abord conduit à supposer que la propagation de la gravitation n'est pas instantanée, mais se fait avec la vitesse de la lumière."
- ^ The Berlin Years: Correspondence, January 1919 – April 1920 (English translation supplement). The Collected Papers of Albert Einstein. Vol. 9. Princeton U.P. p. 30. See also this letter, with commentary, in Sass, Hans-Martin (1979). "Einstein über "wahre Kultur" und die Stellung der Geometrie im Wissenschaftssystem: Ein Brief Albert Einsteins an Hans Vaihinger vom Jahre 1919". Zeitschrift für allgemeine Wissenschaftstheorie (in German). 10 (2): 316–319. doi:10.1007/bf01802352. JSTOR 25170513. S2CID 170178963.
- ^ Darrigol 2004, Secondary sources on relativity
- ^ Galison 2003 and Kragh 1999, Secondary sources on relativity
- ^ Holton (1988), 196–206
- ^ Hentschel, Klaus (1990). Interpretationen und Fehlinterpretationen der speziellen und der allgemeinen Relativitätstheorie durch Zeitgenossen Albert Einsteins (PhD thesis). University of Hamburg. pp. 3–13.
- ^ Miller (1981), 216–217
- ^ Darrigol (2005), 15–18
- ^ Katzir (2005), 286–288
- ^ Whittaker 1953, Secondary sources on relativity
- ^ Poincaré, Selected works in three volumes. page = 682[full citation needed]
- ^ Poincaré, Henri (1905). "Sur la dynamique de l'électron". Comptes rendus des séances de l'Académie des Sciences. 140: 1504–1508.
- ^ Stillwell 2010, pp. 419–435.
- ^ Aleksandrov, P S (28 February 1972). "Poincaré and topology". Russian Mathematical Surveys. 27 (1): 157–168. doi:10.1070/RM1972v027n01ABEH001365. ISSN 0036-0279.
- ^ J. Stillwell, Mathematics and its history, p. 254
- ^ Darwin, G.H. (1900). "Address Delivered by the President, Professor G. H. Darwin, on presenting the Gold Medal of the Society to M. H. Poincaré". Monthly Notices of the Royal Astronomical Society. 60 (5): 406–416. doi:10.1093/mnras/60.5.406. ISSN 0035-8711.
- ^ French: "Mémoire sur les courbes définies par une équation différentielle"
- ^ Kolmogorov, A.N.; Yushkevich, A.P., eds. (24 March 1998). Mathematics of the 19th century. Vol. 3. Springer. pp. 162–174, 283. ISBN 978-3764358457.
- ^ J. Hadamard. L'oeuvre de H. Poincaré. Acta Mathematica, 38 (1921), p. 208
- ^ Toulouse, Édouard, 1910. Henri Poincaré, E. Flammarion, Paris. 2005.
- ^ Toulouse, E. (2013). Henri Poincare. MPublishing. ISBN 9781418165062. Retrieved 10 October 2014.
- ^ Logunov, A. A. (2004), Henri Poincare and Relativity Theory, pp. 3, 63, 187, arXiv:physics/0408077
- ^ a b Charpentier, Éric; Ghys, E.; Lesne, Annick, eds. (2010). The Scientific Legacy of Poincaré. History of Mathematics. Translated by Bowman, Joshua. The London Mathematical Society. pp. 1–2. ISBN 978-0-8218-4718-3.
- ^ Krantz, Steven G. (2010). An Episodic History of Mathematics: Mathematical Culture Through Problem Solving. Washington, DC: Mathematical Association of America. p. 291. ISBN 978-0-88385-766-3. OCLC 501976977.
- ^ Gray, Jeremy (2013). Henri Poincaré: A Scientific Biography. Princeton University Press. p. 195. ISBN 978-0-691-15271-4.
- ^ Rollet, Laurent (19 June 2023). ""My sincere condolences"". European Mathematical Society Magazine (128): 41–50. doi:10.4171/mag/141. ISSN 2747-7894.
- ^ a b Bell, E.T. (1937). Men of Mathematics. Vol. II. Penguin Books. pp. 581, 584.
- ^ a b c Bell, E.T. (1937). Men of Mathematics. Vol. II. Penguin Books. p. 587.
- ^ "Jules Henri Poincaré (1854–1912)". Royal Netherlands Academy of Arts and Sciences. Archived from the original on 5 September 2015. Retrieved 4 August 2015.
- ^ Ginoux, J. M.; Gerini, C. (2013). Henri Poincaré: A Biography Through the Daily Papers. World Scientific. p. 59. doi:10.1142/8956. ISBN 978-981-4556-61-3.
- ^ a b Gray, Jeremy (2013). "The Campaign for Poincaré". Henri Poincaré: A Scientific Biography. Princeton University Press. pp. 194–196.
- ^ Crawford, Elizabeth (1987). The Beginnings of the Nobel Institution: The Science Prizes, 1901–1915. Cambridge University Press. pp. 141–142.
- ^ a b c "Nomination database". Nobelprize.org. Nobel Media AB. Retrieved 24 September 2015.
- ^ Crawford, Elizabeth (13 November 1998). "Nobel: Always the Winners, Never the Losers". Science. 282 (5392): 1256–1257. Bibcode:1998Sci...282.1256C. doi:10.1126/science.282.5392.1256. S2CID 153619456.[dead link]
- ^ Nastasi, Pietro (16 May 2013). "A Nobel Prize for Poincaré?". Lettera Matematica. 1 (1–2): 79–82. doi:10.1007/s40329-013-0005-1.
- ^ Folina, Janet (1992). Poincaré and the Philosophy of Mathematics. London: Palgrave Macmillan UK. p. 145. doi:10.1007/978-1-349-22119-6. ISBN 978-1-349-22121-9.
- ^ Yemima Ben-Menahem, Conventionalism: From Poincare to Quine, Cambridge University Press, 2006, p. 39.
- ^ Gargani Julien (2012), Poincaré, le hasard et l'étude des systèmes complexes, L'Harmattan, p. 124, archived from the original on 4 March 2016, retrieved 5 June 2015
- ^ Poincaré, Henri (2007), Science and Hypothesis, Cosimo, Inc. Press, p. 50, ISBN 978-1-60206-505-5
- ^ Hadamard, Jacques. An Essay on the Psychology of Invention in the Mathematical Field. Princeton Univ Press (1945)
- ^ Poincaré, Henri (1914). "3: Mathematical Creation". Science and Method. Archived from the original on 4 September 2019. Retrieved 4 September 2019.
- ^ Dennett, Daniel C. 1978. Brainstorms: Philosophical Essays on Mind and Psychology. The MIT Press, p. 293
- ^ "Structural Realism": entry by James Ladyman in the Stanford Encyclopedia of Philosophy
Sources
[edit]- Bell, Eric Temple, 1986. Men of Mathematics (reissue edition). Touchstone Books. ISBN 0-671-62818-6.
- Belliver, André, 1956. Henri Poincaré ou la vocation souveraine. Paris: Gallimard.
- Bernstein, Peter L, 1996. "Against the Gods: A Remarkable Story of Risk". (pp. 199–200). John Wiley & Sons.
- Boyer, B. Carl, 1968. A History of Mathematics: Henri Poincaré, John Wiley & Sons.
- Grattan-Guinness, Ivor, 2000. The Search for Mathematical Roots 1870–1940. Princeton Uni. Press.
- Dauben, Joseph (2004) [1993], "Georg Cantor and the Battle for Transfinite Set Theory" (PDF), Proceedings of the 9th ACMS Conference (Westmont College, Santa Barbara, CA), pp. 1–22, archived from the original (PDF) on 13 July 2010. Internet version published in Journal of the ACMS 2004.
- Folina, Janet, 1992. Poincaré and the Philosophy of Mathematics. Macmillan, New York.
- Gray, Jeremy, 1986. Linear differential equations and group theory from Riemann to Poincaré, Birkhauser ISBN 0-8176-3318-9
- Gray, Jeremy, 2013. Henri Poincaré: A scientific biography. Princeton University Press ISBN 978-0-691-15271-4
- Jean Mawhin (October 2005), "Henri Poincaré. A Life in the Service of Science" (PDF), Notices of the AMS, 52 (9): 1036–1044, archived (PDF) from the original on 3 March 2007
- Kolak, Daniel, 2001. Lovers of Wisdom, 2nd ed. Wadsworth.
- Gargani, Julien, 2012. Poincaré, le hasard et l'étude des systèmes complexes, L'Harmattan.
- Murzi, 1998. "Henri Poincaré".
- O'Connor, J. John, and Robertson, F. Edmund, 2002, "Jules Henri Poincaré". University of St. Andrews, Scotland.
- Peterson, Ivars, 1995. Newton's Clock: Chaos in the Solar System (reissue edition). W H Freeman & Co. ISBN 0-7167-2724-2.
- Sageret, Jules, 1911. Henri Poincaré. Paris: Mercure de France.
- Toulouse, E., 1910. Henri Poincaré – (Source biography in French) at University of Michigan Historic Math Collection.
- Stillwell, John (2010). Mathematics and Its History (3rd, illustrated ed.). Springer Science & Business Media. ISBN 978-1-4419-6052-8.
- Papers on Topology: Analysis Situs and Its Five Supplements by Henri Poincaré, translated, with an introduction, by John Stillwell. American Mathematical Society. 2010. ISBN 978-0-8218-5234-7. – Satzer, William J. (26 April 2011). "Review of Papers on Topology: Analysis Situs and Its Five Supplements by Henri Poincaré, translated and edited by John Stillwell". MAA Reviews, Mathematical Association of America. Archived from the original on 26 January 2024. Retrieved 26 January 2024.
- Verhulst, Ferdinand, 2012 Henri Poincaré. Impatient Genius. N.Y.: Springer.
- Henri Poincaré, l'œuvre scientifique, l'œuvre philosophique, by Vito Volterra, Jacques Hadamard, Paul Langevin and Pierre Boutroux, Felix Alcan, 1914.
- Henri Poincaré, l'œuvre mathématique, by Vito Volterra.
- Henri Poincaré, le problème des trois corps, by Jacques Hadamard.
- Henri Poincaré, le physicien, by Paul Langevin.
- Henri Poincaré, l'œuvre philosophique, by Pierre Boutroux.
- This article incorporates material from Jules Henri Poincaré on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.
Further reading
[edit]Secondary sources to work on relativity
[edit]- Cuvaj, Camillo (1969), "Henri Poincaré's Mathematical Contributions to Relativity and the Poincaré Stresses", American Journal of Physics, 36 (12): 1102–1113, Bibcode:1968AmJPh..36.1102C, doi:10.1119/1.1974373
- Darrigol, O. (1995), "Henri Poincaré's criticism of Fin De Siècle electrodynamics", Studies in History and Philosophy of Science, 26 (1): 1–44, Bibcode:1995SHPMP..26....1D, doi:10.1016/1355-2198(95)00003-C
- Darrigol, O. (2000), Electrodynamics from Ampére to Einstein, Oxford: Clarendon Press, ISBN 978-0-19-850594-5
- Darrigol, O. (2004), "The Mystery of the Einstein–Poincaré Connection", Isis, 95 (4): 614–626, Bibcode:2004Isis...95..614D, doi:10.1086/430652, PMID 16011297, S2CID 26997100
- Darrigol, O. (2005), "The Genesis of the theory of relativity" (PDF), Séminaire Poincaré, 1: 1–22, Bibcode:2006eins.book....1D, doi:10.1007/3-7643-7436-5_1, ISBN 978-3-7643-7435-8, archived (PDF) from the original on 28 February 2008
- Galison, P. (2003), Einstein's Clocks, Poincaré's Maps: Empires of Time, New York: W.W. Norton, ISBN 978-0-393-32604-8
- Giannetto, E. (1998), "The Rise of Special Relativity: Henri Poincaré's Works Before Einstein", Atti del XVIII Congresso di Storia della Fisica e dell'astronomia: 171–207
- Giedymin, J. (1982), Science and Convention: Essays on Henri Poincaré's Philosophy of Science and the Conventionalist Tradition, Oxford: Pergamon Press, ISBN 978-0-08-025790-7
- Goldberg, S. (1967), "Henri Poincaré and Einstein's Theory of Relativity", American Journal of Physics, 35 (10): 934–944, Bibcode:1967AmJPh..35..934G, doi:10.1119/1.1973643
- Goldberg, S. (1970), "Poincaré's silence and Einstein's relativity", British Journal for the History of Science, 5: 73–84, doi:10.1017/S0007087400010633, S2CID 123766991
- Holton, G. (1988) [1973], "Poincaré and Relativity", Thematic Origins of Scientific Thought: Kepler to Einstein, Harvard University Press, ISBN 978-0-674-87747-4
- Katzir, S. (2005), "Poincaré's Relativistic Physics: Its Origins and Nature", Phys. Perspect., 7 (3): 268–292, Bibcode:2005PhP.....7..268K, doi:10.1007/s00016-004-0234-y, S2CID 14751280
- Keswani, G.H., Kilmister, C.W. (1983), "Intimations of Relativity: Relativity Before Einstein", Br. J. Philos. Sci., 34 (4): 343–354, doi:10.1093/bjps/34.4.343, S2CID 65257414, archived from the original on 26 March 2009
{{citation}}: CS1 maint: multiple names: authors list (link) - Keswani, G.H. (1965), "Origin and Concept of Relativity, Part I", Br. J. Philos. Sci., 15 (60): 286–306, doi:10.1093/bjps/XV.60.286, S2CID 229320737
- Keswani, G.H. (1965), "Origin and Concept of Relativity, Part II", Br. J. Philos. Sci., 16 (61): 19–32, doi:10.1093/bjps/XVI.61.19, S2CID 229320603
- Keswani, G.H. (1966), "Origin and Concept of Relativity, Part III", Br. J. Philos. Sci., 16 (64): 273–294, doi:10.1093/bjps/XVI.64.273, S2CID 122596290
- Kragh, H. (1999), Quantum Generations: A History of Physics in the Twentieth Century, Princeton University Press, ISBN 978-0-691-09552-3
- Langevin, P. (1913), "L'œuvre d'Henri Poincaré: le physicien", Revue de Métaphysique et de Morale, 21: 703
- Macrossan, M. N. (1986), "A Note on Relativity Before Einstein", Br. J. Philos. Sci., 37 (2): 232–234, CiteSeerX 10.1.1.679.5898, doi:10.1093/bjps/37.2.232, S2CID 121973100, archived from the original on 29 October 2013, retrieved 27 March 2007
- Miller, A.I. (1973), "A study of Henri Poincaré's "Sur la Dynamique de l'Electron", Arch. Hist. Exact Sci., 10 (3–5): 207–328, doi:10.1007/BF00412332, S2CID 189790975
- Miller, A.I. (1981), Albert Einstein's special theory of relativity. Emergence (1905) and early interpretation (1905–1911), Reading: Addison–Wesley, ISBN 978-0-201-04679-3
- Miller, A.I. (1996), "Why did Poincaré not formulate special relativity in 1905?", in Jean-Louis Greffe; Gerhard Heinzmann; Kuno Lorenz (eds.), Henri Poincaré : science et philosophie, Berlin, pp. 69–100
{{citation}}: CS1 maint: location missing publisher (link) - Popp, B.D. (2020), Henri Poincaré: Electrons to Special Relativity, Cham: Springer Nature, ISBN 978-3-030-48038-7
- Schwartz, H. M. (1971), "Poincaré's Rendiconti Paper on Relativity. Part I", American Journal of Physics, 39 (7): 1287–1294, Bibcode:1971AmJPh..39.1287S, doi:10.1119/1.1976641
- Schwartz, H. M. (1972), "Poincaré's Rendiconti Paper on Relativity. Part II", American Journal of Physics, 40 (6): 862–872, Bibcode:1972AmJPh..40..862S, doi:10.1119/1.1986684
- Schwartz, H. M. (1972), "Poincaré's Rendiconti Paper on Relativity. Part III", American Journal of Physics, 40 (9): 1282–1287, Bibcode:1972AmJPh..40.1282S, doi:10.1119/1.1986815
- Scribner, C. (1964), "Henri Poincaré and the principle of relativity", American Journal of Physics, 32 (9): 672–678, Bibcode:1964AmJPh..32..672S, doi:10.1119/1.1970936
- Walter, S. (2005), "Henri Poincaré and the theory of relativity", in Renn, J. (ed.), Albert Einstein, Chief Engineer of the Universe: 100 Authors for Einstein, Berlin: Wiley-VCH, pp. 162–165
- Walter, S. (2007), "Breaking in the 4-vectors: the four-dimensional movement in gravitation, 1905–1910", in Renn, J. (ed.), The Genesis of General Relativity, vol. 3, Berlin: Springer, pp. 193–252
- Whittaker, E.T. (1953), "The Relativity Theory of Poincaré and Lorentz", A History of the Theories of Aether and Electricity: The Modern Theories 1900–1926, London: Nelson
- Zahar, E. (2001), Poincaré's Philosophy: From Conventionalism to Phenomenology, Chicago: Open Court Pub Co, ISBN 978-0-8126-9435-2
Non-mainstream sources
[edit]- Leveugle, J. (2004), La Relativité et Einstein, Planck, Hilbert – Histoire véridique de la Théorie de la Relativitén, Pars: L'Harmattan
- Logunov, A.A. (2004), Henri Poincaré and relativity theory, arXiv:physics/0408077, Bibcode:2004physics...8077L, ISBN 978-5-02-033964-4
External links
[edit]- Works by Henri Poincaré at Project Gutenberg
- Works by or about Henri Poincaré at the Internet Archive
- Works by Henri Poincaré at LibriVox (public domain audiobooks)

- Henri Poincaré's Bibliography
- Internet Encyclopedia of Philosophy: "Henri Poincaré Archived 2 February 2004 at the Wayback Machine" – by Mauro Murzi.
- Internet Encyclopedia of Philosophy: "Poincaré’s Philosophy of Mathematics" – by Janet Folina.
- Henri Poincaré at the Mathematics Genealogy Project
- Henri Poincaré on Information Philosopher
- O'Connor, John J.; Robertson, Edmund F., "Henri Poincaré", MacTutor History of Mathematics Archive, University of St Andrews
- A timeline of Poincaré's life University of Nantes (in French).
- Henri Poincaré Papers University of Nantes (in French).
- Bruce Medal page
- Collins, Graham P., "Henri Poincaré, His Conjecture, Copacabana and Higher Dimensions," Scientific American, 9 June 2004.
- BBC in Our Time, "Discussion of the Poincaré conjecture," 2 November 2006, hosted by Melvyn Bragg.
- Poincare Contemplates Copernicus at MathPages
- High Anxieties – The Mathematics of Chaos (2008) BBC documentary directed by David Malone looking at the influence of Poincaré's discoveries on 20th Century mathematics.
- 1854 births
- 1912 deaths
- Henri Poincaré
- 19th-century French essayists
- 19th-century French male writers
- 19th-century French mathematicians
- 19th-century French non-fiction writers
- 19th-century French philosophers
- 20th-century French essayists
- 20th-century French male writers
- 20th-century French mathematicians
- 20th-century French philosophers
- Algebraic geometers
- Burials at Montparnasse Cemetery
- Chaos theorists
- Continental philosophers
- Corps des mines
- Corresponding members of the Saint Petersburg Academy of Sciences
- Deaths from embolism
- Determinists
- Dynamical systems theorists
- École Polytechnique alumni
- French fluid dynamicists
- Foreign associates of the National Academy of Sciences
- Foreign members of the Royal Society
- French male essayists
- French male non-fiction writers
- French male writers
- French military personnel of the Franco-Prussian War
- French mining engineers
- French geometers
- Hyperbolic geometers
- Lecturers
- French mathematical analysts
- Members of the Académie Française
- Members of the Royal Netherlands Academy of Arts and Sciences
- Mines Paris - PSL alumni
- Officers of the French Academy of Sciences
- Scientists from Nancy, France
- Philosophers of logic
- Philosophers of mathematics
- Philosophers of psychology
- French philosophers of science
- French philosophy academics
- Philosophy writers
- Recipients of the Bruce Medal
- Recipients of the Gold Medal of the Royal Astronomical Society
- French relativity theorists
- Thermodynamicists
- Topologists
- Academic staff of the University of Paris
- Recipients of the Matteucci Medal