Truncated triakis tetrahedron: Difference between revisions
KirbyRider (talk | contribs) No edit summary |
m Updating wikilink to more specific (useful) page Tags: Visual edit Mobile edit Mobile web edit |
||
| (43 intermediate revisions by 18 users not shown) | |||
| Line 1: | Line 1: | ||
{{Distinguish|Triakis truncated tetrahedron|Triakis tetrahedron}} |
|||
{| border="1" bgcolor="#ffffff" cellpadding="5" align="right" style="margin-left:10px" width="250" |
|||
{{refimprove|date=September 2014}} |
|||
| ⚫ | |||
{{Short description|Near-miss Johnson solid with 16 faces}} |
|||
| ⚫ | |||
{{Infobox polyhedron |
|||
|align=center colspan=2|[[Image:Truncated triakis tetrahedron.png|240px|Truncated triakis tetrahedron]] |
|||
| ⚫ | |||
|- |
|||
| type = [[Near-miss Johnson solid]] |
|||
|bgcolor=#e7dcc3|Type||[[Conway polyhedron notation|Conway polyhedron]] |
|||
| ⚫ | |||
|- |
|||
| edges = 42 |
|||
| ⚫ | |||
| vertices = 28 |
|||
|- |
|||
| vertex_config = {{math|4 (5.5.5)<BR>24 (5.5.6)}} |
|||
|bgcolor=#e7dcc3|Edges||42 |
|||
| schläfli = |
|||
|- |
|||
| wythoff = |
|||
|bgcolor=#e7dcc3|Vertices||28 |
|||
| conway = {{math|1=t6kT = dk6tT}} |
|||
|- |
|||
| coxeter = |
|||
| ⚫ | |||
| symmetry = {{math|''T''<sub>''d''</sub>}} |
|||
|- |
|||
| rotation_group = |
|||
|bgcolor=#e7dcc3|[[Vertex configuration]]||4 (5.5.5)<BR>24 (5.5.6) |
|||
| ⚫ | |||
|- |
|||
| properties = [[convex polytope|convex]] |
|||
|bgcolor=#e7dcc3|[[List of spherical symmetry groups|Symmetry group]]||T<sub>d</sub> |
|||
| vertex_figure = |
|||
|- |
|||
| net = Conway_dk6tT_net.png |
|||
|bgcolor=#e7dcc3|Properties||[[Convex polytope|convex]] |
|||
}} |
|||
[[Image:Truncated triakis tetrahedron.gif|thumb]] |
|||
| ⚫ | |||
In [[geometry]], the '''truncated triakis tetrahedron''', or more precisely an '''order-6 truncated triakis tetrahedron''', is a convex [[polyhedron]] with 16 [[Face (geometry)|faces]]: 4 sets of 3 [[pentagon]]s arranged in a [[Tetrahedral symmetry|tetrahedral]] arrangement, with 4 [[hexagon]]s in the gaps. |
|||
| ⚫ | |||
== Construction == |
|||
| ⚫ | |||
[[File:triakistetrahedron.jpg|thumb|center|[[Triakis tetrahedron]]]] |
|||
| ⚫ | |||
Topologically, as a [[near-miss Johnson solid]], the four hexagons corresponding to the face planes of a tetrahedron are triambi, with equal edges but alternating angles, while the pentagons only have reflection symmetry. |
|||
| ⚫ | |||
If all of a triakis tetrahedron's vertices, of both kinds, are truncated, the resulting solid is an irregular icosahedron, whose dual is a ''trihexakis truncated tetrahedron''. |
|||
{{Anchor|order-3 truncated triakis tetrahedron}}Truncation of only the 3-valence vertices yields the '''order-3 truncated triakis tetrahedron''', which looks like a [[tetrahedron]] with each face raised by a low triangular [[frustum]]. The dual to that truncation will be the [[triakis truncated tetrahedron]]. |
|||
[[File:StellaTruncTriakisTetra.png|160px|The full truncation]] |
|||
== Hexakis truncated tetrahedron == |
|||
[[File:Hexakis_truncated_tetrahedron.gif|thumb|Hexakis truncated tetrahedron rotating]] |
|||
The dual of the ''order-6 Truncated triakis tetrahedron'' is called a '''hexakis truncated tetrahedron'''. It is constructed by a [[truncated tetrahedron]] with [[hexagonal pyramid]]s augmented. If all of the triangles are made regular, the polyhedron becomes a [[Near-miss Johnson solid|failed Johnson solid]], with coplanar triangles in a truncated tetrahedron volume. |
|||
{| class=wikitable |
|||
|- align=center |
|||
|[[File:Polyhedron truncated 4a max.png|160px]]<BR>[[truncated tetrahedron]] |
|||
|[[File:Conway_k6tT.png|160px]]<BR>Hexakis truncated tetrahedron |
|||
|[[File:Conway_k6tT_net.png|160px]]<BR>Net |
|||
| ⚫ | |||
| ⚫ | |||
A Triakis Tetrahedron can be fully truncated, not giving out this. The Full truncation is a special type of icosahedron, rather than a hexadecahedron. Another alternate truncation, or the "Low order truncation", will give out what looks like a [[Tetrahedron]] with each face raised by a low [[Pyramidal frustum|Triangular frustum]]. The dual to that truncation will be the "Triakis Truncated Tetrahedron". However, the full truncation is dual to a ''Trihexakis truncated tetrahedron''. |
|||
[[Image:Truncated triakis tetrahedron.png|240px|The common truncation]] [[File:StellaTruncTriakisTetra.png|120px|The Full Truncation]] |
|||
== See also == |
== See also == |
||
* [[Near-miss Johnson solid]] |
* [[Near-miss Johnson solid]] |
||
* [[Truncated tetrakis cube]] |
|||
* [[Truncated triakis octahedron]] |
|||
* [[Truncated triakis icosahedron]] |
|||
== External links == |
== External links == |
||
* [http://www.orchidpalms.com/polyhedra/acrohedra/nearmiss/jsmn.htm Johnson Solid Near Misses: Number |
* [http://www.orchidpalms.com/polyhedra/acrohedra/nearmiss/jsmn.htm Johnson Solid Near Misses: Number 22] |
||
* [http://www.georgehart.com/virtual-polyhedra/conway_notation.html George Hart's Polyhedron generator] - " |
* [http://www.georgehart.com/virtual-polyhedra/conway_notation.html George Hart's Polyhedron generator] - "t6kT" ([[Conway polyhedron notation]]) |
||
{{Near-miss Johnson solids navigator}} |
{{Near-miss Johnson solids navigator}} |
||
{{DEFAULTSORT:Truncated Triakis Tetrahedron}} |
|||
[[Category:Polyhedra]] |
[[Category:Polyhedra]] |
||
[[Category:Truncated tilings]] |
|||
| ⚫ | |||
| ⚫ | |||
[[fr:triakitétraèdre tronqué]] |
|||
[[eo:Senpintigita trilateropiramidigita kvaredro]] |
|||
Latest revision as of 14:13, 29 September 2023
This article needs additional citations for verification. (September 2014) |
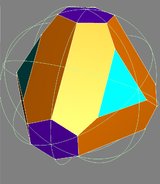
| Truncated triakis tetrahedron | |
|---|---|
 | |
| Type | Near-miss Johnson solid |
| Faces | 4 hexagons 12 irregular pentagons |
| Edges | 42 |
| Vertices | 28 |
| Vertex configuration | 4 (5.5.5) 24 (5.5.6) |
| Conway notation | t6kT = dk6tT |
| Symmetry group | Td |
| Dual polyhedron | Hexakis truncated tetrahedron |
| Properties | convex |
| Net | |
 | |

In geometry, the truncated triakis tetrahedron, or more precisely an order-6 truncated triakis tetrahedron, is a convex polyhedron with 16 faces: 4 sets of 3 pentagons arranged in a tetrahedral arrangement, with 4 hexagons in the gaps.
Construction
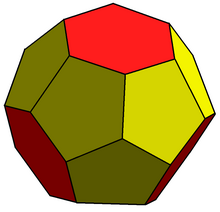
[edit]It is constructed from a triakis tetrahedron by truncating the order-6 vertices. This creates 4 regular hexagon faces, and leaves 12 mirror-symmetric pentagons.
A topologically similar equilateral polyhedron can be constructed by using 12 regular pentagons with 4 equilateral but nonplanar hexagons, each vertex with internal angles alternating between 108 and 132 degrees.
Topologically, as a near-miss Johnson solid, the four hexagons corresponding to the face planes of a tetrahedron are triambi, with equal edges but alternating angles, while the pentagons only have reflection symmetry.
Full truncation
[edit]If all of a triakis tetrahedron's vertices, of both kinds, are truncated, the resulting solid is an irregular icosahedron, whose dual is a trihexakis truncated tetrahedron.
Truncation of only the 3-valence vertices yields the order-3 truncated triakis tetrahedron, which looks like a tetrahedron with each face raised by a low triangular frustum. The dual to that truncation will be the triakis truncated tetrahedron.
Hexakis truncated tetrahedron
[edit]
The dual of the order-6 Truncated triakis tetrahedron is called a hexakis truncated tetrahedron. It is constructed by a truncated tetrahedron with hexagonal pyramids augmented. If all of the triangles are made regular, the polyhedron becomes a failed Johnson solid, with coplanar triangles in a truncated tetrahedron volume.
 truncated tetrahedron |
 Hexakis truncated tetrahedron |
 Net |
See also
[edit]- Near-miss Johnson solid
- Truncated tetrakis cube
- Truncated triakis octahedron
- Truncated triakis icosahedron
External links
[edit]- Johnson Solid Near Misses: Number 22
- George Hart's Polyhedron generator - "t6kT" (Conway polyhedron notation)