Icosidodecahedron: Difference between revisions
KirbyRider (talk | contribs) |
No edit summary |
||
| (136 intermediate revisions by 55 users not shown) | |||
| Line 1: | Line 1: | ||
{{short description|Archimedean solid with 32 faces}} |
|||
{{Semireg polyhedra db|Semireg polyhedron stat table|ID}} |
|||
{{infobox polyhedron |
|||
[[Image:Hoberman Sphere.jpg|thumb|A [[Hoberman sphere]] as an icosidodecahedron]] |
|||
| name = Icosidodecahedron |
|||
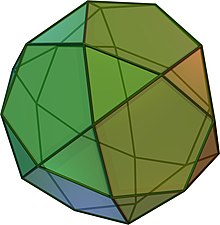
In [[geometry]], an '''icosidodecahedron ''' is a [[polyhedron]] with twenty triangular faces and twelve pentagonal faces. An icosidodecahedron has 30 identical vertices, with two triangles and two pentagons meeting at each, and 60 identical edges, each separating a triangle from a pentagon. As such it is one of the [[Archimedean solid]]s and more particularly, a [[quasiregular polyhedron]]. |
|||
| image = File:Icosidodecahedron.jpg |
|||
| type = [[Archimedean solid]]<br>[[Uniform polyhedron]]<br>[[Quasiregular polyhedron]] |
|||
| faces = 32 |
|||
| edges = 60 |
|||
| vertices = 30 |
|||
| symmetry = [[Icosahedral symmetry]] {{math|I<sub>h</sub>}} |
|||
| angle = 142.62° |
|||
| dual = [[Rhombic triacontahedron]] |
|||
| properties = [[Convex set|convex]] |
|||
| vertex_figure = Polyhedron 12-20 vertfig.svg |
|||
| net = Polyhedron 12-20 net.svg |
|||
}} |
|||
[[File:Icosidodecahedron.stl|thumb|3D model of an icosidodecahedron]] |
|||
In [[geometry]], an '''icosidodecahedron''' or '''pentagonal gyrobirotunda''' is a [[polyhedron]] with twenty (''icosi-'') [[triangular]] faces and twelve (''dodeca-'') [[pentagon]]al faces. An icosidodecahedron has 30 identical [[Vertex (geometry)|vertices]], with two triangles and two pentagons meeting at each, and 60 identical edges, each separating a triangle from a pentagon. As such, it is one of the [[Archimedean solid]]s and more particularly, a [[quasiregular polyhedron]]. |
|||
An icosidodecahedron has icosahedral symmetry, and its first [[stellation]] is the compound of a [[dodecahedron]] and its dual [[icosahedron]], with the vertices of the icosahedron located at the midpoints of the edges of either. |
|||
== Construction == |
|||
Its [[dual polyhedron]] is the [[rhombic triacontahedron]]. An icosidodecahedron can be split along any of six planes to form a pair of [[pentagonal rotunda]]e, which belong among the [[Johnson solid]]s. |
|||
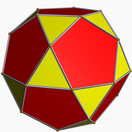
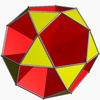
One way to construct the icosidodecahedron is to start with two [[pentagonal rotunda]] by attaching them to their bases. These rotundas cover their decagonal base so that the resulting polyhedron has 32 faces, 30 vertices, and 60 edges. This construction is similar to one of the [[Johnson solids]], the [[pentagonal orthobirotunda]]. The difference is that the icosidodecahedron is constructed by twisting its rotundas by 36°, a process known as [[gyration]], resulting in the pentagonal face connecting to the triangular one. The icosidodecahedron has an alternative name, ''pentagonal gyrobirotunda''.{{r|berman|os}} |
|||
{{multiple image |
|||
| image1 = Icosidodecahedron.png |
|||
| image2 = Dissected icosidodecahedron.png |
|||
| image3 = Pentagonal orthobirotunda solid.png |
|||
| footer = The difference between icosidodecahedron and pentagonal orthobirotunda, and its dissection. |
|||
| align = center |
|||
| total_width = 400 |
|||
}} |
|||
Convenient [[Cartesian coordinates]] for the vertices of an icosidodecahedron with unit edges are given by the [[even permutation]]s of: |
|||
The icosidodecahedron can be considered a [[#Pentagonal_gyrobirotunda|''pentagonal gyrobirotunda'']], as a combination of two [[pentagonal rotunda|rotundae]] (compare [[pentagonal orthobirotunda]], one of the [[Johnson solid]]s). |
|||
<math display="block"> (0, 0, \pm \varphi), \qquad \left(\pm \frac{1}{2}, \pm \frac{\varphi}{2}, \pm \frac{\varphi^2}{2} \right), </math> |
|||
where {{mvar|φ}} denotes the [[golden ratio]].<ref>{{mathworld |title=Icosahedral group |urlname=IcosahedralGroup}}</ref> |
|||
== Properties == |
|||
The [[Wire-frame_model|wire frame figure]] of the icosidodecahedron consists of six [[decagon|flat regular decagons]], meeting in pairs at each of the 30 vertices. |
|||
The surface area of an icosidodecahedron {{mvar|A}} can be determined by calculating the area of all pentagonal faces. The volume of an icosidodecahedron {{mvar|V}} can be determined by slicing it off into two pentagonal rotunda, after which summing up their volumes. Therefore, its surface area and volume can be formulated as:{{r|berman}} |
|||
<math display="block">\begin{align} |
|||
A &= \left(5\sqrt{3}+3\sqrt{25+10\sqrt{5}}\right) a^2 &\approx 29.306a^2 \\ |
|||
V &= \frac{45+17\sqrt{5}}{6}a^3 &\approx 13.836a^3. |
|||
\end{align}</math> |
|||
The [[dihedral angle]] of an icosidodecahedron between pentagon-to-triangle is |
|||
In four-dimensional geometry the icosidodecahedron appears in the [[Regular_polytopes|regular]] [[600-cell]] as the equatorial slice that belongs to the vertex-first passage of the 600-cell through 3D space. In other words: the 30 vertices of the 600-cell which lie at arc distances of 90 degrees on its circumscribed [[hypersphere]] from a pair of opposite vertices, are the vertices of an icosidodecahedron. |
|||
<math display="block"> \arccos \left(-\sqrt{\frac{5 + 2\sqrt{5}}{15}} \right) \approx 142.62^\circ, </math> |
|||
The wire frame figure of the 600-cell consists of 72 flat regular decagons. Six of these are the equatorial decagons to a pair of opposite vertices. They are precisely the six decagons which form the wire frame figure of the icosidodecahedron. |
|||
determined by calculating the angle of a pentagonal rotunda.{{r|williams}} |
|||
An icosidodecahedron has [[icosahedral symmetry]], and its first [[stellation]] is the [[Compound of dodecahedron and icosahedron|compound]] of a [[dodecahedron]] and its dual [[icosahedron]], with the vertices of the icosidodecahedron located at the midpoints of the edges of either. |
|||
The icosidodecahedron is an [[Archimedean solid]], meaning it is a highly symmetric and semi-regular polyhedron, and two or more different regular polygonal faces meet in a vertex.{{r|diudea}} The polygonal faces that meet for every vertex are two equilateral triangles and two regular pentagons, and the [[vertex figure]] of an icosidodecahedron is {{nowrap|(3·5)<sup>2</sup> {{=}} 3<sup>2</sup>·5<sup>2</sup>}. Its [[dual polyhedron]] is [[rhombic triacontahedron]], a [[Catalan solid]].{{r|williams}} |
|||
{{multiple image |
|||
==Cartesian coordinates == |
|||
| align = right | total_width = 400 |
|||
| image1 = Polyhedron 12-20, davinci.png |
|||
| image2 = Spherical icosidodecahedron with colored cicles.png |
|||
| footer = The 60 edges form 6 [[decagon]]s corresponding to [[great circle]]s in the spherical tiling. |
|||
}} |
|||
The icosidodecahedron has 6 central [[decagon]]s. Projected into a sphere, they define 6 [[great circle]]s. {{harvtxt|Fuller|1975}} used these 6 great circles, along with 15 and 10 others in two other polyhedra to define his [[31 great circles of the spherical icosahedron]].{{r|fuller}} |
|||
The long radius (center to vertex) of the icosidodecahedron is in the [[golden ratio]] to its edge length; thus its radius is {{mvar|φ}} if its edge length is 1, and its edge length is {{math|{{sfrac|1|''φ''}}}} if its radius is 1.{{r|williams}} Only a few uniform polytopes have this property, including the four-dimensional [[600-cell]], the three-dimensional icosidodecahedron, and the two-dimensional [[Decagon#The golden ratio in decagon|decagon]]. (The icosidodecahedron is the equatorial cross-section of the 600-cell, and the decagon is the equatorial cross-section of the icosidodecahedron.) These ''radially golden'' polytopes can be constructed, with their radii, from [[Golden triangle (mathematics)|golden triangle]]s which meet at the center, each contributing two radii and an edge. |
|||
Convenient [[Cartesian coordinates]] for the vertices of an icosidodecahedron with unit edges are given by |
|||
* (0,0,±τ) |
|||
* (0,±τ,0) |
|||
* (±τ,0,0) |
|||
* (±1/2, ±τ/2, ±(1+τ)/2) |
|||
* (±τ/2, ±(1+τ)/2, ±1/2) |
|||
* (±(1+τ)/2, ±1/2, ±τ/2) |
|||
where τ is the [[golden ratio]], (1+√5)/2. |
|||
==Related polytopes== |
|||
== Surface area and volume == |
|||
The icosidodecahedron is a [[Rectification (geometry)|rectified]] [[dodecahedron]] and also a rectified [[icosahedron]], existing as the full-edge truncation between these regular solids. |
|||
The surface area ''A'' and the volume ''V'' of the icosidodecahedron of edge length ''a'' are: |
|||
:<math>A = (5\sqrt{3}+3\sqrt{25+10\sqrt{5}}) a^2 \approx 29.3059828a^2</math> |
|||
:<math>V = \frac{1}{6} (45+17\sqrt{5}) a^3 \approx 13.8355259a^3.</math> |
|||
The icosidodecahedron contains 12 pentagons of the [[dodecahedron]] and 20 triangles of the [[icosahedron]]: |
|||
==Related polyhedra== |
|||
{{Icosahedral truncations}} |
|||
The icosidodecahedron exists in a sequence of symmetries of quasiregular polyhedra and tilings with [[vertex configuration]]s (3.''n'')<sup>2</sup>, progressing from tilings of the sphere to the Euclidean plane and into the hyperbolic plane. With [[orbifold notation]] symmetry of *''n''32 all of these tilings are [[wythoff construction]] within a [[fundamental domain]] of symmetry, with generator points at the right angle corner of the domain.<ref>[[Harold Scott MacDonald Coxeter|Coxeter]] ''[[Regular Polytopes (book)|Regular Polytopes]]'', Third edition, (1973), Dover edition, {{ISBN|0-486-61480-8}} (Chapter V: The Kaleidoscope, Section: 5.7 Wythoff's construction)</ref><ref>[http://www.google.com/search?q=Two-Dimensional+Symmetry+Mutation ''Two Dimensional symmetry Mutations'' by Daniel Huson]</ref> |
|||
The icosidodecahedron is a [[Rectification (geometry)|rectified]] [[dodecahedron]] and also a rectified [[icosahedron]], existing as the full-edge truncation between these regular solids. |
|||
{{Quasiregular3 small table}} |
|||
{{Quasiregular5 table}} |
|||
The Icosidodecahedron contains 12 pentagons of the [[dodecahedron]] and 20 triangles of the [[icosahedron]]: |
|||
=== Related polyhedra === |
|||
{| class="wikitable" |
|||
[[File:Icosidecahedron in truncated cube.png|120px|thumb|A topological icosidodecahedron in truncated cube, inserting 6 vertices in center of octagons, and dissecting them into 2 pentagons and 2 triangles.]] |
|||
|- align=center |
|||
The [[truncated cube]] can be turned into an icosidodecahedron by dividing the octagons into two pentagons and two triangles. It has [[pyritohedral symmetry]]. |
|||
!Picture |
|||
|[[Image:Uniform polyhedron-53-t0.png|100px]]<br> '''Dodecahedron''' |
|||
|[[Image:Uniform polyhedron-53-t01.png|100px]]<br> [[Truncated dodecahedron]] |
|||
|[[Image:Uniform polyhedron-53-t1.png|100px]]<br> [[Icosidodecahedron]] |
|||
|[[Image:Uniform polyhedron-53-t12.png|100px]]<br> [[Truncated icosahedron]] |
|||
|[[Image:Uniform polyhedron-53-t2.png|100px]]<br> [[Icosahedron]] |
|||
|- align=center |
|||
![[Coxeter-Dynkin diagram|Coxeter-Dynkin]] |
|||
|{{CDD|node_1|5|node|3|node}} |
|||
|{{CDD|node_1|5|node_1|3|node}} |
|||
|{{CDD|node|5|node_1|3|node}} |
|||
|{{CDD|node|5|node_1|3|node_1}} |
|||
|{{CDD|node|5|node|3|node_1}} |
|||
|} |
|||
=== Pentagonal gyrobirotunda === |
|||
It is also related to the [[Johnson solid]] called a [[pentagonal orthobirotunda]] created by two [[pentagonal rotunda]] connected as mirror images. |
|||
{| class="wikitable" |
|||
|align=center|[[Image:Dissected icosidodecahedron.png|320px]]<BR>(Dissection) |
|||
| |
|||
{| |
|||
|align=center valign=bottom|[[Image:Icosidodecahedron.png|100px]]<BR>Icosidodecahedron<BR>(''pentagonal gyrobirotunda'') |
|||
|- |
|||
|align=center valign=bottom|[[Image:Pentagonal orthobirotunda solid.png|100px]]<BR>Pentagonal orthobirotunda |
|||
|- |
|||
|align=center valign=bottom|[[Image:pentagonal rotunda.png|100px]]<BR>Pentagonal rotunda |
|||
|} |
|||
|} |
|||
Eight [[uniform star polyhedron|uniform star polyhedra]] share the same [[vertex arrangement]]. Of these, two also share the same [[edge arrangement]]: the [[small icosihemidodecahedron]] (having the triangular faces in common), and the [[small dodecahemidodecahedron]] (having the pentagonal faces in common). The vertex arrangement is also shared with the [[uniform polyhedron compound|compounds]] of [[compound of five octahedra|five octahedra]] and of [[compound of five tetrahemihexahedra|five tetrahemihexahedra]]. |
Eight [[uniform star polyhedron|uniform star polyhedra]] share the same [[vertex arrangement]]. Of these, two also share the same [[edge arrangement]]: the [[small icosihemidodecahedron]] (having the triangular faces in common), and the [[small dodecahemidodecahedron]] (having the pentagonal faces in common). The vertex arrangement is also shared with the [[uniform polyhedron compound|compounds]] of [[compound of five octahedra|five octahedra]] and of [[compound of five tetrahemihexahedra|five tetrahemihexahedra]]. |
||
{|class="wikitable" width="400" style="vertical-align:top;text-align:center" |
|||
|align=center|[[Image:Icosidodecahedron.png|100px]]<br>Icosidodecahedron |
|||
{| class="wikitable" width="400" style="vertical-align:top;text-align:center" |
|||
|align=center|[[Image: |
|align=center|[[Image:Small icosihemidodecahedron.png|100px]]<br>[[Small icosihemidodecahedron]] |
||
|align=center|[[Image:Small |
|align=center|[[Image:Small dodecahemidodecahedron.png|100px]]<br>[[Small dodecahemidodecahedron]] |
||
|align=center|[[Image:Small dodecahemidodecahedron.png|100px]]<BR>[[Small dodecahemidodecahedron]] |
|||
|- |
|- |
||
|align=center|[[Image:Great icosidodecahedron.png|100px]]< |
|align=center|[[Image:Great icosidodecahedron.png|100px]]<br>[[Great icosidodecahedron]] |
||
|align=center|[[Image:Great dodecahemidodecahedron.png|100px]]< |
|align=center|[[Image:Great dodecahemidodecahedron.png|100px]]<br>[[Great dodecahemidodecahedron]] |
||
|align=center|[[Image:Great icosihemidodecahedron.png|100px]]< |
|align=center|[[Image:Great icosihemidodecahedron.png|100px]]<br>[[Great icosihemidodecahedron]] |
||
|- |
|- |
||
|align=center|[[Image:Dodecadodecahedron.png|100px]]< |
|align=center|[[Image:Dodecadodecahedron.png|100px]]<br>[[Dodecadodecahedron]] |
||
|align=center|[[Image:Small dodecahemicosahedron.png|100px]]< |
|align=center|[[Image:Small dodecahemicosahedron.png|100px]]<br>[[Small dodecahemicosahedron]] |
||
|align=center|[[Image:Great dodecahemicosahedron.png|100px]]< |
|align=center|[[Image:Great dodecahemicosahedron.png|100px]]<br>[[Great dodecahemicosahedron]] |
||
|- |
|- |
||
|align=center|[[Image:Compound of five octahedra.png|100px]]< |
|align=center|[[Image:Compound of five octahedra.png|100px]]<br>[[Compound of five octahedra]] |
||
|align=center|[[Image:UC18- |
|align=center|[[Image:UC18-5 tetrahemihexahedron.png|100px]]<br>[[Compound of five tetrahemihexahedra]] |
||
|} |
|} |
||
=== Related polychora === |
|||
==Icosidodecahedra in reality and games== |
|||
*In [[Sonic Colors]], a type of obstacle that only appears in Starlight Carnival Act 4 is an icosidodecahedron that has [[Frustum|Frusta]] caved in its pentagonal faces. The obstacle shoots energy balls in a spiral. |
|||
In four-dimensional geometry, the icosidodecahedron appears in the [[Regular polytopes|regular]] [[600-cell]] as the equatorial slice that belongs to the vertex-first passage of the 600-cell through 3D space. In other words: the 30 vertices of the 600-cell which lie at arc distances of 90 degrees on its circumscribed [[hypersphere]] from a pair of opposite vertices, are the vertices of an icosidodecahedron. The wireframe figure of the 600-cell consists of 72 flat regular decagons. Six of these are the equatorial decagons to a pair of opposite vertices, and these six form the wireframe figure of an icosidodecahedron. |
|||
== See also == |
|||
* [[Cuboctahedron]] |
|||
If a [[600-cell]] is [[Stereographic projection|stereographically projected]] to 3-space about any vertex and all points are normalised, the [[geodesic]]s upon which edges fall comprise the icosidodecahedron's [[Barycentric subdivision#Barycentric subdivision of a convex polytope|barycentric subdivision]]. |
|||
* [[Great truncated icosidodecahedron]] |
|||
* [[Icosahedron]] |
|||
== Graph == |
|||
* [[Rhombicosidodecahedron]] |
|||
[[File:Icosidodecahedral graph.png|240px|thumb|The graph of an icosidodecahedron]] |
|||
The [[Skeleton (topology)|skeleton]] of an icosidodecahedron can be represented as the [[Graph (discrete mathematics)|graph]] with 30 [[Vertex (graph theory)|vertices]] and 60 edges, one of the [[Archimedean graph]]s. It is [[quartic graph|quartic]], meaning that each of its vertex is connected by four other vertices.<ref>{{citation|last1=Read|first1=R. C.|last2=Wilson|first2=R. J.|title=An Atlas of Graphs|publisher=[[Oxford University Press]]|year= 1998|page=269}}</ref> |
|||
== Appearance == |
|||
The icosidodecahedron may appears in structural, as in the geodesic dome of the [[Hoberman sphere]]. |
|||
Icosidodecahedra can be found in all eukaryotic cells, including human cells, as Sec13/31 [[COPII]] coat-protein formations.{{r|rs}} |
|||
The icosidodecahedron may also found in popular culture. In [[Star Trek|Star Trek universe]], the Vulcan game of logic [[List_of_games_in_Star_Trek#Kal-toh|Kal-Toh]] has the goal of creating a shape with two nested [[holographic]] icosidodecahedra joined at the midpoints of their segments. |
|||
==See also== |
|||
*[[Cuboctahedron]] |
|||
*[[Great truncated icosidodecahedron]] |
|||
*[[Icosahedron]] |
|||
*[[Rhombicosidodecahedron]] |
|||
*[[Truncated icosidodecahedron]] |
|||
== References == |
== References == |
||
{{reflist|refs= |
|||
* {{The Geometrical Foundation of Natural Structure (book)}} (Section 3-9) |
|||
<ref name=berman>{{cite journal |
|||
== External links == |
|||
| last = Berman | first = Martin |
|||
* {{mathworld2 | urlname = Icosidodecahedron | title = Icosidodecahedron | urlname2 = ArchimedeanSolid | title2 = Archimedean solid}} |
|||
| doi = 10.1016/0016-0032(71)90071-8 |
|||
* {{KlitzingPolytopes|polyhedra.htm|3D convex uniform polyhedra|o3x5o - id}} |
|||
| journal = Journal of the Franklin Institute |
|||
* [http://www.mathconsult.ch/showroom/unipoly/ The Uniform Polyhedra] |
|||
| mr = 290245 |
|||
* [http://www.georgehart.com/virtual-polyhedra/vp.html Virtual Reality Polyhedra] The Encyclopedia of Polyhedra |
|||
| pages = 329–352 |
|||
| title = Regular-faced convex polyhedra |
|||
| volume = 291 |
|||
| year = 1971| issue = 5 |
|||
}}</ref> |
|||
<ref name=diudea>{{cite book |
|||
| last = Diudea | first = M. V. |
|||
| year = 2018 |
|||
| title = Multi-shell Polyhedral Clusters |
|||
| series = Carbon Materials: Chemistry and Physics |
|||
| volume = 10 |
|||
| publisher = [[Springer Science+Business Media|Springer]] |
|||
| isbn = 978-3-319-64123-2 |
|||
| doi = 10.1007/978-3-319-64123-2 |
|||
| url = https://books.google.com/books?id=p_06DwAAQBAJ&pg=PA39 |
|||
| page = 39 |
|||
}}</ref> |
|||
<ref name=fuller>{{cite book |
|||
| last = Fuller | first = R. B. | authorlink = R. Buckminster Fuller |
|||
| title = Synergetics: Explorations in the Geometry of Thinking |
|||
| year = 1975 |
|||
| publisher = MacMillan |
|||
| url = https://books.google.com/books?id=AKDgDQAAQBAJ&dq=31+great+circles&pg=PA183 |
|||
| page = 183–185 |
|||
| isbn = 978-0-02-065320-2 }}</ref> |
|||
<ref name=os>{{cite book |
|||
| last1 = Ogievetsky | first1 = O. |
|||
| last2 = Shlosman | first2 = S. |
|||
| editor-last1 = Novikov | editor-first1 = S. |
|||
| editor-last2 = Krichever | editor-first2 = I. |
|||
| editor-last3 = Ogievetsky | editor-first3 = O. |
|||
| editor-last4 = Shlosman | editor-first4 = S. |
|||
| year = 2021 |
|||
| title = Integrability, Quantization, and Geometry: II. Quantum Theories and Algebraic Geometry |
|||
| contribution = Platonic compounds and cylinders |
|||
| url = https://books.google.com/books?id=UsspEAAAQBAJ&pg=PA477 |
|||
| page = 477 |
|||
| publisher = [[American Mathematical Society]] |
|||
| isbn = 978-1-4704-5592-7 |
|||
}}</ref> |
|||
<ref name=rs>{{cite journal |
|||
| last1 = Russell | first1 = Christopher |
|||
| last2 = Stagg | first2 = Scott |
|||
| title = New Insights into the Structural Mechanisms of the COPII Coat |
|||
| journal = Traffic |
|||
| date = 11 February 2010 |
|||
| volume = 11 | issue = 3 | pages = 303–310 |
|||
| doi = 10.1111/j.1600-0854.2009.01026.x |
|||
| pmid = 20070605 |
|||
| doi-access = free |
|||
}}</ref> |
|||
<ref name=williams>{{cite book |
|||
| last = Williams | first = Robert | authorlink = Robert Williams (geometer) |
|||
| year = 1979 |
|||
| title = The Geometrical Foundation of Natural Structure: A Source Book of Design |
|||
| publisher = Dover Publications, Inc. |
|||
| isbn = 978-0-486-23729-9 |
|||
| url = https://archive.org/details/geometricalfound00will/page/86/mode/1up?view=theater |
|||
| page = 86 |
|||
}}</ref> |
|||
}} |
|||
*{{cite book|author=Cromwell, P.|year=1997|title=Polyhedra|location=United Kingdom|publisher=Cambridge|pages=79–86 ''Archimedean solids''|isbn=0-521-55432-2}} |
|||
==External links== |
|||
*{{mathworld2 |urlname=Icosidodecahedron |title=Icosidodecahedron |urlname2=ArchimedeanSolid |title2=Archimedean solid}} |
|||
*{{KlitzingPolytopes|polyhedra.htm|3D convex uniform polyhedra|o3x5o - id}} |
|||
*[http://www.dr-mikes-math-games-for-kids.com/polyhedral-nets.html?net=1D1NiLVqdeGtmgRYVoqDtRVdULYX8yuwCc3QmkefHkBBQFfG061UUcmoeyIbYKETw4p9pLg3WecHMPxDRy8JGaGKHlYWQJCqLbA3yu66NU9ZKOdvejvHBGtMuZp4O89LBszvnEgWNFbU7I2JwhnVp8hQBn8wSw1ifNCAzgGapWzCkvOVoJPQgcrWxuNXlSA1ESwiCSBVdqj7pKquEaYsKQyb&name=Icosidodecahedron#applet Editable printable net of an icosidodecahedron with interactive 3D view] |
|||
*[http://www.mathconsult.ch/showroom/unipoly/ The Uniform Polyhedra] |
|||
*[http://www.georgehart.com/virtual-polyhedra/vp.html Virtual Reality Polyhedra] The Encyclopedia of Polyhedra |
|||
{{Archimedean solids}} |
{{Archimedean solids}} |
||
| Line 112: | Line 206: | ||
[[Category:Archimedean solids]] |
[[Category:Archimedean solids]] |
||
[[Category:Quasiregular polyhedra]] |
[[Category:Quasiregular polyhedra]] |
||
[[ca:Icosidodecàedre]] |
|||
[[de:Ikosidodekaeder]] |
|||
[[es:Icosidodecaedro]] |
|||
[[eo:Dudek-dekduedro]] |
|||
[[fr:Icosidodécaèdre]] |
|||
[[ko:십이이십면체]] |
|||
[[it:Icosidodecaedro]] |
|||
[[hu:Ikozidodekaéder]] |
|||
[[nl:Icosidodecaëder]] |
|||
[[ja:二十・十二面体]] |
|||
[[pt:Icosidodecaedro]] |
|||
[[ru:Икосододекаэдр]] |
|||
[[th:ทรงสามสิบสองหน้า]] |
|||
[[zh:截半二十面体]] |
|||
Latest revision as of 20:40, 27 November 2024
| Icosidodecahedron | |
|---|---|
 | |
| Type | Archimedean solid Uniform polyhedron Quasiregular polyhedron |
| Faces | 32 |
| Edges | 60 |
| Vertices | 30 |
| Symmetry group | Icosahedral symmetry Ih |
| Dihedral angle (degrees) | 142.62° |
| Dual polyhedron | Rhombic triacontahedron |
| Properties | convex |
| Vertex figure | |
 | |
| Net | |
 | |

In geometry, an icosidodecahedron or pentagonal gyrobirotunda is a polyhedron with twenty (icosi-) triangular faces and twelve (dodeca-) pentagonal faces. An icosidodecahedron has 30 identical vertices, with two triangles and two pentagons meeting at each, and 60 identical edges, each separating a triangle from a pentagon. As such, it is one of the Archimedean solids and more particularly, a quasiregular polyhedron.
Construction
[edit]One way to construct the icosidodecahedron is to start with two pentagonal rotunda by attaching them to their bases. These rotundas cover their decagonal base so that the resulting polyhedron has 32 faces, 30 vertices, and 60 edges. This construction is similar to one of the Johnson solids, the pentagonal orthobirotunda. The difference is that the icosidodecahedron is constructed by twisting its rotundas by 36°, a process known as gyration, resulting in the pentagonal face connecting to the triangular one. The icosidodecahedron has an alternative name, pentagonal gyrobirotunda.[1][2]
Convenient Cartesian coordinates for the vertices of an icosidodecahedron with unit edges are given by the even permutations of: where φ denotes the golden ratio.[3]
Properties
[edit]The surface area of an icosidodecahedron A can be determined by calculating the area of all pentagonal faces. The volume of an icosidodecahedron V can be determined by slicing it off into two pentagonal rotunda, after which summing up their volumes. Therefore, its surface area and volume can be formulated as:[1]
The dihedral angle of an icosidodecahedron between pentagon-to-triangle is determined by calculating the angle of a pentagonal rotunda.[4]
An icosidodecahedron has icosahedral symmetry, and its first stellation is the compound of a dodecahedron and its dual icosahedron, with the vertices of the icosidodecahedron located at the midpoints of the edges of either.
The icosidodecahedron is an Archimedean solid, meaning it is a highly symmetric and semi-regular polyhedron, and two or more different regular polygonal faces meet in a vertex.[5] The polygonal faces that meet for every vertex are two equilateral triangles and two regular pentagons, and the vertex figure of an icosidodecahedron is {{nowrap|(3·5)2 = 32·52}. Its dual polyhedron is rhombic triacontahedron, a Catalan solid.[4]
The icosidodecahedron has 6 central decagons. Projected into a sphere, they define 6 great circles. Fuller (1975) used these 6 great circles, along with 15 and 10 others in two other polyhedra to define his 31 great circles of the spherical icosahedron.[6]
The long radius (center to vertex) of the icosidodecahedron is in the golden ratio to its edge length; thus its radius is φ if its edge length is 1, and its edge length is 1/φ if its radius is 1.[4] Only a few uniform polytopes have this property, including the four-dimensional 600-cell, the three-dimensional icosidodecahedron, and the two-dimensional decagon. (The icosidodecahedron is the equatorial cross-section of the 600-cell, and the decagon is the equatorial cross-section of the icosidodecahedron.) These radially golden polytopes can be constructed, with their radii, from golden triangles which meet at the center, each contributing two radii and an edge.
Related polytopes
[edit]The icosidodecahedron is a rectified dodecahedron and also a rectified icosahedron, existing as the full-edge truncation between these regular solids.
The icosidodecahedron contains 12 pentagons of the dodecahedron and 20 triangles of the icosahedron:
| Family of uniform icosahedral polyhedra | |||||||
|---|---|---|---|---|---|---|---|
| Symmetry: [5,3], (*532) | [5,3]+, (532) | ||||||

|

|

|

|

|

|

|

|
| {5,3} | t{5,3} | r{5,3} | t{3,5} | {3,5} | rr{5,3} | tr{5,3} | sr{5,3} |
| Duals to uniform polyhedra | |||||||

|

|

|

|

|

| ||
| V5.5.5 | V3.10.10 | V3.5.3.5 | V5.6.6 | V3.3.3.3.3 | V3.4.5.4 | V4.6.10 | V3.3.3.3.5 |
The icosidodecahedron exists in a sequence of symmetries of quasiregular polyhedra and tilings with vertex configurations (3.n)2, progressing from tilings of the sphere to the Euclidean plane and into the hyperbolic plane. With orbifold notation symmetry of *n32 all of these tilings are wythoff construction within a fundamental domain of symmetry, with generator points at the right angle corner of the domain.[7][8]
| *n32 orbifold symmetries of quasiregular tilings: (3.n)2 | |||||||
|---|---|---|---|---|---|---|---|
Construction |
Spherical | Euclidean | Hyperbolic | ||||
| *332 | *432 | *532 | *632 | *732 | *832... | *∞32 | |
| Quasiregular figures |

|

|

|

|

|

|

|
| Vertex | (3.3)2 | (3.4)2 | (3.5)2 | (3.6)2 | (3.7)2 | (3.8)2 | (3.∞)2 |
| *5n2 symmetry mutations of quasiregular tilings: (5.n)2 | ||||||||
|---|---|---|---|---|---|---|---|---|
| Symmetry *5n2 [n,5] |
Spherical | Hyperbolic | Paracompact | Noncompact | ||||
| *352 [3,5] |
*452 [4,5] |
*552 [5,5] |
*652 [6,5] |
*752 [7,5] |
*852 [8,5]... |
*∞52 [∞,5] |
[ni,5] | |
| Figures | 
|

|

|

|

|

|

|
|
| Config. | (5.3)2 | (5.4)2 | (5.5)2 | (5.6)2 | (5.7)2 | (5.8)2 | (5.∞)2 | (5.ni)2 |
| Rhombic figures |

|

|

|

|
||||
| Config. | V(5.3)2 | V(5.4)2 | V(5.5)2 | V(5.6)2 | V(5.7)2 | V(5.8)2 | V(5.∞)2 | V(5.∞)2 |
Related polyhedra
[edit]
The truncated cube can be turned into an icosidodecahedron by dividing the octagons into two pentagons and two triangles. It has pyritohedral symmetry.
Eight uniform star polyhedra share the same vertex arrangement. Of these, two also share the same edge arrangement: the small icosihemidodecahedron (having the triangular faces in common), and the small dodecahemidodecahedron (having the pentagonal faces in common). The vertex arrangement is also shared with the compounds of five octahedra and of five tetrahemihexahedra.
Related polychora
[edit]In four-dimensional geometry, the icosidodecahedron appears in the regular 600-cell as the equatorial slice that belongs to the vertex-first passage of the 600-cell through 3D space. In other words: the 30 vertices of the 600-cell which lie at arc distances of 90 degrees on its circumscribed hypersphere from a pair of opposite vertices, are the vertices of an icosidodecahedron. The wireframe figure of the 600-cell consists of 72 flat regular decagons. Six of these are the equatorial decagons to a pair of opposite vertices, and these six form the wireframe figure of an icosidodecahedron.
If a 600-cell is stereographically projected to 3-space about any vertex and all points are normalised, the geodesics upon which edges fall comprise the icosidodecahedron's barycentric subdivision.
Graph
[edit]
The skeleton of an icosidodecahedron can be represented as the graph with 30 vertices and 60 edges, one of the Archimedean graphs. It is quartic, meaning that each of its vertex is connected by four other vertices.[9]
Appearance
[edit]The icosidodecahedron may appears in structural, as in the geodesic dome of the Hoberman sphere.
Icosidodecahedra can be found in all eukaryotic cells, including human cells, as Sec13/31 COPII coat-protein formations.[10]
The icosidodecahedron may also found in popular culture. In Star Trek universe, the Vulcan game of logic Kal-Toh has the goal of creating a shape with two nested holographic icosidodecahedra joined at the midpoints of their segments.
See also
[edit]- Cuboctahedron
- Great truncated icosidodecahedron
- Icosahedron
- Rhombicosidodecahedron
- Truncated icosidodecahedron
References
[edit]- ^ a b Berman, Martin (1971). "Regular-faced convex polyhedra". Journal of the Franklin Institute. 291 (5): 329–352. doi:10.1016/0016-0032(71)90071-8. MR 0290245.
- ^ Ogievetsky, O.; Shlosman, S. (2021). "Platonic compounds and cylinders". In Novikov, S.; Krichever, I.; Ogievetsky, O.; Shlosman, S. (eds.). Integrability, Quantization, and Geometry: II. Quantum Theories and Algebraic Geometry. American Mathematical Society. p. 477. ISBN 978-1-4704-5592-7.
- ^ Weisstein, Eric W. "Icosahedral group". MathWorld.
- ^ a b c Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. p. 86. ISBN 978-0-486-23729-9.
- ^ Diudea, M. V. (2018). Multi-shell Polyhedral Clusters. Carbon Materials: Chemistry and Physics. Vol. 10. Springer. p. 39. doi:10.1007/978-3-319-64123-2. ISBN 978-3-319-64123-2.
- ^ Fuller, R. B. (1975). Synergetics: Explorations in the Geometry of Thinking. MacMillan. p. 183–185. ISBN 978-0-02-065320-2.
- ^ Coxeter Regular Polytopes, Third edition, (1973), Dover edition, ISBN 0-486-61480-8 (Chapter V: The Kaleidoscope, Section: 5.7 Wythoff's construction)
- ^ Two Dimensional symmetry Mutations by Daniel Huson
- ^ Read, R. C.; Wilson, R. J. (1998), An Atlas of Graphs, Oxford University Press, p. 269
- ^ Russell, Christopher; Stagg, Scott (11 February 2010). "New Insights into the Structural Mechanisms of the COPII Coat". Traffic. 11 (3): 303–310. doi:10.1111/j.1600-0854.2009.01026.x. PMID 20070605.
- Cromwell, P. (1997). Polyhedra. United Kingdom: Cambridge. pp. 79–86 Archimedean solids. ISBN 0-521-55432-2.
External links
[edit]- Weisstein, Eric W., "Icosidodecahedron" ("Archimedean solid") at MathWorld.
- Klitzing, Richard. "3D convex uniform polyhedra o3x5o - id".
- Editable printable net of an icosidodecahedron with interactive 3D view
- The Uniform Polyhedra
- Virtual Reality Polyhedra The Encyclopedia of Polyhedra