Intermittency: Difference between revisions
ce |
Citation bot (talk | contribs) Add: s2cid. | Use this bot. Report bugs. | Suggested by Corvus florensis | #UCB_webform 1493/1612 |
||
| (43 intermediate revisions by 27 users not shown) | |||
| Line 1: | Line 1: | ||
{{otheruses}} |
|||
{{Other uses|Intermittent power source}} |
|||
{{short description|Irregular alternation different types of dynamics}} |
|||
{{Refimprove|date=August 2008}} |
|||
{{More citations needed|date=May 2023}} |
|||
| ⚫ | In [[dynamical system]]s, '''intermittency''' is the alternation of phases of apparently periodic and [[Chaos theory|chaotic]] dynamics.<ref>{{cite |
||
{{Primary sources|date=May 2023}} |
|||
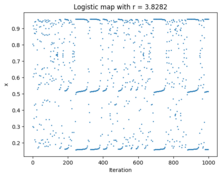
[[File:Intermittency in logistic map.png|thumb|Intermittency in logistic map with <math>r = 3.8282</math>. The trajectory alternates between almost period-3 trajectories and chaotic trajectories. At <math>r = 1 + \sqrt 8 \approx 3.8284</math> a stable period-3 trajectory emerges.]] |
|||
In the apparently periodic phases the behaviour is not quite, but only nearly periodic. Thus, rather than a (truly periodic) series of values such as 2, 4, 2, 4, ... one might have something like 2.0001, 4.0003, 2.0002, 4.0001, 2.0003, 3.9999, 1.8715, 6.7486, ... where the first six values are apparently periodic but where the actually chaotic nature of the system becomes apparent after the value 3.9999 is reached. |
|||
[[File:Intermittency in logistic map, cobweb diagram.png|thumb|The intermittency in logistic map can be understood by looking at the cobweb diagram for logistic map (iterated three times). In the cobweb diagram, there are almost-tangencies where the trajectory can be trapped for a long time.]] |
|||
[[File:Intermittent behavior in Duffing oscillator.png|thumb|Intermittent jumping between two potential wells in the driven [[Duffing equation|Duffing oscillator]]. This is an example of crisis-induced intermittency.]] |
|||
[[File:Intermittent Lorenz Attractor - Chaoscope.jpg|thumb|alt=Intermittency|[[Lorenz attractor]] showing intermittency. The system spends long periods close to the bright periodic orbit, occasionally moving away for phases of chaotic dynamics that cover the rest of the attractor. This is an example of Pomeau–Manneville dynamics.]] |
|||
| ⚫ | In [[dynamical system]]s, '''intermittency''' is the irregular alternation of phases of apparently periodic and [[Chaos theory|chaotic]] dynamics ([[Pomeau–Manneville scenario|Pomeau–Manneville dynamics]]), or different forms of chaotic dynamics (crisis-induced intermittency).<ref>{{cite journal|author=Mingzhou Ding|title=Intermittency|editor=Alwyn Scott|journal=Encyclopedia of Nonlinear Science|url=http://www.ccs.fau.edu/~ding/Intermittency.pdf|publisher=Taylor & Francis|access-date=2006-04-07|archive-date=2011-09-27|archive-url=https://web.archive.org/web/20110927081759/http://www.ccs.fau.edu/~ding/Intermittency.pdf|url-status=dead}}</ref><ref>{{cite book |author=Edward Ott|title=Chaos in dynamical systems|publisher=Cambridge University Press|year=2002|page=323}}</ref> |
||
Experimentally, intermittency appears as long periods of almost periodic behavior interrupted by chaotic behavior. As control variables change, the chaotic behavior become more frequent until the system is fully chaotic. This progression is known as the '''intermittency route to chaos'''. |
|||
Intermittency factor is the fraction of time that motion is [[turbulent]], denoted <math>\mu</math>. |
|||
[[Yves Pomeau|Pomeau]] and Manneville described three routes to intermittency where a nearly periodic system shows irregularly spaced bursts of chaos. <ref>Yves Pomeau and Paul Manneville, Intermittent Transition to Turbulence in Dissipative Dynamical Systems, Commun. Math. Phys. vol. 74, pp. 189–197 1980</ref> These (type I, II and III) correspond to the approach to a [[saddle-node bifurcation]], a subcritical [[Hopf bifurcation]], or an inverse [[period-doubling bifurcation]]. In the apparently periodic phases the behaviour is only nearly periodic, slowly drifting away from an unstable [[periodic orbit]]. Eventually the system gets far enough away from the periodic orbit to be affected by chaotic dynamics in the rest of the [[state space]], until it gets close to the orbit again and returns to the nearly periodic behaviour. Since the time spent near the periodic orbit depends sensitively on how closely the system entered its vicinity (in turn determined by what happened during the chaotic period) the length of each phase is unpredictable. |
|||
In [[technology]], in particular [[electronics]], an '''[[intermittent fault]]''', sometimes called just an "intermittent", is one that does not manifest continuously. These faults are particularly difficult to detect, as they may occur at times when a system is in use, but not when attempts are made to repair it. |
|||
Another kind, on-off intermittency, occurs when a previously transversally stable chaotic attractor with dimension less than the embedding space begins to lose stability. Near unstable orbits within the attractor orbits can escape into the surrounding space, producing a temporary burst before returning to the attractor. <ref>E.Ott and J.C. Sommerer, Blowout bifurcations: the occurrence of riddled basins and on-off intermittency, Physics Letters A, vol. 188, 1994, pp. 39–47</ref> |
|||
In crisis-induced intermittency a chaotic attractor suffers a [[Crisis (dynamical systems)|crisis]], where two or more attractors cross the boundaries of each other's [[basin of attraction]]. As an orbit moves through the first attractor it can cross over the boundary and become attracted to the second attractor, where it will stay until its dynamics moves it across the boundary again. |
|||
Intermittent behaviour is commonly observed in fluid flows that are [[turbulent]] or near the transition to turbulence. In highly [[turbulent]] flows, intermittency is seen in the irregular dissipation of kinetic energy <ref>C. Meneveau and K.R. Sreenivasan, The multifractal nature of turbulent energy dissipation, Journal of Fluid Mechanics, vol. 224, 1991, pp. 429-484</ref> and the anomalous scaling of velocity increments.<ref>F. Anselmet, Y. Gagne, E.J. Hopfinger, R.A. Antonia, High-order velocity structure functions in turbulent shear flows, Journal of Fluid Mechanics, vol. 140, 1984, pp. 63-89</ref> Understanding and modeling atmospheric flow and turbulence under such conditions are further complicated by “turbulence intermittency,” which manifests as periods of strong turbulent activity interspersed in a more quiescent airflow.<ref>{{cite journal |last1=Allouche |first1=Mohammad |last2=Bou-Zeid |first2=Elie |last3=Ansorge |first3=Cedrick |last4=Katul |first4=Gabriel G. |last5=Chamecki |first5=Marcelo |last6=Acevedo |first6=Otavio |last7=Thanekar |first7=Sham |last8=Fuentes |first8=Jose D. |title=The Detection, Genesis, and Modeling of Turbulence Intermittency in the Stable Atmospheric Surface Layer |journal=Journal of the Atmospheric Sciences |date=1 April 2022 |volume=79 |issue=4 |pages=1171–1190 |doi=10.1175/JAS-D-21-0053.1 |s2cid=245955138 |url=https://doi.org/10.1175/JAS-D-21-0053.1 |language=EN |issn=0022-4928}}</ref> It is also seen in the irregular alternation between turbulent and non-turbulent fluid that appear in turbulent [[jet (fluid)|jets]] and other turbulent free shear flows. In [[pipe flow]] and other wall bounded shear flows, there are intermittent puffs that are central to the process of transition from laminar to turbulent flow. Intermittent behavior has also been experimentally demonstrated in circuit oscillators and chemical reactions. |
|||
==See also== |
==See also== |
||
*[[Pomeau–Manneville scenario]] |
|||
*[[Crisis (dynamical systems)]] |
|||
*[[Turbulence|Turbulent flow]] |
*[[Turbulence|Turbulent flow]] |
||
*[[Fluorescence intermittency]] (blinking) of organic molecules and colloidal quantum dots (nanocrystals) |
*[[Fluorescence intermittency]] (blinking) of organic molecules and colloidal quantum dots (nanocrystals) |
||
== |
==References== |
||
{{ |
{{Reflist}} |
||
*{{cite book |
*{{cite book |
||
| last= Staicu |first=A. D. |
| last= Staicu |first=A. D. |
||
| Line 21: | Line 34: | ||
| title = Intermittency in Turbulence |
| title = Intermittency in Turbulence |
||
| url = http://alexandria.tue.nl/extra2/200213784.pdf |
| url = http://alexandria.tue.nl/extra2/200213784.pdf |
||
| publisher = [[University of Technology |
| publisher = [[Eindhoven University of Technology]] |
||
| isbn= |
| isbn= |
||
}} |
}} |
||
| Line 31: | Line 44: | ||
| publisher = [[Cambridge University Press]] |
| publisher = [[Cambridge University Press]] |
||
| bibcode=2000itf..book.....V |
| bibcode=2000itf..book.....V |
||
| isbn = |
| isbn = 0-521-79221-5}} |
||
}} |
|||
==External links== |
|||
* [http://www.ibiblio.org/e-notes/MSet/Intermit.htm Transition to chaos through intermittency] |
|||
[[Category:Dynamical systems]] |
[[Category:Dynamical systems]] |
||
{{physics-stub}} |
|||
[[de:Intermittenz]] |
|||
[[pl:Intermitencja]] |
|||
Latest revision as of 07:52, 11 December 2023
This article needs additional citations for verification. (May 2023) |



In dynamical systems, intermittency is the irregular alternation of phases of apparently periodic and chaotic dynamics (Pomeau–Manneville dynamics), or different forms of chaotic dynamics (crisis-induced intermittency).[1][2]
Experimentally, intermittency appears as long periods of almost periodic behavior interrupted by chaotic behavior. As control variables change, the chaotic behavior become more frequent until the system is fully chaotic. This progression is known as the intermittency route to chaos.
Pomeau and Manneville described three routes to intermittency where a nearly periodic system shows irregularly spaced bursts of chaos. [3] These (type I, II and III) correspond to the approach to a saddle-node bifurcation, a subcritical Hopf bifurcation, or an inverse period-doubling bifurcation. In the apparently periodic phases the behaviour is only nearly periodic, slowly drifting away from an unstable periodic orbit. Eventually the system gets far enough away from the periodic orbit to be affected by chaotic dynamics in the rest of the state space, until it gets close to the orbit again and returns to the nearly periodic behaviour. Since the time spent near the periodic orbit depends sensitively on how closely the system entered its vicinity (in turn determined by what happened during the chaotic period) the length of each phase is unpredictable.
Another kind, on-off intermittency, occurs when a previously transversally stable chaotic attractor with dimension less than the embedding space begins to lose stability. Near unstable orbits within the attractor orbits can escape into the surrounding space, producing a temporary burst before returning to the attractor. [4]
In crisis-induced intermittency a chaotic attractor suffers a crisis, where two or more attractors cross the boundaries of each other's basin of attraction. As an orbit moves through the first attractor it can cross over the boundary and become attracted to the second attractor, where it will stay until its dynamics moves it across the boundary again.
Intermittent behaviour is commonly observed in fluid flows that are turbulent or near the transition to turbulence. In highly turbulent flows, intermittency is seen in the irregular dissipation of kinetic energy [5] and the anomalous scaling of velocity increments.[6] Understanding and modeling atmospheric flow and turbulence under such conditions are further complicated by “turbulence intermittency,” which manifests as periods of strong turbulent activity interspersed in a more quiescent airflow.[7] It is also seen in the irregular alternation between turbulent and non-turbulent fluid that appear in turbulent jets and other turbulent free shear flows. In pipe flow and other wall bounded shear flows, there are intermittent puffs that are central to the process of transition from laminar to turbulent flow. Intermittent behavior has also been experimentally demonstrated in circuit oscillators and chemical reactions.
See also
[edit]- Pomeau–Manneville scenario
- Crisis (dynamical systems)
- Turbulent flow
- Fluorescence intermittency (blinking) of organic molecules and colloidal quantum dots (nanocrystals)
References
[edit]- ^ Mingzhou Ding. Alwyn Scott (ed.). "Intermittency" (PDF). Encyclopedia of Nonlinear Science. Taylor & Francis. Archived from the original (PDF) on 2011-09-27. Retrieved 2006-04-07.
- ^ Edward Ott (2002). Chaos in dynamical systems. Cambridge University Press. p. 323.
- ^ Yves Pomeau and Paul Manneville, Intermittent Transition to Turbulence in Dissipative Dynamical Systems, Commun. Math. Phys. vol. 74, pp. 189–197 1980
- ^ E.Ott and J.C. Sommerer, Blowout bifurcations: the occurrence of riddled basins and on-off intermittency, Physics Letters A, vol. 188, 1994, pp. 39–47
- ^ C. Meneveau and K.R. Sreenivasan, The multifractal nature of turbulent energy dissipation, Journal of Fluid Mechanics, vol. 224, 1991, pp. 429-484
- ^ F. Anselmet, Y. Gagne, E.J. Hopfinger, R.A. Antonia, High-order velocity structure functions in turbulent shear flows, Journal of Fluid Mechanics, vol. 140, 1984, pp. 63-89
- ^ Allouche, Mohammad; Bou-Zeid, Elie; Ansorge, Cedrick; Katul, Gabriel G.; Chamecki, Marcelo; Acevedo, Otavio; Thanekar, Sham; Fuentes, Jose D. (1 April 2022). "The Detection, Genesis, and Modeling of Turbulence Intermittency in the Stable Atmospheric Surface Layer". Journal of the Atmospheric Sciences. 79 (4): 1171–1190. doi:10.1175/JAS-D-21-0053.1. ISSN 0022-4928. S2CID 245955138.
- Staicu, A. D. (2002). Intermittency in Turbulence (PDF). Eindhoven University of Technology.
- Vassilicos, J. C. (2000). Intermittency in turbulent flows. Cambridge University Press. p. 288. Bibcode:2000itf..book.....V. ISBN 0-521-79221-5.


