Linear independence: Difference between revisions
No edit summary |
m Reverted 1 edit by 2A02:8388:8500:A280:A853:253A:B568:535 (talk) to last revision by D.Lazard |
||
| (288 intermediate revisions by more than 100 users not shown) | |||
| Line 1: | Line 1: | ||
{{short description|Vectors whose linear combinations are nonzero}} |
|||
[[File:Linearly independent vectors in R3.svg|thumb|right|Linearly independent vectors in '''R'''<sup>3</sup>.]] |
|||
{{For|linear dependence of random variables|Covariance}} |
|||
[[File:Linearly dependent vectors in R3.svg|thumb|right|Linearly dependent vectors in a plane in '''R'''<sup>3</sup>.]] |
|||
<!--{{technical|date=April 2014}}--> |
|||
{{More citations needed|date=January 2019}}[[File:Vec-indep.png|thumb|right|Linearly independent vectors in <math>\R^3</math>]] |
|||
[[File:Vec-dep.png|thumb|right|Linearly dependent vectors in a plane in <math>\R^3.</math>]] |
|||
In the theory of [[vector space]]s, a [[set (mathematics)|set]] of [[vector (mathematics)|vector]]s is said to be '''{{visible anchor|linearly independent}}''' if there exists no nontrivial [[linear combination]] of the vectors that equals the zero vector. If such a linear combination exists, then the vectors are said to be '''{{visible anchor|linearly dependent}}'''. These concepts are central to the definition of [[Dimension (vector space)|dimension]].<ref>G. E. Shilov, ''[https://books.google.com/books?id=5U6loPxlvQkC&q=dependent+OR+independent+OR+dependence+OR+independence Linear Algebra]'' (Trans. R. A. Silverman), Dover Publications, New York, 1977.</ref> |
|||
<!-- these distinctions are not useful |
|||
* An [[indexed family]] of [[vector space|vector]]s is a '''linearly independent family''' if none of them can be written as a [[linear combination]] of finitely many other vectors in the family. A family of vectors which is not linearly independent is called '''linearly dependent'''. |
|||
* A [[set (mathematics)|set]] of vectors is a '''linearly independent set''' if the set (regarded as a family indexed by itself) is a linearly independent family. |
|||
These two notions are not equivalent: the difference being that in a family we allow repeated elements, while in a set we do not. For example if <math>V</math> is a vector space, then the family <math>F : \{ 1, 2 \} \to V</math> such that <math>f(1) = v</math> and <math>f(2) = v</math> is a {{em|linearly dependent family}}, but the singleton set of the images of that family is <math>\{v\}</math> which is a {{em|linearly independent set}}. |
|||
Both notions are important and used in common, and sometimes even confused in the literature. |
|||
--> |
|||
<!-- this too early |
|||
For instance, in the [[3 dimensional space|three-dimensional]] [[real vector space]] <math>\R^3</math> we have the following example: |
|||
In [[linear algebra]], a [[indexed family|family]] of [[vector space|vector]]s is '''linearly independent''' if none of them can be written as a [[linear combination]] of finitely many other vectors in the family. A family of vectors which is not [[linearly independent]] is called '''[[linearly dependent]]'''. For instance, in the three-dimensional [[real vector space]] <math>\mathbb{R}^3</math> we have the following example. |
|||
:<math> |
:<math> |
||
\begin{matrix} |
\begin{matrix} |
||
| Line 16: | Line 30: | ||
\mbox{dependent}\\ |
\mbox{dependent}\\ |
||
\end{matrix} |
\end{matrix} |
||
</math><!-- weights 9, 5, 4 |
</math>--><!-- weights 9, 5, 4 |
||
Here the first three vectors are linearly independent; but the fourth vector equals 9 times the first plus 5 times the second plus 4 times the third, so the four vectors together are linearly dependent. Linear dependence is a property of the |
Here the first three vectors are linearly independent; but the fourth vector equals 9 times the first plus 5 times the second plus 4 times the third, so the four vectors together are linearly dependent. Linear dependence is a property of the set of vectors, not of any particular vector. For example in this case we could just as well write the first vector as a linear combination of the last three. |
||
:<math>\ |
:<math>\mathbf{v}_1=\left(-\frac{5}{9}\right)\mathbf{v}_2+\left(-\frac{4}{9}\right)\mathbf{v}_3+\frac{1}{9}\mathbf{v}_4 .</math> |
||
--> |
|||
<!-- In [[probability theory]] and [[statistics]] there is an unrelated measure of linear dependence between [[random variable]]s. --> |
|||
A vector space can be of finite dimension or infinite dimension depending on the maximum number of linearly independent vectors. The definition of linear dependence and the ability to determine whether a subset of vectors in a vector space is linearly dependent are central to determining the dimension of a vector space. |
|||
In [[probability theory]] and [[statistics]] there is an unrelated measure of linear dependence between [[random variable]]s. |
|||
== Definition == |
== Definition == |
||
A sequence of vectors <math>\mathbf{v}_1, \mathbf{v}_2, \dots, \mathbf{v}_k</math> from a [[vector space]] {{mvar|V}} is said to be ''linearly dependent'', if there exist [[Scalar (mathematics)|scalars]] <math>a_1, a_2, \dots, a_k,</math> not all zero, such that |
|||
:<math>a_1\mathbf{v}_1 + a_2\mathbf{v}_2 + \cdots + a_k\mathbf{v}_k = \mathbf{0},</math> |
|||
where <math>\mathbf{0}</math> denotes the zero vector. |
|||
This implies that at least one of the scalars is nonzero, say <math>a_1\ne 0</math>, and the above equation is able to be written as |
|||
A finite subset of ''n'' vectors, '''v'''<sub>1</sub>, '''v'''<sub>2</sub>, ..., '''v'''<sub>''n''</sub>, from the vector space ''V'', is '''''linearly dependent''''' if and only if there exists a set of ''n'' scalars, ''a''<sub>1</sub>, ''a''<sub>2</sub>, ..., ''a''<sub>''n''</sub>, not all zero, such that |
|||
:<math>\mathbf{v}_1 = \frac{-a_2}{a_1}\mathbf{v}_2 + \cdots + \frac{-a_k}{a_1} \mathbf{v}_k,</math> |
|||
if <math>k>1,</math> and <math>\mathbf{v}_1 = \mathbf{0}</math> if <math>k=1.</math> |
|||
Thus, a set of vectors is linearly dependent if and only if one of them is zero or a [[linear combination]] of the others. |
|||
:<math> a_1 \mathbf{v}_1 + a_2 \mathbf{v}_2 + \cdots + a_n \mathbf{v}_n = \mathbf{0}. </math> |
|||
A sequence of vectors <math>\mathbf{v}_1, \mathbf{v}_2, \dots, \mathbf{v}_n</math> is said to be ''linearly independent'' if it is not linearly dependent, that is, if the equation |
|||
Note that the zero on the right is the [[Null vector (vector space)|zero vector]], not the number zero. |
|||
:<math>a_1\mathbf{v}_1 + a_2 \mathbf{v}_2 + \cdots + a_n\mathbf{v}_n = \mathbf{0},</math> |
|||
can only be satisfied by <math>a_i=0</math> for <math>i=1,\dots,n.</math> This implies that no vector in the sequence can be represented as a linear combination of the remaining vectors in the sequence. In other words, a sequence of vectors is linearly independent if the only representation of <math>\mathbf 0</math> as a linear combination of its vectors is the trivial representation in which all the scalars <math display="inline">a_i</math> are zero.<ref>{{cite book|last1=Friedberg |last2=Insel |last3=Spence|first1=Stephen |first2=Arnold |first3=Lawrence|title=Linear Algebra|year=2003|publisher=Pearson, 4th Edition|isbn=0130084514|pages=48–49}}</ref> Even more concisely, a sequence of vectors is linearly independent if and only if <math>\mathbf 0</math> can be represented as a linear combination of its vectors in a unique way. |
|||
If a sequence of vectors contains the same vector twice, it is necessarily dependent. The linear dependency of a sequence of vectors does not depend of the order of the terms in the sequence. This allows defining linear independence for a finite set of vectors: A finite set of vectors is ''linearly independent'' if the sequence obtained by ordering them is linearly independent. In other words, one has the following result that is often useful. |
|||
If such scalars do not exist, then the vectors are said to be '''''linearly independent'''''. |
|||
A sequence of vectors is linearly independent if and only if it does not contain the same vector twice and the set of its vectors is linearly independent. |
|||
:<math> a_1 \mathbf{v}_1 + a_2 \mathbf{v}_2 + \cdots + a_n \mathbf{v}_n = \mathbf{0}, </math> |
|||
if and only if ''a''<sub>''i''</sub> = 0 for ''i'' = 1, 2, ..., ''n''. |
|||
===Infinite case=== |
|||
A set of vectors is then said to be ''linearly dependent'' if it is not linearly independent. |
|||
An infinite set of vectors is ''linearly independent'' if every nonempty finite [[subset]] is linearly independent. Conversely, an infinite set of vectors is ''linearly dependent'' if it contains a finite subset that is linearly dependent, or equivalently, if some vector in the set is a linear combination of other vectors in the set. |
|||
An [[indexed family]] of vectors is ''linearly independent'' if it does not contain the same vector twice, and if the set of its vectors is linearly independent. Otherwise, the family is said to be ''linearly dependent''. |
|||
More generally, let ''V'' be a vector space over a [[field (mathematics)|field]] ''K'', and let {'''v'''<sub>''i''</sub> | ''i''∈''I''} be a [[indexed family|family]] of elements of ''V''. The family is ''linearly dependent'' over ''K'' if there exists a family {''a''<sub>''j''</sub> | ''j''∈''J''} of elements of ''K'', not all zero, such that |
|||
A set of vectors which is linearly independent and [[linear span|spans]] some vector space, forms a [[basis (linear algebra)|basis]] for that vector space. For example, the vector space of all [[polynomial]]s in {{mvar|x}} over the reals has the (infinite) subset {{math|1={1, ''x'', ''x''<sup>2</sup>, ...} }} as a basis. |
|||
:<math> \sum_{j \in J} a_j \mathbf{v}_j = \mathbf{0} \,</math> |
|||
== Geometric examples == |
|||
where the index set ''J'' is a nonempty, finite subset of ''I''. |
|||
[[File:Vectores independientes.png|right]] |
|||
* <math>\vec u</math> and <math>\vec v</math> are independent and define the [[plane (geometry)|plane]] P. |
|||
A set ''X'' of elements of ''V'' is ''linearly independent'' if the corresponding family {'''x'''}<sub>'''x'''∈''X''</sub> is linearly independent. |
|||
* <math>\vec u</math>, <math>\vec v</math> and <math>\vec w</math> are dependent because all three are contained in the same plane. |
|||
* <math>\vec u</math> and <math>\vec j</math> are dependent because they are parallel to each other. |
|||
* <math>\vec u</math> , <math>\vec v</math> and <math>\vec k</math> are independent because <math>\vec u</math> and <math>\vec v</math> are independent of each other and <math>\vec k</math> is not a linear combination of them or, equivalently, because they do not belong to a common plane. The three vectors define a three-dimensional space. |
|||
* The vectors <math>\vec o</math> (null vector, whose components are equal to zero) and <math>\vec k</math> are dependent since <math>\vec o = 0 \vec k</math> |
|||
=== Geographic location === |
|||
Equivalently, a family is dependent if a member is in the [[linear span]] of the rest of the family, i.e., a member is a [[linear combination]] of the rest of the family. |
|||
A person describing the location of a certain place might say, "It is 3 miles north and 4 miles east of here." This is sufficient information to describe the location, because the geographic coordinate system may be considered as a 2-dimensional vector space (ignoring altitude and the curvature of the Earth's surface). The person might add, "The place is 5 miles northeast of here." This last statement is ''true'', but it is not necessary to find the location. |
|||
A set of vectors which is linearly independent and [[linear span|spans]] some vector space, forms a [[basis (linear algebra)|basis]] for that vector space. For example, the vector space of all polynomials in ''x'' over the reals has for a basis the (infinite) subset {1, ''x'', ''x''<sup>2</sup>, ...}. |
|||
In this example the "3 miles north" vector and the "4 miles east" vector are linearly independent. That is to say, the north vector cannot be described in terms of the east vector, and vice versa. The third "5 miles northeast" vector is a [[linear combination]] of the other two vectors, and it makes the set of vectors ''linearly dependent'', that is, one of the three vectors is unnecessary to define a specific location on a plane. |
|||
Also note that if altitude is not ignored, it becomes necessary to add a third vector to the linearly independent set. In general, {{mvar|n}} linearly independent vectors are required to describe all locations in {{mvar|n}}-dimensional space. |
|||
== Geometric meaning == |
|||
== Evaluating linear independence == |
|||
A geographic example may help to clarify the concept of linear independence. A person describing the location of a certain place might say, "It is 5 miles north and 6 miles east of here." This is sufficient information to describe the location, because the geographic coordinate system may be considered as a 2-dimensional vector space (ignoring altitude). The person might add, "The place is 7.81 miles northeast of here." Although this last statement is ''true'', it is not necessary. |
|||
=== The zero vector === |
|||
In this example the "5 miles north" vector and the "6 miles east" vector are linearly independent. That is to say, the north vector cannot be described in terms of the east vector, and vice versa. The third "7.81 miles northeast" vector is a [[linear combination]] of the other two vectors, and it makes the set of vectors ''linearly dependent'', that is, one of the three vectors is unnecessary. |
|||
If one or more vectors from a given sequence of vectors <math>\mathbf{v}_1, \dots, \mathbf{v}_k</math> is the zero vector <math>\mathbf{0}</math> then the vector <math>\mathbf{v}_1, \dots, \mathbf{v}_k</math> are necessarily linearly dependent (and consequently, they are not linearly independent). |
|||
Also note that if altitude is not ignored, it becomes necessary to add a third vector to the linearly independent set. In general, ''n'' linearly independent vectors are required to describe any location in ''n''-dimensional space. |
|||
To see why, suppose that <math>i</math> is an index (i.e. an element of <math>\{ 1, \ldots, k \}</math>) such that <math>\mathbf{v}_i = \mathbf{0}.</math> Then let <math>a_{i} := 1</math> (alternatively, letting <math>a_{i}</math> be equal any other non-zero scalar will also work) and then let all other scalars be <math>0</math> (explicitly, this means that for any index <math>j</math> other than <math>i</math> (i.e. for <math>j \neq i</math>), let <math>a_{j} := 0</math> so that consequently <math>a_{j} \mathbf{v}_j = 0 \mathbf{v}_j = \mathbf{0}</math>). |
|||
Simplifying <math>a_1 \mathbf{v}_1 + \cdots + a_k\mathbf{v}_k</math> gives: |
|||
:<math>a_1 \mathbf{v}_1 + \cdots + a_k\mathbf{v}_k = \mathbf{0} + \cdots + \mathbf{0} + a_i \mathbf{v}_i + \mathbf{0} + \cdots + \mathbf{0} = a_i \mathbf{v}_i = a_i \mathbf{0} = \mathbf{0}.</math> |
|||
Because not all scalars are zero (in particular, <math>a_{i} \neq 0</math>), this proves that the vectors <math>\mathbf{v}_1, \dots, \mathbf{v}_k</math> are linearly dependent. |
|||
As a consequence, the zero vector can not possibly belong to any collection of vectors that is linearly ''in''dependent. |
|||
== Example I == |
|||
Now consider the special case where the sequence of <math>\mathbf{v}_1, \dots, \mathbf{v}_k</math> has length <math>1</math> (i.e. the case where <math>k = 1</math>). |
|||
The vectors (1, 1) and (−3, 2) in <math>\mathbb{R}^2</math> are linearly independent. |
|||
A collection of vectors that consists of exactly one vector is linearly dependent if and only if that vector is zero. |
|||
Explicitly, if <math>\mathbf{v}_1</math> is any vector then the sequence <math>\mathbf{v}_1</math> (which is a sequence of length <math>1</math>) is linearly dependent if and only if {{nowrap|<math>\mathbf{v}_1 = \mathbf{0}</math>;}} alternatively, the collection <math>\mathbf{v}_1</math> is linearly independent if and only if <math>\mathbf{v}_1 \neq \mathbf{0}.</math> |
|||
=== Linear dependence and independence of two vectors === |
|||
=== Proof === |
|||
This example considers the special case where there are exactly two vector <math>\mathbf{u}</math> and <math>\mathbf{v}</math> from some real or complex vector space. |
|||
Let λ<sub>1</sub> and λ<sub>2</sub> be two [[real number]]s such that |
|||
The vectors <math>\mathbf{u}</math> and <math>\mathbf{v}</math> are linearly dependent [[if and only if]] at least one of the following is true: |
|||
# <math>\mathbf{u}</math> is a scalar multiple of <math>\mathbf{v}</math> (explicitly, this means that there exists a scalar <math>c</math> such that <math>\mathbf{u} = c \mathbf{v}</math>) or |
|||
# <math>\mathbf{v}</math> is a scalar multiple of <math>\mathbf{u}</math> (explicitly, this means that there exists a scalar <math>c</math> such that <math>\mathbf{v} = c \mathbf{u}</math>). |
|||
If <math>\mathbf{u} = \mathbf{0}</math> then by setting <math>c := 0</math> we have <math>c \mathbf{v} = 0 \mathbf{v} = \mathbf{0} = \mathbf{u}</math> (this equality holds no matter what the value of <math>\mathbf{v}</math> is), which shows that (1) is true in this particular case. Similarly, if <math>\mathbf{v} = \mathbf{0}</math> then (2) is true because <math>\mathbf{v} = 0 \mathbf{u}.</math> |
|||
If <math>\mathbf{u} = \mathbf{v}</math> (for instance, if they are both equal to the zero vector <math>\mathbf{0}</math>) then ''both'' (1) and (2) are true (by using <math>c := 1</math> for both). |
|||
If <math>\mathbf{u} = c \mathbf{v}</math> then <math>\mathbf{u} \neq \mathbf{0}</math> is only possible if <math>c \neq 0</math> ''and'' <math>\mathbf{v} \neq \mathbf{0}</math>; in this case, it is possible to multiply both sides by <math display="inline">\frac{1}{c}</math> to conclude <math display="inline">\mathbf{v} = \frac{1}{c} \mathbf{u}.</math> |
|||
:<math> (1, 1) \lambda_1 + (-3, 2) \lambda_2 = (0, 0) . \,\! </math> |
|||
This shows that if <math>\mathbf{u} \neq \mathbf{0}</math> and <math>\mathbf{v} \neq \mathbf{0}</math> then (1) is true if and only if (2) is true; that is, in this particular case either both (1) and (2) are true (and the vectors are linearly dependent) or else both (1) and (2) are false (and the vectors are linearly ''in''dependent). |
|||
If <math>\mathbf{u} = c \mathbf{v}</math> but instead <math>\mathbf{u} = \mathbf{0}</math> then at least one of <math>c</math> and <math>\mathbf{v}</math> must be zero. |
|||
Moreover, if exactly one of <math>\mathbf{u}</math> and <math>\mathbf{v}</math> is <math>\mathbf{0}</math> (while the other is non-zero) then exactly one of (1) and (2) is true (with the other being false). |
|||
The vectors <math>\mathbf{u}</math> and <math>\mathbf{v}</math> are linearly ''in''dependent if and only if <math>\mathbf{u}</math> is not a scalar multiple of <math>\mathbf{v}</math> ''and'' <math>\mathbf{v}</math> is not a scalar multiple of <math>\mathbf{u}</math>. |
|||
Taking each coordinate alone, this means |
|||
=== Vectors in R<sup>2</sup> === |
|||
:<math> \begin{align} |
|||
'''Three vectors:''' Consider the set of vectors <math>\mathbf{v}_1 = (1, 1),</math> <math>\mathbf{v}_2 = (-3, 2),</math> and <math>\mathbf{v}_3 = (2, 4),</math> then the condition for linear dependence seeks a set of non-zero scalars, such that |
|||
\lambda_1 - 3 \lambda_2 &{}= 0 , \\ |
|||
:<math>a_1 \begin{bmatrix} 1\\1\end{bmatrix} + a_2 \begin{bmatrix} -3\\2\end{bmatrix} + a_3 \begin{bmatrix} 2\\4\end{bmatrix} =\begin{bmatrix} 0\\0\end{bmatrix},</math> |
|||
\lambda_1 + 2 \lambda_2 &{}= 0 . |
|||
or |
|||
\end{align} </math> |
|||
:<math>\begin{bmatrix} 1 & -3 & 2 \\ 1 & 2 & 4 \end{bmatrix}\begin{bmatrix} a_1\\ a_2 \\ a_3 \end{bmatrix}= \begin{bmatrix} 0\\0\end{bmatrix}.</math> |
|||
[[Row reduction|Row reduce]] this matrix equation by subtracting the first row from the second to obtain, |
|||
Solving for λ<sub>1</sub> and λ<sub>2</sub>, we find that λ<sub>1</sub> = 0 and λ<sub>2</sub> = 0. |
|||
:<math>\begin{bmatrix} 1 & -3 & 2 \\ 0 & 5 & 2 \end{bmatrix}\begin{bmatrix} a_1\\ a_2 \\ a_3 \end{bmatrix}= \begin{bmatrix} 0\\0\end{bmatrix}.</math> |
|||
Continue the row reduction by (i) dividing the second row by 5, and then (ii) multiplying by 3 and adding to the first row, that is |
|||
:<math>\begin{bmatrix} 1 & 0 & 16/5 \\ 0 & 1 & 2/5 \end{bmatrix}\begin{bmatrix} a_1\\ a_2 \\ a_3 \end{bmatrix}= \begin{bmatrix} 0\\0\end{bmatrix}.</math> |
|||
Rearranging this equation allows us to obtain |
|||
:<math>\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}\begin{bmatrix} a_1\\ a_2 \end{bmatrix}= \begin{bmatrix} a_1\\ a_2 \end{bmatrix}=-a_3\begin{bmatrix} 16/5\\2/5\end{bmatrix}.</math> |
|||
which shows that non-zero ''a''<sub>''i''</sub> exist such that <math>\mathbf{v}_3 = (2, 4)</math> can be defined in terms of <math>\mathbf{v}_1 = (1, 1)</math> and <math>\mathbf{v}_2 = (-3, 2).</math> Thus, the three vectors are linearly dependent. |
|||
'''Two vectors:''' Now consider the linear dependence of the two vectors <math>\mathbf{v}_1 = (1, 1)</math> and <math>\mathbf{v}_2 = (-3, 2),</math> and check, |
|||
:<math>a_1 \begin{bmatrix} 1\\1\end{bmatrix} + a_2 \begin{bmatrix} -3\\2\end{bmatrix} =\begin{bmatrix} 0\\0\end{bmatrix},</math> |
|||
or |
|||
:<math>\begin{bmatrix} 1 & -3 \\ 1 & 2 \end{bmatrix}\begin{bmatrix} a_1\\ a_2 \end{bmatrix}= \begin{bmatrix} 0\\0\end{bmatrix}.</math> |
|||
The same row reduction presented above yields, |
|||
:<math>\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}\begin{bmatrix} a_1\\ a_2 \end{bmatrix}= \begin{bmatrix} 0\\0\end{bmatrix}.</math> |
|||
This shows that <math>a_i = 0,</math> which means that the vectors <math>\mathbf{v}_1 = (1, 1)</math> and <math>\mathbf{v}_2 = (-3, 2)</math> are linearly independent. |
|||
=== Vectors in R<sup>4</sup> === |
|||
In order to determine if the three vectors in <math>\mathbb{R}^4,</math> |
|||
:<math>\mathbf{v}_1= \begin{bmatrix}1\\4\\2\\-3\end{bmatrix}, \mathbf{v}_2=\begin{bmatrix}7\\10\\-4\\-1\end{bmatrix}, \mathbf{v}_3=\begin{bmatrix}-2\\1\\5\\-4\end{bmatrix}.</math> |
|||
are linearly dependent, form the matrix equation, |
|||
:<math>\begin{bmatrix}1&7&-2\\4& 10& 1\\2&-4&5\\-3&-1&-4\end{bmatrix}\begin{bmatrix} a_1\\ a_2 \\ a_3 \end{bmatrix} = \begin{bmatrix}0\\0\\0\\0\end{bmatrix}.</math> |
|||
Row reduce this equation to obtain, |
|||
:<math>\begin{bmatrix} 1& 7 & -2 \\ 0& -18& 9\\ 0 & 0 & 0\\ 0& 0& 0\end{bmatrix} \begin{bmatrix} a_1\\ a_2 \\ a_3 \end{bmatrix} = \begin{bmatrix}0\\0\\0\\0\end{bmatrix}.</math> |
|||
Rearrange to solve for v<sub>3</sub> and obtain, |
|||
:<math>\begin{bmatrix} 1& 7 \\ 0& -18 \end{bmatrix} \begin{bmatrix} a_1\\ a_2 \end{bmatrix} = -a_3\begin{bmatrix}-2\\9\end{bmatrix}.</math> |
|||
This equation is easily solved to define non-zero ''a''<sub>i</sub>, |
|||
:<math>a_1 = -3 a_3 /2, a_2 = a_3/2,</math> |
|||
where <math>a_3</math> can be chosen arbitrarily. Thus, the vectors <math>\mathbf{v}_1, \mathbf{v}_2,</math> and <math>\mathbf{v}_3</math> are linearly dependent. |
|||
=== Alternative method using determinants === |
=== Alternative method using determinants === |
||
An alternative method |
An alternative method relies on the fact that <math>n</math> vectors in <math>\mathbb{R}^n</math> are linearly '''independent''' [[if and only if]] the [[determinant]] of the [[matrix (mathematics)|matrix]] formed by taking the vectors as its columns is non-zero. |
||
In this case, the matrix formed by the vectors is |
In this case, the matrix formed by the vectors is |
||
:<math>A = \begin{bmatrix}1&-3\\1&2\end{bmatrix} . |
:<math>A = \begin{bmatrix}1&-3\\1&2\end{bmatrix} .</math> |
||
We may write a linear combination of the columns as |
We may write a linear combination of the columns as |
||
:<math> |
:<math>A \Lambda = \begin{bmatrix}1&-3\\1&2\end{bmatrix} \begin{bmatrix}\lambda_1 \\ \lambda_2 \end{bmatrix} .</math> |
||
We are interested in whether ''A''Λ |
We are interested in whether {{math|1=''A''Λ = '''0'''}} for some nonzero vector Λ. This depends on the determinant of <math>A</math>, which is |
||
:<math> |
:<math>\det A = 1\cdot2 - 1\cdot(-3) = 5 \ne 0.</math> |
||
Since the [[determinant]] is non-zero, the vectors (1, 1) and ( |
Since the [[determinant]] is non-zero, the vectors <math>(1, 1)</math> and <math>(-3, 2)</math> are linearly independent. |
||
Otherwise, suppose we have |
Otherwise, suppose we have <math>m</math> vectors of <math>n</math> coordinates, with <math>m < n.</math> Then ''A'' is an ''n''×''m'' matrix and Λ is a column vector with <math>m</math> entries, and we are again interested in ''A''Λ = '''0'''. As we saw previously, this is equivalent to a list of <math>n</math> equations. Consider the first <math>m</math> rows of <math>A</math>, the first <math>m</math> equations; any solution of the full list of equations must also be true of the reduced list. In fact, if {{math|⟨''i''<sub>1</sub>,...,''i''<sub>''m''</sub>⟩}} is any list of <math>m</math> rows, then the equation must be true for those rows. |
||
:<math> |
:<math>A_{\lang i_1,\dots,i_m \rang} \Lambda = \mathbf{0} .</math> |
||
Furthermore, the reverse is true. That is, we can test whether the |
Furthermore, the reverse is true. That is, we can test whether the <math>m</math> vectors are linearly dependent by testing whether |
||
:<math> |
:<math>\det A_{\lang i_1,\dots,i_m \rang} = 0</math> |
||
for all possible lists of |
for all possible lists of <math>m</math> rows. (In case <math>m = n</math>, this requires only one determinant, as above. If <math>m > n</math>, then it is a theorem that the vectors must be linearly dependent.) This fact is valuable for theory; in practical calculations more efficient methods are available. |
||
=== More vectors than dimensions === |
|||
== Example II == |
|||
If there are more vectors than dimensions, the vectors are linearly dependent. This is illustrated in the example above of three vectors in <math>\R^2.</math> |
|||
== Natural basis vectors == |
|||
Let ''V'' = '''R'''<sup>''n''</sup> and consider the following elements in ''V'': |
|||
Let <math>V = \R^n</math> and consider the following elements in <math>V</math>, known as the [[Standard basis|natural basis]] vectors: |
|||
:<math>\begin{matrix} |
:<math>\begin{matrix} |
||
| Line 105: | Line 183: | ||
\mathbf{e}_n & = & (0,0,0,\ldots,1).\end{matrix}</math> |
\mathbf{e}_n & = & (0,0,0,\ldots,1).\end{matrix}</math> |
||
Then |
Then <math>\mathbf{e}_1, \mathbf{e}_2, \ldots, \mathbf{e}_n</math> are linearly independent. |
||
{{math proof| |
|||
=== Proof === |
|||
Suppose that <math>a_1, a_2, \ldots, a_n</math> are real numbers such that |
|||
Suppose that ''a''<sub>1</sub>, ''a''<sub>2</sub>, ..., ''a<sub>n</sub>'' are elements of '''R''' such that |
|||
:<math> |
:<math>a_1 \mathbf{e}_1 + a_2 \mathbf{e}_2 + \cdots + a_n \mathbf{e}_n = \mathbf{0}.</math> |
||
Since |
Since |
||
:<math> |
:<math>a_1 \mathbf{e}_1 + a_2 \mathbf{e}_2 + \cdots + a_n \mathbf{e}_n = \left( a_1 ,a_2 ,\ldots, a_n \right),</math> |
||
then |
then <math>a_i = 0</math> for all <math>i = 1, \ldots, n.</math> |
||
}} |
|||
== Linear independence of functions == |
|||
== Example III == |
|||
Let |
Let <math>V</math> be the [[vector space]] of all differentiable [[function (mathematics)|function]]s of a real variable <math>t</math>. Then the functions <math>e^t</math> and <math>e^{2t}</math> in <math>V</math> are linearly independent. |
||
=== Proof === |
=== Proof === |
||
Suppose |
Suppose <math>a</math> and <math>b</math> are two real numbers such that |
||
: |
:<math>ae ^ t + be ^ {2t} = 0</math> |
||
Take the first derivative of the above equation: |
|||
for ''all'' values of ''t''. We need to show that ''a'' = 0 and ''b'' = 0. In order to do this, we divide through by ''e''<sup>''t''</sup> (which is never zero) and subtract to obtain |
|||
:''be<sup>t</sup>'' = −''a''. |
|||
In other words, the function ''be''<sup>''t''</sup> must be independent of ''t'', which only occurs when ''b'' = 0. It follows that ''a'' is also zero. |
|||
:<math>ae ^ t + 2be ^ {2t} = 0</math> |
|||
== Example IV == |
|||
for {{em|all}} values of <math>t.</math> We need to show that <math>a = 0</math> and <math>b = 0.</math> In order to do this, we subtract the first equation from the second, giving <math>be^{2t} = 0</math>. Since <math>e^{2t}</math> is not zero for some <math>t</math>, <math>b=0.</math> It follows that <math>a = 0</math> too. Therefore, according to the definition of linear independence, <math>e^{t}</math> and <math>e^{2t}</math> are linearly independent. |
|||
The following vectors in '''R'''<sup>4</sup> are linearly dependent. |
|||
:<math> |
|||
\begin{matrix} |
|||
\\ |
|||
\begin{bmatrix}1\\4\\2\\-3\end{bmatrix}, |
|||
\begin{bmatrix}7\\10\\-4\\-1\end{bmatrix} \mathrm{and} |
|||
\begin{bmatrix}-2\\1\\5\\-4\end{bmatrix} |
|||
\\ |
|||
\\ |
|||
\end{matrix} |
|||
</math> |
|||
=== Proof === |
|||
== Space of linear dependencies == |
|||
We need to find scalars <math>\lambda_1</math>, <math>\lambda_2</math> and <math>\lambda_3</math> such that |
|||
A '''linear dependency''' or [[linear relation]] among vectors {{math|'''v'''<sub>1</sub>, ..., '''v'''<sub>''n''</sub>}} is a [[tuple]] {{math|(''a''<sub>1</sub>, ..., ''a''<sub>''n''</sub>)}} with {{mvar|n}} [[scalar (mathematics)|scalar]] components such that |
|||
:<math> |
|||
\begin{matrix} |
|||
\\ |
|||
\lambda_1 \begin{bmatrix}1\\4\\2\\-3\end{bmatrix}+ |
|||
\lambda_2 \begin{bmatrix}7\\10\\-4\\-1\end{bmatrix}+ |
|||
\lambda_3 \begin{bmatrix}-2\\1\\5\\-4\end{bmatrix}= |
|||
\begin{bmatrix}0\\0\\0\\0\end{bmatrix}. |
|||
\end{matrix} |
|||
</math> |
|||
:<math>a_1 \mathbf{v}_1 + \cdots + a_n \mathbf{v}_n= \mathbf{0}.</math> |
|||
Forming the [[simultaneous equation]]s: |
|||
If such a linear dependence exists with at least a nonzero component, then the {{mvar|n}} vectors are linearly dependent. Linear dependencies among {{math|'''v'''<sub>1</sub>, ..., '''v'''<sub>''n''</sub>}} form a vector space. |
|||
:<math> |
|||
\begin{align} |
|||
\lambda_1& \;+ 7\lambda_2& &- 2\lambda_3& = 0\\ |
|||
4\lambda_1& \;+ 10\lambda_2& &+ \lambda_3& = 0\\ |
|||
2\lambda_1& \;- 4\lambda_2& &+ 5\lambda_3& = 0\\ |
|||
-3\lambda_1& \;- \lambda_2& &- 4\lambda_3& = 0\\ |
|||
\end{align} |
|||
</math> |
|||
If the vectors are expressed by their coordinates, then the linear dependencies are the solutions of a homogeneous [[system of linear equations]], with the coordinates of the vectors as coefficients. A [[basis (linear algebra)|basis]] of the vector space of linear dependencies can therefore be computed by [[Gaussian elimination]]. |
|||
we can solve (using, for example, [[Gaussian elimination]]) to obtain: |
|||
:<math> |
|||
\begin{align} |
|||
\lambda_1 &= -3 \lambda_3 /2 \\ |
|||
\lambda_2 &= \lambda_3/2 \\ |
|||
\end{align} |
|||
</math> |
|||
where <math>\lambda_3</math> can be chosen arbitrarily. |
|||
==Generalizations== |
|||
Since these are nontrivial results, the vectors are linearly dependent. |
|||
===Affine independence=== |
|||
== Projective space of linear dependences == |
|||
{{See also|Affine space}} |
|||
A set of vectors is said to be '''affinely dependent''' if at least one of the vectors in the set can be defined as an [[affine combination]] of the others. Otherwise, the set is called '''affinely independent'''. Any affine combination is a linear combination; therefore every affinely dependent set is linearly dependent. Conversely, every linearly independent set is affinely independent. |
|||
A '''linear dependence''' among vectors '''v'''<sub>1</sub>, ..., '''v'''<sub>''n''</sub> is a [[tuple]] (''a''<sub>1</sub>, ..., ''a''<sub>''n''</sub>) with ''n'' [[scalar (mathematics)|scalar]] components, not all zero, such that |
|||
Consider a set of <math>m</math> vectors <math>\mathbf{v}_1, \ldots, \mathbf{v}_m</math> of size <math>n</math> each, and consider the set of <math>m</math> augmented vectors <math display="inline">\left(\left[\begin{smallmatrix} 1 \\ \mathbf{v}_1\end{smallmatrix}\right], \ldots, \left[\begin{smallmatrix}1 \\ \mathbf{v}_m\end{smallmatrix}\right]\right)</math> of size <math>n + 1</math> each. The original vectors are affinely independent if and only if the augmented vectors are linearly independent.<ref name="lp">{{Cite Lovasz Plummer}}</ref>{{Rp|256}} |
|||
:<math>a_1 \mathbf{v}_1 + \cdots + a_n \mathbf{v}_n=0. \,</math> |
|||
===Linearly independent vector subspaces=== |
|||
If such a linear dependence exists, then the ''n'' vectors are linearly dependent. It makes sense to identify two linear dependences if one arises as a non-zero multiple of the other, because in this case the two describe the same linear relationship among the vectors. Under this identification, the set of all linear dependences among '''v'''<sub>1</sub>, ...., '''v'''<sub>''n''</sub> is a [[projective space]]. |
|||
Two vector subspaces <math>M</math> and <math>N</math> of a vector space <math>X</math> are said to be {{em|linearly independent}} if <math>M \cap N = \{0\}.</math><ref name="BNFA">{{Bachman Narici Functional Analysis 2nd Edition}} pp. 3–7</ref> |
|||
== Linear dependence between random variables == |
|||
More generally, a collection <math>M_1, \ldots, M_d</math> of subspaces of <math>X</math> are said to be {{em|linearly independent}} if <math display=inline>M_i \cap \sum_{k \neq i} M_k = \{0\}</math> for every index <math>i,</math> where <math display=inline>\sum_{k \neq i} M_k = \Big\{m_1 + \cdots + m_{i-1} + m_{i+1} + \cdots + m_d : m_k \in M_k \text{ for all } k\Big\} = \operatorname{span} \bigcup_{k \in \{1,\ldots,i-1,i+1,\ldots,d\}} M_k.</math><ref name="BNFA" /> |
|||
The [[covariance]] is sometimes called a measure of "linear dependence" between two [[random variable]]s. That does not mean the same thing as in the context of [[linear algebra]]. When the covariance is normalized, one obtains the [[correlation matrix]]. From it, one can obtain the [[Pearson coefficient]], which gives us the goodness of the fit for the best possible [[linear function]] describing the relation between the variables. In this sense covariance is a linear gauge of dependence. |
|||
The vector space <math>X</math> is said to be a {{em|[[direct sum]]}} of <math>M_1, \ldots, M_d</math> if these subspaces are linearly independent and <math>M_1 + \cdots + M_d = X.</math> |
|||
== See also == |
== See also == |
||
* {{annotated link|Matroid}} |
|||
== References == |
|||
* [[Orthogonality]] |
|||
{{reflist}} |
|||
* [[Matroid]] – a generalization of the concept |
|||
* [[Wronskian#The Wronskian and linear independence|Linear independence of functions]] |
|||
* [[Gramian matrix|Gram determinant]] |
|||
== External links == |
== External links == |
||
* {{springer|title=Linear independence|id=p/l059290}} |
* {{springer|title=Linear independence|id=p/l059290}} |
||
* [http://tutorial.math.lamar.edu/Classes/LinAlg/LinearIndependence.aspx Online Notes] on Linear Independence. |
|||
* [http://mathworld.wolfram.com/LinearlyDependentFunctions.html Linearly Dependent Functions] at WolframMathWorld. |
* [http://mathworld.wolfram.com/LinearlyDependentFunctions.html Linearly Dependent Functions] at WolframMathWorld. |
||
* [http://people.revoledu.com/kardi/tutorial/LinearAlgebra/LinearlyIndependent.html Tutorial and interactive program] on Linear Independence. |
* [http://people.revoledu.com/kardi/tutorial/LinearAlgebra/LinearlyIndependent.html Tutorial and interactive program] on Linear Independence. |
||
* [ |
* [https://www.khanacademy.org/math/linear-algebra/vectors_and_spaces/linear_independence/v/linear-algebra-introduction-to-linear-independence Introduction to Linear Independence] at KhanAcademy. |
||
{{linear algebra}} |
{{linear algebra}} |
||
{{Matrix classes}} |
|||
{{DEFAULTSORT:Linear Independence}} |
|||
[[Category:Abstract algebra]] |
[[Category:Abstract algebra]] |
||
[[Category:Linear algebra]] |
[[Category:Linear algebra]] |
||
[[Category:Articles containing proofs]] |
[[Category:Articles containing proofs]] |
||
[[ar:استقلال خطي]] |
|||
[[bs:Linearna nezavisnost]] |
|||
[[bg:Линейна независимост]] |
|||
[[ca:Independència lineal]] |
|||
[[cs:Lineární závislost]] |
|||
[[de:Lineare Unabhängigkeit]] |
|||
[[es:Dependencia e independencia lineal]] |
|||
[[eo:Lineara sendependeco]] |
|||
[[fa:استقلال خطی]] |
|||
[[fr:Indépendance linéaire]] |
|||
[[ko:일차 독립]] |
|||
[[id:Kebebasan linear]] |
|||
[[is:Línulegt óhæði]] |
|||
[[it:Indipendenza lineare]] |
|||
[[he:תלות לינארית]] |
|||
[[hu:Lineáris függetlenség]] |
|||
[[nl:Lineaire onafhankelijkheid]] |
|||
[[pl:Liniowa niezależność]] |
|||
[[pt:Independência linear]] |
|||
[[ru:Линейная независимость]] |
|||
[[sl:Linearna neodvisnost]] |
|||
[[fi:Lineaarinen riippumattomuus]] |
|||
[[sv:Linjärt oberoende]] |
|||
[[ta:நேரியல் சார்பின்மை]] |
|||
[[uk:Лінійно незалежні вектори]] |
|||
[[ur:لکیری آزادی]] |
|||
[[vi:Độc lập tuyến tính]] |
|||
[[zh:線性無關]] |
|||
Latest revision as of 07:38, 28 June 2024
This article needs additional citations for verification. (January 2019) |


In the theory of vector spaces, a set of vectors is said to be linearly independent if there exists no nontrivial linear combination of the vectors that equals the zero vector. If such a linear combination exists, then the vectors are said to be linearly dependent. These concepts are central to the definition of dimension.[1]
A vector space can be of finite dimension or infinite dimension depending on the maximum number of linearly independent vectors. The definition of linear dependence and the ability to determine whether a subset of vectors in a vector space is linearly dependent are central to determining the dimension of a vector space.
Definition
[edit]A sequence of vectors from a vector space V is said to be linearly dependent, if there exist scalars not all zero, such that
where denotes the zero vector.
This implies that at least one of the scalars is nonzero, say , and the above equation is able to be written as
if and if
Thus, a set of vectors is linearly dependent if and only if one of them is zero or a linear combination of the others.
A sequence of vectors is said to be linearly independent if it is not linearly dependent, that is, if the equation
can only be satisfied by for This implies that no vector in the sequence can be represented as a linear combination of the remaining vectors in the sequence. In other words, a sequence of vectors is linearly independent if the only representation of as a linear combination of its vectors is the trivial representation in which all the scalars are zero.[2] Even more concisely, a sequence of vectors is linearly independent if and only if can be represented as a linear combination of its vectors in a unique way.
If a sequence of vectors contains the same vector twice, it is necessarily dependent. The linear dependency of a sequence of vectors does not depend of the order of the terms in the sequence. This allows defining linear independence for a finite set of vectors: A finite set of vectors is linearly independent if the sequence obtained by ordering them is linearly independent. In other words, one has the following result that is often useful.
A sequence of vectors is linearly independent if and only if it does not contain the same vector twice and the set of its vectors is linearly independent.
Infinite case
[edit]An infinite set of vectors is linearly independent if every nonempty finite subset is linearly independent. Conversely, an infinite set of vectors is linearly dependent if it contains a finite subset that is linearly dependent, or equivalently, if some vector in the set is a linear combination of other vectors in the set.
An indexed family of vectors is linearly independent if it does not contain the same vector twice, and if the set of its vectors is linearly independent. Otherwise, the family is said to be linearly dependent.
A set of vectors which is linearly independent and spans some vector space, forms a basis for that vector space. For example, the vector space of all polynomials in x over the reals has the (infinite) subset {1, x, x2, ...} as a basis.
Geometric examples
[edit]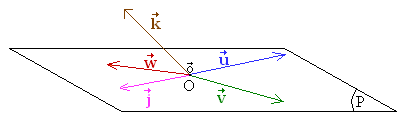
- and are independent and define the plane P.
- , and are dependent because all three are contained in the same plane.
- and are dependent because they are parallel to each other.
- , and are independent because and are independent of each other and is not a linear combination of them or, equivalently, because they do not belong to a common plane. The three vectors define a three-dimensional space.
- The vectors (null vector, whose components are equal to zero) and are dependent since
Geographic location
[edit]A person describing the location of a certain place might say, "It is 3 miles north and 4 miles east of here." This is sufficient information to describe the location, because the geographic coordinate system may be considered as a 2-dimensional vector space (ignoring altitude and the curvature of the Earth's surface). The person might add, "The place is 5 miles northeast of here." This last statement is true, but it is not necessary to find the location.
In this example the "3 miles north" vector and the "4 miles east" vector are linearly independent. That is to say, the north vector cannot be described in terms of the east vector, and vice versa. The third "5 miles northeast" vector is a linear combination of the other two vectors, and it makes the set of vectors linearly dependent, that is, one of the three vectors is unnecessary to define a specific location on a plane.
Also note that if altitude is not ignored, it becomes necessary to add a third vector to the linearly independent set. In general, n linearly independent vectors are required to describe all locations in n-dimensional space.
Evaluating linear independence
[edit]The zero vector
[edit]If one or more vectors from a given sequence of vectors is the zero vector then the vector are necessarily linearly dependent (and consequently, they are not linearly independent). To see why, suppose that is an index (i.e. an element of ) such that Then let (alternatively, letting be equal any other non-zero scalar will also work) and then let all other scalars be (explicitly, this means that for any index other than (i.e. for ), let so that consequently ). Simplifying gives:
Because not all scalars are zero (in particular, ), this proves that the vectors are linearly dependent.
As a consequence, the zero vector can not possibly belong to any collection of vectors that is linearly independent.
Now consider the special case where the sequence of has length (i.e. the case where ). A collection of vectors that consists of exactly one vector is linearly dependent if and only if that vector is zero. Explicitly, if is any vector then the sequence (which is a sequence of length ) is linearly dependent if and only if ; alternatively, the collection is linearly independent if and only if
Linear dependence and independence of two vectors
[edit]This example considers the special case where there are exactly two vector and from some real or complex vector space. The vectors and are linearly dependent if and only if at least one of the following is true:
- is a scalar multiple of (explicitly, this means that there exists a scalar such that ) or
- is a scalar multiple of (explicitly, this means that there exists a scalar such that ).
If then by setting we have (this equality holds no matter what the value of is), which shows that (1) is true in this particular case. Similarly, if then (2) is true because If (for instance, if they are both equal to the zero vector ) then both (1) and (2) are true (by using for both).
If then is only possible if and ; in this case, it is possible to multiply both sides by to conclude This shows that if and then (1) is true if and only if (2) is true; that is, in this particular case either both (1) and (2) are true (and the vectors are linearly dependent) or else both (1) and (2) are false (and the vectors are linearly independent). If but instead then at least one of and must be zero. Moreover, if exactly one of and is (while the other is non-zero) then exactly one of (1) and (2) is true (with the other being false).
The vectors and are linearly independent if and only if is not a scalar multiple of and is not a scalar multiple of .
Vectors in R2
[edit]Three vectors: Consider the set of vectors and then the condition for linear dependence seeks a set of non-zero scalars, such that
or
Row reduce this matrix equation by subtracting the first row from the second to obtain,
Continue the row reduction by (i) dividing the second row by 5, and then (ii) multiplying by 3 and adding to the first row, that is
Rearranging this equation allows us to obtain
which shows that non-zero ai exist such that can be defined in terms of and Thus, the three vectors are linearly dependent.
Two vectors: Now consider the linear dependence of the two vectors and and check,
or
The same row reduction presented above yields,
This shows that which means that the vectors and are linearly independent.
Vectors in R4
[edit]In order to determine if the three vectors in
are linearly dependent, form the matrix equation,
Row reduce this equation to obtain,
Rearrange to solve for v3 and obtain,
This equation is easily solved to define non-zero ai,
where can be chosen arbitrarily. Thus, the vectors and are linearly dependent.
Alternative method using determinants
[edit]An alternative method relies on the fact that vectors in are linearly independent if and only if the determinant of the matrix formed by taking the vectors as its columns is non-zero.
In this case, the matrix formed by the vectors is
We may write a linear combination of the columns as
We are interested in whether AΛ = 0 for some nonzero vector Λ. This depends on the determinant of , which is
Since the determinant is non-zero, the vectors and are linearly independent.
Otherwise, suppose we have vectors of coordinates, with Then A is an n×m matrix and Λ is a column vector with entries, and we are again interested in AΛ = 0. As we saw previously, this is equivalent to a list of equations. Consider the first rows of , the first equations; any solution of the full list of equations must also be true of the reduced list. In fact, if ⟨i1,...,im⟩ is any list of rows, then the equation must be true for those rows.
Furthermore, the reverse is true. That is, we can test whether the vectors are linearly dependent by testing whether
for all possible lists of rows. (In case , this requires only one determinant, as above. If , then it is a theorem that the vectors must be linearly dependent.) This fact is valuable for theory; in practical calculations more efficient methods are available.
More vectors than dimensions
[edit]If there are more vectors than dimensions, the vectors are linearly dependent. This is illustrated in the example above of three vectors in
Natural basis vectors
[edit]Let and consider the following elements in , known as the natural basis vectors:
Then are linearly independent.
Suppose that are real numbers such that
Since
then for all
Linear independence of functions
[edit]Let be the vector space of all differentiable functions of a real variable . Then the functions and in are linearly independent.
Proof
[edit]Suppose and are two real numbers such that
Take the first derivative of the above equation:
for all values of We need to show that and In order to do this, we subtract the first equation from the second, giving . Since is not zero for some , It follows that too. Therefore, according to the definition of linear independence, and are linearly independent.
Space of linear dependencies
[edit]A linear dependency or linear relation among vectors v1, ..., vn is a tuple (a1, ..., an) with n scalar components such that
If such a linear dependence exists with at least a nonzero component, then the n vectors are linearly dependent. Linear dependencies among v1, ..., vn form a vector space.
If the vectors are expressed by their coordinates, then the linear dependencies are the solutions of a homogeneous system of linear equations, with the coordinates of the vectors as coefficients. A basis of the vector space of linear dependencies can therefore be computed by Gaussian elimination.
Generalizations
[edit]Affine independence
[edit]A set of vectors is said to be affinely dependent if at least one of the vectors in the set can be defined as an affine combination of the others. Otherwise, the set is called affinely independent. Any affine combination is a linear combination; therefore every affinely dependent set is linearly dependent. Conversely, every linearly independent set is affinely independent.
Consider a set of vectors of size each, and consider the set of augmented vectors of size each. The original vectors are affinely independent if and only if the augmented vectors are linearly independent.[3]: 256
Linearly independent vector subspaces
[edit]Two vector subspaces and of a vector space are said to be linearly independent if [4] More generally, a collection of subspaces of are said to be linearly independent if for every index where [4] The vector space is said to be a direct sum of if these subspaces are linearly independent and
See also
[edit]- Matroid – Abstraction of linear independence of vectors
References
[edit]- ^ G. E. Shilov, Linear Algebra (Trans. R. A. Silverman), Dover Publications, New York, 1977.
- ^ Friedberg, Stephen; Insel, Arnold; Spence, Lawrence (2003). Linear Algebra. Pearson, 4th Edition. pp. 48–49. ISBN 0130084514.
- ^ Lovász, László; Plummer, M. D. (1986), Matching Theory, Annals of Discrete Mathematics, vol. 29, North-Holland, ISBN 0-444-87916-1, MR 0859549
- ^ a b Bachman, George; Narici, Lawrence (2000). Functional Analysis (Second ed.). Mineola, New York: Dover Publications. ISBN 978-0486402512. OCLC 829157984. pp. 3–7
External links
[edit]- "Linear independence", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- Linearly Dependent Functions at WolframMathWorld.
- Tutorial and interactive program on Linear Independence.
- Introduction to Linear Independence at KhanAcademy.
























































































































![{\textstyle \left(\left[{\begin{smallmatrix}1\\\mathbf {v} _{1}\end{smallmatrix}}\right],\ldots ,\left[{\begin{smallmatrix}1\\\mathbf {v} _{m}\end{smallmatrix}}\right]\right)}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/bedef6dbcd38b445b141b49ec618600e574a614b)










