Preference (economics): Difference between revisions
→Criticism: Altered POV language |
Citation bot (talk | contribs) Added doi. | Use this bot. Report bugs. | Suggested by Abductive | Category:Wikipedia articles needing clarification from March 2024 | #UCB_Category 188/945 |
||
| (325 intermediate revisions by more than 100 users not shown) | |||
| Line 1: | Line 1: | ||
{{Short description|Concept in economics}} |
|||
[[Image:Preference example.jpg|thumb|alt=Example of a preference relation|A simple example of a preference order over three goods]] In [[economics]] and other [[social science]]s, '''preference''' refers to the set of assumptions related to ordering some alternatives, based on the degree of [[happiness]], satisfaction, [[gratification]], enjoyment, or [[utility]] they provide, a process which results in an optimal "[[choice]]" (whether real or theoretical). Although economists are usually not interested in choices or preferences in themselves, they are interested in the theory of choice because it serves as a background for empirical demand analysis.<ref name="Arrow, Kenneth 1958">{{cite journal |last=Arrow |first=Kenneth |year=1958 |title=Utilities, attitudes, choices: a review note |journal=[[Econometrica]] |volume=26 |issue=1 |pages=1–23 |jstor=1907381 }}</ref> |
|||
[[Image:Preference example.svg|thumb|alt=Example of a preference relation|A simple example of a preference order over three goods, in which orange is preferred to a banana, but an apple is preferred to an orange]] In [[economics]], and in other [[social science]]s, '''preference''' refers to an order by which an [[Agent (economics)|agent]], while in search of an "optimal [[choice]]", ranks alternatives based on their respective [[utility]]. ''Preferences'' are evaluations that concern matters of value, in relation to practical reasoning.<ref>{{cite book |last=Broome |first=John |author-link=John Broome (philosopher) |date=1993 |title=Value, Welfare and Morality |publisher=Cambridge University Press |editor1-last=Frey |editor1-first=R. G. |editor2-last=Morris |editor2-first=Christopher |chapter=Can a Humean Be Moderate?}}</ref> Individual preferences are determined by taste, need, ..., as opposed to price, availability or [[personal income]]. [[Classical economics]] assumes that people act in their best (rational) interest.<ref>{{cite book |last1=Blume |first1=Lawrence |editor1-first=Steven N |editor1-last=Durlauf |editor2-first=Lawrence E |editor2-last=Blume |title=The New Palgrave Dictionary of Economics |date=15 December 2016 |publisher=Palgrave Macmillan |location=London |isbn=978-1-349-95121-5 |doi=10.1007/978-1-349-58802-2 }}</ref> In this context, [[rationality]] would dictate that, when given a choice, an individual will select an option that maximizes their [[self-interest]]. But preferences are not always [[transitive relation|transitive]], both because real humans are far from always being rational and because in some situations preferences can form [[cycle (graph theory)|cycles]], in which case there exists no well-defined optimal choice. An example of this is [[Efron dice]]. |
|||
The concept of preference plays a key role in many disciplines, including [[Ethics|moral philosophy]] and [[decision theory]]. The logical properties that preferences possess also have major effects on [[rational choice theory]], which in turn affects all modern economic topics.<ref>{{Cite journal |last1=Hansson |first1=Sven Ove |last2=Grüne-Yanoff |first2=Till |date=May 4, 2018 |title=Preferences |url=https://plato.stanford.edu/entries/preferences/ |journal=Stanford Encyclopedia of Economics}}</ref> |
|||
Using the [[scientific method]], social scientists aim to model how people make practical decisions in order to [[Explanatory research|explain]] the causal underpinnings of human behaviour or to [[Predictive modelling|predict]] future behaviours. Although economists are not typically interested in the specific causes of a person's preferences, they are interested in the theory of choice because it gives a background to empirical [[demand]] analysis.<ref name="Arrow, Kenneth 1958">{{cite journal |last=Arrow |first=Kenneth |year=1958 |title=Utilities, attitudes, choices: a review note |journal=[[Econometrica]] |volume=26 |issue=1 |pages=1–23 |jstor=1907381 |doi=10.2307/1907381 }}</ref> |
|||
'''Stability of preference''' is a deep assumption behind most [[economic model]]s. [[Gary Becker]] drew attention to this with his remark that "the combined assumptions of [[utility maximization problem|maximizing behavior]], [[economic equilibrium|market equilibrium]], and stable preferences, used relentlessly and unflinchingly, form the heart of the economic approach as it is."<ref name="Becker1976">{{cite book |
|||
|last=Becker |
|||
|first=Gary |
|||
|author-link=Gary Becker |
|||
|date=1976 |
|||
|title=The Economic Approach to Human Behavior |
|||
|url=https://www.pauldeng.com/pdf/Becker_the%20economic%20approach%20to%20human%20behavior.pdf |
|||
|access-date=17 January 2022 |
|||
|publisher=University of Chicago Press |
|||
|page=5 |
|||
|isbn=0226041123 |
|||
}}</ref> More complex conditions of adaptive preference were explored by [[Carl Christian von Weizsäcker]] in his paper "The Welfare Economics of Adaptive Preferences" (2005), while remarking that.<ref name="vW2005">{{cite SSRN |
|||
|ssrn=771904 |
|||
|last=von Weizsäcker |
|||
|first=C. Christian |
|||
|date=June 2005 |
|||
|title=The Welfare Economics of Adaptive Preferences |
|||
}}</ref> Traditional [[neoclassical economics]] has worked with the assumption that the preferences of agents in the economy are fixed. This assumption has always been disputed outside neoclassical economics. |
|||
== History == |
== History == |
||
[[Ragnar Frisch]] was the first to |
In 1926, [[Ragnar Frisch]] was the first to develop a mathematical model of preferences in the context of economic demand and utility functions.<ref name="Barten 1982 p. 384">[[Anton Barten|Barten, Anton]] and Volker Böhm. (1982). "Consumer theory", in Kenneth Arrow and Michael Intrilligator (eds.) ''Handbook of mathematical economics. Vol. II'', p. 384</ref> Up to then, economists had used an elaborate theory of demand that omitted ''primitive characteristics'' of people. This omission ceased when, at the end of the 19th and the beginning of the 20th century, [[logical positivism]] predicated the need to relate theoretical concepts to observables.<ref name="econ.hit-u.ac.jp">Gilboa, Itzhak. (2009). [http://www.econ.hit-u.ac.jp/~kmkj/uncertainty/Gilboa_Lecture_Notes.pdf ''Theory of Decision under uncertainty''] {{Webarchive|url=https://web.archive.org/web/20180219002606/http://www.econ.hit-u.ac.jp/~kmkj/uncertainty/Gilboa_Lecture_Notes.pdf |date=2018-02-19 }}. Cambridge: Cambridge university press</ref> Whereas economists in the 18th and 19th centuries felt comfortable theorizing about utility, with the advent of logical positivism in the 20th century, they felt they needed a more empirical structure. Because [[binary relation|binary choices]] are directly observable, they instantly appeal to economists. The search for observables in microeconomics is taken even further by the [[revealed preference|revealed preference theory]], which holds consumers' preferences can be revealed by what they purchase under different circumstances, particularly under different income and price circumstances.<ref name="Roper 2008 p. 243-253">Roper, James and Zin, David. (2008). "A Note on the Pure Theory of Consumer's Behaviour"</ref> |
||
Despite utilitarianism and decision theory, many economists have differing definitions of what a [[rational agent]] is. In the 18th century, utilitarianism gave insight into the utility-maximizing versions of rationality; however, economists still have no consistent definition or understanding of what preferences and rational actors should be analyzed.<ref>{{Cite book | doi=10.1057/978-1-349-95121-5_2138-1| chapter=Rationality| title=The New Palgrave Dictionary of Economics| pages=1–13| year=2008| last1=Blume| first1=Lawrence E.| last2=Easley| first2=David| isbn=978-1-349-95121-5}}</ref> |
|||
Since the pioneer efforts of Frisch in the 1920s, one of the major issues which has pervaded the theory of preferences is the representability of a preference structure with a real-valued function. This has been achieved by mapping it to the mathematical index called ''utility''. [[Gérard Debreu]], influenced by the ideas of the [[bourbaki|Bourbaki group]], championed the axiomatization of consumer theory in the 1950s, and the tools he borrowed from the mathematical field of binary relations have become mainstream since then. Even though the economics of choice can be examined either at the level of utility functions or at the level of preferences, to move from one to the other can be useful. For example, shifting the conceptual basis from an abstract preference relation to an abstract utility scale results in a new mathematical framework, allowing new kinds of conditions on the structure of preference to be formulated and investigated. |
|||
Since the pioneer efforts of Frisch in the 1920s, the representability of a preference structure with a real-valued function is one of the major issues pervading the theory of preferences. This has been achieved by mapping it to the mathematical index called ''utility''. [[John von Neumann|Von Neumann]] and [[Morgenstern's thirteen problems|Morgenstern's]] 1944 book "[[Games and Economic Behavior]]" treated preferences as a formal relation whose properties can be stated axiomatically. These types of axiomatic handling of preferences soon began to influence other economists: Marschak adopted it by 1950, Houthakker employed it in a 1950 paper, and Kenneth Arrow perfected it in his 1951 book "Social Choice and Individual Values".<ref>{{cite web |url=http://128.118.178.162/eps/mhet/papers/0506/0506003.pdf |author=Moscati, Ivan |year=2004 |title=Early Experiments in Consumer Demand Theory |archive-url=https://web.archive.org/web/20140302122147/http://128.118.178.162/eps/mhet/papers/0506/0506003.pdf |archive-date=2014-03-02 |website=128.118.178.162 |others=[[Wayback Machine]]}}</ref> |
|||
Another historical turnpoint can be traced back to 1895, when [[Georg Cantor]], proved in a theorem that if a binary relation is ''linearly ordered'', then it is also isomorphically embeddable in the ordered real numbers. This notion would become very influential for the theory of preferences in economics: by the 1940s prominent authors such as [[Paul Samuelson]], would theorize about people actually having weakly ordered preferences.<ref>Fishburn, Peter. (1994). "Utility and subjective probability", in: Robert Aumann and Sergiu Hart (eds). ''Handbook of game theory. Vol. 2''. Amsterdam: Elsevier Science. pp. 1397-1435.</ref> |
|||
[[Gérard Debreu]], influenced by the ideas of the [[Nicolas Bourbaki|Bourbaki group]], championed the axiomatization of consumer theory in the 1950s, and the tools he borrowed from the mathematical field of binary relations have become mainstream since then. Even though the economics of choice can be examined either at the level of utility functions or at the level of preferences, moving from one to the other can be useful. For example, shifting the conceptual basis from an abstract preference relation to an abstract utility scale results in a new mathematical framework, allowing new conditions on the preference structure to be formulated and investigated. |
|||
==Basic premises== |
|||
In consumer theory, economic actors are thought of as being confronted with a set of possible consumption bundles or commodity space. Of all the available bundles of goods and services, only one is ultimately chosen. The theory of preferences seeks an analytical solution to the problem of getting to this ultimate choice (the optimal choice) using a ''system of preferences'' within a budgetary limitation. Choice is an act, whereas preferences are a state of mind. |
|||
Another historical turning point can be traced back to 1895, when [[Georg Cantor]] proved in a theorem that if a binary relation is ''linearly ordered'', then it is also isomorphic in the ordered real numbers. This notion would become very influential for the theory of preferences in economics: by the 1940s, prominent authors such as [[Paul Samuelson]] would theorize about people having weakly ordered preferences.<ref>Fishburn, Peter (1994). "Utility and subjective probability", in Robert Aumann and Sergiu Hart (eds). ''Handbook of game theory. Vol. 2''. Amsterdam: Elsevier Science. pp. 1397–1435.</ref> |
|||
In reality, people do not necessarily rank or order their preferences in a consistent way. In preference theory, some idealized conditions are regularly imposed on the preferences of economic actors. One of the most important of these idealized conditions is the ''axiom of transitivity''<ref name="Arrow, Kenneth 1958"/>: |
|||
Historically, preference in economics as a form of utility can be categorized as ordinal or cardinal data. Both introduced in the 20th century, cardinal and ordinal utility take opposing theories and mindsets in applying and analyzing preference in utility. Vilfredo Pareto introduced the concept of ordinal utility, while Carl Menger led the idea of cardinal utility. Ordinal utility, in summation, is the direct following of preference, where an optimal choice is taken over a set of parameters. A person is expected to act in their best interests and dedicate their preference to the outcome with the greatest utility. Ordinal utility assumes that an individual will not have the same utility from a preference as any other individual because they likely will not experience the same parameters which cause them to decide a given outcome. Cardinal utility is a function of utility where a person makes a decision based on a preference, and the preference decision is weighted based on a quantitative value of utility. This utility unit is assumed to be universally applicable and constant across all individuals. Cardinal utility also assumes consistency across individuals' decision-making processes, assuming all individuals will have the same preference, with all variables held constant. Marshall found that "a good deal of the analysis of consumer behavior could be greatly simplified by assuming that the [[marginal utility]] of income is constant" (Robert H. Strotz.<ref>[[Robert H. Strotz]]</ref>), however, this cannot be held to the utility of resources and decision-making applied to income. Ordinal and cardinal utility theories provide unique viewpoints on utility, can be used differently to model decision-making preferences and utilization development, and can be used across many applications for economic analysis. |
|||
If alternative <math>A\!</math> is preferred to alternative <math>B\!</math>, and <math>B\!</math> to <math>C\!</math>, then <math>A\!</math> is preferred to <math>C\!</math>. |
|||
== Notation == |
|||
The language of binary relations allow one to write down exactly what is meant by "ranked set of preferences", and thus gives an unambiguous definition of ''order''. A preference relation should not be confused with the order relation <math> \geqslant \!</math> used to indicate which of two real numbers is larger.<ref>Binmore, Ken. (1992). ''Fun and games. A text on game theory''. Lexington: Houghton Mifflin</ref> Order relations satisfy an extra condition: |
|||
There are two fundamental comparative value concepts, namely strict preference (better) and indifference (equal in value to).<ref>Halldén, Sören (1957). "On the Logic of Betterm Lund: Library of Theoria" (10).</ref> These two concepts are expressed in terms of an agent's best wishes; however, they also express objective or intersubjective valid superiority that does not coincide with the pattern of wishes of any person. |
|||
Suppose the set of all states of the world is <math>X</math> and an agent has a preference relation on <math>X</math>. It is common to mark the weak preference relation by <math>\preceq</math>, so that <math>x \preceq y</math> means "the agent wants y at least as much as x" or "the agent weakly prefers y to x". |
|||
<math>A \geqslant B \!</math>, and <math>B \geqslant A \!</math>, implies <math>A = B \!</math> |
|||
The symbol <math>\sim</math> is used as a shorthand to denote an indifference relation: <math>x\sim y \iff (x\preceq y \land y\preceq x)</math>, which reads "the agent is indifferent between y and x", meaning the agent receives the same level of benefit from each. |
|||
which does not always hold in preference relations; hence, an ''indifference relation'' is used in its place (the symbol <math> \sim \!</math> denotes this kind of relation). |
|||
The symbol <math>\prec</math> is used as a shorthand to the strong preference relation: <math>x\prec y \iff (x\preceq y \land y\not\preceq x)</math>), it is redundant inasmuch as the completeness axiom implies it already.<ref>[[Andreu Mas-Colell|Mas-Colell, Andreu]], Michael Whinston and Jerry Green (1995). ''Microeconomic theory''. Oxford: Oxford University Press {{ISBN|0-19-507340-1}}</ref> |
|||
A system of preferences or ''preference structure'' refers to the set of qualitative relations between different alternatives of consumption. For example, if the alternatives are: |
|||
'''Non-satiation of preferences''' |
|||
*Apple |
|||
[[File:Non-Satiated preferences with oranges...jpg|alt=|thumb|A simple example of non-satiated preference, in which a large number of oranges are preferred to a single orange.]] |
|||
*Orange |
|||
Non-satiation refers to the belief any commodity bundle with at least as much of one good and more of the other must provide a higher utility, showing that more is always regarded as "better". This assumption is believed to hold as when consumers are able to discard excess goods at no cost, then consumers can be no worse off with extra goods.<ref>{{Cite journal |last1=Bertoletti |first1=Paolo |last2=Etro |first2=Federico |date=2016 |title=Preferences, entry, and market structure |journal=RAND Journal of Economics|volume=47 |issue=4 |pages=792–821 |doi=10.1111/1756-2171.12155 |hdl=2158/1172593 |hdl-access=free }}</ref> This assumption does not preclude diminishing marginal utility. |
|||
*Banana |
|||
Example |
|||
In this example, a preference structure would be: |
|||
Option A |
|||
"The apple is at least as preferred as the orange", and "The orange is as least as preferred as the Banana". One can use <math>\succsim\!</math> to symbolize that some alternative is "at least as preferred as" another one, which is just a binary relation on the set of alternatives. Therefore: |
|||
* Apple = 5 |
|||
* Orange = 3 |
|||
* Banana = 2 |
|||
Option B |
|||
* Apple = 6 |
|||
* Orange = 4 |
|||
* Banana = 2 |
|||
In this situation, utility from Option B > A, as it contains more apples and oranges with bananas being constant. |
|||
=== Transitivity === |
|||
* Apple <math>\succsim\!</math> Orange |
|||
Transitivity of preferences is a fundamental principle shared by most major {{update after|2031|01|01|text=contemporary}} rational, prescriptive, and descriptive models of decision-making.<ref name="transitivity">{{cite journal |author1=Clintin P. Davis-Stober |author2=Michel Regenwetter |author3=Jason Dana |title=Transitivity of Preferences |journal=Psychological Review |date=2011 |volume=118 |issue=1 |pages=42–56 |doi=10.1037/a0021150 |pmid=21244185 |url=https://www.chapman.edu/research/institutes-and-centers/economic-science-institute/_files/ifree-papers-and-photos/michel-regenwetter1.pdf |access-date=3 February 2022}}</ref> In order to have transitive preferences, a person, player, or agent that prefers choice option A to B and B to C must prefer A to C. The most discussed logical property of preferences are the following: |
|||
* Orange <math>\succsim\!</math> Banana |
|||
* A≽B ∧ B≽C → A≽C (transitivity of weak preference) |
|||
The former qualitative relation can be preserved when mapped into a numerical structure, if we impose certain desirable properties over the binary relation: these are the ''axioms of preference order''. For instance: Let us take the apple and assign it the arbitrary number 5.Then take the orange and let us assign it a value lower than 5, since the orange is less preferred than the apple. If this procedure is extended to the banana, one may prove by induction that if <math>u\!</math> is defined on {apple, orange} and it represents a well-defined binary relation called "at least as preferred as" on this set, then it can be extended to a function <math>u\!</math> defined on {apple, orange, banana} and it will represent "at least as preferred as" on this larger set. |
|||
* A~B ∧ B~C → A~C (transitivity of indifference) |
|||
* A≻B ∧ B≻C → A≻C (transitivity of strict preference) |
|||
Some authors go so far as to assert that a claim of a decision maker's violating transitivity requires evidence beyond any reasonable doubt.<ref name="transitivity" /> But there are scenarios involving a finite set of alternatives where, for any alternative there exists another that a rational agent would prefer. One class of such scenarios involves [[intransitive dice]]. And Schumm gives examples of non-transitivity based on [[Just-noticeable difference]]s.<ref>{{cite journal | jstor=4319930 | author=George F. Schumm | title=Transitivity, Preference and Indifference | journal=Philosophical Studies | volume=52 | number=3 | pages=435–437 | date=Nov 1987 | doi=10.1007/BF00354058 }}</ref> |
|||
Example: |
|||
=== Most commonly used axioms === |
|||
*Apple = 5 |
|||
*Orange = 3 |
|||
*Banana = 2 |
|||
* Order-theoretic: acyclicity, the semi-order property, completeness |
|||
5 > 3 > 2 = u(apple) > u(orange) > u(banana) |
|||
* Topological: continuity, openness, or closeness of the preference sets |
|||
* Linear-space: [[convex preferences|convexity]], homogeneity |
|||
=== Normative interpretations of the axioms === |
|||
and this is consistent with Apple <math>\succsim\!</math> Orange, and with Orange <math>\succsim\!</math> Banana. |
|||
{{more citations needed|section|date=October 2021}} |
|||
Everyday experience suggests that people at least talk about their preferences as if they had personal "standards of judgment" capable of being applied to the particular domain of alternatives that present themselves from time to time.<ref name="Shapley 1974">Shapley, Lloyd and Martin Shubik. (1974). "Game theory in economics". RAND Report R-904/4</ref> Thus, the axioms attempt to model the decision maker's preferences, not over the actual choice, but over the type of desirable procedure (a procedure that any human being would like to follow). [[Behavioral economics]] investigates human behaviour which violates the above axioms. Believing in axioms in a normative way does not imply that everyone must behave according to them.<ref name="econ.hit-u.ac.jp"/> |
|||
Consumers whose preference structures violate transitivity would get exposed to being exploited by some unscrupulous person. For instance, Maria prefers apples to oranges, oranges to bananas, and bananas to apples. Let her be endowed with an apple, which she can trade in a market. Because she prefers bananas to apples, she is willing to pay one cent to trade her apple for a banana. Afterwards, Maria is willing to pay another cent to trade her banana for an orange, the orange for an apple, and so on. There are [[Intransitivity#Occurrences in preferences|other examples]] of this kind of irrational behaviour. |
|||
===Axioms of order=== |
|||
*'''[[total relation|Completeness]]''': for all <math>A\!</math> and <math>B\!</math> we have <math>A\! \succsim\! B\!</math> or <math>B\! \succsim\! A\!</math> or both. |
|||
Completeness implies that some choice will be made, an assertion that is more philosophically questionable. In most applications, the set of consumption alternatives is infinite, and the consumer is unaware of all preferences. For example, one does not have to choose between going on holiday by plane or train. Suppose one does not have enough money to go on holiday anyway. In that case, it is unnecessary to attach a preference order to those alternatives (although it can be nice to dream about what one would do if one won the lottery). However, preference can be interpreted as a hypothetical choice that could be made rather than a conscious state of mind. In this case, completeness amounts to an assumption that the consumers can always make up their minds whether they are indifferent or prefer one option when presented with any pair of options. |
|||
In order for preference theory to be useful mathematically, we need to assume continuity. '''Continuity''' simply means that there are no ‘jumps’ in people’s preferences: if we prefer very large oranges to apples, we will prefer large oranges to apples as well. In mathematical terms, if we prefer point A along a preference curve to point B, points very close to A will also be preferred to B. This allows preference curves to be differentiated. The continuity assumption is "too strong" in the sense that it indeed guarantees the existence of a ''continuous utility function'' representation. Continuity is, therefore, a sufficient condition, but not a necessary one.<ref>{{cite web |url= http://www.policonomics.com/preferences/ |title= Policonomics. Economics made simple|last1= Gallego|first1= Lope|last2= |first2= |date= 2012|work= Preferences |publisher= Open Dictionary|accessdate=16 March 2013}}</ref> |
|||
Under some extreme circumstances, there is no "rational" choice available. For instance, if asked to choose which one of one's children will be killed, as in [[Sophie's Choice (novel)|Sophie's Choice]], there is no rational way out of it. In that case, preferences would be incomplete since "not being able to choose" is not the same as "being indifferent". |
|||
Although some authors include [[reflexive relation|reflexivity]] as one of the axioms required to obtain representability (this axiom states that <math>A\! \succsim\! A\!</math>), it is redundant inasmuch as the completeness axiom implies it already.<ref>[[Andreu Mas-Colell|Mas-Colell, Andreu]], Michael Whinston and Jerry Green (1995). ''Microeconomic theory''. Oxford: Oxford University Press ISBN 0-19-507340-1</ref> |
|||
The ''indifference relation'' ~ is an [[equivalence relation]]. Thus, we have a [[quotient set]] S/~ of [[equivalence class]]es of S, which forms a [[partition of a set|partition]] of S. Each equivalence class is a set of packages that are equally preferred. If there are only two commodities, the equivalence classes can be graphically represented as [[indifference curve]]s. |
|||
==== Most commonly used axioms ==== |
|||
Based on the preference relation on S, we have a preference relation on S/~. As opposed to the former, the latter is [[antisymmetric relation|antisymmetric]] and a [[total order]]. |
|||
* Order-theoretic: acyclicity, transitivity, the semiorder property, completeness |
|||
* Topological: continuity, openness or closedness of the preference sets |
|||
* Linear-space: [[convex preferences|convexity]], homogeneity, translation-invariance |
|||
== Factors which affect consumer preferences == |
|||
=== Normative interpretations of the axioms === |
|||
{{tone|date=October 2021}} |
|||
Everyday experience suggests that people at least talk about their preferences as if they had personal "standards of judgment" capable of being applied to the particular domain of alternatives that present themselves from time to time.<ref name="Shapley 1974">Shapley, Lloyd and Martin Shubik. (1974). "Game theory in economics". RAND Report R-904/4</ref> Thus, the axioms are an attempt to model the decision maker's preferences, not over the actual choice, but over the type of desirable procedure (a procedure that any human being would like to follow). [[Behavioral economics]] investigates inconsistent behavior (i.e. behavior that violates the axioms) of people. Believing in axioms in a normative way does not imply that it is mandatory to behave according to them. Instead, they are a mode of behavior suggested; its what people would like to see themselves following.<ref name="econ.hit-u.ac.jp"/> |
|||
===Indifference curve=== |
|||
Here is an illustrative example of the normative implications of the theory of preferences<ref name="econ.hit-u.ac.jp"/>: Consider a decision maker who needs to make a choice. Assume that this is a choice of where to live or whom to marry and that the decision maker has asked an economist for advice. The economist, who wants to engage in normative science, attempts to tell the decision maker how she should make decisions. |
|||
An [[indifference curve]]<ref>{{Citation |title=Indifference curve |date=2023-02-03 |url=https://en.wikipedia.org/enwiki/w/index.php?title=Indifference_curve&oldid=1137303165 |work=Wikipedia |access-date=2023-06-04 |language=en}}</ref> is a graphical representation that shows the combinations of quantities of two goods for which an individual will have equal preference or utility. It is named as such because the consumer would be indifferent between choosing any combination or bundle of commodities.<ref name="usi.edu">University of Southern Indiana. (2021). Retrieved 26 April 2021, from https://www.usi.edu/business/cashel/331/CONSUMER.pdf</ref> An indifference curve can be detected in a market when the economics of scope is not overly diverse, or the goods and services are part of a perfect market. Any bundles on the same indifference curve have the same utility level. One example of this is [[deodorant]]. Deodorant is similarly priced throughout several different brands. Deodorant also has no major differences in use; therefore, consumers have no preference in what they should use. Indifference curves are negatively sloped because of the non-satiation of preferences, as consumers cannot be indifferent between two bundles if one has more of both goods. The indifference curves are also curved inwards due to [[diminishing marginal utility]], i.e., the reduction in the utility of every additional unit as consumers consume more of the same good. The slope of the indifference curve measures the [[marginal rate of substitution]], which can be defined as the number of units of one good needed to replace one unit of another good without changing the overall utility.<ref>{{Cite book |last=Clower |first=Robert W. |url=https://www.worldcat.org/oclc/18350632 |title=Intermediate microeconomics |date=1988 |publisher=Harcourt Brace Jovanovich |others=Philip E. Graves, Robert L. Sexton |isbn=0-15-541496-8 |location=San Diego |oclc=18350632}}</ref> |
|||
Economist: I suggest that you attach a utility index to each alternative, and choose the alternative with the highest utility. |
|||
===Changes in new technology=== |
|||
Decision Maker: You've been brainwashed. You think only in terms of functions. But this is an important decision, there are people involved, emotions, these are not functions! |
|||
New changes in technology are a big factor in changes of consumer preferences. When an industry has a new competitor who has found ways to make the goods or services work more effectively, it can change the market completely. An example of this is the [[Android (operating system)|Android]] operating system. Some years ago, Android struggled to compete with [[Apple Inc.|Apple]] for market share. With the advances in technology throughout the last five years, they have passed the stagnant Apple brand. Changes in technology examples are but are not limited to increased efficiency, longer-lasting batteries, and a new easier interface for consumers. |
|||
Economist: Would you feel comfortable with cycling among three possible options? Preferring ''x'' to ''y'', and then ''y'' to ''z'', but then again ''z'' to ''x''? |
|||
===Social influence=== |
|||
Decision Maker: No, this is very silly and counterproductive. I told you that there are people involved, and I do not want to play with their feelings. |
|||
Changes in preference can also develop as a result of social interactions among consumers. If decision-makers are asked to make choices in isolation, the results may differ from those if they were to make choices in a group setting. By means of social interactions, individual preferences can evolve without any necessary change to the utility.<ref>{{Cite journal |last1=Fershtman |first1=Chaim |last2=Segal |first2=Uzi |date=2018 |title=Preferences and Social Influence |url=https://www.jstor.org/stable/26528494 |journal=American Economic Journal: Microeconomics |volume=10 |issue=3 |pages=124–142 |doi=10.1257/mic.20160190 |jstor=26528494 |s2cid=51839017 |issn=1945-7669}}</ref> This can be exemplified by taking the example of a group of friends having lunch together. Individuals in such a group may change their food preferences after being exposed to their friends' preferences. Similarly, if an individual tends to be risk-averse but is exposed to a group of risk-seeking people, his preferences may change over time. |
|||
Economist: Good. So now let me tell you a secret: if you follow these two conditions -making decision, and avoid cycling, then you can be described as if you are maximizing a utility function. |
|||
== Types of preferences == |
|||
Consumers whose preference structures violate transitivity would get exposed to being milked by some unscrupulous person. For instance, Maria prefers apples to oranges, oranges to bananas, and bananas to apples. Let her be endowed with an apple, which she can trade in a market. Because she prefers bananas to apples, she is willing to pay, say, one cent to trade her apple for a banana. Afterwards, Maria is willing to pay another cent to trade her banana for an orange, and again the orange for an apple, and so on. There are [[Intransitivity#Occurrences_in_preferences|other examples]] of this kind of "irrational" behaviour. |
|||
[[File:Simple-indifference-curves.svg|thumb|A simple graph showing convex preferences, as the indifference line, curves in{{clarify|reason=The rest of the sentence seems to have been cut off?|date=March 2024}}]] |
|||
=== Convex preferences === |
|||
Completeness implies that some choice will be made, an assertion that is more philosophically questionable. In most applications, the set of consumption alternatives is infinite and the consumer is not conscious of all preferences. For example, one does not have to choose over going on holiday by plane or by train: if one does not have enough money to go on holiday anyway then it is not necessary to attach a preference order to those alternatives (although it can be nice to dream about what one would do if one would win the lottery). However, preference can be interpreted as a hypothetical choice that could be made rather than a conscious state of mind. In this case, completeness amounts to an assumption that the consumers can always make up their mind whether they are indifferent or prefer one option when presented with any pair of options. |
|||
{{Main|Convex preferences}} |
|||
Convex preferences relate to averages between two points on an indifference curve. It comes in two forms, weak and strong. In its weak form, convex preferences state that if <math>A \sim B</math>, then the average of A and B is at least as good as A. In contrast, the average of A and B would be preferred in its strong form. This is why in its strong form, the indifference line curves in, meaning that the average of any two points would result in a point further away from the origin, thus giving a higher utility.<ref>{{Cite journal |last1=Richter |first1=Michael |last2=Rubinst |first2=Ariel |date=December 2019 |title=Convex preferences: A new definition |journal=Theoretical Economics|volume=14 |issue=4 |pages=1169–1183 |doi=10.3982/TE3286 |s2cid=109933565 |doi-access=free |hdl=10419/217099 |hdl-access=free }}</ref> One way to check convexity is to connect two random points on the same indifference curve and draw a straight line through these two points, and then pick one point on the straight line between those two points. If the utility level of the picked point on the straight line is greater than that of those two points, this is a strictly convex preference. Convexity is one of the prerequisites for a rational consumer in the market when maximizing his utility level under the budget constraint. |
|||
=== Concave preferences === |
|||
Under some extreme circumstances there is no "rational" choice available. For instance, if asked to choose which one of one's children will be killed, as in [[Sophie's Choice (novel)|Sophie's Choice]], there is no rational way out of it. In that case preferences would be incomplete, since "not being able to choose" is not the same as "being indifferent". |
|||
Concave preferences are the opposite of convex, where when <math>A \sim B</math>, the average of A and B is worse than A. This is because concave curves slope outwards, meaning an average between two points on the same indifference curve would result in a point closer to the origin, thus giving a lower utility.<ref>{{Cite journal |last=Lahiri |first=Somdeb |date=September 2015 |title=Concave Preferences Over Bundles and the First Fundamental Theorem of Welfare Economics |journal=Social Science Research Network}}</ref> To determine whether the preference is concave or not, one way is still to connect two random points on the same difference curve and draw a straight line through these two points, and then pick one point on the straight line between those two points. If the utility level of the picked point on the straight line is lower than that of those two points, this is a strictly concave preference. |
|||
=== Straight line indifference === |
|||
The ''indifference relation'' ~ is an [[equivalence relation]]. Thus we have a [[quotient set]] S/~ of [[equivalence class]]es of S, which forms a [[partition of a set|partition]] of S. Each equivalence class is a set of packages that is equally preferred. |
|||
Straight-line similarities occur when there are perfect substitutes. Perfect substitutes are goods and/or services that can be used the same way as the good or service it replaces. When <math>A \sim B</math>, the average of A and B will fall on the same indifference line and give the same utility.<ref>{{Cite journal |last=Lipatov |first=Vilen |title=Preempting the Entry of Near Perfect Substitute |journal=Journal of Competition Law & Economics |year=2021 |volume=17 |pages=194–210|doi=10.1093/joclec/nhaa023 }}</ref> |
|||
If there are only two commodities, the equivalence classes can be graphically represented as [[indifference curve]]s. |
|||
[[File:Indifference-curves-perfect-substitutes.svg|thumb|An example of straight line indifference curves, where Good X and Good Y are perfect substitutes. |center]] |
|||
Based on the preference relation on S we have a preference relation on S/~. As opposed to the former, the latter is [[antisymmetric relation|antisymmetric]] and a [[total order]]. |
|||
=== Types of goods affecting preferences === |
|||
When a consumer is faced with a choice between different goods, the type of goods they are choosing between will affect how they make their decision process. To begin with, when there are [[normal good]]s, these goods have a direct correlation with the income the consumer makes, meaning as they make more money, they will choose to consume more of this good, and as their income decreases, they will consume less of the good. However, the opposite is [[inferior good]]s; these negatively correlate with income. Hence, as consumers make less money, they'll consume more inferior goods as they are seen as less desirable, meaning they come with a reduced cost. As they make more money, they'll consume fewer inferior goods and have the money available to buy more desirable goods.<ref>{{Cite journal |last=Cherchye |first=Laurens |date=August 2020 |title=Revealed Preference Analysis with Normal Goods |url=https://www.aeaweb.org/articles/pdf/doi/10.1257/mic.20180133 |journal=American Economic Journal|volume=12 |issue=3 |pages=165–188 |doi=10.1257/mic.20180133 |s2cid=226865939 }}</ref> An example of a normal good would-be branded clothes, as they are more expensive compared to their inferior good counterparts which are non-branded clothes. Goods that are not affected by income as referred to as a [[necessity good]], which are product(s) and services that consumers will buy regardless of the changes in their income levels. These usually include medical care, clothing and basic food. Finally, there are also [[luxury goods]], which are the most expensive and deemed the most desirable. Just like normal goods, as income increases, so is the demand for luxury goods; however, in the case of luxury goods, the greater the income, the greater the demand for luxury goods.<ref>{{Cite journal |last=Mortelmans |first=D. |date=2005 |title=Sign values in processes of distinction: The concept of luxury |volume=157 |pages=497–520}}</ref> |
|||
== Applications to theories of utility == |
== Applications to theories of utility == |
||
In economics, a utility function is often used to represent a preference structure such that <math>u\left(A\right)\geqslant u(B)</math> [[if and only if]] <math>A \succsim |
In economics, a utility function is often used to represent a preference structure such that <math>u\left(A\right)\geqslant u\left(B\right)</math> [[if and only if]] <math>A \succsim B</math>. The idea is to associate each class of indifference with a real number such that if one class is preferred to the other, then the number of the first one is greater than that of the second one. When a preference order is both transitive and complete, it is standard practice to call it a ''rational preference relation'', and the people who comply with it are ''[[rational agent]]s''. A transitive and complete relation is called a [[Strict weak ordering#Total preorders|'' weak order'' (or ''total preorder) '']]. The literature on preferences is far from being standardized regarding terms such as ''complete'', ''partial'', ''strong'', and ''weak''. Together with the terms "total", "linear", "strong complete", "quasi-orders", "pre-orders", and "sub-orders", which also have different meanings depending on the author's taste, there has been an abuse of semantics in the literature.<ref name="Shapley 1974">Shapley, Lloyd and Martin Shubik. (1974). "Game theory in economics". RAND Report R-904/4</ref> |
||
According to Simon Board, a [[Continuous function|continuous]] utility function always exists if <math> \succsim |
According to Simon Board, a [[Continuous function|continuous]] utility function always exists if <math> \succsim </math> is a continuous rational preference relation on <math>R^n</math>.<ref name="Boa2005">{{cite web|last=Board|first=Simon|title=Preferences and Utility|url=http://www.econ.ucla.edu/sboard/teaching/econ11_09/econ11_09_lecture2.pdf|publisher=UCLA|access-date=15 February 2013}}</ref> For any such preference relation, there are many continuous utility functions that represent it. Conversely, every utility function can be used to construct a unique preference relation. |
||
All the above is independent of the prices of the goods and services and |
All the above is independent of the prices of the goods and services and the budget constraints consumers face. These determine the ''feasible'' bundles (which they can afford). According to the standard theory, consumers choose a bundle within their budget such that no other feasible bundle is preferred over it, thus maximizing their utility. |
||
== Primitive equivalents of some known properties of utility functions == |
|||
* An increasing utility function is associated with a monotonic preference relation. |
* An increasing utility function is associated with a [[monotonic]] preference relation. |
||
* [[Quasi-convex function|Quasi-concave]] utility functions are associated with a [[convex preferences|convex preference]] order. When non-convex preferences arise, the [[Shapley–Folkman lemma]] is applicable. |
|||
* A utility function that is non-constant in the neighborhood of x is associated with a locally non-satiated preference order. |
|||
* [[Quasi-convex function|Quasi-concave]] utility functions are associated with a convex preference order. When non-convex preferences arise, the [[Shapley–Folkman lemma]] is applicable. |
|||
* Weakly separable utility functions are associated with the weak separability of preferences. |
|||
=== Lexicographic preferences === |
=== Lexicographic preferences === |
||
[[Lexicographic preferences]] are a special case of preferences that assign an infinite value to a good |
[[Lexicographic preferences]] are a special case of preferences that assign an infinite value to a good when compared with the other goods of a bundle.<ref name="Tanguiane1991">{{Cite book |
||
|last=Tanguiane (Tangian) |first=Andranick |date=1991 |
|||
|title=Aggregation and representation of preferences: introduction to the mathematical theory of democracy |
|||
|chapter = 2. Preferences and goal functions|pages = 23–50 |
|||
|publisher=Springer |location=Berlin-Heidelberg|isbn = 978-3-642-76516-2 |doi=10.1007/978-3-642-76516-2}}</ref> |
|||
Georgescu-Roegen pointed out that the measurability of the utility theory is limited as it excludes lexicographic preferences. Causing an amplified level of awareness placed upon lexicographic preferences as a substitute hypothesis on consumer behaviour.<ref>{{cite journal |last1=Hayakawa |first1=Hiroaki |title=Lexicographic preferences and consumer theory |journal=Journal of Behavioral Economics |volume=7 |issue=1 |date=1978 |pages=17–51|doi=10.1016/0090-5720(78)90013-X }}</ref> |
|||
== Strict versus weak == |
== Strict versus weak == |
||
The possibility of defining a strict preference relation <math>\succ |
The possibility of defining a strict preference relation <math>\succ</math> as distinguished from the weaker one <math>\succsim</math>, and vice versa, suggests in principle an alternative approach of starting with the strict relation <math>\succ</math> as the primitive concept and deriving the weaker one and the indifference relation. However, an indifference relation derived this way will generally not be transitive.<ref name="Barten 1982 p. 384"/> The conditions to avoid such inconsistencies were studied in detail by [[Andranik Tangian]].<ref name="Tanguiane1991" /> According to Kreps "beginning with strict preference makes it easier to discuss non-comparability possibilities".<ref name="Kreps 1990 p. 24">Kreps, David. (1990). ''A Course in Microeconomic Theory''. New Jersey: Princeton University Press</ref> |
||
==Elicitation of preferences== |
|||
== Agreggation == |
|||
Under certain assumptions, individual preferences can be aggregated onto the preferences of a group of people. As a result of agreggation, [[Arrow's impossibility theorem]] states that voting systems sometimes can not convert individual preferences into desirable community-wide acts of choice. |
|||
The mathematical foundations of most common types of preferences — that are representable by quadratic or additive utility functions — laid down by [[Gérard Debreu]]<ref name="Debreu1952">{{Cite journal |
|||
== Expected utility theory == |
|||
|last=Debreu |first=Gérard|year=1952 |
|||
Preference relations can also be applied to a space of simple lotteries, as in [[expected utility hypothesis|expected utility theory]]. In this case a preference structure over lotteries can also be represented by a utility function. |
|||
|title= Definite and semidefinite quadratic forms |journal= Econometrica |volume=20|issue=2|pages=295–300 |
|||
|doi =10.2307/1907852 |
|||
|jstor=1907852}}</ref><ref name="Debreu1960">{{Cite book |
|||
|last=Debreu |first=Gérard|year=1960 |
|||
|chapter= Topological methods in cardinal utility theory |
|||
|editor-last= Arrow|editor-first=Kenneth |
|||
|title= Mathematical Methods in the Social Sciences,1959 |
|||
|publisher= Stanford University Press |
|||
|location= Stanford|pages=16–26|doi= 10.1016/S0377-2217(03)00413-2}}</ref> |
|||
enabled [[Andranik Tangian]] to develop methods for their elicitation. |
|||
In particular, additive and quadratic preference functions in <math>n</math> variables can be constructed from interviews, where questions are aimed at tracing totally <math>n</math> 2D-indifference curves in <math>n - 1</math> coordinate planes.<ref name="Tangian2002">{{Cite journal |
|||
|last=Tangian |first=Andranik|year=2002 |
|||
|title= Constructing a quasi-concave quadratic objective function from interviewing a decision maker |
|||
|journal= European Journal of Operational Research |volume=141|issue=3|pages=608–640 |
|||
| doi=10.1016/S0377-2217(01)00185-0}}</ref><ref name="Tangian2004">{{Cite journal |
|||
|last=Tangian |first=Andranik|year=2004 |
|||
|title= A model for ordinally constructing additive objective functions |
|||
|journal= European Journal of Operational Research |volume=159|issue=2|pages=476–512 |
|||
|doi= 10.1016/S0377-2217(03)00413-2 |
|||
}}</ref> |
|||
== Criticism == |
== Criticism == |
||
Some critics say that rational theories of choice and preference theories rely too heavily on the assumption of invariance, which states that the relation of preference should not depend on the description of the options or on the method of elicitation. |
Some critics say that rational theories of choice and preference theories rely too heavily on the assumption of invariance, which states that the relation of preference should not depend on the description of the options or on the method of elicitation. But without this assumption, one's preferences cannot be represented as maximization of utility.<ref>Slovic, P. (1995). "The Construction of Preference". American Psychologist, Vol. 50, No. 5, pp. 364–371.</ref> |
||
Milton Friedman said that segregating taste factors from objective factors (i.e. prices, income, availability of goods) is conflicting because both are "inextricably interwoven". |
|||
The non-satiation of preferences is another topic that generates debate since it essentially states that "more is better than less". Many argue that this interpretation is flawed and highly subjective. Many critics call for a specification of preference to be able to interpret the non-satiation principle reasonably.<ref>{{Cite journal |last=Higgins |first=Richard S. |date=July 1972 |title=Satiation in Consumer Preference and the Demand Law |url=https://www.jstor.org/stable/1056231 |journal=Southern Economic Journal |volume=39 |issue=1 |pages=116–118 |doi=10.2307/1056231|jstor=1056231 }}</ref> For example, in cases where there is a choice between more pollution and less pollution, consumers would rationally prefer less pollution thus making the non-satiation principle fail. Similar conflicts with the principle can be seen in choices that involve bulky goods in a limited space, such as an excess of furniture in a small house. |
|||
The concept of transitivity is highly debated, with many examples suggesting that it does not generally hold. One of the most well-known is the [[Sorites paradox]], which shows that indifference between small changes in value can be incrementally extended to indifference between large changes in values.<ref>{{cite journal |last1=Luce |first1=Duncan |title=Semiorders and a Theory of Utility Discrimination |url=https://www.imbs.uci.edu/files/personnel/luce/pre1990/1956/Luce_Econometrica_1956.pdf |journal=Econometrica }}</ref> |
|||
Another criticism comes from philosophy. Philosophers cast doubt that when most consumers share the same preference in the same market, which may lead to the result that the shared preference has become somewhat objective, whether the judgments of preferences for each individual will still depend on subjectivity or not.{{clarify|reason=Grammar is convoluted.|date=January 2022}} |
|||
==See also== |
== See also == |
||
{{columns-list|colwidth=15em| |
|||
*[[Arrow's paradox]] |
|||
*[[Behavioral economics]] |
*[[Behavioral economics]] |
||
*[[Convex preferences]] |
*[[Convex preferences]] |
||
*[[Demonstrated preference]] |
|||
*[[Economic subjectivism]] |
*[[Economic subjectivism]] |
||
*[[ |
*[[Gibbard–Satterthwaite theorem]] |
||
*[[Lexicographic preferences]] |
*[[Lexicographic preferences]] |
||
*[[Pairwise comparison]] |
*[[Pairwise comparison (psychology)|Pairwise comparison]] |
||
*[[Preference regression (in marketing)]] |
|||
*[[Preferential voting (disambiguation)]] |
|||
*[[Preferred number]] |
|||
*[[Preference revelation]] |
|||
*[[Revealed preference]] |
*[[Revealed preference]] |
||
*[[ |
*[[Semiorder]] |
||
*[[Strict weak ordering]] |
*[[Strict weak ordering]] |
||
*[[Time preference |
*[[Time preference]] |
||
*[[Indifference curve]] |
|||
*[[Rational choice theory]] |
|||
*[[Ordinal utility]] vs. [[Cardinal utility]] |
|||
*[[TOTREP]] |
|||
}} |
|||
== References == |
== References == |
||
{{Reflist}} |
{{Reflist}} |
||
*Kreps, David (1990). ''A Course in Microeconomic Theory''. New Jersey: Princeton University Press. ISBN 0-691-04264-0 |
|||
{{microeconomics-footer}} |
{{microeconomics-footer}} |
||
| Line 137: | Line 207: | ||
{{DEFAULTSORT:Preference (Economics)}} |
{{DEFAULTSORT:Preference (Economics)}} |
||
[[Category:Microeconomics]] |
[[Category:Microeconomics]] |
||
[[Category: |
[[Category:Utility]] |
||
Latest revision as of 05:17, 2 April 2024

In economics, and in other social sciences, preference refers to an order by which an agent, while in search of an "optimal choice", ranks alternatives based on their respective utility. Preferences are evaluations that concern matters of value, in relation to practical reasoning.[1] Individual preferences are determined by taste, need, ..., as opposed to price, availability or personal income. Classical economics assumes that people act in their best (rational) interest.[2] In this context, rationality would dictate that, when given a choice, an individual will select an option that maximizes their self-interest. But preferences are not always transitive, both because real humans are far from always being rational and because in some situations preferences can form cycles, in which case there exists no well-defined optimal choice. An example of this is Efron dice.
The concept of preference plays a key role in many disciplines, including moral philosophy and decision theory. The logical properties that preferences possess also have major effects on rational choice theory, which in turn affects all modern economic topics.[3]
Using the scientific method, social scientists aim to model how people make practical decisions in order to explain the causal underpinnings of human behaviour or to predict future behaviours. Although economists are not typically interested in the specific causes of a person's preferences, they are interested in the theory of choice because it gives a background to empirical demand analysis.[4]
Stability of preference is a deep assumption behind most economic models. Gary Becker drew attention to this with his remark that "the combined assumptions of maximizing behavior, market equilibrium, and stable preferences, used relentlessly and unflinchingly, form the heart of the economic approach as it is."[5] More complex conditions of adaptive preference were explored by Carl Christian von Weizsäcker in his paper "The Welfare Economics of Adaptive Preferences" (2005), while remarking that.[6] Traditional neoclassical economics has worked with the assumption that the preferences of agents in the economy are fixed. This assumption has always been disputed outside neoclassical economics.
History
[edit]In 1926, Ragnar Frisch was the first to develop a mathematical model of preferences in the context of economic demand and utility functions.[7] Up to then, economists had used an elaborate theory of demand that omitted primitive characteristics of people. This omission ceased when, at the end of the 19th and the beginning of the 20th century, logical positivism predicated the need to relate theoretical concepts to observables.[8] Whereas economists in the 18th and 19th centuries felt comfortable theorizing about utility, with the advent of logical positivism in the 20th century, they felt they needed a more empirical structure. Because binary choices are directly observable, they instantly appeal to economists. The search for observables in microeconomics is taken even further by the revealed preference theory, which holds consumers' preferences can be revealed by what they purchase under different circumstances, particularly under different income and price circumstances.[9]
Despite utilitarianism and decision theory, many economists have differing definitions of what a rational agent is. In the 18th century, utilitarianism gave insight into the utility-maximizing versions of rationality; however, economists still have no consistent definition or understanding of what preferences and rational actors should be analyzed.[10]
Since the pioneer efforts of Frisch in the 1920s, the representability of a preference structure with a real-valued function is one of the major issues pervading the theory of preferences. This has been achieved by mapping it to the mathematical index called utility. Von Neumann and Morgenstern's 1944 book "Games and Economic Behavior" treated preferences as a formal relation whose properties can be stated axiomatically. These types of axiomatic handling of preferences soon began to influence other economists: Marschak adopted it by 1950, Houthakker employed it in a 1950 paper, and Kenneth Arrow perfected it in his 1951 book "Social Choice and Individual Values".[11]
Gérard Debreu, influenced by the ideas of the Bourbaki group, championed the axiomatization of consumer theory in the 1950s, and the tools he borrowed from the mathematical field of binary relations have become mainstream since then. Even though the economics of choice can be examined either at the level of utility functions or at the level of preferences, moving from one to the other can be useful. For example, shifting the conceptual basis from an abstract preference relation to an abstract utility scale results in a new mathematical framework, allowing new conditions on the preference structure to be formulated and investigated.
Another historical turning point can be traced back to 1895, when Georg Cantor proved in a theorem that if a binary relation is linearly ordered, then it is also isomorphic in the ordered real numbers. This notion would become very influential for the theory of preferences in economics: by the 1940s, prominent authors such as Paul Samuelson would theorize about people having weakly ordered preferences.[12]
Historically, preference in economics as a form of utility can be categorized as ordinal or cardinal data. Both introduced in the 20th century, cardinal and ordinal utility take opposing theories and mindsets in applying and analyzing preference in utility. Vilfredo Pareto introduced the concept of ordinal utility, while Carl Menger led the idea of cardinal utility. Ordinal utility, in summation, is the direct following of preference, where an optimal choice is taken over a set of parameters. A person is expected to act in their best interests and dedicate their preference to the outcome with the greatest utility. Ordinal utility assumes that an individual will not have the same utility from a preference as any other individual because they likely will not experience the same parameters which cause them to decide a given outcome. Cardinal utility is a function of utility where a person makes a decision based on a preference, and the preference decision is weighted based on a quantitative value of utility. This utility unit is assumed to be universally applicable and constant across all individuals. Cardinal utility also assumes consistency across individuals' decision-making processes, assuming all individuals will have the same preference, with all variables held constant. Marshall found that "a good deal of the analysis of consumer behavior could be greatly simplified by assuming that the marginal utility of income is constant" (Robert H. Strotz.[13]), however, this cannot be held to the utility of resources and decision-making applied to income. Ordinal and cardinal utility theories provide unique viewpoints on utility, can be used differently to model decision-making preferences and utilization development, and can be used across many applications for economic analysis.
Notation
[edit]There are two fundamental comparative value concepts, namely strict preference (better) and indifference (equal in value to).[14] These two concepts are expressed in terms of an agent's best wishes; however, they also express objective or intersubjective valid superiority that does not coincide with the pattern of wishes of any person.
Suppose the set of all states of the world is and an agent has a preference relation on . It is common to mark the weak preference relation by , so that means "the agent wants y at least as much as x" or "the agent weakly prefers y to x".
The symbol is used as a shorthand to denote an indifference relation: , which reads "the agent is indifferent between y and x", meaning the agent receives the same level of benefit from each.
The symbol is used as a shorthand to the strong preference relation: ), it is redundant inasmuch as the completeness axiom implies it already.[15]
Non-satiation of preferences

Non-satiation refers to the belief any commodity bundle with at least as much of one good and more of the other must provide a higher utility, showing that more is always regarded as "better". This assumption is believed to hold as when consumers are able to discard excess goods at no cost, then consumers can be no worse off with extra goods.[16] This assumption does not preclude diminishing marginal utility.
Example
Option A
- Apple = 5
- Orange = 3
- Banana = 2
Option B
- Apple = 6
- Orange = 4
- Banana = 2
In this situation, utility from Option B > A, as it contains more apples and oranges with bananas being constant.
Transitivity
[edit]Transitivity of preferences is a fundamental principle shared by most major contemporary rational, prescriptive, and descriptive models of decision-making.[17] In order to have transitive preferences, a person, player, or agent that prefers choice option A to B and B to C must prefer A to C. The most discussed logical property of preferences are the following:
- A≽B ∧ B≽C → A≽C (transitivity of weak preference)
- A~B ∧ B~C → A~C (transitivity of indifference)
- A≻B ∧ B≻C → A≻C (transitivity of strict preference)
Some authors go so far as to assert that a claim of a decision maker's violating transitivity requires evidence beyond any reasonable doubt.[17] But there are scenarios involving a finite set of alternatives where, for any alternative there exists another that a rational agent would prefer. One class of such scenarios involves intransitive dice. And Schumm gives examples of non-transitivity based on Just-noticeable differences.[18]
Most commonly used axioms
[edit]- Order-theoretic: acyclicity, the semi-order property, completeness
- Topological: continuity, openness, or closeness of the preference sets
- Linear-space: convexity, homogeneity
Normative interpretations of the axioms
[edit]This section needs additional citations for verification. (October 2021) |
Everyday experience suggests that people at least talk about their preferences as if they had personal "standards of judgment" capable of being applied to the particular domain of alternatives that present themselves from time to time.[19] Thus, the axioms attempt to model the decision maker's preferences, not over the actual choice, but over the type of desirable procedure (a procedure that any human being would like to follow). Behavioral economics investigates human behaviour which violates the above axioms. Believing in axioms in a normative way does not imply that everyone must behave according to them.[8]
Consumers whose preference structures violate transitivity would get exposed to being exploited by some unscrupulous person. For instance, Maria prefers apples to oranges, oranges to bananas, and bananas to apples. Let her be endowed with an apple, which she can trade in a market. Because she prefers bananas to apples, she is willing to pay one cent to trade her apple for a banana. Afterwards, Maria is willing to pay another cent to trade her banana for an orange, the orange for an apple, and so on. There are other examples of this kind of irrational behaviour.
Completeness implies that some choice will be made, an assertion that is more philosophically questionable. In most applications, the set of consumption alternatives is infinite, and the consumer is unaware of all preferences. For example, one does not have to choose between going on holiday by plane or train. Suppose one does not have enough money to go on holiday anyway. In that case, it is unnecessary to attach a preference order to those alternatives (although it can be nice to dream about what one would do if one won the lottery). However, preference can be interpreted as a hypothetical choice that could be made rather than a conscious state of mind. In this case, completeness amounts to an assumption that the consumers can always make up their minds whether they are indifferent or prefer one option when presented with any pair of options.
Under some extreme circumstances, there is no "rational" choice available. For instance, if asked to choose which one of one's children will be killed, as in Sophie's Choice, there is no rational way out of it. In that case, preferences would be incomplete since "not being able to choose" is not the same as "being indifferent".
The indifference relation ~ is an equivalence relation. Thus, we have a quotient set S/~ of equivalence classes of S, which forms a partition of S. Each equivalence class is a set of packages that are equally preferred. If there are only two commodities, the equivalence classes can be graphically represented as indifference curves. Based on the preference relation on S, we have a preference relation on S/~. As opposed to the former, the latter is antisymmetric and a total order.
Factors which affect consumer preferences
[edit]This article's tone or style may not reflect the encyclopedic tone used on Wikipedia. (October 2021) |
Indifference curve
[edit]An indifference curve[20] is a graphical representation that shows the combinations of quantities of two goods for which an individual will have equal preference or utility. It is named as such because the consumer would be indifferent between choosing any combination or bundle of commodities.[21] An indifference curve can be detected in a market when the economics of scope is not overly diverse, or the goods and services are part of a perfect market. Any bundles on the same indifference curve have the same utility level. One example of this is deodorant. Deodorant is similarly priced throughout several different brands. Deodorant also has no major differences in use; therefore, consumers have no preference in what they should use. Indifference curves are negatively sloped because of the non-satiation of preferences, as consumers cannot be indifferent between two bundles if one has more of both goods. The indifference curves are also curved inwards due to diminishing marginal utility, i.e., the reduction in the utility of every additional unit as consumers consume more of the same good. The slope of the indifference curve measures the marginal rate of substitution, which can be defined as the number of units of one good needed to replace one unit of another good without changing the overall utility.[22]
Changes in new technology
[edit]New changes in technology are a big factor in changes of consumer preferences. When an industry has a new competitor who has found ways to make the goods or services work more effectively, it can change the market completely. An example of this is the Android operating system. Some years ago, Android struggled to compete with Apple for market share. With the advances in technology throughout the last five years, they have passed the stagnant Apple brand. Changes in technology examples are but are not limited to increased efficiency, longer-lasting batteries, and a new easier interface for consumers.
Social influence
[edit]Changes in preference can also develop as a result of social interactions among consumers. If decision-makers are asked to make choices in isolation, the results may differ from those if they were to make choices in a group setting. By means of social interactions, individual preferences can evolve without any necessary change to the utility.[23] This can be exemplified by taking the example of a group of friends having lunch together. Individuals in such a group may change their food preferences after being exposed to their friends' preferences. Similarly, if an individual tends to be risk-averse but is exposed to a group of risk-seeking people, his preferences may change over time.
Types of preferences
[edit]
Convex preferences
[edit]Convex preferences relate to averages between two points on an indifference curve. It comes in two forms, weak and strong. In its weak form, convex preferences state that if , then the average of A and B is at least as good as A. In contrast, the average of A and B would be preferred in its strong form. This is why in its strong form, the indifference line curves in, meaning that the average of any two points would result in a point further away from the origin, thus giving a higher utility.[24] One way to check convexity is to connect two random points on the same indifference curve and draw a straight line through these two points, and then pick one point on the straight line between those two points. If the utility level of the picked point on the straight line is greater than that of those two points, this is a strictly convex preference. Convexity is one of the prerequisites for a rational consumer in the market when maximizing his utility level under the budget constraint.
Concave preferences
[edit]Concave preferences are the opposite of convex, where when , the average of A and B is worse than A. This is because concave curves slope outwards, meaning an average between two points on the same indifference curve would result in a point closer to the origin, thus giving a lower utility.[25] To determine whether the preference is concave or not, one way is still to connect two random points on the same difference curve and draw a straight line through these two points, and then pick one point on the straight line between those two points. If the utility level of the picked point on the straight line is lower than that of those two points, this is a strictly concave preference.
Straight line indifference
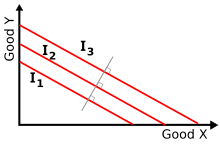
[edit]Straight-line similarities occur when there are perfect substitutes. Perfect substitutes are goods and/or services that can be used the same way as the good or service it replaces. When , the average of A and B will fall on the same indifference line and give the same utility.[26]
Types of goods affecting preferences
[edit]When a consumer is faced with a choice between different goods, the type of goods they are choosing between will affect how they make their decision process. To begin with, when there are normal goods, these goods have a direct correlation with the income the consumer makes, meaning as they make more money, they will choose to consume more of this good, and as their income decreases, they will consume less of the good. However, the opposite is inferior goods; these negatively correlate with income. Hence, as consumers make less money, they'll consume more inferior goods as they are seen as less desirable, meaning they come with a reduced cost. As they make more money, they'll consume fewer inferior goods and have the money available to buy more desirable goods.[27] An example of a normal good would-be branded clothes, as they are more expensive compared to their inferior good counterparts which are non-branded clothes. Goods that are not affected by income as referred to as a necessity good, which are product(s) and services that consumers will buy regardless of the changes in their income levels. These usually include medical care, clothing and basic food. Finally, there are also luxury goods, which are the most expensive and deemed the most desirable. Just like normal goods, as income increases, so is the demand for luxury goods; however, in the case of luxury goods, the greater the income, the greater the demand for luxury goods.[28]
Applications to theories of utility
[edit]In economics, a utility function is often used to represent a preference structure such that if and only if . The idea is to associate each class of indifference with a real number such that if one class is preferred to the other, then the number of the first one is greater than that of the second one. When a preference order is both transitive and complete, it is standard practice to call it a rational preference relation, and the people who comply with it are rational agents. A transitive and complete relation is called a weak order (or total preorder) . The literature on preferences is far from being standardized regarding terms such as complete, partial, strong, and weak. Together with the terms "total", "linear", "strong complete", "quasi-orders", "pre-orders", and "sub-orders", which also have different meanings depending on the author's taste, there has been an abuse of semantics in the literature.[19]
According to Simon Board, a continuous utility function always exists if is a continuous rational preference relation on .[29] For any such preference relation, there are many continuous utility functions that represent it. Conversely, every utility function can be used to construct a unique preference relation.
All the above is independent of the prices of the goods and services and the budget constraints consumers face. These determine the feasible bundles (which they can afford). According to the standard theory, consumers choose a bundle within their budget such that no other feasible bundle is preferred over it, thus maximizing their utility.
Primitive equivalents of some known properties of utility functions
[edit]- An increasing utility function is associated with a monotonic preference relation.
- Quasi-concave utility functions are associated with a convex preference order. When non-convex preferences arise, the Shapley–Folkman lemma is applicable.
Lexicographic preferences
[edit]Lexicographic preferences are a special case of preferences that assign an infinite value to a good when compared with the other goods of a bundle.[30]
Georgescu-Roegen pointed out that the measurability of the utility theory is limited as it excludes lexicographic preferences. Causing an amplified level of awareness placed upon lexicographic preferences as a substitute hypothesis on consumer behaviour.[31]
Strict versus weak
[edit]The possibility of defining a strict preference relation as distinguished from the weaker one , and vice versa, suggests in principle an alternative approach of starting with the strict relation as the primitive concept and deriving the weaker one and the indifference relation. However, an indifference relation derived this way will generally not be transitive.[7] The conditions to avoid such inconsistencies were studied in detail by Andranik Tangian.[30] According to Kreps "beginning with strict preference makes it easier to discuss non-comparability possibilities".[32]
Elicitation of preferences
[edit]The mathematical foundations of most common types of preferences — that are representable by quadratic or additive utility functions — laid down by Gérard Debreu[33][34] enabled Andranik Tangian to develop methods for their elicitation. In particular, additive and quadratic preference functions in variables can be constructed from interviews, where questions are aimed at tracing totally 2D-indifference curves in coordinate planes.[35][36]
Criticism
[edit]Some critics say that rational theories of choice and preference theories rely too heavily on the assumption of invariance, which states that the relation of preference should not depend on the description of the options or on the method of elicitation. But without this assumption, one's preferences cannot be represented as maximization of utility.[37]
Milton Friedman said that segregating taste factors from objective factors (i.e. prices, income, availability of goods) is conflicting because both are "inextricably interwoven".
The non-satiation of preferences is another topic that generates debate since it essentially states that "more is better than less". Many argue that this interpretation is flawed and highly subjective. Many critics call for a specification of preference to be able to interpret the non-satiation principle reasonably.[38] For example, in cases where there is a choice between more pollution and less pollution, consumers would rationally prefer less pollution thus making the non-satiation principle fail. Similar conflicts with the principle can be seen in choices that involve bulky goods in a limited space, such as an excess of furniture in a small house.
The concept of transitivity is highly debated, with many examples suggesting that it does not generally hold. One of the most well-known is the Sorites paradox, which shows that indifference between small changes in value can be incrementally extended to indifference between large changes in values.[39]
Another criticism comes from philosophy. Philosophers cast doubt that when most consumers share the same preference in the same market, which may lead to the result that the shared preference has become somewhat objective, whether the judgments of preferences for each individual will still depend on subjectivity or not.[clarification needed]
See also
[edit]References
[edit]- ^ Broome, John (1993). "Can a Humean Be Moderate?". In Frey, R. G.; Morris, Christopher (eds.). Value, Welfare and Morality. Cambridge University Press.
- ^ Blume, Lawrence (15 December 2016). Durlauf, Steven N; Blume, Lawrence E (eds.). The New Palgrave Dictionary of Economics. London: Palgrave Macmillan. doi:10.1007/978-1-349-58802-2. ISBN 978-1-349-95121-5.
- ^ Hansson, Sven Ove; Grüne-Yanoff, Till (May 4, 2018). "Preferences". Stanford Encyclopedia of Economics.
- ^ Arrow, Kenneth (1958). "Utilities, attitudes, choices: a review note". Econometrica. 26 (1): 1–23. doi:10.2307/1907381. JSTOR 1907381.
- ^ Becker, Gary (1976). The Economic Approach to Human Behavior (PDF). University of Chicago Press. p. 5. ISBN 0226041123. Retrieved 17 January 2022.
- ^ von Weizsäcker, C. Christian (June 2005). "The Welfare Economics of Adaptive Preferences". SSRN 771904.
- ^ a b Barten, Anton and Volker Böhm. (1982). "Consumer theory", in Kenneth Arrow and Michael Intrilligator (eds.) Handbook of mathematical economics. Vol. II, p. 384
- ^ a b Gilboa, Itzhak. (2009). Theory of Decision under uncertainty Archived 2018-02-19 at the Wayback Machine. Cambridge: Cambridge university press
- ^ Roper, James and Zin, David. (2008). "A Note on the Pure Theory of Consumer's Behaviour"
- ^ Blume, Lawrence E.; Easley, David (2008). "Rationality". The New Palgrave Dictionary of Economics. pp. 1–13. doi:10.1057/978-1-349-95121-5_2138-1. ISBN 978-1-349-95121-5.
- ^ Moscati, Ivan (2004). "Early Experiments in Consumer Demand Theory" (PDF). 128.118.178.162. Wayback Machine. Archived from the original (PDF) on 2014-03-02.
- ^ Fishburn, Peter (1994). "Utility and subjective probability", in Robert Aumann and Sergiu Hart (eds). Handbook of game theory. Vol. 2. Amsterdam: Elsevier Science. pp. 1397–1435.
- ^ Robert H. Strotz
- ^ Halldén, Sören (1957). "On the Logic of Betterm Lund: Library of Theoria" (10).
- ^ Mas-Colell, Andreu, Michael Whinston and Jerry Green (1995). Microeconomic theory. Oxford: Oxford University Press ISBN 0-19-507340-1
- ^ Bertoletti, Paolo; Etro, Federico (2016). "Preferences, entry, and market structure". RAND Journal of Economics. 47 (4): 792–821. doi:10.1111/1756-2171.12155. hdl:2158/1172593.
- ^ a b Clintin P. Davis-Stober; Michel Regenwetter; Jason Dana (2011). "Transitivity of Preferences" (PDF). Psychological Review. 118 (1): 42–56. doi:10.1037/a0021150. PMID 21244185. Retrieved 3 February 2022.
- ^ George F. Schumm (Nov 1987). "Transitivity, Preference and Indifference". Philosophical Studies. 52 (3): 435–437. doi:10.1007/BF00354058. JSTOR 4319930.
- ^ a b Shapley, Lloyd and Martin Shubik. (1974). "Game theory in economics". RAND Report R-904/4
- ^ "Indifference curve", Wikipedia, 2023-02-03, retrieved 2023-06-04
- ^ University of Southern Indiana. (2021). Retrieved 26 April 2021, from https://www.usi.edu/business/cashel/331/CONSUMER.pdf
- ^ Clower, Robert W. (1988). Intermediate microeconomics. Philip E. Graves, Robert L. Sexton. San Diego: Harcourt Brace Jovanovich. ISBN 0-15-541496-8. OCLC 18350632.
- ^ Fershtman, Chaim; Segal, Uzi (2018). "Preferences and Social Influence". American Economic Journal: Microeconomics. 10 (3): 124–142. doi:10.1257/mic.20160190. ISSN 1945-7669. JSTOR 26528494. S2CID 51839017.
- ^ Richter, Michael; Rubinst, Ariel (December 2019). "Convex preferences: A new definition". Theoretical Economics. 14 (4): 1169–1183. doi:10.3982/TE3286. hdl:10419/217099. S2CID 109933565.
- ^ Lahiri, Somdeb (September 2015). "Concave Preferences Over Bundles and the First Fundamental Theorem of Welfare Economics". Social Science Research Network.
- ^ Lipatov, Vilen (2021). "Preempting the Entry of Near Perfect Substitute". Journal of Competition Law & Economics. 17: 194–210. doi:10.1093/joclec/nhaa023.
- ^ Cherchye, Laurens (August 2020). "Revealed Preference Analysis with Normal Goods". American Economic Journal. 12 (3): 165–188. doi:10.1257/mic.20180133. S2CID 226865939.
- ^ Mortelmans, D. (2005). "Sign values in processes of distinction: The concept of luxury". 157: 497–520.
{{cite journal}}: Cite journal requires|journal=(help) - ^ Board, Simon. "Preferences and Utility" (PDF). UCLA. Retrieved 15 February 2013.
- ^ a b Tanguiane (Tangian), Andranick (1991). "2. Preferences and goal functions". Aggregation and representation of preferences: introduction to the mathematical theory of democracy. Berlin-Heidelberg: Springer. pp. 23–50. doi:10.1007/978-3-642-76516-2. ISBN 978-3-642-76516-2.
- ^ Hayakawa, Hiroaki (1978). "Lexicographic preferences and consumer theory". Journal of Behavioral Economics. 7 (1): 17–51. doi:10.1016/0090-5720(78)90013-X.
- ^ Kreps, David. (1990). A Course in Microeconomic Theory. New Jersey: Princeton University Press
- ^ Debreu, Gérard (1952). "Definite and semidefinite quadratic forms". Econometrica. 20 (2): 295–300. doi:10.2307/1907852. JSTOR 1907852.
- ^ Debreu, Gérard (1960). "Topological methods in cardinal utility theory". In Arrow, Kenneth (ed.). Mathematical Methods in the Social Sciences,1959. Stanford: Stanford University Press. pp. 16–26. doi:10.1016/S0377-2217(03)00413-2.
- ^ Tangian, Andranik (2002). "Constructing a quasi-concave quadratic objective function from interviewing a decision maker". European Journal of Operational Research. 141 (3): 608–640. doi:10.1016/S0377-2217(01)00185-0.
- ^ Tangian, Andranik (2004). "A model for ordinally constructing additive objective functions". European Journal of Operational Research. 159 (2): 476–512. doi:10.1016/S0377-2217(03)00413-2.
- ^ Slovic, P. (1995). "The Construction of Preference". American Psychologist, Vol. 50, No. 5, pp. 364–371.
- ^ Higgins, Richard S. (July 1972). "Satiation in Consumer Preference and the Demand Law". Southern Economic Journal. 39 (1): 116–118. doi:10.2307/1056231. JSTOR 1056231.
- ^ Luce, Duncan. "Semiorders and a Theory of Utility Discrimination" (PDF). Econometrica.















