Jacobi elliptic functions: Difference between revisions
| (641 intermediate revisions by more than 100 users not shown) | |||
| Line 1: | Line 1: | ||
{{Short description|Mathematical function}} |
|||
In [[mathematics]], the '''Jacobi elliptic functions''' are a set of basic [[elliptic function]]s, and auxiliary [[theta function]]s, that are of historical importance. Many of their features show up in important structures and have direct relevance to some applications (e.g. the equation of a [[pendulum]]—also see [[pendulum (mathematics)]]). They also have useful analogies to the functions of [[trigonometry]], as indicated by the matching notation ''sn'' for ''sin''. The Jacobi elliptic functions are used more often in practical problems than the [[Weierstrass elliptic functions]] as they do not require notions of complex analysis to be defined and/or understood. They were introduced by {{harvs|txt|first=Carl Gustav Jakob |last=Jacobi|authorlink=Carl Gustav Jakob Jacobi|year=1829}}. |
|||
In [[mathematics]], the '''Jacobi elliptic functions''' are a set of basic [[elliptic function]]s. They are found in the description of the [[pendulum (mechanics)|motion of a pendulum]], as well as in the design of electronic [[elliptic filter]]s. While [[trigonometry|trigonometric functions]] are defined with reference to a circle, the Jacobi elliptic functions are a generalization which refer to other [[conic section]]s, the ellipse in particular. The relation to trigonometric functions is contained in the notation, for example, by the matching notation <math>\operatorname{sn}</math> for <math>\sin</math>. The Jacobi elliptic functions are used more often in practical problems than the [[Weierstrass elliptic functions]] as they do not require notions of complex analysis to be defined and/or understood. They were introduced by {{harvs|txt|first=Carl Gustav Jakob |last=Jacobi|authorlink=Carl Gustav Jakob Jacobi|year=1829}}. [[Carl Friedrich Gauss]] had already studied special Jacobi elliptic functions in 1797, the [[lemniscate elliptic functions]] in particular,<ref>{{Cite book |last1=Armitage |first1=J. V. |last2=Eberlein| first2=W. F. |title=Elliptic Functions |publisher=Cambridge University Press |year=2006 |edition=First |isbn=978-0-521-78078-0}} p. 48</ref> but his work was published much later. |
|||
== |
==Overview== |
||
[[Image:JacobiFunctionAbstract.png| |
[[Image:JacobiFunctionAbstract.png|322px|thumb|The fundamental rectangle in the complex plane of <math>u</math>]] |
||
There are twelve Jacobian elliptic functions. Each of the twelve corresponds to an arrow drawn from one corner of a rectangle to another. The corners of the rectangle are labeled, by convention, s, c, d and n. The rectangle is understood to be lying on the [[complex plane]], so that s is at the origin, c is at the point ''K'' on the real axis, d is at the point ''K'' + ''iK<nowiki>'</nowiki>'' and n is at point ''iK<nowiki>'</nowiki>'' on the imaginary axis. The numbers ''K'' and ''K' '' are called the [[quarter period]]s. The twelve Jacobian elliptic functions are then pq, where each of p and q is a different one of the letters s, c, d, n. |
|||
There are twelve Jacobi elliptic functions denoted by <math>\operatorname{pq}(u, m)</math>, where <math>\mathrm p</math> and <math>\mathrm q</math> are any of the letters <math>\mathrm c</math>, <math>\mathrm s</math>, <math>\mathrm n</math>, and <math>\mathrm d</math>. (Functions of the form <math>\operatorname{pp}(u,m)</math> are trivially set to unity for notational completeness.) <math>u</math> is the argument, and <math>m</math> is the parameter, both of which may be complex. In fact, the Jacobi elliptic functions are [[meromorphic function|meromorphic]] in both <math>u</math> and <math>m</math>.<ref name="Walker">{{cite journal |last1=Walker |first1=Peter |date=2003 |title=The Analyticity of Jacobian Functions with Respect to the Parameter k |url=https://www.jstor.org/stable/3560143 |bibcode=2003RSPSA.459.2569W |journal=Proceedings of the Royal Society |volume=459 |issue=2038 |pages=2569–2574|doi=10.1098/rspa.2003.1157 |jstor=3560143 |s2cid=121368966 }}</ref> The distribution of the zeros and poles in the <math>u</math>-plane is well-known. However, questions of the distribution of the zeros and poles in the <math>m</math>-plane remain to be investigated.<ref name="Walker"/> |
|||
The Jacobian elliptic functions are then the unique doubly periodic, [[meromorphic]] functions satisfying the following three properties: |
|||
* There is a simple zero at the corner p, and a simple pole at the corner q. |
|||
* The step from p to q is equal to half the period of the function pq ''u''; that is, the function pq ''u'' is periodic in the direction pq, with the period being twice the distance from p to q. The function pq ''u'' is also periodic in the other two directions, with a period such that the distance from p to one of the other corners is a quarter period. |
|||
* If the function pq ''u'' is expanded in terms of ''u'' at one of the corners, the leading term in the expansion has a coefficient of 1. In other words, the leading term of the expansion of pq ''u'' at the corner p is ''u''; the leading term of the expansion at the corner q is 1/''u'', and the leading term of an expansion at the other two corners is 1. |
|||
In the complex plane of the argument <math>u</math>, the twelve functions form a repeating lattice of simple [[Zeros and poles|poles and zeroes]].<ref name="DLMF22">{{cite web|url=http://dlmf.nist.gov/22|title=NIST Digital Library of Mathematical Functions (Release 1.0.17)|editor-last=Olver|editor-first=F. W. J.|display-editors=et al |date=2017-12-22|publisher=National Institute of Standards and Technology|access-date=2018-02-26 }}</ref> Depending on the function, one repeating parallelogram, or unit cell, will have sides of length <math>2K</math> or <math>4K</math> on the real axis, and <math>2K'</math> or <math>4K'</math> on the imaginary axis, where <math>K=K(m)</math> and <math>K'=K(1-m)</math> are known as the [[quarter period]]s with <math>K(\cdot)</math> being the [[elliptic integral]] of the first kind. The nature of the unit cell can be determined by inspecting the "auxiliary rectangle" (generally a parallelogram), which is a rectangle formed by the origin <math>(0,0)</math> at one corner, and <math>(K,K')</math> as the diagonally opposite corner. As in the diagram, the four corners of the auxiliary rectangle are named <math>\mathrm s</math>, <math>\mathrm c</math>, <math>\mathrm d</math>, and <math>\mathrm n</math>, going counter-clockwise from the origin. The function <math>\operatorname{pq}(u,m)</math> will have a zero at the <math>\mathrm p</math> corner and a pole at the <math>\mathrm q</math> corner. The twelve functions correspond to the twelve ways of arranging these poles and zeroes in the corners of the rectangle. |
|||
More generally, there is no need to impose a rectangle; a parallelogram will do. However, if ''K'' and ''iK' '' are kept on the real and imaginary axis respectively, then the Jacobi elliptic functions pq ''u'' will be real functions when ''u'' is real. |
|||
When the argument <math>u</math> and parameter <math>m</math> are real, with <math>0 < m < 1</math>, <math>K</math> and <math>K'</math> will be real and the auxiliary parallelogram will in fact be a rectangle, and the Jacobi elliptic functions will all be real valued on the real line. |
|||
Since the Jacobian elliptic functions are doubly periodic in <math>u</math>, they factor through a [[torus]] – in effect, their domain can be taken to be a torus, just as cosine and sine are in effect defined on a circle. Instead of having only one circle, we now have the product of two circles, one real and the other imaginary. The complex plane can be replaced by a [[complex torus]]. The circumference of the first circle is <math>4K</math> and the second <math>4K'</math>, where <math>K</math> and <math>K'</math> are the [[quarter period]]s. Each function has two zeroes and two poles at opposite positions on the torus. Among the points {{nowrap|<math>0</math>, <math>K</math>, <math>K + iK'</math>, <math>iK'</math>}} there is one zero and one pole. |
|||
The Jacobian elliptic functions are then doubly periodic, meromorphic functions satisfying the following properties: |
|||
* There is a simple zero at the corner <math>\mathrm p</math>, and a simple pole at the corner <math>\mathrm q</math>. |
|||
* The complex number <math>\mathrm p-\mathrm q</math> is equal to half the period of the function <math>\operatorname{pq} u</math>; that is, the function <math>\operatorname{pq} u</math> is periodic in the direction <math>\operatorname{pq}</math>, with the period being <math>2(\mathrm p-\mathrm q)</math>. The function <math>\operatorname{pq} u</math> is also periodic in the other two directions <math>\mathrm{pp}'</math> and <math>\mathrm{pq}'</math>, with periods such that <math>\mathrm p-\mathrm p'</math> and <math>\mathrm p-\mathrm q'</math> are quarter periods. |
|||
{{multiple image |
|||
|align=center |
|||
|footer=Plots of four Jacobi Elliptic Functions in the complex plane of <math>u</math>, illustrating their double periodic behavior. Images generated using a version of the [[domain coloring]] method.<ref>{{Cite web|url=https://github.com/nschloe/cplot|title=cplot, Python package for plotting complex-valued functions|website=[[GitHub]] }}</ref> All have values of <math>k=\sqrt{m}</math> equal to <math>0.8</math>. |
|||
| image1 = Ellipj-sn-08.png |
|||
| alt1=Elliptic Jacobi function <math>\operatorname{sn}</math>, <math>k=0.8</math> |
|||
| caption1=Jacobi elliptic function <math>\operatorname{sn}</math> |
|||
| image2 = Ellipj-cn08.png |
|||
| alt2=Elliptic Jacobi function <math>\operatorname{cn}</math>, <math>k=0.8</math> |
|||
| caption2=Jacobi elliptic function <math>\operatorname{cn}</math> |
|||
| image3 = Ellipj-dn08.png |
|||
| alt3=Elliptic Jacobi function <math>\operatorname{dn}</math>, <math>k=0.8</math> |
|||
| caption3=Jacobi elliptic function <math>\operatorname{dn}</math> |
|||
| image4 = Ellipj-sc08.png |
|||
| alt4=Elliptic Jacobi function <math>\operatorname{sc}</math>, <math>k=0.8</math> |
|||
| caption4=Jacobi elliptic function <math>\operatorname{sc}</math> |
|||
}} |
|||
{{clear}} |
|||
==Notation== |
==Notation== |
||
The elliptic functions can be given in a variety of notations, which can make the subject unnecessarily confusing. Elliptic functions are functions of two variables. The first variable might be given in terms of the '''amplitude''' |
The elliptic functions can be given in a variety of notations, which can make the subject unnecessarily confusing. Elliptic functions are functions of two variables. The first variable might be given in terms of the '''amplitude''' <math>\varphi</math>, or more commonly, in terms of <math>u</math> given below. The second variable might be given in terms of the '''parameter''' <math>m</math>, or as the '''[[elliptic modulus]]''' <math>k</math>, where <math>k^2=m</math>, or in terms of the '''[[modular angle]]''' <math>\alpha</math>, where <math>m=\sin^2\alpha</math>. The complements of <math>k</math> and <math>m</math> are defined as <math>m'=1-m</math> and <math display="inline">k' = \sqrt{m'}</math>. These four terms are used below without comment to simplify various expressions. |
||
The twelve Jacobi elliptic functions are generally written as <math>\operatorname{pq}(u, m)</math> where <math>\mathrm p</math> and <math>\mathrm q</math> are any of the letters <math>\mathrm c</math>, <math>\mathrm s</math>, <math>\mathrm n</math>, and <math>\mathrm d</math>. Functions of the form <math>\operatorname{pp}(u,m)</math> are trivially set to unity for notational completeness. The “major” functions are generally taken to be <math>\operatorname{cn}(u,m)</math>, <math>\operatorname{sn}(u,m)</math> and <math>\operatorname{dn}(u,m)</math> from which all other functions can be derived and expressions are often written solely in terms of these three functions, however, various symmetries and generalizations are often most conveniently expressed using the full set. (This notation is due to [[Christof Gudermann|Gudermann]] and [[James Whitbread Lee Glaisher|Glaisher]] and is not Jacobi's original notation.) |
|||
Throughout this article, <math>\operatorname{pq}(u,t^2)=\operatorname{pq}(u;t)</math>. |
|||
The functions are notationally related to each other by the multiplication rule: (arguments suppressed) |
|||
:<math>\operatorname{pq}\cdot \operatorname{p'q'}= \operatorname{pq'}\cdot \operatorname{p'q}</math> |
|||
from which other commonly used relationships can be derived: |
|||
:<math>\frac{\operatorname{pr}}{\operatorname{qr}}=\operatorname{pq}</math> |
|||
:<math>\operatorname{pr}\cdot \operatorname{rq}=\operatorname{pq}</math> |
|||
:<math>\frac{1}{\operatorname{qp}}=\operatorname{pq}</math> |
|||
The multiplication rule follows immediately from the identification of the elliptic functions with the [[Neville theta function]]s<ref name="Neville1944">{{cite book |last=Neville |first=Eric Harold |date=1944 |title=Jacobian Elliptic Functions |url=https://archive.org/details/jacobianelliptic00neviuoft |location=Oxford |publisher=Oxford University Press |author-link=Eric Harold Neville}}</ref> |
|||
:<math>\operatorname{pq}(u,m)=\frac{\theta_\operatorname{p}(u,m)}{\theta_\operatorname{q}(u,m)}</math> |
|||
Also note that: |
|||
: <math>K(m)=K(k^2)=\int_0^1\frac{dt}{\sqrt{(1-t^2)(1-mt^2)}}=\int_0^1\frac{dt}{\sqrt{(1-t^2)(1-k^2t^2)}}. </math> |
|||
=={{anchor|sn|cn|dn|am}}Definition in terms of inverses of elliptic integrals== |
|||
[[File:Modell der elliptischen Funktion φ=am (u, k) durch eine Fläche -Schilling V, 1 - 317-.jpg|thumb|Model of the Jacobi amplitude (measured along vertical axis) as a function of independent variables ''u'' and the modulus ''k'']] |
|||
There is a definition, relating the elliptic functions to the inverse of the [[Elliptic integral#Incomplete elliptic integral of the first kind|incomplete elliptic integral of the first kind]] <math>F</math>. These functions take the parameters <math>u</math> and <math>m</math> as inputs. The <math>\varphi</math> that satisfies |
|||
:<math>u=F(\varphi,m)=\int_0^\varphi \frac{\mathrm d\theta} {\sqrt {1-m \sin^2 \theta}}</math> |
|||
is called the '''Jacobi amplitude''': |
|||
:<math>\operatorname{am}(u,m)=\varphi.</math> |
|||
In this framework, the ''elliptic sine'' sn ''u'' (Latin: ''sinus amplitudinis'') is given by |
|||
:<math>\operatorname {sn} (u,m) = \sin \operatorname{am}(u,m)</math> |
|||
and the ''elliptic cosine'' cn ''u'' (Latin: ''cosinus amplitudinis'') is given by |
|||
:<math>\operatorname {cn} (u,m) = \cos \operatorname{am}(u,m)</math> |
|||
and the ''delta amplitude'' dn ''u'' (Latin: ''delta amplitudinis'')<ref group="note">If <math>u\in\mathbb{R}</math> and <math>m</math> is restricted to <math>[0,1]</math>, then <math>\operatorname{dn}(u,m)</math> can be also written as <math>\sqrt {1-m\sin^2 \operatorname{am}(u,m)}.</math></ref> |
|||
==Definition as inverses of elliptic integrals== |
|||
[[File:sn-k-08.png|right|thumb|300px|Elliptic Jacobi function, sn, corresponding to k=0.8, generated using a version of the [[Domain coloring]] method.<ref>http://nbviewer.ipython.org/github/empet/Math/blob/master/DomainColoring.ipynb</ref>]] |
|||
:<math>\operatorname {dn} (u,m) = \frac{\mathrm d}{\mathrm du}\operatorname{am}(u,m).</math> |
|||
The above definition, in terms of the unique meromorphic functions satisfying certain properties, is quite abstract. There is a simpler, but completely equivalent definition, giving the elliptic functions as inverses of the incomplete [[elliptic integral]] of the first kind. Let |
|||
In the above, the value <math>m</math> is a free parameter, usually taken to be real such that <math>0\leq m \leq 1</math> (but can be complex in general), and so the elliptic functions can be thought of as being given by two variables, <math>u</math> and the parameter <math>m</math>. The remaining nine elliptic functions are easily built from the above three (<math>\operatorname{sn}</math>, <math>\operatorname{cn}</math>, <math>\operatorname{dn}</math>), and are given in a section below. Note that when <math>\varphi=\pi/2</math>, that <math>u</math> then equals the [[quarter period]] <math>K</math>. |
|||
In the most general setting, <math>\operatorname{am}(u,m)</math> is a [[multivalued function]] (in <math>u</math>) with infinitely many [[Branch point|logarithmic branch points]] (the branches differ by integer multiples of <math>2\pi</math>), namely the points <math>2sK(m)+(4t+1)K(1-m)i</math> and <math>2sK(m)+(4t+3)K(1-m)i</math> where <math>s,t\in\mathbb{Z}</math>.<ref name="sala">{{cite journal |last=Sala |first=Kenneth L. |date=November 1989 |title=Transformations of the Jacobian Amplitude Function and Its Calculation via the Arithmetic-Geometric Mean|url=https://epubs.siam.org/doi/abs/10.1137/0520100 |journal=SIAM Journal on Mathematical Analysis|volume=20|issue=6|pages=1514–1528|doi=10.1137/0520100 }}</ref> This multivalued function can be made single-valued by cutting the complex plane along the line segments joining these branch points (the cutting can be done in non-equivalent ways, giving non-equivalent single-valued functions), thus making <math>\operatorname{am}(u,m)</math> [[Analytic function|analytic]] everywhere except on the [[Branch point#Branch cuts|branch cuts]]. In contrast, <math>\sin\operatorname{am}(u,m)</math> and other elliptic functions have no branch points, give consistent values for every branch of <math>\operatorname{am}</math>, and are [[meromorphic function|meromorphic]] in the whole complex plane. Since every elliptic function is meromorphic in the whole complex plane (by definition), <math>\operatorname{am}(u,m)</math> (when considered as a single-valued function) is not an elliptic function. |
|||
:<math>u=\int_0^\phi \frac{\mathrm d\theta} {\sqrt {1-m \sin^2 \theta}}\, . </math> |
|||
However, a particular cutting for <math>\operatorname{am}(u,m)</math> can be made in the <math>u</math>-plane by line segments from <math>2sK(m)+(4t+1)K (1-m)i</math> to <math>2sK(m)+(4t+3)K(1-m)i</math> with <math>s,t\in\mathbb{Z}</math>; then it only remains to define <math>\operatorname{am}(u,m)</math> at the branch cuts by continuity from some direction. Then <math>\operatorname{am}(u,m)</math> becomes single-valued and singly-periodic in <math>u</math> with the minimal period <math>4iK(1-m)</math> and it has singularities at the logarithmic branch points mentioned above. If <math>m\in\mathbb{R}</math> and <math>m\le 1</math>, <math>\operatorname{am}(u,m)</math> is continuous in <math>u</math> on the real line. When <math>m>1</math>, the branch cuts of <math>\operatorname{am}(u,m)</math> in the <math>u</math>-plane cross the real line at <math>2(2s+1)K(1/m)/\sqrt{m}</math> for <math>s\in\mathbb{Z}</math>; therefore for <math>m>1</math>, <math>\operatorname{am}(u,m)</math> is not continuous in <math>u</math> on the real line and jumps by <math>2\pi</math> on the discontinuities. |
|||
Then the elliptic function sn ''u'' is given by |
|||
But defining <math>\operatorname{am}(u,m)</math> this way gives rise to very complicated branch cuts in the <math>m</math>-plane (''not'' the <math>u</math>-plane); they have not been fully described as of yet. |
|||
:<math>\operatorname {sn}\; u = \sin \phi\,</math> |
|||
Let |
|||
and cn ''u'' is given by |
|||
:<math>E(\varphi,m)=\int_0^{\varphi}\sqrt{1-m\sin^2\theta}\,\mathrm d\theta</math> |
|||
be the [[Elliptic integral#Incomplete elliptic integral of the second kind|incomplete elliptic integral of the second kind]] with parameter <math>m</math>. |
|||
Then the '''Jacobi epsilon''' function can be defined as |
|||
:<math>\operatorname {cn}\; u = \cos \phi</math> |
|||
:<math>\mathcal{E}(u,m)=E(\operatorname{am}(u,m),m)</math> |
|||
for <math>u\in\mathbb{R}</math> and <math>0<m<1</math> and by [[analytic continuation]] in each of the variables otherwise: the Jacobi epsilon function is meromorphic in the whole complex plane (in both <math>u</math> and <math>m</math>). Alternatively, throughout both the <math>u</math>-plane and <math>m</math>-plane,<ref>{{dlmf|first1=W. P.|last1=Reinhardt|first2=P. L.|last2=Walker|id=22.16.E17|title=Jacobian Elliptic Functions}}</ref> |
|||
:<math>\mathcal{E} (u,m)=\int_0^u \operatorname{dn}^2(t,m)\, \mathrm dt;</math> |
|||
<math>\mathcal{E}</math> is well-defined in this way because all [[Residue (complex analysis)|residues]] of <math>t\mapsto\operatorname{dn}(t,m)^2</math> are zero, so the integral is path-independent. So the Jacobi epsilon relates the incomplete elliptic integral of the first kind to the incomplete elliptic integral of the second kind: |
|||
:<math>E(\varphi,m)=\mathcal{E}(F(\varphi,m),m).</math> |
|||
The Jacobi epsilon function is not an elliptic function, but it appears when differentiating the Jacobi elliptic functions with respect to the parameter. |
|||
The '''Jacobi zn''' function is defined by |
|||
and |
|||
:<math>\operatorname{zn}(u,m)=\mathcal{E}(u,m)-\frac{E(m)}{K(m)}u.</math> |
|||
It is a singly periodic function which is meromorphic in <math>u</math>, but not in <math>m</math> (due to the branch cuts of <math>E</math> and <math>K</math>). Its minimal period in <math>u</math> is <math>2K(m)</math>. It is related to the [[Elliptic integrals#Jacobi zeta function|Jacobi zeta function]] by <math>Z(\varphi,m)=\operatorname{zn}(F(\varphi,m),m).</math> |
|||
Historically, the Jacobi elliptic functions were first defined by using the amplitude. In more modern texts on elliptic functions, the Jacobi elliptic functions are defined by other means, for example by ratios of theta functions (see below), and the amplitude is ignored. |
|||
:<math>\operatorname {dn}\; u = \sqrt {1-m\sin^2 \phi}\, .</math> |
|||
[[File:Modell der elliptischen Funktion φ=am (u, k) durch eine Fläche -Schilling V, 1 - 317-.jpg|thumb|Model of amplitude (measured along vertical axis) as a function of independent variables ''u'' and ''k'']] |
|||
Here, the angle <math>\phi</math> is called the '''amplitude'''. On occasion, dn ''u'' = Δ(''u'') is called the '''delta amplitude'''. In the above, the value ''m'' is a free parameter, usually taken to be real, 0 ≤ ''m'' ≤ 1, and so the elliptic functions can be thought of as being given by two variables, the amplitude <math>\phi</math> and the parameter ''m''. |
|||
In modern terms, the relation to elliptic integrals would be expressed by <math>\operatorname{sn}(F(\varphi,m),m)=\sin\varphi</math> (or <math>\operatorname{cn}(F(\varphi,m),m)=\cos\varphi</math>) instead of <math>\operatorname{am}(F(\varphi,m),m)=\varphi</math>. |
|||
The remaining nine elliptic functions are easily built from the above three, and are given in a section below. |
|||
==Definition as trigonometry: the Jacobi ellipse== |
|||
Note that when <math>\phi=\pi/2</math>, that ''u'' then equals the [[quarter period]] ''K''. |
|||
[[File:Jacobi Elliptic Functions (on Jacobi Ellipse).svg|right|thumb|upright=1.5|Plot of the Jacobi ellipse (''x''<sup>2</sup> + ''y''<sup>2</sup>/''b''<sup>2</sup> = 1, ''b'' real) and the twelve Jacobi elliptic functions ''pq''(''u'',''m'') for particular values of angle ''φ'' and parameter ''b''. The solid curve is the ellipse, with ''m'' = 1 − 1/''b''<sup>2</sup> and ''u'' = ''F''(''φ'',''m'') where ''F''(⋅,⋅) is the [[elliptic integral]] of the first kind (with parameter <math>m=k^2</math>). The dotted curve is the unit circle. Tangent lines from the circle and ellipse at ''x'' = cd crossing the ''x''-axis at dc are shown in light grey.]] |
|||
<math> \cos \varphi, \sin \varphi </math> are defined on the unit circle, with radius ''r'' = 1 and angle <math>\varphi =</math> arc length of the unit circle measured from the positive ''x''-axis. Similarly, Jacobi elliptic functions are defined on the unit ellipse,{{citation needed|reason= see talk of this section.|date=July 2016}} with ''a'' = 1. Let |
|||
==Definition as trigonometry== |
|||
<math> \cos \theta, \sin \theta </math> are defined on the unit circle, with ''r'' = 1. Similarly, Jacobi elliptic functions |
|||
are defined on the unit ellipse, with ''a'' = 1. Let |
|||
:<math> |
:<math> |
||
\begin{align} |
\begin{align} |
||
& x^2 + \frac{y^2}{b^2} = 1, \\ |
& x^2 + \frac{y^2}{b^2} = 1, \quad b > 1, \\ |
||
& m = 1 - \frac |
& m = 1 - \frac{1}{b^2}, \quad 0 < m < 1, \\ |
||
& x = r \cos \ |
& x = r \cos \varphi, \quad y = r \sin \varphi |
||
\end{align} |
\end{align} |
||
</math> |
</math> |
||
then: |
then: |
||
:<math> r( \ |
:<math> r( \varphi,m) = \frac{1} {\sqrt {1-m \sin^2 \varphi}}\, . </math> |
||
For each angle <math>\varphi</math> the parameter |
|||
Replace radians on the unit circle by ''u'' on the unit ellipse, where: |
|||
:<math>u = u(\varphi,m)=\int_0^\varphi r(\theta,m) \, d\theta</math> |
|||
(the incomplete elliptic integral of the first kind) is computed. |
|||
On the unit circle (<math>a=b=1</math>), <math>u</math> would be an arc length. |
|||
However, the relation of <math>u</math> to the [[Ellipse#Arc length|arc length of an ellipse]] is more complicated.<ref>{{dlmf|first=B. C.|last=Carlson|id=19.8.E13|title=Elliptic Integrals}}</ref> |
|||
Let <math>P=(x,y)=(r \cos\varphi, r\sin\varphi)</math> be a point on the ellipse, and let <math>P'=(x',y')=(\cos\varphi,\sin\varphi)</math> be the point where the unit circle intersects the line between <math>P</math> and the origin <math>O</math>. |
|||
:<math> \cos \varphi= x , </math> |
|||
Then the familiar relations from the unit circle: |
|||
:<math>u = u(\varphi,m)=\int_0^\varphi r(\theta,m) \, d\theta </math> |
|||
:<math> x' = \cos \varphi, \quad y' = \sin \varphi</math> |
|||
read for the ellipse: |
|||
:<math>x' = \operatorname{cn}(u,m),\quad y' = \operatorname{sn}(u,m).</math> |
|||
So the projections of the intersection point <math>P'</math> of the line <math>OP</math> with the unit circle on the ''x''- and ''y''-axes are simply <math>\operatorname{cn}(u,m)</math> and <math>\operatorname{sn}(u,m)</math>. These projections may be interpreted as 'definition as trigonometry'. In short: |
|||
:<math> \operatorname{cn}(u,m) = \frac{x}{r(\varphi,m)}, \quad \operatorname{sn}(u,m) = \frac{y}{r(\varphi,m)}, \quad \operatorname{dn}(u,m) = \frac{1}{r(\varphi,m)}. </math> |
|||
then: |
|||
For the <math>x</math> and <math>y</math> value of the point <math>P</math> with |
|||
:<math>\operatorname{cn}(u,m)=x,\quad \operatorname{sn}(u,m) = \frac y b,\quad \operatorname{dn}(u,m) = \frac 1 {r(\varphi,m)} . </math> |
|||
<math>u</math> and parameter <math>m</math> we get, after inserting the relation: |
|||
:<math>r(\varphi,m) = \frac 1 {\operatorname{dn}(u,m)} </math> |
|||
into: <math>x = r(\varphi,m) \cos (\varphi), y = r(\varphi,m) \sin (\varphi)</math> that: |
|||
:<math> x = \frac{\operatorname{cn}(u,m)} {\operatorname{dn}(u,m)},\quad y = \frac{\operatorname{sn}(u,m)} {\operatorname{dn}(u,m)}.</math> |
|||
The latter relations for the ''x''- and ''y''-coordinates of points on the unit ellipse may be considered as generalization of the relations <math> x = \cos \varphi, y = \sin \varphi</math> for the coordinates of points on the unit circle. |
|||
The following table summarizes the expressions for all Jacobi elliptic functions pq(u,m) in the variables (''x'',''y'',''r'') and (''φ'',dn) with <math display="inline">r = \sqrt{x^2+y^2}</math> |
|||
==Definition in terms of theta functions== |
|||
{| class="wikitable" style="text-align:center" |
|||
|+ Jacobi elliptic functions pq[''u'',''m''] as functions of {''x'',''y'',''r''} and {''φ'',dn} |
|||
!colspan="2" rowspan="2"| |
|||
!colspan="4"|q |
|||
|- |
|||
! c |
|||
! s |
|||
! n |
|||
! d |
|||
|- |
|||
!rowspan="6"|p |
|||
|- |
|||
! c |
|||
|1 || <math>x/y=\cot(\varphi)</math> || <math>x/r=\cos(\varphi)</math> || <math>x=\cos(\varphi)/\operatorname{dn}</math> |
|||
|- |
|||
! s |
|||
|<math>y/x=\tan(\varphi)</math> || 1 ||<math>y/r=\sin(\varphi)</math> || <math>y=\sin(\varphi)/\operatorname{dn}</math> |
|||
|- |
|||
! n |
|||
|<math>r/x=\sec(\varphi)</math> || <math>r/y=\csc(\varphi)</math> || 1 || <math>r=1/\operatorname{dn}</math> |
|||
|- |
|||
! d |
|||
| <math>1/x=\sec(\varphi)\operatorname{dn}</math> || <math>1/y=\csc(\varphi)\operatorname{dn}</math> || <math>1/r=\operatorname{dn} </math> || 1 |
|||
|} |
|||
==Definition in terms of the Jacobi theta functions== |
|||
Equivalently, Jacobi elliptic functions can be defined in terms of his [[theta function]]s. If we abbreviate <math>\vartheta(0;\tau)</math> as <math>\vartheta</math>, and <math>\vartheta_{01}(0;\tau), \vartheta_{10}(0;\tau), \vartheta_{11}(0;\tau)</math> respectively as <math>\vartheta_{01}, \vartheta_{10}, \vartheta_{11}</math> (the ''theta constants'') then the [[elliptic modulus]] ''k'' is <math>k=\left({\vartheta_{10} \over \vartheta}\right)^2</math>. If we set <math>u = \pi \vartheta^2 z</math>, we have |
|||
===Using elliptic integrals=== |
|||
[[File:cn-k-08.png|right|thumb|300px|Elliptic Jacobi function, cn, k=0.8]] |
|||
Equivalently, Jacobi's elliptic functions can be defined in terms of the [[theta function]]s.<ref>{{cite book |last1=Whittaker |first1=Edmund Taylor |authorlink1=Edmund T. Whittaker |last2=Watson |first2=George Neville |authorlink2=George N. Watson |date= 1927 |page=492 |edition=4th |title=A Course of Modern Analysis |title-link=A Course of Modern Analysis |publisher= Cambridge University Press}}</ref> With <math>z,\tau\in\mathbb{C}</math> such that <math>\operatorname{Im}\tau >0</math>, let |
|||
[[File:dn-k-08.png|right|thumb|300px|Elliptic Jacobi function, dn, k=0.8]] |
|||
:<math>\mbox{sn}(u; k) = -{\vartheta \vartheta_{11}(z;\tau) \over \vartheta_{10} \vartheta_{01}(z;\tau)}</math> |
|||
:<math>\theta_1(z|\tau)=\displaystyle\sum_{n=-\infty}^\infty (-1)^{n-\frac12}e^{(2n+1)iz+\pi i\tau\left(n+\frac12\right)^2},</math> |
|||
<!-- extra blank line between two lines of "displayed" [[TeX]], for legibility --> |
|||
:<math>\theta_2(z|\tau)=\displaystyle\sum_{n=-\infty}^\infty e^{(2n+1)iz+\pi i\tau \left(n+\frac12\right)^2},</math> |
|||
:<math>\theta_3(z|\tau)=\displaystyle\sum_{n=-\infty}^\infty e^{2niz+\pi i\tau n^2},</math> |
|||
:<math>\theta_4(z|\tau)=\displaystyle\sum_{n=-\infty}^\infty (-1)^n e^{2niz+\pi i\tau n^2}</math> |
|||
and <math>\theta_2(\tau)=\theta_2(0|\tau)</math>, <math>\theta_3(\tau)=\theta_3(0|\tau)</math>, <math>\theta_4(\tau)=\theta_4(0|\tau)</math>. Then with <math>K=K(m)</math>, <math>K'=K(1-m)</math>, <math>\zeta=\pi u/(2K)</math> and <math>\tau=iK'/K</math>, |
|||
:<math>\ |
:<math>\begin{align}\operatorname{sn}(u,m)&=\frac{\theta_3(\tau)\theta_1(\zeta|\tau)}{\theta_2(\tau)\theta_4(\zeta|\tau)},\\ |
||
\operatorname{cn}(u,m)&=\frac{\theta_4(\tau)\theta_2(\zeta|\tau)}{\theta_2(\tau)\theta_4(\zeta|\tau)},\\ |
|||
\operatorname{dn}(u,m)&=\frac{\theta_4(\tau)\theta_3(\zeta|\tau)}{\theta_3(\tau)\theta_4(\zeta|\tau)}.\end{align}</math> |
|||
The Jacobi zn function can be expressed by theta functions as well: |
|||
<!-- extra blank line between two lines of "displayed" [[TeX]], for legibility --> |
|||
:<math>\begin{align}\operatorname{zn}(u,m)&=\frac{\pi}{2K}\frac{\theta_{4}'(\zeta|\tau)}{\theta_{4}(\zeta|\tau)}\\ &=\frac{\pi}{2K}\frac{\theta_{3}'(\zeta|\tau)}{\theta_{3}(\zeta|\tau)}+m\frac{\operatorname{sn}(u,m)\operatorname{cn}(u,m)}{\operatorname{dn}(u,m)}\\ |
|||
&=\frac{\pi}{2K}\frac{\theta_{2}'(\zeta|\tau)}{\theta_{2}(\zeta|\tau)}+\frac{\operatorname{dn}(u,m)\operatorname{sn}(u,m)}{\operatorname{cn}(u,m)}\\ |
|||
&=\frac{\pi}{2K}\frac{\theta_{1}'(\zeta|\tau)}{\theta_{1}(\zeta|\tau)}-\frac{\operatorname{cn}(u,m)\operatorname{dn}(u,m)}{\operatorname{sn}(u,m)}\end{align}</math> |
|||
where <math>'</math> denotes the partial derivative with respect to the first variable. |
|||
===Using modular inversion=== |
|||
:<math>\mbox{dn}(u; k) = {\vartheta_{01} \vartheta(z;\tau) \over \vartheta \vartheta_{01}(z;\tau)}</math> |
|||
In fact, the definition of the Jacobi elliptic functions in Whittaker & Watson is stated a little bit differently than the one given above (but it's equivalent to it) and relies on modular inversion: [[Modular lambda function|The function]] <math>\lambda</math>, defined by |
|||
[[File:The region F1 for modular inversion.jpg|thumb|The region <math>F_1</math> in the complex plane. It is bounded by two semicircles from below, by a ray from the left and by a ray from the right.]] |
|||
:<math>\lambda (\tau)=\frac{\theta_2(\tau)^4}{\theta_3(\tau)^4},</math> |
|||
assumes every value in <math>\mathbb{C}-\{0,1\}</math> ''once and only once''<ref>{{cite journal |last=Cox |first=David Archibald |authorlink1=David A. Cox |date=January 1984 |title=The Arithmetic-Geometric Mean of Gauss|url=https://www.researchgate.net/publication/248675540 |journal=L'Enseignement Mathématique|volume=30|issue=2|pages=290}}</ref> in |
|||
:<math>F_1-(\partial F_1\cap\{\tau\in\mathbb{H}:\operatorname{Re}\tau <0\})</math> |
|||
where <math>\mathbb{H}</math> is the upper half-plane in the complex plane, <math>\partial F_1</math> is the boundary of <math>F_1</math> and |
|||
:<math>F_1=\{\tau\in\mathbb{H}:\left|\operatorname{Re}\tau\right|\le 1,\left|\operatorname{Re}(1/\tau)\right|\le 1\}.</math> |
|||
In this way, each <math>m\,\overset{\text{def}}{=}\,\lambda (\tau)\in\mathbb{C}-\{0,1\}</math> can be associated with ''one and only one'' <math>\tau</math>. Then Whittaker & Watson define the Jacobi elliptic functions by |
|||
:<math>\begin{align}\operatorname{sn}(u,m)&=\frac{\theta_3(\tau)\theta_1(\zeta |\tau)}{\theta_2(\tau)\theta_4(\zeta|\tau)},\\ |
|||
\operatorname{cn}(u,m)&=\frac{\theta_4(\tau)\theta_2(\zeta |\tau)}{\theta_2(\tau)\theta_4(\zeta|\tau)},\\ |
|||
\operatorname{dn}(u,m)&=\frac{\theta_4(\tau)\theta_3(\zeta |\tau)}{\theta_3(\tau)\theta_4(\zeta|\tau)}\end{align}</math> |
|||
where <math>\zeta=u/\theta_3(\tau)^2</math>. |
|||
In the book, they place an additional restriction on <math>m</math> (that <math>m\notin (-\infty,0)\cup (1,\infty)</math>), but it is in fact not a necessary restriction (see the Cox reference). Also, if <math>m=0</math> or <math>m=1</math>, the Jacobi elliptic functions degenerate to non-elliptic functions which is described below. |
|||
==Definition in terms of Neville theta functions== |
|||
Since the Jacobi functions are defined in terms of the elliptic modulus ''k''(τ), we need to invert this and find τ in terms of ''k''. We start from <math>k' = \sqrt{1-k^2}</math>, the ''complementary modulus''. As a function of τ it is |
|||
The Jacobi elliptic functions can be defined very simply using the [[Neville theta functions]]:<ref name="WolframJE"/> |
|||
:<math>k'(\tau) = \left({\vartheta_{01} \over \vartheta}\right)^2.</math> |
|||
:<math>\operatorname{pq}(u,m)=\frac{\theta_\operatorname{p}(u,m)}{\theta_\operatorname{q}(u,m)}</math> |
|||
Let us first define |
|||
Simplifications of complicated products of the Jacobi elliptic functions are often made easier using these identities. |
|||
:<math>\ell = {1 \over 2} {1-\sqrt{k'} \over 1+\sqrt{k'}} = |
|||
{1 \over 2} {\vartheta - \vartheta_{01} \over \vartheta + \vartheta_{01}}.</math> |
|||
== Jacobi transformations== |
|||
Then define the [[nome (mathematics)|nome]] ''q'' as <math>q = \exp (\pi i \tau)</math> and expand <math>\ell</math> as a [[power series]] in the nome ''q'', we obtain |
|||
===The Jacobi imaginary transformations=== |
|||
:<math>\ell = {q + q^9 + q^{25} + \cdots \over 1 + 2q^4 + 2q^{16} + \cdots}.</math> |
|||
[[File:JacobiElliptic.HT.svg|right|thumb|upright=1.5|Plot of the degenerate Jacobi curve (''x''<sup>2</sup> + ''y''<sup>2</sup>/''b''<sup>2</sup> = 1, ''b'' = ∞) and the twelve Jacobi Elliptic functions pq(''u'',1) for a particular value of angle ''φ''. The solid curve is the degenerate ellipse (''x''<sup>2</sup> = 1) with ''m'' = 1 and ''u'' = ''F''(''φ'',1) where ''F''(⋅,⋅) is the [[elliptic integral]] of the first kind. The dotted curve is the unit circle. Since these are the Jacobi functions for ''m'' = 0 (circular trigonometric functions) but with imaginary arguments, they correspond to the six hyperbolic trigonometric functions.]] |
|||
[[Reversion of series]] now gives |
|||
The Jacobi imaginary transformations relate various functions of the imaginary variable ''i u'' or, equivalently, relations between various values of the ''m'' parameter. In terms of the major functions:<ref name="W&W">{{cite book |last1=Whittaker |first1=E.T. |last2=Watson |first2=G.N.|date=1940 |title=A Course in Modern Analysis |url=https://archive.org/details/courseofmodernan00whit |location=New York, USA |publisher=The MacMillan Co.|isbn=978-0-521-58807-2|author-link=A Course of Modern Analysis}}</ref>{{rp|506}} |
|||
:<math>q = \ell + 2\ell^5 + 15\ell^9 + 150\ell^{13} + 1707\ell^{17} + 20910\ell^{21} + 268616\ell^{25} + \cdots.</math> |
|||
:<math>\operatorname{cn}(u, m)= \operatorname{nc}(i\,u,1\!-\!m)</math> |
|||
Since we may reduce to the case where the imaginary part of τ is greater than or equal to 1/2 sqrt(3), we can assume the absolute value of ''q'' is less than or equal to exp(-1/2 sqrt(3) π) ~ 0.0658; for values this small the above series converges very rapidly and easily allows us to find the appropriate value for ''q''. |
|||
:<math>\operatorname{sn}(u, m)= -i \operatorname{sc}(i\,u,1\!-\!m)</math> |
|||
:<math>\operatorname{dn}(u, m)= \operatorname{dc}(i\,u,1\!-\!m)</math> |
|||
Using the multiplication rule, all other functions may be expressed in terms of the above three. The transformations may be generally written as <math>\operatorname{pq}(u,m)=\gamma_{\operatorname{pq}} \operatorname{pq}'(i\,u,1\!-\!m)</math>. The following table gives the <math>\gamma_{\operatorname{pq}} \operatorname{pq}'(i\,u,1\!-\!m)</math> for the specified pq(''u,m'').<ref name="WolframJE">{{cite web |url=http://functions.wolfram.com/EllipticFunctions/JacobiAmplitude/introductions/JacobiPQs/ShowAll.html |title=Introduction to the Jacobi elliptic functions |date=2018 |website=The Wolfram Functions Site |publisher=Wolfram Research, Inc. |access-date=January 7, 2018}}</ref> (The arguments <math>(i\,u,1\!-\!m)</math> are suppressed) |
|||
==Minor functions== |
|||
:{| class="wikitable" style="text-align:center" |
|||
|+ Jacobi Imaginary transformations <math>\gamma_{\operatorname{pq}}\operatorname{pq}'(i\,u,1\!-\!m)</math> |
|||
!colspan="2" rowspan="2"| |
|||
!colspan="4"|q |
|||
|- |
|||
! c |
|||
! s |
|||
! n |
|||
! d |
|||
|- |
|||
!rowspan="6"|p |
|||
|- |
|||
! c |
|||
| 1 || i ns || nc || nd |
|||
|- |
|||
! s |
|||
| −''i'' sn || 1 || −''i'' sc || −''i'' sd |
|||
|- |
|||
! n |
|||
| cn || ''i'' cs || 1 || cd |
|||
|- |
|||
! d |
|||
| dn || ''i'' ds || dc || 1 |
|||
|} |
|||
Since the [[Hyperbolic functions|hyperbolic trigonometric functions]] are proportional to the circular trigonometric functions with imaginary arguments, it follows that the Jacobi functions will yield the hyperbolic functions for m=1.<ref name="Neville1944"/>{{rp|249}} In the figure, the Jacobi curve has degenerated to two vertical lines at ''x'' = 1 and ''x'' = −1. |
|||
Reversing the order of the two letters of the function name results in |
|||
the reciprocals of the three functions above: |
|||
=== The Jacobi real transformations === |
|||
The Jacobi real transformations<ref name="Neville1944"/>{{rp|308}} yield expressions for the elliptic functions in terms with alternate values of ''m''. The transformations may be generally written as <math>\operatorname{pq}(u,m)=\gamma_{\operatorname{pq}} \operatorname{pq}'(k\,u,1/m)</math>. The following table gives the <math>\gamma_{\operatorname{pq}} \operatorname{pq}'(k\,u,1/m)</math> for the specified pq(''u,m'').<ref name="WolframJE"/> (The arguments <math>(k\,u,1/m)</math> are suppressed) |
|||
:{| class="wikitable" style="text-align:center" |
|||
|+ Jacobi real transformations <math>\gamma_{\operatorname{pq}}\operatorname{pq}'(k\,u,1/m)</math> |
|||
!colspan="2" rowspan="2"| |
|||
!colspan="4"|q |
|||
|- |
|||
! c |
|||
! s |
|||
! n |
|||
! d |
|||
|- |
|||
!rowspan="6"|p |
|||
|- |
|||
! c |
|||
| <math>1 </math> ||<math>k\operatorname{ds} </math> || <math> \operatorname{dn} </math> || <math> \operatorname{dc} </math> |
|||
|- |
|||
! s |
|||
|<math>\frac 1 k \operatorname{sd} </math> || <math>1</math> || <math>\frac 1 k \operatorname{sn} </math> || <math>\frac 1 k \operatorname{sc} </math> |
|||
|- |
|||
! n |
|||
| <math> \operatorname{nd} </math> || <math>k \operatorname{ns} </math> || <math>1</math> || <math> \operatorname{nc} </math> |
|||
|- |
|||
! d |
|||
| <math> \operatorname{cd} </math> || <math>k \operatorname{cs} </math> || <math> \operatorname{cn} </math> || <math> 1 </math> |
|||
|} |
|||
=== Other Jacobi transformations === |
|||
Jacobi's real and imaginary transformations can be combined in various ways to yield three more simple transformations |
|||
.<ref name="Neville1944"/>{{rp|214}} The real and imaginary transformations are two transformations in a group ([[Dihedral group of order 6|D<sub>3</sub>]] or [[anharmonic group]]) of six transformations. If |
|||
:<math>\mu_R(m) = 1/m</math> |
|||
is the transformation for the ''m'' parameter in the real transformation, and |
|||
:<math>\mu_I(m) = 1-m = m'</math> |
|||
is the transformation of ''m'' in the imaginary transformation, then the other transformations can be built up by successive application of these two basic transformations, yielding only three more possibilities: |
|||
:<math> |
:<math> |
||
\begin{align} |
\begin{align} |
||
\mu_{IR}(m)&=&\mu_I(\mu_R(m))&=&-m'/m \\ |
|||
\operatorname{ns}(u) & = \frac{1}{\operatorname{sn}(u)} \\[8pt] |
|||
\mu_{RI}(m)&=&\mu_R(\mu_I(m))&=&1/m' \\ |
|||
\operatorname{nc}(u) & = \frac{1}{\operatorname{cn}(u)} \\[8pt] |
|||
\mu_{RIR}(m)&=&\mu_R(\mu_I(\mu_R(m)))&=&-m/m' |
|||
\operatorname{nd}(u) & = \frac{1}{\operatorname{dn}(u)} |
|||
\end{align} |
\end{align} |
||
</math> |
|||
These five transformations, along with the identity transformation (''μ''<sub>''U''</sub>(''m'') = ''m'') yield the six-element group. With regard to the Jacobi elliptic functions, the general transformation can be expressed using just three functions: |
|||
:<math>\operatorname{cs}(u,m)=\gamma_i \operatorname{cs'}(\gamma_i u, \mu_i(m))</math> |
|||
:<math>\operatorname{ns}(u,m)=\gamma_i \operatorname{ns'}(\gamma_i u, \mu_i(m))</math> |
|||
:<math>\operatorname{ds}(u,m)=\gamma_i \operatorname{ds'}(\gamma_i u, \mu_i(m))</math> |
|||
where ''i'' = U, I, IR, R, RI, or RIR, identifying the transformation, γ<sub>i</sub> is a multiplication factor common to these three functions, and the prime indicates the transformed function. The other nine transformed functions can be built up from the above three. The reason the cs, ns, ds functions were chosen to represent the transformation is that the other functions will be ratios of these three (except for their inverses) and the multiplication factors will cancel. |
|||
The following table lists the multiplication factors for the three ps functions, the transformed ''m''{{'}}s, and the transformed function names for each of the six transformations.<ref name="Neville1944"/>{{rp|214}} (As usual, ''k''<sup>2</sup> = ''m'', 1 − ''k''<sup>2</sup> = ''k''<sub>1</sub><sup>2</sup> = ''m''′ and the arguments (<math>\gamma_i u, \mu_i(m)</math>) are suppressed) |
|||
:{| class="wikitable" style="text-align:center" |
|||
|+ Parameters for the six transformations |
|||
!Transformation i||<math>\gamma_i</math>||<math>\mu_i(m)</math>||cs'||ns'||ds' |
|||
|- |
|||
! U |
|||
| 1 || m || cs || ns || ds |
|||
|- |
|||
! I |
|||
| i || m' || ns || cs || ds |
|||
|- |
|||
! IR |
|||
| i k || −m'/m || ds || cs || ns |
|||
|- |
|||
! R |
|||
| k || 1/m || ds || ns || cs |
|||
|- |
|||
! RI |
|||
|i k<sub>1</sub>|| 1/m' || ns || ds || cs |
|||
|- |
|||
! RIR |
|||
| k<sub>1</sub> || −m/m' || cs || ds || ns |
|||
|- |
|||
|} |
|||
Thus, for example, we may build the following table for the RIR transformation.<ref name="WolframJE"/> The transformation is generally written <math>\operatorname{pq}(u,m)=\gamma_{\operatorname{pq}}\,\operatorname{pq'}(k'\,u,-m/m')</math> (The arguments <math>(k'\,u,-m/m')</math> are suppressed) |
|||
:{| class="wikitable" style="text-align:center" |
|||
|+ The RIR transformation <math>\gamma_{\operatorname{pq}}\,\operatorname{pq'}(k'\,u,-m/m')</math> |
|||
!colspan="2" rowspan="2"| |
|||
!colspan="4"|q |
|||
|- |
|||
! c |
|||
! s |
|||
! n |
|||
! d |
|||
|- |
|||
!rowspan="6"|p |
|||
|- |
|||
! c |
|||
|1|| k' cs || cd || cn |
|||
|- |
|||
! s |
|||
|<math>\frac{1}{k'}</math> sc|| 1 ||<math>\frac{1}{k'}</math> sd ||<math> \frac{1}{k'}</math> sn |
|||
|- |
|||
! n |
|||
| dc || <math>k'</math> ds || 1 || dn |
|||
|- |
|||
! d |
|||
| nc || <math>k'</math> ns || nd || 1 |
|||
|} |
|||
The value of the Jacobi transformations is that any set of Jacobi elliptic functions with any real-valued parameter ''m'' can be converted into another set for which <math>0<m\le 1/2</math> and, for real values of ''u'', the function values will be real.<ref name="Neville1944"/>{{rp|p. 215}} |
|||
===Amplitude transformations=== |
|||
In the following, the second variable is suppressed and is equal to <math>m</math>: |
|||
:<math>\sin(\operatorname{am}(u+v)+\operatorname{am}(u-v))=\frac{2\operatorname{sn}u\operatorname{cn}u\operatorname{dn}v}{1-m\operatorname{sn}^2u\operatorname{sn}^2v},</math> |
|||
:<math>\cos(\operatorname{am}(u+v)-\operatorname{am}(u-v))=\dfrac{\operatorname{cn}^2v-\operatorname{sn}^2v\operatorname{dn}^2u}{1-m\operatorname{sn}^2u\operatorname{sn}^2v}</math> |
|||
where both identities are valid for all <math>u,v,m\in\mathbb{C}</math> such that both sides are well-defined. |
|||
With |
|||
:<math>m_1=\left(\frac{1-\sqrt{m'}}{1+\sqrt{m'}}\right)^2,</math> |
|||
we have |
|||
:<math>\cos (\operatorname{am}(u,m)+\operatorname{am}(K-u,m))=-\operatorname{sn}((1-\sqrt{m'})u,1/m_1),</math> |
|||
:<math>\sin(\operatorname{am}(\sqrt{m'}u,-m/m')+\operatorname{am}((1-\sqrt{m'})u,1/m_1))=\operatorname{sn}(u,m),</math> |
|||
:<math>\sin(\operatorname{am}((1+\sqrt{m'})u,m_1)+\operatorname{am}((1-\sqrt{m'})u,1/m_1))=\sin(2\operatorname{am}(u,m))</math> |
|||
where all the identities are valid for all <math>u,m\in\mathbb{C}</math> such that both sides are well-defined. |
|||
==The Jacobi hyperbola== |
|||
[[File:Jacobi Elliptic Functions (on Jacobi Hyperbola).svg|right|thumb|upright=1.5|Plot of the Jacobi hyperbola (''x''<sup>2</sup> + ''y''<sup>2</sup>/''b''<sup>2</sup> = 1, ''b'' imaginary) and the twelve Jacobi Elliptic functions pq(''u'',''m'') for particular values of angle ''φ'' and parameter ''b''. The solid curve is the hyperbola, with ''m'' = 1 − 1/''b''<sup>2</sup> and ''u'' = ''F''(''φ'',''m'') where ''F''(⋅,⋅) is the [[elliptic integral]] of the first kind. The dotted curve is the unit circle. For the ds-dc triangle, ''σ'' = sin(''φ'')cos(''φ'').]] |
|||
Introducing complex numbers, our ellipse has an associated hyperbola: |
|||
:<math> x^2 - \frac{y^2}{b^2} = 1 </math> |
|||
from applying Jacobi's imaginary transformation<ref name="WolframJE"/> to the elliptic functions in the above equation for ''x'' and ''y''. |
|||
:<math> x = \frac{1} {\operatorname{dn}(u,1-m)},\quad y = \frac{ \operatorname{sn}(u,1-m)} {\operatorname{dn}(u,1-m)}</math> |
|||
It follows that we can put <math> x=\operatorname{dn}(u,1-m), y=\operatorname{sn}(u,1-m)</math>. So our ellipse has a dual ellipse with m replaced by 1-m. This leads to the complex torus mentioned in the Introduction.<ref>{{Cite web|url=https://paramanands.blogspot.co.uk/2011/01/elliptic-functions-complex-variables.html#.WlHhTbp2t9A|title = Elliptic Functions: Complex Variables}}</ref> Generally, m may be a complex number, but when m is real and m<0, the curve is an ellipse with major axis in the x direction. At m=0 the curve is a circle, and for 0<m<1, the curve is an ellipse with major axis in the y direction. At ''m'' = 1, the curve degenerates into two vertical lines at ''x'' = ±1. For ''m'' > 1, the curve is a hyperbola. When ''m'' is complex but not real, ''x'' or ''y'' or both are complex and the curve cannot be described on a real ''x''-''y'' diagram. |
|||
=={{anchor|ns|nc|nd|sc|sd|dc|ds|cs|cd|pg}}Minor functions== |
|||
Reversing the order of the two letters of the function name results in the reciprocals of the three functions above: |
|||
:<math> |
|||
\operatorname{ns}(u) = \frac{1}{\operatorname{sn}(u)}, \qquad \operatorname{nc}(u) = \frac{1}{\operatorname{cn}(u)}, \qquad |
|||
\operatorname{nd}(u) = \frac{1}{\operatorname{dn}(u)}. |
|||
</math> |
</math> |
||
Similarly, the ratios of the three primary functions correspond to the first letter of the numerator followed by the first letter of the denominator: |
Similarly, the ratios of the three primary functions correspond to the first letter of the numerator followed by the first letter of the denominator: |
||
[[File:sc-k-08.png|right|thumb|300px|Elliptic Jacobi function, sc, ''k'' = 0.8]] |
|||
:<math> |
:<math> |
||
\begin{align} |
\begin{align} |
||
\operatorname{sc}(u) |
\operatorname{sc}(u) = \frac{\operatorname{sn}(u)}{\operatorname{cn}(u)}, \qquad |
||
\operatorname{sd}(u) |
\operatorname{sd}(u) = \frac{\operatorname{sn}(u)}{\operatorname{dn}(u)}, \qquad \operatorname{dc}(u) = \frac{\operatorname{dn}(u)}{\operatorname{cn}(u)}, \qquad \operatorname{ds}(u) = \frac{\operatorname{dn}(u)}{\operatorname{sn}(u)}, \qquad \operatorname{cs}(u) = \frac{\operatorname{cn}(u)}{\operatorname{sn}(u)}, \qquad |
||
\operatorname{ |
\operatorname{cd}(u) = \frac{\operatorname{cn}(u)}{\operatorname{dn}(u)}. |
||
\operatorname{ds}(u) & = \frac{\operatorname{dn}(u)}{\operatorname{sn}(u)} \\[8pt] |
|||
\operatorname{cs}(u) & = \frac{\operatorname{cn}(u)}{\operatorname{sn}(u)} \\[8pt] |
|||
\operatorname{cd}(u) & = \frac{\operatorname{cn}(u)}{\operatorname{dn}(u)} |
|||
\end{align} |
\end{align} |
||
</math> |
</math> |
||
More compactly, we have |
More compactly, we have |
||
:<math>\operatorname{pq}(u)=\frac{\operatorname{ |
:<math>\operatorname{pq}(u)=\frac{\operatorname{pn}(u)}{\operatorname{qn}(u)}</math> |
||
where |
where p and q are any of the letters s, c, d. |
||
== Periodicity, poles, and residues == |
|||
(This notation is due to [[Christof Gudermann|Gudermann]] and [[James Whitbread Lee Glaisher|Glaisher]] and is not Jacobi's original notation.) |
|||
[[File:JacobiEllipticFunctions.svg|thumb|Plots of the phase for the twelve Jacobi Elliptic functions pq(u,m) as a function complex argument u, with poles and zeroes indicated. The plots are over one full cycle in the real and imaginary directions with the colored portion indicating phase according to the color wheel at the lower right (which replaces the trivial dd function). Regions with absolute value below 1/3 are colored black, roughly indicating the location of a zero, while regions with absolute value above 3 are colored white, roughly indicating the position of a pole. All plots use ''m'' = 2/3 with ''K'' = ''K''(''m''), ''K''′ = ''K''(1 − ''m''), ''K''(⋅) being the complete elliptic integral of the first kind. Arrows at the poles point in direction of zero phase. Right and left arrows imply positive and negative real residues respectively. Up and down arrows imply positive and negative imaginary residues respectively.]] |
|||
==Addition theorems== |
|||
In the complex plane of the argument ''u'', the Jacobi elliptic functions form a repeating pattern of poles (and zeroes). The residues of the poles all have the same absolute value, differing only in sign. Each function pq(''u'',''m'') has an "inverse function" (in the multiplicative sense) qp(''u'',''m'') in which the positions of the poles and zeroes are exchanged. The periods of repetition are generally different in the real and imaginary directions, hence the use of the term "doubly periodic" to describe them. |
|||
The functions satisfy the two algebraic relations |
|||
For the Jacobi amplitude and the Jacobi epsilon function: |
|||
:<math>\operatorname{cn}^2(u,k) + \operatorname{sn}^2(u,k) = 1,\,</math> |
|||
:<math>\operatorname{am}(u+2K,m)=\operatorname{am}(u,m)+\pi,</math> |
|||
:<math>\operatorname{am}(u+4iK',m)=\operatorname{am}(u,m),</math> |
|||
:<math>\mathcal{E}(u+2K,m)=\mathcal{E}(u,m)+2E,</math> |
|||
:<math>\mathcal{E}(u+2iK',m)=\mathcal{E}(u,m)+2iE \frac{K'}{K}-\frac{\pi i}{K}</math> |
|||
where <math>E(m)</math> is the [[Elliptic integral#Complete elliptic integral of the second kind|complete elliptic integral of the second kind]] with parameter <math>m</math>. |
|||
The double periodicity of the Jacobi elliptic functions may be expressed as: |
|||
:<math>\operatorname{dn}^2(u,k) + k^2 \ \operatorname{sn}^2(u,k) = 1.\,</math> |
|||
:<math>\operatorname{pq}(u + 2 \alpha K(m) + 2 i \beta K(1-m)\,,\,m)=(-1)^\gamma \operatorname{pq}(u,m)</math> |
|||
From this we see that (cn, sn, dn) parametrizes an [[elliptic curve]] which is the intersection of the two [[quadric]]s defined by the above two equations. We now may define a group law for points on this curve by the addition formulas for the Jacobi functions |
|||
where ''α'' and ''β'' are any pair of integers. ''K''(⋅) is the complete elliptic integral of the first kind, also known as the [[quarter period]]. The power of negative unity (''γ'') is given in the following table: |
|||
:<math> |
|||
:{| class="wikitable" style="text-align:center" |
|||
|+ <math>\gamma</math> |
|||
!colspan="2" rowspan="2"| |
|||
!colspan="4"|q |
|||
|- |
|||
! c |
|||
! s |
|||
! n |
|||
! d |
|||
|- |
|||
!rowspan="6"|p |
|||
|- |
|||
! c |
|||
|0||β || α + β || α |
|||
|- |
|||
! s |
|||
|β || 0 || α || α + β |
|||
|- |
|||
! n |
|||
| α + β || α || 0 || β |
|||
|- |
|||
! d |
|||
| α || α + β || β || 0 |
|||
|} |
|||
When the factor (−1)<sup>''γ''</sup> is equal to −1, the equation expresses quasi-periodicity. When it is equal to unity, it expresses full periodicity. It can be seen, for example, that for the entries containing only α when α is even, full periodicity is expressed by the above equation, and the function has full periods of 4''K''(''m'') and 2''iK''(1 − ''m''). Likewise, functions with entries containing only ''β'' have full periods of 2K(m) and 4''iK''(1 − ''m''), while those with α + β have full periods of 4''K''(''m'') and 4''iK''(1 − ''m''). |
|||
In the diagram on the right, which plots one repeating unit for each function, indicating phase along with the location of poles and zeroes, a number of regularities can be noted: The inverse of each function is opposite the diagonal, and has the same size unit cell, with poles and zeroes exchanged. The pole and zero arrangement in the auxiliary rectangle formed by (0,0), (''K'',0), (0,''K''′) and (''K'',''K''′) are in accordance with the description of the pole and zero placement described in the introduction above. Also, the size of the white ovals indicating poles are a rough measure of the absolute value of the residue for that pole. The residues of the poles closest to the origin in the figure (i.e. in the auxiliary rectangle) are listed in the following table: |
|||
:{| class="wikitable" style="text-align:center; width:200px”" |
|||
|+ Residues of Jacobi Elliptic Functions |
|||
!colspan="2" rowspan="2"| |
|||
!colspan="4"|q |
|||
|- |
|||
! width="40pt"|c |
|||
! width="40pt"|s |
|||
! width="40pt"|n |
|||
! width="40pt"|d |
|||
|- |
|||
!rowspan="6"|p |
|||
|- |
|||
! height="40pt" |c |
|||
| ||1||<math>-\frac{i}{k}</math>||<math>-\frac{1}{k}</math> |
|||
|- |
|||
! height="40pt" |s |
|||
| <math>-\frac{1}{k'}</math>|| ||<math>\frac{1}{k}</math>||<math>-\frac{i}{k\,k'}</math> |
|||
|- |
|||
! height="40pt" |n |
|||
|<math>-\frac{1}{k'}</math>||1|| ||<math>-\frac{i}{k'}</math> |
|||
|- |
|||
! height="40pt" | d |
|||
| -1 || 1 || <math>-i</math> || |
|||
|- |
|||
|} |
|||
When applicable, poles displaced above by 2''K'' or displaced to the right by 2''K''′ have the same value but with signs reversed, while those diagonally opposite have the same value. Note that poles and zeroes on the left and lower edges are considered part of the unit cell, while those on the upper and right edges are not. |
|||
The information about poles can in fact be used to [[Characterization (mathematics)|characterize]] the Jacobi elliptic functions:<ref>{{cite book |last1=Whittaker |first1=Edmund Taylor |authorlink1=Edmund T. Whittaker |last2=Watson |first2=George Neville |authorlink2=George N. Watson |date= 1927 |pages=504–505 |edition=4th |title=A Course of Modern Analysis |title-link=A Course of Modern Analysis |publisher= Cambridge University Press}}</ref> |
|||
The function <math>u\mapsto\operatorname{sn}(u,m)</math> is the unique elliptic function having simple poles at <math>2rK+(2s+1)iK'</math> (with <math>r,s\in\mathbb{Z}</math>) with residues <math>(-1)^r/\sqrt{m}</math> taking the value <math>0</math> at <math>0</math>. |
|||
The function <math>u\mapsto\operatorname{cn}(u,m)</math> is the unique elliptic function having simple poles at <math>2rK+(2s+1)iK'</math> (with <math>r,s\in\mathbb{Z}</math>) with residues <math>(-1)^{r+s-1}i/\sqrt{m}</math> taking the value <math>1</math> at <math>0</math>. |
|||
The function <math>u\mapsto\operatorname{dn}(u,m)</math> is the unique elliptic function having simple poles at <math>2rK+(2s+1)iK'</math> (with <math>r,s\in\mathbb{Z}</math>) with residues <math>(-1)^{s-1}i</math> taking the value <math>1</math> at <math>0</math>. |
|||
==Special values== |
|||
Setting <math>m=-1</math> gives the [[lemniscate elliptic functions]] <math>\operatorname{sl}</math> and <math>\operatorname{cl}</math>: |
|||
:<math>\operatorname{sl}u=\operatorname{sn}(u,-1),\quad \operatorname{cl}u=\operatorname{cd}(u,-1)=\frac{\operatorname{cn}(u,-1)}{\operatorname{dn}(u,-1)}.</math> |
|||
When <math>m=0</math> or <math>m=1</math>, the Jacobi elliptic functions are reduced to non-elliptic functions: |
|||
{| class="wikitable" |
|||
|- |
|||
! Function |
|||
! ''m'' = 0 |
|||
! ''m'' = 1 |
|||
|- |
|||
| <math>\operatorname{sn}(u,m)</math> |
|||
| <math>\sin u</math> |
|||
| <math>\tanh u</math> |
|||
|- |
|||
| <math>\operatorname{cn}(u,m)</math> |
|||
| <math>\cos u</math> |
|||
| <math>\operatorname{sech} u</math> |
|||
|- |
|||
| <math>\operatorname{dn}(u,m)</math> |
|||
| <math>1</math> |
|||
| <math>\operatorname{sech} u</math> |
|||
|- |
|||
| <math>\operatorname{ns}(u,m)</math> |
|||
| <math>\csc u</math> |
|||
| <math>\coth u</math> |
|||
|- |
|||
| <math>\operatorname{nc}(u,m)</math> |
|||
| <math>\sec u</math> |
|||
| <math>\cosh u</math> |
|||
|- |
|||
| <math>\operatorname{nd}(u,m)</math> |
|||
| <math>1</math> |
|||
| <math>\cosh u</math> |
|||
|- |
|||
| <math>\operatorname{sd}(u,m)</math> |
|||
| <math>\sin u</math> |
|||
| <math>\sinh u</math> |
|||
|- |
|||
| <math>\operatorname{cd}(u,m)</math> |
|||
| <math>\cos u</math> |
|||
| <math>1</math> |
|||
|- |
|||
| <math>\operatorname{cs}(u,m)</math> |
|||
| <math>\cot u</math> |
|||
| <math>\operatorname{csch} u</math> |
|||
|- |
|||
| <math>\operatorname{ds}(u,m)</math> |
|||
| <math>\csc u</math> |
|||
| <math>\operatorname{csch} u</math> |
|||
|- |
|||
| <math>\operatorname{dc}(u,m)</math> |
|||
| <math>\sec u</math> |
|||
| <math>1</math> |
|||
|- |
|||
| <math>\operatorname{sc}(u,m)</math> |
|||
| <math>\tan u</math> |
|||
| <math>\sinh u</math> |
|||
|} |
|||
For the Jacobi amplitude, <math>\operatorname{am}(u,0)=u</math> and <math>\operatorname{am}(u,1)=\operatorname{gd}u</math> where <math>\operatorname{gd}</math> is the [[Gudermannian function]]. |
|||
In general if neither of p,q is d then <math>\operatorname{pq}(u,1)=\operatorname{pq}(\operatorname{gd}(u),0)</math>. |
|||
==Identities== |
|||
===Half angle formula=== |
|||
<math display="block">\operatorname{sn}\left(\frac{u}{2},m\right)=\pm\sqrt{\frac{1-\operatorname{cn}(u,m)}{1+\operatorname{dn}(u,m)}}</math> |
|||
<math display="block">\operatorname{cn}\left(\frac{u}{2},m\right)=\pm\sqrt{\frac{\operatorname{cn}(u,m)+\operatorname{dn}(u,m)}{1+\operatorname{dn}(u,m)}}</math> |
|||
<math display="block">\operatorname{cn}\left(\frac{u}{2},m\right)=\pm\sqrt{\frac{m'+\operatorname{dn}(u,m)+m\operatorname{cn}(u,m)}{1+\operatorname{dn}(u,m)}}</math> |
|||
===K formulas=== |
|||
'''Half K formula''' |
|||
<math display="block">\operatorname{sn}\left[\tfrac{1}{2}K(k); k\right] = \frac{\sqrt{2}}{\sqrt{1+k} + \sqrt{1-k}} </math> |
|||
<math display="block">\operatorname{cn}\left[\tfrac{1}{2}K(k); k\right] = \frac{\sqrt{2}\,\sqrt[4]{1-k^2}}{\sqrt{1+k} + \sqrt{1-k}} </math> |
|||
<math display="block"> \operatorname{dn}\left[\tfrac{1}{2}K(k); k\right] = \sqrt[4]{1-k^2} </math> |
|||
'''Third K formula''' |
|||
:<math>\operatorname{sn}\left[\frac{1}{3}K\left(\frac{x^3}{\sqrt{x^6+1}+1}\right);\frac{x^3}{\sqrt{x^6+1}+1}\right] = |
|||
\frac{\sqrt{2\sqrt{x^4-x^2+1}-x^2+2}+\sqrt{x^2+1}-1}{\sqrt{2\sqrt{x^4-x^2+1}-x^2+2}+\sqrt{x^2+1}+1} </math> |
|||
To get ''x''<sup>3</sup>, we take the tangent of twice the arctangent of the modulus. |
|||
Also this equation leads to the sn-value of the third of ''K'': |
|||
:<math>k^2s^4-2k^2s^3+2s-1 = 0 </math> |
|||
:<math>s = \operatorname{sn}\left[\tfrac{1}{3}K(k); k\right] </math> |
|||
These equations lead to the other values of the Jacobi-Functions: |
|||
:<math>\operatorname{cn}\left[\tfrac{2}{3}K(k); k\right] = 1 - \operatorname{sn}\left[\tfrac{1}{3}K(k); k\right] </math> |
|||
:<math>\operatorname{dn}\left[\tfrac{2}{3}K(k); k\right] = 1/\operatorname{sn}\left[\tfrac{1}{3}K(k); k\right] - 1 </math> |
|||
'''Fifth K formula''' |
|||
Following equation has following solution: |
|||
:<math>4k^2x^6+8k^2x^5+2(1-k^2)^2x-(1-k^2)^2 = 0 </math> |
|||
:<math>x = \frac{1}{2}-\frac{1}{2}k^2\operatorname{sn}\left[\tfrac{2}{5}K(k); k\right]^2 \operatorname{sn}\left[\tfrac{4}{5}K(k); k\right]^2 = \frac{\operatorname{sn}\left[\frac{4}{5}K(k); k\right]^2-\operatorname{sn}\left[\frac{2}{5}K(k); k\right]^2}{2\operatorname{sn}\left[\frac{2}{5}K(k); k\right]\operatorname{sn}\left[\frac{4}{5}K(k); k\right]} </math> |
|||
To get the sn-values, we put the solution x into following expressions: |
|||
:<math>\operatorname{sn}\left[\tfrac{2}{5}K(k); k\right] = (1 + k^2)^{-1/2}\sqrt{2(1-x-x^2)(x^2+1-x\sqrt{x^2+1})} </math> |
|||
:<math>\operatorname{sn}\left[\tfrac{4}{5}K(k); k\right] = (1 + k^2)^{-1/2}\sqrt{2(1-x-x^2)(x^2+1+x\sqrt{x^2+1})} </math> |
|||
=== Relations between squares of the functions === |
|||
Relations between squares of the functions can be derived from two basic relationships (Arguments (''u'',''m'') suppressed): |
|||
<math display="block">\operatorname{cn}^2+\operatorname{sn}^2=1</math> |
|||
<math display="block">\operatorname{cn}^2+m' \operatorname{sn}^2=\operatorname{dn}^2</math> |
|||
where ''m + m' ''= 1. Multiplying by any function of the form ''nq'' yields more general equations: |
|||
<math display="block">\operatorname{cq}^2+\operatorname{sq}^2=\operatorname{nq}^2</math> |
|||
<math display="block">\operatorname{cq}^2{}+m' \operatorname{sq}^2=\operatorname{dq}^2</math> |
|||
With ''q'' = ''d'', these correspond trigonometrically to the equations for the unit circle (<math>x^2+y^2=r^2</math>) and the unit ellipse (<math>x^2{}+m' y^2=1</math>), with ''x'' = ''cd'', ''y'' = ''sd'' and ''r'' = ''nd''. Using the multiplication rule, other relationships may be derived. For example: |
|||
<math display="block"> |
|||
-\operatorname{dn}^2{}+m'= -m\operatorname{cn}^2 = m\operatorname{sn}^2-m |
|||
</math> |
|||
<math display="block"> |
|||
-m'\operatorname{nd}^2{}+m'= -mm'\operatorname{sd}^2 = m\operatorname{cd}^2-m |
|||
</math> |
|||
<math display="block"> |
|||
m'\operatorname{sc}^2{}+m'= m'\operatorname{nc}^2 = \operatorname{dc}^2-m |
|||
</math> |
|||
<math display="block"> |
|||
\operatorname{cs}^2{}+m'=\operatorname{ds}^2=\operatorname{ns}^2-m |
|||
</math> |
|||
=== Addition theorems === |
|||
The functions satisfy the two square relations (dependence on ''m'' suppressed) |
|||
<math display="block">\operatorname{cn}^2(u) + \operatorname{sn}^2(u) = 1,\,</math> |
|||
<math display="block">\operatorname{dn}^2(u) + m \operatorname{sn}^2(u) = 1.\,</math> |
|||
From this we see that (cn, sn, dn) parametrizes an [[elliptic curve]] which is the intersection of the two [[quadric]]s defined by the above two equations. We now may define a group law for points on this curve by the addition formulas for the Jacobi functions<ref name="DLMF22" /> |
|||
<math display="block"> |
|||
\begin{align} |
\begin{align} |
||
\operatorname{cn}(x+y) & = |
\operatorname{cn}(x+y) & = |
||
{\operatorname{cn}(x) |
{\operatorname{cn}(x) \operatorname{cn}(y) |
||
- \operatorname{sn}(x) |
- \operatorname{sn}(x) \operatorname{sn}(y) \operatorname{dn}(x) \operatorname{dn}(y) |
||
\over {1 - |
\over {1 - m \operatorname{sn}^2 (x) \operatorname{sn}^2 (y)}}, \\[8pt] |
||
\operatorname{sn}(x+y) & = |
\operatorname{sn}(x+y) & = |
||
{\operatorname{sn}(x) |
{\operatorname{sn}(x) \operatorname{cn}(y) \operatorname{dn}(y) + |
||
\operatorname{sn}(y) |
\operatorname{sn}(y) \operatorname{cn}(x) \operatorname{dn}(x) |
||
\over {1 - |
\over {1 - m \operatorname{sn}^2 (x) \operatorname{sn}^2 (y)}}, \\[8pt] |
||
\operatorname{dn}(x+y) & = |
\operatorname{dn}(x+y) & = |
||
{\operatorname{dn}(x) |
{\operatorname{dn}(x) \operatorname{dn}(y) - m \operatorname{sn}(x) \operatorname{sn}(y) \operatorname{cn}(x) \operatorname{cn}(y) |
||
- |
\over {1 - m \operatorname{sn}^2 (x) \operatorname{sn}^2 (y)}}. |
||
\over {1 - k^2 \;\operatorname{sn}^2 (x)\; \operatorname{sn}^2 (y)}}. |
|||
\end{align} |
\end{align} |
||
</math> |
</math> |
||
The Jacobi epsilon and zn functions satisfy a quasi-addition theorem: |
|||
==Relations between squares of the functions== |
|||
<math display="block">\begin{align}\mathcal{E}(x+y,m)&=\mathcal{E}(x,m)+\mathcal{E}(y,m)-m\operatorname{sn}(x,m)\operatorname{sn}(y,m)\operatorname{sn}(x+y,m),\\ |
|||
\operatorname{zn}(x+y,m)&=\operatorname{zn}(x,m)+\operatorname{zn}(y,m)-m\operatorname{sn}(x,m)\operatorname{sn}(y,m)\operatorname{sn}(x+y,m).\end{align}</math> |
|||
Double angle formulae can be easily derived from the above equations by setting ''x'' = ''y''.<ref name="DLMF22" /> Half angle formulae<ref name="WolframJE" /><ref name="DLMF22" /> are all of the form: |
|||
:<math> |
|||
-\operatorname{dn}^2(u)+m_1= -m\;\operatorname{cn}^2(u) = m\;\operatorname{sn}^2(u)-m |
|||
</math> |
|||
<math display="block">\operatorname{pq}(\tfrac{1}{2}u,m)^2 = f_{\mathrm p}/f_{\mathrm q}</math> |
|||
:<math> |
|||
-m_1\;\operatorname{nd}^2(u)+m_1= -mm_1\;\operatorname{sd}^2(u) = m\;\operatorname{cd}^2(u)-m |
|||
</math> |
|||
where: |
|||
:<math> |
|||
<math display="block">f_{\mathrm c} = \operatorname{cn}(u,m)+\operatorname{dn}(u,m)</math> |
|||
<math display="block">f_{\mathrm s} = 1-\operatorname{cn}(u,m)</math> |
|||
</math> |
|||
<math display="block">f_{\mathrm n} = 1+\operatorname{dn}(u,m)</math> |
|||
<math display="block">f_{\mathrm d} = (1+\operatorname{dn}(u,m))-m(1-\operatorname{cn}(u,m))</math> |
|||
==Jacobi elliptic functions as solutions of nonlinear ordinary differential equations== |
|||
:<math> |
|||
===Derivatives with respect to the first variable=== |
|||
\operatorname{cs}^2(u)+m_1=\operatorname{ds}^2(u)=\operatorname{ns}^2(u)-m |
|||
The [[derivative]]s of the three basic Jacobi elliptic functions (with respect to the first variable, with <math>m</math> fixed) are: |
|||
</math> |
|||
<math display=block>\frac{\mathrm{d}}{\mathrm{d}z} \operatorname{sn}(z) = \operatorname{cn}(z) \operatorname{dn}(z),</math> |
|||
<math display=block>\frac{\mathrm{d}}{\mathrm{d}z} \operatorname{cn}(z) = -\operatorname{sn}(z) \operatorname{dn}(z),</math> |
|||
<math display=block>\frac{\mathrm{d}}{\mathrm{d}z} \operatorname{dn}(z) = - m \operatorname{sn}(z) \operatorname{cn}(z).</math> |
|||
These can be used to derive the derivatives of all other functions as shown in the table below (arguments (u,m) suppressed): |
|||
where ''m'' + ''m''<sub>1</sub> = 1 and ''m'' = ''k''<sup>2</sup>. |
|||
{| class="wikitable" style="text-align:center" |
|||
Additional relations between squares can be obtained by noting that pq<sup>2</sup> · qp<sup>2</sup> = 1 and that pq = pr / qr where p, q, r are any of the letters s, c, d, n and ss = cc = dd = nn = 1. |
|||
|+ Derivatives <math>\frac{\mathrm d}{\mathrm du} \operatorname{pq}(u,m)</math> |
|||
!colspan="2" rowspan="2"| |
|||
!colspan="4"|q |
|||
|- |
|||
! c |
|||
! s |
|||
! n |
|||
! d |
|||
|- |
|||
!rowspan="6"|p |
|||
|- |
|||
! c |
|||
|0 ||−ds ns ||−dn sn || −m' nd sd |
|||
|- |
|||
! s |
|||
|dc nc || 0 ||cn dn || cd nd |
|||
|- |
|||
! n |
|||
|dc sc || −cs ds || 0 || ''m'' cd sd |
|||
|- |
|||
! d |
|||
|m' nc sc || −cs ns || −''m'' cn sn ||0 |
|||
|} |
|||
Also |
|||
:<math>\frac{\mathrm d}{\mathrm dz}\mathcal{E}(z)=\operatorname{dn}(z)^2.</math> |
|||
With the [[#Addition theorems|addition theorems above]] and for a given ''m'' with 0 < ''m'' < 1 the major functions are therefore solutions to the following nonlinear [[ordinary differential equation]]s: |
|||
* <math>\operatorname{am}(x)</math> solves the differential equations <math>\frac{\mathrm d^2y}{\mathrm dx^2}+m\sin (y)\cos (y)=0</math> and |
|||
:<math>\left(\frac{\mathrm dy}{\mathrm dx}\right)^2=1-m\sin(y)^2</math> (for <math>x</math> not on a branch cut) |
|||
* <math>\operatorname{sn}(x)</math> solves the differential equations <math>\frac{\mathrm{d}^2 y}{\mathrm{d}x^2} + (1+m) y - 2 m y^3 = 0</math> and <math> \left(\frac{\mathrm{d} y}{\mathrm{d}x}\right)^2 = (1-y^2) (1-m y^2)</math> |
|||
* <math>\operatorname{cn}(x)</math> solves the differential equations <math>\frac{\mathrm{d}^2 y}{\mathrm{d}x^2} + (1-2m) y + 2 m y^3 = 0</math> and <math> \left(\frac{\mathrm{d} y}{\mathrm{d}x}\right)^2 = (1-y^2) (1-m + my^2)</math> |
|||
* <math>\operatorname{dn}(x)</math> solves the differential equations <math>\frac{\mathrm{d}^2 y}{\mathrm{d}x^2} - (2 - m) y + 2 y^3 = 0</math> and <math> \left(\frac{\mathrm{d} y}{\mathrm{d}x}\right)^2 = (y^2 - 1) (1 - m - y^2)</math> |
|||
The function which exactly solves the [[Pendulum (mechanics)#Simple gravity pendulum|pendulum differential equation]], |
|||
:<math>\frac{\mathrm d^2 \theta}{\mathrm dt^2}+c\sin \theta=0,</math> |
|||
with initial angle <math>\theta_0</math> and zero initial angular velocity is |
|||
:<math>\begin{align}\theta&=2\arcsin (\sqrt{m}\operatorname{cd}(\sqrt{c}t,m))\\ |
|||
&=2\operatorname{am}\left(\frac{1+\sqrt{m}}{2}(\sqrt{c}t+K),\frac{4\sqrt{m}}{(1+\sqrt{m})^2}\right)-2\operatorname{am}\left(\frac{1+\sqrt{m}}{2}(\sqrt{c}t-K),\frac{4\sqrt{m}}{(1+\sqrt{m})^2}\right)-\pi\end{align}</math> |
|||
where <math>m=\sin (\theta_0/2)^2</math>, <math>c>0</math> and <math>t\in\mathbb{R}</math>. |
|||
===Derivatives with respect to the second variable=== |
|||
With the first argument <math>z</math> fixed, the derivatives with respect to the second variable <math>m</math> are as follows: |
|||
:<math>\begin{align}\frac{\mathrm d}{\mathrm dm}\operatorname{sn}(z)&=\frac{\operatorname{dn}(z)\operatorname{cn}(z)((1-m)z-\mathcal{E}(z)+m\operatorname{cd}(z)\operatorname{sn}(z))}{2m(1-m)},\\ |
|||
\frac{\mathrm d}{\mathrm dm}\operatorname{cn}(z)&=\frac{\operatorname{sn}(z)\operatorname{dn}(z)((m-1)z+\mathcal{E}(z)-m\operatorname{sn}(z)\operatorname{cd}(z))}{2m(1-m)},\\ |
|||
\frac{\mathrm d}{\mathrm dm}\operatorname{dn}(z)&=\frac{\operatorname{sn}(z)\operatorname{cn}(z)((m-1)z+\mathcal{E}(z)-\operatorname{dn}(z)\operatorname{sc}(z))}{2(1-m)},\\ |
|||
\frac{\mathrm d}{\mathrm dm}\mathcal{E}(z)&=\frac{\operatorname{cn}(z)(\operatorname{sn}(z)\operatorname{dn}(z)-\operatorname{cn}(z)\mathcal{E}(z))}{2(1-m)}-\frac{z}{2}\operatorname{sn}(z)^2.\end{align}</math> |
|||
==Expansion in terms of the nome== |
==Expansion in terms of the nome== |
||
Let the [[nome (mathematics)|nome]] be <math>q=\exp(-\pi K'/K)</math> and let |
Let the [[nome (mathematics)|nome]] be <math>q=\exp(-\pi K'(m)/K(m))=e^{i\pi \tau}</math>, <math>\operatorname{Im}(\tau)>0</math>, <math>m=k^2</math> and let <math>v=\pi u /(2K(m))</math>. Then the functions have expansions as [[Lambert series]] |
||
:<math>\operatorname{am}(u,m)=\frac{\pi u}{2K(m)}+2\sum_{n=1}^\infty \frac{q^n}{n(1+q^{2n})}\sin (2nv),</math> |
|||
:<math>\operatorname{sn}(u)=\frac{2\pi}{ |
:<math>\operatorname{sn}(u,m)=\frac{2\pi}{kK(m)} |
||
\sum_{n=0}^\infty \frac{q^{n+1/2}}{1-q^{2n+1}} \sin ((2n+1)v),</math> |
\sum_{n=0}^\infty \frac{q^{n+1/2}}{1-q^{2n+1}} \sin ((2n+1)v),</math> |
||
:<math>\operatorname{cn}(u)=\frac{2\pi}{ |
:<math>\operatorname{cn}(u,m)=\frac{2\pi}{kK(m)} |
||
\sum_{n=0}^\infty \frac{q^{n+1/2}}{1+q^{2n+1}} \cos ((2n+1)v),</math> |
\sum_{n=0}^\infty \frac{q^{n+1/2}}{1+q^{2n+1}} \cos ((2n+1)v),</math> |
||
:<math>\operatorname{dn}(u)=\frac{\pi}{2K} + \frac{2\pi}{K} |
:<math>\operatorname{dn}(u,m)=\frac{\pi}{2K(m)} + \frac{2\pi}{K(m)} |
||
\sum_{n=1}^\infty \frac{q^{n}}{1+q^{2n}} \cos (2nv) |
\sum_{n=1}^\infty \frac{q^{n}}{1+q^{2n}} \cos (2nv),</math> |
||
:<math>\operatorname{zn}(u,m)=\frac{2\pi}{K(m)}\sum_{n=1}^\infty \frac{q^n}{1-q^{2n}}\sin (2nv)</math> |
|||
==Jacobi elliptic functions as solutions of nonlinear ordinary differential equations== |
|||
The [[derivative]]s of the three basic Jacobi elliptic functions are: |
|||
when <math>\left|\operatorname{Im}(u/K)\right|<\operatorname{Im}(iK'/K).</math> |
|||
:<math> |
|||
\frac{\mathrm{d}}{\mathrm{d}z}\, \mathrm{sn}\,(z) = \mathrm{cn}\,(z)\, \mathrm{dn}\,(z),</math> |
|||
Bivariate power series expansions have been published by Schett.<ref>{{cite journal|first1=Alois|last1=Schett |title=Properties of the Taylor series expansion coefficients of the Jacobian Elliptic Functions|year=1976|journal=Math. Comp.|volume=30|number=133|pages=143–147|doi=10.1090/S0025-5718-1976-0391477-3| mr=0391477|s2cid=120666361 }}</ref> |
|||
<!-- extra blank line between two lines of "displayed" [[TeX]] for legibility --> |
|||
==Fast computation== |
|||
:<math>\frac{\mathrm{d}}{\mathrm{d}z}\, \mathrm{cn}\,(z) = -\mathrm{sn}\,(z)\, \mathrm{dn}\,(z),</math> |
|||
The theta function ratios provide an efficient way of computing the Jacobi elliptic functions. There is an alternative method, based on the [[arithmetic-geometric mean]] and [[Landen's transformation]]s:<ref name="sala"/> |
|||
Initialize |
|||
<!-- extra blank line between two lines of "displayed" [[TeX]] for legibility --> |
|||
:<math>a_0=1,\, b_0=\sqrt{1-m}</math> |
|||
where <math>0<m<1</math>. |
|||
Define |
|||
:<math>a_n=\frac{a_{n-1}+b_{n-1}}{2},\, b_n=\sqrt{a_{n-1}b_{n-1}},\, c_n=\frac{a_{n-1}-b_{n-1}}{2}</math> |
|||
where <math>n\ge 1</math>. |
|||
Then define |
|||
:<math>\varphi_N=2^N a_N u</math> |
|||
for <math>u\in\mathbb{R}</math> and a fixed <math>N\in\mathbb{N}</math>. If |
|||
:<math>\varphi_{n-1}=\frac{1}{2}\left(\varphi_n+\arcsin \left(\frac{c_n}{a_n}\sin \varphi_n\right)\right)</math> |
|||
for <math>n\ge 1</math>, then |
|||
:<math>\operatorname{am}(u,m)=\varphi_0,\quad \operatorname{zn}(u,m)=\sum_{n=1}^N c_n\sin\varphi_n</math> |
|||
as <math>N\to\infty</math>. This is notable for its rapid convergence. It is then trivial to compute all Jacobi elliptic functions from the Jacobi amplitude <math>\operatorname{am}</math> on the real line.<ref group="note">For the <math>\operatorname{dn}</math> function, |
|||
<math>\operatorname{dn}(u,m)=\frac{\operatorname{cn}(u,m)}{\operatorname{sn}(K(m)-u,m)}</math> can be used.</ref> |
|||
In conjunction with the addition theorems for elliptic functions (which hold for complex numbers in general) and the Jacobi transformations, the method of computation described above can be used to compute all Jacobi elliptic functions in the whole complex plane. |
|||
:<math>\frac{\mathrm{d}}{\mathrm{d}z}\, \mathrm{dn}\,(z) = - k^2 \mathrm{sn}\,(z)\, \mathrm{cn}\,(z). |
|||
Another method of fast computation of the Jacobi elliptic functions via the arithmetic–geometric mean, avoiding the computation of the Jacobi amplitude, is due to Herbert E. Salzer:<ref>{{cite journal |last=Salzer |first=Herbert E. |date=July 1962 |title=Quick calculation of Jacobian elliptic functions|journal=Communications of the ACM|volume=5|issue=7|pages=399|doi=10.1145/368273.368573 |s2cid=44953400 |doi-access=free }}</ref> |
|||
Let |
|||
:<math>0\le m\le 1,\,0\le u\le K(m),\, a_0=1,\, b_0=\sqrt{1-m},</math> |
|||
:<math>a_{n+1}=\frac{a_n+b_n}{2},\, b_{n+1}=\sqrt{a_n b_n},\,c_{n+1}=\frac{a_n-b_n}{2}.</math> |
|||
Set |
|||
:<math>\begin{align}y_N&=\frac{a_N}{\sin (a_Nu)}\\ |
|||
y_{N-1}&=y_N+\frac{a_Nc_N}{y_N}\\ |
|||
y_{N-2}&=y_{N-1}+\frac{a_{N-1}c_{N-1}}{y_{N-1}}\\ |
|||
\vdots&=\vdots\\ |
|||
y_0&=y_1+\frac{m}{4y_1}.\end{align}</math> |
|||
Then |
|||
:<math>\begin{align}\operatorname{sn}(u,m)&=\frac{1}{y_0}\\ |
|||
\operatorname{cn}(u,m)&=\sqrt{1-\frac{1}{y_0^2}}\\ |
|||
\operatorname{dn}(u,m)&=\sqrt{1-\frac{m}{y_0^2}}\end{align}</math> |
|||
as <math>N\to\infty</math>. |
|||
Yet, another method for a rapidly converging fast computation of the Jacobi elliptic sine function found in the literature is shown below.<ref>{{Cite journal |last=Smith |first=John I. |date=May 5, 1971 |title=The Even- and Odd-Mode Capacitance Parameters for Coupled Lines in Suspended Substrate |url=https://ieeexplore.ieee.org/document/1127543 |journal=IEEE Transactions on Microwave Theory and Techniques |volume=MTT-19 |issue=5 |pages=430 |doi=10.1109/TMTT.1971.1127543 |bibcode=1971ITMTT..19..424S |via=IEEE Xplore}}</ref> |
|||
Let: |
|||
:<math>\begin{align} |
|||
&a_0 = u &b_0 = \frac{1-\sqrt{1-m}}{1+\sqrt{1-m}} \\ |
|||
&a_1 = \frac{a_0}{1+b_0} &b_1 = \frac{1-\sqrt{1-b^2_0 }}{1+\sqrt{1-b^2_0}}\\ |
|||
&\vdots = \vdots &\vdots = \vdots \\ |
|||
&a_n = \frac{a_{n-1}}{1+b_{n-1}} &b_n = \frac{1-\sqrt{1-b^2_{n-1}}}{1+\sqrt{1-b^2_{n-1}}}\\ |
|||
\end{align}</math> |
|||
Then set: |
|||
:<math>\begin{align} |
|||
y_{n+1} &= \sin(a_n) \\ |
|||
y_{n} &= \frac{y_{n+1}(1+b_n)}{1+y^2_{n+1}b_n} \\ |
|||
\vdots &= \vdots\\ |
|||
y_0 &= \frac{y_1(1+b_0)}{1+y^2_1b_0} \\ |
|||
\end{align}</math> |
|||
Then: |
|||
:<math>\operatorname{sn}(u,m) = y_0 \text{ as }n \rightarrow\infty</math>. |
|||
==Approximation in terms of hyperbolic functions== |
|||
The Jacobi elliptic functions can be expanded in terms of the hyperbolic functions. When <math>m</math> is close to unity, such that <math>m'^2</math> and higher powers of <math>m'</math> can be neglected, we have:<ref>{{dlmf|first1=W. P.|last1=Reinhardt|first2=P. L.|last2=Walker|id=22.10|title=Jacobian Elliptic Functions}}</ref><ref>{{dlmf|first1=W. P.|last1=Reinhardt|first2=P. L.|last2=Walker|id=22.16.E8|title=Jacobian Elliptic Functions}}</ref> |
|||
* sn(''u''): <math display="block">\operatorname{sn} (u,m)\approx \tanh (u)+\frac{1}{4}m'(\sinh (u)\cosh (u) -u)\operatorname{sech}^2 (u).</math> |
|||
* cn(''u''): <math display="block">\operatorname{cn} (u,m)\approx \operatorname{sech} (u)-\frac{1}{4} m'(\sinh (u)\cosh (u) -u)\tanh (u) \operatorname{sech} (u).</math> |
|||
* dn(''u''): <math display="block">\operatorname{dn} (u,m) \approx \operatorname{sech} (u)+\frac{1}{4} m'(\sinh (u)\cosh(u) +u)\tanh (u) \operatorname{sech} (u) .</math> |
|||
For the Jacobi amplitude, |
|||
<math display="block">\operatorname{am} (u,m) \approx \operatorname{gd} (u)+\frac{1}{4}m'(\sinh (u)\cosh (u) -u)\operatorname{sech} (u) .</math> |
|||
==Continued fractions== |
|||
Assuming real numbers <math>a,p</math> with <math>0<a<p</math> and the [[Nome (mathematics)|nome]] <math>q=e^{\pi i \tau}</math>, <math>\operatorname{Im}(\tau)>0</math> with [[Theta function|elliptic modulus]] <math display="inline">k(\tau)=\sqrt{1-k'(\tau)^2}=(\vartheta_{10}(0;\tau)/\vartheta_{00}(0;\tau))^2</math>. If <math>K[\tau]=K(k(\tau))</math>, where <math>K(x)=\pi/2\cdot {}_2F_1(1/2,1/2;1;x^2)</math> is the [[complete elliptic integral of the first kind]], then holds the following [[Continued fraction|continued fraction expansion]]<ref name="bagis-evaluations">N.Bagis.(2020)."Evaluations of series related to Jacobi elliptic functions". preprint https://www.researchgate.net/publication/331370071_Evaluations_of_Series_Related_to_Jacobi_Elliptic_Functions</ref> |
|||
:<math> |
|||
\begin{align} |
|||
&\frac{\textrm{dn}\left((p/2-a)\tau K\left[\frac{p\tau}{2}\right];k\left(\frac{p\tau}{2}\right)\right)}{\sqrt{k'\left(\frac{p\tau}{2}\right)}} = \frac{\sum^\infty_{n=-\infty}q^{p/2 n^2+(p/2-a)n}}{\sum^\infty_{n=-\infty}(-1)^nq^{p/2 n^2+(p/2-a)n}}\\[4pt] |
|||
={}&-1+\frac{2}{1-{}} \, \frac{q^a+q^{p-a}}{1-q^p+{}} \, \frac{(q^a+q^{2p-a})(q^{a+p}+q^{p-a})}{1-q^{3p}+{}} \, \frac{q^p(q^a+q^{3p-a})(q^{a+2p}+q^{p-a})}{1-q^{5p}+{}} \, \frac{q^{2p}(q^a+q^{4p-a})(q^{a+3p}+q^{p-a})}{1-q^{7p}+{}}\cdots |
|||
\end{align} |
|||
</math> |
</math> |
||
Known continued fractions involving <math>\textrm{sn}(t),\textrm{cn}(t)</math> and <math>\textrm{dn}(t)</math> with elliptic modulus <math>k</math> are |
|||
For <math>z\in\Complex</math>, <math>|k|<1</math>:<ref name="wall-analytic-theory">H.S. Wall. (1948). "Analytic Theory of Continued Fractions", Van Nostrand, New York.</ref> pg. 374 |
|||
With the [[#Addition theorems|addition theorems above]] and for a given ''k'' with 0 < ''k'' < 1 they therefore are solutions to the following nonlinear [[ordinary differential equation]]s: |
|||
:<math>\int^{\infty}_{0}\textrm{sn}(t)e^{-tz}\, \mathrm dt=\frac{1}{1^2(1+k^2)+z^2-{}} \, \frac{1\cdot 2^2\cdot 3k^2}{3^2(1+k^2)+z^2-{}} \, \frac{3\cdot 4^2\cdot 5k^2}{5^2(1+k^2)+z^2-{}}\cdots</math> |
|||
For <math>z \in \Complex\setminus\{0\}</math>, <math>|k|<1</math>:<ref name="wall-analytic-theory"/> pg. 375 |
|||
* <math>\mathrm{sn}\,(x)</math> solves the differential equations |
|||
: |
:<math>\int^{\infty}_{0}\textrm{sn}^2(t)e^{-t z}\,\mathrm dt=\frac{2z^{-1}}{2^2(1+k^2)+z^2-{}} \, \frac{2\cdot 3^2\cdot 4k^2}{4^2(1+k^2)+z^2-{}} \, \frac{4\cdot 5^2\cdot 6k^2}{6^2(1+k^2)+z^2-{}}\cdots</math> |
||
: and |
|||
:: <math> \left(\frac{\mathrm{d} y}{\mathrm{d}x}\right)^2 = (1-y^2) (1-k^2 y^2)</math> |
|||
For <math>z\in\Complex\setminus\{0\}</math>, <math>|k|<1</math>:<ref name="perron">Perron, O. (1957). "Die Lehre von den Kettenbruchen", Band II, B.G. Teubner, Stuttgart.</ref> pg. 220 |
|||
* <math>\mathrm{cn}\,(x)</math> solves the differential equations |
|||
: |
:<math>\int^\infty_0 \textrm{cn}(t)e^{-t z}\, \mathrm dt=\frac{1}{z+{}} \, \frac{1^2}{z+{}} \, \frac{2^2k^2}{z+{}}\, \frac{3^2}{z+{}} \, \frac{4^2k^2}{z+{}} \, \frac{5^2}{z+{}} \cdots</math> |
||
: and |
|||
:: <math> \left(\frac{\mathrm{d} y}{\mathrm{d}x}\right)^2 = (1-y^2) (1-k^2 + k^2 y^2)</math> |
|||
For <math>z\in\Complex\setminus\{0\}</math>, <math>|k|<1</math>:<ref name="wall-analytic-theory"/> pg. 374 |
|||
* <math>\mathrm{dn}\,(x)</math> solves the differential equations |
|||
: |
:<math>\int^\infty_0\textrm{dn}(t)e^{-t z}\, \mathrm dt=\frac{1}{z+{}} \, \frac{1^2k^2}{z+{}} \, \frac{2^2}{z+{}} \, \frac{3^2k^2}{z+{}} \, \frac{4^2}{z+{}} \, \frac{5^2k^2}{z+{}} \cdots</math> |
||
: and |
|||
:: <math> \left(\frac{\mathrm{d} y}{\mathrm{d}x}\right)^2 = (y^2 - 1) (1 - k^2 - y^2)</math> |
|||
For <math>z\in\Complex</math>, <math>|k|<1</math>:<ref name="wall-analytic-theory"/> pg. 375 |
|||
== Inverse functions == |
|||
:<math>\int^{\infty}_{0}\frac{\textrm{sn}(t)\textrm{cn}(t)}{\textrm{dn}(t)}e^{-tz}\, \mathrm dt=\frac{1}{2\cdot 1^2(2-k^2)+z^2-{}} \, \frac{1\cdot 2^2\cdot 3k^4}{2\cdot 3^2(2-k^2)+z^2-{}} \, \frac{3\cdot 4^2\cdot 5k^4}{2\cdot 5^2(2-k^2)+z^2-{}}\cdots</math> |
|||
== {{anchor|arcsn|arccn|arcdn}}Inverse functions == |
|||
The inverses of the Jacobi elliptic functions can be defined similarly to the [[inverse trigonometric functions]]; if <math>x=\mathrm{sn}(\xi, k)</math>, <math>\xi=\mathrm{arcsn}(x, k)</math>. They can be represented as elliptic integrals,<ref>{{dlmf|title=§22.15 Inverse Functions|first1=W. P.|last1=Reinhardt|first2=P. L.|last2=Walker|id=22.15}}</ref><ref>{{cite web|last=Ehrhardt|first=Wolfgang|title=The AMath and DAMath Special Functions: Reference Manual and Implementation Notes|url=http://www.wolfgang-ehrhardt.de/specialfunctions.pdf|accessdate=17 July 2013|page=42}}</ref> and power series representations have been found.<ref>{{cite journal|last=Carlson|first=B. C.|title=Power series for inverse Jacobian elliptic functions|journal=Mathematics of Computation|year=2008|volume=77|pages=1615–1621|url=http://www.ams.org/journals/mcom/2008-77-263/S0025-5718-07-02049-2/S0025-5718-07-02049-2.pdf|accessdate=17 July 2013|doi=10.1090/s0025-5718-07-02049-2}}</ref> |
|||
The inverses of the Jacobi elliptic functions can be defined similarly to the [[inverse trigonometric functions]]; if <math>x=\operatorname{sn}(\xi, m)</math>, <math>\xi=\operatorname{arcsn}(x, m)</math>. They can be represented as elliptic integrals,<ref>{{dlmf|title=§22.15 Inverse Functions|first1=W. P.|last1=Reinhardt|first2=P. L.|last2=Walker|id=22.15}}</ref><ref>{{cite web|last=Ehrhardt|first=Wolfgang|title=The AMath and DAMath Special Functions: Reference Manual and Implementation Notes|url=http://www.wolfgang-ehrhardt.de/specialfunctions.pdf|access-date=17 July 2013|page=42|archive-url=https://web.archive.org/web/20160731033441/http://www.wolfgang-ehrhardt.de/specialfunctions.pdf|archive-date=31 July 2016|url-status=dead}}</ref><ref>{{cite book|last1=Byrd|first1=P.F.|last2=Friedman|first2=M.D.|title=Handbook of Elliptic Integrals for Engineers and Scientists|date=1971|publisher=Springer-Verlag|location=Berlin|edition=2nd}}</ref> and power series representations have been found.<ref>{{cite journal|last=Carlson|first=B. C.|title=Power series for inverse Jacobian elliptic functions|journal=Mathematics of Computation|year=2008|volume=77|issue=263|pages=1615–1621|url=https://www.ams.org/journals/mcom/2008-77-263/S0025-5718-07-02049-2/S0025-5718-07-02049-2.pdf|access-date=17 July 2013|doi=10.1090/s0025-5718-07-02049-2|bibcode=2008MaCom..77.1615C|doi-access=free}}</ref><ref name="DLMF22"/> |
|||
*<math>\operatorname{arcsn}(x,m) = \int_0^x \frac{\mathrm{d}t}{\sqrt{(1-t^2)(1-mt^2)}}</math> |
|||
*<math>\operatorname{arccn}(x,m) =\int_x^1 \frac{\mathrm{d}t}{\sqrt{(1-t^2)(1-m+mt^2)}}</math> |
|||
*<math>\operatorname{arcdn}(x,m) = \int_x^1 \frac{\mathrm{d}t}{\sqrt{(1-t^2)(t^2+m-1)}}</math> |
|||
== Map projection == |
== Map projection == |
||
| Line 237: | Line 887: | ||
== See also== |
== See also== |
||
* [[Elliptic integral]] |
|||
* [[Elliptic curve]] |
* [[Elliptic curve]] |
||
* [[Schwarz–Christoffel mapping]] |
* [[Schwarz–Christoffel mapping]] |
||
* [[Carlson symmetric form]] |
* [[Carlson symmetric form]] |
||
* [[Weierstrass's elliptic functions]] |
|||
* [[theta function|Jacobi theta function]] |
* [[theta function|Jacobi theta function]] |
||
* [[Ramanujan theta function]] |
* [[Ramanujan theta function]] |
||
* [[Dixon elliptic functions]] |
|||
* [[Abel elliptic functions]] |
|||
* [[Weierstrass elliptic function]] |
|||
* [[Lemniscate elliptic functions]] |
|||
==Notes== |
==Notes== |
||
{{reflist}} |
{{reflist|group=note}} |
||
==Citations== |
|||
{{Reflist}} |
|||
==References== |
==References== |
||
* {{AS ref|16|569}} |
* {{AS ref|16|569}} |
||
* [[Naum Akhiezer|N. I. Akhiezer]], ''Elements of the Theory of Elliptic Functions'' |
* [[Naum Akhiezer|N. I. Akhiezer]], ''Elements of the Theory of Elliptic Functions'' (1970) Moscow, translated into English as ''AMS Translations of Mathematical Monographs Volume 79'' (1990) AMS, Rhode Island {{ISBN|0-8218-4532-2}} |
||
* [[Alfred Cardew Dixon|A. C. Dixon]] [ |
* [[Alfred Cardew Dixon|A. C. Dixon]] [https://archive.org/details/117736039 The elementary properties of the elliptic functions, with examples] (Macmillan, 1894) |
||
* [[Alfred George Greenhill]] [ |
* [[Alfred George Greenhill]] [https://archive.org/details/applicationselli00greerich The applications of elliptic functions] (London, New York, Macmillan, 1892) |
||
* Edmund T. Whittaker, George Neville Watson: ''A Course in Modern Analysis''. 4th ed. Cambridge, England: Cambridge University Press, 1990. S. 469–470. |
|||
* H. Hancock [http://www.archive.org/details/lecturestheorell00hancrich Lectures on the theory of elliptic functions] (New York, J. Wiley & sons, 1910) |
|||
*{{Citation | last1=Jacobi | first1=C. G. J. | title=Fundamenta nova theoriae functionum ellipticarum | url= |
* H. Hancock [https://archive.org/details/lecturestheorell00hancrich Lectures on the theory of elliptic functions] (New York, J. Wiley & sons, 1910) |
||
*{{Citation | last1=Jacobi | first1=C. G. J. | title=Fundamenta nova theoriae functionum ellipticarum | url=https://archive.org/details/fundamentanovat00jacogoog | publisher=Königsberg | language=la | isbn=978-1-108-05200-9 | id=Reprinted by Cambridge University Press 2012 | year=1829}} |
|||
*{{dlmf|first=William P. |last=Reinhardt|first2=Peter L. |last2=Walker|id=22|title=Jacobian Elliptic Functions}} |
*{{dlmf|first=William P. |last=Reinhardt|first2=Peter L. |last2=Walker|id=22|title=Jacobian Elliptic Functions}} |
||
* {{in lang|fr}} [[P. Appell]] and E. Lacour [https://archive.org/details/principestheorie00apperich Principes de la théorie des fonctions elliptiques et applications] (Paris, Gauthier Villars, 1897) |
|||
* [[E. T. Whittaker]] and [[G. N. Watson]] ''[[A Course of Modern Analysis]]'', (1940, 1996) Cambridge University Press. ISBN 0-521-58807-3 |
|||
* {{fr |
* {{in lang|fr}} G. H. Halphen [https://archive.org/details/traitedesfonctio01halprich Traité des fonctions elliptiques et de leurs applications (vol. 1)] (Paris, Gauthier-Villars, 1886–1891) |
||
* {{ |
* {{in lang|fr}} G. H. Halphen [https://archive.org/details/traitedesfonctio02halprich Traité des fonctions elliptiques et de leurs applications (vol. 2)] (Paris, Gauthier-Villars, 1886–1891) |
||
* {{ |
* {{in lang|fr}} G. H. Halphen [https://archive.org/details/traitedesfonctio03halprich Traité des fonctions elliptiques et de leurs applications (vol. 3)] (Paris, Gauthier-Villars, 1886–1891) |
||
* {{ |
* {{in lang|fr}} J. Tannery and J. Molk [http://gallica.bnf.fr/notice?N=FRBNF37258233 Eléments de la théorie des fonctions elliptiques. Tome I, Introduction. Calcul différentiel. Ire partie] (Paris : Gauthier-Villars et fils, 1893) |
||
* {{ |
* {{in lang|fr}} J. Tannery and J. Molk [http://gallica.bnf.fr/notice?N=FRBNF37258241 Eléments de la théorie des fonctions elliptiques. Tome II, Calcul différentiel. IIe partie] (Paris : Gauthier-Villars et fils, 1893) |
||
* {{ |
* {{in lang|fr}} J. Tannery and J. Molk [http://gallica.bnf.fr/notice?N=FRBNF37258245 Eléments de la théorie des fonctions elliptiques. Tome III, Calcul intégral. Ire partie, Théorèmes généraux. Inversion] (Paris : Gauthier-Villars et fils, 1893) |
||
* {{ |
* {{in lang|fr}} J. Tannery and J. Molk [http://gallica.bnf.fr/notice?N=FRBNF37258246 Eléments de la théorie des fonctions elliptiques. Tome IV, Calcul intégral. IIe partie, Applications] (Paris : Gauthier-Villars et fils, 1893) |
||
* {{fr |
* {{in lang|fr}} C. Briot and J. C. Bouquet [http://gallica.bnf.fr/notice?N=FRBNF30162167 Théorie des fonctions elliptiques] ( Paris : Gauthier-Villars, 1875) |
||
* Toshio Fukushima: ''Fast Computation of Complete Elliptic Integrals and Jacobian Elliptic Functions''. 2012, [[National Astronomical Observatory of Japan]] (国立天文台) |
|||
* {{fr icon}} C. Briot and J. C. Bouquet [http://gallica.bnf.fr/notice?N=FRBNF30162167 Théorie des fonctions elliptiques] ( Paris : Gauthier-Villars, 1875) |
|||
* Lowan, Blanch und Horenstein: ''On the Inversion of the q-Series Associated with Jacobian Elliptic Functions''. Bull. Amer. Math. Soc. 48, 1942 |
|||
* H. Ferguson, D. E. Nielsen, G. Cook: ''A partition formula for the integer coefficients of the theta function nome''. Mathematics of computation, Volume 29, Nummer 131, Juli 1975 |
|||
* J. D. Fenton and R. S. Gardiner-Garden: ''Rapidly-convergent methods for evaluating elliptic integrals and theta and elliptic functions''. J. Austral. Math. Soc. (Series B) 24, 1982, S. 57 |
|||
* Adolf Kneser: ''Neue Untersuchung einer Reihe aus der Theorie der elliptischen Funktionen''. J. reine u. angew. Math. 157, 1927. pages 209 – 218 |
|||
==External links== |
==External links== |
||
| Line 272: | Line 932: | ||
{{DEFAULTSORT:Jacobi Elliptic Functions}} |
{{DEFAULTSORT:Jacobi Elliptic Functions}} |
||
[[Category:Jacobi elliptic functions| ]] |
|||
[[Category:Elliptic functions]] |
[[Category:Elliptic functions]] |
||
[[Category:Special functions]] |
|||
Latest revision as of 01:03, 1 September 2024
In mathematics, the Jacobi elliptic functions are a set of basic elliptic functions. They are found in the description of the motion of a pendulum, as well as in the design of electronic elliptic filters. While trigonometric functions are defined with reference to a circle, the Jacobi elliptic functions are a generalization which refer to other conic sections, the ellipse in particular. The relation to trigonometric functions is contained in the notation, for example, by the matching notation for . The Jacobi elliptic functions are used more often in practical problems than the Weierstrass elliptic functions as they do not require notions of complex analysis to be defined and/or understood. They were introduced by Carl Gustav Jakob Jacobi (1829). Carl Friedrich Gauss had already studied special Jacobi elliptic functions in 1797, the lemniscate elliptic functions in particular,[1] but his work was published much later.
Overview
[edit]
There are twelve Jacobi elliptic functions denoted by , where and are any of the letters , , , and . (Functions of the form are trivially set to unity for notational completeness.) is the argument, and is the parameter, both of which may be complex. In fact, the Jacobi elliptic functions are meromorphic in both and .[2] The distribution of the zeros and poles in the -plane is well-known. However, questions of the distribution of the zeros and poles in the -plane remain to be investigated.[2]
In the complex plane of the argument , the twelve functions form a repeating lattice of simple poles and zeroes.[3] Depending on the function, one repeating parallelogram, or unit cell, will have sides of length or on the real axis, and or on the imaginary axis, where and are known as the quarter periods with being the elliptic integral of the first kind. The nature of the unit cell can be determined by inspecting the "auxiliary rectangle" (generally a parallelogram), which is a rectangle formed by the origin at one corner, and as the diagonally opposite corner. As in the diagram, the four corners of the auxiliary rectangle are named , , , and , going counter-clockwise from the origin. The function will have a zero at the corner and a pole at the corner. The twelve functions correspond to the twelve ways of arranging these poles and zeroes in the corners of the rectangle.
When the argument and parameter are real, with , and will be real and the auxiliary parallelogram will in fact be a rectangle, and the Jacobi elliptic functions will all be real valued on the real line.
Since the Jacobian elliptic functions are doubly periodic in , they factor through a torus – in effect, their domain can be taken to be a torus, just as cosine and sine are in effect defined on a circle. Instead of having only one circle, we now have the product of two circles, one real and the other imaginary. The complex plane can be replaced by a complex torus. The circumference of the first circle is and the second , where and are the quarter periods. Each function has two zeroes and two poles at opposite positions on the torus. Among the points , , , there is one zero and one pole.
The Jacobian elliptic functions are then doubly periodic, meromorphic functions satisfying the following properties:
- There is a simple zero at the corner , and a simple pole at the corner .
- The complex number is equal to half the period of the function ; that is, the function is periodic in the direction , with the period being . The function is also periodic in the other two directions and , with periods such that and are quarter periods.
Notation
[edit]The elliptic functions can be given in a variety of notations, which can make the subject unnecessarily confusing. Elliptic functions are functions of two variables. The first variable might be given in terms of the amplitude , or more commonly, in terms of given below. The second variable might be given in terms of the parameter , or as the elliptic modulus , where , or in terms of the modular angle , where . The complements of and are defined as and . These four terms are used below without comment to simplify various expressions.
The twelve Jacobi elliptic functions are generally written as where and are any of the letters , , , and . Functions of the form are trivially set to unity for notational completeness. The “major” functions are generally taken to be , and from which all other functions can be derived and expressions are often written solely in terms of these three functions, however, various symmetries and generalizations are often most conveniently expressed using the full set. (This notation is due to Gudermann and Glaisher and is not Jacobi's original notation.)
Throughout this article, .
The functions are notationally related to each other by the multiplication rule: (arguments suppressed)
from which other commonly used relationships can be derived:
The multiplication rule follows immediately from the identification of the elliptic functions with the Neville theta functions[5]
Also note that:
Definition in terms of inverses of elliptic integrals
[edit]
There is a definition, relating the elliptic functions to the inverse of the incomplete elliptic integral of the first kind . These functions take the parameters and as inputs. The that satisfies
is called the Jacobi amplitude:
In this framework, the elliptic sine sn u (Latin: sinus amplitudinis) is given by
and the elliptic cosine cn u (Latin: cosinus amplitudinis) is given by
and the delta amplitude dn u (Latin: delta amplitudinis)[note 1]
In the above, the value is a free parameter, usually taken to be real such that (but can be complex in general), and so the elliptic functions can be thought of as being given by two variables, and the parameter . The remaining nine elliptic functions are easily built from the above three (, , ), and are given in a section below. Note that when , that then equals the quarter period .
In the most general setting, is a multivalued function (in ) with infinitely many logarithmic branch points (the branches differ by integer multiples of ), namely the points and where .[6] This multivalued function can be made single-valued by cutting the complex plane along the line segments joining these branch points (the cutting can be done in non-equivalent ways, giving non-equivalent single-valued functions), thus making analytic everywhere except on the branch cuts. In contrast, and other elliptic functions have no branch points, give consistent values for every branch of , and are meromorphic in the whole complex plane. Since every elliptic function is meromorphic in the whole complex plane (by definition), (when considered as a single-valued function) is not an elliptic function.
However, a particular cutting for can be made in the -plane by line segments from to with ; then it only remains to define at the branch cuts by continuity from some direction. Then becomes single-valued and singly-periodic in with the minimal period and it has singularities at the logarithmic branch points mentioned above. If and , is continuous in on the real line. When , the branch cuts of in the -plane cross the real line at for ; therefore for , is not continuous in on the real line and jumps by on the discontinuities.
But defining this way gives rise to very complicated branch cuts in the -plane (not the -plane); they have not been fully described as of yet.
Let
be the incomplete elliptic integral of the second kind with parameter .
Then the Jacobi epsilon function can be defined as
for and and by analytic continuation in each of the variables otherwise: the Jacobi epsilon function is meromorphic in the whole complex plane (in both and ). Alternatively, throughout both the -plane and -plane,[7]
is well-defined in this way because all residues of are zero, so the integral is path-independent. So the Jacobi epsilon relates the incomplete elliptic integral of the first kind to the incomplete elliptic integral of the second kind:
The Jacobi epsilon function is not an elliptic function, but it appears when differentiating the Jacobi elliptic functions with respect to the parameter.
The Jacobi zn function is defined by
It is a singly periodic function which is meromorphic in , but not in (due to the branch cuts of and ). Its minimal period in is . It is related to the Jacobi zeta function by
Historically, the Jacobi elliptic functions were first defined by using the amplitude. In more modern texts on elliptic functions, the Jacobi elliptic functions are defined by other means, for example by ratios of theta functions (see below), and the amplitude is ignored.
In modern terms, the relation to elliptic integrals would be expressed by (or ) instead of .
Definition as trigonometry: the Jacobi ellipse
[edit]
are defined on the unit circle, with radius r = 1 and angle arc length of the unit circle measured from the positive x-axis. Similarly, Jacobi elliptic functions are defined on the unit ellipse,[citation needed] with a = 1. Let
then:
For each angle the parameter
(the incomplete elliptic integral of the first kind) is computed. On the unit circle (), would be an arc length. However, the relation of to the arc length of an ellipse is more complicated.[8]
Let be a point on the ellipse, and let be the point where the unit circle intersects the line between and the origin . Then the familiar relations from the unit circle:
read for the ellipse:
So the projections of the intersection point of the line with the unit circle on the x- and y-axes are simply and . These projections may be interpreted as 'definition as trigonometry'. In short:
For the and value of the point with and parameter we get, after inserting the relation:
into: that:
The latter relations for the x- and y-coordinates of points on the unit ellipse may be considered as generalization of the relations for the coordinates of points on the unit circle.
The following table summarizes the expressions for all Jacobi elliptic functions pq(u,m) in the variables (x,y,r) and (φ,dn) with
| q | |||||
|---|---|---|---|---|---|
| c | s | n | d | ||
| p | |||||
| c | 1 | ||||
| s | 1 | ||||
| n | 1 | ||||
| d | 1 | ||||
Definition in terms of the Jacobi theta functions
[edit]Using elliptic integrals
[edit]Equivalently, Jacobi's elliptic functions can be defined in terms of the theta functions.[9] With such that , let
and , , . Then with , , and ,
The Jacobi zn function can be expressed by theta functions as well:
where denotes the partial derivative with respect to the first variable.
Using modular inversion
[edit]In fact, the definition of the Jacobi elliptic functions in Whittaker & Watson is stated a little bit differently than the one given above (but it's equivalent to it) and relies on modular inversion: The function , defined by

assumes every value in once and only once[10] in
where is the upper half-plane in the complex plane, is the boundary of and
In this way, each can be associated with one and only one . Then Whittaker & Watson define the Jacobi elliptic functions by
where . In the book, they place an additional restriction on (that ), but it is in fact not a necessary restriction (see the Cox reference). Also, if or , the Jacobi elliptic functions degenerate to non-elliptic functions which is described below.
Definition in terms of Neville theta functions
[edit]The Jacobi elliptic functions can be defined very simply using the Neville theta functions:[11]
Simplifications of complicated products of the Jacobi elliptic functions are often made easier using these identities.
Jacobi transformations
[edit]The Jacobi imaginary transformations
[edit]
The Jacobi imaginary transformations relate various functions of the imaginary variable i u or, equivalently, relations between various values of the m parameter. In terms of the major functions:[12]: 506
Using the multiplication rule, all other functions may be expressed in terms of the above three. The transformations may be generally written as . The following table gives the for the specified pq(u,m).[11] (The arguments are suppressed)
Jacobi Imaginary transformations q c s n d p c 1 i ns nc nd s −i sn 1 −i sc −i sd n cn i cs 1 cd d dn i ds dc 1
Since the hyperbolic trigonometric functions are proportional to the circular trigonometric functions with imaginary arguments, it follows that the Jacobi functions will yield the hyperbolic functions for m=1.[5]: 249 In the figure, the Jacobi curve has degenerated to two vertical lines at x = 1 and x = −1.
The Jacobi real transformations
[edit]The Jacobi real transformations[5]: 308 yield expressions for the elliptic functions in terms with alternate values of m. The transformations may be generally written as . The following table gives the for the specified pq(u,m).[11] (The arguments are suppressed)
Jacobi real transformations q c s n d p c s n d
Other Jacobi transformations
[edit]Jacobi's real and imaginary transformations can be combined in various ways to yield three more simple transformations .[5]: 214 The real and imaginary transformations are two transformations in a group (D3 or anharmonic group) of six transformations. If
is the transformation for the m parameter in the real transformation, and
is the transformation of m in the imaginary transformation, then the other transformations can be built up by successive application of these two basic transformations, yielding only three more possibilities:
These five transformations, along with the identity transformation (μU(m) = m) yield the six-element group. With regard to the Jacobi elliptic functions, the general transformation can be expressed using just three functions:
where i = U, I, IR, R, RI, or RIR, identifying the transformation, γi is a multiplication factor common to these three functions, and the prime indicates the transformed function. The other nine transformed functions can be built up from the above three. The reason the cs, ns, ds functions were chosen to represent the transformation is that the other functions will be ratios of these three (except for their inverses) and the multiplication factors will cancel.
The following table lists the multiplication factors for the three ps functions, the transformed m's, and the transformed function names for each of the six transformations.[5]: 214 (As usual, k2 = m, 1 − k2 = k12 = m′ and the arguments () are suppressed)
Parameters for the six transformations Transformation i cs' ns' ds' U 1 m cs ns ds I i m' ns cs ds IR i k −m'/m ds cs ns R k 1/m ds ns cs RI i k1 1/m' ns ds cs RIR k1 −m/m' cs ds ns
Thus, for example, we may build the following table for the RIR transformation.[11] The transformation is generally written (The arguments are suppressed)
The RIR transformation q c s n d p c 1 k' cs cd cn s sc 1 sd sn n dc ds 1 dn d nc ns nd 1
The value of the Jacobi transformations is that any set of Jacobi elliptic functions with any real-valued parameter m can be converted into another set for which and, for real values of u, the function values will be real.[5]: p. 215
Amplitude transformations
[edit]In the following, the second variable is suppressed and is equal to :
where both identities are valid for all such that both sides are well-defined.
With
we have
where all the identities are valid for all such that both sides are well-defined.
The Jacobi hyperbola
[edit]
Introducing complex numbers, our ellipse has an associated hyperbola:
from applying Jacobi's imaginary transformation[11] to the elliptic functions in the above equation for x and y.
It follows that we can put . So our ellipse has a dual ellipse with m replaced by 1-m. This leads to the complex torus mentioned in the Introduction.[13] Generally, m may be a complex number, but when m is real and m<0, the curve is an ellipse with major axis in the x direction. At m=0 the curve is a circle, and for 0<m<1, the curve is an ellipse with major axis in the y direction. At m = 1, the curve degenerates into two vertical lines at x = ±1. For m > 1, the curve is a hyperbola. When m is complex but not real, x or y or both are complex and the curve cannot be described on a real x-y diagram.
Minor functions
[edit]Reversing the order of the two letters of the function name results in the reciprocals of the three functions above:
Similarly, the ratios of the three primary functions correspond to the first letter of the numerator followed by the first letter of the denominator:
More compactly, we have
where p and q are any of the letters s, c, d.
Periodicity, poles, and residues
[edit]
In the complex plane of the argument u, the Jacobi elliptic functions form a repeating pattern of poles (and zeroes). The residues of the poles all have the same absolute value, differing only in sign. Each function pq(u,m) has an "inverse function" (in the multiplicative sense) qp(u,m) in which the positions of the poles and zeroes are exchanged. The periods of repetition are generally different in the real and imaginary directions, hence the use of the term "doubly periodic" to describe them.
For the Jacobi amplitude and the Jacobi epsilon function:
where is the complete elliptic integral of the second kind with parameter .
The double periodicity of the Jacobi elliptic functions may be expressed as:
where α and β are any pair of integers. K(⋅) is the complete elliptic integral of the first kind, also known as the quarter period. The power of negative unity (γ) is given in the following table:
q c s n d p c 0 β α + β α s β 0 α α + β n α + β α 0 β d α α + β β 0
When the factor (−1)γ is equal to −1, the equation expresses quasi-periodicity. When it is equal to unity, it expresses full periodicity. It can be seen, for example, that for the entries containing only α when α is even, full periodicity is expressed by the above equation, and the function has full periods of 4K(m) and 2iK(1 − m). Likewise, functions with entries containing only β have full periods of 2K(m) and 4iK(1 − m), while those with α + β have full periods of 4K(m) and 4iK(1 − m).
In the diagram on the right, which plots one repeating unit for each function, indicating phase along with the location of poles and zeroes, a number of regularities can be noted: The inverse of each function is opposite the diagonal, and has the same size unit cell, with poles and zeroes exchanged. The pole and zero arrangement in the auxiliary rectangle formed by (0,0), (K,0), (0,K′) and (K,K′) are in accordance with the description of the pole and zero placement described in the introduction above. Also, the size of the white ovals indicating poles are a rough measure of the absolute value of the residue for that pole. The residues of the poles closest to the origin in the figure (i.e. in the auxiliary rectangle) are listed in the following table:
Residues of Jacobi Elliptic Functions q c s n d p c 1 s n 1 d -1 1
When applicable, poles displaced above by 2K or displaced to the right by 2K′ have the same value but with signs reversed, while those diagonally opposite have the same value. Note that poles and zeroes on the left and lower edges are considered part of the unit cell, while those on the upper and right edges are not.
The information about poles can in fact be used to characterize the Jacobi elliptic functions:[14]
The function is the unique elliptic function having simple poles at (with ) with residues taking the value at .
The function is the unique elliptic function having simple poles at (with ) with residues taking the value at .
The function is the unique elliptic function having simple poles at (with ) with residues taking the value at .
Special values
[edit]Setting gives the lemniscate elliptic functions and :
When or , the Jacobi elliptic functions are reduced to non-elliptic functions:
| Function | m = 0 | m = 1 |
|---|---|---|
For the Jacobi amplitude, and where is the Gudermannian function.
In general if neither of p,q is d then .
Identities
[edit]Half angle formula
[edit]
K formulas
[edit]Half K formula
Third K formula
To get x3, we take the tangent of twice the arctangent of the modulus.
Also this equation leads to the sn-value of the third of K:
These equations lead to the other values of the Jacobi-Functions:
Fifth K formula
Following equation has following solution:
To get the sn-values, we put the solution x into following expressions:
Relations between squares of the functions
[edit]Relations between squares of the functions can be derived from two basic relationships (Arguments (u,m) suppressed): where m + m' = 1. Multiplying by any function of the form nq yields more general equations:
With q = d, these correspond trigonometrically to the equations for the unit circle () and the unit ellipse (), with x = cd, y = sd and r = nd. Using the multiplication rule, other relationships may be derived. For example:
Addition theorems
[edit]The functions satisfy the two square relations (dependence on m suppressed)
From this we see that (cn, sn, dn) parametrizes an elliptic curve which is the intersection of the two quadrics defined by the above two equations. We now may define a group law for points on this curve by the addition formulas for the Jacobi functions[3]
The Jacobi epsilon and zn functions satisfy a quasi-addition theorem:
Double angle formulae can be easily derived from the above equations by setting x = y.[3] Half angle formulae[11][3] are all of the form:
where:
Jacobi elliptic functions as solutions of nonlinear ordinary differential equations
[edit]Derivatives with respect to the first variable
[edit]The derivatives of the three basic Jacobi elliptic functions (with respect to the first variable, with fixed) are:
These can be used to derive the derivatives of all other functions as shown in the table below (arguments (u,m) suppressed):
| q | |||||
|---|---|---|---|---|---|
| c | s | n | d | ||
| p | |||||
| c | 0 | −ds ns | −dn sn | −m' nd sd | |
| s | dc nc | 0 | cn dn | cd nd | |
| n | dc sc | −cs ds | 0 | m cd sd | |
| d | m' nc sc | −cs ns | −m cn sn | 0 | |
Also
With the addition theorems above and for a given m with 0 < m < 1 the major functions are therefore solutions to the following nonlinear ordinary differential equations:
- solves the differential equations and
- (for not on a branch cut)
- solves the differential equations and
- solves the differential equations and
- solves the differential equations and
The function which exactly solves the pendulum differential equation,
with initial angle and zero initial angular velocity is
where , and .
Derivatives with respect to the second variable
[edit]With the first argument fixed, the derivatives with respect to the second variable are as follows:
Expansion in terms of the nome
[edit]Let the nome be , , and let . Then the functions have expansions as Lambert series
when
Bivariate power series expansions have been published by Schett.[15]
Fast computation
[edit]The theta function ratios provide an efficient way of computing the Jacobi elliptic functions. There is an alternative method, based on the arithmetic-geometric mean and Landen's transformations:[6]
Initialize
where . Define
where . Then define
for and a fixed . If
for , then
as . This is notable for its rapid convergence. It is then trivial to compute all Jacobi elliptic functions from the Jacobi amplitude on the real line.[note 2]
In conjunction with the addition theorems for elliptic functions (which hold for complex numbers in general) and the Jacobi transformations, the method of computation described above can be used to compute all Jacobi elliptic functions in the whole complex plane.
Another method of fast computation of the Jacobi elliptic functions via the arithmetic–geometric mean, avoiding the computation of the Jacobi amplitude, is due to Herbert E. Salzer:[16]
Let
Set
Then
as .
Yet, another method for a rapidly converging fast computation of the Jacobi elliptic sine function found in the literature is shown below.[17]
Let:
Then set:
Then:
- .
Approximation in terms of hyperbolic functions
[edit]The Jacobi elliptic functions can be expanded in terms of the hyperbolic functions. When is close to unity, such that and higher powers of can be neglected, we have:[18][19]
- sn(u):
- cn(u):
- dn(u):
For the Jacobi amplitude,
Continued fractions
[edit]Assuming real numbers with and the nome , with elliptic modulus . If , where is the complete elliptic integral of the first kind, then holds the following continued fraction expansion[20]
Known continued fractions involving and with elliptic modulus are
For , :[21] pg. 374
For , :[21] pg. 375
For , :[22] pg. 220
For , :[21] pg. 374
For , :[21] pg. 375
Inverse functions
[edit]The inverses of the Jacobi elliptic functions can be defined similarly to the inverse trigonometric functions; if , . They can be represented as elliptic integrals,[23][24][25] and power series representations have been found.[26][3]
Map projection
[edit]The Peirce quincuncial projection is a map projection based on Jacobian elliptic functions.
See also
[edit]- Elliptic curve
- Schwarz–Christoffel mapping
- Carlson symmetric form
- Jacobi theta function
- Ramanujan theta function
- Dixon elliptic functions
- Abel elliptic functions
- Weierstrass elliptic function
- Lemniscate elliptic functions
Notes
[edit]Citations
[edit]- ^ Armitage, J. V.; Eberlein, W. F. (2006). Elliptic Functions (First ed.). Cambridge University Press. ISBN 978-0-521-78078-0. p. 48
- ^ a b Walker, Peter (2003). "The Analyticity of Jacobian Functions with Respect to the Parameter k". Proceedings of the Royal Society. 459 (2038): 2569–2574. Bibcode:2003RSPSA.459.2569W. doi:10.1098/rspa.2003.1157. JSTOR 3560143. S2CID 121368966.
- ^ a b c d e Olver, F. W. J.; et al., eds. (2017-12-22). "NIST Digital Library of Mathematical Functions (Release 1.0.17)". National Institute of Standards and Technology. Retrieved 2018-02-26.
- ^ "cplot, Python package for plotting complex-valued functions". GitHub.
- ^ a b c d e f Neville, Eric Harold (1944). Jacobian Elliptic Functions. Oxford: Oxford University Press.
- ^ a b Sala, Kenneth L. (November 1989). "Transformations of the Jacobian Amplitude Function and Its Calculation via the Arithmetic-Geometric Mean". SIAM Journal on Mathematical Analysis. 20 (6): 1514–1528. doi:10.1137/0520100.
- ^ Reinhardt, W. P.; Walker, P. L. (2010), "Jacobian Elliptic Functions", in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248.
- ^ Carlson, B. C. (2010), "Elliptic Integrals", in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248.
- ^ Whittaker, Edmund Taylor; Watson, George Neville (1927). A Course of Modern Analysis (4th ed.). Cambridge University Press. p. 492.
- ^ Cox, David Archibald (January 1984). "The Arithmetic-Geometric Mean of Gauss". L'Enseignement Mathématique. 30 (2): 290.
- ^ a b c d e f "Introduction to the Jacobi elliptic functions". The Wolfram Functions Site. Wolfram Research, Inc. 2018. Retrieved January 7, 2018.
- ^ Whittaker, E.T.; Watson, G.N. (1940). A Course in Modern Analysis. New York, USA: The MacMillan Co. ISBN 978-0-521-58807-2.
- ^ "Elliptic Functions: Complex Variables".
- ^ Whittaker, Edmund Taylor; Watson, George Neville (1927). A Course of Modern Analysis (4th ed.). Cambridge University Press. pp. 504–505.
- ^ Schett, Alois (1976). "Properties of the Taylor series expansion coefficients of the Jacobian Elliptic Functions". Math. Comp. 30 (133): 143–147. doi:10.1090/S0025-5718-1976-0391477-3. MR 0391477. S2CID 120666361.
- ^ Salzer, Herbert E. (July 1962). "Quick calculation of Jacobian elliptic functions". Communications of the ACM. 5 (7): 399. doi:10.1145/368273.368573. S2CID 44953400.
- ^ Smith, John I. (May 5, 1971). "The Even- and Odd-Mode Capacitance Parameters for Coupled Lines in Suspended Substrate". IEEE Transactions on Microwave Theory and Techniques. MTT-19 (5): 430. Bibcode:1971ITMTT..19..424S. doi:10.1109/TMTT.1971.1127543 – via IEEE Xplore.
- ^ Reinhardt, W. P.; Walker, P. L. (2010), "Jacobian Elliptic Functions", in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248.
- ^ Reinhardt, W. P.; Walker, P. L. (2010), "Jacobian Elliptic Functions", in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248.
- ^ N.Bagis.(2020)."Evaluations of series related to Jacobi elliptic functions". preprint https://www.researchgate.net/publication/331370071_Evaluations_of_Series_Related_to_Jacobi_Elliptic_Functions
- ^ a b c d H.S. Wall. (1948). "Analytic Theory of Continued Fractions", Van Nostrand, New York.
- ^ Perron, O. (1957). "Die Lehre von den Kettenbruchen", Band II, B.G. Teubner, Stuttgart.
- ^ Reinhardt, W. P.; Walker, P. L. (2010), "§22.15 Inverse Functions", in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248.
- ^ Ehrhardt, Wolfgang. "The AMath and DAMath Special Functions: Reference Manual and Implementation Notes" (PDF). p. 42. Archived from the original (PDF) on 31 July 2016. Retrieved 17 July 2013.
- ^ Byrd, P.F.; Friedman, M.D. (1971). Handbook of Elliptic Integrals for Engineers and Scientists (2nd ed.). Berlin: Springer-Verlag.
- ^ Carlson, B. C. (2008). "Power series for inverse Jacobian elliptic functions" (PDF). Mathematics of Computation. 77 (263): 1615–1621. Bibcode:2008MaCom..77.1615C. doi:10.1090/s0025-5718-07-02049-2. Retrieved 17 July 2013.
References
[edit]- Abramowitz, Milton; Stegun, Irene Ann, eds. (1983) [June 1964]. "Chapter 16". Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Applied Mathematics Series. Vol. 55 (Ninth reprint with additional corrections of tenth original printing with corrections (December 1972); first ed.). Washington D.C.; New York: United States Department of Commerce, National Bureau of Standards; Dover Publications. p. 569. ISBN 978-0-486-61272-0. LCCN 64-60036. MR 0167642. LCCN 65-12253.
- N. I. Akhiezer, Elements of the Theory of Elliptic Functions (1970) Moscow, translated into English as AMS Translations of Mathematical Monographs Volume 79 (1990) AMS, Rhode Island ISBN 0-8218-4532-2
- A. C. Dixon The elementary properties of the elliptic functions, with examples (Macmillan, 1894)
- Alfred George Greenhill The applications of elliptic functions (London, New York, Macmillan, 1892)
- Edmund T. Whittaker, George Neville Watson: A Course in Modern Analysis. 4th ed. Cambridge, England: Cambridge University Press, 1990. S. 469–470.
- H. Hancock Lectures on the theory of elliptic functions (New York, J. Wiley & sons, 1910)
- Jacobi, C. G. J. (1829), Fundamenta nova theoriae functionum ellipticarum (in Latin), Königsberg, ISBN 978-1-108-05200-9, Reprinted by Cambridge University Press 2012
- Reinhardt, William P.; Walker, Peter L. (2010), "Jacobian Elliptic Functions", in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248.
- (in French) P. Appell and E. Lacour Principes de la théorie des fonctions elliptiques et applications (Paris, Gauthier Villars, 1897)
- (in French) G. H. Halphen Traité des fonctions elliptiques et de leurs applications (vol. 1) (Paris, Gauthier-Villars, 1886–1891)
- (in French) G. H. Halphen Traité des fonctions elliptiques et de leurs applications (vol. 2) (Paris, Gauthier-Villars, 1886–1891)
- (in French) G. H. Halphen Traité des fonctions elliptiques et de leurs applications (vol. 3) (Paris, Gauthier-Villars, 1886–1891)
- (in French) J. Tannery and J. Molk Eléments de la théorie des fonctions elliptiques. Tome I, Introduction. Calcul différentiel. Ire partie (Paris : Gauthier-Villars et fils, 1893)
- (in French) J. Tannery and J. Molk Eléments de la théorie des fonctions elliptiques. Tome II, Calcul différentiel. IIe partie (Paris : Gauthier-Villars et fils, 1893)
- (in French) J. Tannery and J. Molk Eléments de la théorie des fonctions elliptiques. Tome III, Calcul intégral. Ire partie, Théorèmes généraux. Inversion (Paris : Gauthier-Villars et fils, 1893)
- (in French) J. Tannery and J. Molk Eléments de la théorie des fonctions elliptiques. Tome IV, Calcul intégral. IIe partie, Applications (Paris : Gauthier-Villars et fils, 1893)
- (in French) C. Briot and J. C. Bouquet Théorie des fonctions elliptiques ( Paris : Gauthier-Villars, 1875)
- Toshio Fukushima: Fast Computation of Complete Elliptic Integrals and Jacobian Elliptic Functions. 2012, National Astronomical Observatory of Japan (国立天文台)
- Lowan, Blanch und Horenstein: On the Inversion of the q-Series Associated with Jacobian Elliptic Functions. Bull. Amer. Math. Soc. 48, 1942
- H. Ferguson, D. E. Nielsen, G. Cook: A partition formula for the integer coefficients of the theta function nome. Mathematics of computation, Volume 29, Nummer 131, Juli 1975
- J. D. Fenton and R. S. Gardiner-Garden: Rapidly-convergent methods for evaluating elliptic integrals and theta and elliptic functions. J. Austral. Math. Soc. (Series B) 24, 1982, S. 57
- Adolf Kneser: Neue Untersuchung einer Reihe aus der Theorie der elliptischen Funktionen. J. reine u. angew. Math. 157, 1927. pages 209 – 218




































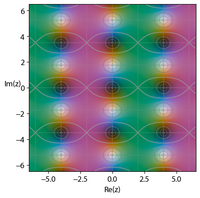


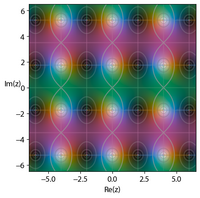

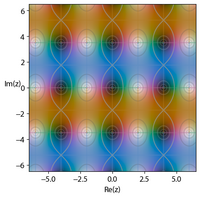






























































































































































































































![{\displaystyle \operatorname {sn} \left[{\tfrac {1}{2}}K(k);k\right]={\frac {\sqrt {2}}{{\sqrt {1+k}}+{\sqrt {1-k}}}}}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/ed82907c77897c29b197ad49d191e97568af3a0f)
![{\displaystyle \operatorname {cn} \left[{\tfrac {1}{2}}K(k);k\right]={\frac {{\sqrt {2}}\,{\sqrt[{4}]{1-k^{2}}}}{{\sqrt {1+k}}+{\sqrt {1-k}}}}}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/3438731cb1b1b39124a6e4675420fb84a8e89bba)
![{\displaystyle \operatorname {dn} \left[{\tfrac {1}{2}}K(k);k\right]={\sqrt[{4}]{1-k^{2}}}}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/e5257c49ceccef91f2fca3a910e76ee9b0271e33)
![{\displaystyle \operatorname {sn} \left[{\frac {1}{3}}K\left({\frac {x^{3}}{{\sqrt {x^{6}+1}}+1}}\right);{\frac {x^{3}}{{\sqrt {x^{6}+1}}+1}}\right]={\frac {{\sqrt {2{\sqrt {x^{4}-x^{2}+1}}-x^{2}+2}}+{\sqrt {x^{2}+1}}-1}{{\sqrt {2{\sqrt {x^{4}-x^{2}+1}}-x^{2}+2}}+{\sqrt {x^{2}+1}}+1}}}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/3a55b698b1f4a2c82dd98b9a357808c81a574a1f)

![{\displaystyle s=\operatorname {sn} \left[{\tfrac {1}{3}}K(k);k\right]}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/7d02d4647e1efcb10a29246750edb36cd609ebdd)
![{\displaystyle \operatorname {cn} \left[{\tfrac {2}{3}}K(k);k\right]=1-\operatorname {sn} \left[{\tfrac {1}{3}}K(k);k\right]}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/b8ff147f7bba74210bfc2aecb6a7d5f1e631e593)
![{\displaystyle \operatorname {dn} \left[{\tfrac {2}{3}}K(k);k\right]=1/\operatorname {sn} \left[{\tfrac {1}{3}}K(k);k\right]-1}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/5e954723c754da74da208796a92de7a6f1c12ee3)

![{\displaystyle x={\frac {1}{2}}-{\frac {1}{2}}k^{2}\operatorname {sn} \left[{\tfrac {2}{5}}K(k);k\right]^{2}\operatorname {sn} \left[{\tfrac {4}{5}}K(k);k\right]^{2}={\frac {\operatorname {sn} \left[{\frac {4}{5}}K(k);k\right]^{2}-\operatorname {sn} \left[{\frac {2}{5}}K(k);k\right]^{2}}{2\operatorname {sn} \left[{\frac {2}{5}}K(k);k\right]\operatorname {sn} \left[{\frac {4}{5}}K(k);k\right]}}}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/a4e1e2cac70ecfaac820bc6e651c16b587c5a0a4)
![{\displaystyle \operatorname {sn} \left[{\tfrac {2}{5}}K(k);k\right]=(1+k^{2})^{-1/2}{\sqrt {2(1-x-x^{2})(x^{2}+1-x{\sqrt {x^{2}+1}})}}}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/59616f297795198522bd003f6538789e21df3610)
![{\displaystyle \operatorname {sn} \left[{\tfrac {4}{5}}K(k);k\right]=(1+k^{2})^{-1/2}{\sqrt {2(1-x-x^{2})(x^{2}+1+x{\sqrt {x^{2}+1}})}}}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/4f2f49ed0b51dbe9f0a15ecf90ff0884df9c86f8)












![{\displaystyle {\begin{aligned}\operatorname {cn} (x+y)&={\operatorname {cn} (x)\operatorname {cn} (y)-\operatorname {sn} (x)\operatorname {sn} (y)\operatorname {dn} (x)\operatorname {dn} (y) \over {1-m\operatorname {sn} ^{2}(x)\operatorname {sn} ^{2}(y)}},\\[8pt]\operatorname {sn} (x+y)&={\operatorname {sn} (x)\operatorname {cn} (y)\operatorname {dn} (y)+\operatorname {sn} (y)\operatorname {cn} (x)\operatorname {dn} (x) \over {1-m\operatorname {sn} ^{2}(x)\operatorname {sn} ^{2}(y)}},\\[8pt]\operatorname {dn} (x+y)&={\operatorname {dn} (x)\operatorname {dn} (y)-m\operatorname {sn} (x)\operatorname {sn} (y)\operatorname {cn} (x)\operatorname {cn} (y) \over {1-m\operatorname {sn} ^{2}(x)\operatorname {sn} ^{2}(y)}}.\end{aligned}}}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/4bfd8c48734ac156351213c7c745a30b682fcb6f)

































































![{\displaystyle K[\tau ]=K(k(\tau ))}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/3b9e0c6bdeff30398693bc75ee3916b13a57d11a)

![{\displaystyle {\begin{aligned}&{\frac {{\textrm {dn}}\left((p/2-a)\tau K\left[{\frac {p\tau }{2}}\right];k\left({\frac {p\tau }{2}}\right)\right)}{\sqrt {k'\left({\frac {p\tau }{2}}\right)}}}={\frac {\sum _{n=-\infty }^{\infty }q^{p/2n^{2}+(p/2-a)n}}{\sum _{n=-\infty }^{\infty }(-1)^{n}q^{p/2n^{2}+(p/2-a)n}}}\\[4pt]={}&-1+{\frac {2}{1-{}}}\,{\frac {q^{a}+q^{p-a}}{1-q^{p}+{}}}\,{\frac {(q^{a}+q^{2p-a})(q^{a+p}+q^{p-a})}{1-q^{3p}+{}}}\,{\frac {q^{p}(q^{a}+q^{3p-a})(q^{a+2p}+q^{p-a})}{1-q^{5p}+{}}}\,{\frac {q^{2p}(q^{a}+q^{4p-a})(q^{a+3p}+q^{p-a})}{1-q^{7p}+{}}}\cdots \end{aligned}}}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/aef2c799ca80eecd7e2fdb629c2148326e37c57d)















![{\displaystyle [0,1]}](https://wikimedia.org/enwiki/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)

