6-cube: Difference between revisions
m →Projections: an hexeract → a hexeract |
|||
| (45 intermediate revisions by 13 users not shown) | |||
| Line 1: | Line 1: | ||
{{Short description|6-dimensional hypercube}} |
|||
{| class="wikitable" align="right" style="margin-left:10px" width="250" |
{| class="wikitable" align="right" style="margin-left:10px" width="250" |
||
!bgcolor=#e7dcc3 colspan=2|6-cube<BR>Hexeract |
!bgcolor=#e7dcc3 colspan=2|6-cube<BR>Hexeract |
||
| Line 10: | Line 11: | ||
|bgcolor=#e7dcc3|[[Schläfli symbol]]|| {4,3<sup>4</sup>} |
|bgcolor=#e7dcc3|[[Schläfli symbol]]|| {4,3<sup>4</sup>} |
||
|- |
|- |
||
|bgcolor=#e7dcc3|[[Coxeter |
|bgcolor=#e7dcc3|[[Coxeter diagram]]||{{CDD|node_1|4|node|3|node|3|node|3|node|3|node}} |
||
|- |
|- |
||
|bgcolor=#e7dcc3|5-faces||12 [[5-cube|{4,3,3,3}]] [[File:5-cube graph.svg|25px]] |
|bgcolor=#e7dcc3|5-faces||12 [[5-cube|{4,3,3,3}]] [[File:5-cube graph.svg|25px]] |
||
| Line 32: | Line 33: | ||
|bgcolor=#e7dcc3|Dual||[[6-orthoplex]] [[File:6-orthoplex.svg|25px]] |
|bgcolor=#e7dcc3|Dual||[[6-orthoplex]] [[File:6-orthoplex.svg|25px]] |
||
|- |
|- |
||
|bgcolor=#e7dcc3|Properties||[[Convex polytope|convex]] |
|bgcolor=#e7dcc3|Properties||[[Convex polytope|convex]], [[Hanner polytope]] |
||
|} |
|} |
||
In [[geometry]], a '''6-cube''' is a six-[[dimension]]al [[hypercube]] with 64 [[Vertex (geometry)|vertices]], 192 [[Edge (geometry)|edge]]s, 240 square [[Face (geometry)|faces]], 160 cubic [[Cell (mathematics)|cells]], 60 [[tesseract]] [[4-face]]s, and 12 [[5-cube]] [[5-face]]s. |
In [[geometry]], a '''6-cube''' is a six-[[dimension]]al [[hypercube]] with 64 [[Vertex (geometry)|vertices]], 192 [[Edge (geometry)|edge]]s, 240 square [[Face (geometry)|faces]], 160 cubic [[Cell (mathematics)|cells]], 60 [[tesseract]] [[4-face]]s, and 12 [[5-cube]] [[5-face]]s. |
||
| Line 40: | Line 41: | ||
== Related polytopes== |
== Related polytopes== |
||
It is a part of an infinite family of polytopes, called [[hypercube]]s. The [[Dual polytope|dual]] of a 6-cube can be called a [[6-orthoplex]], and is a part of the infinite family of [[cross-polytope]]s. |
It is a part of an infinite family of polytopes, called [[hypercube]]s. The [[Dual polytope|dual]] of a 6-cube can be called a [[6-orthoplex]], and is a part of the infinite family of [[cross-polytope]]s. It is composed of various [[5-cubes]], at perpendicular angles on the u-axis, forming coordinates (x,y,z,w,v,u).<ref>{{Cite web|url=https://www.researchgate.net/publication/361688598_A_New_Six-Dimensional_Hyper-Chaotic_System|title=(PDF) A New Six-Dimensional Hyper-Chaotic System}}</ref><ref>{{Cite web|url=https://www.sciencedirect.com/science/article/pii/S0747717188800105|title=An improved projection operation for cylindrical algebraic decomposition of three-dimensional space - ScienceDirect}}</ref> |
||
Applying an ''[[Alternation (geometry)|alternation]]'' operation, deleting alternating vertices of the 6-cube, creates another [[uniform polytope]], called a [[6-demicube]], (part of an infinite family called [[demihypercube]]s), which has 12 [[5-demicube]] and 32 [[5-simplex]] facets. |
Applying an ''[[Alternation (geometry)|alternation]]'' operation, deleting alternating vertices of the 6-cube, creates another [[uniform polytope]], called a [[6-demicube]], (part of an infinite family called [[demihypercube]]s), which has 12 [[5-demicube]] and 32 [[5-simplex]] facets. |
||
== As a configuration== |
|||
This [[Regular 4-polytope#As configurations|configuration matrix]] represents the 6-cube. The rows and columns correspond to vertices, edges, faces, cells, 4-faces and 5-faces. The diagonal numbers say how many of each element occur in the whole 6-cube. The nondiagonal numbers say how many of the column's element occur in or at the row's element.<ref>Coxeter, Regular Polytopes, sec 1.8 Configurations</ref><ref>Coxeter, Complex Regular Polytopes, p.117</ref> |
|||
<math>\begin{bmatrix}\begin{matrix}64 & 6 & 15 & 20 & 15 & 6 \\ 2 & 192 & 5 & 10 & 10 & 5 \\ 4 & 4 & 240 & 4 & 6 & 4 \\ 8 & 12 & 6 & 160 & 3 & 3 \\ 16 & 32 & 24 & 8 & 60 & 2 \\ 32 & 80 & 80 & 40 & 10 & 12 \end{matrix}\end{bmatrix}</math> |
|||
== Cartesian coordinates == |
== Cartesian coordinates == |
||
[[Cartesian coordinates]] for the vertices of a 6-cube centered at the origin and edge length 2 are |
[[Cartesian coordinates]] for the vertices of a 6-cube centered at the origin and edge length 2 are |
||
: (±1,±1,±1,±1,±1,±1) |
: (±1,±1,±1,±1,±1,±1) |
||
while the interior of the same consists of all points (x<sub>0</sub>, x<sub>1</sub>, x<sub>2</sub>, x<sub>3</sub>, x<sub>4</sub>, x<sub>5</sub>) with |
while the interior of the same consists of all points (x<sub>0</sub>, x<sub>1</sub>, x<sub>2</sub>, x<sub>3</sub>, x<sub>4</sub>, x<sub>5</sub>) with −1 < x<sub>i</sub> < 1. |
||
== Construction == |
== Construction == |
||
There are three [[Coxeter group]]s associated with the 6-cube, one [[regular polytope|regular]], with the C<sub>6</sub> or [4,3,3,3,3] [[Coxeter group]], and a half symmetry (D<sub>6</sub>) or [3<sup>3,1,1</sup>] Coxeter group. The lowest symmetry construction is based on [[hyperrectangle]]s, [[cartesian product]s of lower dimensional hypercubes. |
There are three [[Coxeter group]]s associated with the 6-cube, one [[regular polytope|regular]], with the C<sub>6</sub> or [4,3,3,3,3] [[Coxeter group]], and a half symmetry (D<sub>6</sub>) or [3<sup>3,1,1</sup>] Coxeter group. The lowest symmetry construction is based on [[hyperrectangle]]s or [[proprism]]s, [[cartesian product]]s of lower dimensional hypercubes. |
||
{| class=wikitable |
{| class="wikitable sortable" |
||
!Name |
!Name |
||
![[Coxeter diagram|Coxeter]] |
![[Coxeter diagram|Coxeter]] |
||
| Line 63: | Line 69: | ||
|{{CDD|node_1|4|node|3|node|3|node|3|node|3|node}}<BR>{{CDD|node_f1|3|node|3|node|3|node|3|node|4|node}} |
|{{CDD|node_1|4|node|3|node|3|node|3|node|3|node}}<BR>{{CDD|node_f1|3|node|3|node|3|node|3|node|4|node}} |
||
|{4,3,3,3,3} |
|{4,3,3,3,3} |
||
|[4,3 |
|[4,3,3,3,3]||46080 |
||
|- align=center |
|- align=center |
||
![[Quasiregular polytope|Quasiregular]] 6-cube |
![[Quasiregular polytope|Quasiregular]] 6-cube |
||
|{{CDD|node_f1|3|node|3|node|3|node|split1|nodes}} |
|{{CDD|node_f1|3|node|3|node|3|node|split1|nodes}} |
||
| |
| |
||
|[3<sup> |
|[3,3,3,3<sup>1,1</sup>]||23040 |
||
| ⚫ | |||
| ⚫ | |||
|- align=center |
|- align=center |
||
| ⚫ | |||
|{{CDD|node_1|4|node|3|node|3|node|3|node|2|node_1}} |
|{{CDD|node_1|4|node|3|node|3|node|3|node|2|node_1}} |
||
||{4,3,3,3}×{}||[4,3,3,3, |
||{4,3,3,3}×{}||[4,3,3,3,2]||7680 |
||
|- align=center |
|||
| ⚫ | |||
| ⚫ | |||
|- align=center |
|- align=center |
||
|{{CDD|node_1|4|node|3|node|3|node|2|node_1|4|node}} |
|{{CDD|node_1|4|node|3|node|3|node|2|node_1|4|node}} |
||
||{4,3,3}×{4}||[4,3,3,2,4]||3072 |
||{4,3,3}×{4}||[4,3,3,2,4]||3072 |
||
|- align=center |
|- align=center |
||
|{{CDD|node_1|4|node|3|node|2|node_1| |
|{{CDD|node_1|4|node|3|node|2|node_1|4|node|3|node}} |
||
||{4,3 |
||{4,3}<sup>2</sup>||[4,3,2,4,3]||2304 |
||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
|- align=center |
|- align=center |
||
|{{CDD|node_1|4|node|3|node|2|node_1|4|node|2|node_1}} |
|{{CDD|node_1|4|node|3|node|2|node_1|4|node|2|node_1}} |
||
||{4,3}×{4}×{}||[4,3,2,4,2]||768 |
||{4,3}×{4}×{}||[4,3,2,4,2]||768 |
||
|- align=center |
|- align=center |
||
|{{CDD|node_1|4 |
|{{CDD|node_1|4|node|2|node_1|4|node|2|node_1|4|node}} |
||
||{4 |
||{4}<sup>3</sup>||[4,2,4,2,4]||512 |
||
|- align=center |
|- align=center |
||
|{{CDD|node_1|4|node| |
|{{CDD|node_1|4|node|3|node|2|node_1|2|node_1|2|node_1}} |
||
||{4}×{}<sup> |
||{4,3}×{}<sup>3</sup>||[4,3,2,2,2]||384 |
||
|- align=center |
|- align=center |
||
|{{CDD|node_1|4|node|2|node_1|4|node|2|node_1|2|node_1}} |
|{{CDD|node_1|4|node|2|node_1|4|node|2|node_1|2|node_1}} |
||
||{4}<sup>2</sup>×{}<sup>2</sup>||[4,2,4,2,2]|| |
||{4}<sup>2</sup>×{}<sup>2</sup>||[4,2,4,2,2]||256 |
||
|- align=center |
|- align=center |
||
|{{CDD|node_1|4|node|2|node_1| |
|{{CDD|node_1|4|node|2|node_1|2|node_1|2|node_1|2|node_1}} |
||
||{4}<sup> |
||{4}×{}<sup>4</sup>||[4,2,2,2,2]||128 |
||
|- align=center |
|- align=center |
||
|{{CDD|node_1|2|node_1|2|node_1|2|node_1|2|node_1|2|node_1}} |
|{{CDD|node_1|2|node_1|2|node_1|2|node_1|2|node_1|2|node_1}} |
||
| Line 104: | Line 109: | ||
|} |
|} |
||
== |
== Projections == |
||
{| class=wikitable |
{| class=wikitable |
||
|+ [[orthographic projection]]s |
|+ [[orthographic projection]]s |
||
| Line 159: | Line 164: | ||
|[[File:Hexeract.ogv|280px]]<br>6-cube 6D simple rotation through 2Pi with 6D perspective projection to 3D. |
|[[File:Hexeract.ogv|280px]]<br>6-cube 6D simple rotation through 2Pi with 6D perspective projection to 3D. |
||
|[[File:6Cube-QuasiCrystal.png|280px]]<br>6-cube [[quasicrystal]] structure orthographically projected<br> to 3D using the [[golden ratio]]. |
|[[File:6Cube-QuasiCrystal.png|280px]]<br>6-cube [[quasicrystal]] structure orthographically projected<br> to 3D using the [[golden ratio]]. |
||
|- |
|||
|[[File:Hexeract-q1q4-q2q5-q3q6.gif|280px]]<br>A 3D [[Perspective (graphical)|perspective projection]] of a hexeract undergoing a triple [[rotation]] about the X-W1, Y-W2 and Z-W3 [[Orthogonal coordinates|orthogonal]] [[Rotation plane|planes]]. |
|||
|} |
|} |
||
== Related polytopes== |
== Related polytopes== |
||
The 64 vertices of a 6-cube also represent a regular skew 4-polytope {4,3,4 | 4}. Its net can be seen as a 4×4×4 matrix of 64 cubes, a periodic subset of the [[cubic honeycomb]], {4,3,4}, in 3-dimensions. It has 192 edges, and 192 square faces. Opposite faces fold together into a 4-cycle. Each fold direction adds 1 dimension, raising it into 6-space. |
|||
The ''6-cube'' is 6th in a series of [[hypercube]]: |
|||
{{Hypercube polytopes}} |
|||
This polytope is one of 63 [[ |
This polytope is one of 63 [[uniform 6-polytope]]s generated from the B<sub>6</sub> [[Coxeter plane]], including the regular 6-cube or [[6-orthoplex]]. |
||
{{Hexeract family}} |
{{Hexeract family}} |
||
== References == |
== References == |
||
<references /> |
|||
* [[Coxeter|Coxeter, H.S.M.]] ''[[Regular Polytopes (book)|Regular Polytopes]]'', (3rd edition, 1973), Dover edition, {{ISBN|0-486-61480-8}} p. 296, Table I (iii): Regular Polytopes, three regular polytopes in n-dimensions (n>=5) |
* [[Coxeter|Coxeter, H.S.M.]] ''[[Regular Polytopes (book)|Regular Polytopes]]'', (3rd edition, 1973), Dover edition, {{ISBN|0-486-61480-8}} p. 296, Table I (iii): Regular Polytopes, three regular polytopes in n-dimensions (n>=5) |
||
* {{KlitzingPolytopes|polypeta.htm|6D uniform polytopes (polypeta)|o3o3o3o3o4x - ax}} |
* {{KlitzingPolytopes|polypeta.htm|6D uniform polytopes (polypeta)|o3o3o3o3o4x - ax}} |
||
Latest revision as of 02:39, 11 July 2024
| 6-cube Hexeract | |
|---|---|
 Orthogonal projection inside Petrie polygon Orange vertices are doubled, and the center yellow has 4 vertices | |
| Type | Regular 6-polytope |
| Family | hypercube |
| Schläfli symbol | {4,34} |
| Coxeter diagram | |
| 5-faces | 12 {4,3,3,3} |
| 4-faces | 60 {4,3,3} |
| Cells | 160 {4,3} |
| Faces | 240 {4} |
| Edges | 192 |
| Vertices | 64 |
| Vertex figure | 5-simplex |
| Petrie polygon | dodecagon |
| Coxeter group | B6, [34,4] |
| Dual | 6-orthoplex |
| Properties | convex, Hanner polytope |
In geometry, a 6-cube is a six-dimensional hypercube with 64 vertices, 192 edges, 240 square faces, 160 cubic cells, 60 tesseract 4-faces, and 12 5-cube 5-faces.
It has Schläfli symbol {4,34}, being composed of 3 5-cubes around each 4-face. It can be called a hexeract, a portmanteau of tesseract (the 4-cube) with hex for six (dimensions) in Greek. It can also be called a regular dodeca-6-tope or dodecapeton, being a 6-dimensional polytope constructed from 12 regular facets.
Related polytopes
[edit]It is a part of an infinite family of polytopes, called hypercubes. The dual of a 6-cube can be called a 6-orthoplex, and is a part of the infinite family of cross-polytopes. It is composed of various 5-cubes, at perpendicular angles on the u-axis, forming coordinates (x,y,z,w,v,u).[1][2]
Applying an alternation operation, deleting alternating vertices of the 6-cube, creates another uniform polytope, called a 6-demicube, (part of an infinite family called demihypercubes), which has 12 5-demicube and 32 5-simplex facets.
As a configuration
[edit]This configuration matrix represents the 6-cube. The rows and columns correspond to vertices, edges, faces, cells, 4-faces and 5-faces. The diagonal numbers say how many of each element occur in the whole 6-cube. The nondiagonal numbers say how many of the column's element occur in or at the row's element.[3][4]
Cartesian coordinates
[edit]Cartesian coordinates for the vertices of a 6-cube centered at the origin and edge length 2 are
- (±1,±1,±1,±1,±1,±1)
while the interior of the same consists of all points (x0, x1, x2, x3, x4, x5) with −1 < xi < 1.
Construction
[edit]There are three Coxeter groups associated with the 6-cube, one regular, with the C6 or [4,3,3,3,3] Coxeter group, and a half symmetry (D6) or [33,1,1] Coxeter group. The lowest symmetry construction is based on hyperrectangles or proprisms, cartesian products of lower dimensional hypercubes.
| Name | Coxeter | Schläfli | Symmetry | Order |
|---|---|---|---|---|
| Regular 6-cube | {4,3,3,3,3} | [4,3,3,3,3] | 46080 | |
| Quasiregular 6-cube | [3,3,3,31,1] | 23040 | ||
| hyperrectangle | {4,3,3,3}×{} | [4,3,3,3,2] | 7680 | |
| {4,3,3}×{4} | [4,3,3,2,4] | 3072 | ||
| {4,3}2 | [4,3,2,4,3] | 2304 | ||
| {4,3,3}×{}2 | [4,3,3,2,2] | 1536 | ||
| {4,3}×{4}×{} | [4,3,2,4,2] | 768 | ||
| {4}3 | [4,2,4,2,4] | 512 | ||
| {4,3}×{}3 | [4,3,2,2,2] | 384 | ||
| {4}2×{}2 | [4,2,4,2,2] | 256 | ||
| {4}×{}4 | [4,2,2,2,2] | 128 | ||
| {}6 | [2,2,2,2,2] | 64 |
Projections
[edit]| Coxeter plane | B6 | B5 | B4 |
|---|---|---|---|
| Graph | 
|

|

|
| Dihedral symmetry | [12] | [10] | [8] |
| Coxeter plane | Other | B3 | B2 |
| Graph | 
|

|

|
| Dihedral symmetry | [2] | [6] | [4] |
| Coxeter plane | A5 | A3 | |
| Graph | 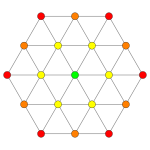
|

| |
| Dihedral symmetry | [6] | [4] |
| 3D Projections | |
6-cube 6D simple rotation through 2Pi with 6D perspective projection to 3D. |
 6-cube quasicrystal structure orthographically projected to 3D using the golden ratio. |
 A 3D perspective projection of a hexeract undergoing a triple rotation about the X-W1, Y-W2 and Z-W3 orthogonal planes. | |
Related polytopes
[edit]The 64 vertices of a 6-cube also represent a regular skew 4-polytope {4,3,4 | 4}. Its net can be seen as a 4×4×4 matrix of 64 cubes, a periodic subset of the cubic honeycomb, {4,3,4}, in 3-dimensions. It has 192 edges, and 192 square faces. Opposite faces fold together into a 4-cycle. Each fold direction adds 1 dimension, raising it into 6-space.
The 6-cube is 6th in a series of hypercube:

|

|

|

|

|

|

|

|

|

|
| Line segment | Square | Cube | 4-cube | 5-cube | 6-cube | 7-cube | 8-cube | 9-cube | 10-cube |
This polytope is one of 63 uniform 6-polytopes generated from the B6 Coxeter plane, including the regular 6-cube or 6-orthoplex.
References
[edit]- ^ "(PDF) A New Six-Dimensional Hyper-Chaotic System".
- ^ "An improved projection operation for cylindrical algebraic decomposition of three-dimensional space - ScienceDirect".
- ^ Coxeter, Regular Polytopes, sec 1.8 Configurations
- ^ Coxeter, Complex Regular Polytopes, p.117
- Coxeter, H.S.M. Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8 p. 296, Table I (iii): Regular Polytopes, three regular polytopes in n-dimensions (n>=5)
- Klitzing, Richard. "6D uniform polytopes (polypeta) o3o3o3o3o4x - ax".
External links
[edit]- Weisstein, Eric W. "Hypercube". MathWorld.
- Olshevsky, George. "Measure polytope". Glossary for Hyperspace. Archived from the original on 4 February 2007.
- Multi-dimensional Glossary: hypercube Garrett Jones
































































