Generalised beam theory: Difference between revisions
Mark viking (talk | contribs) →top: Add context |
→References: Category |
||
| (19 intermediate revisions by 10 users not shown) | |||
| Line 1: | Line 1: | ||
{{short description|Engineering theory}} |
|||
{{Underlinked|date=January 2018}} |
|||
In [[structural engineering]] and [[mechanical engineering]], '''generalised beam theory (GBT)''' is a one-dimensional theory used to mathematically model how beams bend and twist under various loads. It is a generalization of classical [[Euler–Bernoulli beam theory]] that approximates a beam as an assembly of thin-walled plates that are constrained to deform as a [[linear combination]] of specified deformation [[Normal mode|modes]].<ref name="deMiranda2013">{{cite journal|last1=de Miranda|first1=Stefano|last2=Gutiérrez|first2=Alejandro|last3=Miletta|first3=Rosario|last4=Ubertini|first4=Francesco|title=A generalized beam theory with shear deformation|journal=Thin-Walled Structures|date=June 2013|volume=67|pages=88–100|doi=10.1016/j.tws.2013.02.012}}</ref> |
|||
== History== |
|||
| ⚫ | |||
| ⚫ | <ref>{{cite journal|last1=Silvestre|first1=N|last2=Camotim|first2=D|title=Second-order generalised beam theory for arbitrary orthotropic materials|journal=Thin-Walled |
||
| ⚫ | Its origin is due to Richard Schardt (1966). Since then many other authors have extended the initial (first-order elastic) GBT formulations developed by Schardt and his co-workers.<ref>{{cite journal|last1=Schardt|first1=Richard|title=Generalised Beam Theory – an adequate method for coupled stability problems|journal=Thin-Walled Structures|date=1994|volume=19|issue=2–4|pages=161–180|doi=10.1016/0263-8231(94)90027-2}}</ref><ref>{{cite journal|last1=Davies|first1=JM|title=Recent research advances in cold-formed steel structures|journal=Journal of Constructional Steel Research|date=2000|volume=55|issue=1–3|doi=10.1016/S0143-974X(99)00089-9|pages=267–288}}</ref> Many extensions and applications of GBT have been developed by Camotim ([[Instituto Superior Técnico]], University of Lisbon, Portugal) and collaborators, since the beginning of the 21st century. |
||
| ⚫ | The theory can be applied without restrictions to any prismatic thin-walled structural member exhibiting straight or curved axial axis (any loading, any cross-section geometry, any boundary conditions) |
||
| ⚫ | <ref>{{cite journal|last1=Silvestre|first1=N|last2=Camotim|first2=D|title=Second-order generalised beam theory for arbitrary orthotropic materials|journal=Thin-Walled Structures|date=2002|volume=40|issue=9|pages=791–820|doi=10.1016/S0263-8231(02)00026-5}}</ref><ref>{{cite journal|last1=Borges Dinis|first1=P|last2=Camotim|first2=D|last3=Silvestre|first3=N|title=GBT formulation to analyse the buckling behaviour of thin-walled members with arbitrarily 'branched'open cross-sections|journal=Thin-Walled Structures|date=2006|volume=44|issue=1|pages=20–38|doi=10.1016/j.tws.2005.09.005}}</ref><ref>{{cite journal|last1=Camotim|first1=D|last2=Basaglia|first2=C|last3=Silvestre|first3=N|title=GBT buckling analysis of thin-walled steel frames: a state-of-the-art report|journal=Thin-Walled Structures|date=2010|volume=48|issue=10|pages=726–743|doi=10.1016/j.tws.2009.12.003}}</ref><ref>{{cite journal|last1=Abambres|first1=M|last2=Camotim|first2=D|last3=Silvestre|first3=N|title=GBT-based elastic–plastic post-buckling analysis of stainless steel thin-walled members|journal=Thin-Walled Structures|date=2014|volume=83|issue=October|pages=85–102|doi=10.1016/j.tws.2014.01.004|s2cid=120053099|url=https://hal.archives-ouvertes.fr/hal-02450449/file/4th%20ISSSES%202012%20Paper_Abambres%2C%20Camotim%2C%20Silvestre.pdf}}</ref><ref>{{cite journal|last1=Abambres|first1=M|last2=Camotim|first2=D|last3=Silvestre|first3=N|last4=Rasmussen|first4=KJR|title=GBT-based structural analysis of elastic–plastic thin-walled members|journal=Computers & Structures|date=2014|volume=136|issue=May|pages=1–23|doi=10.1016/j.compstruc.2014.01.001|s2cid=122047967|url=https://hal.archives-ouvertes.fr/hal-02450457/file/SSRC%202013%20Paper_Abambres%20et%20al.pdf}}</ref><ref>{{cite journal|last1=Bebiano|first1=R|last2=Gonçalves|first2=R|last3=Camotim|first3=D|title=A cross-section analysis procedure to rationalise and automate the performance of GBT-based structural analyses|journal=Thin-Walled Structures|date=2015|volume=92|issue=July|pages=29–47|doi=10.1016/j.tws.2015.02.017}}</ref><ref>{{cite journal|last1=Gonçalves|first1=R|last2=Camotim|first2=D|title=GBT deformation modes for curved thin-walled cross-sections based on a mid-line polygonal approximation|journal=Thin-Walled Structures|volume=103|date=2016|issue=January|pages=231–243|doi=10.1016/j.tws.2015.12.025}}</ref> |
||
== Description == |
|||
| ⚫ | GBT has |
||
| ⚫ | The theory can be applied without restrictions to any prismatic thin-walled structural member exhibiting straight or curved axial axis (any [[Structural load|loading]], any [[Cross section (geometry)|cross-section geometry]], any boundary conditions). GBT is in some ways analogous to the [[finite strip method]]<ref name="deMiranda2013" /> and can be a more computationally efficient method than modeling a beam with a full 2D or 3D [[finite element method]] to predict the member structural behavior. |
||
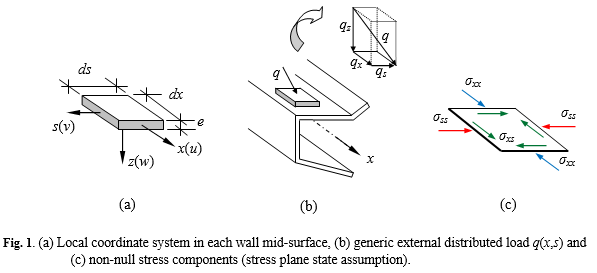
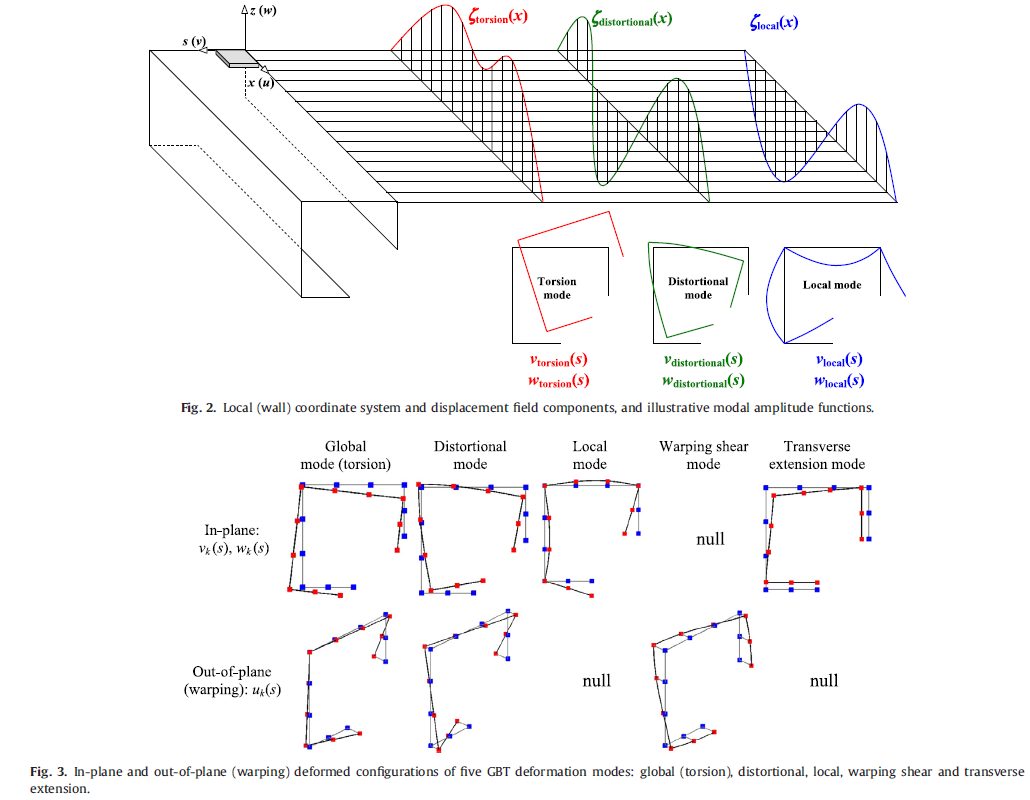
| ⚫ | GBT has been widely recognized as an efficient approach to analyzing thin-walled members and structural systems. The efficiency arises mostly from its modal nature – the [[Displacement field (mechanics)|displacement field]] is expressed as a linear combination of cross-section deformation modes whose amplitudes vary continuously along the member length (x axis) - see Figures 2-3. Due to GBT assumptions inherent to a thin-walled member, only 3 non-null stress components are considered in the formulations (see Fig. 1). |
||
Membrane displacement field (i.e., in the cross-section mid-surface): |
Membrane displacement field (i.e., in the cross-section mid-surface): |
||
| Line 19: | Line 23: | ||
<!-- [[File:GBT membrane displacement field.png|GBT membrane displacement field]] --> |
<!-- [[File:GBT membrane displacement field.png|GBT membrane displacement field]] --> |
||
The GBT modal nature makes it possible to (i) acquire in-depth knowledge on the mechanics of the thin-walled member behaviour and (ii) judiciously exclude, from subsequent similar GBT analyses, those deformation modes found to play no (or negligible) role in the particular behaviour under scrutiny |
The GBT modal nature makes it possible to (i) acquire in-depth knowledge on the mechanics of the thin-walled member behaviour and (ii) judiciously exclude, from subsequent similar GBT analyses, those deformation modes found to play no (or negligible) role in the particular behaviour under scrutiny. Eliminating modes that play no role reduces the number of degrees of freedom involved in a GBT analysis and increases its computational efficiency. GBT has proven useful in the understanding of the structural behaviour under analysis as well as in its computational efficiency.<ref name="deMiranda2013" /> |
||
The investigation, application and dissemination of GBT will certainly last during many more years. |
|||
[[File:Gbt3.png|Gbt3]] |
[[File:Gbt3.png|Gbt3]] |
||
| Line 30: | Line 32: | ||
{{reflist}} |
{{reflist}} |
||
[[Category:Beam theory]] |
|||
[[Category:Civil engineering]] |
|||
[[Category:Structural engineering]] |
|||
[[Category:Mechanical engineering]] |
[[Category:Mechanical engineering]] |
||
[[Category:Aerospace engineering]] |
|||
Latest revision as of 16:31, 2 December 2023
In structural engineering and mechanical engineering, generalised beam theory (GBT) is a one-dimensional theory used to mathematically model how beams bend and twist under various loads. It is a generalization of classical Euler–Bernoulli beam theory that approximates a beam as an assembly of thin-walled plates that are constrained to deform as a linear combination of specified deformation modes.[1]
History
[edit]Its origin is due to Richard Schardt (1966). Since then many other authors have extended the initial (first-order elastic) GBT formulations developed by Schardt and his co-workers.[2][3] Many extensions and applications of GBT have been developed by Camotim (Instituto Superior Técnico, University of Lisbon, Portugal) and collaborators, since the beginning of the 21st century. [4][5][6][7][8][9][10]
Description
[edit]The theory can be applied without restrictions to any prismatic thin-walled structural member exhibiting straight or curved axial axis (any loading, any cross-section geometry, any boundary conditions). GBT is in some ways analogous to the finite strip method[1] and can be a more computationally efficient method than modeling a beam with a full 2D or 3D finite element method to predict the member structural behavior.
GBT has been widely recognized as an efficient approach to analyzing thin-walled members and structural systems. The efficiency arises mostly from its modal nature – the displacement field is expressed as a linear combination of cross-section deformation modes whose amplitudes vary continuously along the member length (x axis) - see Figures 2-3. Due to GBT assumptions inherent to a thin-walled member, only 3 non-null stress components are considered in the formulations (see Fig. 1).
Membrane displacement field (i.e., in the cross-section mid-surface):
The GBT modal nature makes it possible to (i) acquire in-depth knowledge on the mechanics of the thin-walled member behaviour and (ii) judiciously exclude, from subsequent similar GBT analyses, those deformation modes found to play no (or negligible) role in the particular behaviour under scrutiny. Eliminating modes that play no role reduces the number of degrees of freedom involved in a GBT analysis and increases its computational efficiency. GBT has proven useful in the understanding of the structural behaviour under analysis as well as in its computational efficiency.[1]
References
[edit]- ^ a b c de Miranda, Stefano; Gutiérrez, Alejandro; Miletta, Rosario; Ubertini, Francesco (June 2013). "A generalized beam theory with shear deformation". Thin-Walled Structures. 67: 88–100. doi:10.1016/j.tws.2013.02.012.
- ^ Schardt, Richard (1994). "Generalised Beam Theory – an adequate method for coupled stability problems". Thin-Walled Structures. 19 (2–4): 161–180. doi:10.1016/0263-8231(94)90027-2.
- ^ Davies, JM (2000). "Recent research advances in cold-formed steel structures". Journal of Constructional Steel Research. 55 (1–3): 267–288. doi:10.1016/S0143-974X(99)00089-9.
- ^ Silvestre, N; Camotim, D (2002). "Second-order generalised beam theory for arbitrary orthotropic materials". Thin-Walled Structures. 40 (9): 791–820. doi:10.1016/S0263-8231(02)00026-5.
- ^ Borges Dinis, P; Camotim, D; Silvestre, N (2006). "GBT formulation to analyse the buckling behaviour of thin-walled members with arbitrarily 'branched'open cross-sections". Thin-Walled Structures. 44 (1): 20–38. doi:10.1016/j.tws.2005.09.005.
- ^ Camotim, D; Basaglia, C; Silvestre, N (2010). "GBT buckling analysis of thin-walled steel frames: a state-of-the-art report". Thin-Walled Structures. 48 (10): 726–743. doi:10.1016/j.tws.2009.12.003.
- ^ Abambres, M; Camotim, D; Silvestre, N (2014). "GBT-based elastic–plastic post-buckling analysis of stainless steel thin-walled members" (PDF). Thin-Walled Structures. 83 (October): 85–102. doi:10.1016/j.tws.2014.01.004. S2CID 120053099.
- ^ Abambres, M; Camotim, D; Silvestre, N; Rasmussen, KJR (2014). "GBT-based structural analysis of elastic–plastic thin-walled members" (PDF). Computers & Structures. 136 (May): 1–23. doi:10.1016/j.compstruc.2014.01.001. S2CID 122047967.
- ^ Bebiano, R; Gonçalves, R; Camotim, D (2015). "A cross-section analysis procedure to rationalise and automate the performance of GBT-based structural analyses". Thin-Walled Structures. 92 (July): 29–47. doi:10.1016/j.tws.2015.02.017.
- ^ Gonçalves, R; Camotim, D (2016). "GBT deformation modes for curved thin-walled cross-sections based on a mid-line polygonal approximation". Thin-Walled Structures. 103 (January): 231–243. doi:10.1016/j.tws.2015.12.025.